Как умножать корни
Знак корня (v) означает квадратный корень из некоторого числа. Знак корня встречается не только в алгебре, но и в повседневной жизни, например, в деревообрабатывающем производстве, которое включает расчет относительных размеров. Вы можете умножить два любых корня с одинаковыми показателями (степени корня). Если у корней разные показатели, необходимо привести корни к одному показателю. Если вы хотите узнать, как умножить корни с или без множителей, прочитайте эту статью.
Ваши действия
Способ 1 из 3: Умножение корней без множителей
Убедитесь, что корни имеют одинаковый показатель (степень). Степень записывается слева над знаком корня. Если степени нет, то корень считается квадратным (то есть его степень 2) и его можно умножить на другие квадратные корни (об умножение корней с разными показателями читайте далее). Вот несколько примеров умножения корней с одинаковыми показателями:
- Пример 1: v(18) x v(2) = ?
- Пример 2: v(10) x v(5) = ?
- Пример 3: 3v(3) x 3v(9) = ?
Перемножьте числа под корнем. Вот как это делается:
- Пример 1: v(18) x v(2) = v(36)
- Пример 2: v(10) x v(5) = v(50)
- Пример 3: 3v(3) x 3v(9) = 3v(27)
Упростите подкоренное выражение. При умножении корней полученное подкоренное выражение можно упростить (не всегда) до произведения некоторого числа (или выражения) на полный квадрат или куб. Вот как это делается:
- Пример 1: v(36) = 6. 36 является квадратом числа 6, потому что 6*6=36.
- Пример 2: v(50) = v(25*2) = v([5*5]*2) = 5v(2). Число 50 можно разложить на произведение чисел 25 и 2. Корень из 25 равен 5, поэтому выносим 5 за знак корня и таким образом упрощаем подкоренное выражение.
- Если внести число 5 обратно под знак корня, оно возводится в квадрат и вы получаете число 25 под знаком корня.
- Пример 3: 3v(27) = 3. Кубический корень из числа 27 равен 3, потому что 3*3*3 = 27.
Способ 2 из 3: Умножение корней с множителями
Умножьте множители. Множитель – число, стоящее перед знаком корня. Если его нет, то множитель равен 1. Перемножьте множители. Вот как это делается:
- Пример 1: 3v(2) x v(10) = 3v(?)
- Пример 2: 4v(3) x 3v(6) = 12v(?)
Умножьте числа под знаком корня. После того, как вы перемножили множители, перемножьте числа под знаком корня. Вот как это делается:
- Пример 1: 3v(2) x v(10) = 3v(2 x 10) = 3v(20)
- Пример 2: 4v(3) x 3v(6) = 12v(3 x 6) = 12v(18)
Your ads will be inserted here by
Easy Plugin for AdSense.
Please go to the plugin admin page to
Paste your ad code OR
Suppress this ad slot.Упростите подкоренное выражение. Далее упростите полученные значения под знаком корня, вынеся соответствующие числа за знак корня. После этого просто перемножьте эти вынесенные числа и множители, стоящие перед знаком корня. Вот как это делается:
- 3v(20) = 3v(4 x 5) = 3v([2 x 2] x 5) = (3 x 2)v(5) = 6v(5)
- 12v(18) = 12v(9 x 2) = 12v(3 x 3 x 2) = (12 x 3)v(2) = 36v(2)
Способ 3 из 3: Умножение корней с разными показателями
Найдите НОК (наименьшее общее кратное) показателей. НОК показателей — наименьшее число, которое делится на оба показателя. Найдите НОК показателей для следующего выражения:3v(5) x 2v(2) = ?
- Показатели равны 3 и 2. Число 6 является НОК этих двух чисел, потому что это наименьшее число, которое делится без остатка как на 3, так и на 2: 6/3=2 и 6/2=3. Чтобы умножить корни, их показатель должен быть равен 6.
Запишите каждый корень с НОК в качестве нового показателя. Вот как записать выражение с новым показателем:
Найдите числа, на которые вы должны умножить каждый исходный показатель, чтобы получить НОК. В выражении 3v(5) вам нужно умножить показатель 3 на 2, чтобы получить 6. В выражении 2v(2) вам нужно умножить показатель 2 на 3, чтобы получить 6.
Возведите число, стоящее под знаком корня, в степень равную числу, найденному в предыдущем шаге. Для первого выражения возведите 5 в степень 2. Для второго выражение возведите 2 в степень 3. Вот как это будет выглядеть:
- 2 —> 6v(5) = 6v(5)2
- 3 —> 6v(2) = 6v(2)3
Проделайте операцию возведения в степень и запишите результат под знаком корня. Вот как это делается:
- 6v(5)2 = 6v(5 x 5) = 6v25
- 6v(2)3 = 6v(2 x 2 x 2) = 6v8
Перемножьте числа под знаком корня: 6v(8 x 25)
Запишите ответ. 6v(8 x 25) = 6v(200). В некоторых случаях вы можете упростить подкоренное выражение, например, найдя множитель числа 200, из которого можно взять корень 6 степени. Но в данном случае выражение не упрощается.
Рекомендации
- Знак корня является еще одним способом записи дробных показателей. Например, квадратный корень из любого числа есть это число в степени 1/2; кубический корень из любого числа есть это число в степени 1/3 и так далее.
- Множитель – число, стоящее непосредственно перед знаком корня. Так, например, в выражении 2(квадратный корень)5, число 5 является подкоренным выражением, а число 2 — множителем. Когда множитель и корень записаны рядом, то это означает их умножение: 2*(квадратный корень)5.
- Если «множитель» отделяется от корня знаком плюс или минус, то это уже вообще не множитель — это отдельный член выражения и операции с ним проводятся отдельно от корня.
Похожие публикации
wikisurv.ru
Иррациональные выражения. Преобразование иррациональных выражений
Выражения, содержащие корень, который нельзя извлечь, называются иррациональными или радикальными.
Примеры:
– иррациональные выражения
Сложение и вычитание
При сложении или вычитании иррациональных выражений их пишут одно за другим с сохранением их знаков.
Примеры:
В некоторых случаях с помощью преобразования можно сделать иррациональные выражения подобными, то есть имеющими одинаковые показатели корней и подкоренные числа (или выражения), а затем сделать приведение.
Примеры:
Умножение и деление
При умножении иррациональных выражений с одинаковыми показателями корней перемножаются их подкоренные числа или выражения:
При делении иррациональных выражений с одинаковыми показателями корней подкоренное число или выражение делимого делится на подкоренное число или выражение делителя:
Примеры:
Возведение в степень
Чтобы возвести в степень иррациональное выражение, следует возвести в степень подкоренное число или выражение:
Примеры:
При возведении в n-ю степень знак корня отбрасывается, так как возведение числа (или выражения) в n-ю степень и извлечение из него корня n-ой степени – это взаимно сокращающиеся действия:
Извлечение корня
Чтобы извлечь корень из иррационального выражения, следует показатели корней перемножить:
, так как
Пример:
С помощью таких преобразований можно упростить извлечение корней 4-й, 6-й, 8-й, 9-й и т. п. степеней из чисел.
Примеры:
Сокращение корней
Величина иррационального выражения не изменится, если показатель корня и подкоренного выражения умножить или разделить на одно и то же число:
так как извлечение корня и возведение в степень – это взаимно сокращающиеся действия, если их показатели равны.
На этом свойстве основано сокращение корней и приведение их к одному показателю.
Сокращение корней – это деление показателей корня и подкоренного числа (или выражения) на одно и то же число, если оно является общим множителем для всех показателей.
Примеры:
Приведение корней к одному показателю
Приведение корней к общему показателю имеет большое сходство с приведением дробей к общему знаменателю. Рассмотрим два способа:
- Показатели корней не имеют общих множителей. В этом случае показатель каждого корня и его подкоренное число (или выражение) умножают на произведение остальных корней.
Рассмотрим три выражения:
,
так как у данных показателей нет общего множителя, то просто перемножаем все показатели между собой, полученный результат и станет общим показателем. После приведения к общему показателю выражения будут иметь следующий вид:
- Показатели корней имеют общий множитель. В этом случае надо найти НОК показателей и умножить показатель каждого корня на недостающий множитель.
Рассмотрим два выражения:
,
НОК (4, 6) = 12, значит для первого выражения дополнительным множителем будет 3, а для второго 2. После приведения к общему показателю выражения будут иметь следующий вид:
При умножении и делении иррациональных выражений с разными показателями, их приводят к общему показателю, а затем уже умножают или делят их подкоренные числа или выражения.
Примеры:
naobumium.info
Как умножать корни — Как? Так!
Содержимое:
3 метода:
Знак корня (√) означает квадратный корень из некоторого числа. Знак корня встречается не только в алгебре, но и в повседневной жизни, например, в деревообрабатывающем производстве, которое включает расчет относительных размеров. Вы можете умножить два любых корня с одинаковыми показателями (степени корня). Если у корней разные показатели, необходимо привести корни к одному показателю. Если вы хотите узнать, как умножить корни с или без множителей, прочитайте эту статью.
Шаги
Метод 1 Умножение корней без множителей
- 1 Убедитесь, что корни имеют одинаковый показатель (степень). Степень записывается слева над знаком корня. Если степени нет, то корень считается квадратным (то есть его степень 2) и его можно умножить на другие квадратные корни (об умножении корней с разными показателями читайте далее). Вот несколько примеров умножения корней с одинаковыми показателями:
- Пример 1: √(18) x √(2) = ?
- Пример 2: √(10) x √(5) = ?
- Пример 3: 3√(3) x 3√(9) = ?
- 2 Перемножьте числа под корнем. Вот как это делается:
- Пример 1: √(18) x √(2) = √(36)
- Пример 2: √(10) x √(5) = √(50)
- Пример 3: 3√(3) x 3√(9) = 3√(27)
- 3 . При умножении корней полученное подкоренное выражение можно упростить (не всегда) до произведения некоторого числа (или выражения) на полный квадрат или куб. Вот как это делается:
- Пример 1: √(36) = 6. 36 является квадратом числа 6, потому что 6*6=36.
- Пример 2: √(50) = √(25*2) = √([5*5]*2) = 5√(2). Число 50 можно разложить на произведение чисел 25 и 2. Корень из 25 равен 5, поэтому выносим 5 за знак корня и таким образом упрощаем подкоренное выражение.
- Если внести число 5 обратно под знак корня, оно возводится в квадрат, и вы получите число 25 под знаком корня.
- Пример 3: 3√(27) = 3. Кубический корень из числа 27 равен 3, потому что 3*3*3 = 27.
Метод 2 Умножение корней с множителями
- 1 Умножьте множители. Множитель – число, стоящее перед знаком корня. Если его нет, то множитель равен 1. Перемножьте множители. Вот как это делается:
- Пример 1: 3√(2) x √(10) = 3√(?)
- Пример 2: 4√(3) x 3√(6) = 12√(?)
- 2 Умножьте числа под знаком корня. После того как вы перемножили множители, перемножьте числа под знаком корня. Вот как это делается:
- Пример 1: 3√(2) x √(10) = 3√(2 x 10) = 3√(20)
- Пример 2: 4√(3) x 3√(6) = 12√(3 x 6) = 12√(18)
- 3 Упростите подкоренное выражение. Далее упростите полученные значения под знаком корня, вынеся соответствующие числа за знак корня. После этого просто перемножьте эти вынесенные числа и множители, стоящие перед знаком корня. Вот как это делается:
- 3√(20) = 3√(4 x 5) = 3√([2 x 2] x 5) = (3 x 2)√(5) = 6√(5)
- 12√(18) = 12√(9 x 2) = 12√(3 x 3 x 2) = (12 x 3)√(2) = 36√(2)
Метод 3 Умножение корней с разными показателями
- 1 Найдите НОК (наименьшее общее кратное) показателей. НОК показателей – наименьшее число, которое делится на оба показателя. Найдите НОК показателей для следующего выражения:3√(5) x 2√(2) = ?
- Показатели равны 3 и 2. Число 6 является НОК этих двух чисел, потому что это наименьшее число, которое делится без остатка как на 3, так и на 2: 6/3=2 и 6/2=3. Чтобы умножить корни, их показатель должен быть равен 6.
- 2 Запишите каждый корень с НОК в качестве нового показателя. Вот как записать выражение с новым показателем:
- 3 Найдите числа, на которые вы должны умножить каждый исходный показатель, чтобы получить НОК. В выражении 3√(5) вам нужно умножить показатель 3 на 2, чтобы получить 6. В выражении 2√(2) вам нужно умножить показатель 2 на 3, чтобы получить 6.
- 4 Возведите число, стоящее под знаком корня, в степень равную числу, найденному в предыдущем шаге. Для первого выражения возведите 5 в степень 2. Для второго выражения возведите 2 в степень 3. Вот как это будет выглядеть:
- 2 —> 6√(5) = 6√(5)2
- 3 —> 6√(2) = 6√(2)3
- 5 Проделайте операцию возведения в степень и запишите результат под знаком корня. Вот как это делается:
- 6√(5)2 = 6√(5 x 5) = 6√25
- 6√(2)3 = 6√(2 x 2 x 2) = 6√8
- 6 Перемножьте числа под знаком корня: 6√(8 x 25)
- 7 Запишите ответ. 6√(8 x 25) = 6√(200). В некоторых случаях вы можете упростить подкоренное выражение, например, найдя множитель числа 200, из которого можно взять корень 6 степени. Но в данном случае выражение не упрощается.
Советы
- Если «множитель» отделяется от корня знаком плюс или минус, то это уже вообще не множитель – это отдельный член выражения, и операции с ним проводятся отдельно от корня.
- Знак корня является еще одним способом записи дробных показателей. Например, квадратный корень из любого числа есть это число в степени 1/2; кубический корень из любого числа есть это число в степени 1/3 и так далее.
- Множитель – число, стоящее непосредственно перед знаком корня. Так, например, в выражении 2(квадратный корень)5, число 5 является подкоренным выражением, а число 2 – множителем. Когда множитель и корень записаны рядом, то это означает их умножение: 2*(квадратный корень)5.
Похожие статьи
Прислал: Новикова Ксения . 2017-11-12 13:11:09
kak-otvet.imysite.ru
Как умножать корни » VripMaster
Знак корня (√) означает квадратный корень из некоторого числа. Знак корня встречается не только в алгебре, но и в повседневной жизни, например, в деревообрабатывающем производстве, которое включает расчет относительных размеров. Вы можете умножить два любых корня с одинаковыми показателями (степени корня). Если у корней разные показатели, необходимо привести корни к одному показателю. Если вы хотите узнать, как умножить корни с или без множителей, прочитайте эту статью.
Умножение корней без множителей
-
 Убедитесь, что корни имеют одинаковый показатель (степень). Степень записывается слева над знаком корня. Если степени нет, то корень считается квадратным (то есть его степень 2) и его можно умножить на другие квадратные корни (об умножении корней с разными показателями читайте далее). Вот несколько примеров умножения корней с одинаковыми показателями:
Убедитесь, что корни имеют одинаковый показатель (степень). Степень записывается слева над знаком корня. Если степени нет, то корень считается квадратным (то есть его степень 2) и его можно умножить на другие квадратные корни (об умножении корней с разными показателями читайте далее). Вот несколько примеров умножения корней с одинаковыми показателями:- Пример 1: √(18) x √(2) = ?
- Пример 2: √(10) x √(5) = ?
- Пример 3: √(3) x √(9) = ?
-
 Перемножьте числа под корнем. Вот как это делается:
Перемножьте числа под корнем. Вот как это делается:- Пример 1: √(18) x √(2) = √(36)
- Пример 2: √(10) x √(5) = √(50)
- Пример 3: √(3) x √(9) = √(27)
-
 Упростите подкоренное выражение. При умножении корней полученное подкоренное выражение можно упростить (не всегда) до произведения некоторого числа (или выражения) на полный квадрат или куб. Вот как это делается:
Упростите подкоренное выражение. При умножении корней полученное подкоренное выражение можно упростить (не всегда) до произведения некоторого числа (или выражения) на полный квадрат или куб. Вот как это делается:- Пример 1: √(36) = 6. 36 является квадратом числа 6, потому что 6*6=36.
- Пример 2: √(50) = √(25*2) = √([5*5]*2) = 5√(2). Число 50 можно разложить на произведение чисел 25 и 2. Корень из 25 равен 5, поэтому выносим 5 за знак корня и таким образом упрощаем подкоренное выражение.
- Если внести число 5 обратно под знак корня, оно возводится в квадрат, и вы получите число 25 под знаком корня.
- Пример 3: √(27) = 3. Кубический корень из числа 27 равен 3, потому что 3*3*3 = 27.
Умножение корней с множителями
-
 Умножьте множители. Множитель – число, стоящее перед знаком корня. Если его нет, то множитель равен 1. Перемножьте множители. Вот как это делается:
Умножьте множители. Множитель – число, стоящее перед знаком корня. Если его нет, то множитель равен 1. Перемножьте множители. Вот как это делается:- Пример 1: 3√(2) x √(10) = 3√(?)
- Пример 2: 4√(3) x 3√(6) = 12√(?)
-
 Умножьте числа под знаком корня. После того как вы перемножили множители, перемножьте числа под знаком корня. Вот как это делается:
Умножьте числа под знаком корня. После того как вы перемножили множители, перемножьте числа под знаком корня. Вот как это делается:- Пример 1: 3√(2) x √(10) = 3√(2 x 10) = 3√(20)
- Пример 2: 4√(3) x 3√(6) = 12√(3 x 6) = 12√(18)
-
 Упростите подкоренное выражение. Далее упростите полученные значения под знаком корня, вынеся соответствующие числа за знак корня. После этого просто перемножьте эти вынесенные числа и множители, стоящие перед знаком корня. Вот как это делается:
Упростите подкоренное выражение. Далее упростите полученные значения под знаком корня, вынеся соответствующие числа за знак корня. После этого просто перемножьте эти вынесенные числа и множители, стоящие перед знаком корня. Вот как это делается:- 3√(20) = 3√(4 x 5) = 3√([2 x 2] x 5) = (3 x 2)√(5) = 6√(5)
- 12√(18) = 12√(9 x 2) = 12√(3 x 3 x 2) = (12 x 3)√(2) = 36√(2)
Умножение корней с разными показателями
-
 Найдите НОК (наименьшее общее кратное) показателей. НОК показателей – наименьшее число, которое делится на оба показателя. Найдите НОК показателей для следующего выражения:√(5) x √(2) = ?
Найдите НОК (наименьшее общее кратное) показателей. НОК показателей – наименьшее число, которое делится на оба показателя. Найдите НОК показателей для следующего выражения:√(5) x √(2) = ?- Показатели равны 3 и 2. Число 6 является НОК этих двух чисел, потому что это наименьшее число, которое делится без остатка как на 3, так и на 2: 6/3=2 и 6/2=3. Чтобы умножить корни, их показатель должен быть равен 6.
-
 Запишите каждый корень с НОК в качестве нового показателя. Вот как записать выражение с новым показателем:
Запишите каждый корень с НОК в качестве нового показателя. Вот как записать выражение с новым показателем: -

Найдите числа, на которые вы должны умножить каждый исходный показатель, чтобы получить НОК. В выражении √(5) вам нужно умножить показатель 3 на 2, чтобы получить 6. В выражении √(2) вам нужно умножить показатель 2 на 3, чтобы получить 6.
-
 Возведите число, стоящее под знаком корня, в степень равную числу, найденному в предыдущем шаге. Для первого выражения возведите 5 в степень 2. Для второго выражения возведите 2 в степень 3. Вот как это будет выглядеть:
Возведите число, стоящее под знаком корня, в степень равную числу, найденному в предыдущем шаге. Для первого выражения возведите 5 в степень 2. Для второго выражения возведите 2 в степень 3. Вот как это будет выглядеть:- —> √(5) = √(5)
- —> √(2) = √(2)
-
 Проделайте операцию возведения в степень и запишите результат под знаком корня. Вот как это делается:
Проделайте операцию возведения в степень и запишите результат под знаком корня. Вот как это делается:- √(5) = √(5 x 5) = √25
- √(2) = √(2 x 2 x 2) = √8
-

Перемножьте числа под знаком корня: √(8 x 25)
-

Запишите ответ. √(8 x 25) = √(200). В некоторых случаях вы можете упростить подкоренное выражение, например, найдя множитель числа 200, из которого можно взять корень 6 степени. Но в данном случае выражение не упрощается.
Советы
- Если «множитель» отделяется от корня знаком плюс или минус, то это уже вообще не множитель – это отдельный член выражения, и операции с ним проводятся отдельно от корня.
- Знак корня является еще одним способом записи дробных показателей. Например, квадратный корень из любого числа есть это число в степени 1/2; кубический корень из любого числа есть это число в степени 1/3 и так далее.
- Множитель – число, стоящее непосредственно перед знаком корня. Так, например, в выражении 2(квадратный корень)5, число 5 является подкоренным выражением, а число 2 – множителем. Когда множитель и корень записаны рядом, то это означает их умножение: 2*(квадратный корень)5.
vripmaster.com
3 методика:Умножение корней без множителейУмножение корней с множителямиУмножение корней с разными показателями Знак корня (√) означает квадратный корень из некоторого числа. Знак корня встречается не только в алгебре, но и в повседневной жизни, например, в деревообрабатывающем производстве, которое включает расчет относительных размеров. Вы можете умножить два любых корня с одинаковыми показателями (степени корня). Если у корней разные показатели, необходимо привести корни к одному показателю. Если вы хотите узнать, как умножить корни с или без множителей, прочитайте эту статью. ШагиМетод 1 из 3: Умножение корней без множителей
Метод 2 из 3: Умножение корней с множителями
Метод 3 из 3: Умножение корней с разными показателями
Советы
|
ves-mir.3dn.ru
Какие трудности ждут тех, кто взялся выполнять сложение корней? :: SYL.ru
Тема про квадратные корни является обязательной в школьной программе курса математики. Без них не обойтись при решении квадратных уравнений. А позже появляется необходимость не только извлекать корни, но и выполнять с ними другие действия. Среди них достаточно сложные: возведение в степень, умножение и деление. Но есть и достаточно простые: вычитание и сложение корней. Кстати, они только на первый взгляд кажутся такими. Выполнить их без ошибок не всегда оказывается просто для того, кто только начинает с ними знакомиться.
Что такое математический корень?
Это действие возникло в противовес возведению в степень. Математика предполагает наличие двух противоположных операций. На сложение существует вычитание. Умножению противостоит деление. Обратное действие степени — это извлечение соответствующего корня.

Если в степени стоит двойка, то и корень будет квадратным. Он является самым распространенным в школьной математике. У него даже нет указания, что он квадратный, то есть возле него не приписывается цифра 2. Математическая запись этого оператора (радикала) представлена на рисунке.
Из описанного действия плавно вытекает его определение. Чтобы извлечь квадратный корень из некоторого числа, нужно выяснить, какое даст при умножении на себя подкоренное выражение. Это число и будет квадратным корнем. Если записать это математически, то получится следующее: х*х=х2=у, значит √у=х.
Какие действия с ними можно выполнять?
По своей сути корень — это дробная степень, у которой в числителе стоит единица. А знаменатель может быть любым. Например, у квадратного корня он равен двум. Поэтому все действия, которые можно выполнить со степенями, будут справедливы и для корней.
И требования к этим действиям у них одинаковые. Если умножение, деление и возведение в степень не встречают затруднений у учеников, то сложение корней, как и их вычитание, иногда приводит в замешательство. А все потому что хочется выполнить эти операции без оглядки на знак корня. И здесь начинаются ошибки.

По каким правилам выполняется их сложение и вычитание?
Сначала нужно запомнить два категорических «нельзя»:
- нельзя выполнять сложение и вычитание корней, как у простых чисел, то есть невозможно записать подкоренные выражения суммы под один знак и выполнять с ними математические операции;
- нельзя складывать и вычитать корни с разными показателями, например квадратный и кубический.
Наглядный пример первого запрета: √6 + √10 ≠ √16, но √(6 + 10) = √16.
Во втором случае лучше ограничиться упрощением самих корней. А в ответе оставить их сумму.
Теперь к правилам
- Найти и сгруппировать подобные корни. То есть те, у которых не только стоят одинаковые числа под радикалом, но и они сами с одним показателем.
- Выполнить сложение корней, объединенных в одну группу первым действием. Оно легко осуществимо, потому что нужно только сложить значения, которые стоят перед радикалами.
- Извлечь корни в тех слагаемых, в которых подкоренное выражение образует целый квадрат. Другими словами, не оставлять ничего под знаком радикала.
- Упростить подкоренные выражения. Для этого нужно разложить их на простые множители и посмотреть, не дадут ли они квадрата какого-либо числа. Понятно, что это справедливо, если речь идет о квадратном корне. Когда показатель степени три или четыре, то и простые множители должны давать куб или четвертую степень числа.
- Вынести из-под знака радикала множитель, который дает целую степень.
- Посмотреть, не появилось ли опять подобных слагаемых. Если да, то снова выполнить второе действие.

В ситуации, когда задача не требует точного значения корня, его можно вычислить на калькуляторе. Бесконечную десятичную дробь, которая высветится в его окошке, округлить. Чаще всего это делают до сотых. А потом выполнять все операции для десятичных дробей.
Рекомендация: после разложения на простые множители нужно сделать проверку. То есть умножить их друг на друга и проверить, получается ли исходное значение.
Это вся информация о том, как выполняется сложение корней. Примеры, расположенные ниже, проиллюстрируют вышесказанное.
Первое задание
Вычислить значение выражений:
а) √2 + 3√32 + ½ √128 — 6√18;
б) √75 — √147 + √48 — 1/5 √300;
в) √275 — 10√11 + 2√99 + √396.
Решение.
а) Если следовать приведенному выше алгоритму, то видно, что для первых двух действий в этом примере ничего нет. Зато можно упростить некоторые подкоренные выражения.
Например, 32 разложить на два множителя 2 и 16; 18 будет равно произведению 9 и 2; 128 — это 2 на 64. Учитывая это, выражение будет записано так:
√2 + 3√(2 * 16) + ½ √(2 * 64) — 6 √(2 * 9).
Теперь нужно вынести из-под знака радикала те множители, которые дают квадрат числа. Это 16=42, 9=32, 64=82. Выражение примет вид:
√2 + 3 * 4√2 + ½ * 8 √2 — 6 * 3√2.
Нужно немного упростить запись. Для этого производится умножение коэффициентов перед знаками корня:
√2 + 12√2 + 4 √2 — 12√2.
В этом выражении все слагаемые оказались подобными. Поэтому их нужно просто сложить. В ответе получится: 5√2.
б) Подобно предыдущему примеру, сложение корней начинается с их упрощения. Подкоренные выражения 75, 147, 48 и 300 будут представлены такими парами: 5 и 25, 3 и 49, 3 и 16, 3 и 100. В каждой из них имеется число, которое можно вынести из-под знака корня:
5√5 — 7√3 + 4√3 — 1/5 * 10√3.
После упрощения получается ответ: 5√5 — 5√3. Его можно оставить в таком виде, но лучше вынести общий множитель 5 за скобку: 5 (√5 — √3).
в) И снова разложение на множители: 275 = 11 * 25, 99 = 11 * 9, 396 = 11 * 36. После вынесения множителей из-под знака корня имеем:
5√11 — 10√11 + 2 * 3√11 + 6√11. После приведения подобных слагаемых получим результат: 7√11.
Пример с дробными выражениями
√(45/4) — √20 — 5√(1/18) — 1/6 √245 + √(49/2).

На множители нужно будет разложить такие числа: 45 = 5 * 9, 20 = 4 * 5, 18 = 2 * 9, 245 = 5 * 49. Аналогично уже рассмотренным, нужно вынести множители из-под знака корня и упростить выражение:
3/2 √5 — 2√5 — 5/ 3 √(½) — 7/6 √5 + 7 √(½) = (3/2 — 2 — 7/6) √5 — (5/3 — 7) √(½) = — 5/3 √5 + 16/3 √(½).
Это выражение требует того, чтобы избавиться от иррациональности в знаменателе. Для этого нужно умножить на √2/√2 второе слагаемое:
— 5/3 √5 + 16/3 √(½) * √2/√2 = — 5/3 √5 + 8/3 √2.
Для полноты действий нужно выделить целую часть у множителей перед корнями. У первого она равна 1, у второго — 2.
www.syl.ru
как умножить корень из 3 на корень из 3 ?
по свойствам. . так корни одной степени то умножение можно занести под знак корня. . и получится корень из 3 умножить на 3..=корень из 9=3
Устно, молча и за одну секунду —просто сказать ответ — 3 !!!
Получится корень из 3 в квадрате ))) т. е. Ответ «3»
Корень из 3=1.73205080757. 1.73205080757*1.73205080757=3
Только при умножении подкореные выражения можно внести под один корень, т. е под конрем мы умножаем 3 на 3 получается 9 и выносим из под корня ответ 3
корень из 3 умножить на корень из 3 будет корень из 9, а из девяти извлечь корень и будет просто 3
touch.otvet.mail.ru

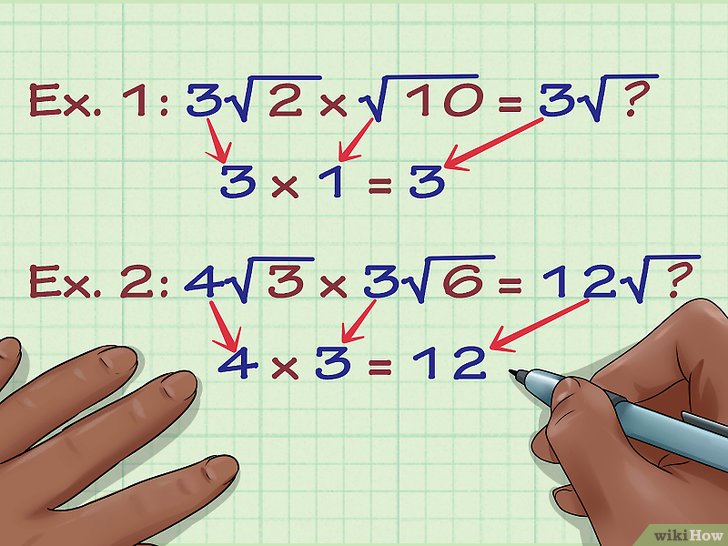
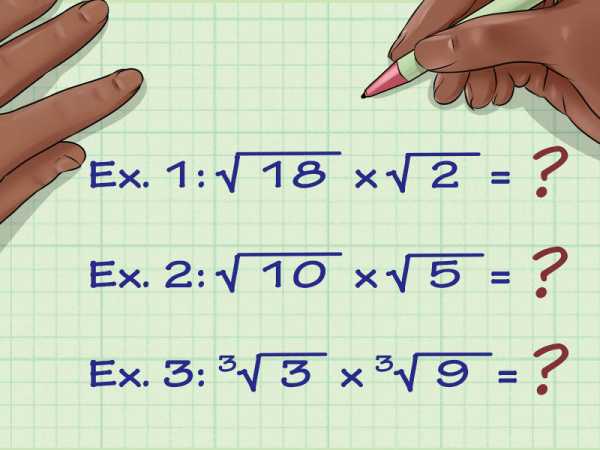 Убедитесь, что корни имеют одинаковый показатель (степень). Степень записывается слева над знаком корня. Если степени нет, то корень считается квадратным (то есть его степень 2) и его можно умножить на другие квадратные корни (об умножении корней с разными показателями читайте далее). Вот несколько примеров умножения корней с одинаковыми показателями:
Убедитесь, что корни имеют одинаковый показатель (степень). Степень записывается слева над знаком корня. Если степени нет, то корень считается квадратным (то есть его степень 2) и его можно умножить на другие квадратные корни (об умножении корней с разными показателями читайте далее). Вот несколько примеров умножения корней с одинаковыми показателями: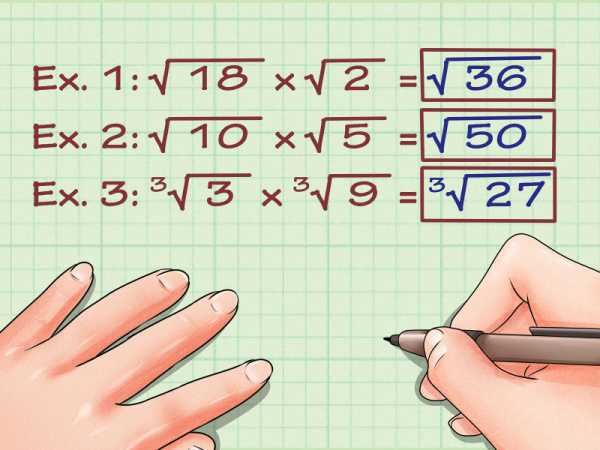 Перемножьте числа под корнем. Вот как это делается:
Перемножьте числа под корнем. Вот как это делается: Упростите подкоренное выражение. При умножении корней полученное подкоренное выражение можно упростить (не всегда) до произведения некоторого числа (или выражения) на полный квадрат или куб. Вот как это делается:
Упростите подкоренное выражение. При умножении корней полученное подкоренное выражение можно упростить (не всегда) до произведения некоторого числа (или выражения) на полный квадрат или куб. Вот как это делается: Умножьте множители. Множитель – число, стоящее перед знаком корня. Если его нет, то множитель равен 1. Перемножьте множители. Вот как это делается:
Умножьте множители. Множитель – число, стоящее перед знаком корня. Если его нет, то множитель равен 1. Перемножьте множители. Вот как это делается: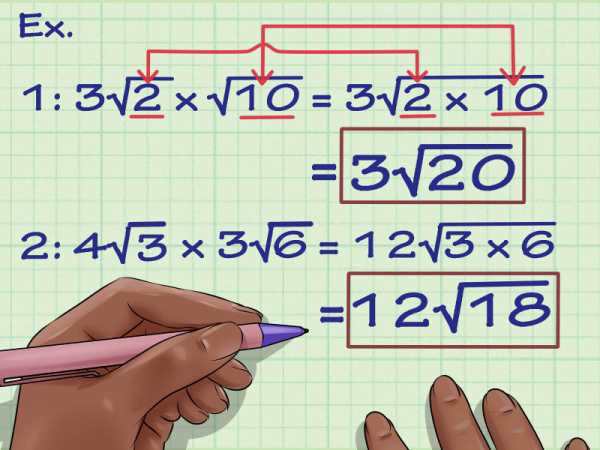 Умножьте числа под знаком корня. После того как вы перемножили множители, перемножьте числа под знаком корня. Вот как это делается:
Умножьте числа под знаком корня. После того как вы перемножили множители, перемножьте числа под знаком корня. Вот как это делается: Упростите подкоренное выражение. Далее упростите полученные значения под знаком корня, вынеся соответствующие числа за знак корня. После этого просто перемножьте эти вынесенные числа и множители, стоящие перед знаком корня. Вот как это делается:
Упростите подкоренное выражение. Далее упростите полученные значения под знаком корня, вынеся соответствующие числа за знак корня. После этого просто перемножьте эти вынесенные числа и множители, стоящие перед знаком корня. Вот как это делается: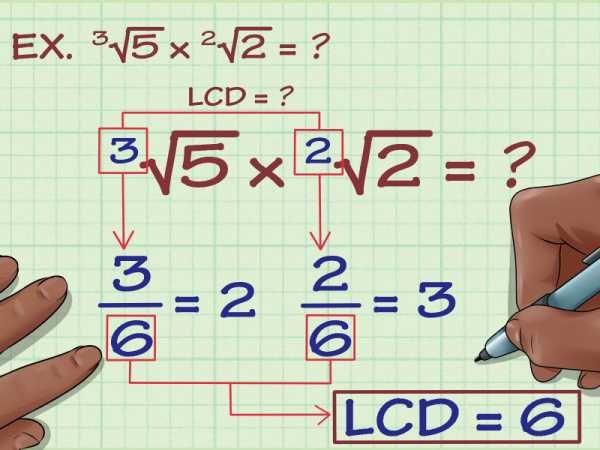 Найдите НОК (наименьшее общее кратное) показателей. НОК показателей – наименьшее число, которое делится на оба показателя. Найдите НОК показателей для следующего выражения:√(5) x √(2) = ?
Найдите НОК (наименьшее общее кратное) показателей. НОК показателей – наименьшее число, которое делится на оба показателя. Найдите НОК показателей для следующего выражения:√(5) x √(2) = ?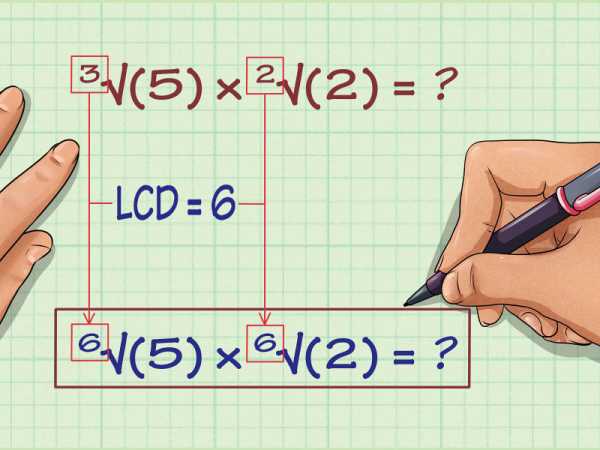 Запишите каждый корень с НОК в качестве нового показателя. Вот как записать выражение с новым показателем:
Запишите каждый корень с НОК в качестве нового показателя. Вот как записать выражение с новым показателем: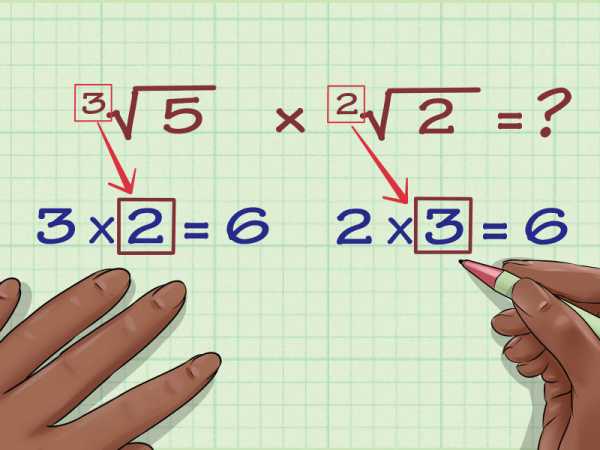
 Возведите число, стоящее под знаком корня, в степень равную числу, найденному в предыдущем шаге. Для первого выражения возведите 5 в степень 2. Для второго выражения возведите 2 в степень 3. Вот как это будет выглядеть:
Возведите число, стоящее под знаком корня, в степень равную числу, найденному в предыдущем шаге. Для первого выражения возведите 5 в степень 2. Для второго выражения возведите 2 в степень 3. Вот как это будет выглядеть: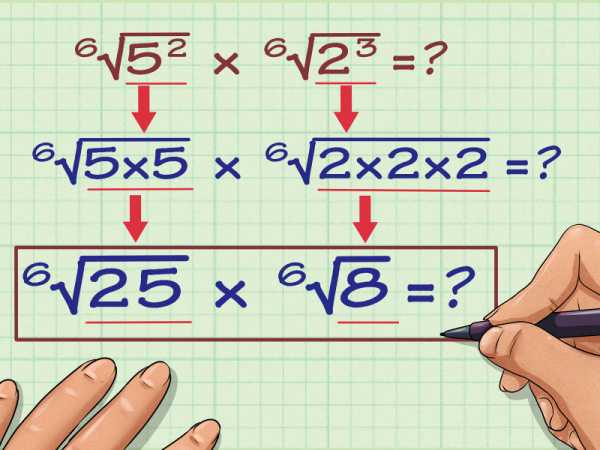 Проделайте операцию возведения в степень и запишите результат под знаком корня. Вот как это делается:
Проделайте операцию возведения в степень и запишите результат под знаком корня. Вот как это делается: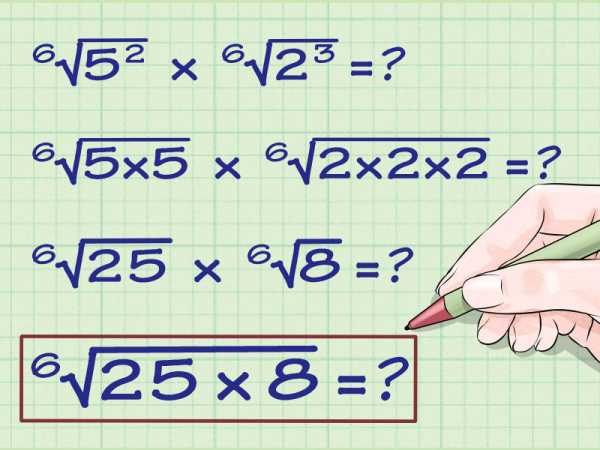
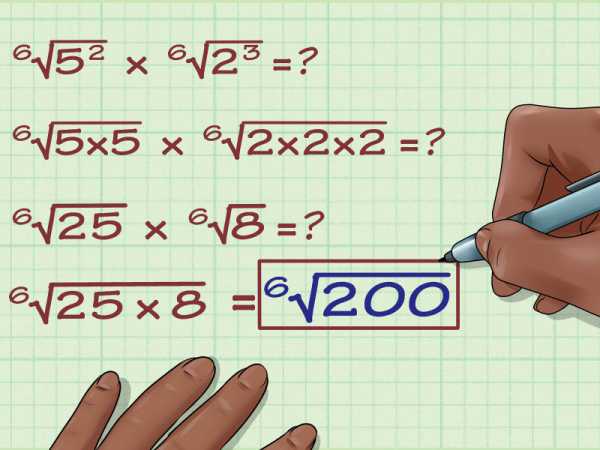

 Адрес для вставки QR-кода числа 516, размер 500×500:
Адрес для вставки QR-кода числа 516, размер 500×500:



 – квадратная матрица коэффициентов
при неизвестных;
– квадратная матрица коэффициентов
при неизвестных; – вектор-столбец неизвестных; – вектор-столбец правых частей системы.
По правилу Крамера системыn неизвестными
имеет единственное решение, если
определитель системы отличен от нуля
и
значение каждого из неизвестных
вычисляется как отношение двух
определителей порядкаn,
т. е.
– вектор-столбец неизвестных; – вектор-столбец правых частей системы.
По правилу Крамера системыn неизвестными
имеет единственное решение, если
определитель системы отличен от нуля
и
значение каждого из неизвестных
вычисляется как отношение двух
определителей порядкаn,
т. е.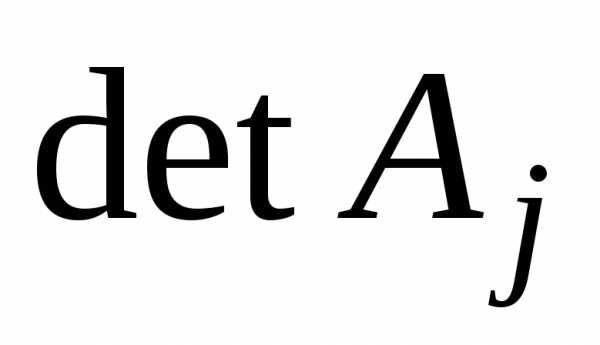 –
определитель матрицы, получаемый заменой j-го столбца матрицы А столбцом
правых частей.
–
определитель матрицы, получаемый заменой j-го столбца матрицы А столбцом
правых частей.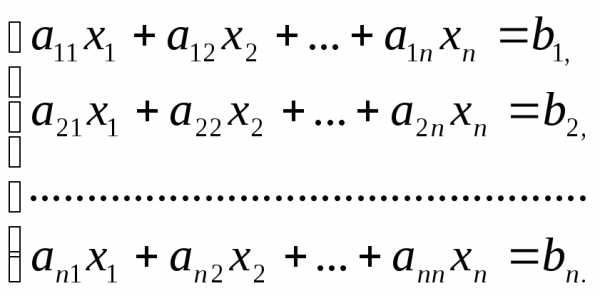 (2.1)
(2.1) i = 1,…, n.
i = 1,…, n. приi > j, т. е. все
элементы ниже главной диагонали равны
нулю. Тогда из последнего уравнения
сразу определяем
приi > j, т. е. все
элементы ниже главной диагонали равны
нулю. Тогда из последнего уравнения
сразу определяем 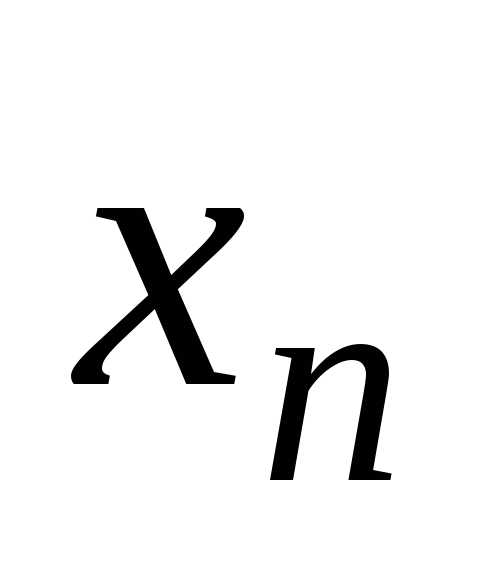 .
Подставляя
.
Подставляя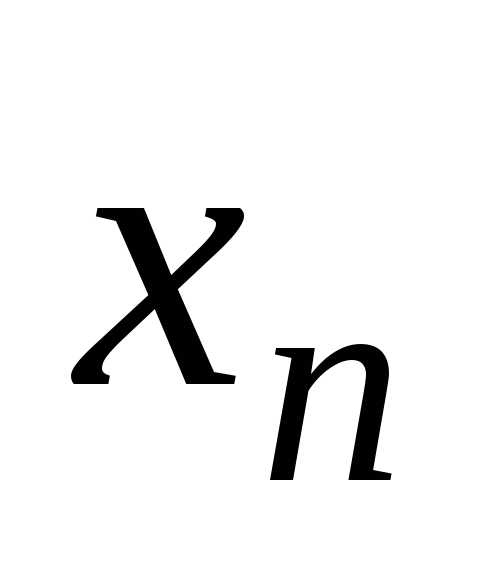 в
предпоследнее уравнение, находим
в
предпоследнее уравнение, находим  и т. д.
и т. д. 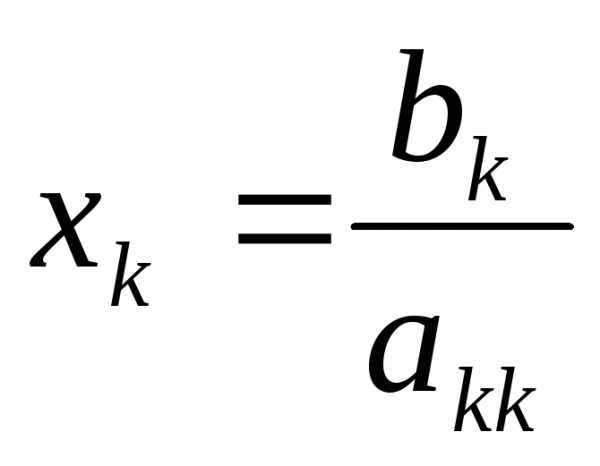 при k = n (2.2)
при k = n (2.2)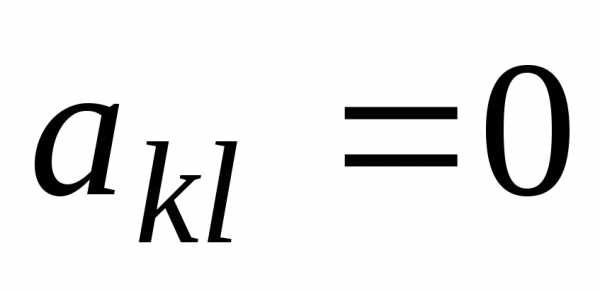 .
.  обратится
в нуль. То же проделаем со всеми остальными
уравнениями. В результате все коэффициенты
первого столбца, лежащие ниже главной
диагонали, обратятся в нуль. Затем,
используя второе уравнение, обратим в
нуль соответствующие коэффициенты
второго столбца. Последовательно
продолжая этот процесс, приведем матрицу
систему к верхней треугольной форме.
обратится
в нуль. То же проделаем со всеми остальными
уравнениями. В результате все коэффициенты
первого столбца, лежащие ниже главной
диагонали, обратятся в нуль. Затем,
используя второе уравнение, обратим в
нуль соответствующие коэффициенты
второго столбца. Последовательно
продолжая этот процесс, приведем матрицу
систему к верхней треугольной форме.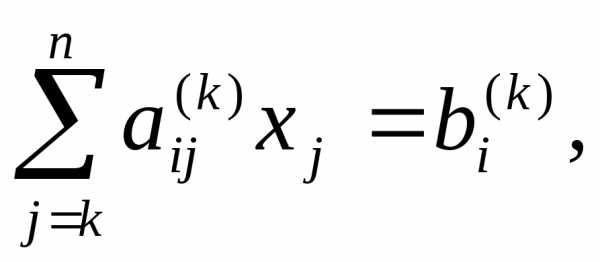
 m > k и вычтем из m-й строки.
Первый ненулевой элемент этой строки
обратится в нуль, а остальные изменятся
по формулам
m > k и вычтем из m-й строки.
Первый ненулевой элемент этой строки
обратится в нуль, а остальные изменятся
по формулам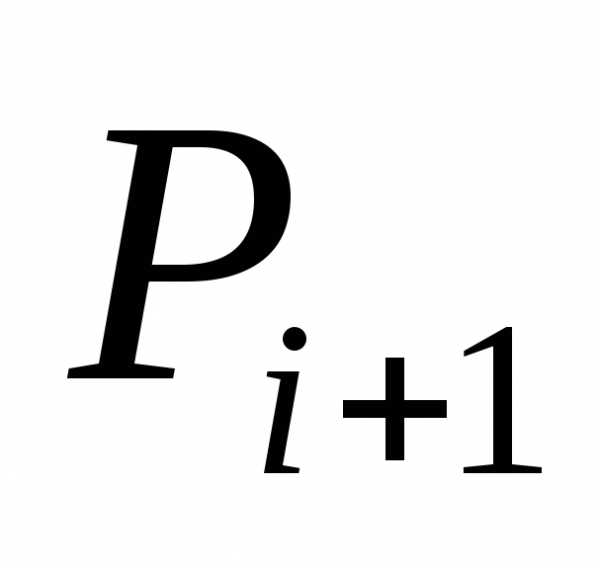 и
и через
через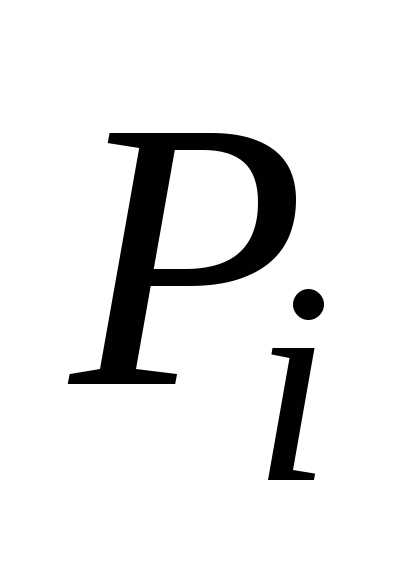 и
и и получение соотношения для
и получение соотношения для и
и .
.
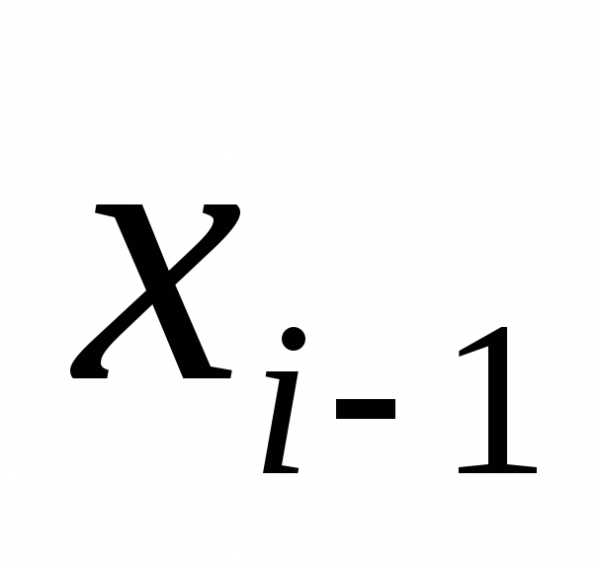 в каждом уравнении системы. Получаемая
в результате прямого хода система
содержит в каждом уравнении только два
неизвестных
в каждом уравнении системы. Получаемая
в результате прямого хода система
содержит в каждом уравнении только два
неизвестных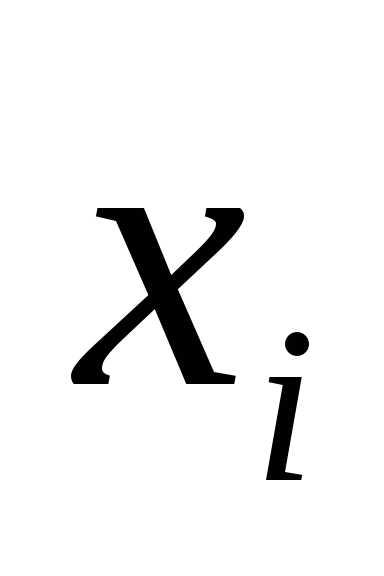 и
и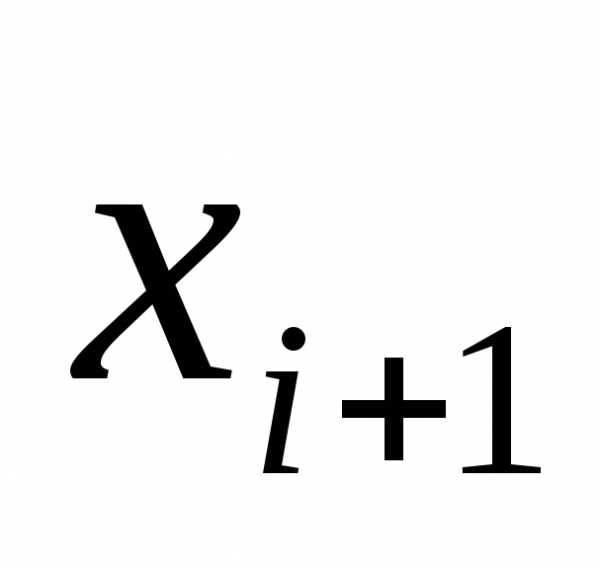 ,
и матрица ее – верхняя треугольная с
двумя диагоналями. Запишемi-ю строку
преобразованной двухдиагональной
матрицы в виде
,
и матрица ее – верхняя треугольная с
двумя диагоналями. Запишемi-ю строку
преобразованной двухдиагональной
матрицы в виде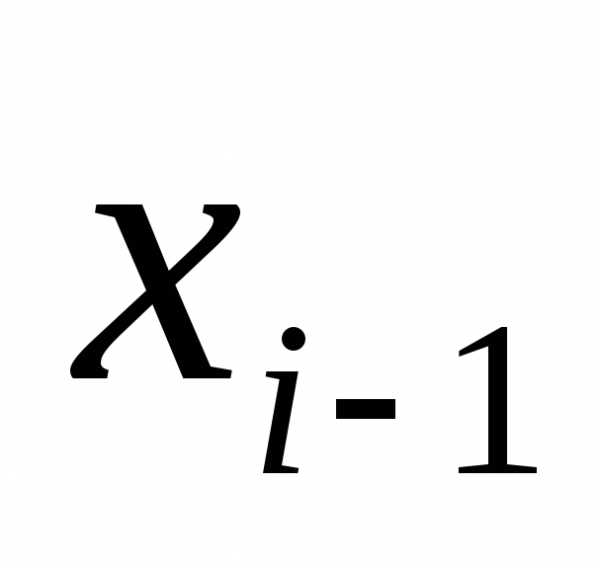 в систему (3.1), получим соотношение
в систему (3.1), получим соотношение Начальные значения коэффициентов
Начальные значения коэффициентов в рассмотренной схеме вычислений не
требуются, так как значения коэффициентов
в рассмотренной схеме вычислений не
требуются, так как значения коэффициентов вычисляются
только через коэффициенты первого
уравнения системы (3.1): приi = 1 из (3.1)
получаем соотношение
Сравнивая это выражение с (3.2) приi =1, получаем
а значение
вычисляются
только через коэффициенты первого
уравнения системы (3.1): приi = 1 из (3.1)
получаем соотношение
Сравнивая это выражение с (3.2) приi =1, получаем
а значение в обратном ходе вычисляем по соотношениюДля начала обратного хода метода прогонки
необходимо для вычислениязадать значение
в обратном ходе вычисляем по соотношениюДля начала обратного хода метода прогонки
необходимо для вычислениязадать значение .
Так как
.
Так как ,
то из первого соотношения (3.3) вытекает,
что
,
то из первого соотношения (3.3) вытекает,
что и, следовательно, можно задать любое
значение для
и, следовательно, можно задать любое
значение для Обычно полагают
Обычно полагают  ,и тогда
,и тогда 



 © OddLabs, 2011-2019 |
Правильность результатов не гарантируется
© OddLabs, 2011-2019 |
Правильность результатов не гарантируется

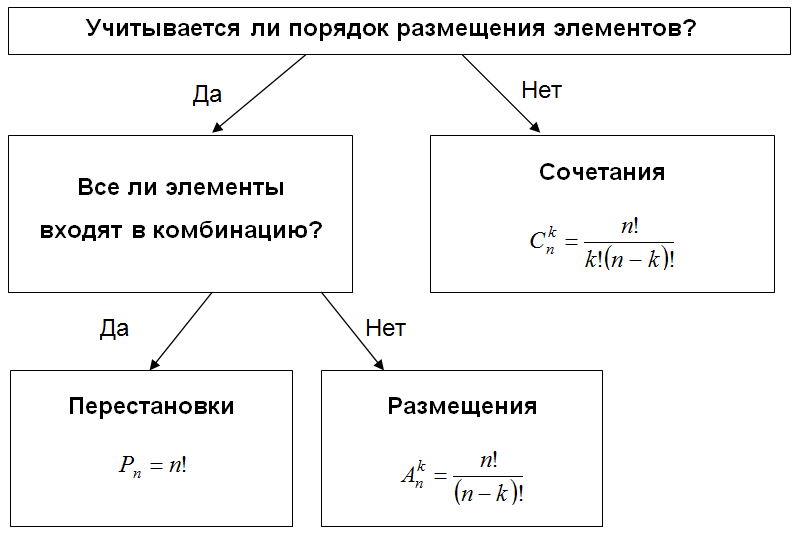
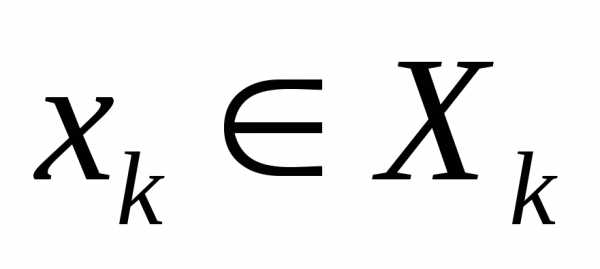 .
Элемент
.
Элемент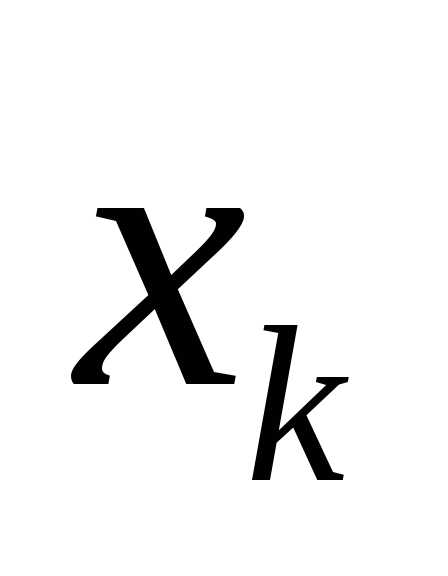 называетсяk-ой
координатой (или k-ой
координатой) кортежа
называетсяk-ой
координатой (или k-ой
координатой) кортежа  .
. ,.
Декартово произведение этих множеств
обозначается так.
,.
Декартово произведение этих множеств
обозначается так.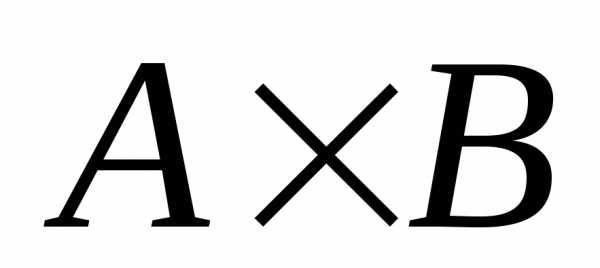 и
и 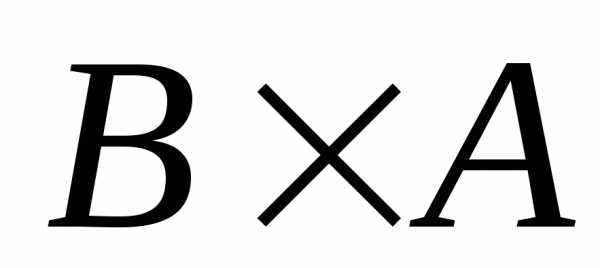 различны, хотя они содержат одинаковое
число элементов. Различны и множества
, и
– первое состоит из троек (a,b,c),
второе – из пар вида ((a,b),c),
а третье – из пар вида (a,(b,c)),
где во всех трех случаях
различны, хотя они содержат одинаковое
число элементов. Различны и множества
, и
– первое состоит из троек (a,b,c),
второе – из пар вида ((a,b),c),
а третье – из пар вида (a,(b,c)),
где во всех трех случаях  ,
,  ,
, 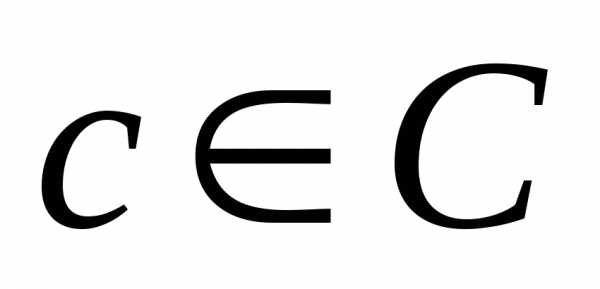 .
. ,
то справедливо равенство
,
то справедливо равенство )
= 11, n(
)
= 11, n( )
= 8,
)
= 8,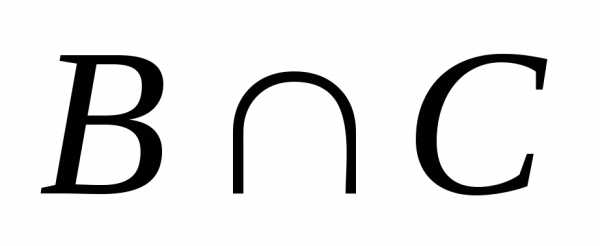 )
= 12, n()
= 6.
)
= 12, n()
= 6.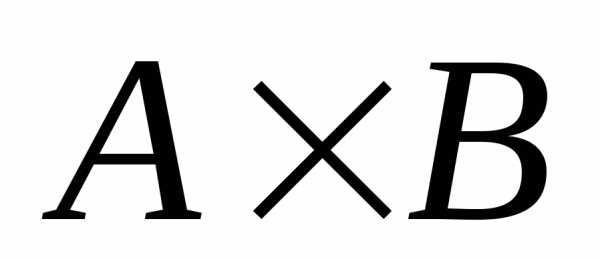 состоит из пар вида (a,b),
где
состоит из пар вида (a,b),
где  ,
, 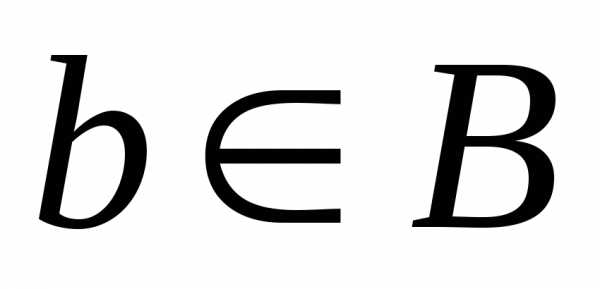 .
Если
и ,
то эти пары можно записать в виде
следующей таблицы:
.
Если
и ,
то эти пары можно записать в виде
следующей таблицы: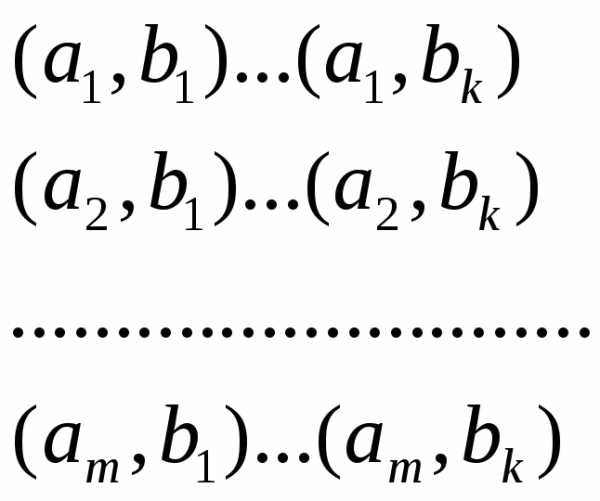
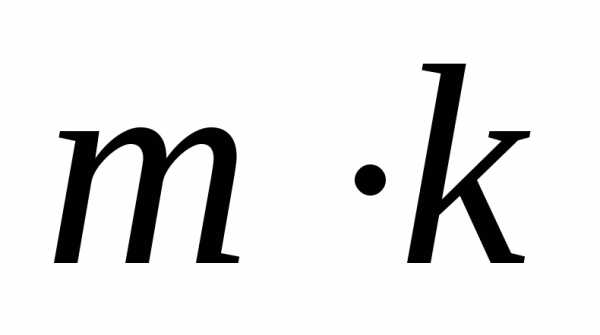 ,
то есть.
С помощью метода математической индукции
формула обобщается на любое число
множеств.
,
то есть.
С помощью метода математической индукции
формула обобщается на любое число
множеств.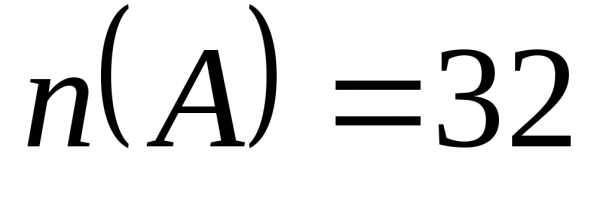 ,
,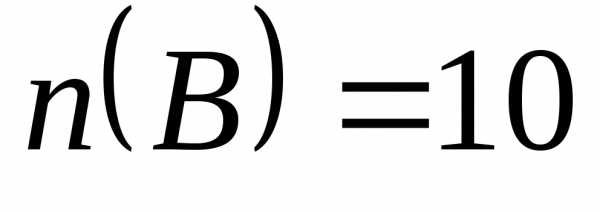 .
. способами, при любом выборе первой
координаты вторая выбирается
способами, при любом выборе первой
координаты вторая выбирается способами, при любом выборе первых двух
координат третья выбирается
способами, при любом выборе первых двух
координат третья выбирается способами и так далее доk-ой
координаты включительно, то общее число
полученных таким образом картежей равно
способами и так далее доk-ой
координаты включительно, то общее число
полученных таким образом картежей равно 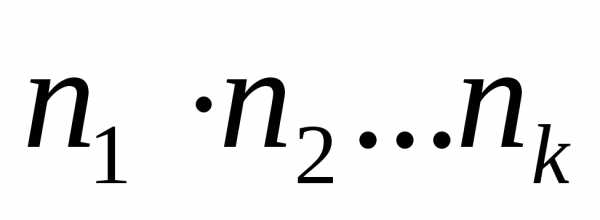
 (букваA
от французского слова arrangement
– размещение. Черта сверху указывает
на возможность повторения элементов).
(букваA
от французского слова arrangement
– размещение. Черта сверху указывает
на возможность повторения элементов). .
(8)
.
(8)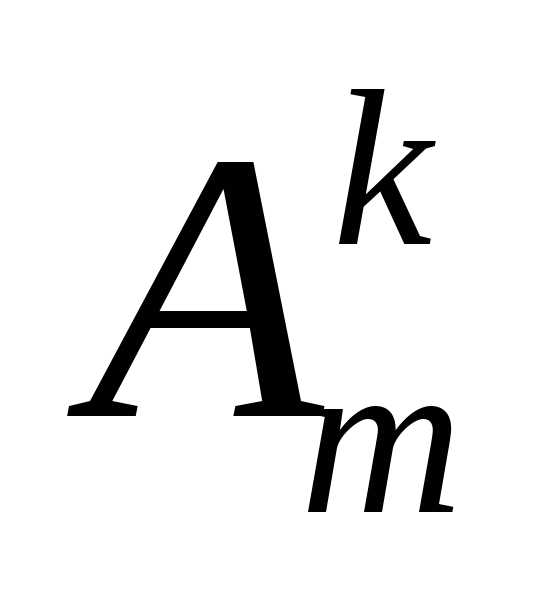 .
Число размещений без повторений изm
элементов по k находится по формуле
.
Число размещений без повторений изm
элементов по k находится по формуле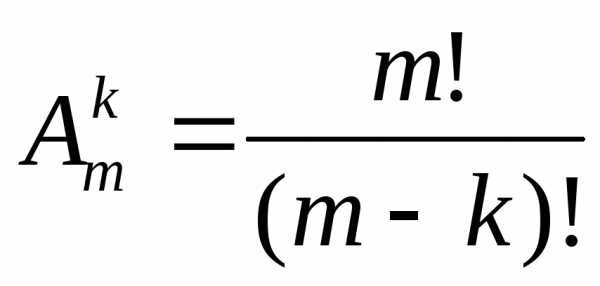 . (9)
. (9)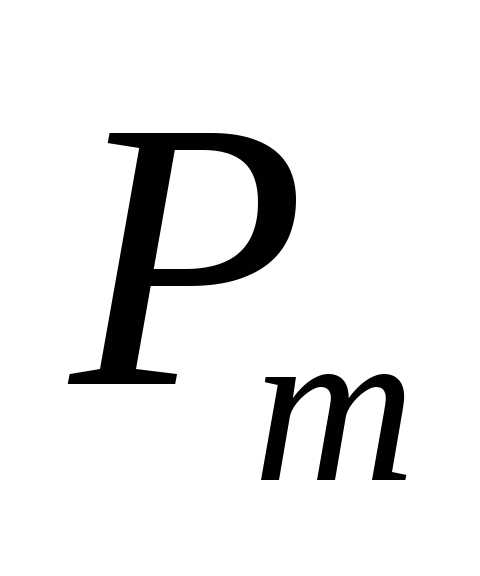 от французского словаpermutation
– перестановка и находятся по формуле
от французского словаpermutation
– перестановка и находятся по формуле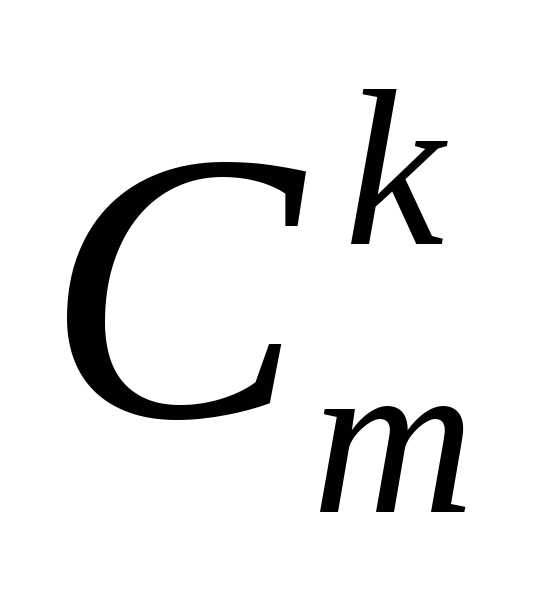 .
От французского словаcombination
– комбинация.
.
От французского словаcombination
– комбинация.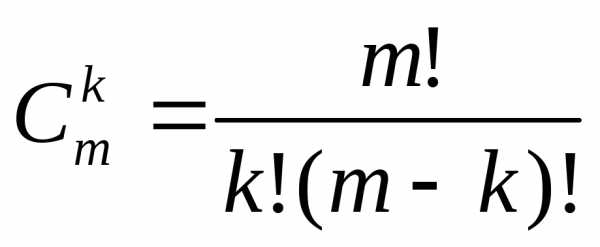 . (11)
. (11) входит
входит раз, …, а буква
раз, …, а буква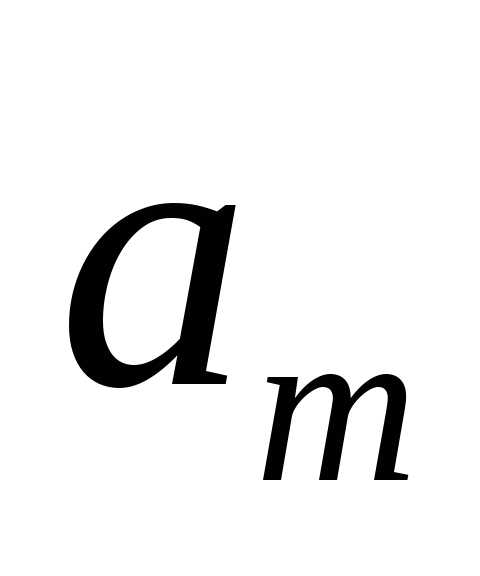 входит
входит раз. Число таких перестановок обозначают.
раз. Число таких перестановок обозначают.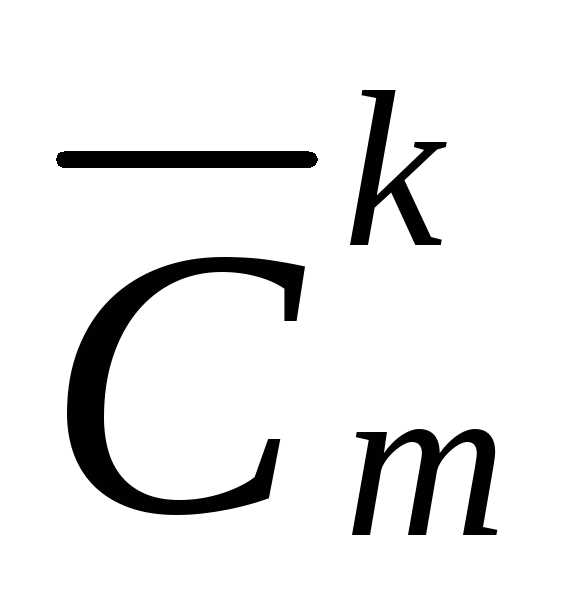 ,
,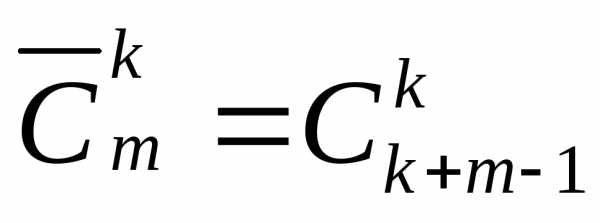 . (2)
. (2)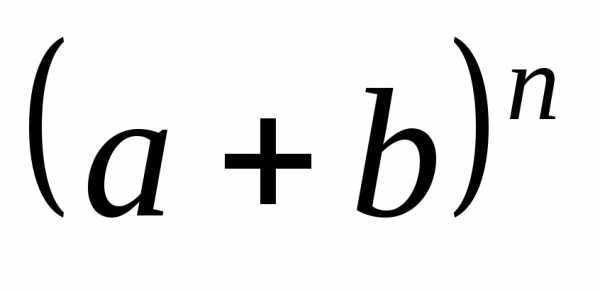 .
Эта формула носит название формулы
бинома Ньютона и имеет вид
.
Эта формула носит название формулы
бинома Ньютона и имеет вид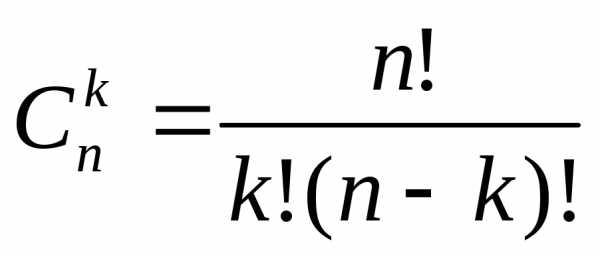 .
.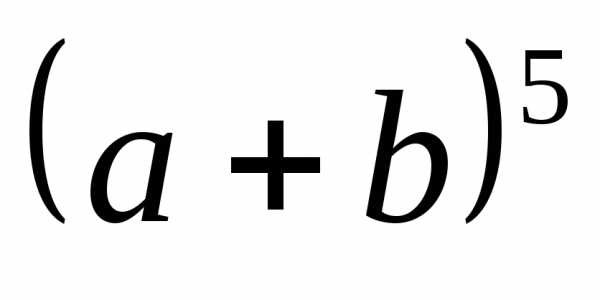 .
.