Квадратные уравнения (способы решения)
Разделы: Математика
Необходимость решать уравнения не только первой, но и второй степени ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.
Квадратные уравнения умели решать около 2000 лет до нашей эры в Вавилоне. Применяя современную алгебраическую запись, можно сказать, что в их книгописных текстах встречаются, кроме неполных, и такие, как полные квадратные уравнения.
Определение
Уравнение вида ax2 + bx + c = 0, где a, b, c — действительные числа, причем a ≠ 0, называют квадратным уравнением.
Если a = 1 , то квадратное уравнение называют приведенным; если a ≠ 1, то неприведенным .
Числа a, b, c носят следующие названия: a — первый коэффициент, b — второй коэффициент, c — свободный член.
| Корни уравнения ax2 + bx + c = 0 находят по формуле |
Выражение D = b2— 4ac называют дискриминантом квадратного уравнения.
- если D < 0, то уравнение не имеет действительных корней;
- если D = 0, то уравнение имеет один действительный корень;
- если D > 0, то уравнение имеет два действительных корня.
В случае, когда D = 0, иногда говорят, что квадратное уравнение имеет два одинаковых корня.
Формулы
Полное квадратное уравнение
Неполные квадратные уравнения
Если в квадратном уравнении ax2 + bx + c = 0 второй коэффициент b или свободный член c равен нулю, то квадратное уравнение называется неполным.
Неполные уравнения выделяют потому, что для отыскания их корней можно не пользоваться формулой корней квадратного уравнения — проще решить уравнение методом разложения его левой части на множители.
Способы решения неполных квадратных уравнений:
- c = 0, то уравнение примет вид
ax2 + bx = 0.
x(ax + b) = 0 ,
x = 0 или ax + b = 0, x = —b : a. - b = 0, то уравнение примет вид
ax2 + c = 0,
x2 = —c / a,
x1, 2 = ±√(-c / a). - b = 0 и c = 0 , то уравнение примет вид
ax2 = 0,
x = 0
Решение неполного квадратного уравнения
Квадратные уравнения с комплексными переменными
Сначала рассмотрим простейшее квадратное уравнение z2 = a, где a-заданное число, а z-неизвестное. На множестве действительных чисел это уравнение:
- имеет один корень z = 0, если а = 0;
- имеет два действительных корня z1, 2 = ±√a
- Не имеет действительных корней, если a < 0
Решение квадратных уравнений с помощью графиков
Не используя формул квадратное уравнение можно решить графическим способом. Например x2 + x + 1 = 0.
Решим уравнение. Для этого построим два графика y = x2; y = x + 1.
y = x2, квадратичная функция, график парабола.
y = x + 1, линейная функция, график прямая.
Графики пересекаются в двух точках, уравнение имеет два корня.
Ответ: x ≈ -0,6; x ≈ 2,6.
Решение задач с помощью квадратных уравнений
| Процессы | Скорость км/ч | Время ч. | Расстояние км. |
|---|---|---|---|
| Вверх по реке | 10 — x | 35 / (10 — x) | 35 |
| Вверх по протоку | 10 — x + 1 | 18 / (10 — x + 1) | 18 |
| V течения | x | ||
| V притока | x + 1 |
Зная, что скорость в стоячей воде равна 10 км/ч, составим уравнение.
ОДЗ: ∀ x ≠ 9, 10.
Практикум
т.к. D1
Ответ: корней нет.
Ответ: x = 2,5.
Заключение
Ещё в древности люди пользовались ими не зная, что это – квадратные уравнения.
В наше время невозможно представить себе решение как простейших, так и сложных задач не только в математике, но и в других точных науках, без применения решения квадратных уравнений.
Надеюсь и вы открыли для себя что-нибудь новое
Презентация
20.06.2009
Поделиться страницей:urok.1sept.ru
Вывод формулы корней полного квадратного уравнения. Решение приведенных квадратных уравнений и уравнений с четным вторым коэффициентом
Разделы: Математика
Устный счет:
1. При каком значении Х , выражение принимает минимальное значение
а) ; б)
2. Зависимость y(x) выражается формулой y = 13x + 1
выразить x(y)
3. Не решая уравнения, определить, равносильны ли они:
4. Выделить полный квадрат:
5. Вычислить пары чисел , удовлетворяющих условиям
| а) m + n = 4 mn = 4 |
б) m + n = –3 mn = –18 |
- Какое уравнение называется полным?
- Что такое корни квадратного уравнения?
- Сколько корней может иметь квадратное уравнение?
Теорема. Квадратное уравнение не может иметь более двух различных корней.
Доказательство:
Предположим, что уравнение три различных корня:
Если уравнение имеет корень, то после подстановки его в уравнение получится верное числовое равенство:
(1)
(2)
(3)
из (2) отнимаем (1)
–
_____________________
В каком случае произведение равно 0?
Так как = > 0 = > a+ b = 0. (4)
Из (3) вычтем (2)
–
_________________
= > a+ b = 0 (5)
Из (4) отнимем (5)
–
________________
а0 = > = > ,
а по условию пришли
к противоречию.
Давайте решим уравнение:
Самостоятельно:
a)
Вместе:
б)
Нравится ли этот способ? Нет! Тогда будем рассуждать иначе:
(формулу для нахождения корней квадратного уравнения учить проговаривать словами).
– дискриминант квадратного уравнения.
По теореме, доказанной нами , уравнение не может иметь более двух корней.
Количество корней зависит от D.
1). D > 0
2). D = 0
3). D < 0 – уравнение действительных корней не имеет.
Решить уравнения:
1)
– корней нет.
2)
D = 49–48 = 1
3)
D = 25 + 12 = 37
Если в уравнении b = 2k ,то уравнение имеет вид
D =
Диктант(один ученик на внутренней доске, в это время двое по карточкам)
1) Вычислить дискриминант квадратного
уравнения D = 100
2) Найти корни квадратного уравнения х = 3 и
3) При каком условии полное квадратное уравнение
имеет один корень D = 0
4) При каком условии полное квадратное уравнение
не имеет корней.
5) Решить уравнение D < 0.
После диктанта ребята меняются тетрадями и проверяют задание , исправляют ошибки и задают вопросы ученику у доски.
Все проверяют работу учеников на доске, которым были даны карточки.
1)
а) Решить уравнение
б) При каком m можно представить в виде квадрата двучлена выражение
а)
б)
2)
1. Решить уравнение
2. При каком а уравнение имеет один корень
Этим учащимся задаются вопросы и ставится оценка.
Итог урока
– Какие уравнения мы сегодня решали?
– Сколько корней может иметь квадратное
уравнение?
– С помощью чего мы их решали?
Когда D = 0, то …
D < 0, то …
D > 0, то …
3.03.2008
Поделиться страницей:urok.1sept.ru
Квадратные уравнения и его корни
Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, иррациональных уравнений и неравенств. Решение многих задач математики, физики и практики сводится к решению алгебраических уравнений.
В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения.
Однако имеются и другие приёмы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения.
Данные приёмы решения заслуживают внимания, поскольку они не отражены в школьных учебниках математики.
Овладение данными приёмами поможет мне экономить время и эффективно решать уравнения.
Потребность в быстром решении обусловлена применением тестовой системы вступительных экзаменов.
Квадратным уравнением называется уравнение ах² + bх + с = 0, где а≠0, а, b,с – заданные числа числа, х – неизвестное.
Коэффициенты а, b,с квадратного уравнения называют так: а- первым или старшим коэффициентом, b-вторым коэффициентом, с-свободным членом.
Неполное квадратное уравнение
Квадратное уравнение ах² + bх + с = 0 называют неполным, если хотя бы один из коэффициентов b или с равен нулю.
1) ах² = 0, х=0
2) ах² + с = 0, ах² = -с
1. если с>0, то нет действительных корней
2. если с
3) ах² + bх = 0, х(ах+в)=0 х=0 или ах=- в х=- в/а
Пример1: 5х²=0 х=0
Ответ: х= 0
Пример2: 3х² — 27 = 0
3х²=27 х²=9 х 1,2=
Ответ: х1,2 =
Пример3: х²+7=0 х²=-7
Ответ: нет действительных корней
Пример4: х²- 6х=0 х(х-6)=0 х1=0 или х2=6
Ответ: х1=0; х2=6
3. История квадратных уравнений.
Квадратные уравнения в Древнем Вавилоне.
Необходимость решать уравнения не только первой, но и второй степени ещё в древности была вызвана потребность решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет назад до н. э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:
Правило решения этих уравнений, изложено в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты переводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
Как составлял и решал Диофант квадратные уравнения.
В “Арифметике” Диофант нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.
Вот, к примеру, одна из его задач.
Задача 11. “Найти два числа, зная, что их сумма равна 20, а произведение – 96”.
Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так если бы они были равны, то их произведение равнялось бы не96, а 100. Таким образом, одно из них будет больше половины их суммы, т. е. 10 – x. Разность между ними 2x. Отсюда уравнение
(10 + x) (10 – x) = 96, или же
100 – x² = 96, x² – 4 = 0 (1)
Отсюда x = 2. Одно из искомых чисел равно 12, другое 8. Решение x = -2 для Диофанта не существует, так как греческая математика знала только положительные числа.
Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравнения y (20 – y) = 96 y² – 20y + 96 = 0 (2)
Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удаётся свести задачу к решению не полного квадратного уравнения(1).
Квадратные уравнения в Индии
Задачи на квадратные уравнения встречаются уже в 499г. В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее:
«Как солнце блеском своим затмевает звёзды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи».
Одна из задач знаменитого индийского математика XIIв. Бхаскары:
Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений. Часть страницы из алгебры Бхаскары (вычисление корней).
Квадратные уравнения у ал-Хорезми
В алгебраическом трактате ал-Хорезми даётся классификация линейных уравнений и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
1) “Квадраты равны корнями”, т. е. ax² = bx.
2) “Квадраты равны числу”, т. е. ax²= c.
3) “Корни равны числу”, т. е. ax = c
4) “Квадраты и числа равны корням”, т. е. ax² + c = bx/
5) “Квадраты и корни равны числу”, т. е. ax² + bx = c.
6) “Корни и числа равны квадратам”, т. е. bx + c + ax²
Для ал-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приёмами ал-джабар и ал-мукабала. Его решения, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида ал-Хорезми, как и все математики до 17 века, не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений ал-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.
Квадратные уравнения в Европе XIII — XVIIв. в.
Формулы решения квадратных уравнений по образцу ал-Хорезми в Европе были впервые изложены в книге “Книге абака”, написанной в 1202 г. Итальянским математиком Леонардо Фибоначчи. Этот объёмистый труд, в котором отражено влияние математики как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические примеры задач и первый в Европе подошёл к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других стран Европы. Многие задачи из “Книги абака” переходили почти во все европейские учебники 16 – 17 веков и частично 18 века.
Общие правило решения квадратных уравнений, приведённых к единому каноническому виду x² + bx = c, при всевозможных комбинациях знаков коэффициентов b, c было сформулировано в Европе лишь в 1544 г. М. Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в 16 веке учитывают, помимо положительных, и отрицательные корни. Лишь в 17 веке благодаря трудам Жирара, Декарта, Ньютона и других учёных способов решения квадратных уравнений принимает современный вид.
4. Решение квадратных уравнений.
4. 1 Метод выделения полного квадрата
Пример1: решить квадратное уравнение х² + 2х – 3=0
➢ Преобразуем это уравнение так: х² + 2х = 3, х² + 2х +1= 3+1,
(х + 1)² = 4.
Следовательно, х+1=2 или х+1= -2, откуда х1=1, х2= -3.
Решая уравнение, мы преобразовали его так, что в левой части получился квадрат двучлена, а правая часть не содержит неизвестное.
4. 2 Решение квадратных уравнений по формуле.
ах² + bх + с = 0
D=b²- 4ac
Если D =0,то х=
Если D>0,то
Если D
Пример1: х² — 4х +5 =0
D=16-4·1·5
D
Пример2: 2х² + 3х + 1 = 0
D=9-4·2·1=1 х1=
Ответ: -1; — ½
4. 3 Теорема Виета
Если — корни уравнения х² + bх + c = 0, то справедливы формулы
Т. е. сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Пример1: х² — 14х – 15 =0
Ответ: 15; -1
Теорема Виета aх² + bх + c = 0 x1 + x2 = — b/a x1· x2 = c/a
По праву достойна в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше, скажи, постоянства такого:
Умножишь ты корни – и дробь уж готова?
В числителе с , в знаменателе а.
А сумма корней тоже дроби равна.
Хоть с минусом дробь, что за беда.
В числителе в, b знаменателе а.
5. Приёмы устного решения квадратного уравнения.
1. Свойства коэффициентов квадратного уравнения:
Если в квадратном уравнении ах² + bх + с = 0 сумма коэффициентов а + в + с = 0, то х1 = 1; х2 = с/а.
Пример: 5х² — 8х +3 = 0
Так как 5 – 8 + 3 = 0, то х1 = 1; х2 = 0,6
Если в квадратном уравнении ах² + bх + с = 0 выполняется равенство а + с = в, то х1 = -1; х2 = — с/а.
Пример: 5х² + 8х +3 = 0
Так как 5 + 3 = 8, то х1 = — 1; х2 = — 0,6
Пример. Решить уравнения с большими коэффициентами:
5. 2 Приём «Переброски»:
Пример1:
2х² — 11х +5=0 х²-11х+10=0
делим на 2
Пример2:
6х² — 7х – 3 = 0 х² — 7х -18 = 0
делим на 6
Ответ:1,5; -1/3
6. Комплексные числа.
Решение многих задач физики и техники приводит к квадратным уравнениям с отрицательным дискриминантом. Эти уравнения не имеют решения в области действительных чисел. Но решение многих таких задач имеет вполне определенный физический смысл. Значение величин, получающихся в результате решения указанных уравнений, назвали комплексными числами. Комплексные числа широко использовал отец русской авиации Н. Е. Жуковский (1847 – 1921) при разработке теории крыла, автором которой он является. Комплексные числа и функции от комплексного переменного находят применение во многих вопросах науки и техники.
Цель настоящей работы знакомство с историей появления комплексных чисел, с действиями с комплексными числами, решение уравнений с комплексным переменным.
7. Действия с комплексными числами.
Рассмотрим решение квадратного уравнения х²+1=0. Отсюда х²=-1. Число х, квадрат которого равен –1, называется мнимой единицей и обозначается i. Таким образом i²=-1, откуда i=. Решение квадратного уравнения, например, х² –8х+25=0, можно записать следующим образом: х=4=4=4=
=43=43i.
Числа вида 4+3i и 4-3i называют комплексными числами. В общем виде комплексное число записывается а+bi, где a и b- действительные числа, а i – мнимая единица. Число а называется действительной частью комплексного числа, bi-мнимой частью этого числа, b- коэффициентом мнимой части комплексного числа.
Сложение комплексных чисел. Суммой двух комплексных чисел z1=a+bi и z2=c+di называется комплексное число z=(a+c)+(b+d)i. Числа a+bi и a-bi называются сопряженными. Их сумма равна действительному числу 2а, (а+bi)+(а-bi)=2а. Числа а+bi и -a-bi называются противоположными. Их сумма равна нулю. Комплексные числа равны, если равны их действительные части и коэффициенты мнимых частей: а+bi=c+di, если a=c, b=d. Комплексное число равно нулю тогда, когда его действительная часть и коэффициент мнимой части равны нулю, т. е. z=a+bi=0, если a=0,b=0. Действительные числа являются частным случаем комплексных чисел. Если b=0, то a+bi=a — действительное число. Если а=0, b0, то a+bi=bi – чисто мнимое число. Для комплексных чисел справедливы переместительный и сочетательный законы сложения. Их справедливость следует из того, что сложение комплексных чисел по существу сводится к сложению действительных частей и коэффициентов мнимых частей, а они являются действительными числами, для которых справедливы указанные законы.
Вычитание комплексных чисел определяется как действие, обратное сложению: разностью двух комплексных чисел a+ bi и c+di называется комплексное число х+уi, которое в сумме с вычитаемым дает уменьшаемое. Отсюда, исходя из определения сложения и равенства комплексных чисел получим два уравнения, из которых найдем, что х=а-с, у=b-d. Значит, (а+bi)-(c+di)=(a-c)+ (b-d)i.
Произведение комплексных чисел z1=a+bi и z2=c+di называется комплексное число z = (ac-bd)+(ad+bc)i, z1z2= (a+bi)(c+di)=(ac-bd)+(ad+bc)i. Легко проверить, что умножение комплексных чисел можно выполнять как умножение многочленов с заменой i2 на –1. Для умножения комплексных чисел также справедливы переместительный и сочетательный законы, а также распределительный закон умножения по отношению к сложению.
Из определения умножения получим, что произведение сопряженных комплексных чисел равно действительному числу: (a +bi)(a-bi)=a2+b2
Деление комплексных чисел, кроме деления на нуль, определяется как действие, обратное умножению. Конкретное правило деления получим, записав частное в виде дроби и умножив числитель и знаменатель этой дроби на число, сопряженное со знаменателем:(a+bi):(c+di) =. = = +i.
Степень числа i является периодической функцией показателя с периодом 4. Действительно, i2 =-1, i3 =-i, i4 = 1, i4n = (i4)n = 1n = 1, i4n+1=i, i4n+2 =-1, i4n+3 =-i.
Квадратное уравнение с комплексным неизвестным.
Рассмотрим сначала простейшее квадратное уравнение z2=a, где а — заданное число, z — неизвестное.
На множестве действительных чисел это уравнение:
1) имеет один корень z=0, если а=0;
2) имеет два действительных корня z1,2=, если а>0;
3) не имеет действительных корней, если а
На множестве комплексных чисел это уравнение всегда имеет корень.
Задача 1. Найти комплексные корни уравнения z2=a, если:
1) а = -1; 2) а = -25; 3) а = -3.
1)z2 = -1. Так как i2 = -1, то это уравнение можно записать в виде z2 = i2, или z2- i2 = 0. Отсюда, раскладывая левую часть на множители, получаем
(z-i)(z+i)=0, z1=i, z2=-i.
Ответ. z1,2=i.
2) z2 = -25. Учитывая, что i2 = -1,преобразуем это уравнение: z2=(-1)25, z2=i252, z2-52i=0, (z-5i)(z+5i)=0, откуда z1=5i, z2=-5i.
Ответ. z 1,2=5i.
3) z2=-3, z2=i2()2, z2-()2i2=0, (z-i)(z+i)=0, z1 =i, z 2=-i.
Ответ. z1,2=i.
Вообще уравнение z2=a, где а
Используя равенство i2=-1, квадратные корни из отрицательных чисел принято записывать так: =i, =i=2i, = i.
Итак, определен для любого действительного числа а (положительного, отрицательного и нуля). Поэтому любое квадратное уравнение az2+bz+c=0, где а,b,с- действительные числа, а0, имеет корни. Эти корни находятся по известной формуле:
Задача 2. Решить уравнение z2-4z+13=0. По формуле находим: z1,2= = = = =23i.
Заметим, что найденные в этой задаче корни являются сопряженными: z1=2+3i и z2=2-3i. Найдем сумму и произведение этих корней: z1+z2=(2+3i)+(2-3i)=4, z1z2=(2+3i)(2-3i)=13.
Число 4 — это 2-й коэффициент уравнения z2-4z+13=0, взятый с противоположным знаком, а число 13 — свободный член, то есть в этом случае справедлива теорема Виета. Она справедлива для любого квадратного уравнения: если z1 и z2 — корни уравнения az2+bz+c=0, z1+z2= -, z1z2=.
Задача 3. Составить приведенное квадратное уравнение с действительными коэффициентами, имеющее корень z1=-1-2i.
Второй корень z2 уравнения является числом, сопряженным с данным корнем z1, то есть z2=-1+2i. По теореме Виета находим
P=-(z1+z2)=2, q=z1z2=5. Ответ z²+2z+5=0.
8. Заключение.
В данной работе рассмотрены способы решения квадратных уравнений. А также рассмотрены приёмы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения.
Данные приёмы решения заслуживают внимания, поскольку они не отражены в школьных учебниках математики. Овладение данными приёмами поможет мне экономить время и эффективно решать уравнения. Потребность в быстром решении обусловлена применением тестовой системы вступительных экзаменов.
В настоящем работе дано понятие комплексных чисел, история их возникновения. Рассмотрены примеры действий с комплексными числами. Приведены примеры решения уравнений с комплексным переменным, что позволяет решить любые квадратные уравнения, даже с отрицательным дискриминантом.
Таким образом, цели работы — рассмотреть способы решения квадратных уравнений: метод выделения полного квадрата, решение квадратных уравнений по формуле, теорема Виета; изучить приёмы устного решения квадратного уравнения; рассмотреть решение квадратного уравнения с комплексными неизвестными — достигнуты.
www.hintfox.com
Формулы корней квадратных уравнений | Учеба-Легко.РФ
Пусть дано квадратное уравнение ах2 + bх + с = 0.
Применим к квадратному трехчлену ах2 + bх + с те же преобразования, которые мы выполняли в § 13, когда доказывали теорему о том, что графиком функции у = ах2 + bх + с является парабола.
Имеем
Обычно выражение b2 — 4ас обозначают буквой D и называют дискриминантом квадратного уравнения ах2 + bх + с = 0 (или дискриминантом квадратного трехчлена ах + bх + с).
Таким образом
Значит, квадратное уравнение ах2 + их + с = О можно переписать в виде
Любое квадратное уравнение можно преобразовать к виду (1), удобному, как мы сейчас убедимся, для того, чтобы определять число корней квадратного уравнения и находить эти корни.
Доказательство. Если D < 0, то правая часть уравнения (1) — отрицательное число; в то же время левая часть уравнения (1) при любых значениях х принимает неотрицательные значения. Значит, нет ни одного значения х, которое удовлетворяло бы уравнению (1), а потому уравнение (1) не имеет корней.
Пример 1. Решить уравнение 2x2 + 4х + 7 = 0.
Решение. Здесь а = 2, b = 4, с = 7,
D = b2-4ac = 42. 4. 2. 7 = 16-56 = -40.
Так как D < 0, то по теореме 1 данное квадратное уравнение не имеет корней.
Доказательство. Если D = 0, то уравнение (1) принимает вид
— единственный корень уравнения.
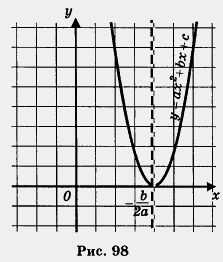
Замечание 1. Помните ли вы, что х = — — абсцисса вершины параболы, которая служит графиком функции у = ах2 + их + с? Почему именно это
значение оказалось единственным корнем квадратного уравнения ах2 + их + с — 0? «Ларчик» открывается просто: если D — 0, то, как мы установили ранее,
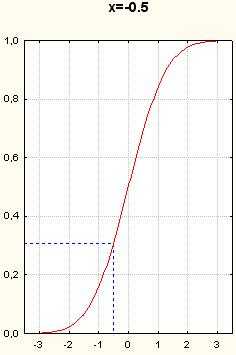
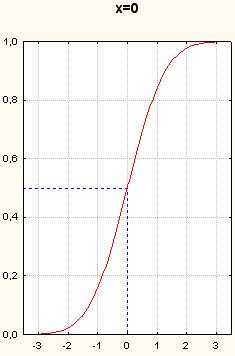
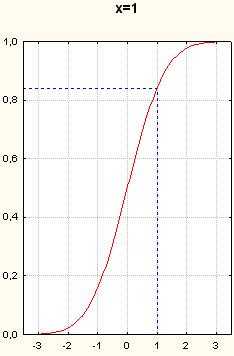
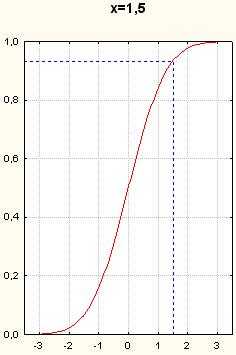
Графиком же функции является парабола с вершиной в точке (см., например, рис. 98). Значит, абсцисса вершины параболы и единственный корень квадратного уравнения при D = 0 — одно и то же число.
Пример 2. Решить уравнение 4x2 — 20x + 25 = 0.
Решение. Здесь а = 4, b = -20, с = 25, D = b2 — 4ас = (-20)2 — 4 • 4 • 25 = 400 — 400 = 0.
Так как D = 0, то по теореме 2 данное квадратное уравнение имеет один корень. Этот корень находится по формуле
Ответ: 2,5.
Замечание 2. Обратите внимание, что 4х2 — 20х +25 — полный квадрат: 4х2 — 20х + 25 = (2х — 5)2.
Если бы мы это заметили сразу, то решили бы уравнение так: (2х — 5)2 = 0, значит, 2х — 5 = 0, откуда получаем х = 2,5. Вообще, если D = 0, то
ах2 + bх + с = — это мы отметили ранее в замечании 1.
Если D > 0, то квадратное уравнение ах2 + bх + с = 0 имеет два корня, которые находятся по формулам
Доказательство. Перепишем квадратное уравнение ах2 + Ьх + с = 0 в виде (1)
Положим
По условию, D > 0, значит, правая часть уравнения положительное число. Тогда из уравнения (2) получаем, что

Итак, заданное квадратное уравнение имеет два корня:
Замечание 3. В математике довольно редко бывает так, чтобы введенный термин не имел, образно выражаясь, житейской подоплеки. Возьмем новое
понятие — дискриминант. Вспомните слово «дискриминация». Что оно означает? Оно означает унижение одних и возвышение других, т.е. различное отноше-
ние к различным пюдям. Оба слова (и дискриминант, и дискриминация) происходят от латинского discriminans — «различающий». Дискриминант различает квадратные уравнения по числу корней.
Пример 3. Решить уравнение Зх2 + 8х — 11 = 0.
Решение. Здесь а = 3, b = 8, с = — 11,
D = b2 — 4ас = 82 — 4 • 3 • (-11) = 64 + 132 = 196.
Так как D > 0, то по теореме 3 данное квадратное уравнение имеет два корня. Эти корни находятся по формулам (3)
Фактически мы с вами выработали следующее правило:
Правило решения уравнения
ах2 + bх + с = 0

Это правило универсально, оно применимо как к полным, так и к неполным квадратным уравнениям. Однако неполные квадратные уравнения обычно по этому правилу не решают, их удобнее решать так, как мы это делали в предыдущем параграфе.
Пример 4. Решить уравнения:
а) х2 + Зх — 5 = 0; б) — 9x2 + 6х — 1 = 0; в) 2х2-х + 3,5 = 0.
Р е ш е н и е. а) Здесь а = 1, b = 3, с = — 5,
D = b2 — 4ас = З2 — 4 • 1 • (- 5) = 9 + 20 = 29.
Так как D > 0, то данное квадратное уравнение имеет два корня. Эти корни находим по формулам (3)
б) Как показывает опыт, удобнее иметь дело с квадратными уравнениями, у которых старший коэффициент положителен. Поэтому сначала умножим обе части уравнения на -1, получим
9x2 — 6x + 1 = 0.
Здесь а = 9, b = -6, с = 1, D = b2 — 4ас = 36 — 36 = 0.
Так как D = 0, то данное квадратное уравнение имеет один корень. Этот корень находится по формуле х = — . Значит,
Это уравнение можно было решить по-другому: так как
9х2 — 6x + 1 = (Зх — IJ, то получаем уравнение (Зх — I)2 = 0, откуда находим Зх — 1 = 0, т. е. х = .
в) Здесь а = 2, b = — 1, с = 3,5, D = b2 — 4ас = 1 — 4 • 2 • 3,5= 1 — 28 = — 27. Так как D < 0, то данное квадратное уравнение не имеет корней.
Математики — люди практичные, экономные. Зачем, говорят они, пользоваться таким длинным правилом решения квадратного уравнения, лучше сразу написать общую формулу:
Если окажется, что дискриминант D = b2 — 4ас — отрицательное число, то записанная формула не имеет смысла (под знаком квадратного корня находится отрицательное число), значит, корней нет. Если же окажется, что дискриминант равен нулю, то получаем
т. е. один корень (говорят также, что квадратное уравнение в этом случае имеет два одинаковых корня:
Наконец, если окажется, что b2 — 4ас > 0, то получаются два корня х1и х2, которые вычисляются по тем же формулам (3), что указаны выше.
Само число в этом случае положительно (как всякий квадратный корень из положительного числа), а двойной знак перед ним означает, что в одном случае (при отыскании х1 ) это положительное число прибавляется к числу — b, а в другом случае (при отыскании х2) это положительное число вы-
читается из числа — b.
У вас есть свобода выбора. Хотите —- решайте квадратное уравнение подробно, используя сформулированное выше правило; хотите — запишите сразу формулу (4) и с ее помощью делайте необходимые выводы.
Пример 5. Решить уравнения:
Решение, а) Конечно, можно использовать формулы (4) или (3), учитывая, что в данном случае Но зачем выполнять действия с дробями, когда проще и, главное, приятнее иметь дело с целыми числами? Давайте освободимся от знаменателей. Для этого нужно умножить обе части уравнения на 12, т. е. на наименьший общий знаменатель дробей, служащих коэффициентами уравнения. Получим
откуда 8х2 + 10x — 7 = 0.
А теперь воспользуемся формулой (4)
б) Мы снова имеем уравнение с дробными коэффициентами: а = 3, b = — 0,2, с = 2,77. Умножим обе части уравнения на 100, тогда получим уравнение с целыми коэффициентами:
300x2 — 20x + 277 = 0.
Далее воспользуемся формулой (4):
Простая прикидка показывает, что дискриминант (подкоренное выражение) — отрицательное число. Значит, уравнение не имеет корней.
Пример 6. Решить уравнение
Решение. Здесь, в отличие от предыдущего примера, предпочтительнее действовать по правилу, а не по сокращенной формуле (4).
Имеем а = 5, b = -, с = 1, D = b2 — 4ас = (- ) 2 — 4 • 5 • 1 = 60 — 20 = 40. Так как D > 0, то квадратное уравнение имеет два корня, которые будем искать по формулам (3)
Пример 7. Решить уравнение
х2 — (2р + 1)x +(р2+р-2) = 0
Решение. Это квадратное уравнение отличается от всех рассмотренных до сих пор квадратных уравнений тем, что в роли коэффициентов выступают не конкретные числа, а буквенные выражения. Такие уравнения называют уравнениями с буквенными коэффициентами или уравнениями с параметрами. В данном случае параметр (буква) р входит в состав второго коэффициента и свободного члена уравнения.
Найдем дискриминант:
Пример 8. Решить уравнение рx2 + (1 — р) х — 1 = 0.
Решение. Это также уравнение с параметром р, но, в отличие от предыдущего примера, его нельзя сразу решать по формулам (4) или (3). Дело в том, что указанные формулы применимы к квадратным уравнениям, а про заданное уравнение мы этого пока сказать не можем. В самом деле, а вдруг р = 0? Тогда
уравнение примет вид 0 • x2+ (1-0)x- 1 = 0, т. е. х — 1 = 0, откуда получаем х = 1. Вот если точно известно, что , то можно применять формулы корней квадратного уравнения:
uclg.ru






 Список использованной литературы
Список использованной литературы

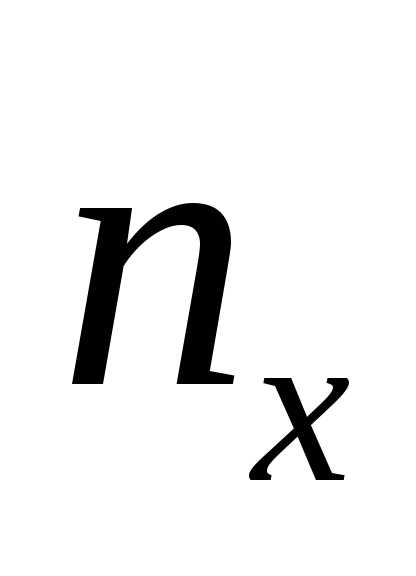 раз, одно и то же значение случайной
величиныY может встретиться
раз, одно и то же значение случайной
величиныY может встретиться 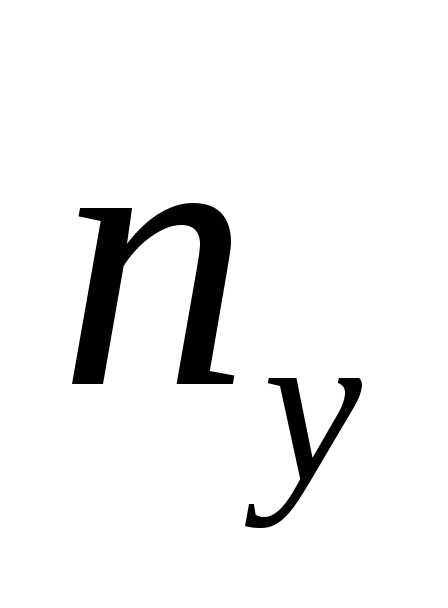 раз, а одна и та же пара чисел (х, у)
может наблюдаться
раз, а одна и та же пара чисел (х, у)
может наблюдаться 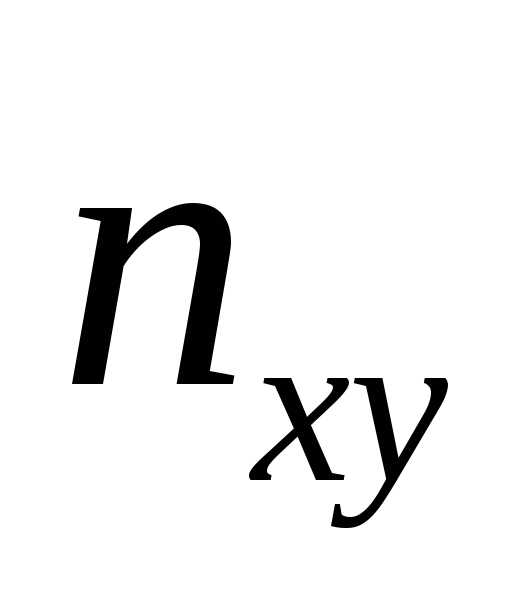 раз. Поэтому данные наблюдений группируют,
т.е. подсчитывают частоты
раз. Поэтому данные наблюдений группируют,
т.е. подсчитывают частоты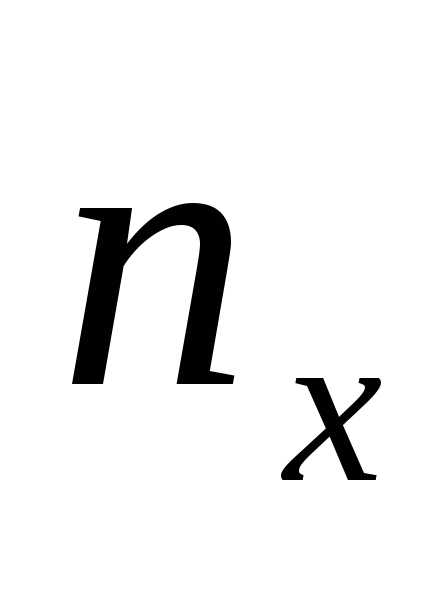 ,,
,,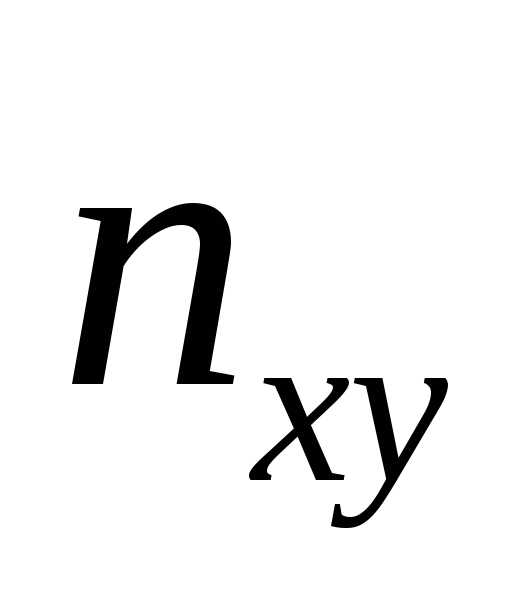 . Все сгруппированные данные за-писывают
в виде таблицы, которую называют корреляционной.
. Все сгруппированные данные за-писывают
в виде таблицы, которую называют корреляционной.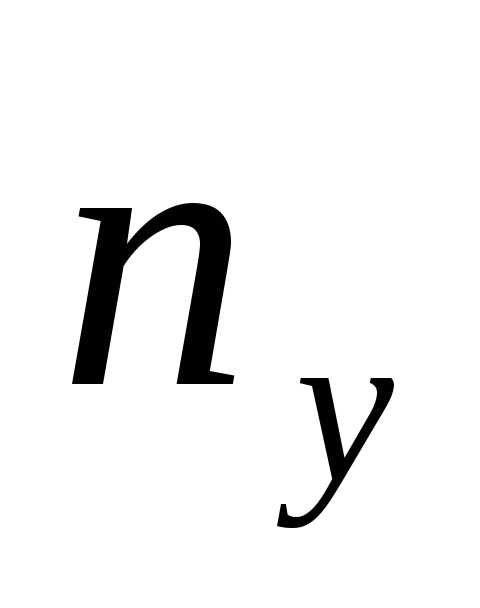
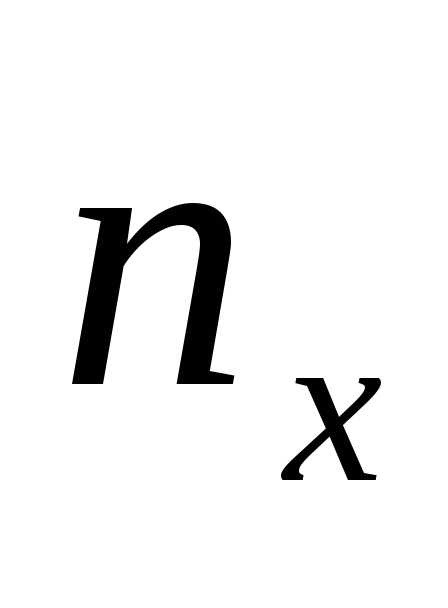
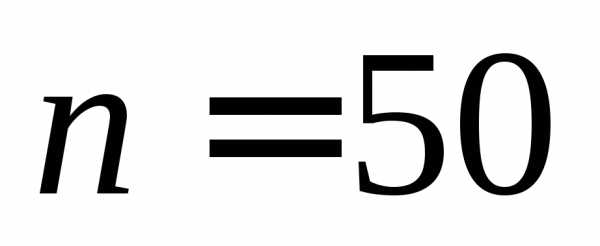
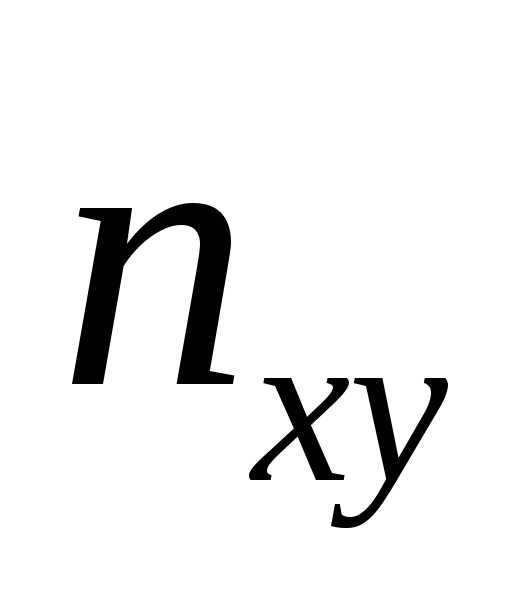 наблюдаемых
пар значений случайных величин Х и Y. Например, частота 6
указывает, что пара чисел (4,
1)
наблюдалась 6
раз. Все
частоты помещены в прямоугольнике,
стороны которого проведены жирными
линиями.
наблюдаемых
пар значений случайных величин Х и Y. Например, частота 6
указывает, что пара чисел (4,
1)
наблюдалась 6
раз. Все
частоты помещены в прямоугольнике,
стороны которого проведены жирными
линиями.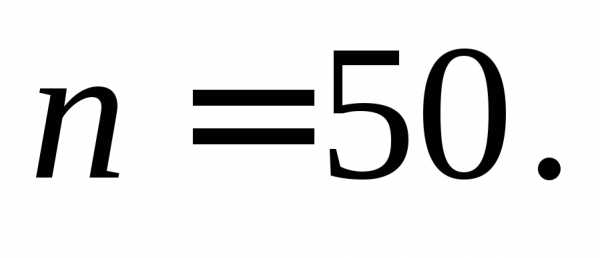
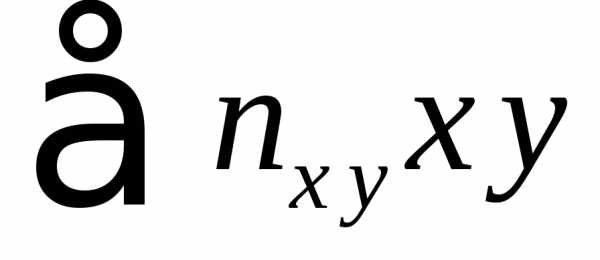 учтено, что пара
(х, у)
наблюдалась
учтено, что пара
(х, у)
наблюдалась 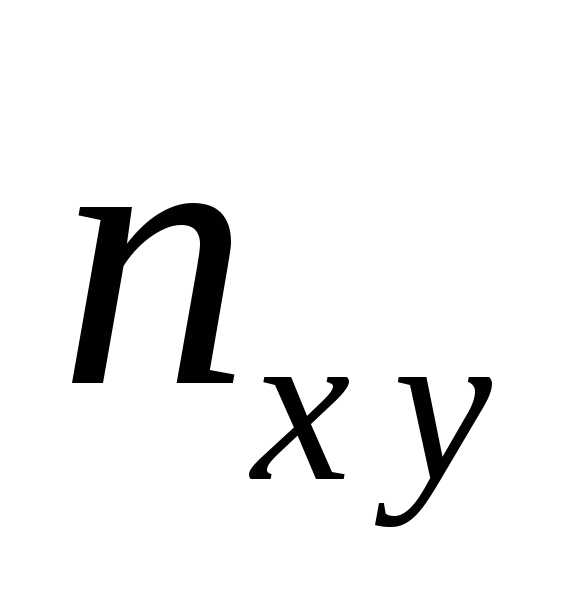 раз, а
и
раз, а
и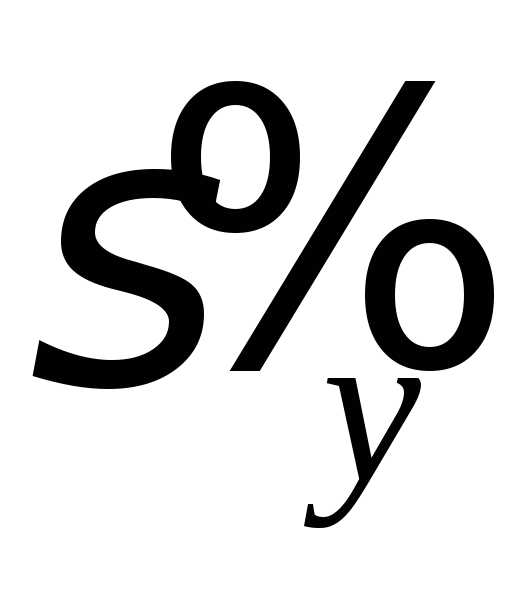
выборочные средние квадратические
отклонения случайных величин Х и Y.
выборочные средние квадратические
отклонения случайных величин Х и Y.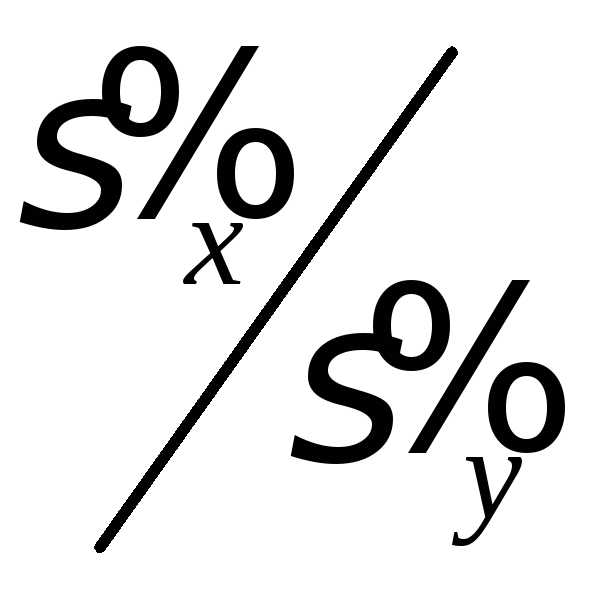 и назовем это выражение выборочным
коэффициентом корреляции
и назовем это выражение выборочным
коэффициентом корреляции
 мал, то линейная связь считается слабой
и ее можно не принимать во внимание.
Если же выборочный коэффициент корреляции
мал, то линейная связь считается слабой
и ее можно не принимать во внимание.
Если же выборочный коэффициент корреляции близок к1,
то линейная связь сильная и к ней следует
относиться практически как к функциональной.
В противном случае, связь принято считать
статистической. И, наконец, при
близок к1,
то линейная связь сильная и к ней следует
относиться практически как к функциональной.
В противном случае, связь принято считать
статистической. И, наконец, при 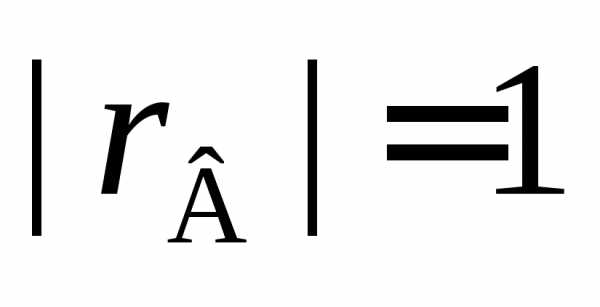 связь между случайными величинамиХ и Y имеет строго линейный характер.
связь между случайными величинамиХ и Y имеет строго линейный характер. является лишь оценкой теоретического
коэффициента корреляции
является лишь оценкой теоретического
коэффициента корреляции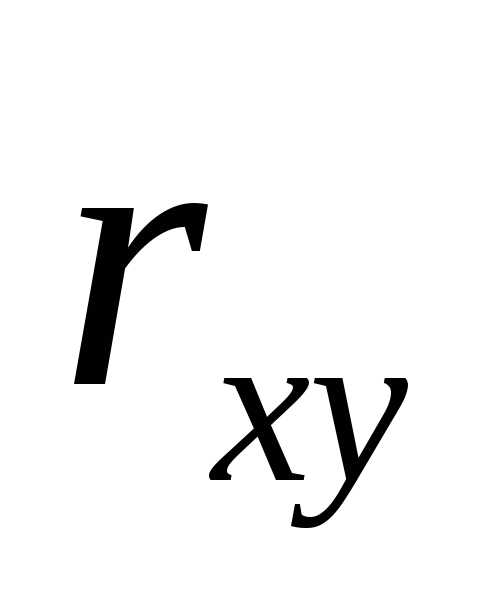 генеральной сово-купности, поэтому
возникает необходимость проверить
гипотезу о значи-мости выборочного
коэффициента корреляции
генеральной сово-купности, поэтому
возникает необходимость проверить
гипотезу о значи-мости выборочного
коэффициента корреляции . Однако, если
выборка имеет достаточно большой
объем и хорошо представляет генеральную
совокупность, т.е. является репрезентативной,
то вывод (гипотезу) о ли-нейной зависимости
между случайными величинами Х и Y , полученный по данным выборки, можно
распространить и на всю генеральную
сово-купность.
. Однако, если
выборка имеет достаточно большой
объем и хорошо представляет генеральную
совокупность, т.е. является репрезентативной,
то вывод (гипотезу) о ли-нейной зависимости
между случайными величинами Х и Y , полученный по данным выборки, можно
распространить и на всю генеральную
сово-купность. 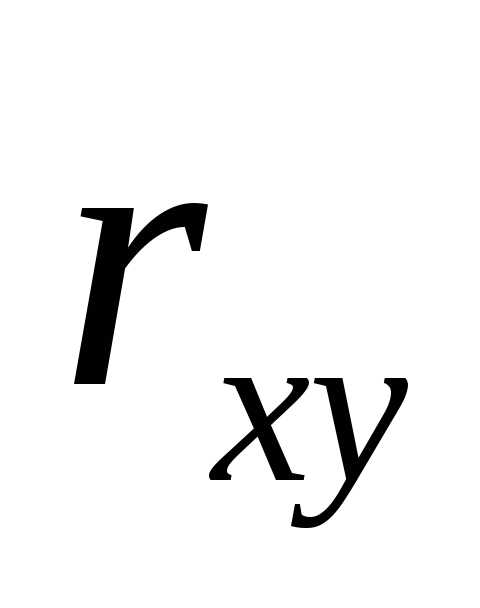 генеральной
совокупности (если она распределена
нормально) можно воспользоваться
формулой
генеральной
совокупности (если она распределена
нормально) можно воспользоваться
формулой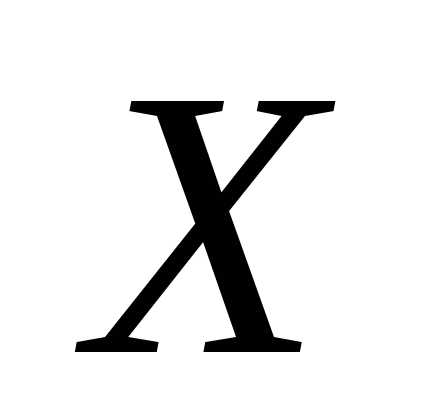 и
и ограничиваются изучением зависимости
между одной из них и условным математическим
ожиданием другой. Знание статистической зависимости
позволяет прогнозировать, что значение
зависимой случайной переменной будет
находиться в некотором интервале, если
независимая переменная примет определенное
значение. С помощью вероятностных
методов можно вычислить вероятность
того, что ошибка прогноза не выйдет за
определенные границы.
ограничиваются изучением зависимости
между одной из них и условным математическим
ожиданием другой. Знание статистической зависимости
позволяет прогнозировать, что значение
зависимой случайной переменной будет
находиться в некотором интервале, если
независимая переменная примет определенное
значение. С помощью вероятностных
методов можно вычислить вероятность
того, что ошибка прогноза не выйдет за
определенные границы.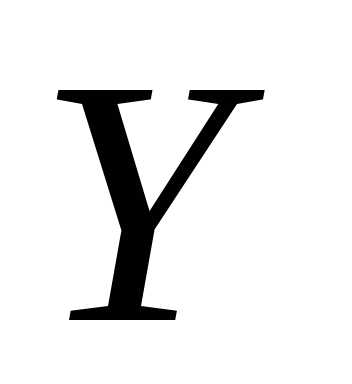 по
по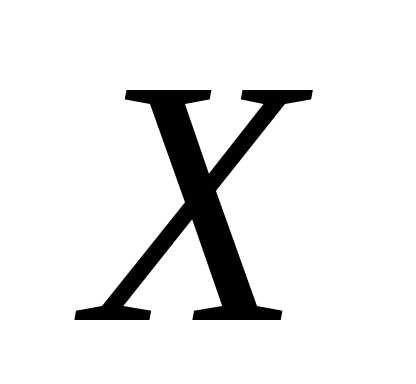 (или
(или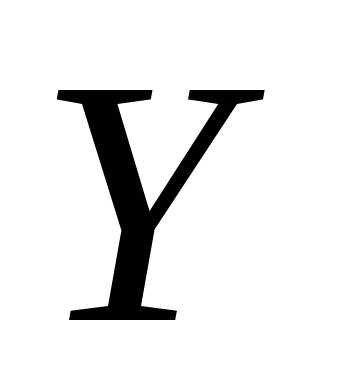 на
на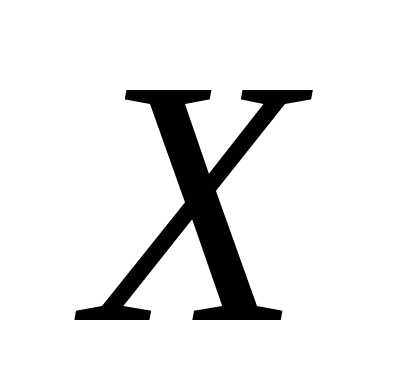 ) называется условное среднее значение
случайной переменной
) называется условное среднее значение
случайной переменной 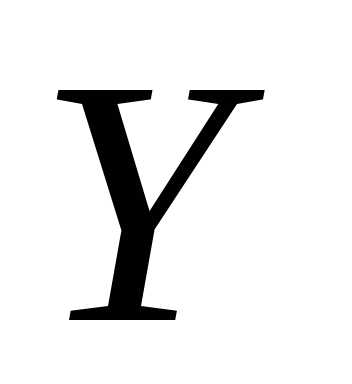 как функция
как функция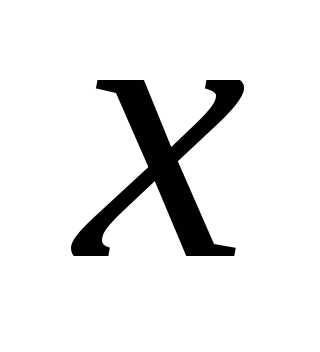 и некоторого числа параметров, которые
находятся методом наименьших квадратов
по наблюденным значениям двумерной
случайной величины
и некоторого числа параметров, которые
находятся методом наименьших квадратов
по наблюденным значениям двумерной
случайной величины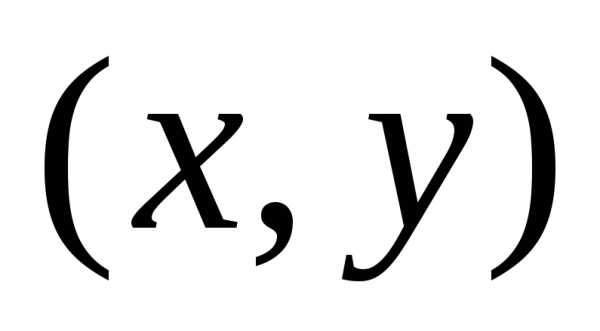 .
Эта кривая называется такжеэмпирическим
уравнением регрессии или просто уравнением регрессии.
.
Эта кривая называется такжеэмпирическим
уравнением регрессии или просто уравнением регрессии.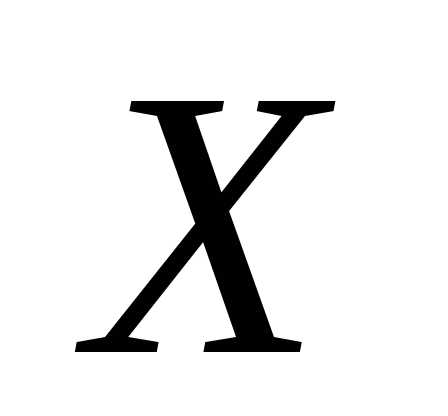 и
и случайные переменные, Пару случайных
чисел
случайные переменные, Пару случайных
чисел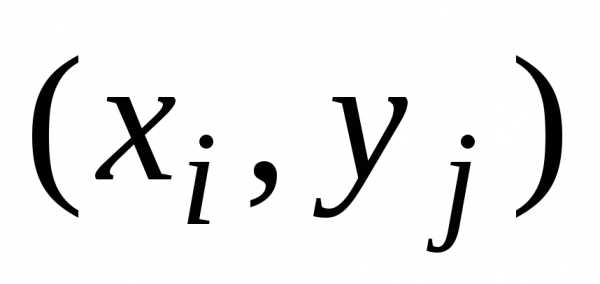 можно
изобразить графически в виде точки с
координатами
можно
изобразить графически в виде точки с
координатами 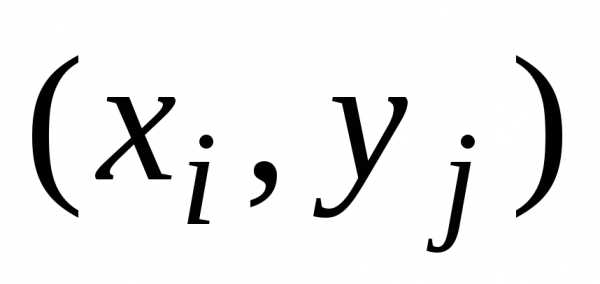 .
Аналогично можно изобразить всю выборку.
.
Аналогично можно изобразить всю выборку.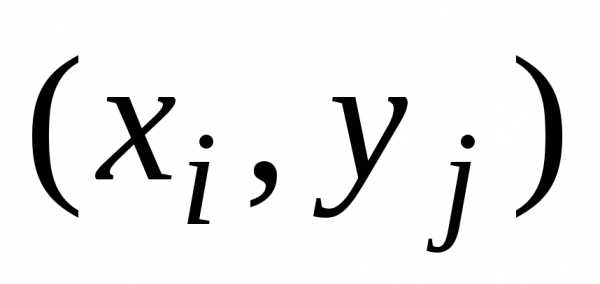 называетсякорреляционным
полем .
называетсякорреляционным
полем .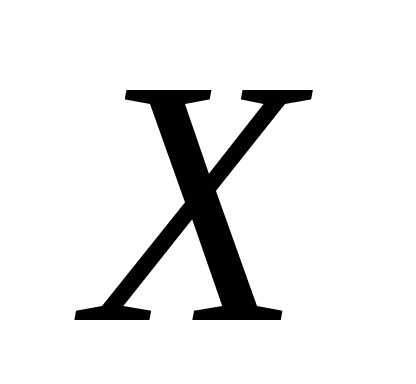 и
и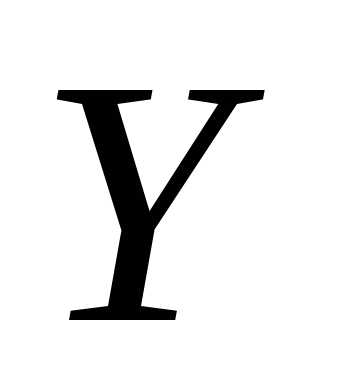 ,
если она существует.
,
если она существует. — объем выполненных работ,
— объем выполненных работ,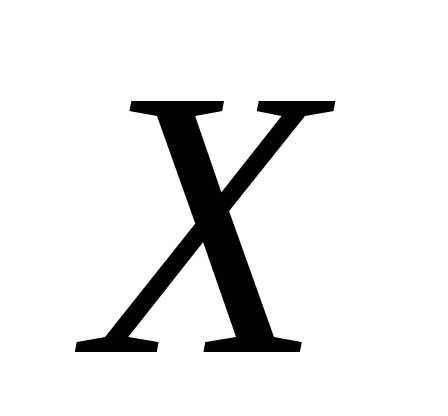 – накладные расходы. Для случайного
вектора (
– накладные расходы. Для случайного
вектора ( )
получена выборка, которую можно
представить с помощью корреляционной
таблицы
)
получена выборка, которую можно
представить с помощью корреляционной
таблицы
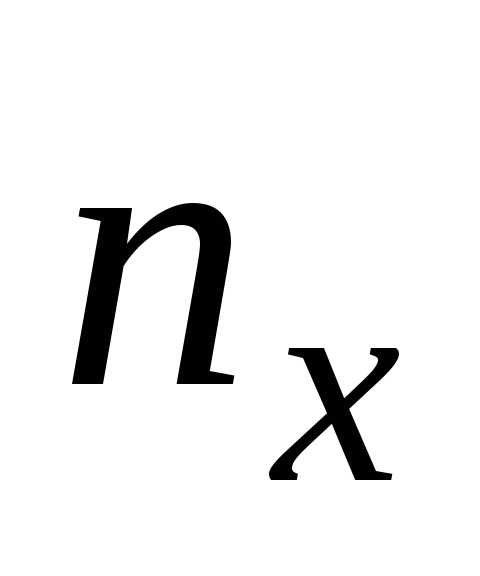
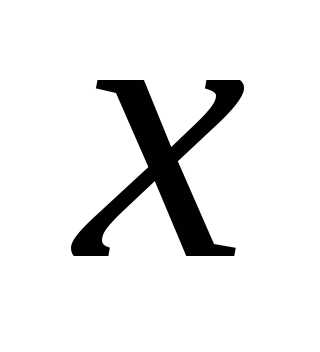 и
и и значения середин интервалов. В ячейки,
образованные пересечением строк и
столбцов помещают частоты
и значения середин интервалов. В ячейки,
образованные пересечением строк и
столбцов помещают частоты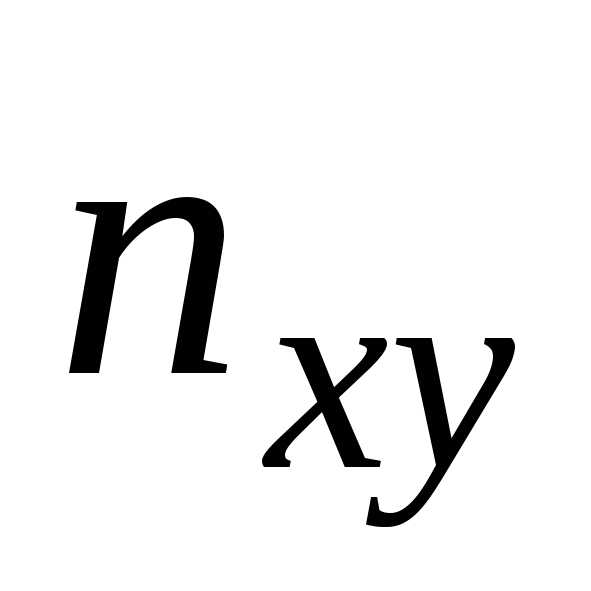 попадания пар значений
попадания пар значений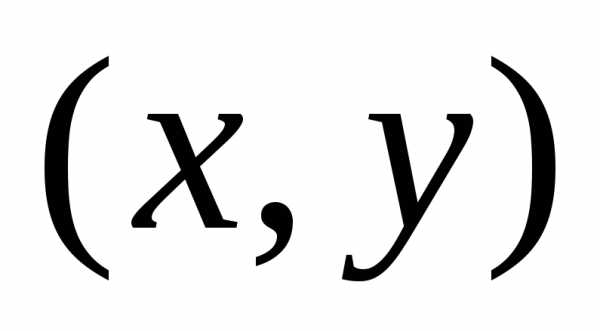 в соответствующие интервалы. В последней
строке и последнем столбце находятся
значения
в соответствующие интервалы. В последней
строке и последнем столбце находятся
значения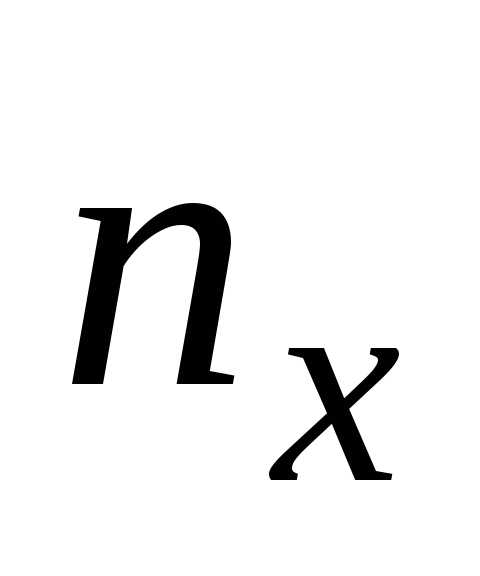 и
и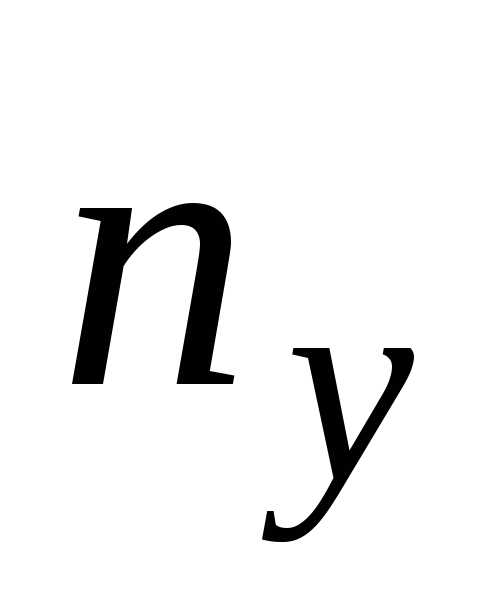 — суммы
— суммы по соответствующим столбцу и строке ,
где
по соответствующим столбцу и строке ,
где 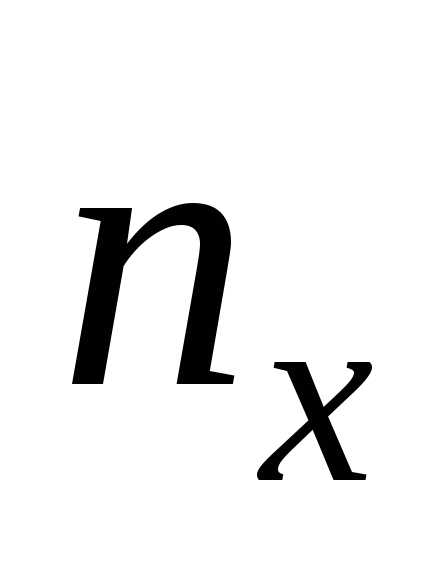 – суммарная частота наблюдаемого
значения признака
– суммарная частота наблюдаемого
значения признака 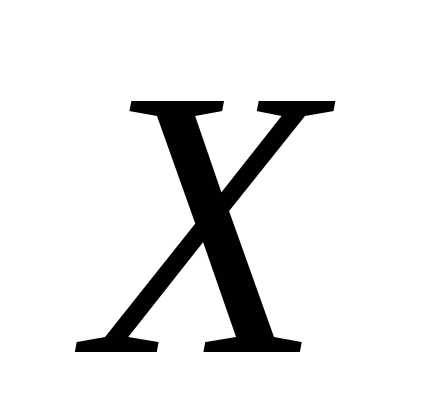 при всех значениях
при всех значениях ,
,  – суммарная частота наблюдаемого
значения признака
– суммарная частота наблюдаемого
значения признака  при
всех значениях
при
всех значениях ,
,  –частота
появления пары значений признаков
–частота
появления пары значений признаков 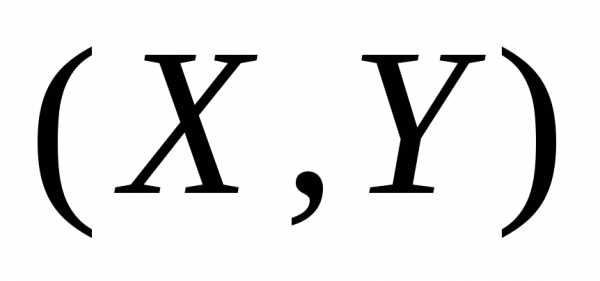 .При
этом выполняются равенства
.При
этом выполняются равенства —
объем выборки.
—
объем выборки.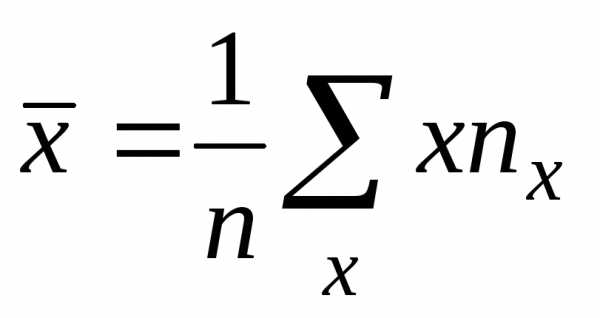 ,
, 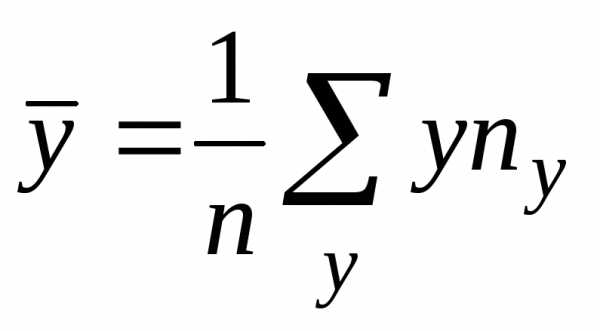 ,
(2)
,
(2)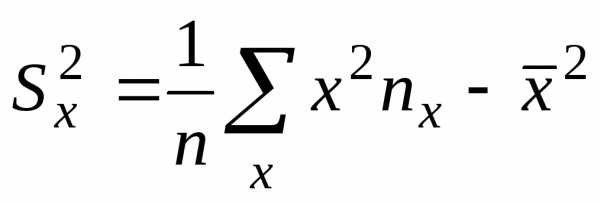 ,
, 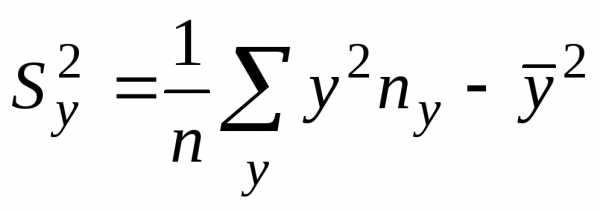 .
(3)
.
(3)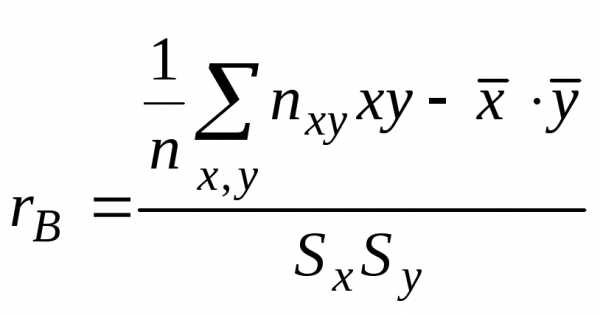 (4)
(4)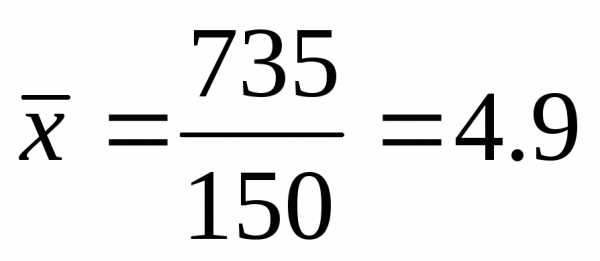 ,
, 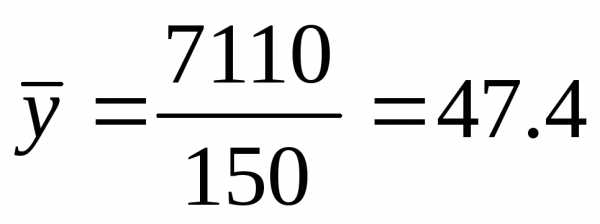
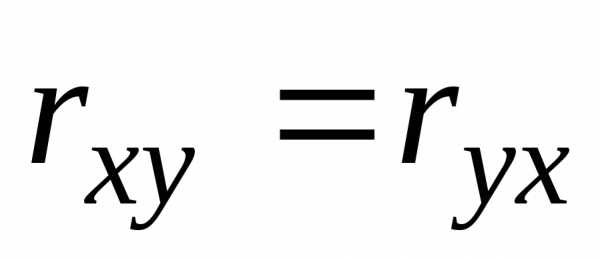 ,
поэтому выборочный коэффициент корреляции
обозначают просто
,
поэтому выборочный коэффициент корреляции
обозначают просто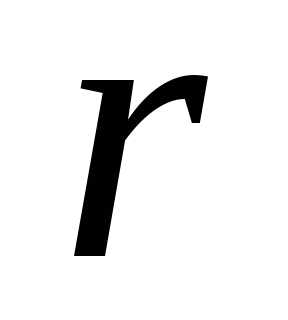 .
.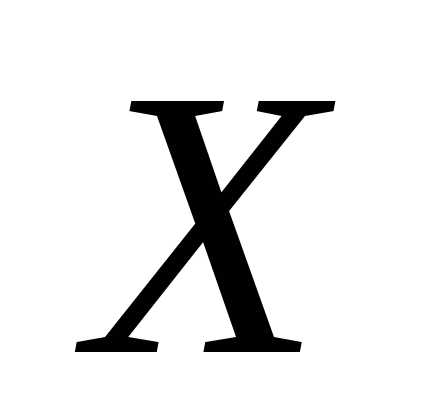 и
и подчиняется
нормальному закону,
подчиняется
нормальному закону,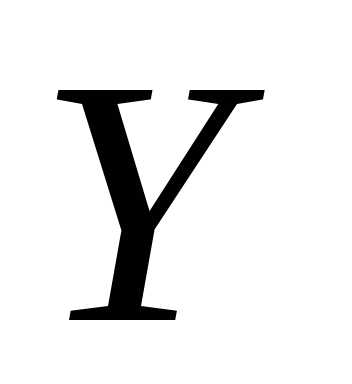 на
на имеет вид
имеет вид на
на имеет вид
имеет вид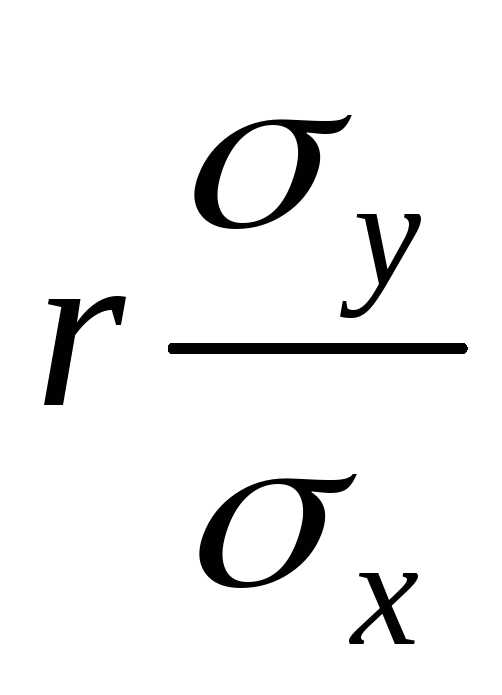 и
и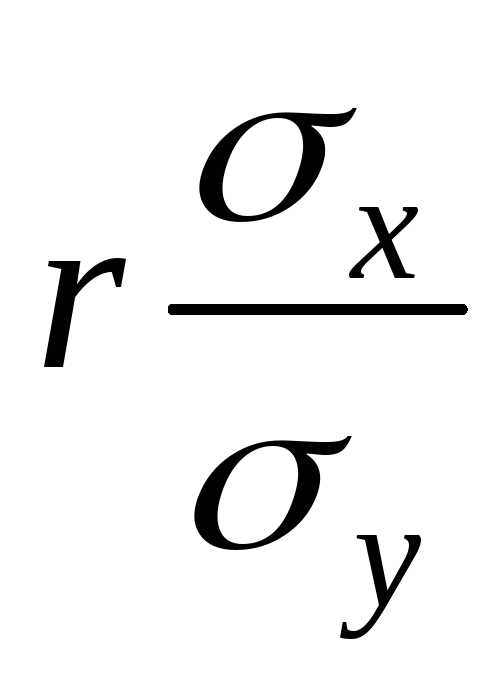 называются коэффициентами регрессии.
называются коэффициентами регрессии. наи
наи на
на имеют вид
имеют вид на
на
 на
на
 )
в зависимости от изменения аргумента
)
в зависимости от изменения аргумента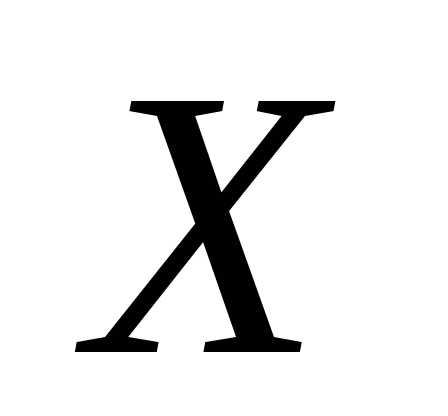 (или
(или ).
).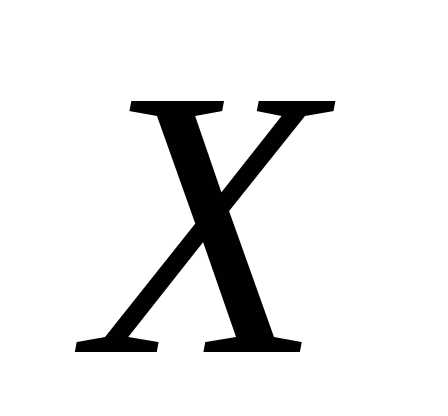 и
и .
Равенство нулю выборочного коэффициента
корреляции еще не свидетельствует о
равенстве нулю самого коэффициента
корреляции, а, следовательно, о
некоррелированности случайных величин
.
Равенство нулю выборочного коэффициента
корреляции еще не свидетельствует о
равенстве нулю самого коэффициента
корреляции, а, следовательно, о
некоррелированности случайных величин и
и .
Чтобы выяснить, находятся ли случайные
величины в корреляционной зависимости,
нужно проверить значимость выборочного
коэффициента корреляции
.
Чтобы выяснить, находятся ли случайные
величины в корреляционной зависимости,
нужно проверить значимость выборочного
коэффициента корреляции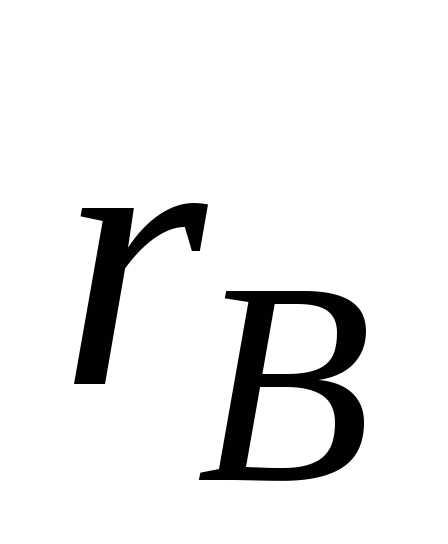 ,
т.е. установить, достаточна ли его
величина для обоснованного вывода о
наличии корреляционной связи. Для этого
проверяют нулевую гипотезу
,
т.е. установить, достаточна ли его
величина для обоснованного вывода о
наличии корреляционной связи. Для этого
проверяют нулевую гипотезу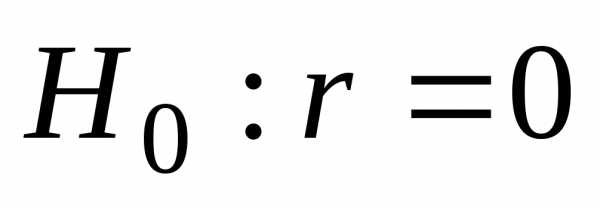 ,
т.е. случайные величины в генеральной
совокупности не коррелированы.
Альтернативная гипотеза.
Предполагая, что имеется двумерное
нормальное распределение случайных
переменных, вычисляют статистику
,
т.е. случайные величины в генеральной
совокупности не коррелированы.
Альтернативная гипотеза.
Предполагая, что имеется двумерное
нормальное распределение случайных
переменных, вычисляют статистику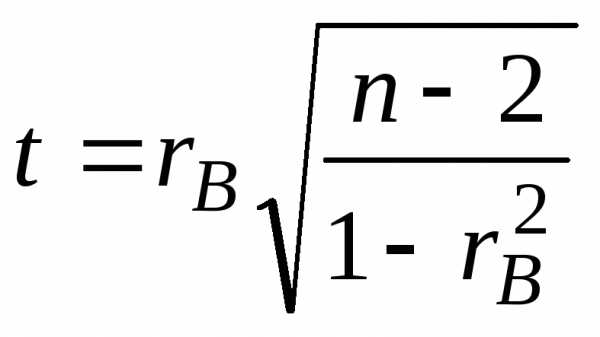 ,
(8)
,
(8) и числу степеней свободынаходят по таблицам распределения
Стьюдента критическое значение
и числу степеней свободынаходят по таблицам распределения
Стьюдента критическое значение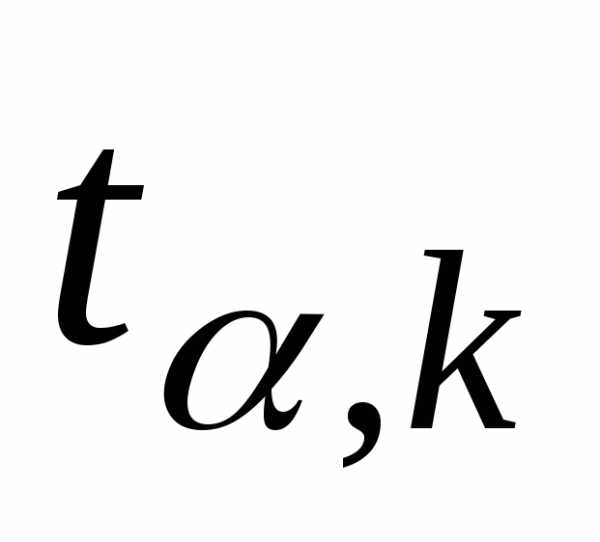 ,
удовлетворяющее условию.
Если
,
удовлетворяющее условию.
Если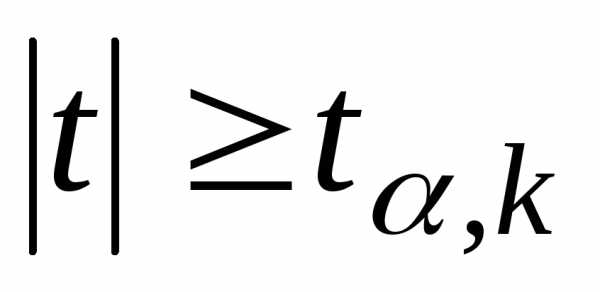 ,
то нулевую гипотезу об отсутствии
корреляционной связи между переменными
,
то нулевую гипотезу об отсутствии
корреляционной связи между переменными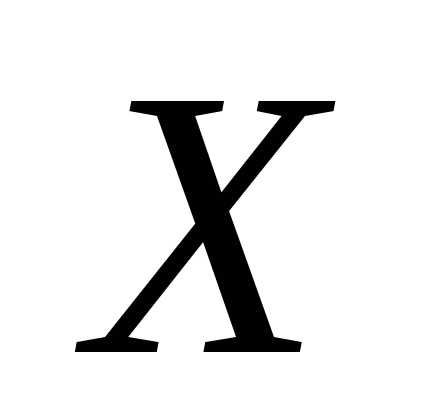 и
и следует отвергнуть. В этом случае
переменные являются зависимыми. Если
следует отвергнуть. В этом случае
переменные являются зависимыми. Если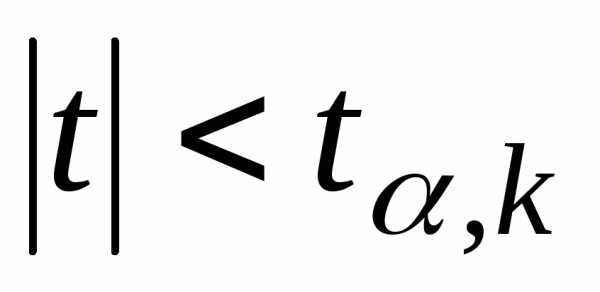 ,
то нет оснований отвергать нулевую
гипотезу.
,
то нет оснований отвергать нулевую
гипотезу. и числу степеней свободынайдем критическую точку
и числу степеней свободынайдем критическую точку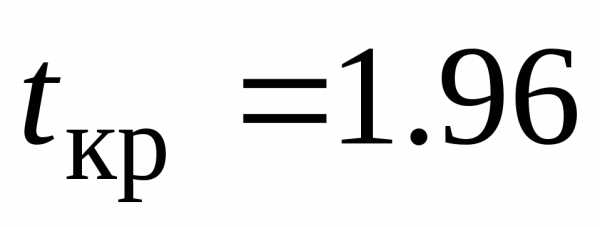 .
Так как
.
Так как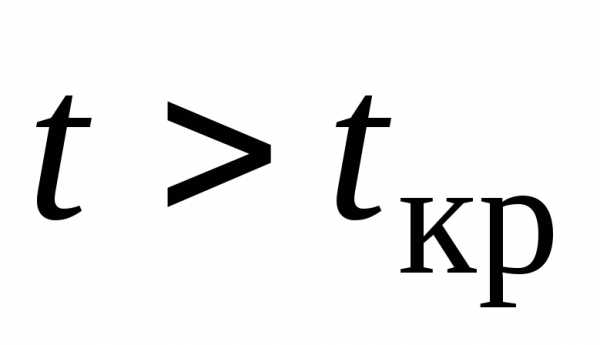 ,
то нулевая гипотеза отвергается.
Рассматриваемые случайные величины
являются коррелированными и , следовательно,
зависимыми.
,
то нулевая гипотеза отвергается.
Рассматриваемые случайные величины
являются коррелированными и , следовательно,
зависимыми.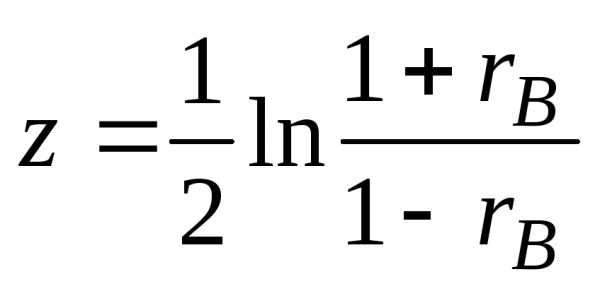 .
Отсюда.
.
Отсюда. хорошо аппроксимируется нормальным
распределением с параметрамии
хорошо аппроксимируется нормальным
распределением с параметрамии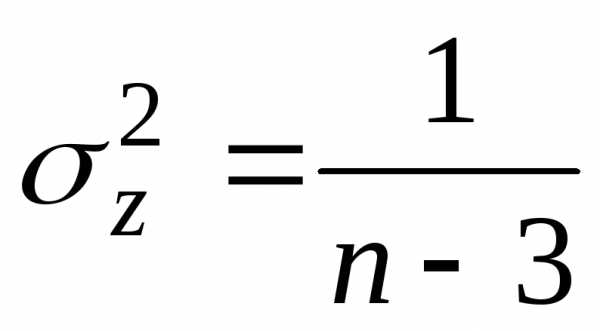 .
.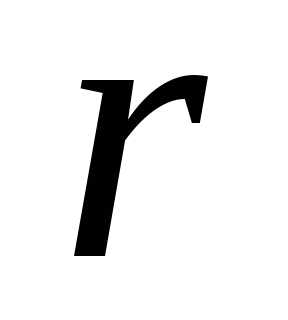 имеет вид.
Величины
имеет вид.
Величины и
и находят по таблицам
находят по таблицам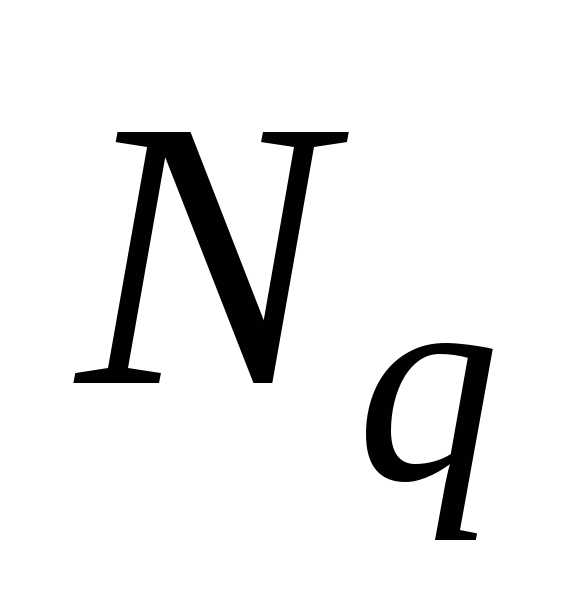 –
нормированная функция Лапласа для
–
нормированная функция Лапласа для %
доверительного интервала.
%
доверительного интервала. имеет распределение Стьюдента сстепенями свободы. Регрессионный анализ
имеет распределение Стьюдента сстепенями свободы. Регрессионный анализ и наблюдавшимся признаком
и наблюдавшимся признаком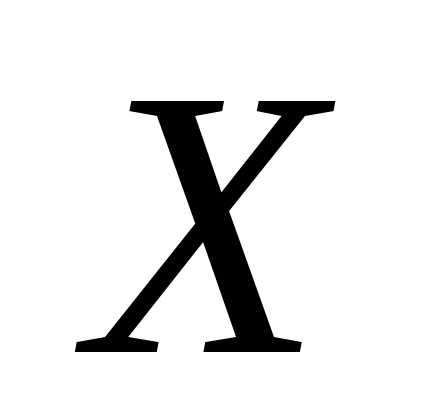 ,
оценка функции регрессии. Рассмотрим
вначале линейный регрессионный анализ
в котором условное математическое
ожидание можно представить в виде
линейной функции от оцениваемых
параметров
,
оценка функции регрессии. Рассмотрим
вначале линейный регрессионный анализ
в котором условное математическое
ожидание можно представить в виде
линейной функции от оцениваемых
параметров называются коэффициентами регрессии.
Оценки этих параметров обозначим
называются коэффициентами регрессии.
Оценки этих параметров обозначим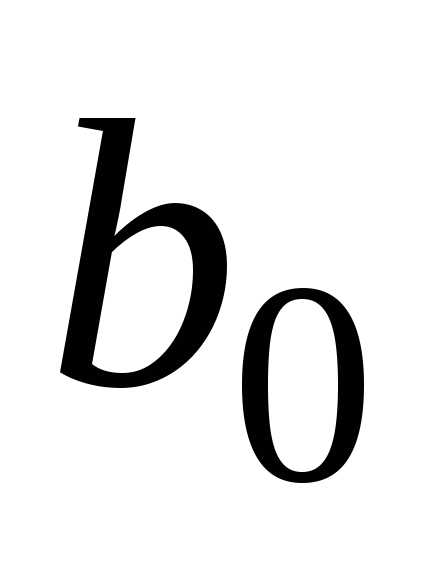 и
и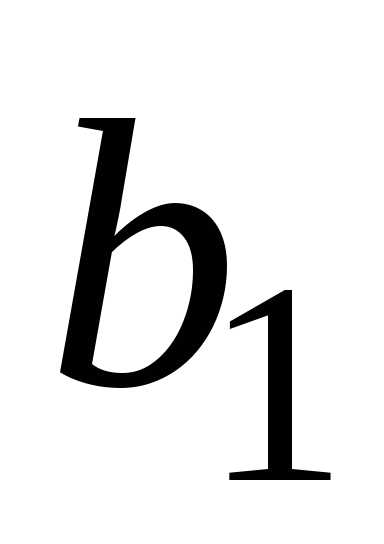 .
Подставляя эти оценки в формулу (9)
вместо параметров, получим линейное
уравнение регрессии
.
Подставляя эти оценки в формулу (9)
вместо параметров, получим линейное
уравнение регрессии от вычисленных по уравнению регрессии
от вычисленных по уравнению регрессии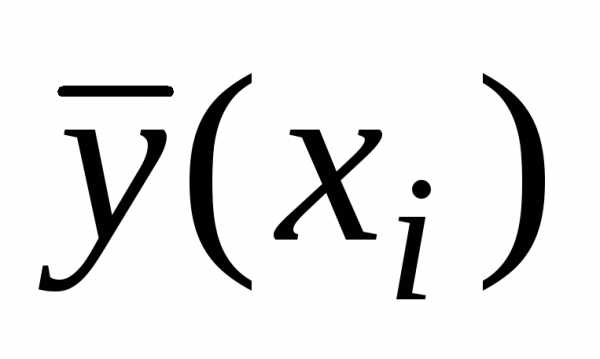 ,
т. е. условия минимума величины
,
т. е. условия минимума величины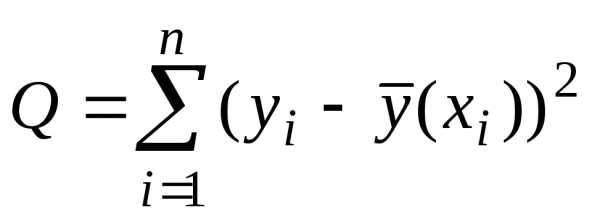 (11)
(11) по переменным
по переменным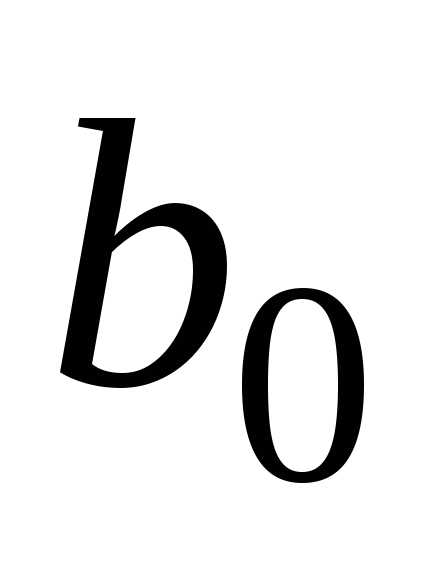 и
и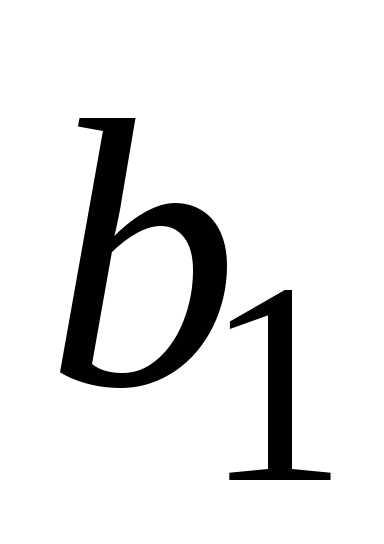 .
В результате получим систему нормальных
уравнений
.
В результате получим систему нормальных
уравнений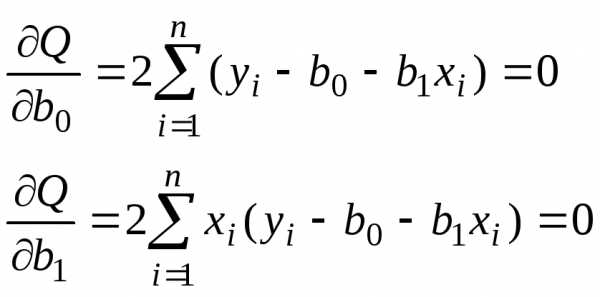 (13)
(13)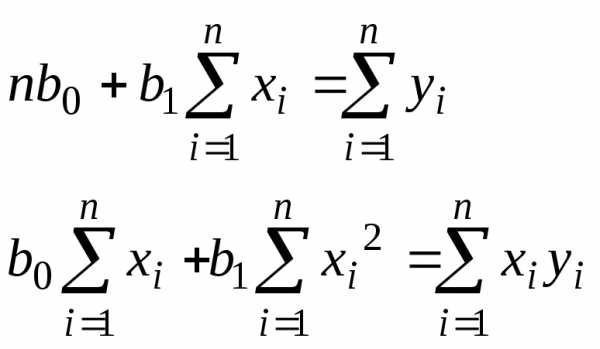 (14)
(14)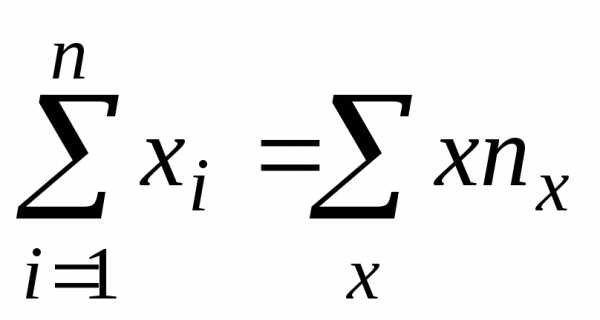 ,
,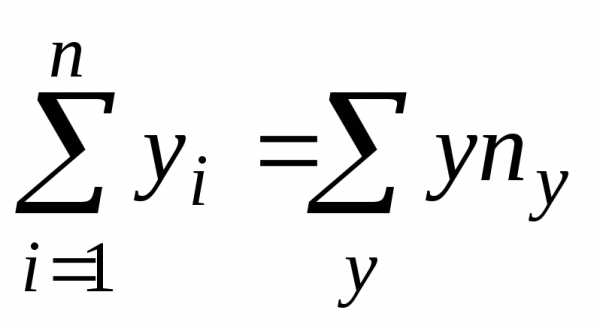 ,
,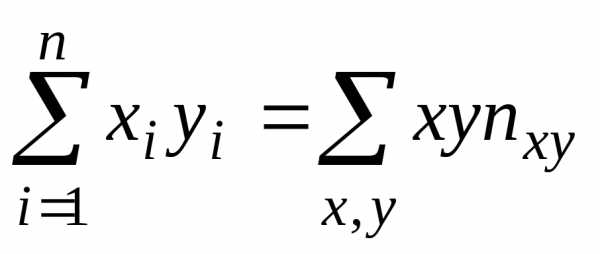 ,
,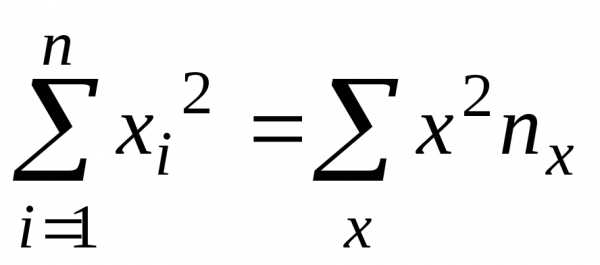 (15)
(15) ,
, ,
, соответствующие частоты:
соответствующие частоты: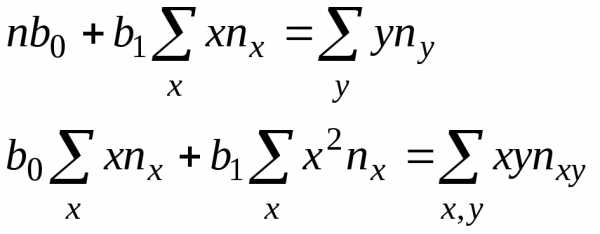 (16)
(16) и
и и уравнение регрессии.
и уравнение регрессии. и
и нелинейная,
то условное математическое ожидание
является нелинейной функцией. Пусть,
например,.
Оценки параметров
нелинейная,
то условное математическое ожидание
является нелинейной функцией. Пусть,
например,.
Оценки параметров обозначим
обозначим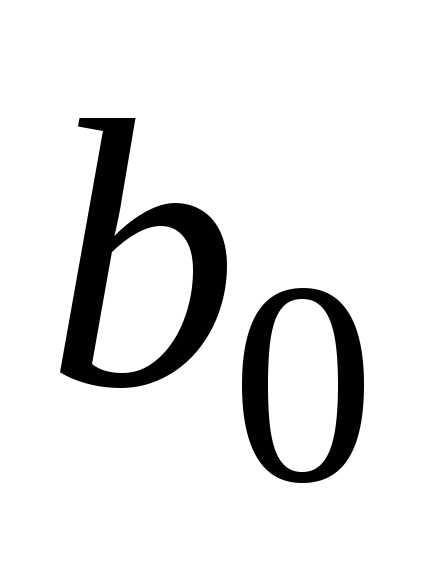 ,
,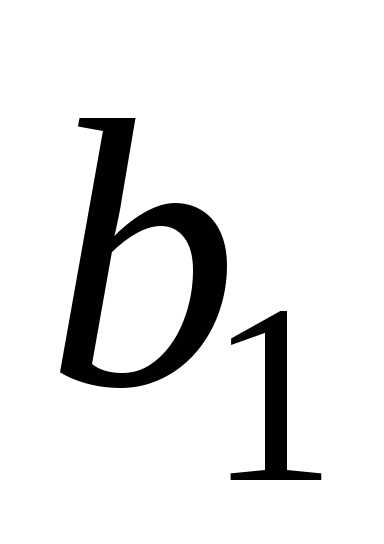 ,
,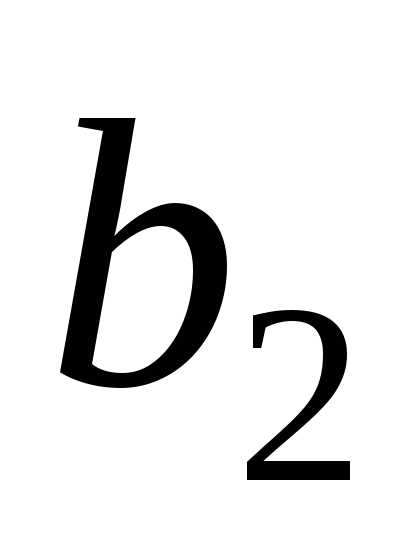 .
В этом случае система нормальных
уравнений имеет вид
.
В этом случае система нормальных
уравнений имеет вид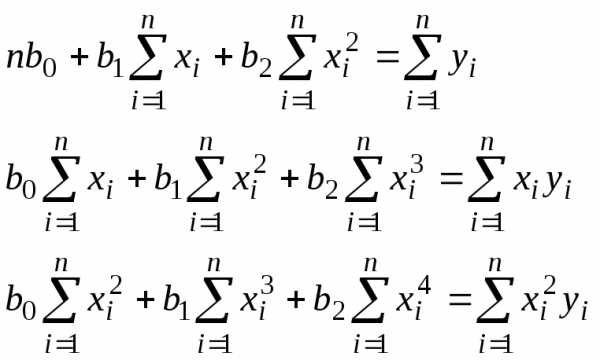 (17)
(17)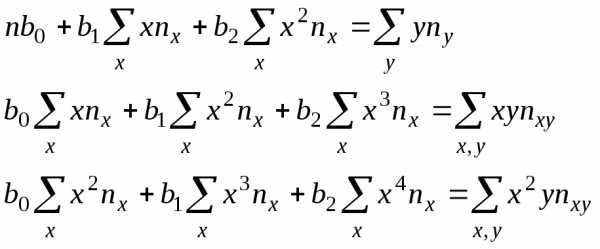 (18)
(18)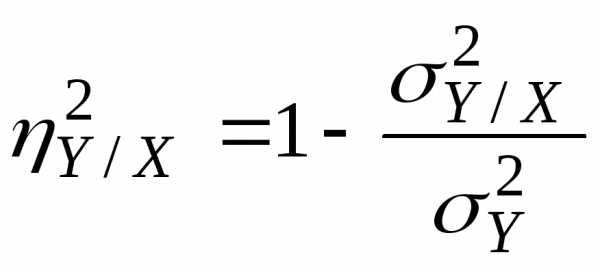
 .
В этом случае вместо дисперсий используются
их статистические оценки. Тогда
.
В этом случае вместо дисперсий используются
их статистические оценки. Тогда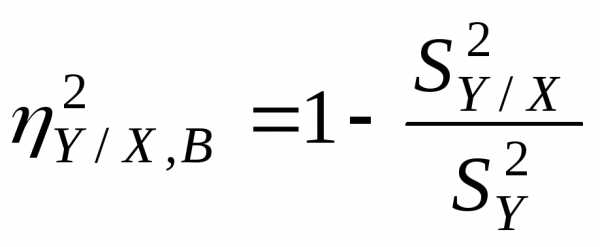 (19)
(19)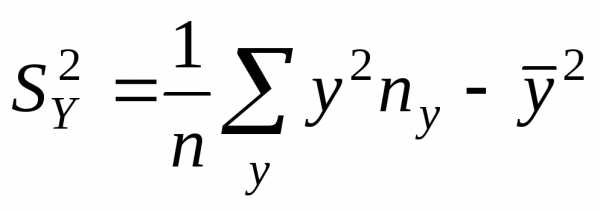 ,
,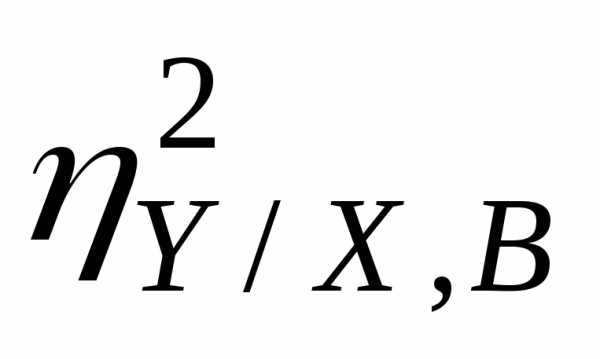 вычисляется по данным корреляционной
таблицы с помощью формулы
вычисляется по данным корреляционной
таблицы с помощью формулы относительно безусловного среднего
арифметического
относительно безусловного среднего
арифметического .
.

 наступления события
наступления события в каждом испытании постоянна и
удовлетворяет двойному неравенству
в каждом испытании постоянна и
удовлетворяет двойному неравенству ,
а число независимых испытаний
,
а число независимых испытаний достаточно велико, то вероятностьможет быть вычислена по следующей
приближённой формуле
достаточно велико, то вероятностьможет быть вычислена по следующей
приближённой формуле .
. (Н.Ф.Л)
(Н.Ф.Л) :
: .
. нечётна. Действительно, после замены
переменных
нечётна. Действительно, после замены
переменных

 ;
;
 можно полагать что,следовательно, все значения этой функции
расположены в отрезке [-0,5; 0,5], при этом
наименьшим являетсязатем функция медленно растёт и обращается
в нуль, т.е.
можно полагать что,следовательно, все значения этой функции
расположены в отрезке [-0,5; 0,5], при этом
наименьшим являетсязатем функция медленно растёт и обращается
в нуль, т.е. а затем возрастает доСледовательно, на всей
числовой прямой является строго
возрастающей функцией, т.е. если
а затем возрастает доСледовательно, на всей
числовой прямой является строго
возрастающей функцией, т.е. если  то
то обосновывается на основании несобственного
интеграла Пуассона.
обосновывается на основании несобственного
интеграла Пуассона. и для
и для ;
для значений
;
для значений следует воспользоваться той же таблицей
с учётом равенства
следует воспользоваться той же таблицей
с учётом равенства ,
преобразуем равенство (15), так:
,
преобразуем равенство (15), так: ),
с учётом чётности подынтегральной
функции получим
),
с учётом чётности подынтегральной
функции получим появится в
появится в независимых испытаниях не менее
независимых испытаниях не менее раз и не более
раз и не более раз, вычисляется формулой:
раз, вычисляется формулой: ,
, ,
, ,
, ,
, .
Вычисляем
.
Вычисляем (И.В.
или Ф.Л.)
(И.В.
или Ф.Л.) и поэтому имеется также ё таблица
приближённых значений (см. в конце книги,
приложение).
и поэтому имеется также ё таблица
приближённых значений (см. в конце книги,
приложение). ,,
,, .
. ,
, .
Воспользуемся интегральной теоремой
Муавра-Лапласа:
.
Воспользуемся интегральной теоремой
Муавра-Лапласа: ;
; независимых испытаний, в каждом из
которых вероятность наступления события
независимых испытаний, в каждом из
которых вероятность наступления события равна,а относительная частота в каждой серии
испытания равна
равна,а относительная частота в каждой серии
испытания равна найти вероятность отклонение
относительной частоты
от постоянной вероятности
найти вероятность отклонение
относительной частоты
от постоянной вероятности появления события
появления события по абсолютной величине не превышает
заданного числа
по абсолютной величине не превышает
заданного числа Другими словами, найти вероятность:
Другими словами, найти вероятность:  ,
как бы ни было мало
,
как бы ни было мало ,
имеет место предельное равенство
,
имеет место предельное равенство в
одном испытании. Сначала установим
следующее равенство при любом
в
одном испытании. Сначала установим
следующее равенство при любом и достаточно большом
и достаточно большом :
: .
. легко заметить, что имеет место двойное
неравенство.
Обозначим
легко заметить, что имеет место двойное
неравенство.
Обозначим получим
получим ==
2
==
2 .
. .
Найти вероятность того, что среди
случайно отобранных 400 деталей
относительная частота появления
нестандартных деталей отклонится от
.
Найти вероятность того, что среди
случайно отобранных 400 деталей
относительная частота появления
нестандартных деталей отклонится от по абсолютной величине не более чем на
0,03.
по абсолютной величине не более чем на
0,03.
 =2
=2 .
.
 этих проб от вероятности
этих проб от вероятности ,
по модулю не превышающей 0,03.
,
по модулю не превышающей 0,03. .
. .
Сколько деталей надо отобрать, чтобы с
вероятностью 0,9999 можно было бы утверждать,
что относительная частота нестандартных
деталей (среди отобранных), отклоняется
от
.
Сколько деталей надо отобрать, чтобы с
вероятностью 0,9999 можно было бы утверждать,
что относительная частота нестандартных
деталей (среди отобранных), отклоняется
от по
модулю не более, чем на 0,03. Найти это
количество
по
модулю не более, чем на 0,03. Найти это
количество
 .
По формуле (13) имеем
.
По формуле (13) имеем .
. сходится по вероятности к истинной
вероятности этого же события, т.е.
справедлива оценка снизу
сходится по вероятности к истинной
вероятности этого же события, т.е.
справедлива оценка снизу ,
, от
испытания к испытанию остается неизменным
и равным
от
испытания к испытанию остается неизменным
и равным при этом
при этом  .
.
 равносильно двойному неравенству
равносильно двойному неравенству
 распределена
по биномиальному закону. Эта случайная
величина представляет собой число
успехов
распределена
по биномиальному закону. Эта случайная
величина представляет собой число
успехов в серии из
в серии из испытаний, в каждом из которых может
появиться успех с вероятностью
испытаний, в каждом из которых может
появиться успех с вероятностью или неуспех с вероятностью
или неуспех с вероятностью .Вероятность
того, что в серии из
.Вероятность
того, что в серии из испытаний появится
испытаний появится успехов равна
успехов равна и
и вычисление вероятности по формуле (1)
представляет значительные трудности.
Например, если,,,
то
вычисление вероятности по формуле (1)
представляет значительные трудности.
Например, если,,,
то достаточно велико, а
достаточно велико, а не мало, так что ().
Введем обозначение
не мало, так что ().
Введем обозначение .
(2)
.
(2) ,
т.е.
,
т.е. ,
то вероятность того, что в серии из
,
то вероятность того, что в серии из испытаний
будет
испытаний
будет успехов равна
успехов равна эту вероятность можно выразить через
функцию
эту вероятность можно выразить через
функцию :
:
 (3)
(3) ,
а аргумент
,
а аргумент .
. успехов в серии из
успехов в серии из испытаний равна
испытаний равна ,
,,
получим
,
,,
получим ,
справедливая при достаточно больших
значениях
,
справедливая при достаточно больших
значениях .
. при
этом
(5)
при
этом
(5) при
этом
(6)
при
этом
(6) ,
а значит
,
а значит .
Подставляя это выражение в (8) и учитывая
(5) и (6), получим
.
Подставляя это выражение в (8) и учитывая
(5) и (6), получим .
. и не малых значениях
и не малых значениях функция биномиального распределения
имеет вид функции нормированного
нормального распределения с
функция биномиального распределения
имеет вид функции нормированного
нормального распределения с и
и .
.
 ,
т.е.
,
т.е. ,
то вероятность того, что в серии из
,
то вероятность того, что в серии из испытаний число успехов находится в
промежутке
испытаний число успехов находится в
промежутке определяется с помощью функции Лапласа
определяется с помощью функции Лапласа — функция Лапласа.
— функция Лапласа. (12)
(12)
 и
и ,
, и не малых значениях
и не малых значениях функция биномиального распределения
имеет вид функции нормированного
нормального распределения с
функция биномиального распределения
имеет вид функции нормированного
нормального распределения с и
и .
. и
и расположены симметрично относительно
математического ожидания
расположены симметрично относительно
математического ожидания ,
т.е.и,
то формула (13) примет вид
,
т.е.и,
то формула (13) примет вид ,
, ,
, ,
, ,.
,. – количество выпадений герба при 700
бросках. Она распределена биномиально
с.
Значение,
следовательно, можно применить локальную
формулу Муавра – Лапласа.
– количество выпадений герба при 700
бросках. Она распределена биномиально
с.
Значение,
следовательно, можно применить локальную
формулу Муавра – Лапласа. – количество выпадений герба при 700
бросках. Она распределена биномиально
с.
Значение,
следовательно, можно применить
интегральную формулу Муавра – Лапласа.
– количество выпадений герба при 700
бросках. Она распределена биномиально
с.
Значение,
следовательно, можно применить
интегральную формулу Муавра – Лапласа. ,
, ,,,.
,,,. ,
, ,,,
,,, .
. .
. соответствует значение аргумента
соответствует значение аргумента .
Следовательно,
.
Следовательно, и.
Для определения границ, между которыми
заключено число изделий первого сорта,
имеем неравенство.
Отсюда.
и.
Для определения границ, между которыми
заключено число изделий первого сорта,
имеем неравенство.
Отсюда. достаточно велико, а вероятность
удовлетворяет,
для вычисления биномиальных вероятностей
используют приближенные теоремы Муавра
– Лапласа.
достаточно велико, а вероятность
удовлетворяет,
для вычисления биномиальных вероятностей
используют приближенные теоремы Муавра
– Лапласа. наступления события
наступления события в каждом испытании постоянна и
удовлетворяет условиям
в каждом испытании постоянна и
удовлетворяет условиям ,
а число независимых испытаний
,
а число независимых испытаний достаточно
велико, то вероятность
достаточно
велико, то вероятность может бить вычислена по следующей
приближённой формуле
может бить вычислена по следующей
приближённой формуле
 ),
позволяющую найти приближенное значение
),
позволяющую найти приближенное значение  при достаточно больших значениях
при достаточно больших значениях ,
где функция
,
где функция  (Ф. Г.)
(Ф. Г.) разность
разность стремится к
стремится к вместе с
вместе с и
и .
Воспользуемся формулой Стрилинга,
дляТогда с учетом формулы Бернулли после
некоторых преобразований получим
.
Воспользуемся формулой Стрилинга,
дляТогда с учетом формулы Бернулли после
некоторых преобразований получим получим
получим
 приведена таблица
значений (см. приложение?).
приведена таблица
значений (см. приложение?). :
: чётная, т.е.
чётная, т.е.  , и для
, и для можно считать,
можно считать,
 ,
по условию задачии
,
по условию задачии ,
тоТогда на основании таблицы значений
функции
,
тоТогда на основании таблицы значений
функции получим.
По формуле (12) получим
получим.
По формуле (12) получим с помощью формулы Бернулли очень трудно
сосчитать.
с помощью формулы Бернулли очень трудно
сосчитать.
 .
Если
.
Если то
то и
если
и
если то
то потому, чтоp+q = 1.
потому, чтоp+q = 1. берут число не менее 10., отсюда следует,
чтоесли p или q близко к нулю,тем больше нужно братьn.
берут число не менее 10., отсюда следует,
чтоесли p или q близко к нулю,тем больше нужно братьn. раз и не более
раз и не более раз,
раз,  ,
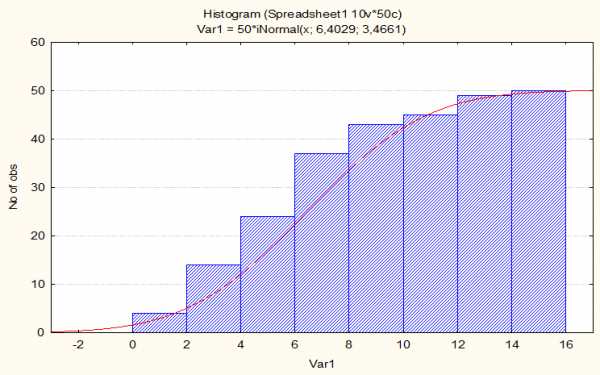
равна
,
равна








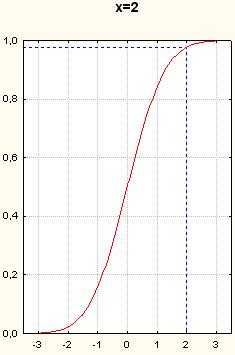
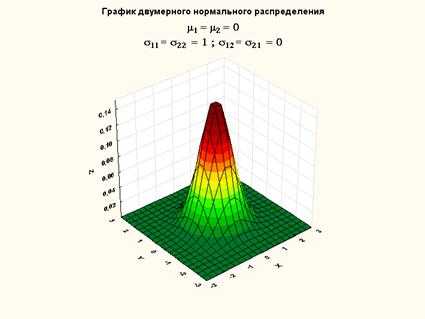



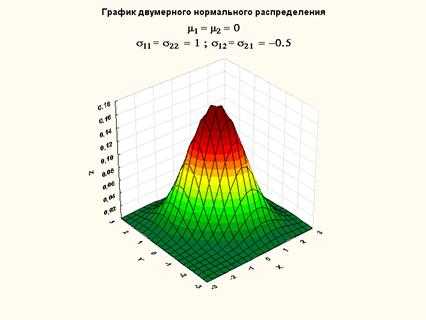



 ,
определённая на множестве
,
определённая на множестве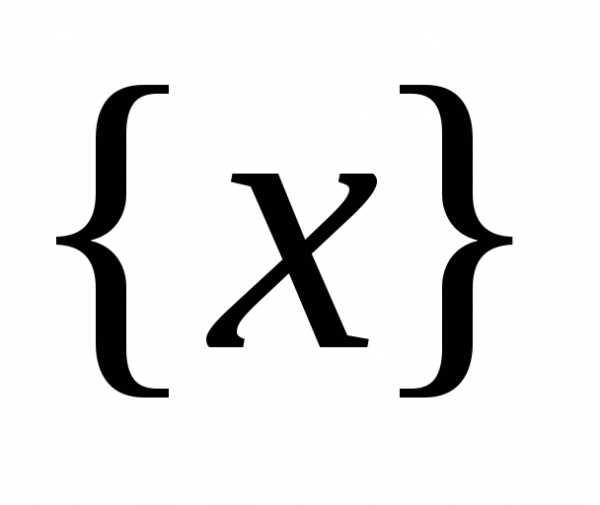 .
Пусть имеется точкаa,
быть может и не принадлежащая
.
Пусть имеется точкаa,
быть может и не принадлежащая 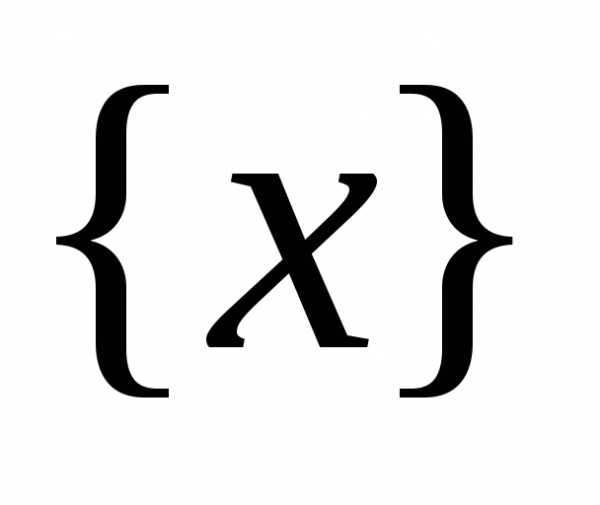 ,
но такая, что в любой
,
но такая, что в любой -окрестности
точкиa имеются точки множества
-окрестности
точкиa имеются точки множества 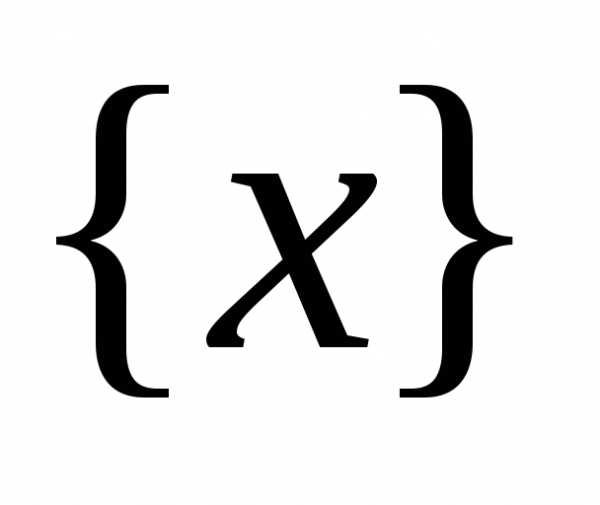 ,
отличные отa.
Например:
,
точкаa не принадлежит
,
отличные отa.
Например:
,
точкаa не принадлежит 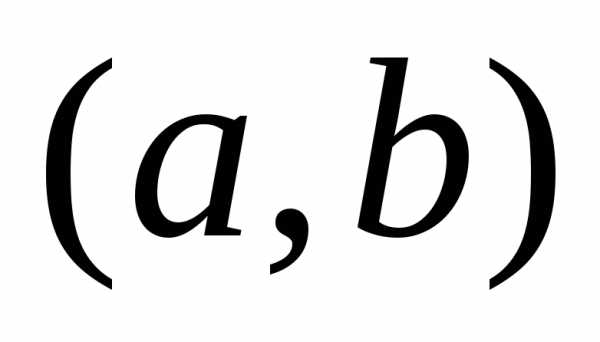 ,
но любая
,
но любая -окрестностьсодержит точки, принадлежащие
-окрестностьсодержит точки, принадлежащие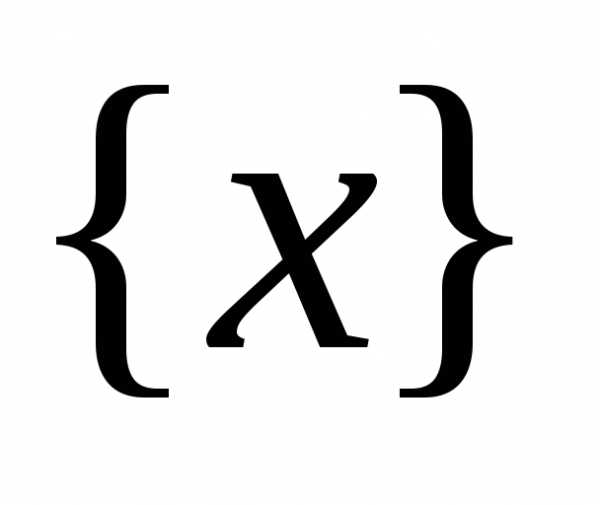 и отличные отa.
и отличные отa.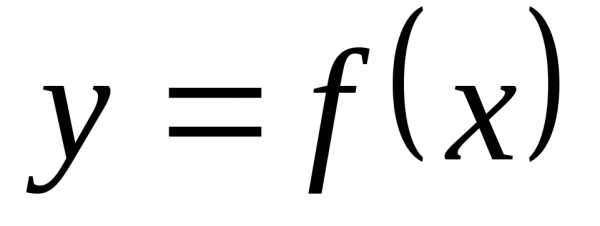 в точке a (или при
),
если для любой последовательности
значений аргумента,
сходящейся кa и состоящей из чисел
в точке a (или при
),
если для любой последовательности
значений аргумента,
сходящейся кa и состоящей из чисел  ,
отличных отa,
соответствующая последовательность
значений функции
сходится к числуb.
,
отличных отa,
соответствующая последовательность
значений функции
сходится к числуb. в точке a,
если для любого сколь угодно малого
положительного числа
в точке a,
если для любого сколь угодно малого
положительного числа  найдётся отвечающее ему положительное
число
найдётся отвечающее ему положительное
число такое, что для всех значений аргументаx,
удовлетворяющих условию
,
справедливо неравенство.
такое, что для всех значений аргументаx,
удовлетворяющих условию
,
справедливо неравенство. или
или 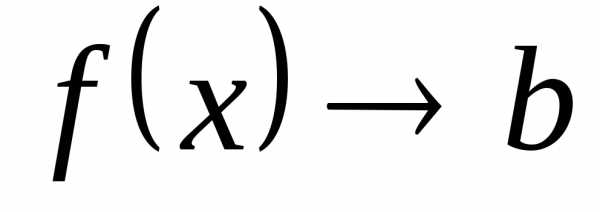 при.
при.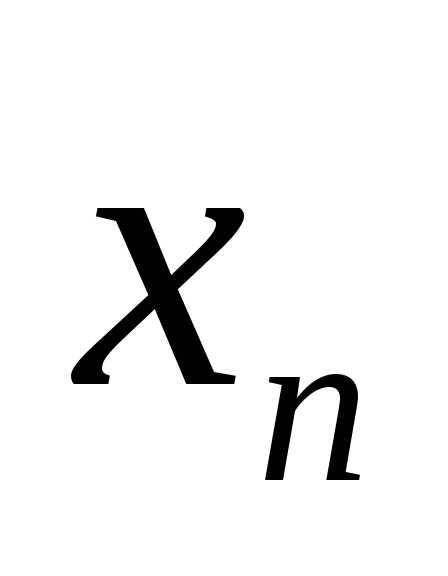 должны быть отличны отa:
функция
должны быть отличны отa:
функция  может быть не определена в точке a.
Определение 12.1 явно содержит это
требование, в определении 12.2 неравенство
может быть не определена в точке a.
Определение 12.1 явно содержит это
требование, в определении 12.2 неравенство 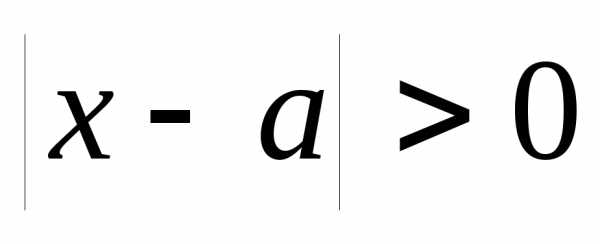 означает
означает  . ☼
. ☼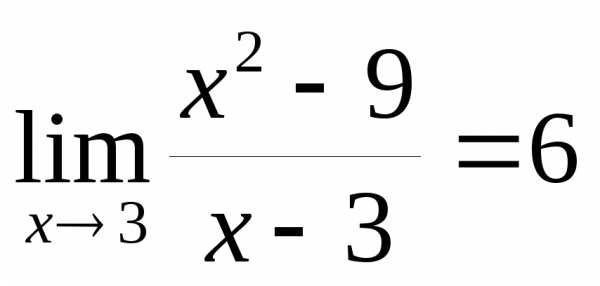 .
. может иметь в точке a только один предел, так как имеется
единственный предел последовательности
может иметь в точке a только один предел, так как имеется
единственный предел последовательности 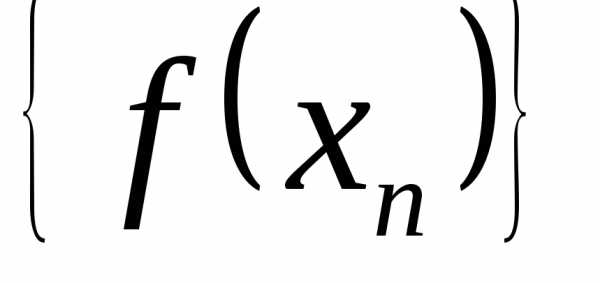 в определении 12.1, а определение 12.2
эквивалентно определению 12.1.☼
в определении 12.1, а определение 12.2
эквивалентно определению 12.1.☼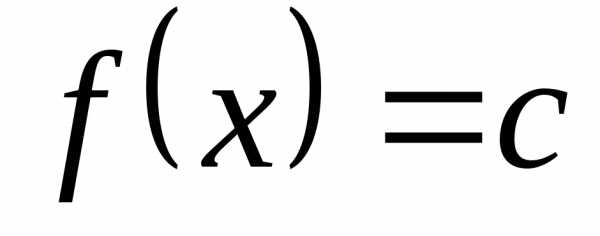 .
.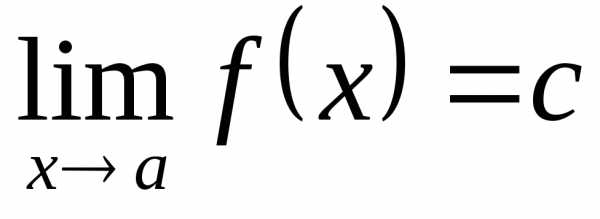 ,
так как любая последовательность ,
сходящаяся к числу a,
порождает последовательность
.
,
так как любая последовательность ,
сходящаяся к числу a,
порождает последовательность
.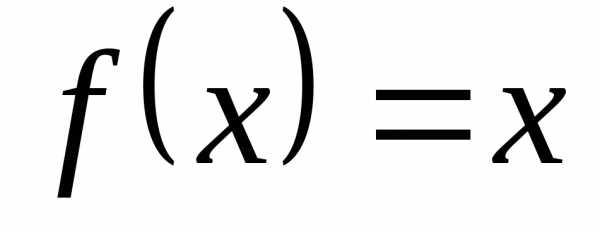 .
.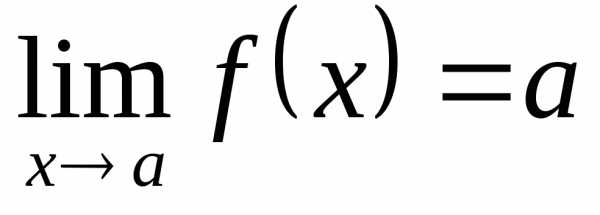 ,
так как последовательности и совпадают.
,
так как последовательности и совпадают. – функция Дирихле, – не имеет предела:
для рациональных чисел при,
для иррациональных при
– функция Дирихле, – не имеет предела:
для рациональных чисел при,
для иррациональных при .
Это противоречит определению 12.1.
.
Это противоречит определению 12.1. в точке
в точке 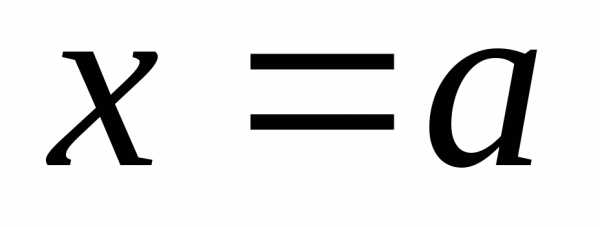 ,
если для любой последовательности
значений аргумента ,
сходящейся к a,
элементы
,
если для любой последовательности
значений аргумента ,
сходящейся к a,
элементы  которой больше (меньше)a,
соответствующая последовательность значений функции сходится к b.
которой больше (меньше)a,
соответствующая последовательность значений функции сходится к b. равны, то в точкеa существует предельное значение этой
функции, равное указанным односторонним
предельным значениям.
равны, то в точкеa существует предельное значение этой
функции, равное указанным односторонним
предельным значениям. :
: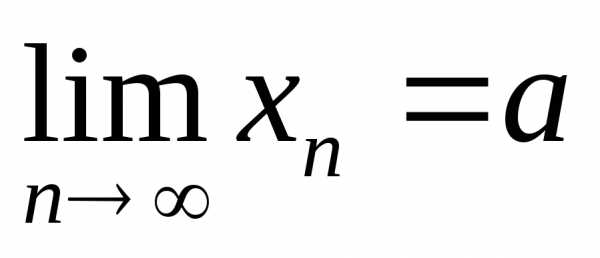 (
(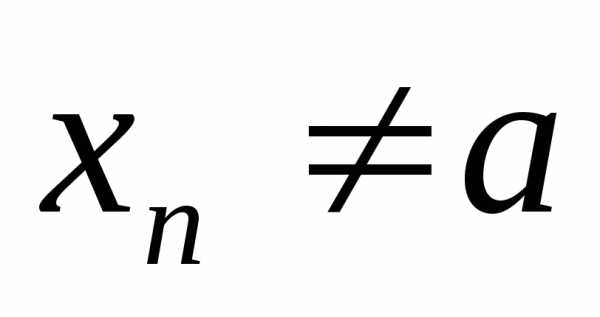 для любогоn). Пусть
подпоследовательность
для любогоn). Пусть
подпоследовательность 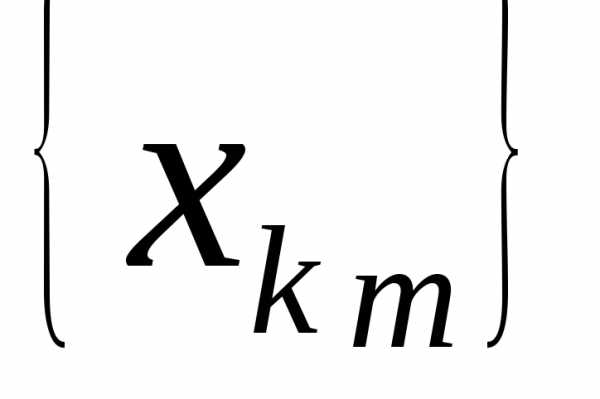 состоит из всех
состоит из всех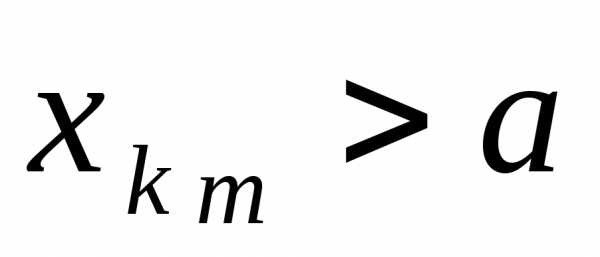 ,
а подпоследовательность
,
а подпоследовательность  из всех
из всех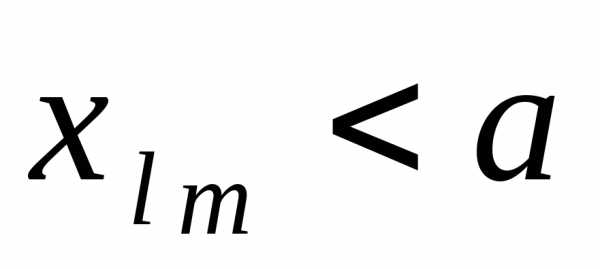 . По условию:
:
. По условию:
: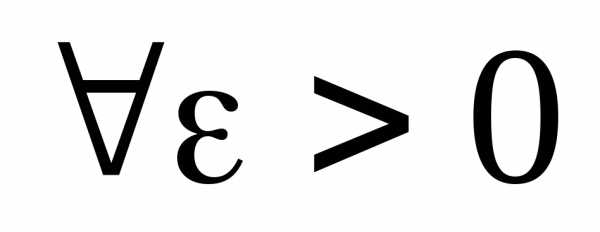 ; ,
; ,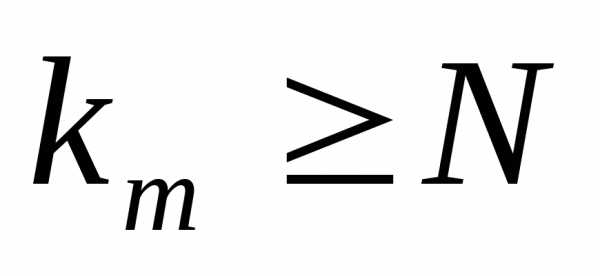 ;,
;,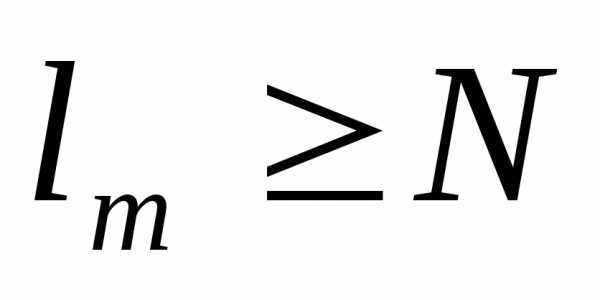 . Так как
и
. Так как
и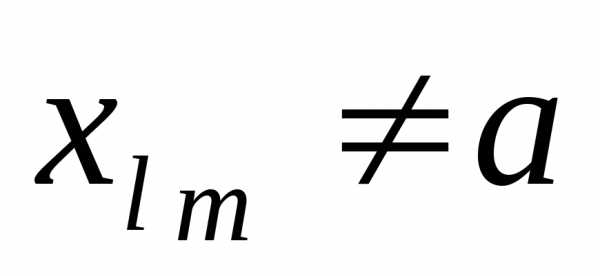 ,
то есть неравенствами охвачены все
элементы
,
то есть неравенствами охвачены все
элементы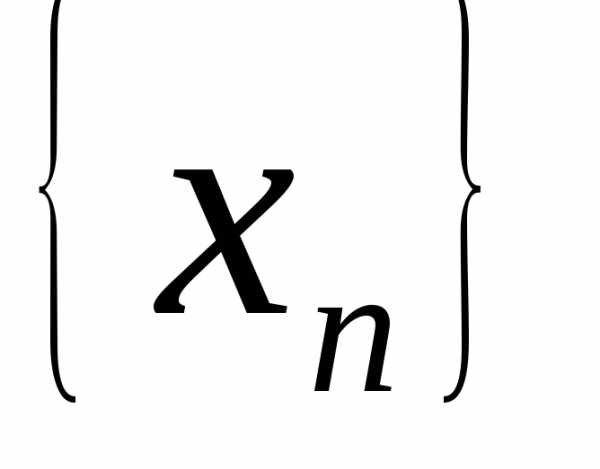 ,
то при всех
,
то при всех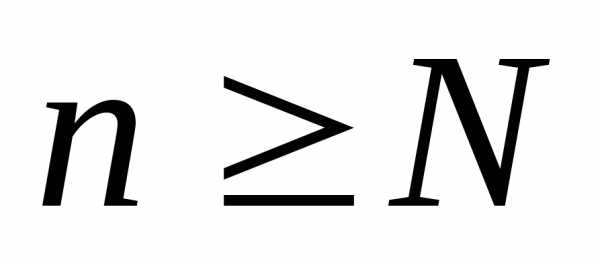 выполняется неравенство .
■
выполняется неравенство .
■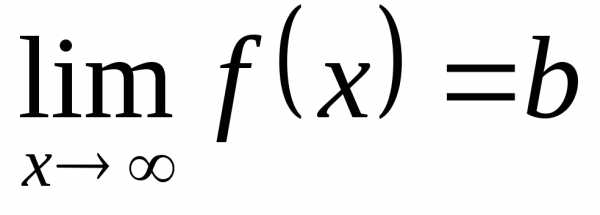 .
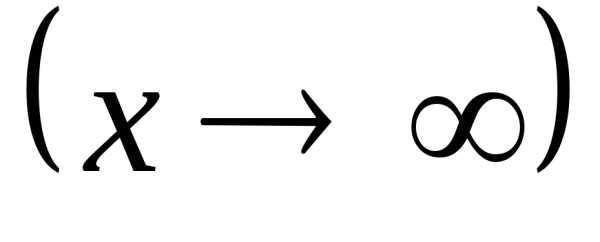
.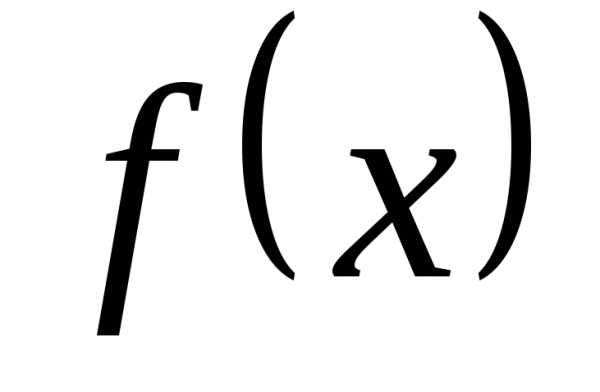 при
стремлении аргумента x к положительной (отрицательной)
бесконечности,
если для любой бесконечно большой
последовательности значений аргумента,
элементы которой, начиная с некоторого
номера, положительны (отрицательны),
соответствующая последовательность
сходится к b.
при
стремлении аргумента x к положительной (отрицательной)
бесконечности,
если для любой бесконечно большой
последовательности значений аргумента,
элементы которой, начиная с некоторого
номера, положительны (отрицательны),
соответствующая последовательность
сходится к b.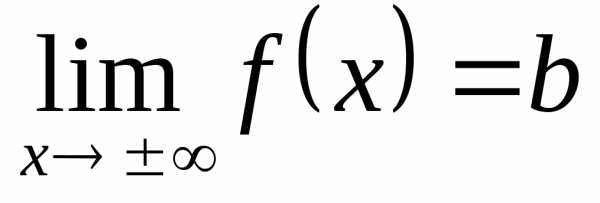 .
. имела в точкеa конечный предел, необходимо и достаточно,
чтобы в точке a функция
имела в точкеa конечный предел, необходимо и достаточно,
чтобы в точке a функция  удовлетворяла условию Коши: для любого
сколь угодно малого
удовлетворяла условию Коши: для любого
сколь угодно малого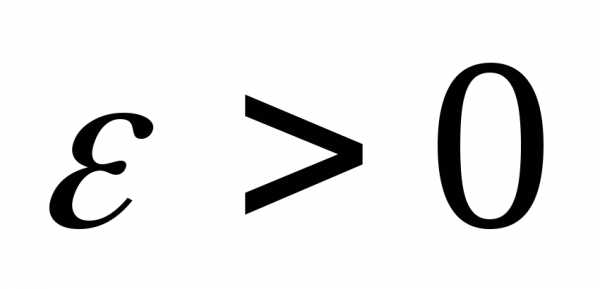 найдется
найдется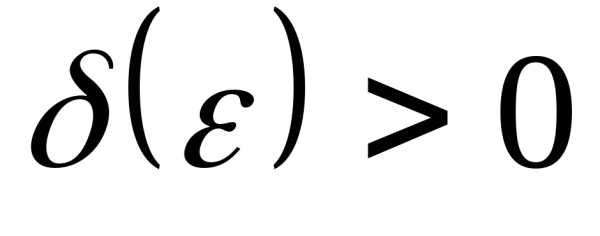 такое, что для любых двух значений
аргумента
такое, что для любых двух значений
аргумента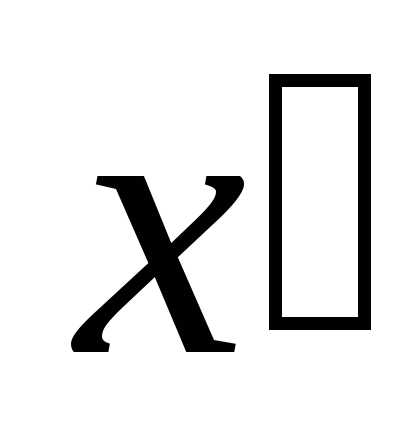 и
и ,
удовлетворяющих условиям;,
справедливо неравенство.
,
удовлетворяющих условиям;,
справедливо неравенство.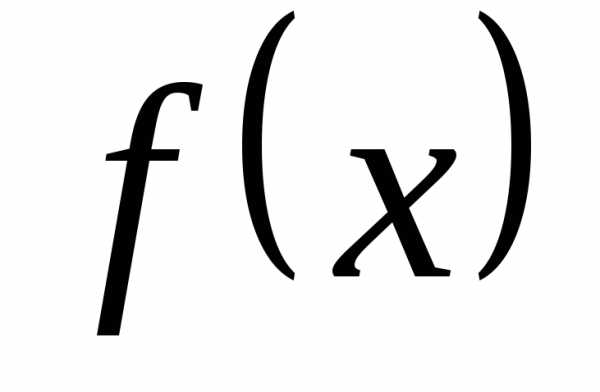 и
и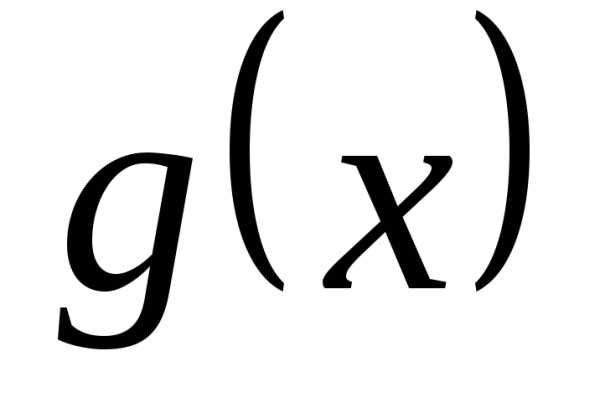 заданы на одном и том же множестве
заданы на одном и том же множестве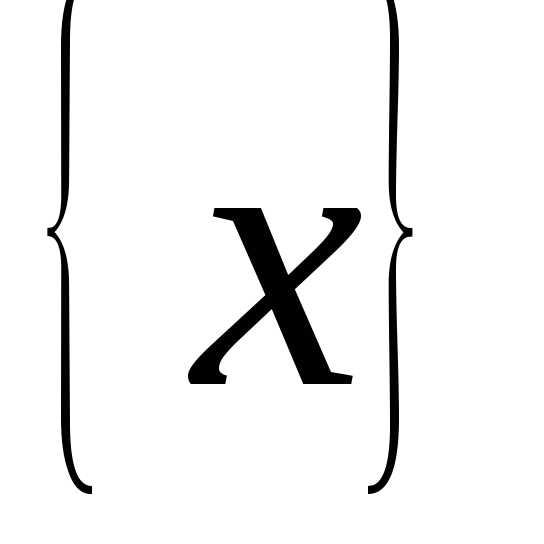 и имеют в точкеa пределы, равные b и c.
Тогда
и имеют в точкеa пределы, равные b и c.
Тогда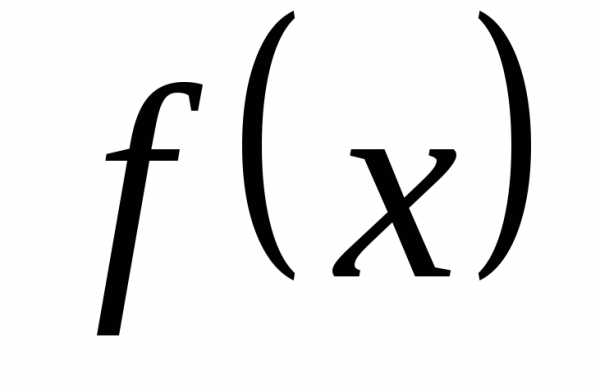 и
и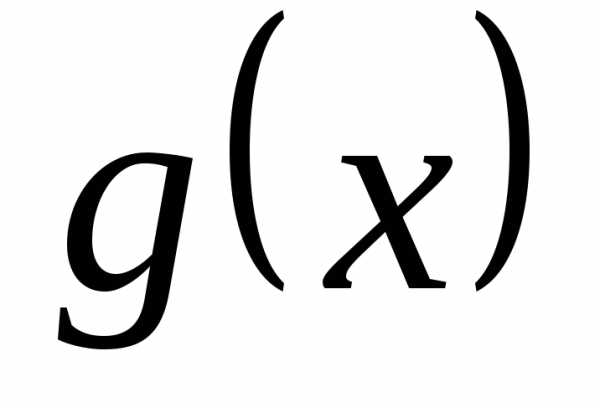 .
Соответствующие последовательности
.
Соответствующие последовательности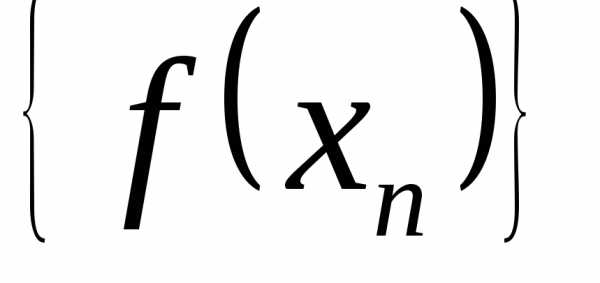 и
и значений этих функций имеют пределыb и c.
Но тогда, в силу теорем 9.3-9.5, последовательности
,и
значений этих функций имеют пределыb и c.
Но тогда, в силу теорем 9.3-9.5, последовательности
,и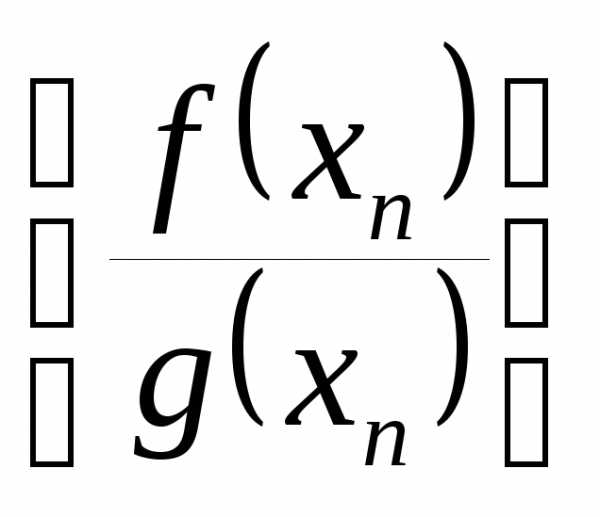 при
при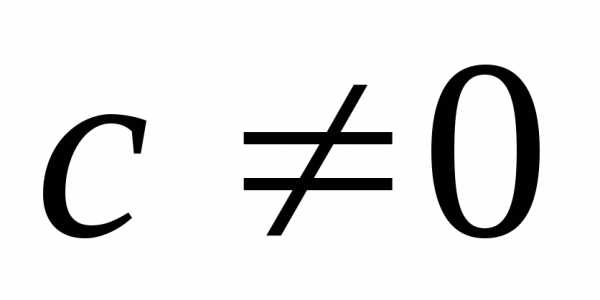 имеют пределы, соответственно равные
имеют пределы, соответственно равные ,
, и.
Согласно определению 12.1 предела функции,
это означает, что , , . ■
и.
Согласно определению 12.1 предела функции,
это означает, что , , . ■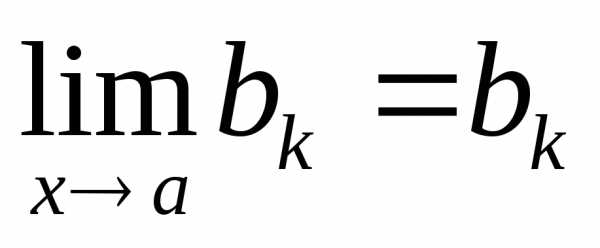 ,
,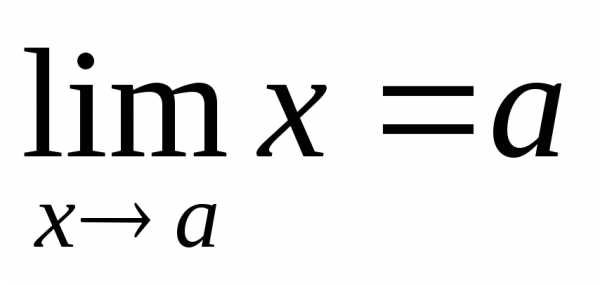 ,
то
,
то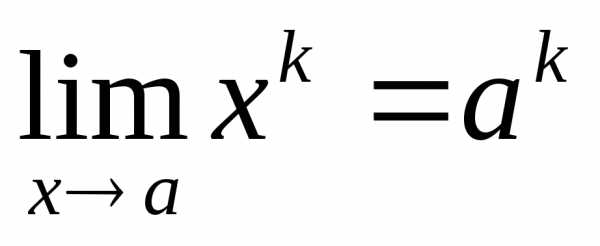 и. ■
и. ■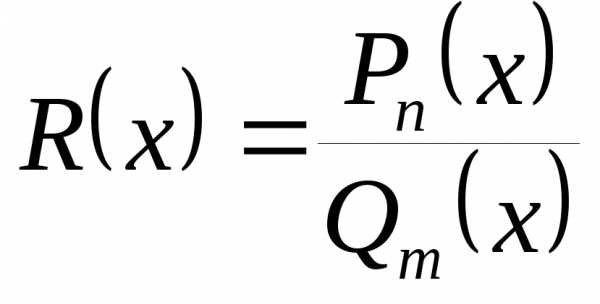 )
имеет предел в любой точке,
не являющейся корнем её знаменателя,
причём
)
имеет предел в любой точке,
не являющейся корнем её знаменателя,
причём называетсябесконечно
малой в точке
называетсябесконечно
малой в точке  (при),
если
(при),
если .
. ,
– бесконечно малая функция в любой
точке,
в силу утверждения 12.3:
,
– бесконечно малая функция в любой
точке,
в силу утверждения 12.3: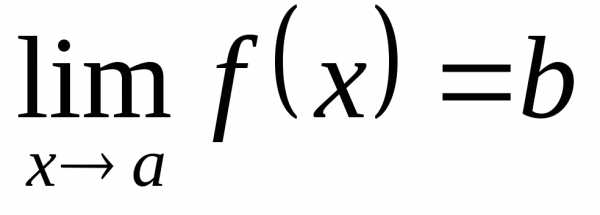 ,
то
– бесконечно малая в точкеa.
Отсюда следует специальное представление
функции
,
где
,
то
– бесконечно малая в точкеa.
Отсюда следует специальное представление
функции
,
где .
Говорят, что функция
.
Говорят, что функция асимптотически равнаb при
.☼
асимптотически равнаb при
.☼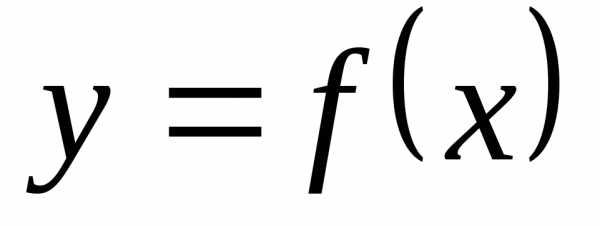 называетсябесконечно
большой в точке
называетсябесконечно
большой в точке  справа
(слева),
если для любой последовательности
справа
(слева),
если для любой последовательности  :
: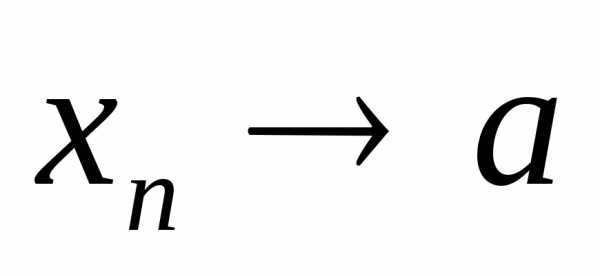 при,
при,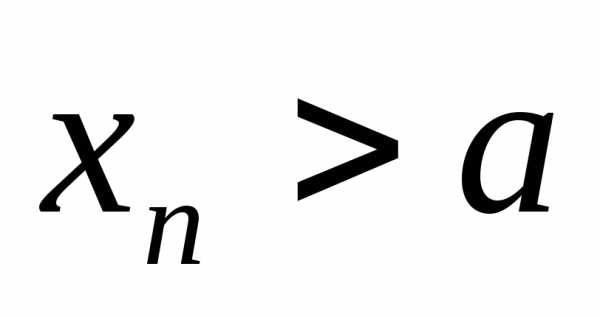 (
(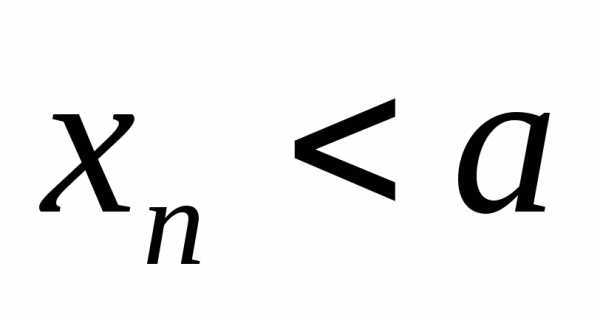 ),
соответствующая последовательность
),
соответствующая последовательность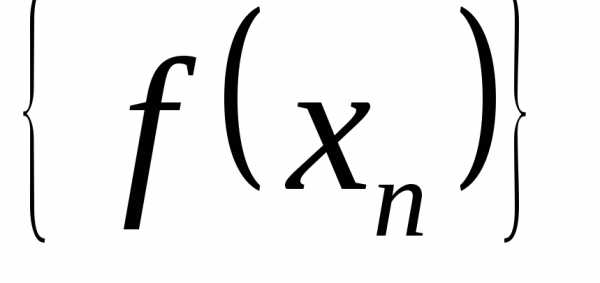 значений функции является бесконечно
большой последовательностью определённого
знака.
значений функции является бесконечно
большой последовательностью определённого
знака.
 является бесконечно большой при
является бесконечно большой при ,
, .
. вблизи точки
вблизи точки .
Так как она определена лишь при
.
Так как она определена лишь при ,
то вблизи
,
то вблизи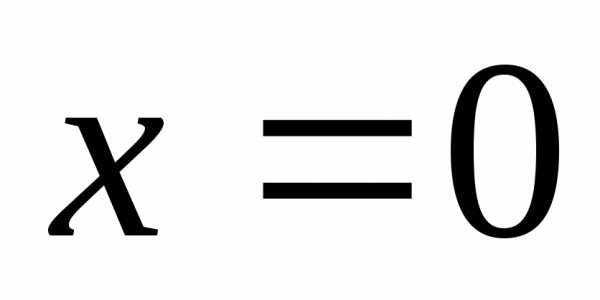 её можно исследовать только при:
её можно исследовать только при: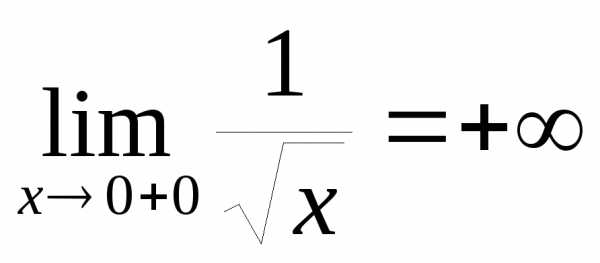 .
То есть функция
.
То есть функция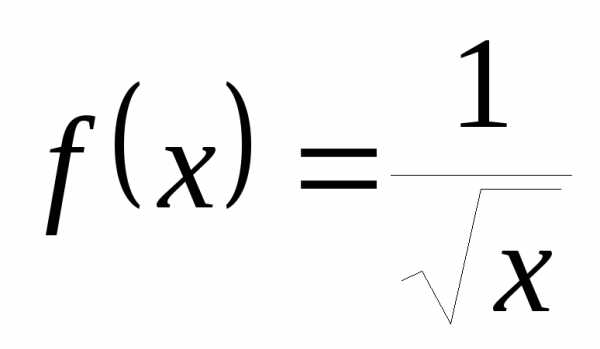 – положительная бесконечно большая
при.
– положительная бесконечно большая
при.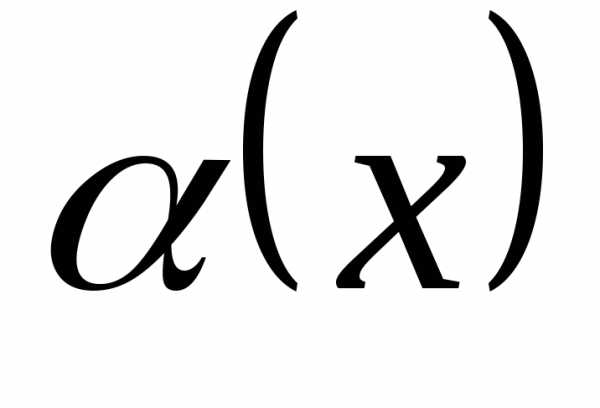 и
и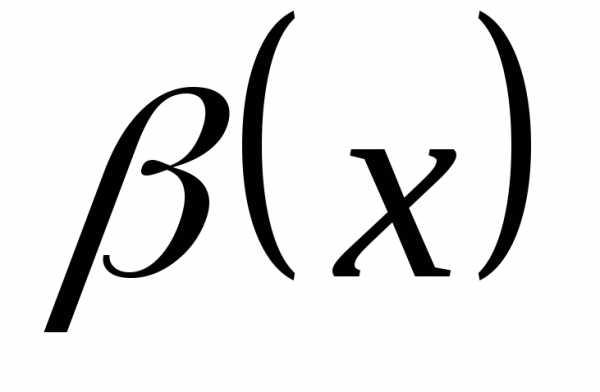 – две бесконечно малые в точке
– две бесконечно малые в точке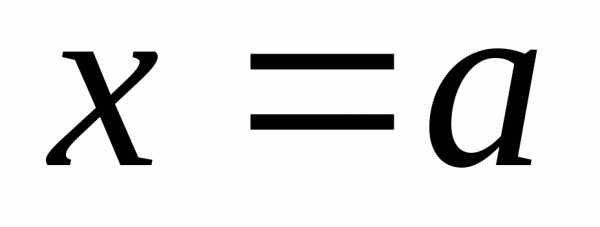 функции и пусть существует
функции и пусть существует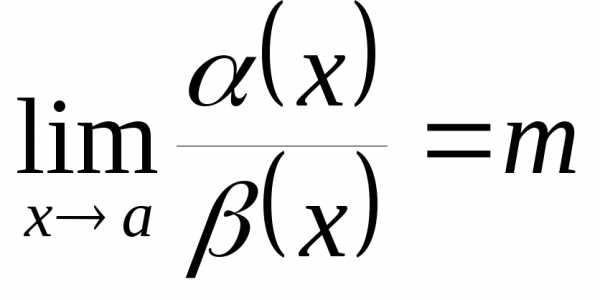 .
Если
.
Если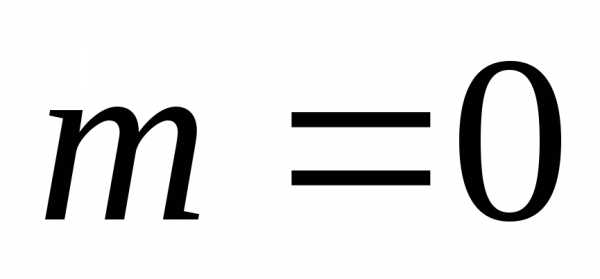 ,
то
,
то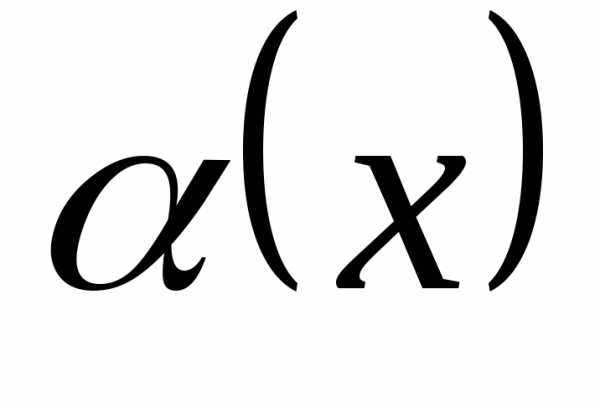 –бесконечно
малая более высокого порядка,
чем
–бесконечно
малая более высокого порядка,
чем 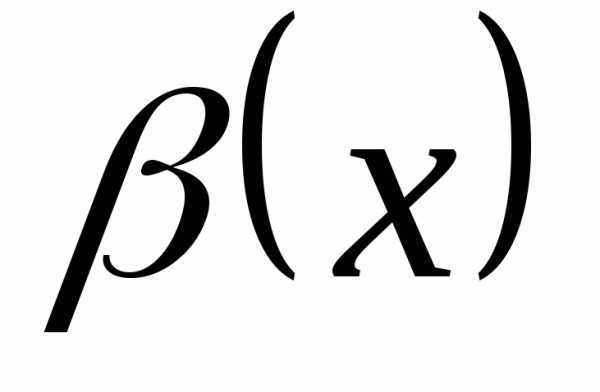 . Если
. Если 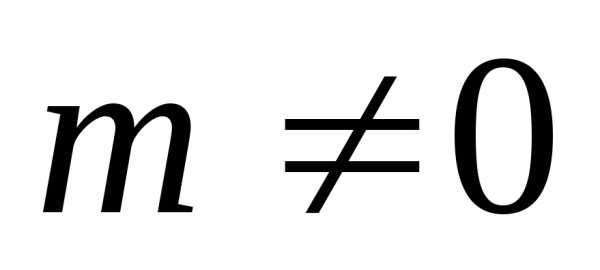 ,
то
,
то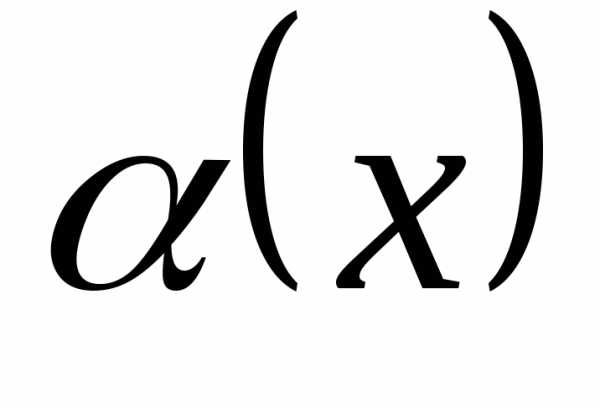 и
и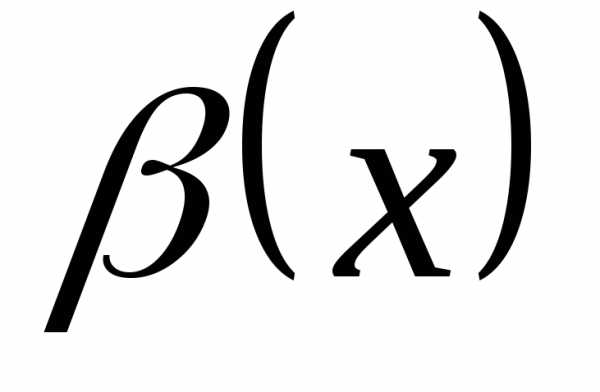 –бесконечно
малые одного порядка. Если
–бесконечно
малые одного порядка. Если  ,
то
,
то и
и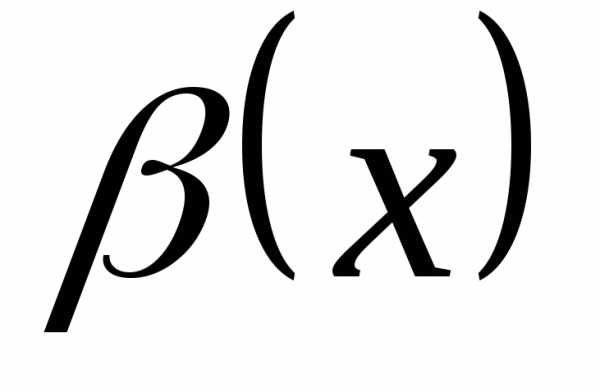 –эквивалентные
бесконечно малые.
–эквивалентные
бесконечно малые.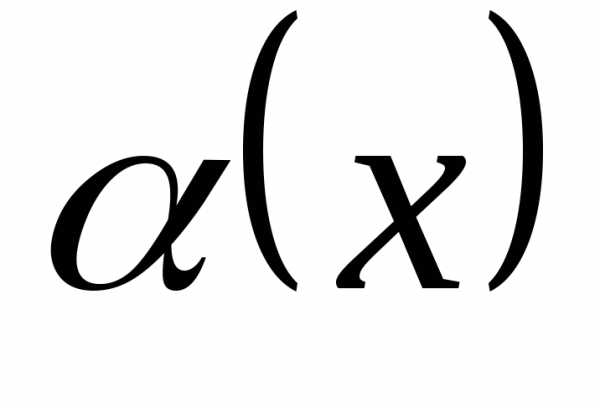 имеет порядок малостиm,
если
имеет порядок малостиm,
если 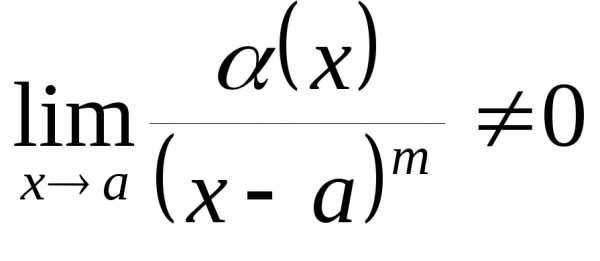 .
. (
( равноo малое от
равноo малое от  ),
если
),
если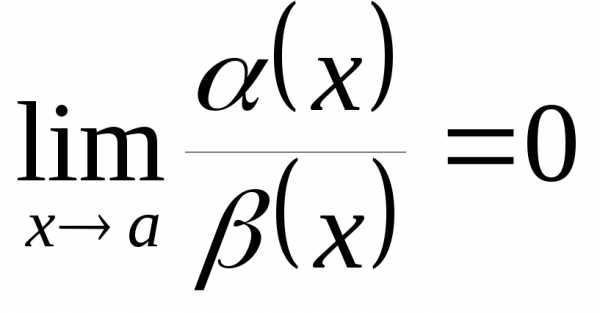 .
. – бесконечно малые одного порядка при
– бесконечно малые одного порядка при  ,
так как
,
так как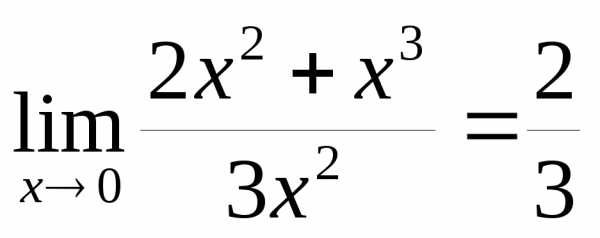 .
. – эквивалентные бесконечно малые при
– эквивалентные бесконечно малые при  ,
так как
,
так как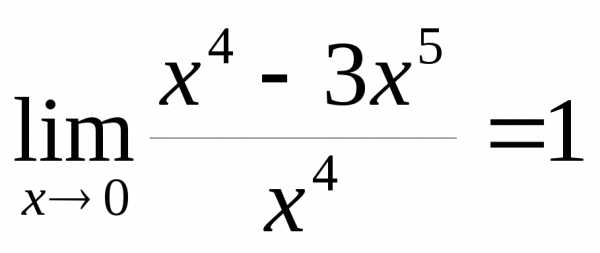 .
.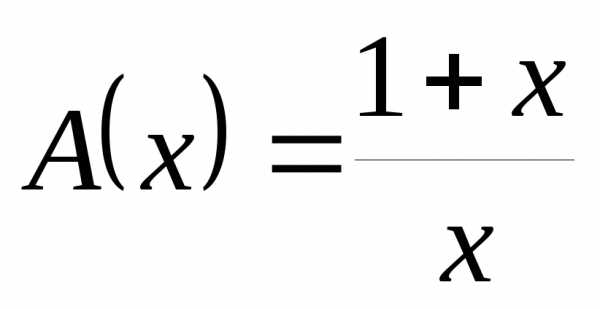 и
и 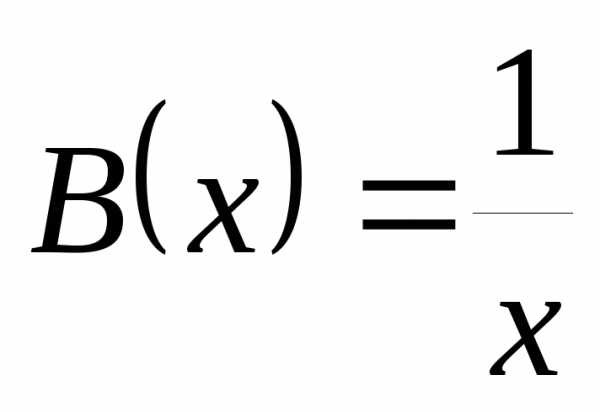 имеют одинаковый порядок роста при
имеют одинаковый порядок роста при  справа и слева, так как
справа и слева, так как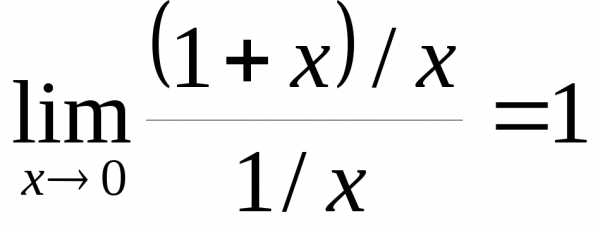 .
.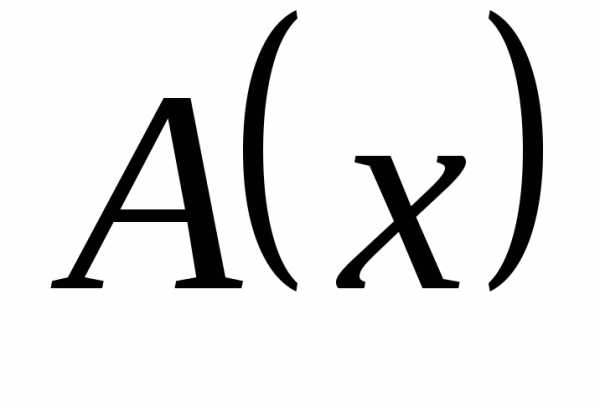 и
и 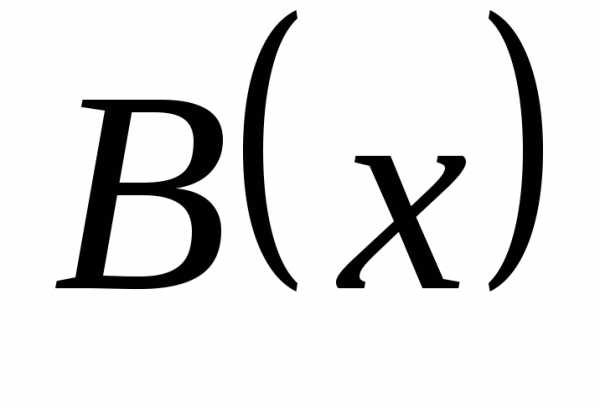 – бесконечно большие в точке
– бесконечно большие в точке  справа функции одного знака: , .
Если
справа функции одного знака: , .
Если  ,
то
,
то 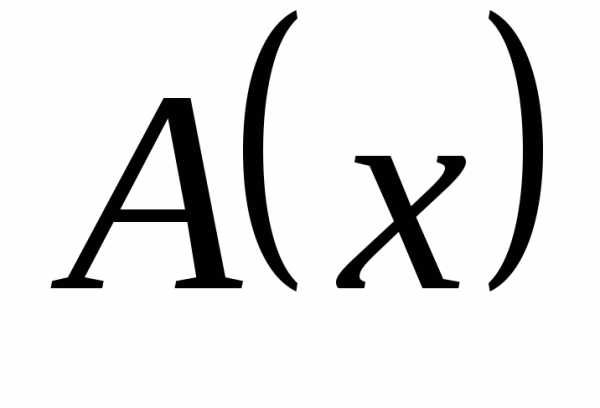 имеет
более высокий порядок роста в точке a справа, чем
имеет
более высокий порядок роста в точке a справа, чем 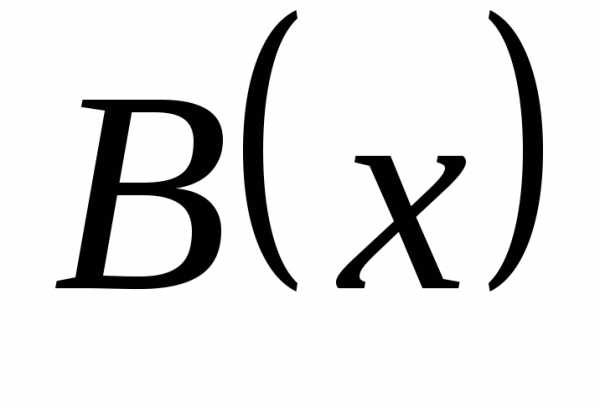 .
Если
.
Если 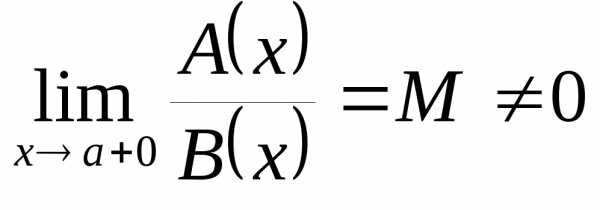 ,
то
,
то 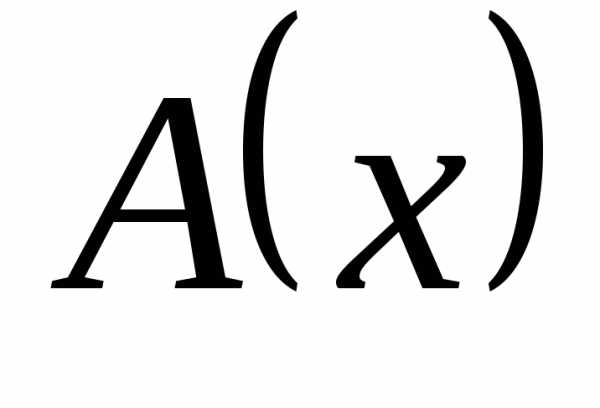 и
и 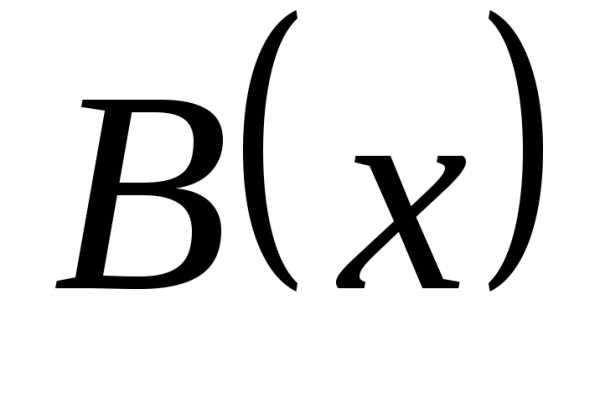 имеют в точке a справа одинаковый порядок роста. Если
имеют в точке a справа одинаковый порядок роста. Если 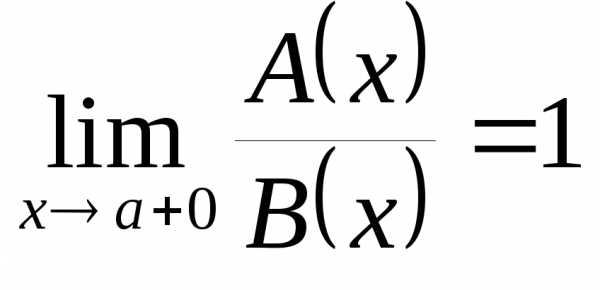 ,
то
,
то  и
и 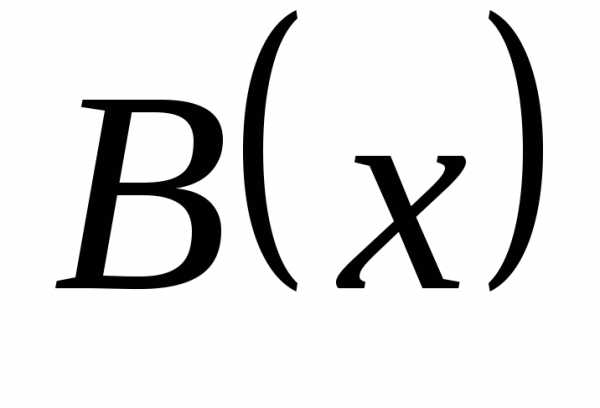 – эквивалентные
бесконечно большие функции.
– эквивалентные
бесконечно большие функции. ,
то
,
то 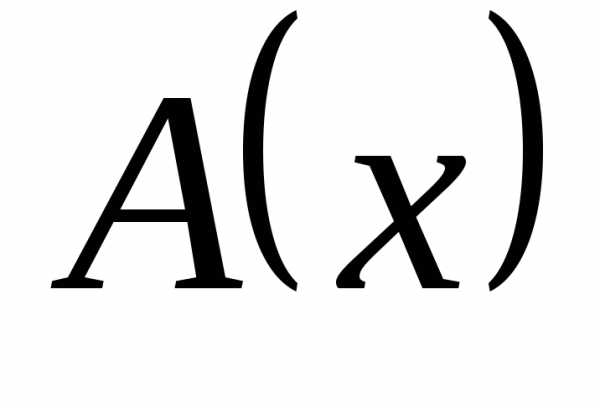 – бесконечно большая более низкого
порядка, чем
– бесконечно большая более низкого
порядка, чем 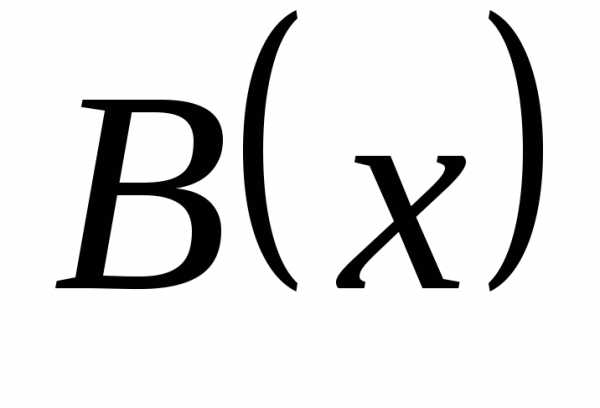 .
А
.
А 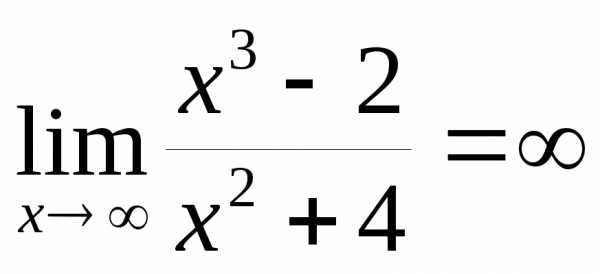 ,
поэтому
,
поэтому  – бесконечно большая более высокого
порядка, чем
– бесконечно большая более высокого
порядка, чем  .
.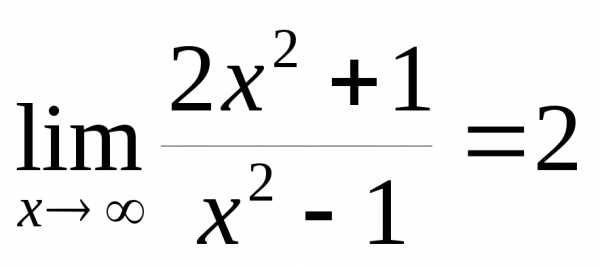 – таким образом,
– таким образом,  и
и 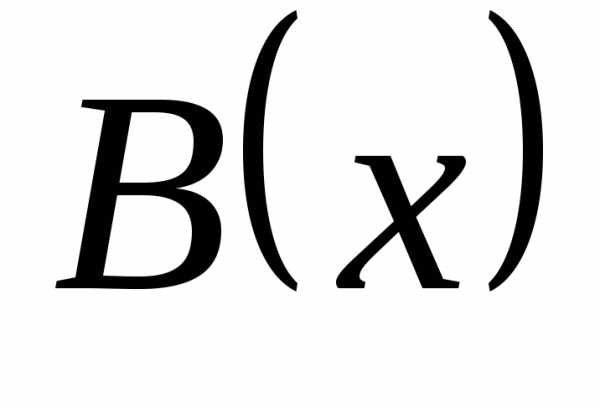 – бесконечно большие одного порядка
(один порядок роста).
– бесконечно большие одного порядка
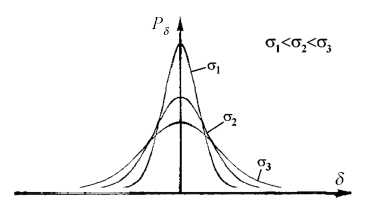
(один порядок роста).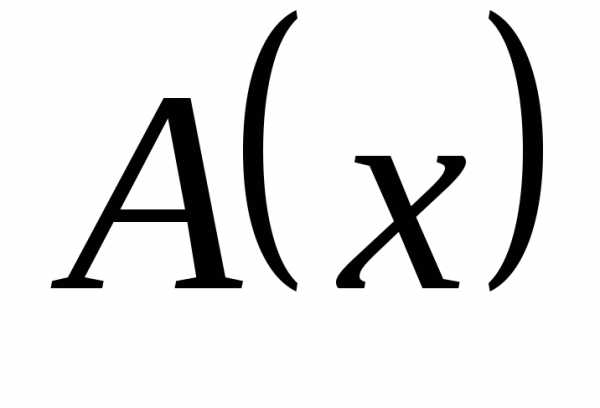 – бесконечно большая второго порядка
по отношению к
– бесконечно большая второго порядка
по отношению к 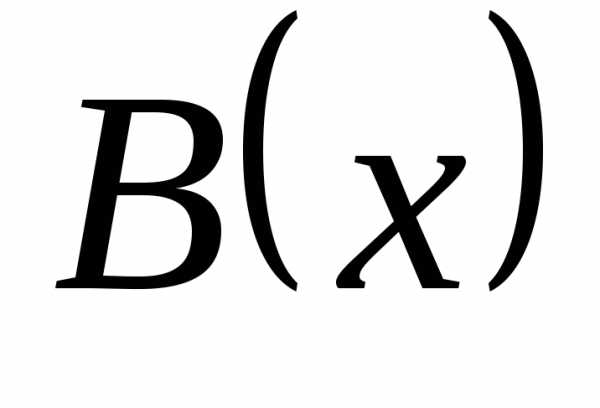 .
. .
. ,
, – многочлены степенейm и k соответственно, то
– многочлены степенейm и k соответственно, то 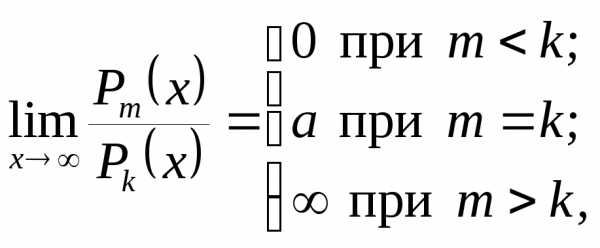 гдеа – отношение коэффициентов при старших
степенях многочленов.
гдеа – отношение коэффициентов при старших
степенях многочленов. 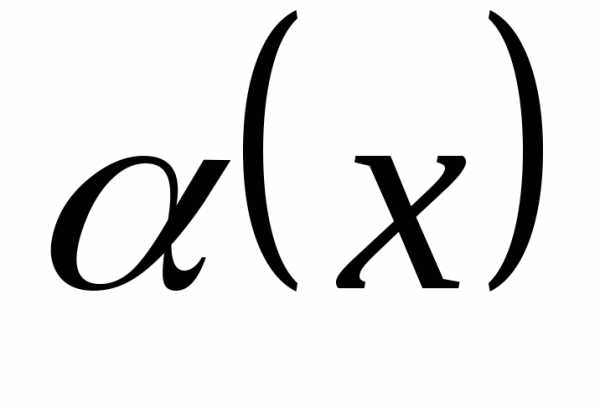 – бесконечно малая при
– бесконечно малая при
 ,
то функция
,
то функция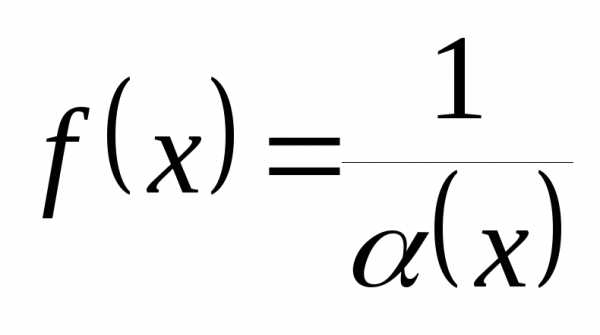 является бесконечно большой при
является бесконечно большой при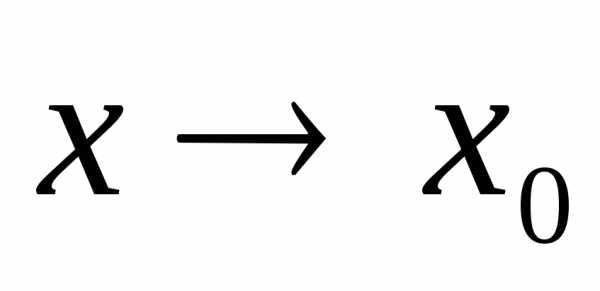
 .
. – бесконечно большая при
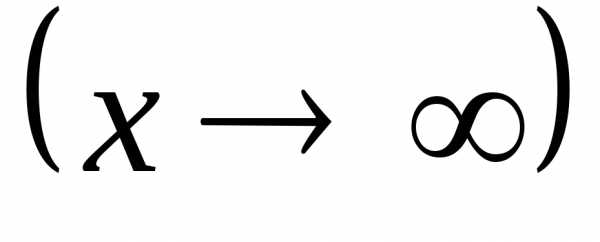
– бесконечно большая при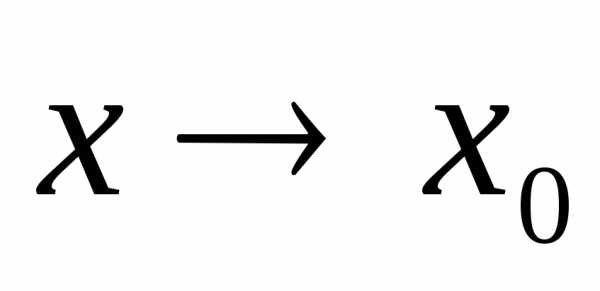
 ,
то функция
,
то функция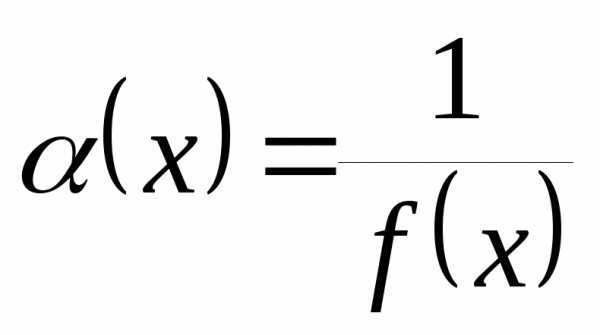 является бесконечно малой при
является бесконечно малой при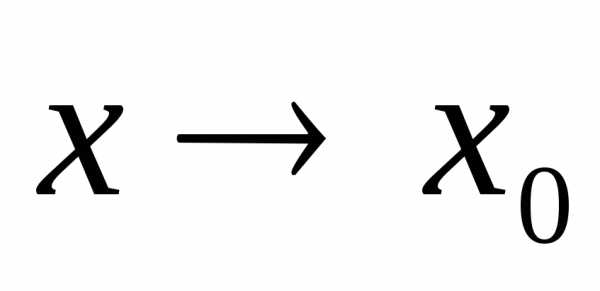
 .
.
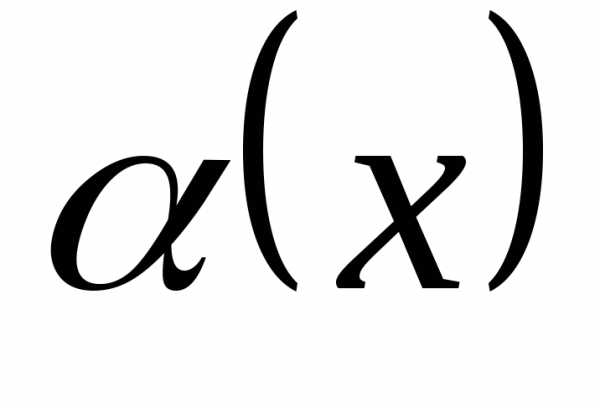 – бесконечно малая, то есть
.
Таким образом,
– бесконечно малая, то есть
.
Таким образом, 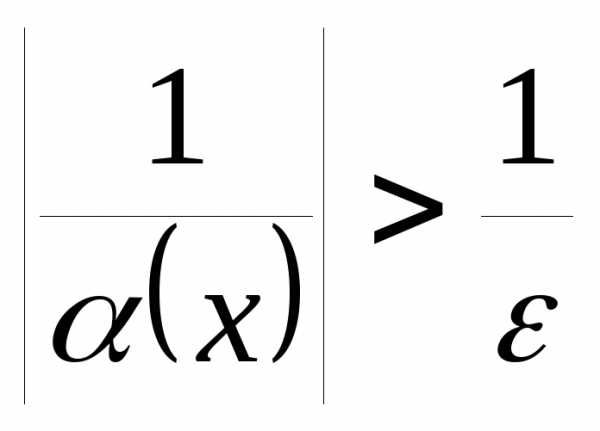 ,
отсюда
,
отсюда 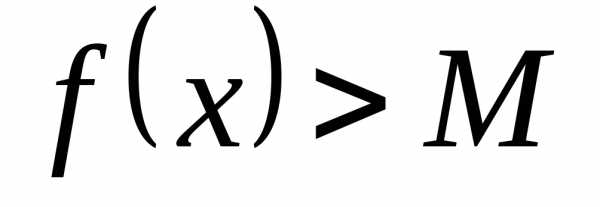 ,
где
,
где 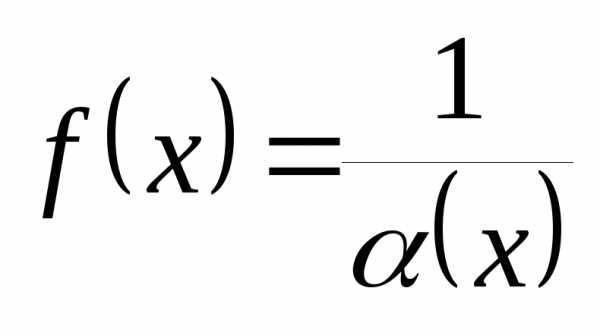 ,
,  .
Получаем, что функция
.
Получаем, что функция  – бесконечно большая.
– бесконечно большая. – бесконечно большая величина. При
– бесконечно большая величина. При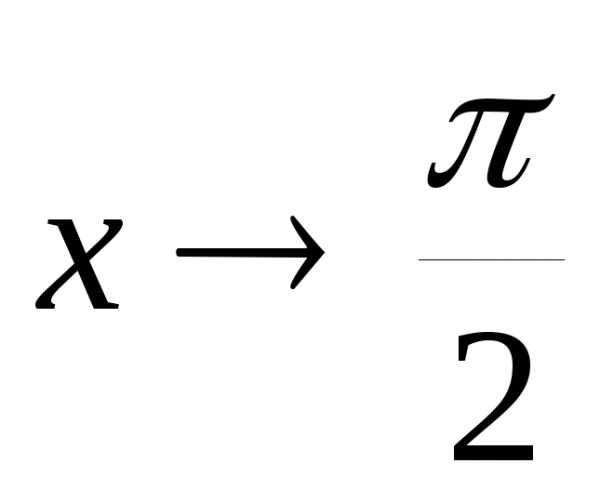 функция
функция – бесконечно большая, а– бесконечно малая.
– бесконечно большая, а– бесконечно малая.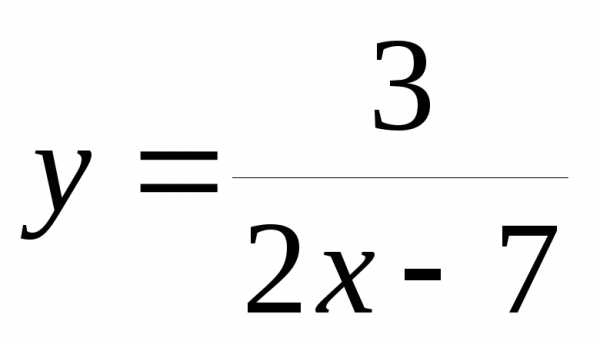 при– бесконечно малая, а
при– бесконечно малая, а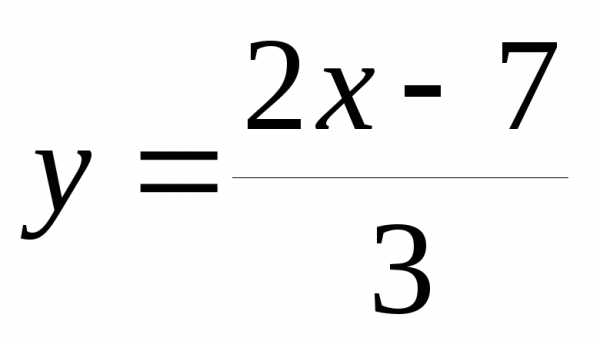 – бесконечно большая.
– бесконечно большая.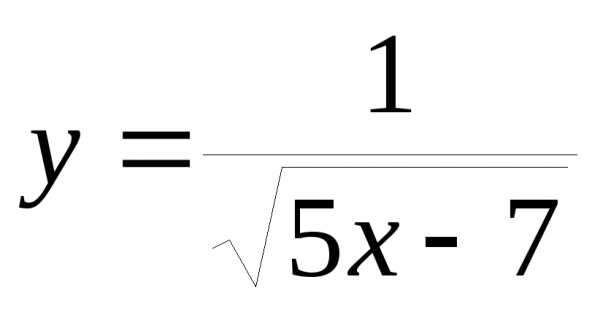 – бесконечно малая.
– бесконечно малая.

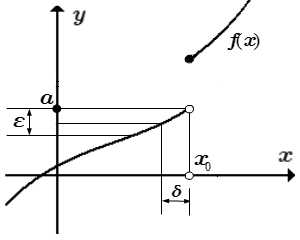

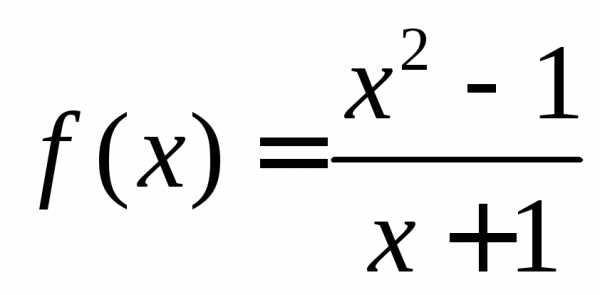 не определена при значении
не определена при значении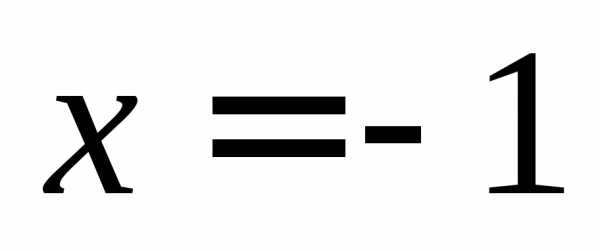 ,
так как при нем знаменатель обращается
в нуль. Таким образом, при
,
так как при нем знаменатель обращается
в нуль. Таким образом, при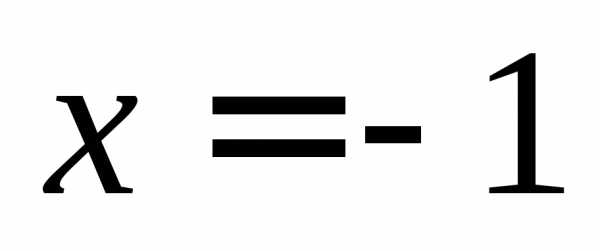 функция имеет разрыв (рисунок 2.1).
функция имеет разрыв (рисунок 2.1).

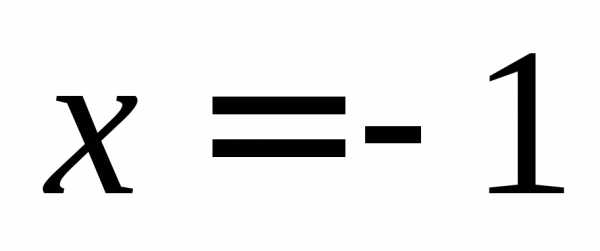 равным,
то получим функцию непрерывную на всей
числовой оси. Математически это
записывается как
равным,
то получим функцию непрерывную на всей
числовой оси. Математически это
записывается как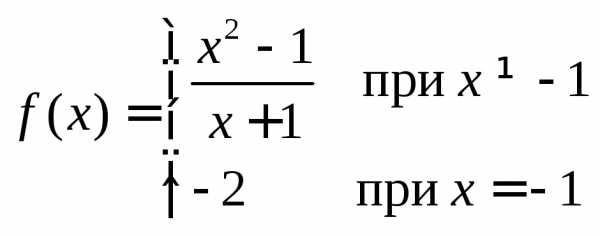
 —
точка разрыва функции
—
точка разрыва функции ,
но возможно найти для нее в точке
,
но возможно найти для нее в точке такое значение А, при котором измененная
функция
такое значение А, при котором измененная
функция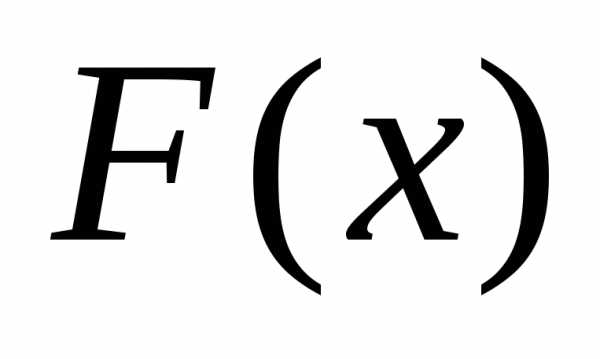 станет
непрерывной, то это число А называетсяпределом
функции
станет
непрерывной, то это число А называетсяпределом
функции 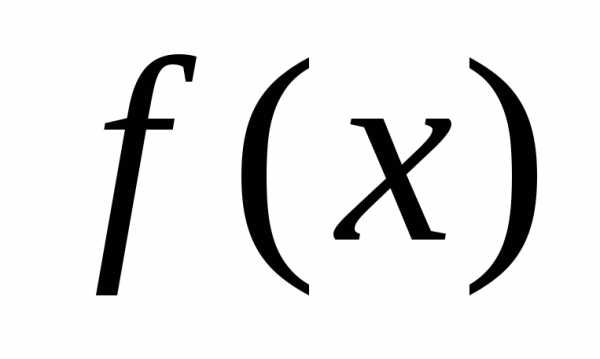 в точке
в точке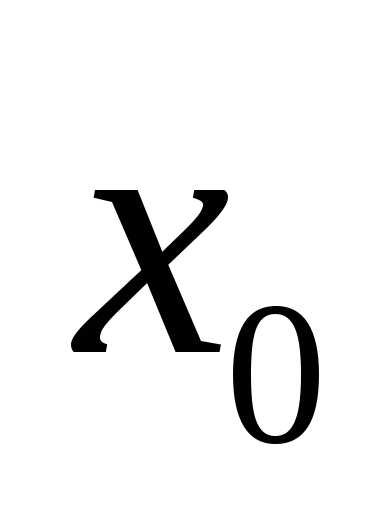 ,
а точка
,
а точка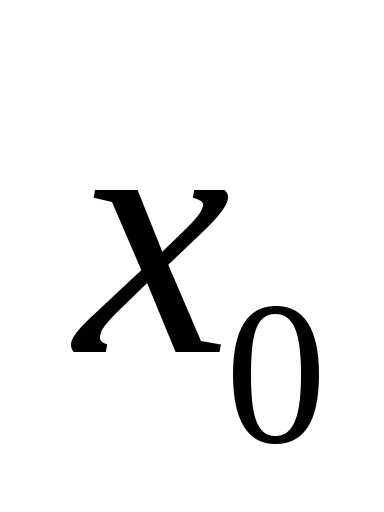 — точкой устранимого разрыва.
— точкой устранимого разрыва.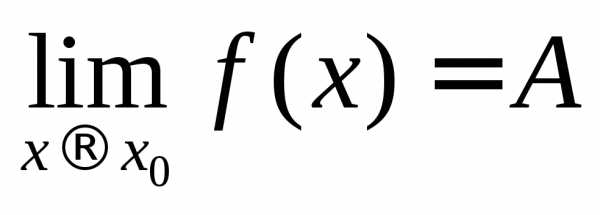
 в точке
в точке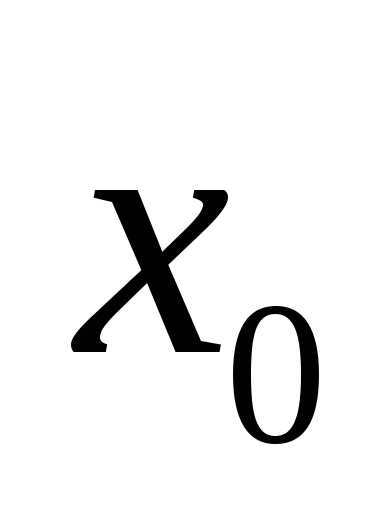 означает, что функция
означает, что функция приближенно равна
приближенно равна для всех значений
для всех значений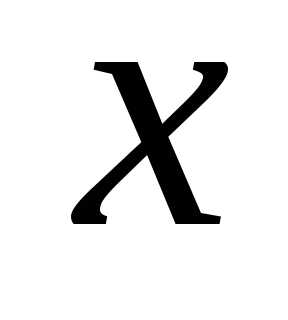 ,
близких к
,
близких к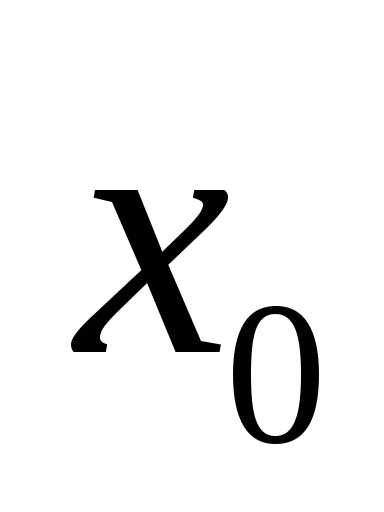 .
. ,
если, задав произвольное как угодно
малое положительное число,
можно найти такое
>0 (зависящее от ),
что для всех x,
лежащих в
— окрестности числа
,
если, задав произвольное как угодно
малое положительное число,
можно найти такое
>0 (зависящее от ),
что для всех x,
лежащих в
— окрестности числа 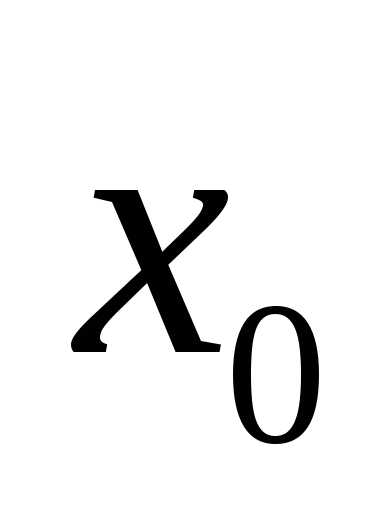 ,
т.е. дляx,
удовлетворяющих неравенству
,
значения функцииf(x) будут лежать в
— окрестности числа А, т.е.
.
,
т.е. дляx,
удовлетворяющих неравенству
,
значения функцииf(x) будут лежать в
— окрестности числа А, т.е.
.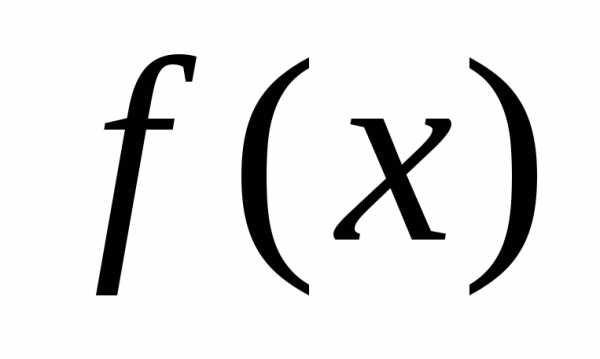 при
при .
Для построения этого рисунка необходимо
выполнить следующие действия:
.
Для построения этого рисунка необходимо
выполнить следующие действия: и отметить точки
и отметить точки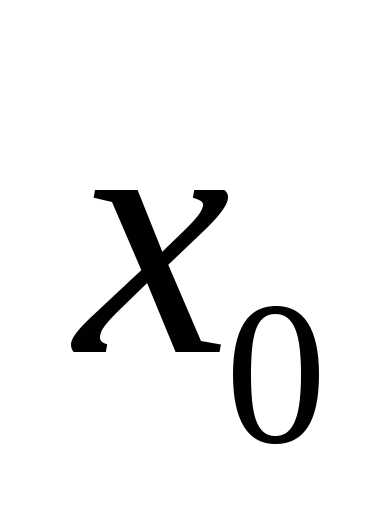 иА;
иА;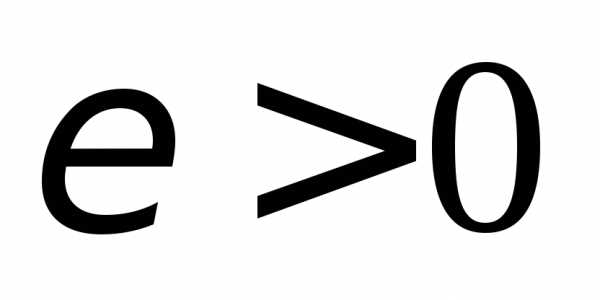 ;
;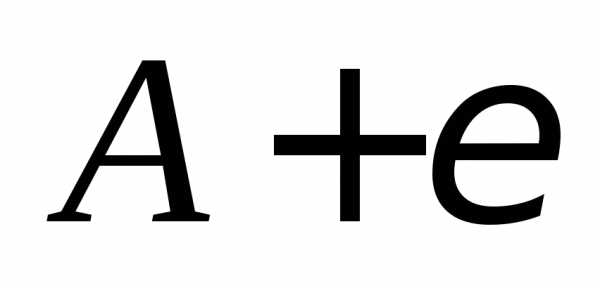 ,
,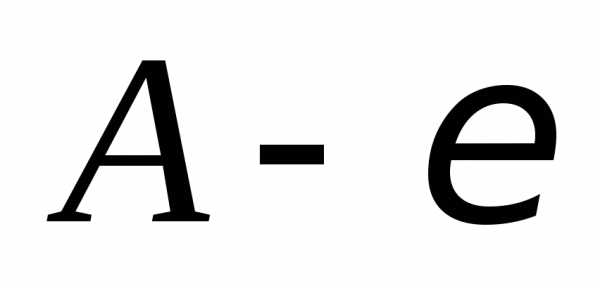 и графику функции построить
и графику функции построить окрестность
точки
окрестность
точки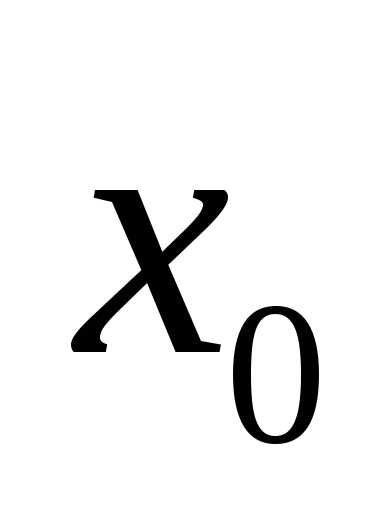 .
Расстояния от точки
.
Расстояния от точки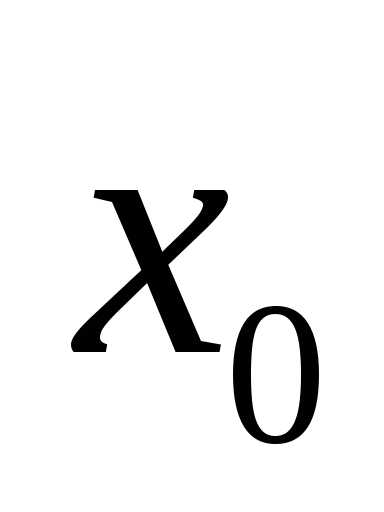 до точек
до точек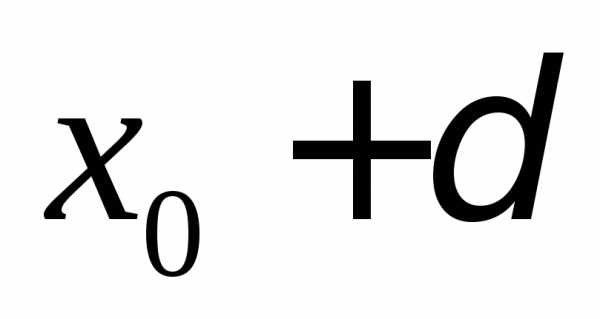 и
и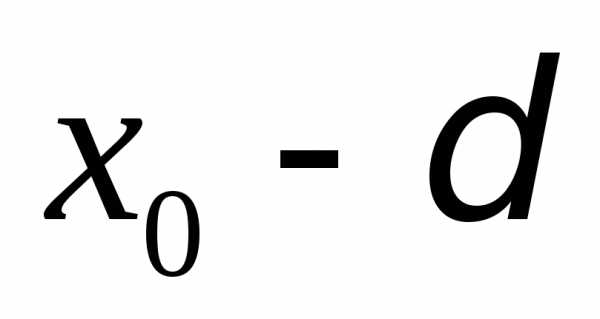 должны быть равными, поэтому из двух
полученных отрезков следует взять
меньший и отложить его в обе стороны
от точки
должны быть равными, поэтому из двух
полученных отрезков следует взять
меньший и отложить его в обе стороны
от точки ;
;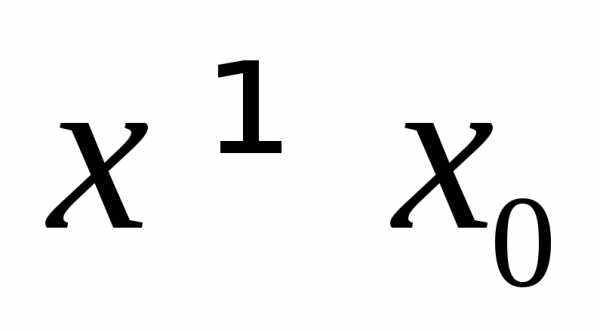 ,
принадлежащую окрестности точки
,
принадлежащую окрестности точки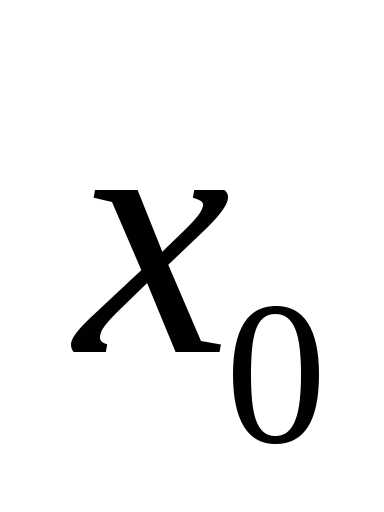 ,
и по графику функции найти значение
,
и по графику функции найти значение ,
которое должно попасть в построенную
окрестность точкиА.
,
которое должно попасть в построенную
окрестность точкиА.
 и при этом
и при этом  ,
то пишут .
Если, в частности,
,
то пишут .
Если, в частности,  ,
то вместо символа 0+0 пишут +0.
,
то вместо символа 0+0 пишут +0. и при этом
и при этом 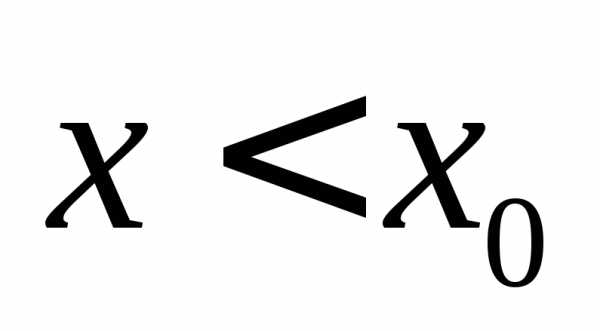 ,
то пишут .
,
то пишут . и
и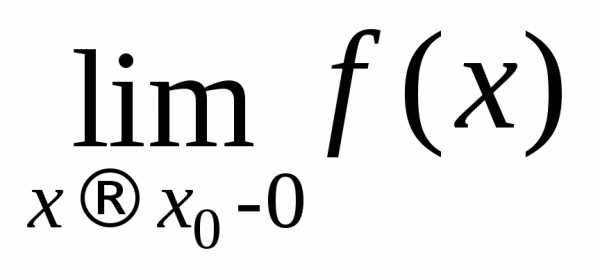 называются соответственнопределом
справа и пределом слева функции f(x) в точке
называются соответственнопределом
справа и пределом слева функции f(x) в точке  .
. необходимо и достаточно, чтобы
необходимо и достаточно, чтобы 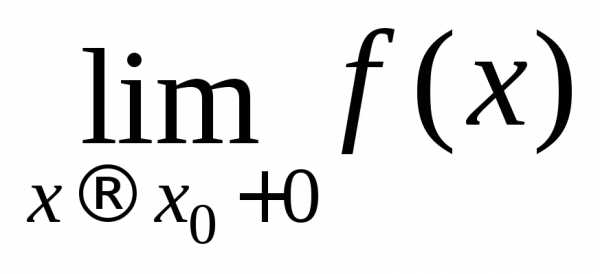 =
=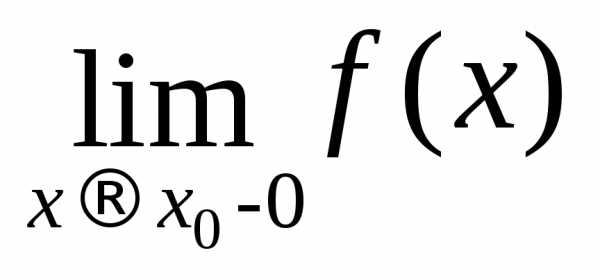 .
.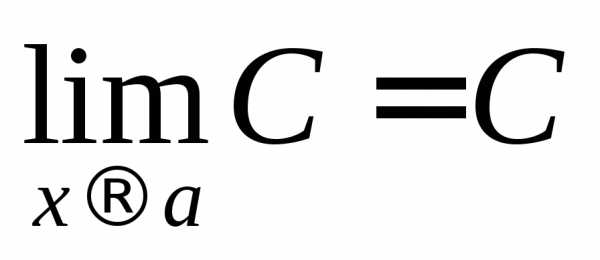 .
.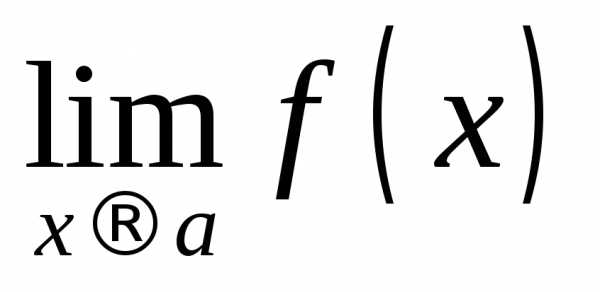 следует начинать с подстановки значения
следует начинать с подстановки значения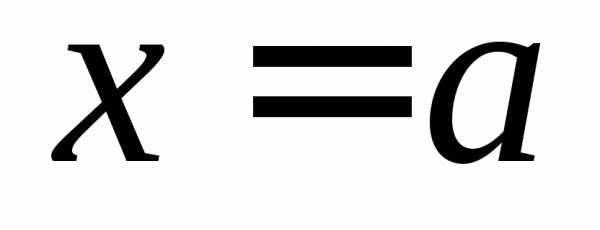 в выражение для функции. При этом если
получается числовое значение 0 или,
то искомый предел найден.
в выражение для функции. При этом если
получается числовое значение 0 или,
то искомый предел найден. .
.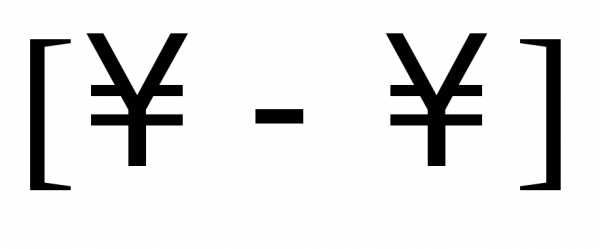 ,
, ,
, ,
, ,
, ,
,
 называютсянеопределённостями.
называютсянеопределённостями. ,
то для нахождения предела нужно
преобразовать функцию так, чтобы раскрыть
эту неопределенность.
,
то для нахождения предела нужно
преобразовать функцию так, чтобы раскрыть
эту неопределенность. обычно получается, когда задан предел
отношения двух многочленов. В этом
случае, для вычисления предела
рекомендуется разложить многочлены на
множители и сократить на общий множитель.
Этот множитель равен нулю при предельном
значениих.
обычно получается, когда задан предел
отношения двух многочленов. В этом
случае, для вычисления предела
рекомендуется разложить многочлены на
множители и сократить на общий множитель.
Этот множитель равен нулю при предельном
значениих.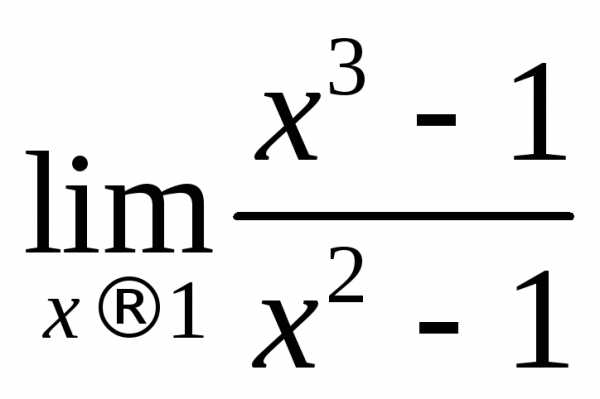 .
.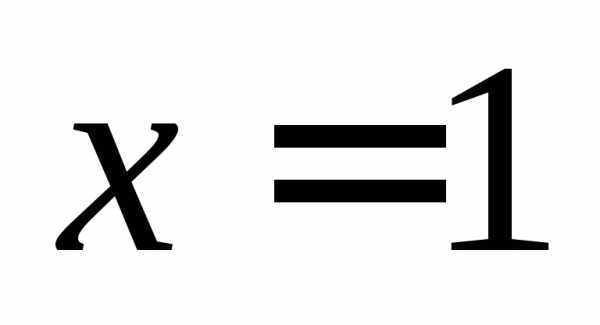 ,
получим неопределенность:
,
получим неопределенность: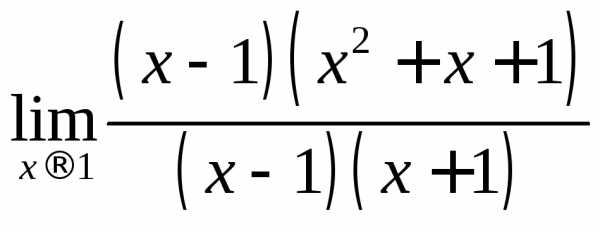 ;
;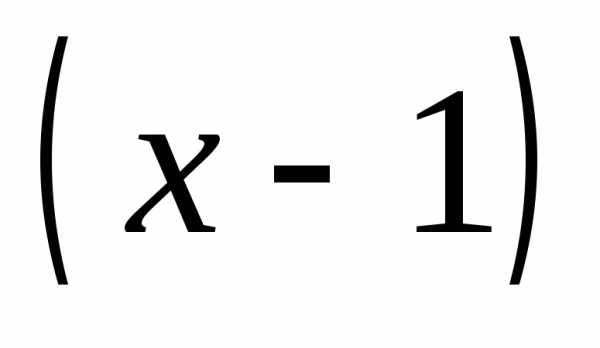 и получим
и получим получается, когда задан предел отношения
двух многочленов при.
В этом случае для вычисления рекомендуется
разделить оба многочлена нахв старшей степени.
получается, когда задан предел отношения
двух многочленов при.
В этом случае для вычисления рекомендуется
разделить оба многочлена нахв старшей степени.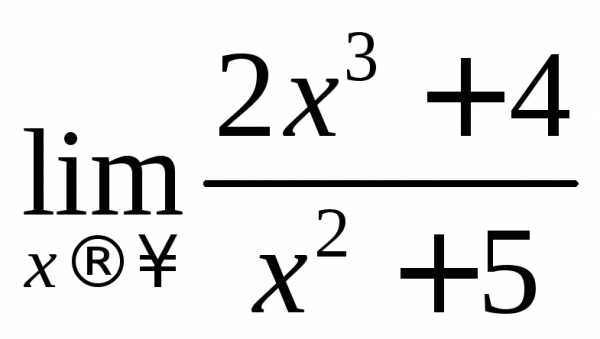 .
. ,
поэтому разделим все члены выражения
наx3.
,
поэтому разделим все члены выражения
наx3. .
. .
.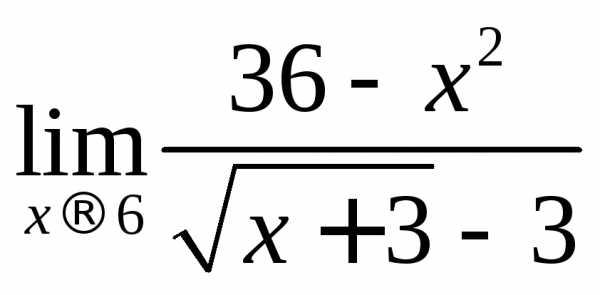
 или (1)∞часто используются первый
и второй замечательные пределы:
или (1)∞часто используются первый
и второй замечательные пределы: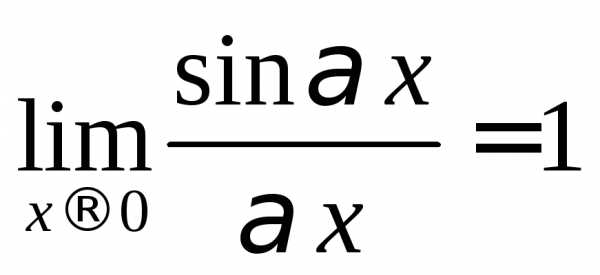
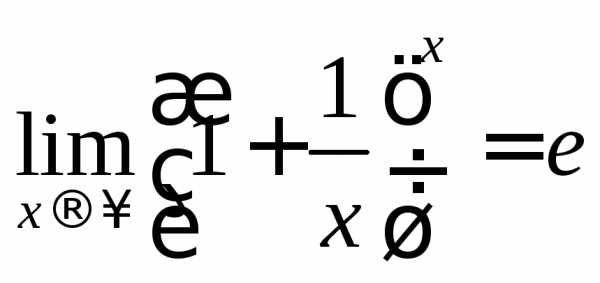 и
и 
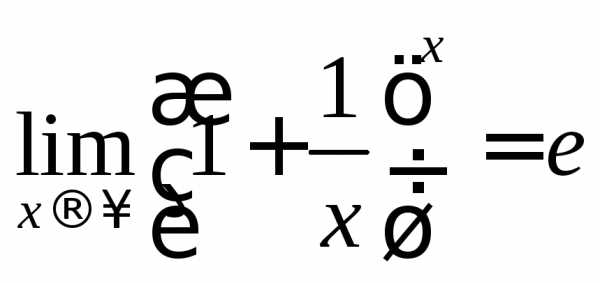
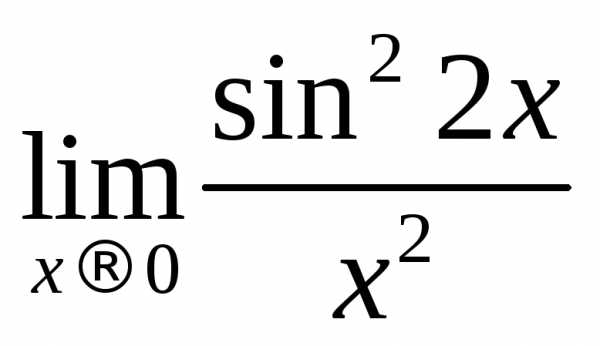
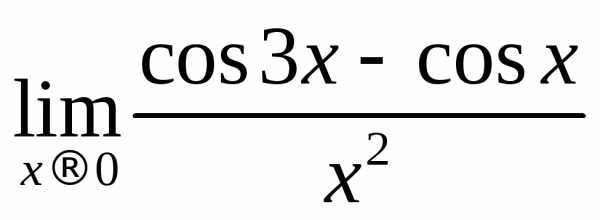 .
.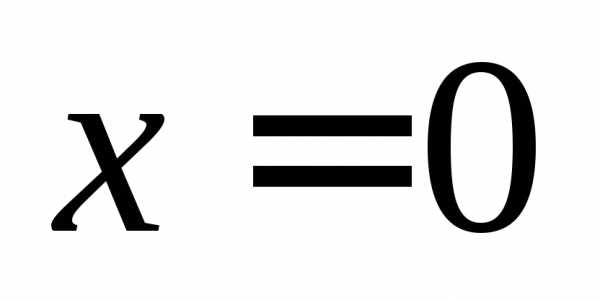 получим неопределенность:
получим неопределенность: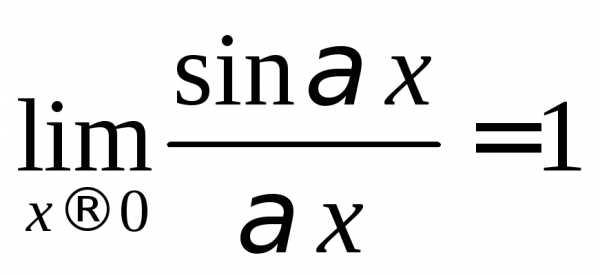 .
.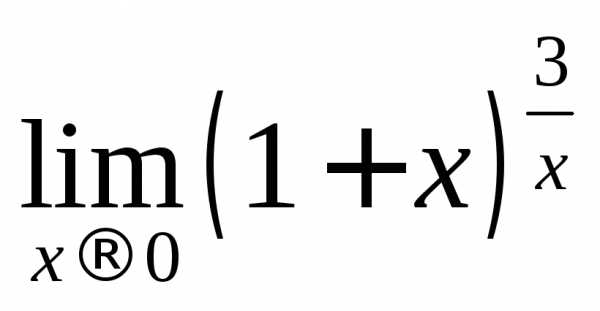
 или
или можно использовать правило Лопиталя,
которое основано на следующей теореме.
можно использовать правило Лопиталя,
которое основано на следующей теореме.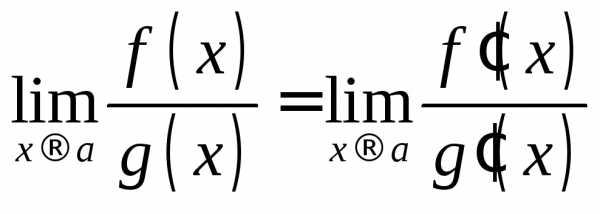

 ,
имеем неопределенность вида
,
имеем неопределенность вида .
Применяя правило Лопиталя, получим
.
Применяя правило Лопиталя, получим