Математические методы
Министерство
образования и науки Республики Казахстан
Северо-Казахстанский
государственный университет им. М.
Козыбаева
М.В.
Погребицкая
В
ПСИХОЛОГИИ
Учебно-методическое
пособие
для
студентов психологических и
педагогических
специальностей
Петропавловск
2004
ББК
88
УДК
311:189.9
П
43
Издается
по решению
Учебно-методического
Совета
СКГУ им. М.Козыбаева
(протокол
№ 9 от 24.06.2004г.)
Рецензент:
кандидат
физико-математических наук, доцент Е.
Акжигитов
Погребицкая
М.В.
П
43 | Математические
методы в психологии: Учебно-методическое
пособие. – Петропавловск,
СКГУ,
2004.-
228
с. |
Учебно-методическое
пособие содержит системное изложение
математических методов в применении
к задачам экспериментальных психологических
исследований. В доступной форме, не
требующей значительной подготовки,
рассматриваются основные методы
обработки данных, включая непараметрические
критерии оценки различий и корреляционный
анализ. Приведены многочисленные примеры
такой обработки и предложены многовариантные
лабораторные работы для развития
практических навыков решения задач.
Пособие
предназначено для студентов психологических
и педагогических специальностей, а
также может быть использовано студентами,
обучающимися по кредитной и дистанционной
технологиям, исследователями в области
психологии, социологии, педагогики,
медицины и биологии.
УДК
311:189.9
Погребицкая
М.В., 2004
Северо-Казахстанский
государственный университет им.
М.Козыбаева, 2004
Содержание
| От
автора……………………………………………………… | 7 |
| Введение……………………………………………………… | 9 |
| | |
Раздел I. | ОПИСАТЕЛЬНАЯ
СТАТИСТИКА | |
| | |
| Тема
1. Измерения в психологии……………………….. | 15 |
| Признаки
и переменные………………………….
| 15 |
| Шкалы
измерения…………………………………
| 16 |
| Вопросы
и упражнения…………………………… | 18 |
| Тема
2. Представление данных………………………… | 20 |
| Группировка
данных………………………………
| 20 |
| Табулирование
данных…………………………..
| 21 |
| Ранговый
порядок …………………………………
| 23 |
| Распределение
частот……………………………
| 25 |
| Статистические
ряды……………………………..
| 27 |
| Понятие
распределения и гистограммы………
| 29 |
| Вопросы
и упражнения…………………………… | 33 |
| Тема
3. Меры центральной тенденции………………… | 34 |
| Мода………………………..………………………..
| 34 |
| Медиана………………………..……………………
| 36 |
| Среднее………………………..……………………
| 38 |
| Мода,
медиана и среднее значение объединенных
групп………………………………
| 40 |
| Интерпретация
моды, медианы и среднего…..
| 41 |
| Выбор
меры центральной тенденции………….
| 42 |
| Вопросы
и упражнения…………………………… | 45 |
| Тема
4. Меры изменчивости…………………………….. | 46 |
| Размах………………………..……………………..
| 47 |
| Дисперсия
и стандартное отклонение…………
| 47 |
| Стандартизированные
данные………………….
| 51 |
| Вопросы
и упражнения…………………………… | 53 |
| Тема
5. Распределение признака. Нормальное
распределение…………………………………… | 55 |
| Параметры
распределения………………………
| 55 |
| Нормальное
распределение…………………….
| 56 |
| Асимметрия…………………………………………
| 60 |
| Эксцесс………………………..…………………….
| 61 |
| Применение
нормального распределения……
| 62 |
| Вопросы
и упражнения…………………………… | 64 |
| Тема
6. Понятие выборки………………………………… | 65 |
| Полное
и выборочное исследования…………..
| 66 |
| Зависимые
и независимые выборки……………
| 67 |
| Требования
к выборке……………………………
| 67 |
| Репрезентативность
выборки……………………
| 69 |
| Формирование
выборки………………………….
| 71 |
| Определение
объема выборки………………….
| 72 |
| Вопросы
и упражнения…………………………… | 76 |
| | |
Раздел II. | ОБЩИЕ
ПРИНЦИПЫ ПРОВЕРКИ СТАТИСТИЧЕСКИХ
ГИПОТЕЗ | |
| | |
| Тема
7. Статистические гипотезы и критерии………. | 78 |
| Статистические
гипотезы…………………………
| 79 |
| Статистические
критерии………………………..
| 81 |
| Параметрические
и непараметрические методы………………………………………………
| 83 |
| Уровни
статистической значимости……………
| 85 |
| Правило
отклонения нулевой и принятия
альтернативной гипотезы………………………..
| 86 |
| Мощность
критериев………………………………
| 89 |
| Вопросы
и упражнения…………………………… | 90 |
| Тема
8. Классификация психологических
задач, решаемых с помощью статистических
методов………………………..…………………… | 92 |
| Классификация
задач…………………………….
| 92 |
| Принятие
решения о задаче и методе обработки
………………………..…………………
| 97 |
| Вопросы
и упражнения…………………………… | 98 |
| | |
Раздел III. | СТАТИСТИЧЕСКИЕ КРИТЕРИИ | |
| | |
| Тема
9. Корреляционный анализ……………………….. | 100 |
| Понятие
корреляционной связи…………………
| 100 |
| Коэффициент
ранговой корреляции rs Спирмена………………………..………………….
| 105 |
| Коэффициент
линейной корреляции Пирсона
| 110 |
| Расчет
уровней значимости коэффициентов
корреляции………………………..………………..
| 114 |
| Коэффициент
корреляции …………………….
| 115 |
| Вопросы
и упражнения…………………………… | 118 |
| Тема
10. Выявление различий в уровне
исследуемого признака………………………… | 120 |
| Постановка
задачи………………………………..
| 120 |
| Q
— критерий Розенбаума…………………………
| 122 |
| S
— критерии тенденций Джонкира………………
| 126 |
| Вопросы
и упражнения…………………………… | 131 |
| Тема
11. Оценка достоверности сдвига в
значениях исследуемого признака………………………… | 132 |
| Постановка
задачи………………………………..
| 132 |
| Т
— критерий Вилкоксона………………………….
| 136 |
| Вопросы
и упражнения…………………………… | 140 |
| Тема
12. Критерии согласия распределений и
многофункциональные критерии…………… | 141 |
| Постановка
задачи………………………………..
| 141 |
| 2 критерий Пирсона………………………………
| 142 |
| —
критерий Колмогорова-Смирнова…………..
| 160 |
| Критерий
* — угловое преобразование
Фишера………………………………………………
| 167 |
| Вопросы
и упражнения…………………………… | 175 |
| | |
| Заключение………………………..………………………… | 176 |
| Приложение
1. Статистические таблицы критических
значений………………………..……………………………… | 179 |
| Приложение
2. Лабораторные работы по дисциплине
«Математические методы в психологии»
………………. | 194 |
| Приложение
3. Описание статистических функций
табличного процессора Microsoft
Excel………………….. | 210 |
| Приложение
4. Применение пакета анализа табличного
процессора Microsoft
Excel
для решения статистических
задач………………………..……………… | 220 |
| Приложение
5. Литература………………………………… | 227 |
ОТ
АВТОРА
Применение
математических методов для обработки
экспериментального материала в психологии
– неотъемлемая часть профессиональных
навыков современного психолога.
Математические
методы – это мощный инструмент,
позволяющий успешно ориентироваться
в море экспериментальных данных и
избегать логических и содержательных
ошибок в работе психолога.
Наиболее естественным
путем, которым математика проникает в
психологию, является математическая
статистика, применение которой позволяет
психологу обосновывать экспериментальные
планы, обобщать данные экспериментов,
выявлять различия между группами
испытуемых, находить зависимости между
экспериментальными данными, строить
статистические прогнозы.
Настоящее
учебно-методическое пособие призвано
решить следующие задачи:
повысить уровень
математической культуры студентов-психологов;
привить навыки
самостоятельной работы в условиях
кредитной технологии и дистанционного
обучения;
дать представление
об основных статистических
процедурах;
научить студентов
самостоятельно проводить первоначальную
статистическую обработку экспериментальных
данных;
сформировать
основы статистического мышления
студентов;
научить студентов
правильно выбирать методы обработки
экспериментальных данных и оценивать
полученные результаты;
научить студентов
грамотно подготавливать данные для
работы со статистическими пакетами на
ЭВМ;
привить
навыки использования инструментов
среды Microsoft
Excel
для нахождения различного рода
статистик.
Материал для
пособия подобран с учетом требований
Государственных общеобязательных
стандартов образования РК к содержанию
первой части дисциплины «Математические
методы в психологии» по специальностям
520930 «Психология», 020940 «Психология»,
031440 «Педагогика и психология», 050106
«Педагогика и психология» и 050503
«Психология».
Большинство
рассматриваемых в руководстве методов
являются непараметрическими, что
расширяет их возможности применения в
психологии по сравнению с традиционными
параметрическими методами. Пособие
содержит большое количество практических
примеров и задач.
В руководство
включены также 10 многовариантных
лабораторных работ, выполнение которых
возможно с применением и без применения
статистических пакетов на ЭВМ. В одном
из приложений приводятся описания
статистических функций табличного
процессора Excel, входящего
в состав пакета программMicrosoftOffice. Приложение 4 содержит
рекомендации к использованию встроенного
пакета анализа в Excel.
ВВЕДЕНИЕ
В настоящее время
использование математических методов
в развитии новых психологических теорий
стало необходимостью. Математические
процедуры входят в такие разделы
психологии, как психометрика,
психодиагностика, дифференциальная
психология, психогенетика. Многие
психологические концепции подвергаются
сомнению на основании того, что они не
подтверждены статистически.
С другой стороны,
психологу можно совершать открытия, не
привлекая математики. Существует
множество теорий в психологии,
сформулированных без поддержки
математики, например, теория психоанализа,
бихевиоральная концепция, аналитическая
психология.
Психология
отличается от многих наук тем, что не
имеет собственных единиц измерения и
берет их «напрокат», например, у физики
(секунды, миллиметры, градусы).
Тем не менее, применение математического
аппарата в большинстве исследований
проще, чем доказательство, что в этом
не было необходимости. В любом случае
математика систематизирует мышление
и позволяет выявить закономерности, на
первый взгляд, не всегда очевидные.
Можно выделить три
стадии процесса математизации
психологической науки.
Первая стадия – это
применение математических методов для
анализа и обработки результатов
экспериментов и наблюдений и установление
простейших количественных закономерностей
(психофизический закон, экспоненциальная
кривая научения).
Вторая стадия
заключалась в попытке моделирования
психических процессов и явлений с
помощью готового математического
аппарата, разработанного ранее для
других наук.
Третий этап
математизации (современный этап)
характеризуется разработкой
специализированного математического
аппарата для исследования и моделирования
психических процессов и явлений,
формирования математической психологии
как самостоятельного раздела теоретической
(абстрактно-аналитической) психологии.
В основе предмета
«Математические методы в психологии»
лежит «математическая статистика»– наука о случайных явлениях, включающая
описание случайных явлений, проверку
гипотез, изучение причинных зависимостей.
Распространенное
отношение к статистике – смесь
благоговения с цинизмом, подозрением
и презрением. Однажды кто-то заметил:
«Есть маленькая ложь, есть большая
ложь, а есть статистика». Необоснованное
применение методов статистики может
повлечь за собой ситуацию, в которой
человек, держа голову в холодильнике,
а ноги в печи, говорит: «В среднем я
чувствую себя прекрасно». Отказ от
широко распространенного мнения о
статистике – это не только путь к новым
открытиям и закономерностям в различных
областях познания, но и лучшая защита
от цифрового абсурда.
Первоначально
статистикой (statistics)
называлось изучение государственных
дел. В XVII
в. в Европе горстка математиков проводила
небольшие частные исследования,
которые впоследствии оформились в
теорию вероятностей. Эти исследования,
проведенные, в частности, Блезом Паскалем
(1623-1662гг.) и Пьером Ферма (1601-1665гг.),
выполнялись по просьбе Шевалье де Мере,
азартного игрока, которому было особенно
важно понять природу удачи.
На
первоначальное развитие статистических
методов оказало влияние их происхождение.
У статистики были «мать», которой нужно
было представлять регулярные отчеты
правительственных подразделений (слова
«штат» и «статистика» происходят от
одного латинского корня –status),
и «отец» – честный карточный игрок,
который полагался на математику,
усиливавшую его ловкость – умение брать
решающие взятки в азартных играх. От
«матери» ведут свое происхождение счет,
измерение, описание, табулирование,
упорядочение и проведение переписей,
т.е. все то, что привело к современной
описательной статистике. От предприимчивого
интеллектуала – «отца» – в конечном
счете, возникла современная теория
статистического вывода, непосредственно
базирующаяся на теории вероятностей.
Недавнее дополнение, называемое
планированием экспериментов, опирается
в основном на сочетание теории вероятностей
с несколько элементарной, но удивительной
логикой.
Начала
статистической теории измерений положены
Карлом Фридрихом Гауссом – королем
математиков, как его называли современники,
– в первой половине XIX
века в связи с его занятиями астрономией
и геодезией. С 1807 г. и до самой смерти в
1855 г. Гаусс заведовал кафедрой математики
Геттингенского университета и одновременно
был директором обсерватории в Геттингене.
В его основном труде по астрономии
«Теория движения небесных тел» содержится
способ определения орбит планет по
наблюдениям, который опирается на
развитую им же классическую теорию
ошибок измерений. Таким образом,
метрология оказывается тесно связанной
со статистической теорией измерений.
Естественно было
ожидать, что дальнейшее развитие
математической статистики будет
стимулироваться новыми проблемами
метрологии.
Важной
сферой применения методов математической
статистики является массовое производство.
Первые идеи в этой области принадлежат
одному из директоров крупных пивоваренных
заводов Гиннеса в Англии. В начале XX
в. он прочитал книгу по теории вероятностей
и подумал, что «из этого можно делать
деньги». Позвав к себе Уильяма Госсета,
младшего служащего завода, директор
предложил ему поехать в единственный
в то время центр статистических
исследований в Лондоне для учебы под
руководством крупнейшего статистика,
биолога и философа Карла Пирсона,
основателя журнала «Биометрика».
У.Госсет
проявил инициативу и выдающиеся
способности и вскоре приступил к
самостоятельным исследованиям. Их
результаты были весьма значительны:
одни представляли несомненную ценность
для пивоварения, другие – большой
теоретический интерес. Естественно
возникла проблема их публикации. Но
устав пивоваренной компании Гиннеса
запрещал работникам публикацию
результатов исследований. Однако
компания дала согласие на публикацию
работ по теоретическим вопросам
статистики (что было нарушением устава),
но решила не связывать результаты с
именем одного из служащих компании,
дабы конкуренты не могли догадаться о
пользе, которую несет статистика для
пивоварения. В результате научный мир
был изумлен рядом первоклассных
статей в журнале «Биометрика»,
опубликованных начиная с 1908 г. под
псевдонимом «Student»,
что значит «Студент», но в нашей литературе
принято писать «Стьюдент». Эти работы
совершили переворот в статистике,
так как они содержат неклассическую
постановку задачи и точное ее решение.
Сейчас положение
совершенно иное: не только плодотворно
развиваются области психологии,
широко использующие математические
методы, но даже на психологических
факультетах и в ряде гуманитарных,
биологических и медицинских вузов
читается обязательный курс математики,
включающий элементы математической
статистики.
Основными разделами
математической статистики считаются
разделы описательной статистики, теория
статистического вывода, планирование
и анализ экспериментов.
Описательная
статистика включает в себя
табулирование, представление и
описание совокупностей данных. Эти
данные могут быть либо количественными,
как, например, измерения роста и веса,
либо качественными, как, например,
пол и тип личности. Описательная
статистика упорядочивает и систематизирует
имеющуюся информацию, облегчает
понимание изучаемого явления.
Наиболее ярким
примером статистического описания
служат результаты переписи населения,
представленные в виде соответствующих
таблиц, графиков и показателей
распределения населения по демографическим
и социальным признакам.
Всякая большая
группа испытуемых, относительно которых
мы хотим провести исследование и
собираемся делать выводы, называется генеральной совокупностью.
Выборка–
это часть испытуемых,выделенная
из генеральной совокупности для
проведения эксперимента.
Теория
статистического вывода– это
формализованная система методов решения
задач, в которой выводятся свойства
генеральной совокупности данных путем
исследования выборки.
Например, директор
крупного концерна хочет определить
долю сотрудников, которые положительно
относятся к введению нового графика
работы. Излишне было бы опрашивать
каждого сотрудника, если бы можно было
надежно определить такую долю по
выборке минимальным объемом, скажем, в
100 человек. Но какова доля тех сотрудников,
которые положительно отнеслись в этой
выборке из 100 человек, по отношению к
доле во всей совокупности сотрудников?
Ответ можно получить благодаря теории
статистического вывода. Таким образом,
задача статистического вывода состоит
в том, чтобы предсказать свойства всей
совокупности, зная свойства только
выборки из этой совокупности. Эти выводы
делаются и производятся с помощью
методов описательной статистики
посредством описания как свойств
выборок, так и совокупностей.
Планирование
и анализ экспериментов представляет собой
третью важную ветвь статистических
методов, разработанную для обнаружения
и проверки причинных связей между
переменными.
К особенностям
применения математических методов
обработки в психологии относятся
следующие утверждения:
чем
ближе к реальности экспериментальные
данные, тем надежнее результат
математического исследования;
при
использовании математических методов
для анализа и обработки результатов
экспериментов и наблюдений большую
часть успеха исследования составляют
определение типа решаемой задачи и
выбор метода решения;
важную
часть решения задачи занимает
интерпретация полученного результата.
studfiles.net
Математические методы — это… Что такое Математические методы?
- Математические методы
применяются для обработки полученных методом опроса и эксперимента данных, а также для установления количественных зависимостей между изучаемыми явлениями. Они помогают оценить результаты эксперимента, повышают надежность выводов, дают основание для теоретических обобщений. К математическим методам относят методы: регистрации, ранжирования, шкалирования (см. регистрация, ранжирование, шкалирование).
Исследовательская деятельность. Словарь.— М.: УЦ «Перспектива».
Е.А. Шашенкова.
2010.
- Магистратура
- Метод идеализации
Смотреть что такое «Математические методы» в других словарях:
МАТЕМАТИЧЕСКИЕ МЕТОДЫ — в демографии, служат для количеств. и качеств, анализа демографич. процессов, используются при расчёте разл. демографич. показателей. М. м. применяются, во первых, в теоретич. анализе взаимосвязей между характеристиками разл. демографич.… … Демографический энциклопедический словарь
Математические методы в социологии — Математические методы в социологии методы статистического анализа статистических данных и методы математического моделирования социальных явлений и процессов. Компьютерная социология использование возможностей компьютерной техники для … Википедия
МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ГЕОЛОГИИ — использование математических методов в геологических исследованиях обеспечивает воспроизводимость результатов, позволяет максимально унифицировать форму представления материала и производить его обработку сообразно системе строгих, логически… … Геологическая энциклопедия
математические методы в биологии — сущ., кол во синонимов: 1 • мамба (3) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Математические методы в экономике — Эта статья или раздел описывает ситуацию применительно лишь к одному региону. Вы можете помочь Википедии, добавив информацию для других стран и регионов. Математические методы в экономике научное направление в экономике, посвящённое и … Википедия
Математические методы в управлении войсками — количественные и символико логические методы анализа, оценки и прогнозирования обстановки, подготовки на этой основе управленческих решений и их оптимизации. Среди известных М.м.у.в. наибольшее распространение получили методы теории вероятностей … Пограничный словарь
МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ИНЖЕНЕРНОЙ ПСИХОЛОГИИ — совокупность алгоритмов, основанных на теоретических положениях и идеях определенного раздела математики и позволяющих осуществить комплексный анализ закономерностей и соотношений. Применение М. м. в инженерной психологии развивается по трем… … Энциклопедический словарь по психологии и педагогике
экономико-математические методы — эконометрика — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] экономико математические методы ЭММ Обобщающее название комплекса экономических и математических… … Справочник технического переводчика
Экономико-математические методы (ЭММ) — [economico mathematical methods] обобщающее название комплекса экономических и математических научных дисциплин, объединенных для изучения экономики. Введено академиком В.С.Немчиновым в начале 60 х годов. Встречаются высказывания о том, что… … Экономико-математический словарь
Экономика и математические методы — Cписок значений слова или словосочетания со ссылками на … Википедия
Книги
- Математические методы социальных технологий, Курбатов В.И., В учебном пособии изложены математические модели и методы их анализа, апробированные при изучении демографических, экономических и социальных процессов. Рассмотрены математические модели… Категория: Социология, политология Издатель: ВУЗОВСКАЯ КНИГА, Производитель: ВУЗОВСКАЯ КНИГА, Подробнее Купить за 1053 грн (только Украина)
- Математические методы, Т. Л. Партыка, И. И. Попов, Рассматриваются прикладные математические методы и модели, в том числе методы математического программирования (поиск экстремума, линейное и динамическое программирование), многосвязные… Категория: Разработка программного обеспечения Серия: Профессиональное образование Издатель: Форум, Инфра-М, Подробнее Купить за 674 руб
- Математические методы, Т. Л. Партыка, И. И. Попов, Рассматриваются прикладные математические методы и модели, в том числе методы математического программирования (поиск экстремума, линейное и динамическое программирование), многосвязные… Категория: Учебники для ВУЗов Серия: Профессиональное образование Издатель: Форум, Инфра-М, Производитель: Форум, Инфра-М, Подробнее Купить за 500 грн (только Украина)
Другие книги по запросу «Математические методы» >>
research_activities.academic.ru
Методы математического анализа — Энциклопедия по экономике
Прежде чем применить методы математического анализа для вычисления параметров уравнения тренда, необходимо выявить тип тенденции, а эта задача не является чисто математической. Наличие колебаний уровней крайне усложняет выявление типа тенденции и требует всестороннего подхода к этой проблеме, прежде всего качественного изучения характера развития объекта. При этом нужно дать ответ на такие вопросы
[c.321]
Методы математического анализа Дифференциальное, интегральное и вариационное исчисление и др.
[c.430]
Решение этого комплекса задач осуществляется на единой математической основе. Помимо сетевых моделей при расчете календарно-плановых нормативов использованы методы математического анализа, комбинаторно-эвристические процедуры и теория математической статистики.
[c.45]
Данная глава посвящена моделированию фактического распределения сделок с помощью регулируемого распределения, то есть поиску функции и ее подходящих параметров, которые моделируют фактическую функцию плотности вероятности торговых P L с двумя точками перегиба. Вы можете использовать уже известные функции и методы, например, полиномиальную интерполяцию или экстраполяцию, интерполяцию и экстраполяцию рациональной функции (частные многочленов), или использовать сплайн-интерполяцию. После того как теоретическая функция найдена, можно определить ассоциированные вероятности тем же методом расчета интеграла, который использовался при поиске ассоциированных вероятностей регулируемого распределения, или рассчитать интеграл с помощью методов математического анализа. Одна из целей этой книги — позволить трейдерам, использующим немеханические системы, применять те же методы управления счетом, что и трейдерам, использующим механические системы. Регулируемое распределение требует расчета параметров, они относятся к первым четырем моментам распределения. Именно эти моменты — расположение, масштаб, асимметрия и эксцесс — описывают распределение. Таким образом, кто-либо, торгующий по немеханическому методу, например по волнам Эллиотта,
[c.141]
Первоначально, когда еще в природе не существовало компьютерной техники, а методы математического анализа в силу сложности расчетов никто не пытался применить для анализа динамики цен, трейдеры вручную, используя лишь логарифмические линейки, рисовали графики, на которых откладывали прямые линии. Позже были найдены закономерности в соотношении этих линий и графиков цен. Так возникли трендовые линии, модели и фигуры.
[c.35]
Исторически классический технический анализ развивался следующим образом. Первоначально, когда еще в природе не существовало компьютерной техники, а методы математического анализа в силу сложности расчетов никто не пытался применять для анализа динамики цен, трейдеры вручную, ис-
[c.243]
Методы математического анализа
[c.140]
Использование методов математического анализа для управления производством сводится в основном к отысканию максимумов (или минимумов) различных функциональных зависимостей, которые имеются на предприятии. Если имеется функциональная зависимость общего вида у=-рО ), то точка экстремума должна удовлетворять условию g — 0. Иными словами, необходимо сначала продифференцировать функцию, затем приравнять ее к нулю, затем определить соответствующее значение х. Например, имеем зависимость
[c.140]
Следует помнить, что если функция имеет несколько минимумов или максимумов, то методы математического,. анализа не дают гарантии нахождения самой максимальной или самой минимальной точки.
[c.141]
В настоящее время происходит также синтез аналитических методов математического анализа и вычислительной математики. В последние десятилетия появились универсальные пакеты символьных вычислений, которые позволяют без знания алгоритмов и программ решать на компьютере сложнейшие численные и аналитические задачи быстро отыскивать производные и экстремумы сложных функций, строить графики, решать системы уравнений и многое другое.
[c.14]
Наличие функциональных зависимостей социально-экономических явлений позволяет использовать для решения экономических проблем методы математического анализа. Поэтому необходимо познакомиться с ними. Это знакомство мы начнем со способов задания функции.
[c.22]
Наличие функциональных зависимостей позволяет использовать для решения экономических проблем методы математического анализа. В качестве примеров функциональных зависимостей можно привести следующие функции, имеющие смысл в некоторой области значений аргумента
[c.94]
В последнее время стали применяться методы математического анализа работы энергосистем на электронно-счетных машинах. Такой анализ в первую очередь производится в объединенных и крупных энергосистемах и позволяет выявить резервы дальнейшего снижения себестоимости энергии.
[c.405]
Иными словами, методика программирования — это одна из глав прикладной математики. Другими главами являются методика применения теории вероятностей, теория сложных систем, теория численных методов математического анализа, методика решения некорректно поставленных задач 7 и многие другие.
[c.5]
Буржуазным экономистам нельзя верить ни в одном слове, раз речь заходит об общей теории политической экономии 2. Исследования буржуазных ученых могут представлять определенный интерес лишь со стороны использования статистических материалов, некоторых методов математического анализа, данных отраслевых и специальных экономик о технико-экономических сдвигах в хозяйстве.
[c.541]
Еще до официального признания в рамках государственной политики необходимости перехода от планово-распределительной системы с командно-административными принципами управления к рыночным отношениям было известно, что дать полное формализованное описание системы управления для сложных систем практически невозможно. Причиной этому являются протекающие в управляемой системе (или внешней для нее среде) процессы, при описании которых не удается воспользоваться информацией об их внутренней структуре или принципах формирования, а также недоступность информации и чрезмерные затраты на ее получение. Это особенно характерно для рыночной экономики и при ее формировании. Поэтому в настоящей работе наибольшее внимание уделено методикам, которые позволяют принимать и обосновывать решения при неопределенности экономических данных и ситуаций, недостатке фактической информации об окружающей среде, ее перспективах, что вызывает наибольшие затруднения у специалистов в условиях рыночных отношений. Это вариантные методы математического анализа возможных линий поведения и связанных с ними исходов. Среди них в настоящей главе рассмотрены теория игр, разновидность имитационной модели, теория графов, эвристические методы при использовании методов экспертных оценок, теория вероятностей в сочетании с другими методами. В составе аналитических расчетов задействованы также приемы факторного анализа, балансовых методов и др.
[c.55]
Применяя методы математического анализа и математической статистики, можно заранее рассчитать репрезентативность выборки информации и ее соответствие генеральной совокупности.
[c.546]
Многообразие и сложность проблемы пропорций нашли свое отражение в различных подходах к исследуемой проблеме. Большинство авторов используют в работе метод математического анализа, иногда полностью отвлекаясь от назначения изделия, законов формирования его материальной структуры. Этот метод позволяет выявить наличие пропорций, но не объясняет, к сожалению, как и почему применена именно эта пропорция и какой художественный эффект при этом был достигнут. Отсюда ограниченность математических методов и ошибочность вывода о том, что достаточно установить строгую пропорциональность, как сразу изделие приобретает гармоничную завершенность и эстетическую выразительность.
[c.190]
Вывод. Для проведения сравнительной оценки семи предприятий использовано пять оценочных показателей. Расчеты, проведенные с использованием метода математического анализа, показали, что более точное распределение мест дал метод Дельфи, где учтена значимость показателей, используемых для сравнительной оценки предприятий.
[c.288]
Обработка прогнозных данных не требует от риск-менеджера фундаментальных знаний различных методов математического анализа. Это позволит оптимизировать структуру подразделения по управлению риском предприятия, распределив нагрузку между специалистами различного профиля (финансистами, математиками, юристами), и оптимизировать затраты на содержание данного подразделения.
[c.581]
Математический анализ. Математический анализ подразумевает вычисление теоретических ранних и поздних дат начала и завершения всех работ проекта без учета ограничений со стороны набора ресурсов. В результате получается не расписание, а скорее показатель количества временных периодов, в рамках которых работа должна быть запланирована с данными ресурсами и прочими известными ограничениями. Наиболее известны следующие методы математического анализа
[c.73]
Кроме балансового в плановой работе используются и другие методы экономического анализа и синтеза, прямого счета, расчета по факторам, экстраполяции и итерации, экономико-математические методы (линейного программирования, динамического программирования, матричный и др.), метод экономико-математического моделирования.
[c.72]
При современных масштабах производства эффективная работа по плановому руководству отдельными предприятиями и отраслью немыслима без широкого внедрения математических методов в анализ и планирование и без электронно-вычислительной техники. В настоящее время ведутся исследования и разрабатывается теория планирования, в основе которой лежат балансовый метод, метод моделирования и метод выбора оптимального варианта производственной программы. В частности, благоприятные перспективы имеет матричный (балансовый) метод планирования деятельности предприятий, основанный на применении матричной алгебры.
[c.129]
Курс Оценка стоимости предприятия (бизнеса) имеет связь с такими дисциплинами, как «Теория и практика оценочной деятельности», «Правовые основы оценочной деятельности», «Математические методы оценки» » Анализ финансовой отчетности», «Бухгалтерский учет», «Микро и макроэкономика», «Бизнес-планирование».
[c.311]
Критерии и способы оценки сравнительной экономической эффективности проектов детально излагаются в главе 5. Однако вопросы, рассматриваемые на стадии ТЭО, настолько широки и разноплановы, что одних экономических критериев здесь явно недостаточно. Формальные методы математической оптимизации здесь играют подчиненную роль. А главное внимание обращено на творческую проработку ft анализ имеющихся альтернатив. Оценку их эффективности дают с помощью целой группы экономических, социальных, экологических, технико-технологических, а нередко — и международных аспектов. Наиболее удачный вариант проектных решений принимают к осуществлению и утверждают в виде «Технического задания на разработку проекта строительства предприятия» (ТЗ).
[c.55]
Кроме метода элиминирования, для определения характера и степени зависимости технико-экономических показателей от различных факторов в процессе анализа используют методы математической статистики, в частности, корреляционный метод, требующий современные средства вычислительной техники.
[c.389]
Чем удачнее подобрана модель, тем точнее она отражает характерные черты анализируемого процесса, тем достовернее полученные результаты. К построению моделей подходят по-разному используют методы математического программирования (линейное, динамичное, выпуклое, стохастическое), сетевого и матричного планирования, математической статистики (дисперсионный и регрессионный анализы, группировка совокупностей по статистическим критериям) и т.д.
[c.33]
При анализе фактических и расчетных показателей эффективности организационно-технических мероприятий обычно применяют методы математической статистики (уравнения корреляции, дисперсионный анализ, теорию вероятностей, законы больших чисел, метод полного факторного анализа, метод наименьших квадратов, математической обработки динамических рядов и т. д.). Следует иметь в виду, что математические методы и ЭВМ следует использовать при качественном анализе основных критериев и показателей эффективностей, выявлении взаимообусловленных связей и зависимостей.
[c.98]
В связи с различиями в структурности проблем в планировании существуют различные методы разработки и обоснования оптимальности планов. К ним относятся методы экономического анализа балансовый технико-экономических расчетов, системного анализа, экономико-математические методы, экспертные (оценочные).
[c.143]
В последнее время особое значение придается применению различных экономико-математических методов для анализа показателей, характеризующих развитие экономики, в том числе для анализа себестоимости.
[c.23]
Одновременно с этим методом в нефтяной промышленности применим метод индексного анализа себестоимости, а также трансцендентная кинетическая производственная функция как экономико-математическая модель [28]. Одним из главных условий получения хороших результатов является правильный выбор исходных статистических показателей, от которых зависит в значительной степени точность расчетов.
[c.23]
При наличии такого согласованного набора показателей нашей небольшой группе уже не нужно было разводить долгих философских дискуссий о том, к какому из характерных регионов США следует отнести тот или иной город, или о том, что в таком-то районе экономика вообще развита хорошо, и поэтому наши продажи должны здесь пойти вверх. Подобные обсуждения заменил математический анализ. Членам группы оставалось только сравнить коэффициент эффективности любого города с показателями других городов и с наличием или отсутствием маркетинговой активности в этих городах. Самое главное, они получили метод экстраполяции потенциального объема продаж в таких городах, где до сих пор никаких маркетинговых мероприятий еще не проводилось. В результате оказалось, что многие небольшие города имеют весьма неплохие перспективы.
[c.47]
В число основных традиционных способов и приемов экономического анализа входят исчисление относительных и средних величин сравнение группировка индексный метод метод цепных подстановок балансовый метод. К математическим методам экономического анализа можно
[c.14]
Для решения данной задачи использованы методы математической статистики, в частности, корреляционно-регрессионный анализ.
[c.104]
Так, к оптимизационным точным методам можно отнести методы теории оптимальных процессов, некоторые методы математического программирования и методы исследования операций. К оптимизационным приближенным методам относятся отдельные методы математического программирования, методы исследования операций, методы экономической кибернетики, методы математической теории планирования экстремальных экспериментов, эвристические методы. К неоптимизационным точным методам относятся методы элементарной математики и классические методы математического анализа, эконометрические методы. К неоптимизационным приближенным методам относятся метод статистических испытаний и другие методы математической статистики.
[c.98]
Ряд экономических задач в области проектирования и эксплуатации оборудования, используемого в газоразделении, может с успехом решаться обычными методами классического анализа (выбор оптимальной толщины изоляции, оценка сравнительной экономической эффективности различных типов теп-лообменных аппаратов, выбор оптимального размера предприятий и пр.). Приведем пример использования метода математического анализа при решении экономической задачи (выбор оптимальной толщины изоляции агрегатов глубокого охлаждения).
[c.198]
С начала XX в. в учебных курсах микроэкономического анализа изме] лось и понимание метода экономической теории. Менялись и взгляды методику ее преподавания. В 40—50-е гг. главной задачей преподавания с ло внедрение методов математического анализа. Об этом свидетельствует ник Гарвардского университета, написанный Дж. Хендерсоном и Р Кн н том в 1958 г. Он был высоко оценен такими выдающимися исследователя как Э. Хансен, У. Баумоль, Э. Чемберлин. Вучебнике излагается куре мик экономического анализа для неэкономических специальностей, полност переложенный на язык математики. Повсеместное внедрение математик ких методов как в научные исследования, так и в изложение учебного мл» риала, позволило более строго и стройно изложить основные теоретическ положения, проверить теоретические системы навнутреннююлогику, обл чило проверку теорий с помощью статистических данных.
[c.362]
Целевая функция / может быть недифференцируемой, что затрудняет применение классических методов математического анализа.
[c.84]
Неоптимизационные точные методы элементарной математики классические методы математического анализа эконометричес-кие методы.
[c.219]
В прогнозировании можно идти двумя путями. Первый — попытаться причинно-следственный механизм, т.е. найти факторы, опреде-поведение прогнозируемого показателя, прогноз по которым либо известен, либо его дать несложно. Этот путь приводит к экономико-математическому моделированию, построению модели поведения экономического объекта. В настоящее время данный путь широко используется при прогнозировании природопользования. Второй путь — не вдаваясь в механику движения, попытаться предсказать будущее положение, анали-временной ряд изолированно. В современной практике прогнозиро-природопользования такие методы изолированного анализа и про-почти не применяются, но преимущество этих методов диктует необходимость их более широкого применения.
[c.31]
Из различных возможных направлений развития отрасли необходимо отобрать наилучшие с учетом имеющихся возможностей. С этой целью составленные прогнозы подвергают тщательному анализу. Значительное количество неопределенностей обусловли-ваег вероятностный характер прогнозов. В случае, если предвидение будущего выполняется с помощью статистических методов, вероятность осуществления прогноза определяется с помощью методов математической статистики. На основе статистических методов находят верхнюю и нижнюю границы значения прогнозируемых параметров (например, производительность труда, себестоимость продукции).
[c.90]
economy-ru.info
Методы математические — Энциклопедия по экономике
Основой для составления годовых планов товарооборота нефтеснабсбытовых управлений могут служить краткосрочные прогнозы, разработанные с применением экономико-математических методов, в числе которых наиболее приемлемы в указанном прогнозировании — методы математической статистики.
[c.146]
Из методов математического программирования наиболее широко используются матричный и симплексный. Каждый из них-имеет свой алгоритм решения.
[c.73]
Сущность статистического контроля качества продукции состоит в том, что на предприятии с помощью методов математической
[c.123]
Чтобы успешно проводить исследования, необходимо разработать их методику, ознакомиться с методами математической статистики, основами логики, нужно научиться обобщать факты, и, что самое главное, безукоризненно знать предмет исследований.
[c.33]
Процесс разработки в условиях АСУП задач перспективного развития предприятия включает следующее 1) определение круга решаемых проблем и искомых результатов 2) локализацию системы, т. е. определение комплекса входящих в нее объектов и связей рассматриваемой системы с отраслью и народным хозяйством 3) выбор периода планирования 4) выбор типа экстремальной задачи в зависимости от характера решаемых проблем, специфики оптимизируемой системы, длительности периода планирования и т. д. 5) установление критерия оптимальности 6) определение возможных вариантов развития отдельных объектов системы — перспектив реконструкции или модернизации действующих объектов предприятий, возможность расширения предприятия за счет строительства новых объектов основного и вспомогательного производства, варианты совершенствования технологии и т. д. 7) формулирование условий, в которых осуществляется деятельность всей рассматриваемой системы и отдельных ее объектов, включая внешние и внутренние ее связи 8) формализацию задачи, т. е. описание условий деятельности системы и целевой функции в виде экономико-математической модели 9) подготовку исходной информации, определение числовых значений параметров экономико-математической модели 10) решение возникающих экстремальных задач отыскания лучшего варианта развития системы с использованием методов математического программирования и ЭВМ И) ана-. лиз полученных результатов 12) выдачу необходимой исходной информации, включая результаты выполненных расчетов в АСУП, для решения комплексной задачи в масштабе отрасли.
[c.420]
Метод уравнений. Сущность метода математических уравнений состоит в следующем.
[c.220]
Критерии и способы оценки сравнительной экономической эффективности проектов детально излагаются в главе 5. Однако вопросы, рассматриваемые на стадии ТЭО, настолько широки и разноплановы, что одних экономических критериев здесь явно недостаточно. Формальные методы математической оптимизации здесь играют подчиненную роль. А главное внимание обращено на творческую проработку ft анализ имеющихся альтернатив. Оценку их эффективности дают с помощью целой группы экономических, социальных, экологических, технико-технологических, а нередко — и международных аспектов. Наиболее удачный вариант проектных решений принимают к осуществлению и утверждают в виде «Технического задания на разработку проекта строительства предприятия» (ТЗ).
[c.55]
Применение методов математического моделирования при подготовке. производства
[c.100]
Математическое моделирование технологических процессов основывается на теории процесса как результате соответствующих исследований. Однако нередко встречаются процессы столь сложные, что теоретическое изучение их механизма требует весьма длительных сроков, тогда как задачи оптимизации подлежат решению в более короткое время. Поэтому для моделирования технологических процессов используются методы математической статистики, позволяющие на основе эксперимента давать математическое описание очень сложных или малоизученных процессов.
[c.100]
Математико-статистическое моделирование основывается на методах математической статистики, теории вероятностей, теории корреляции и других. Эффективность применения этих методов была значительно повышена
[c.100]
Во всех перечисленных выше методах математического программирования коэффициенты ограничений и оптимизируемой функции рассматриваются как величины, не зависящие от времени. Поэтому эти методы пригодны для решения только статических задач. Для исследования динамических процессов и явлений применяют метод динамического программирования, в
[c.153]
В общем виде функциональная зависимость удельных эксплуатационных затрат у от факториальных признаков (х, d, z, V, w, R) выражается по методу математической статистики следующим уравнением связи
[c.156]
Кроме метода элиминирования, для определения характера и степени зависимости технико-экономических показателей от различных факторов в процессе анализа используют методы математической статистики, в частности, корреляционный метод, требующий современные средства вычислительной техники.
[c.389]
Чем удачнее подобрана модель, тем точнее она отражает характерные черты анализируемого процесса, тем достовернее полученные результаты. К построению моделей подходят по-разному используют методы математического программирования (линейное, динамичное, выпуклое, стохастическое), сетевого и матричного планирования, математической статистики (дисперсионный и регрессионный анализы, группировка совокупностей по статистическим критериям) и т.д.
[c.33]
Оптимизация производственной программы предприятия. Для выбора более рациональных вариантов смешения компонентов в товарные нефтепродукты и для расчета оптимальной производственной программы на нефтеперерабатывающих предприятиях применяют методы математического программирования.
[c.73]
При анализе фактических и расчетных показателей эффективности организационно-технических мероприятий обычно применяют методы математической статистики (уравнения корреляции, дисперсионный анализ, теорию вероятностей, законы больших чисел, метод полного факторного анализа, метод наименьших квадратов, математической обработки динамических рядов и т. д.). Следует иметь в виду, что математические методы и ЭВМ следует использовать при качественном анализе основных критериев и показателей эффективностей, выявлении взаимообусловленных связей и зависимостей.
[c.98]
Одним из наиболее известных методов является система Аккорд (автоматизация контроля и координации оптимальных режимов деятельности). Оптимизация рабочей силы в этой системе выполняется по программе Дельта . Идея алгоритма этой программы сводится к использованию метода линейного программирования на сети. Можно отметить достаточную строгость применяемого в этом методе математического аппарата. Недостаток этого метода заключается в том, что оптимизация проводится без учета механизации работ (путем добавления или изменения одних рабочих).
[c.47]
Зависимость отдельных составляющих целевой функции от числа пунктов разгрузки, включенных в какой-либо вариант внешнего транспортного обеспечения и условно рассматриваемых как непрерывные функции в области целочисленных величин числа пунктов разгрузки пгв, представлена на рис. 27. Как видно из рисунка, с увеличением числа пунктов разгрузки возрастают суммарные затраты на их организацию и уменьшаются транспортные расходы по доставке труб к месту работ. Следовательно, целевая функция как сумма указанных составляющих имеет экстремум при некотором значении числа пунктов разгрузки. Учитывая нелинейную зависимость функционала и его отдельных составляющих от числа вводимых пунктов разгрузки и искомых переменных, для решения поставленной задачи не могут быть применены классические методы математического программирования (например,. линейного). Как известно из курса высшей математики, математическое программирование — область математики, разрабатывающая теорию и методы решения многомерных экстремальных задач с ограничениями, т. е. задач на экстремум функции многих переменных с ограничениями на область изменения этих переменных. Само название программирование взято из линейного программирования, где оно обычно обозначает распределение наилучшим образом ограниченных ресурсов для достижения поставленных целей. Следовательно, термин программирование здесь можно заменить термином планирование .
[c.145]
Данный метод поиска оптимального набора пунктов разгрузки можно отнести к области эвристического (логического) программирования. Как и в большинстве других методов математического программирования, вначале находят опорное решение рассматриваемой задачи (так называемый допустимый план). Затем последовательно за конечное число шагов (итераций) находят допустимое решение, соответствующее минимуму целевой функции. На каждом шаге определяют новое допустимое решение, которому соответствует меньшее значение целевой функции, чем ее значение на предыдущем допустимом решении.
[c.146]
Обработка данных методами математической статистики заключается в следующем
[c.57]
Ввиду того, что межремонтный период работы турбобура при одинаковом долоте и методе бурения изменяется в весьма широких пределах вследствие влияния случайных причин, результаты промысловых данных были отработаны методами математической статистики, описанной в предыдущем параграфе. Для этого составляли вариационный ряд значений межремонтного периода работы турбобура в зависимости от вида бурения и диаметра скважины. После предварительного исключения из вариационного ряда грубых промахов для каждого варианта определяли среднее взвешенное значение признака, среднеквадратическое отклонение и предельную случайную погрешность, коэффициент вариации и степень точно сти при вероятности 0,80 и данном числе степеней свободы.
[c.60]
Для выяснения этих вопросов полученные показатели работы долот в обоих вариантах бурения были обработаны методами математической статистики, описанной в IV главе.
[c.205]
Для решения данной задачи использованы методы математической статистики, в частности, корреляционно-регрессионный анализ.
[c.104]
Выборочный контроль качества продукции основан на применении методов математической статистики для проверки соответствия качества контролируемой партии изделий установленным требованиям по выборочным характеристикам малой выборки из партии.
[c.174]
Таким образом, анализ с применением методов математической статистики дает возможность установить, в какой мере каждый из объективно действующих факторов и вся их совокупность влияют на уровень производительности труда, что позволяет в какой-то мере управлять величиной производительности труда. Решение этой задачи имеет большое значение для научно обоснованного планирования, особенно на перспективный период.
[c.89]
При выполнении анализа технико-экономической эффективности НИР выбор методов и средств зависит не только от целей анализа, но и от объема исходной информации, которая есть на данной стадии НИР. Так, на стадии разработки технического задания имеется весьма ограниченный круг данных, поэтому, естественно, расчеты по узкому кругу укрупненных показателей носят ориентировочный характер. Широко используются методы экстраполяции, моделирования, аналогов и т. д. При оформлении результатов НИР, когда имеются уже основные характеристики исследуемого объекта, расчеты, обосновывающие целесообразность проведения ОКР и внедрения объекта в производство, должны быть сделаны значительно более точно с использованием информации, накопленной в процессе проведения НИР. На этой стадии могут широко применяться методы математического моделирования, учитывающие структуру объекта, его основные конструкторские характеристики, результаты исследования физических моделей и т. д.
[c.88]
При применении методов математического планирования эксперимента применяется bj — 3.
[c.90]
В условиях конструкторской подготовки производства весьма трудно обеспечить равномерную по календарным срокам сдачу технической документации на опытные образцы. Выявленные в процессе проектирования недочеты конструкции, необходимость конструкторских доработок и изменений, естественно, вызывает многочисленные отклонения от плановых сроков и, как следствие, неравномерное поступление заказов в экспериментальные цехи. В таких условиях большую роль играет применение математических приемов, позволяющих оперативно маневрировать ресурсами и обеспечить выравнивание загрузки производственных участков. В частности, оптимизация загрузки опытного производства, маневрирование ресурсами могут выполняться методами математического моделирования.
[c.130]
Корреляционный анализ, основанный на использовании методов математической статистики при обработке исходных данных, позволяет выявить комплексное влияние на величину себестоимости ряда основных, наиболее существенных факторов. При использовании этого метода себестоимость серийного изготовления проектируемого изделия рассматривается как функция выбранных его характеристик
[c.142]
Большое количество промежуточных расчетов, требующихся для определения приведенных затрат и годового эффекта, заставляет учитывать еще одну характерную особенность технико-экономического анализа. Поскольку объем исходной информации по проектируемой машине (особенно на ранних стадиях проектирования) весьма ограничен, для этих расчетов привлекается разнообразный статистический материал и используются различные методы математической статистики. Как бы совершенна ни была зависимость, разработанная для расчета того или иного показателя, погрешность в полученных
[c.148]
В настоящее время широко используется метод установления нормативной численности работающих, основанный на изучении влияния различных факторов на объем работ. На основании данных о фактической численности работников, занятых выполнением тех или иных трудовых функций, и численных значений факторов по группе базовых предприятий с применением метода математической статистики для данной группы
[c.262]
Новые возможности для использования всех рассмотренных выше методов открываются применением в планировании методов экономико-математического моделирования. Так, например, аппарат межотраслевого моделирования позволяет увязать баланс народного хозяйства с системой материальных балансов, с отраслевыми расчетами потребности в продукции и структуры затрат на ее производство, с расчетами по капитальному строительству, уровню жизни населения и др., а в конечном счете — поставить и решить задачу оптимизации межотраслевых связей. Тем самым балансовый метод получает свое дальнейшее развитие за счет применения методов межотраслевого моделирования и оптимального планирования. Методы сетевого планирования, матричной алгебры, оптимизации выступают в качестве инструментов практической реализации программно-целевого подхода, а методы математической статистики находят широкое применение в прогнозировании.
[c.95]
Однако практическое применение экономико-математических методов в нашей стране стало реально осуществимым к началу 60-х годов благодаря появлению и быстрому развитию электронной вычислительной техники. В эти годы были построены первые отчетные и экспериментальные плановые межотраслевые балансы, решены первые задачи оптимального развития и размещения производства, рассчитаны прогнозы отдельных экономических показателей с помощью методов математической статистики.
[c.117]
В составе задач первой очереди АСПР Госплана СССР около 80% их общего числа относится к задачам прямой обработки данных и 20%—к задачам, реализуемым с использованием экономико-математических моделей. Среди задач первого из этих классов (класс А) примерно 60% относится к прямым плановым расчетам и 40%—к информационно-поисковым и справочным задачам. Среди задач второго из этих классов (класс Б) наиболее широко представлены задачи, решаемые на основе народнохозяйственных межотраслевых моделей и моделей оптимального планирования. Задачи типа БЗ, решаемые с использованием методов математической статистики, пока еще не нашли широкого применения.
[c.178]
Основная цель планирования технической подготовки производства определение сроков выполнения всего комплекса работ п отдельных его этапов. Эффективность организации технической подготовки определяется правильным выбором методов планирования, планово-учетных единиц планирования, своевременностью разработки п обоснованностью системы норм и нормативов трудоемкости п продолжительности выполнения ра-бдокументы организации работ технической подготовки производства. Один метод планирования заключается в разработке календарных линейных графиков по этапам работ другой в разработке сетевого графика с применением методов математической статистики и электронно-вычислительной техники. Качество норм и нормативов предопределяет обоснованность плановых показателей п позволяет с высокой степенью достоверности оцепить результаты труда исполнителей.
[c.72]
Из различных возможных направлений развития отрасли необходимо отобрать наилучшие с учетом имеющихся возможностей. С этой целью составленные прогнозы подвергают тщательному анализу. Значительное количество неопределенностей обусловли-ваег вероятностный характер прогнозов. В случае, если предвидение будущего выполняется с помощью статистических методов, вероятность осуществления прогноза определяется с помощью методов математической статистики. На основе статистических методов находят верхнюю и нижнюю границы значения прогнозируемых параметров (например, производительность труда, себестоимость продукции).
[c.90]
Методы математического моделирования процессов позволяют существенно уменьшить объем и продолжительность проектных разработок и могут быть использованы как для решения проектных задач при создании новых промышленных объектов, так и для оптимизации уже осуществленных технологических режимов. Математическое описание содержит необходимые исходные данные для автоматизации управления технологическими процессами описывающие уравнения вводят в ЭЦВМ, которая на их основе выдает команды для постоянного поддержания оптимального технологического режима.
[c.100]
Ввиду того, что показатели работы долот при бурении с отклонителем и на прямой трубе изменяются в сравнительно большом диапазоне, а количество их ограничено, то для установления точности и надежности исследуемых показателей и случайности или неслучайности различия между ними фактические промысловые данные должны быть обработаны методами математической статистики [56]. При этом исходят из известной теории П. Л. Че-бышева, что при достаточно большом числе наблюдений среднее оказывается вполне определенной величиной, вытекающей из общих условий процесса. Чем больше число наблюдений, тем ближе подходит среднее их значение к своему математическому ожиданию, представляющему собой среднюю величину возможных зна-
[c.56]
Ввиду ограниченности количества данных при работе с двумя сопоставимыми отклоняющими компоновками необходимо установить точность и надежность средних значений показателей работы долот в обоих вариантах, а также выяснить, случайно или не случайно различие между ними. С этой целью полученные показатели работы долот в обоих вариантах бурения были обработаны методами математической статистики, описанной в главе IV. В результате этого данные, содержащие грубые ошибки, исключались из рассмотрения и не вошли в табл. 43. При этом было установлено, что средняя проходка на трехшарошечное долото Б-269С при бурении с кривыми переводниками с углом смещения осей резьб 2 и 2,5° составляет соответственно 30,7 и 24,4 м исправленное среднемвадратичбское отклонение 10,0 и 7,26 м коэффициент вариации 32,6 и 27,5% точность 2,70 и 1,67 м при вероятности 0,80.
[c.184]
Обработка параметров искривления ствола методами математической статистики [23] показала, что при бурении опытными долотами ЗВ-190С приращение искривления ствола на 10 м проходки на 24% больше, чем при бурении серийными долотами ОМ-576-190С (1,37е против 1,09°).
[c.215]
В последние годы на основе теоретического обобщения передовой практики советскими учеными и практическими работниками разработан ряд новых принципов и подходов, способствующих рационализации всею комплекса работ по подготовке производства. Успешно внедряются в практику методы организации комплексной подготовки производства, обеспечивающей реализацию процессов создания и внедрения новой техники По единому плану, во нзаим-ной связи и обусловленности. Значительно расширен диапазон методов технико-экономического анализа технических и организационных решений при проектировании новой техники, технологии и организации производства. Создана методология функционально-стоимостного анализа и определены конкретные пути его реализации в условиях социалистической промышленности. Широкое применение находят программно-целевые методы планирования и организации работ по созданию новых видов продукции. Разработаны процедуры планирования, методические принципы формирования нормативной базы, методы математического и имитационного моделирования. Определены формы и способы организации подготовки производства в системах автоматизированного проектирования.
[c.309]
economy-ru.info
МАТЕМАТИЧЕСКИЕ МЕТОДЫ — это… Что такое МАТЕМАТИЧЕСКИЕ МЕТОДЫ?
МАТЕМАТИЧЕСКИЕ МЕТОДЫ в демографии, служат для количеств. и качеств, анализа демографич. процессов, используются при расчёте разл. демографич. показателей. М. м. применяются, во-первых, в теоретич. анализе взаимосвязей между характеристиками разл. демографич. процессов и состава и числ. нас. главным образом на основе моделей демографических. Во-вторых, для расчёта или приближённой оценки отд. количеств. мер, в т. ч. производных показателей, рассчитываемых на основе демографич. моделей (напр., истинный коэфф. естеств. прироста, сила смертности и др.), а также непосредственных характеристик нас. и демографич. процессов, к-рые в силу тех или иных причин не были получены при сборе данных демографич. статистики (определение данных по 1-летним возрастам исходя из 5-летних возрастных групп, для заполнения пропусков в динамич.
рядах показателей и их экстраполяции и др.). В-третьих, для анализа и матем. описания, а также прогноза связей между отд. демографич. показателями (напр., биометрический анализ, формула Брасса в типовых таблицах смертности). Кроме того, в рамках статистич. методов выделяются теоретико-вероятностные и математико-статистические.
В основе применения М. м. в демографии лежит формализация демографич. процесса, в ходе к-рой приходится абстрагироваться от целого ряда качеств. характеристик, черт и свойств нас. Так, применяя методы матем. анализа, приходится не учитывать, что числ. нас. или число демографич. событий суть целые величины, изменяющиеся прерывно, в дискретных моделях предполагается несущественным распределение событий внутри годичного интервала времени и т. д. Применение М. м. допустимо в той мере, в какой формальные допущения не искажают существа изучаемых процессов или явлений.
В совр. демографии применяются методы матем. анализа (интегральное и дифференциальное исчисления, теория рядов и т. п.) и дифференциальных уравнений при построении непрерывных моделей демографич. процессов. Интегральные уравнения служат гл. обр. для описания процесса воспроиз-ва нас. в непрерывной модели (см. Интегральное уравнение). Методы матричной алгебры применяются в дискретных демографич. моделях (см., напр., Модели воспроизводства населения) при перспективных расчётах нас. Теоретико-вероятностные методы используются при построении стохастич. демографич. моделей (напр., имитационных моделей рождаемости). Правила вычисления вероятностей сложных событий лежат в основе расчётов демографич. таблиц, определения т. н. чистых и комбинированных вероятностей (напр., вероятность овдовения к данному возрасту при условии отсутствия развода, вероятность рождения ребёнка или вступления в брак в данном возрастном интервале при наличии или отсутствии смертности и т. д.).
В практике демографич. расчётов важное место занимают методы вычислит. математики; интерполяция и экстраполяция, численное интегрирование (см., напр., Борткевича поправка) и др.
М. м. применялись в демографии на всём протяжении её истории, использование ЭВМ значительно расширило их возможности и повысило точность расчётов.
Венецкии И. Г., Математические методы в демографии, М., 1971; Боярский А. Я., Население и методы его изучения, М., 1975; Keyfitz N., Introduction to the mathematics of population, Reading (Mass.), L., 1968.
Е. М. Андреев.
Демографический энциклопедический словарь. — М.: Советская энциклопедия.
Главный редактор Д.И. Валентей.
1985.
demography.academic.ru
Классификация экономико-математических методов
Особенностью
решения задач управления экономикой
является необходимость учета при их
решении множества переменных величин,
характеризующих постоянно изменяющиеся
производственные условия.
Так
как число сочетаний этих величин в
течение определенного времени могло
быть достаточно большим, то возможно
существование значительного числа
вариантов решений. Отсюда большая
размерность решаемых задач. В этих
условиях простой перебор и сравнение
всех возможных вариантов решения
конкретной задачи нереально из-за
большой трудоемкости вычислений. Поэтому
требуются специальные методы, позволяющие
достаточно быстро и с достаточной
степенью обоснованности найти искомое
решение. Эти методы получили название
экономико-математических методов.
Поскольку
целью изучения экономико-математических
методов является раскрытие механизма
их реализации, определение области
наиболее эффективного использования,
то в качестве классификационного
признака можно принять, например,
характер используемого математического
аппарата. По этому признаку можно
выделить методы классической и прикладной
математики (рис.1).
Методы
классической математики включают
математический анализ и теорию
вероятностей. Методы математического
анализа в свою очередь могут быть
классифицированы на дифференциальное
и вариационное исчисления. Эти методы
целесообразно использовать при расчете
параметров календарно-плановых
нормативов: определение размеров партии
деталей, длительности производственного
цикла, для оперативного регулирования
производства и др.
Группа
методов прикладной математики обширна
по номенклатуре, неоднородна по составу
элементарных расчетов, способам их
реализации, применяемым приемам и т.д.
По общности указанных признаков методы
рассматриваемой группы можно
классифицировать следующим образом:
методы оптимального программирования,
математической статистики, комбинаторные
методы, теории расписаний, игр, массового
обслуживания, управление запасами,
метод экспертных оценок.
Экономико-математические
методы
1. Методы классической математики
1.1.
Матема-
тический
анализ
2.
Методы прикладной математики
1.2.
Теория
вероят-
ности
2.2.
Матема-
тическая
статистика
2.1.
Оптимальное
программи-
рование
2.1.1.
Линейное
2.1.2.
Вероятность
2.1.5.
Выпуклое
2.2.1.
Корреляцион-
ный анализ
Дифференци-
альное
исчисление
2.1.6.
Квадратичное
2.2.2.
Регрессионный анализ
2.6.
Теория массового обслуживания
2.4. Теория игр
2.3.
Комбина-
торные
методы
2.2.3.
Дисперсионный анализ
2.2.4.
Факторный анализ
2.7.
Теория управления запасами
2.8.
Метод экспертных оценок
2.5.
Теория расписания
2.1.3.
Целочисленное
1.1.2.
Вариационное исчисление
2.1.4.
Нелинейное
2.1.7.
Динамическое
2.1.8.
Параметрическое
2.1.9. Блочное
Рис.
1 – Классификация экономико-математических
методов
Методы
математической статистики используются
для нахождения и раскрытия закономерностей,
свойственных большим совокупностям
однородных объектов. При этом изучается
не каждый элемент совокупности, а
определенная выборка. Полученные
характеристики такой выборки могут
использоваться: 1) для сравнительной
оценки элементов различных совокупностей
или их характеристик, 2) для установления
связей между отдельными величинами, 3)
для прогнозирования на этой основе
развития системы в будущем. Математическая
статистика включает: корреляционный,
регрессионный, дисперсионный, факторный
анализы и др.
Оптимальное
программирование – это комплекс
специальных методов, обеспечивающих в
условиях множества возможных решений
выбор такого, которое является наилучшим
(оптимальным) по заданному критерию при
определенных ограничивающих условиях.
Оптимальное программирование –
эффективный инструмент решения задач
управления. В их числе: линейное,
вероятностное, целочисленное (дискретное)
программирование, нелинейное, выпуклое,
квадратичное, динамическое, параметрическое,
блочное и др.
В
математике решаемые на оптимум задачи
называются экстремальными. В них
требуется отыскать максимум или минимум
некоторой целевой функции.
Линейное
программирование используется при
решении задач в том случае, когда целевая
функция и ограничения выражены линейными
зависимостями. Эти методы в настоящее
время являются наиболее разработанными,
относительно простыми и понятными для
широкого использования. Существуют
эффективные алгоритмы для использования
вычислительной техники при их реализации.
Многие процессы допускают линейную
интерпретацию, а некоторые нелинейные
зависимости могут быть сведены к линейным
для ограниченного числа ситуаций.
Однако
в некоторых случаях применение линейных
методов искажает получаемые результаты,
что приводит к необходимости использования
и других методов.
Если
в системе равенств или неравенств
содержатся случайные элементы, но
зависимости между переменными линейные,
то такая задача решается методами
вероятностного программирования. Если
при нахождении неизвестных переменных
необходимо, чтобы одна из них или
несколько принимали только целочисленные
значения, то в этом случае при решении
такой задачи необходимо использовать
методы целочисленного программирования.
Методы
нелинейного программирования используются
тогда, когда целевая функция, или хотя
бы одно ограничение, выражены нелинейной
зависимостью. В числе методов нелинейного
программирования можно выделить
квадратичное и выпуклое программирование.
Выпуклое
программирование представляет собой
совокупность специальных методов
решения нелинейных экстремальных задач,
у которых выпуклы либо целевая функция,
либо ограничительные условия.
Квадратичное
программирование – это совокупность
методов решения особого класса
экстремальных задач, в которых ограничения
линейны, а целевая функция является
многочленом второй степени.
Методы
динамического программирования могут
применяться для решения оптимизационных
задач, в которых необходимо рассматривать
процесс управления или производства в
пространстве или во времени, т.е. в
развитии. Весь процесс поиска оптимального
решения представляется в виде определенной
последовательности шагов, для каждого
из которых находится оптимальное
решение, влияющее на последующие шаги
(принцип многошаговости Р.Беллмана).
В
моделях реальных экономических систем
коэффициенты целевой функции или
ограничения могут являться не постоянными
величинами, а изменяться в течение
определенного периода времени под
воздействием различных факторов. В этом
случае эффективными будут методы
параметрического программирования.
Модели,
содержащие большое число показателей,
очень сложны в реализации. Поэтому в
тех случаях, когда это возможно, их
преобразуют в несколько моделей меньшей
размерности. Полученные локальные
задачи решаются совместно с использованием
специальных методов, наиболее известным
из которых является метод разложения
Данцига-Вульфа. Это методы блочного
программирования.
Для
решения задач методами математического
программирования используются
комбинаторные методы, например, ветвей
и границ. В случае «трудной» задачи она
заменяется на набор задач, представляющих
ветвь. Чем больше ветвей, тем большее
значение получает целевая функция.
Граница предельной ветви достигается
в том случае, если значение критерия не
улучшается. К этим методам близко
подходят эвристические, основные на
опыте, интуиции исполнителя.
Когда
приходится принимать решения в условиях
неопределенноcти,
причем такое решение должно обеспечивать
наибольший эффект или наименьшие потери,
целесообразно пользоваться методами
теории игр.
Предметом
исследования теории массового обслуживания
являются вероятностные модели реальных
систем обслуживания, в которых в случайные
моменты времени возникают заявки на
обслуживание и имеются устройства для
обслуживания этих заявок. В экономике:
заявка – спрос на продукцию определенного
вида, обслуживающее устройство –
предприятия.
Теория
расписаний представляет собой систему
методов, позволяющих упорядочить во
времени использование системы машин
для обработки некоторого множества
изделий. При этом должны быть выполнены
определенные технологические условия
и обеспечено достижение оптимального
значения заранее заданного критерия
качества расписания.
studfiles.net
Математические методы экономических исследований
Международный институт
экономики и права
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ЭКОНОМИЧЕСКИХ ИССЛЕДОВАНИЙ
Контрольная работа
Тема 1. Системы, системный подход, системный анализ. Основные термины, определения, технологии
1. Понятие системы.
2. Системный подход, принципы системного подхода.
3. Системный анализ: постановка задачи, декомпозиция, композиция системы, исследование системы.
4. Структура системы.
Краткое содержание темы
Вообще строго определенного понятия системы в настоящее время не существует. Однако, для целей экономического исследования наиболее приемлемым будет следующее определение:
Система — это целостная совокупность элементов любого типа, взаимосвязанных между собой, взаимодействие которых обеспечивает достижение поставленной цели.
Таким образом, для системы характерно наличие:
· совокупности элементов;
· взаимосвязи элементов через структуру;
· взаимодействия;
· целенаправленности.
Элемент системы — это структурная единица системы, не подлежащая делению в данных условиях рассмотрения системы.
Основным свойством системы является то, что она обладает характеристиками, принципиально отличными от характеристик составляющих ее элементов. Только интегративное взаимодействие ее элементов позволяет системе достигнуть уникальных свойств.
Системный подход — это конкретно-научный метод диалектической методологии, имеющей общенаучное значение. Методология изучения системы как единого целого, состоящего из отдельных частей, с различных точек зрения формализации позволяет сформулировать следующие принципы системного подхода.
Принцип конечной цели: абсолютный приоритет конечной (глобальной ) цели.
Принцип единства: совместное рассмотрение системы как целого и как совокупности частей (элементов).
Принцип связности: рассмотрение любой части совместно с ее связями с окружением.
Принцип модульного построения: выделение модулей (подсистем) в системе и рассмотрение ее как совокупность подсистем.
Принцип иерархии: выделение иерархии частей (элементов) и (или) их ранжирование.
Принцип функциональности: совместное рассмотрение структуры и функций с приоритетом функций над структурой.
Принцип развития: учет изменяемости системы, ее способности к развитию, расширению, замене частей, накапливанию информации.
Принцип децентрализации: сочетание в принимаемых решениях управления централизации и децентрализации.
Принцип неопределенности: учет неопределенностей и случайностей в системе.
Совокупность приемов и методов для изучения сложных систем представляет собой системный анализ. Системный анализ — это средство и технология системного подхода.
Рассмотрим основные этапы системного анализа.
1. Постановка задачи. Она включает:
· определение объекта исследования;
· постановку целей;
· задание критериев для изучения объекта и управления им.
Этап слабоформализуем. Успех постановки задачи определяется в основном искусством и опытом системного аналитика, глубиной понимания им поставленной проблемы.
2. Структуризация и очертание границ (декомпозиция) изучаемой системы. Она включает:
· разбиение совокупности всех объектов и процессов, отвечающих поставленной цели, на два класса: собственно исследуемую систему и внешнюю среду;
· изучение процессов взаимодействия объектов (элементов) системы и внешней среды.
Этап слабоформализуем. Он основан на искусстве и опыте проводящих этот этап специалистов.
Разбиение объектов и процессов осуществляется в результате последовательного перебора и включения в систему объектов и процессов, оказывающих заметное влияние на процесс достижения поставленной цели.
3. Составление модели изучаемой системы (как правило, математической).
Параметризация — первый этап этого процесса. Осуществляется описание элементов системы и элементарных воздействий с помощью тех или иных параметров. Параметры могут принимать как непрерывные, так и дискретные числовые значения, а также значения в виде признаков, которые не могут быть охарактеризованы с помощью обычных числовых параметров, а различаются качественно (например: теплый, холодный, плохой, хороший).
Установление различного рода зависимостей между введенными параметрами. Характер этих зависимостей может быть любым. Количественные (числовые) параметры связываются зависимостями типа систем уравнений (обыкновенных алгебраических или дифференциальных). Качественные параметры связываются зависимостями типа таблиц. В общем случае могут встречаться комбинации зависимостей различных типов.
Зависимости между параметрами в системах задаются в общем случае не простыми формулами, а произвольными алгоритмами с использованием любых средств как количественных, так и описательных.
Выделение подсистем и установление их иерархии преследует цель не только упрощения описания системы. Этот процесс дает возможность осуществлять уточнение первоначальной структуризации (разбиения на элементы) и параметризации системы.
Результатом этого этапа является законченная математическая модель системы, описанная на формальном языке.
4. Исследование полученной (построенной) системы — четвертый этап системного анализа.
Первая задача этапа — прогноз развития изучаемой системы.
Для решения этой задачи задают различные предположения о внешних воздействиях на систему в течение рассматриваемого периода и с помощью модели определяют распределение значений, характеризующих систему параметров для любых фиксированных моментов времени.
Термин “прогноз развития” подчеркивает то обстоятельство, что для системы нельзя определить единственную траекторию развития, можно определить лишь множество таких траекторий. При этом каждая траектория может реализоваться в действительности лишь с той или иной степенью вероятности.
Получив прогноз развития изучаемой системы, производят анализ его результатов на соответствие заданным целям и критериям и вырабатывают предложения по улучшению управления и т.д., пока не получится удовлетворяющий результат.
Под структурой системы понимается организация системы из отдельных элементов с их взаимосвязями, которые определяются распределением функций и целей, выполняемых системой.
Структура — это способ организации целого из составных частей .
Эффективность структуры определяется качеством, значением, формой и содержанием ее составных частей, а также местом, которое занимают они в целом, и существующими между ними отношениями.
По принципам управления и подчиненности различают структуры (системы): централизованные, децентрализованные, смешанные.
Централизованная система: задания отдельным элементам системы выдаются лишь одним элементом более высокого уровня.
Децентрализованная система: решения отдельными элементами системы принимаются независимо и не корректируются системой более высокого уровня.
В смешанной системе некоторые функции или этапы выполняются по централизованной системе, а другие — по децентрализованной.
По числу уровней иерархии различают системы: одноуровневые, многоуровневые.
Многоуровневые могут быть однородными и неоднородными.
По выполняемым функциям и целевому назначению различают системы: физические, экономические, биологические, общественные, информационные и т.д.
В зависимости от числа элементов системы и связей между ними различают системы фиксированной (жесткой) и изменяемой (управляемой или переменной) структуры.
По принципам разбиения систем на подсистемы различают структуры систем, в которых элементы объединяются по функциональному и (или) объектному принципам. При объектном разбиении различают структуры отраслевых систем, региональных систем, территориальных систем.
1. Методы математической статистики.
2. Методы исследования операций и оптимизации.
3. Кибернетические методы.
4. Методы экспертных оценок.
Краткое содержание темы
Основой моделирования экономических систем и протекающих в них процессов являются экономико-математические методы. Рассмотрим состав и структуру экономико-математических методов, применяемых в современной экономической науке и практике.
К старейшим и наиболее используемым классам экономико-математических методов относятся методы математической статистики. Эти методы используются для анализа деятельности экономических систем и включают в себя следующие направления:
· расчет и интерпретация статистических характеристик экономических процессов;
· рег
mirznanii.com











 мала, то из формулы (2) следует, что малы
слагаемые.
Поэтому, если не рассматривать значения,
которым соответствует малая вероятность
(такие значения практически невозможны),
то все остальные значения
мала, то из формулы (2) следует, что малы
слагаемые.
Поэтому, если не рассматривать значения,
которым соответствует малая вероятность
(такие значения практически невозможны),
то все остальные значения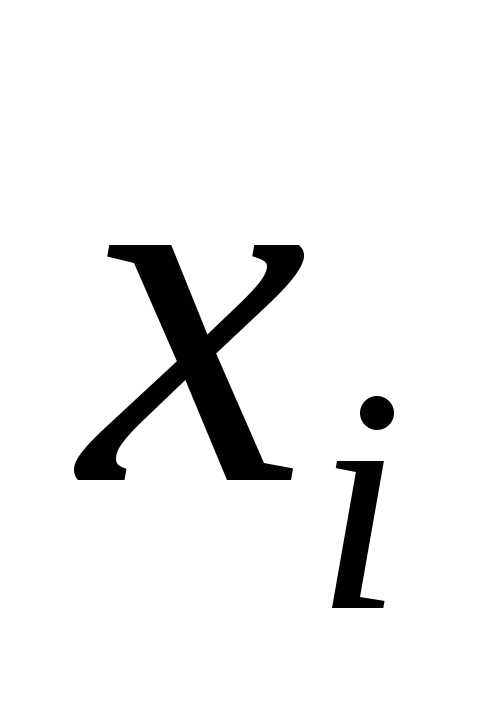 мало отклоняются от математического
ожидания
мало отклоняются от математического
ожидания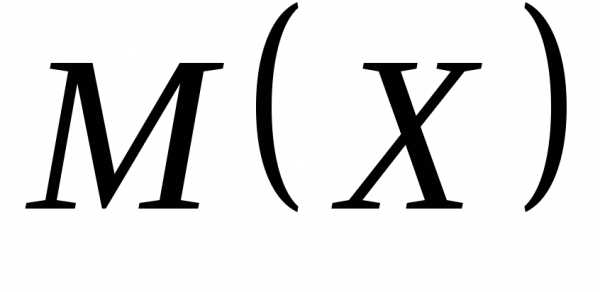 .
Следовательно,при
малой дисперсии возможные значения
случайной величины концентрируются
около ее математического ожидания (за
исключением, может быть, сравнительно
малого числа отдельных значений). Если
дисперсия
.
Следовательно,при
малой дисперсии возможные значения
случайной величины концентрируются
около ее математического ожидания (за
исключением, может быть, сравнительно
малого числа отдельных значений). Если
дисперсия 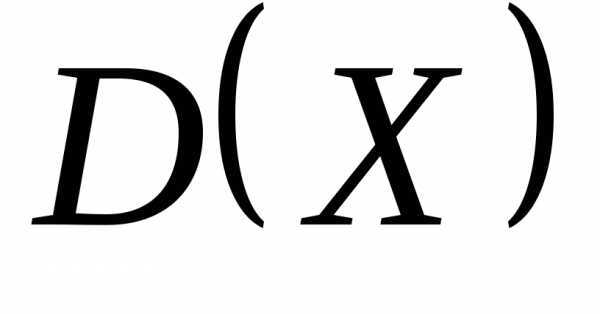 велика, то это означает большой разброс
значений случайной величины, концентрация
значений случайной величины около
какого-нибудь центра исключается.
велика, то это означает большой разброс
значений случайной величины, концентрация
значений случайной величины около
какого-нибудь центра исключается.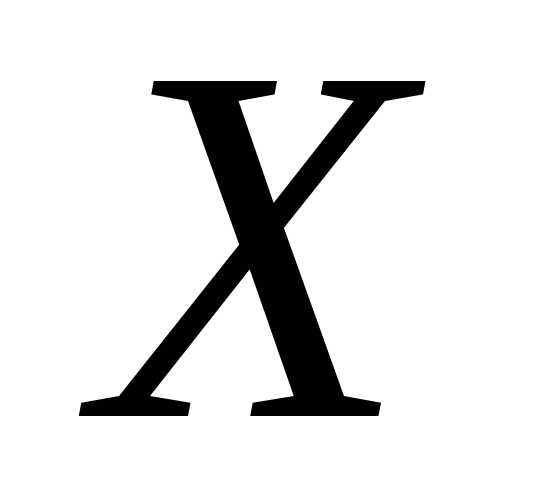 и
и имеют следующее законы распределения
имеют следующее законы распределения

 и
и одинаковы, однако дисперсии различны.
Дисперсия случайной величины
одинаковы, однако дисперсии различны.
Дисперсия случайной величины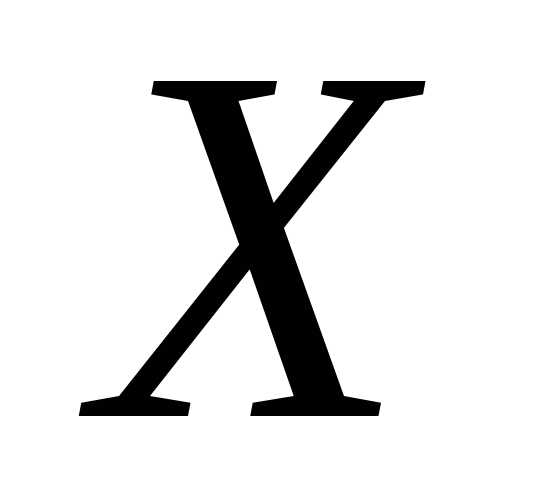 мала и мы видим, что ее значение
сконцентрированы около ее математического
ожидания.
Напротив, значения случайной величины
мала и мы видим, что ее значение
сконцентрированы около ее математического
ожидания.
Напротив, значения случайной величины значительно рассеяны относительно,
а поэтому дисперсия
значительно рассеяны относительно,
а поэтому дисперсия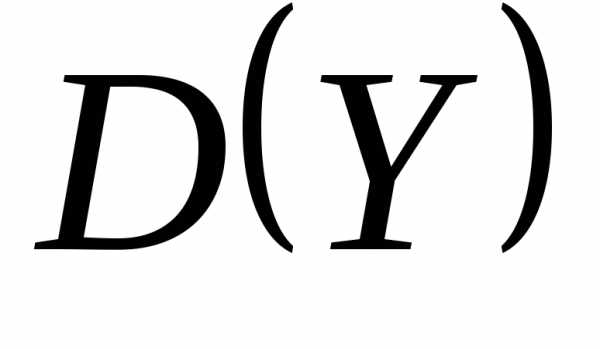 имеет большое значение. ●
имеет большое значение. ●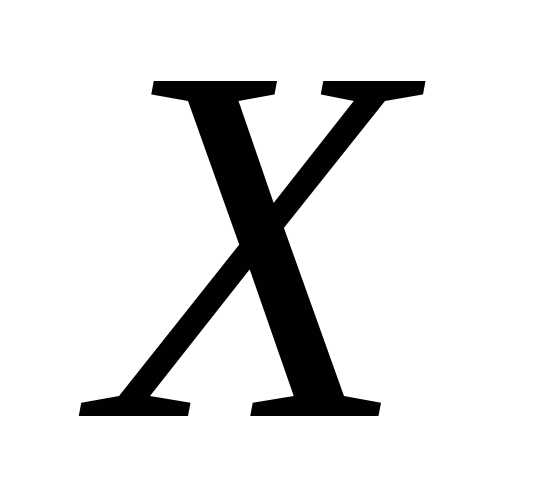 и
и  от их математических ожиданий называется корреляционным
моментом этих
величин
от их математических ожиданий называется корреляционным
моментом этих
величин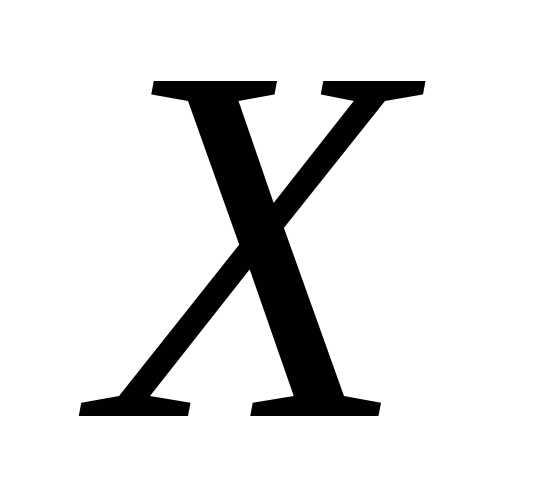 и
и независимы, то, воспользовавшись
свойствами 6 и 7 математических ожиданий,
находим
независимы, то, воспользовавшись
свойствами 6 и 7 математических ожиданий,
находим Y]
= D[X]+D[Y]. если случайные величины Х и Y независимы
Y]
= D[X]+D[Y]. если случайные величины Х и Y независимы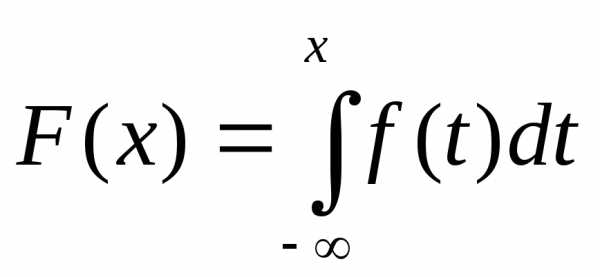 то функция f(x)
называется плотностью распределения
вероятности.
то функция f(x)
называется плотностью распределения
вероятности.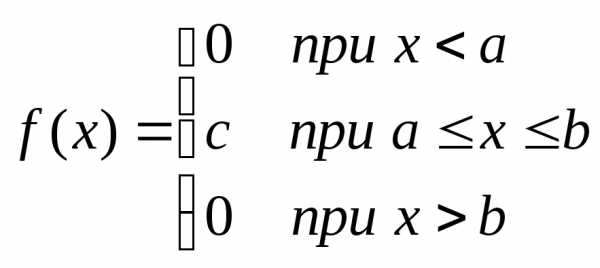
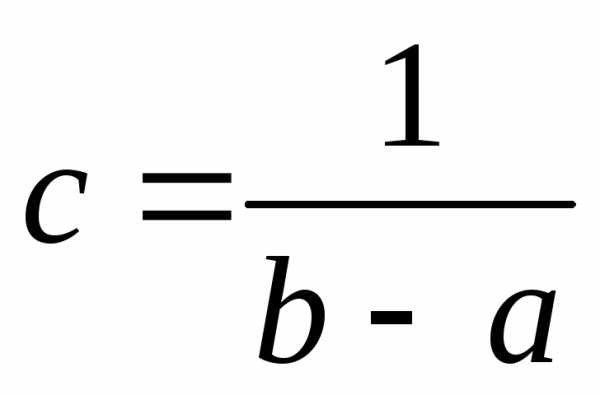 .
.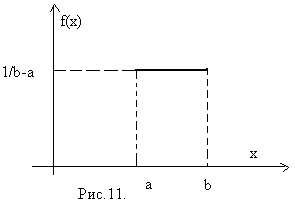 рафик
плотности распределения приведен на
рисунке. Если какой-либо отрезок [α,β]целиком содержится в [а,b],то вероятность попадания в него случайной
величины Х равна
рафик
плотности распределения приведен на
рисунке. Если какой-либо отрезок [α,β]целиком содержится в [а,b],то вероятность попадания в него случайной
величины Х равна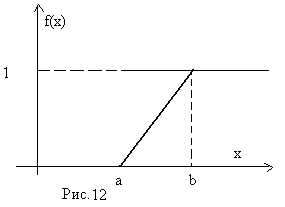 .
.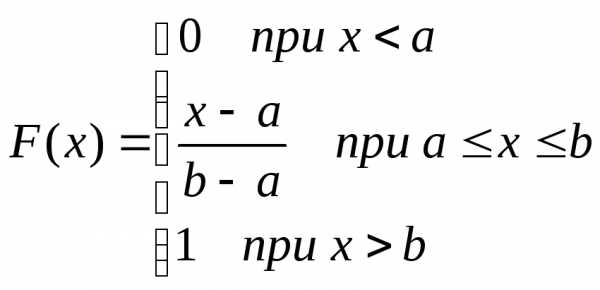
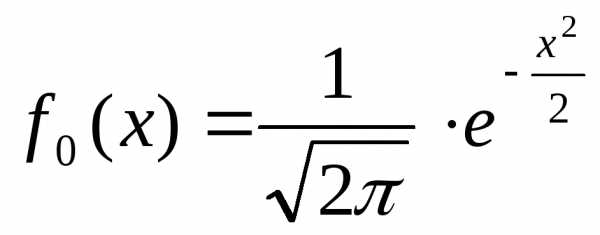
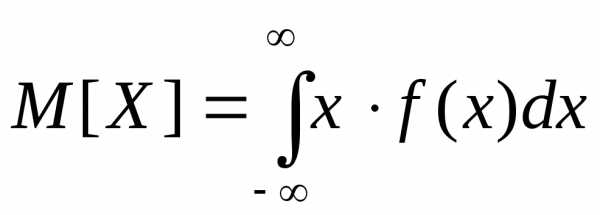
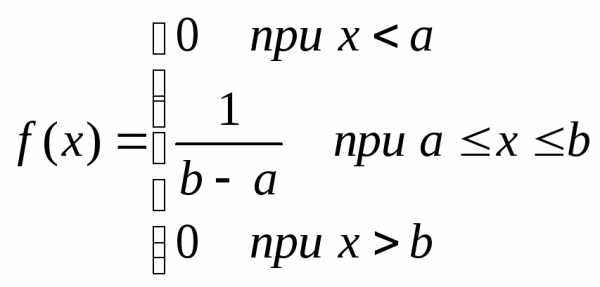
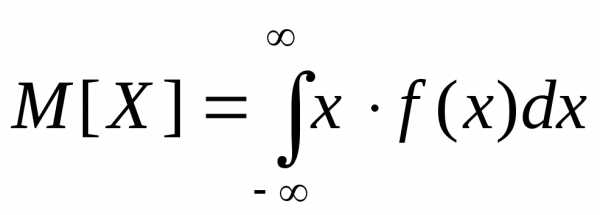
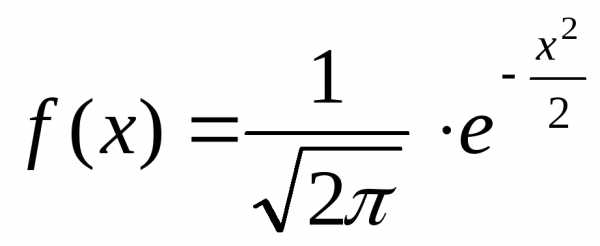
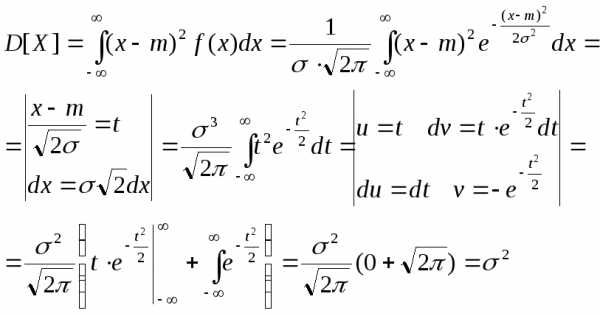
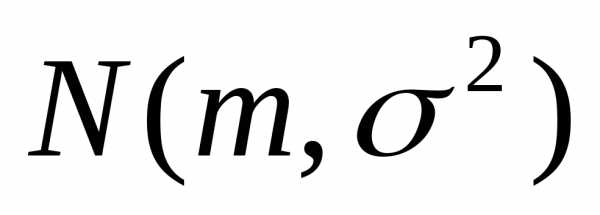 которая имеет график, представленный
на рисунке.
которая имеет график, представленный
на рисунке. — любая первообразная для подынтегральной
функции
— любая первообразная для подынтегральной
функции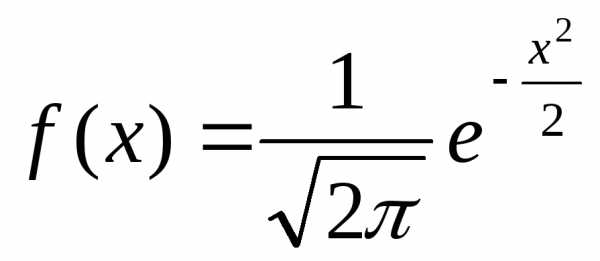
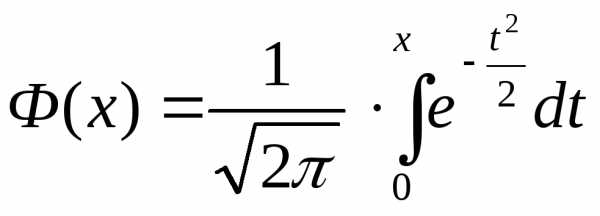
 + 2
+ 2 + 3
+ 3 =
= 
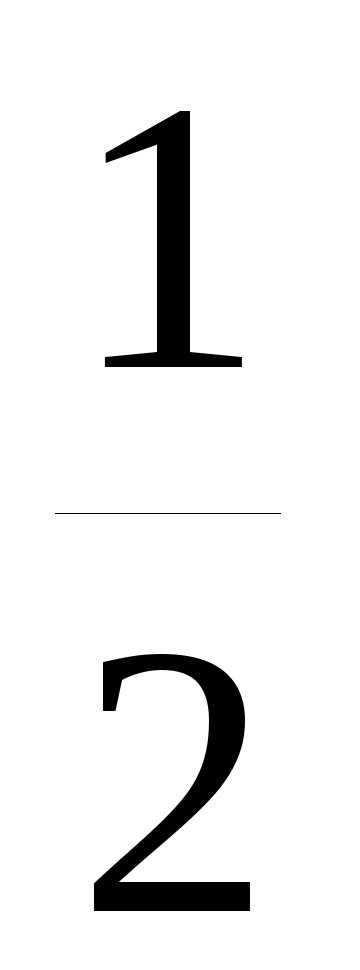 +
+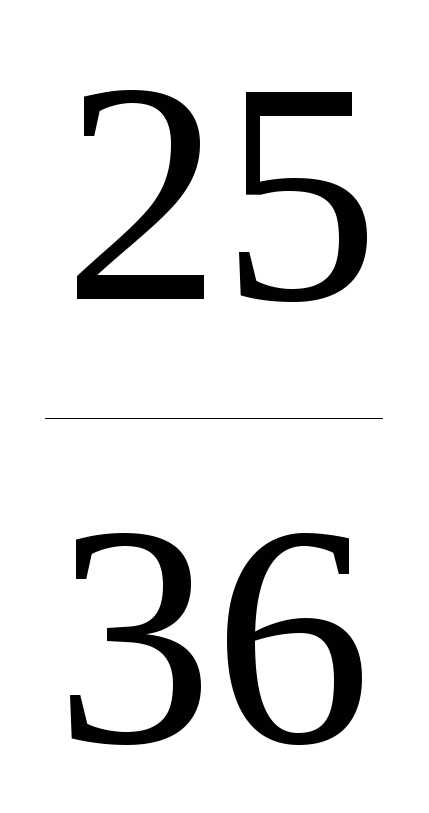
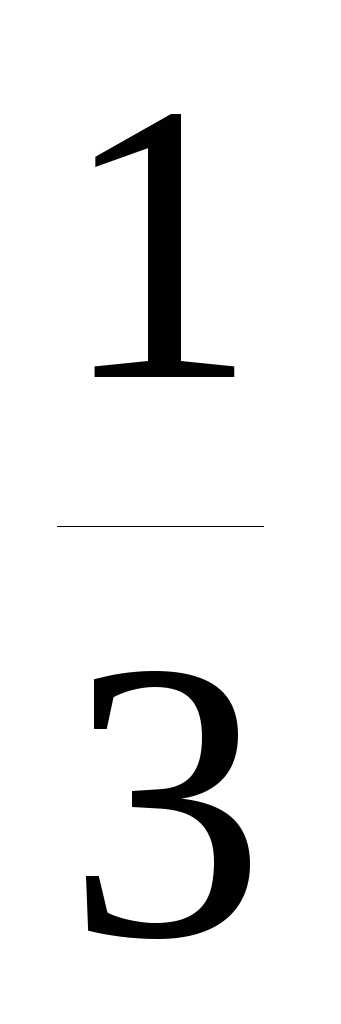 +
+
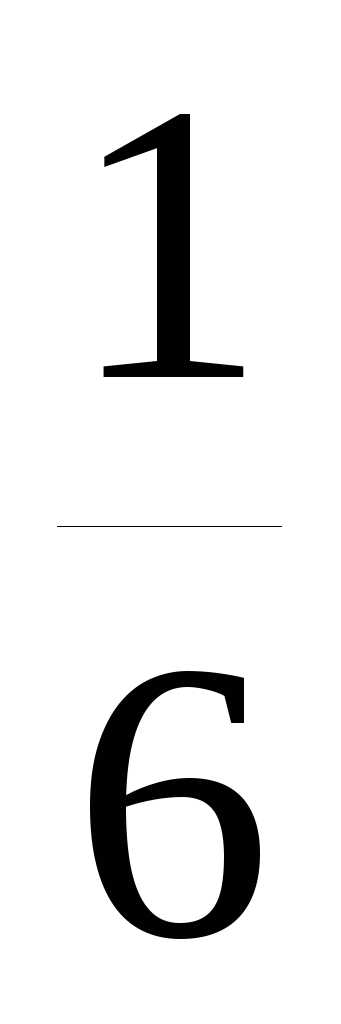 =
=
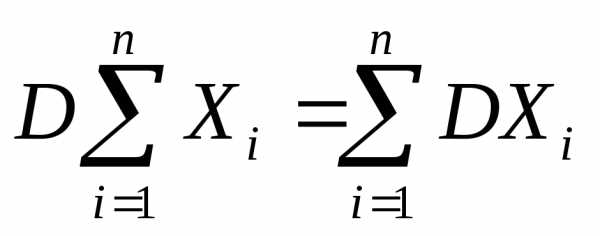
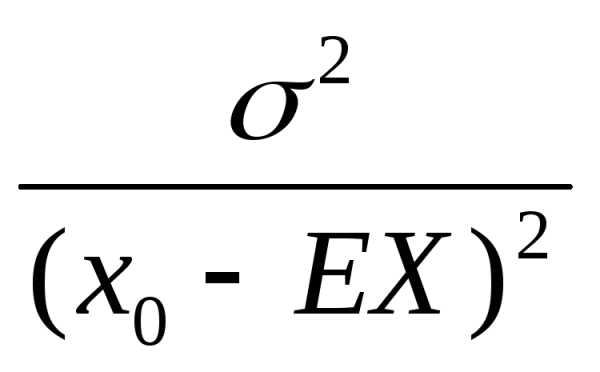
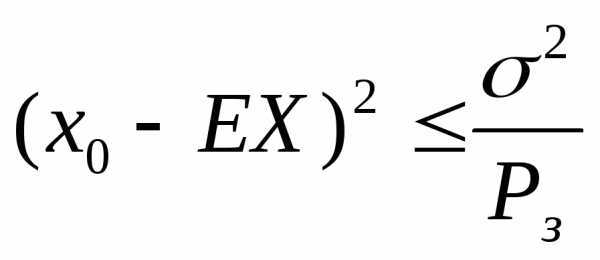 и
и 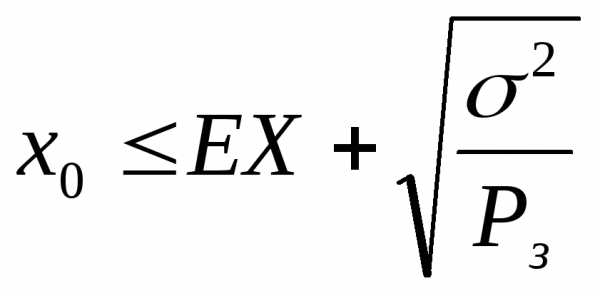
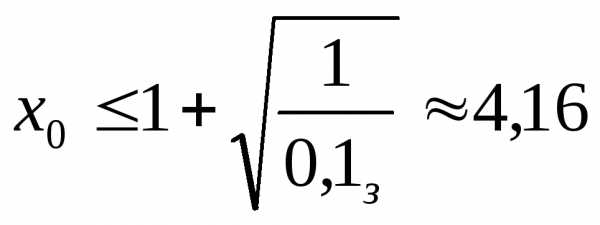
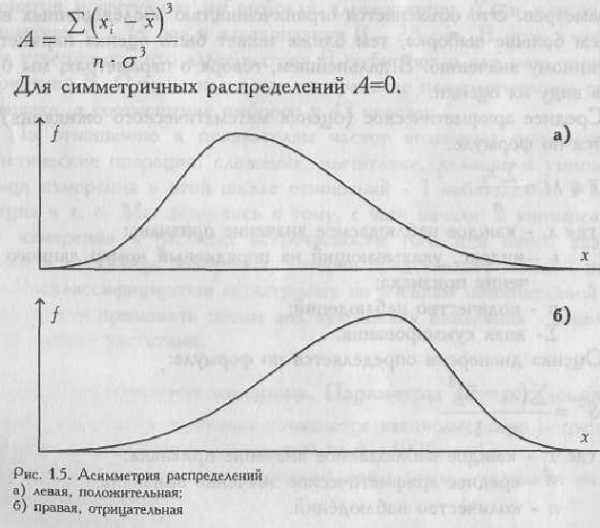
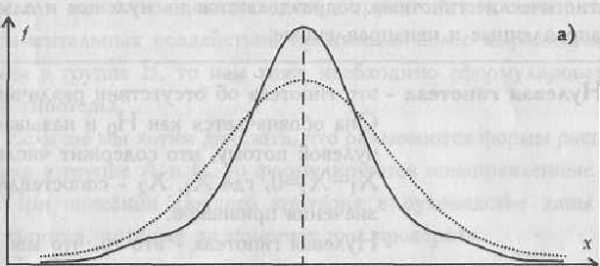
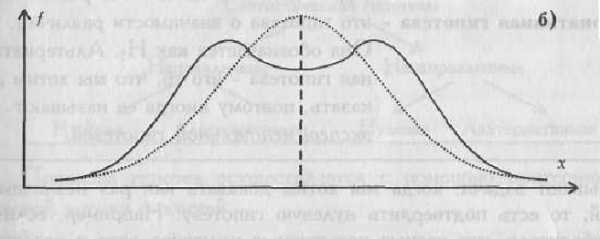
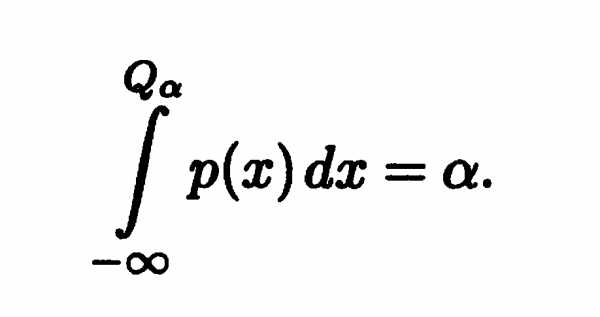
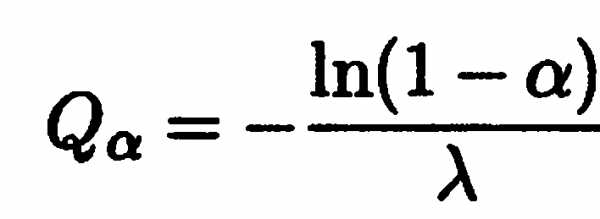 ,
а медиана равна
,
а медиана равна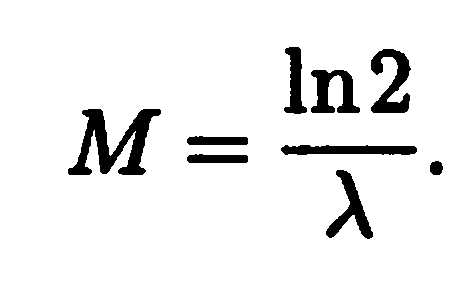
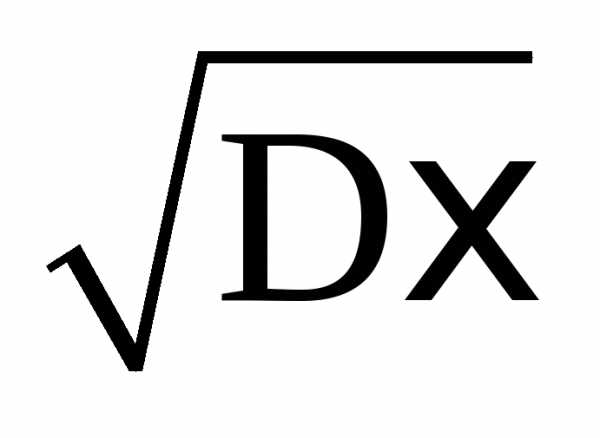 (2.19)
(2.19)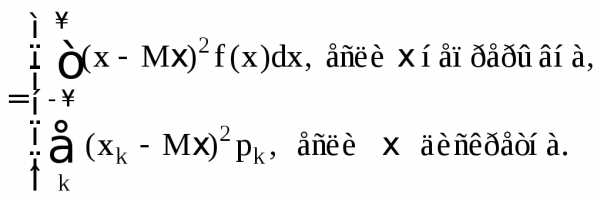 (2.20)
(2.20)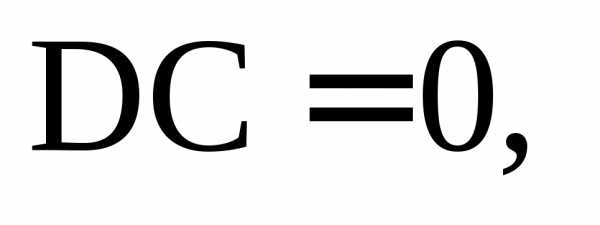 если.
если. независимы.
независимы.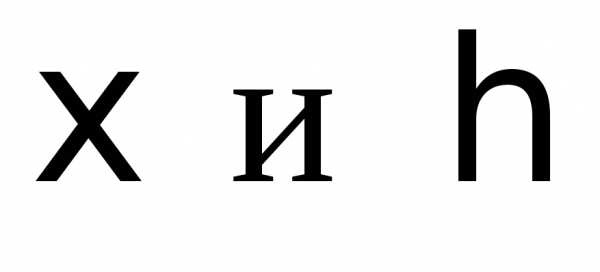 независимы – это с одной стороны; с
другой стороны
независимы – это с одной стороны; с
другой стороны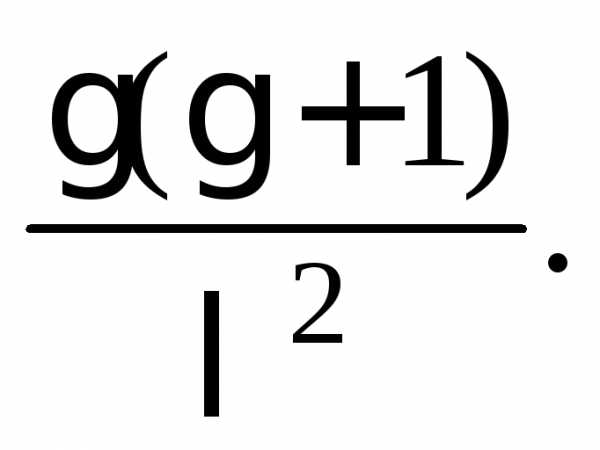 Из примера 16 возьмем величину
Из примера 16 возьмем величину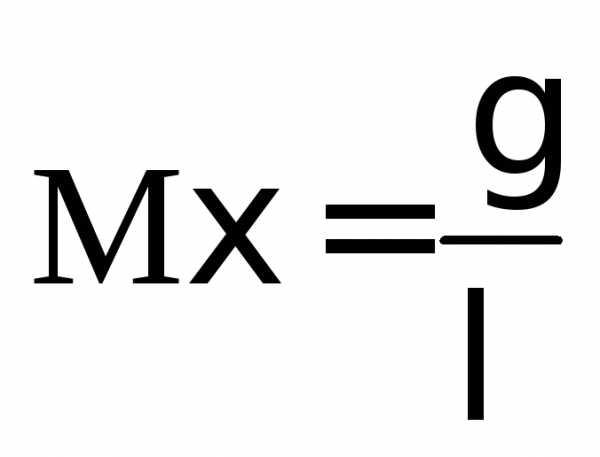
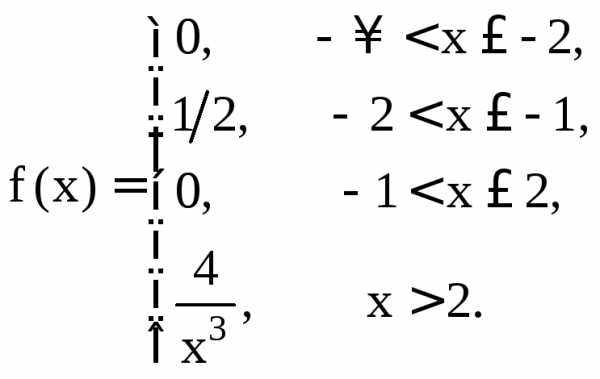
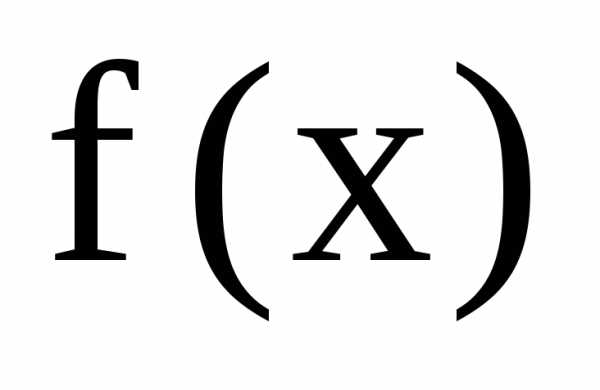 удовлетворяет, в частности,
удовлетворяет, в частности, cл.
величины
cл.
величины  называется
число
называется
число cл.
величины
cл.
величины  называется число
называется число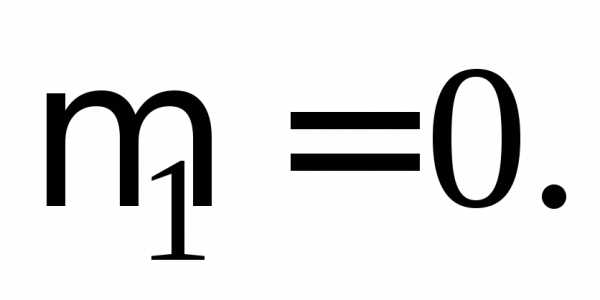
 сл. величины ξ называются число
сл. величины ξ называются число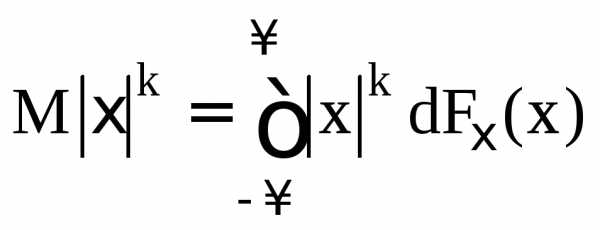 .
. и Мо ξ соответственно.
и Мо ξ соответственно. –
определяется из соотношения.
Из определения следует, что медиана сл.
величины – это любое решение уравнения
–
определяется из соотношения.
Из определения следует, что медиана сл.
величины – это любое решение уравнения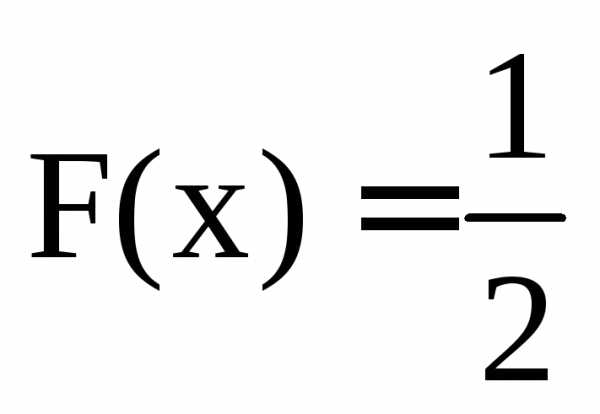 .
Поскольку решение этого уравнения не
единственно, то медиана сл. величины
определяется неоднозначно.
.
Поскольку решение этого уравнения не
единственно, то медиана сл. величины
определяется неоднозначно.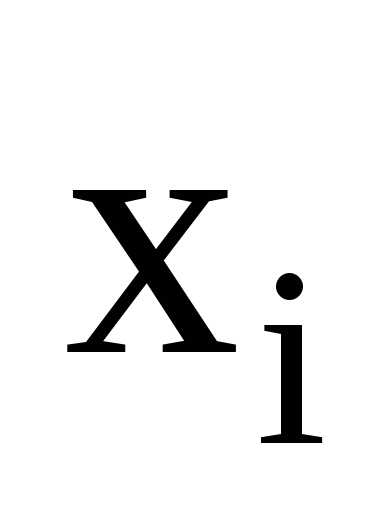 ,
для которого
,
для которого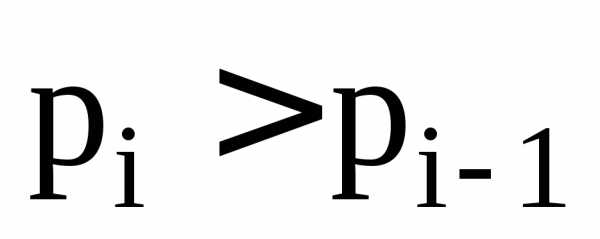 и
и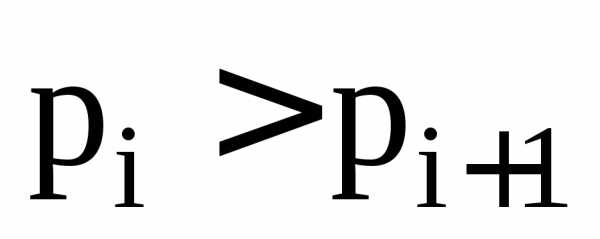 ,
при этом все ее значения должны быть
расположены в порядке возрастания.
,
при этом все ее значения должны быть
расположены в порядке возрастания.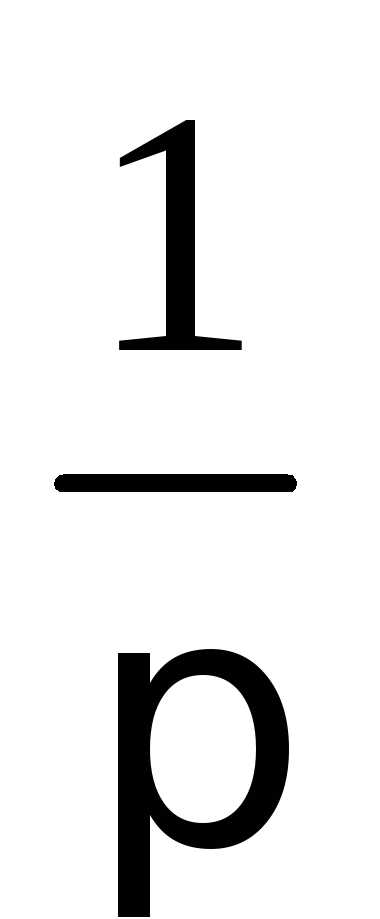 .
Следовательно, Мо ξ = 0.
.
Следовательно, Мо ξ = 0.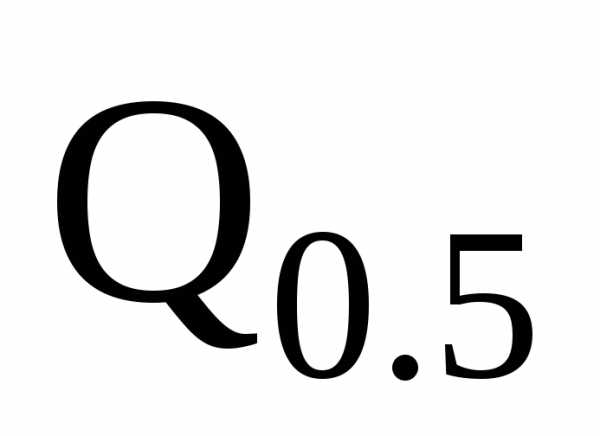 – это медиана случайной величиныMe :
– это медиана случайной величиныMe :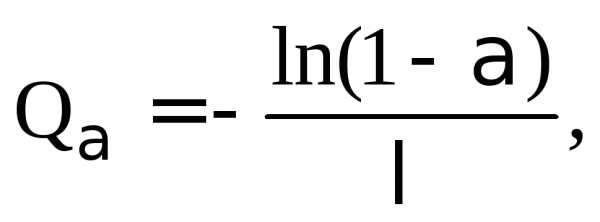
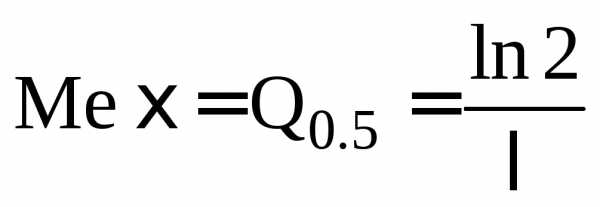 .
. сл. величины
называется число
сл. величины
называется число 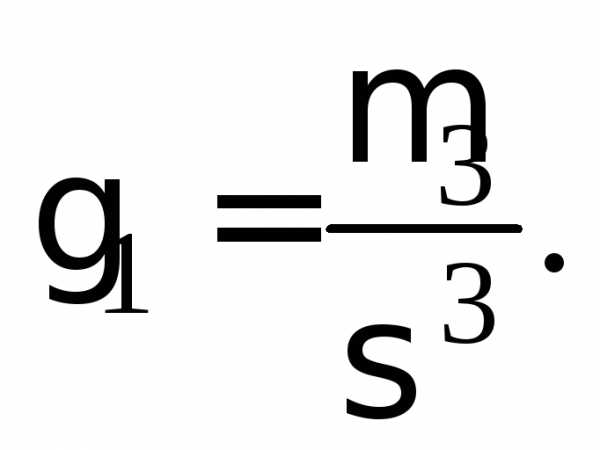 Еслидля
любого х, то
Еслидля
любого х, то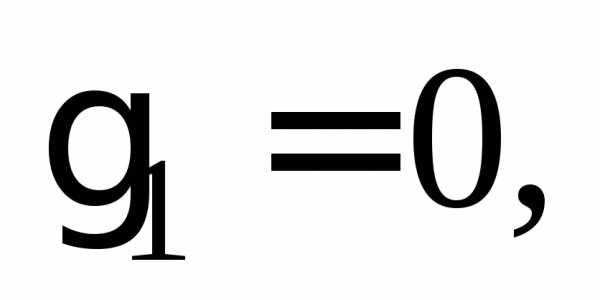 так как в этом случае все центральные
моменты нечетных порядков равны нулю.
Равенство вероятностей означает, что
сл. величина распределена симметрично
относительно своего математического
ожидания.
так как в этом случае все центральные
моменты нечетных порядков равны нулю.
Равенство вероятностей означает, что
сл. величина распределена симметрично
относительно своего математического
ожидания. >
0, то функция плотности распределения
по отношению к ее математическому
ожиданию имеет сдвиг вправо; для
>
0, то функция плотности распределения
по отношению к ее математическому
ожиданию имеет сдвиг вправо; для < 0 – влево.
< 0 – влево. для случайной величины, имеющей нормальный
закон распределения.
для случайной величины, имеющей нормальный
закон распределения.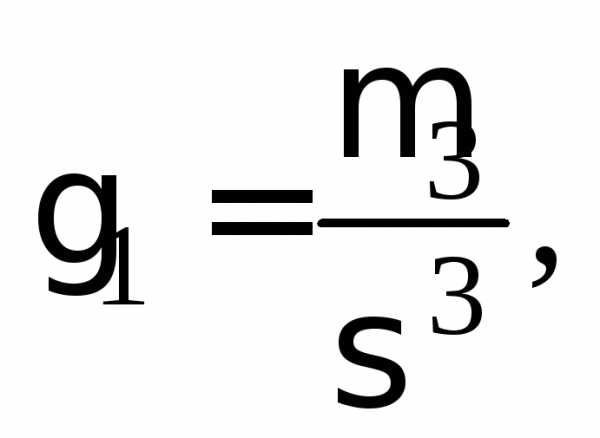 вычислим составляющие этойформулы:
– интеграл от нечетной подынтегральной
функции по симметричному промежутку.
Тогда
вычислим составляющие этойформулы:
– интеграл от нечетной подынтегральной
функции по симметричному промежутку.
Тогда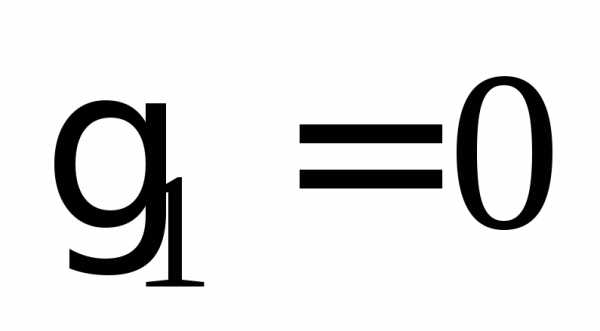 .
.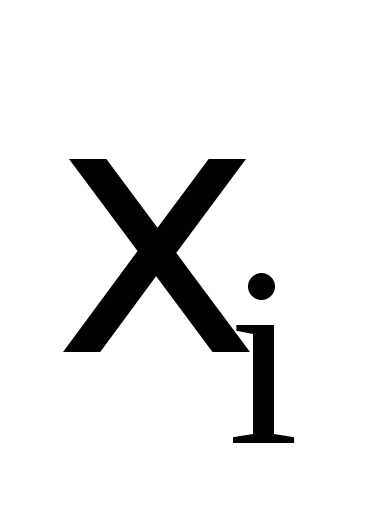 переходить к сл. величине
переходить к сл. величине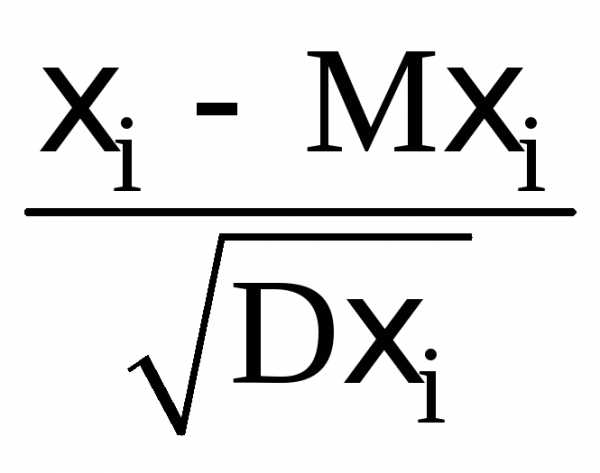 .
Вновь полученные сл. величины имеют те
же значения
.
Вновь полученные сл. величины имеют те
же значения ,
что и исходные.
,
что и исходные. сл. величины
называется число
сл. величины
называется число 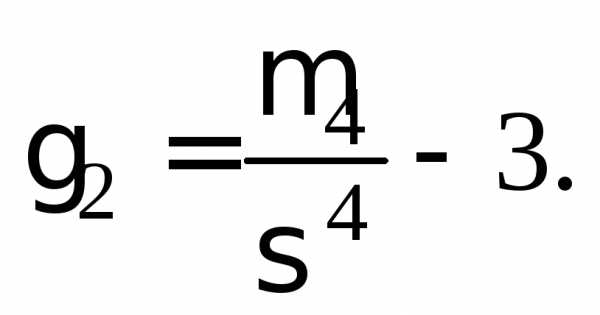 Эксцесс, как правило, используется для
характеристики симметричности
унимодальных распределений.
Эксцесс, как правило, используется для
характеристики симметричности
унимодальных распределений. = 0, так как
= 0, так как > 0, то кривая плотности распределения
более островершинна, чем при нормальном
распределении; если
> 0, то кривая плотности распределения
более островершинна, чем при нормальном
распределении; если < 0, то кривая плотности распределения
более плоская, чем при нормальном
распределении. При этом справедливо
замечание относительно преобразования
сравниваемых сл. величин, сделанное
выше. Более подробно эти вопросы можно
изучить по специальной литературе по
теории вероятностей и математической
статистике.
< 0, то кривая плотности распределения
более плоская, чем при нормальном
распределении. При этом справедливо
замечание относительно преобразования
сравниваемых сл. величин, сделанное
выше. Более подробно эти вопросы можно
изучить по специальной литературе по
теории вероятностей и математической
статистике.


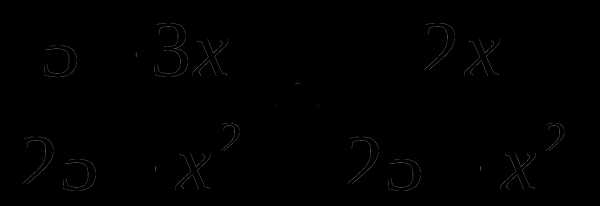 при
при  .
.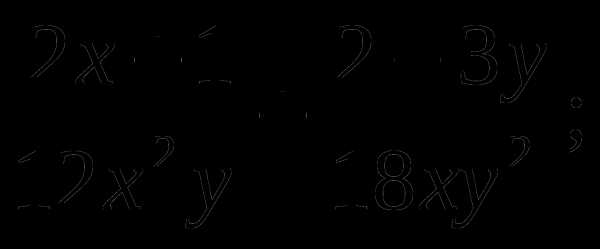 в)
в)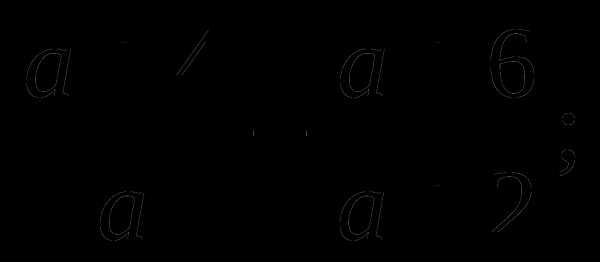 г)
г) 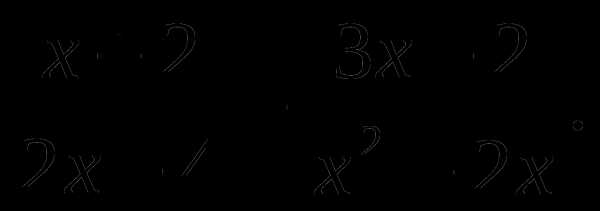
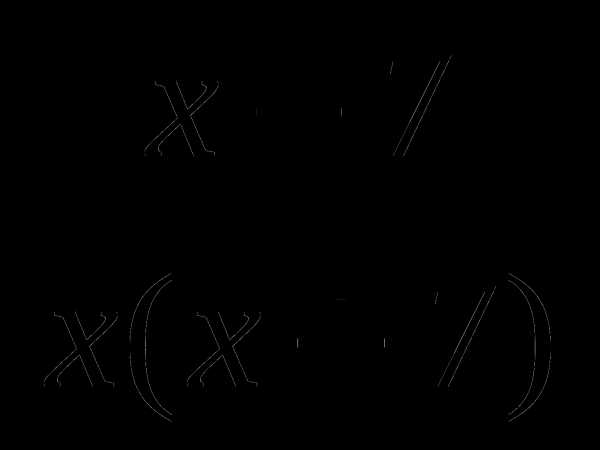
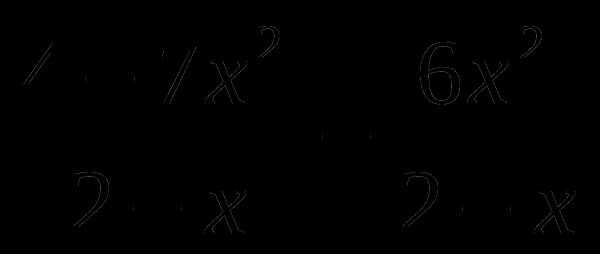 при
при 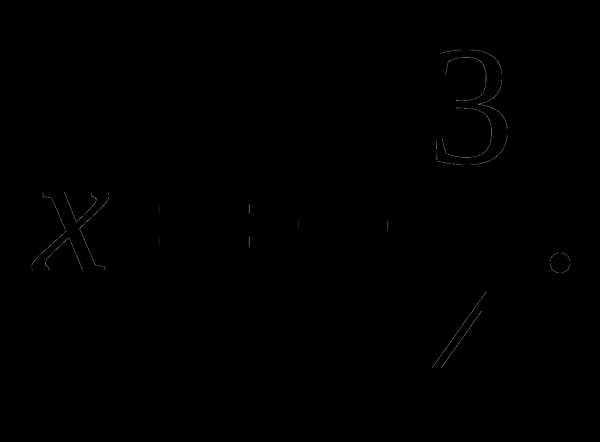
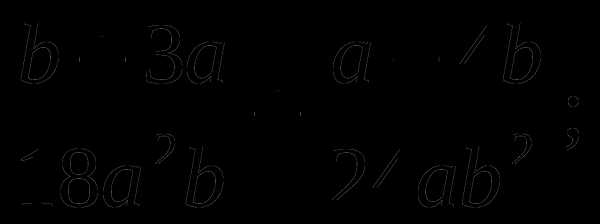 в)
в)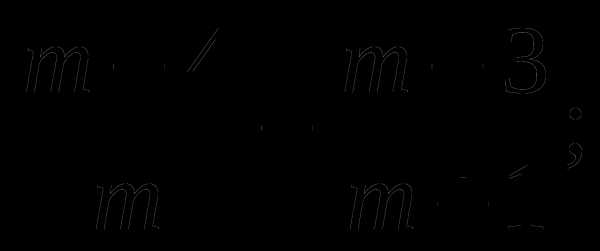 г)
г) 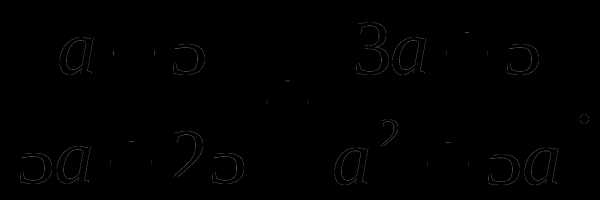
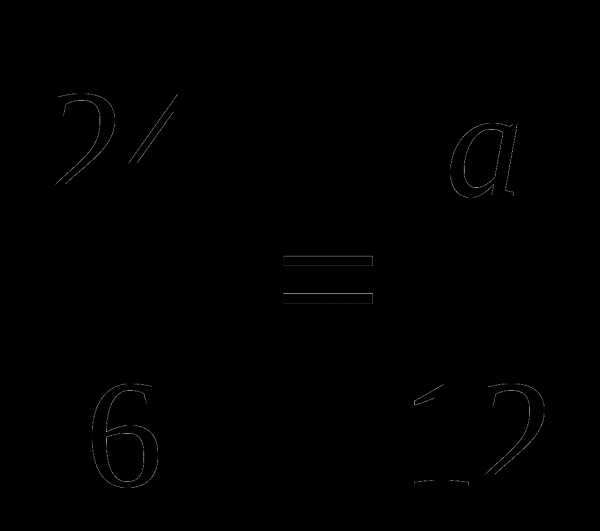 ; 2)
; 2) 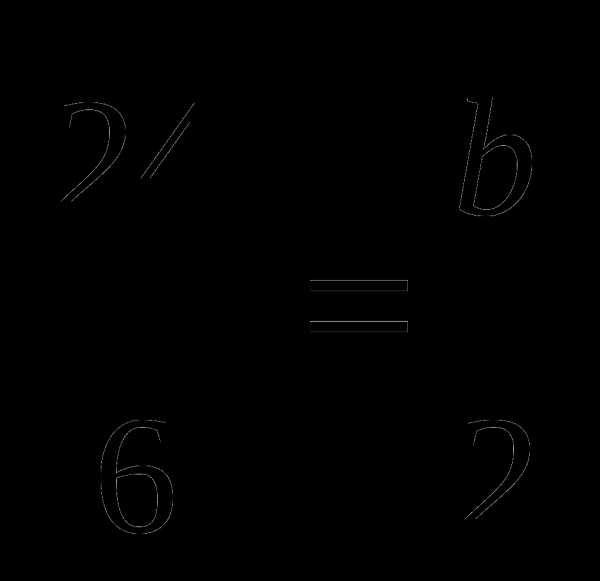 ; 3)
; 3) 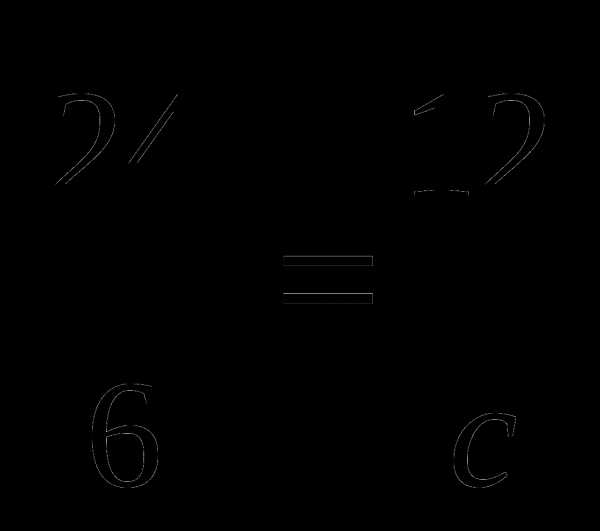 ; 4)
; 4) 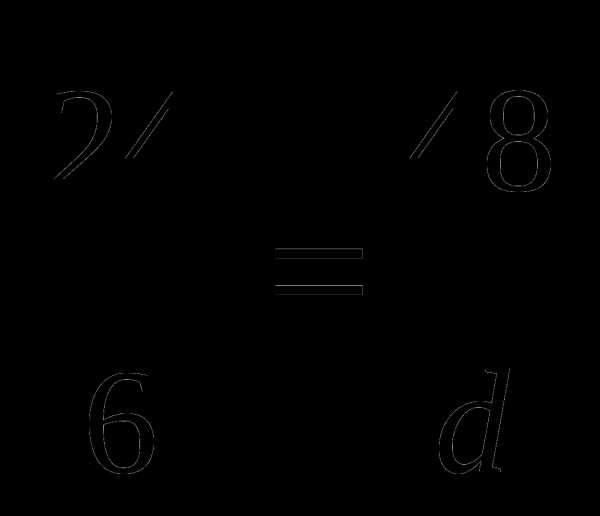 ?
? .
. ;
; ;
; ;
; ,
,  .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6)  ?
? ;
; ;
; ;
;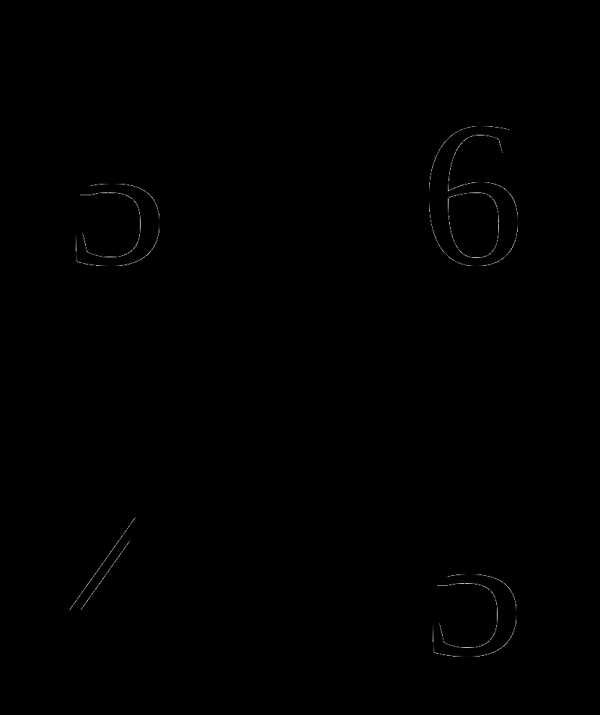 .
.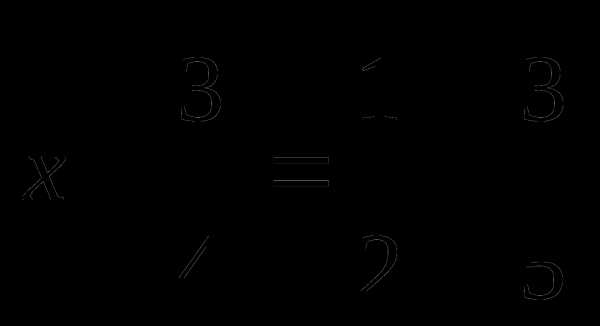 .
. ;
; ;
;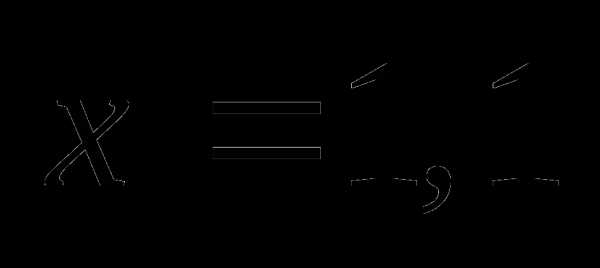 ;
;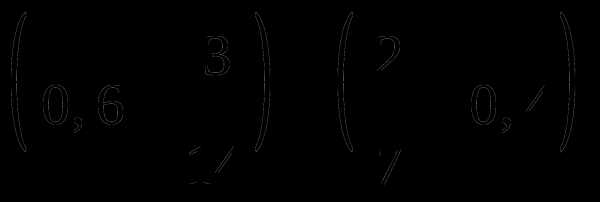 .
.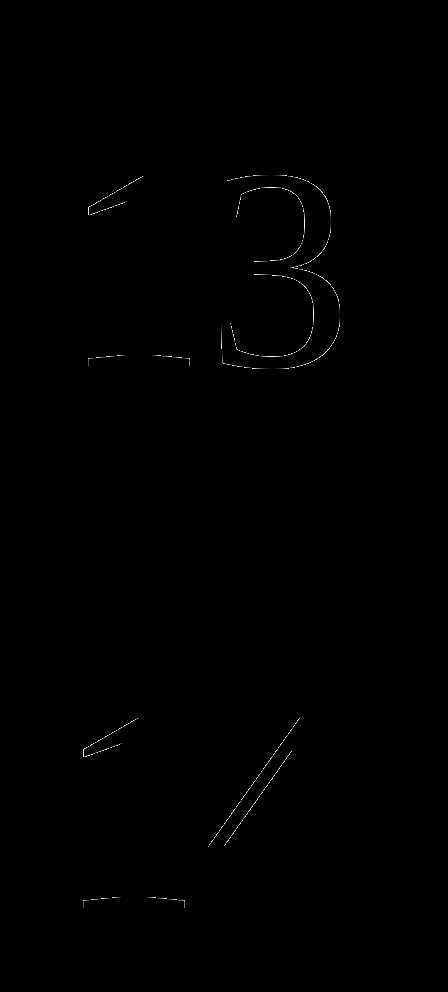 ;
;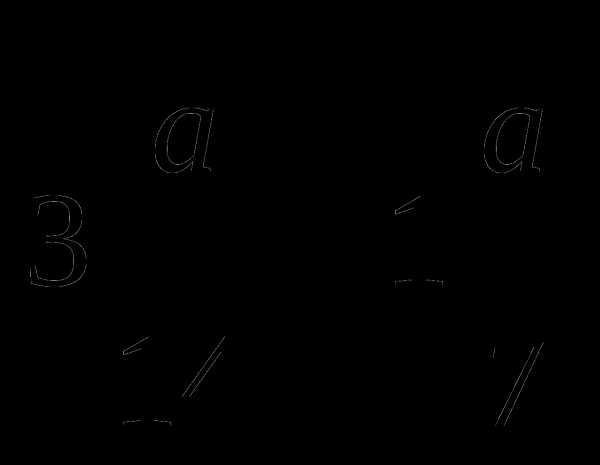 равно 2?
равно 2?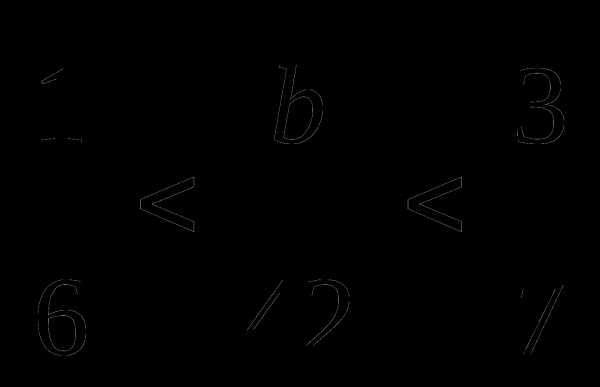 ?
?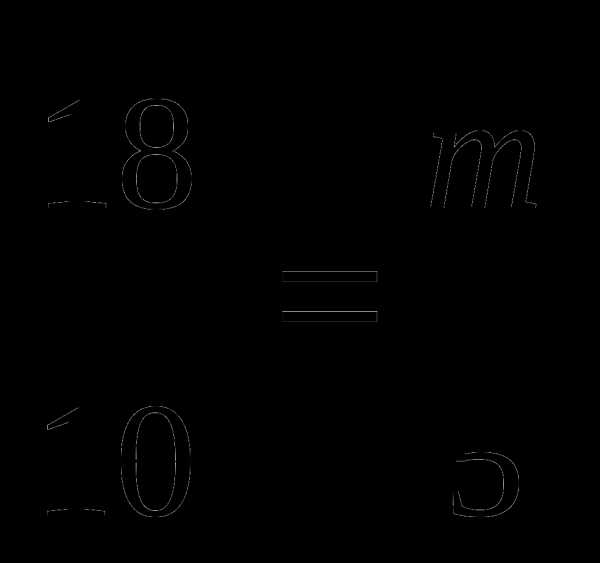 ; 2)
; 2) 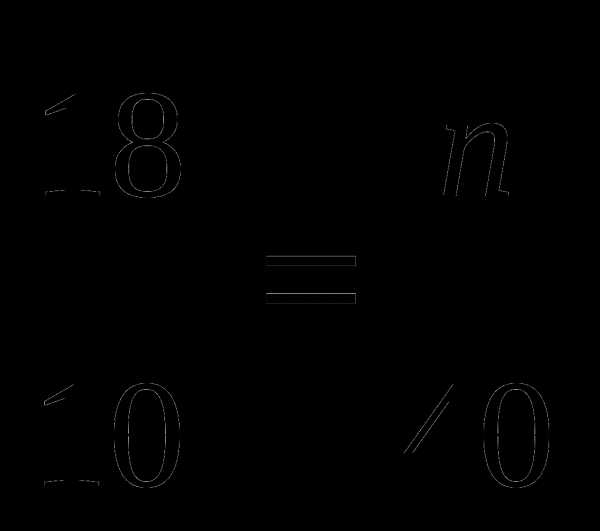 ; 3)
; 3) 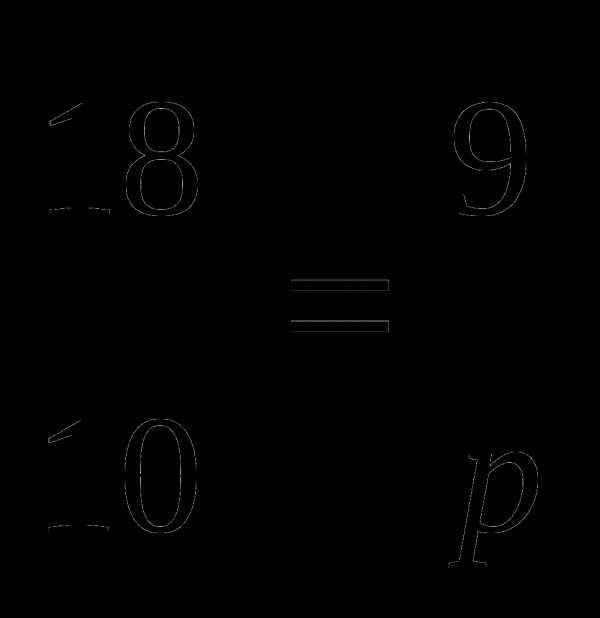 ; 4)
; 4) 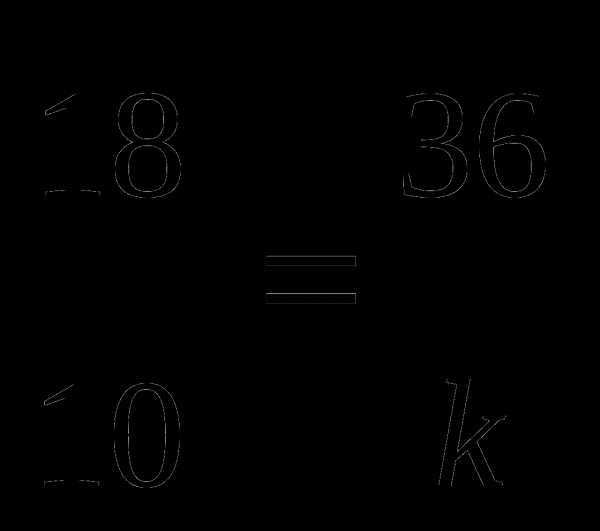 ?
? .
. ;
; ;
; ;
; ,
,  и
и  .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6)  ?
? ;
; ;
; ;
; .
.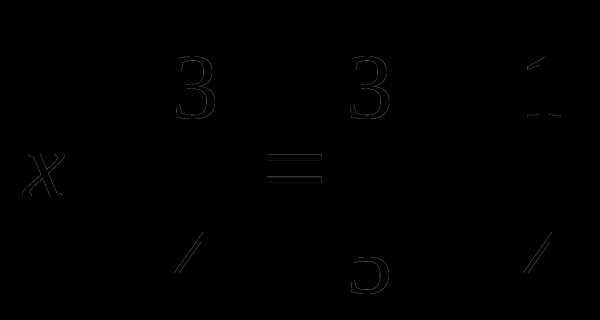 .
.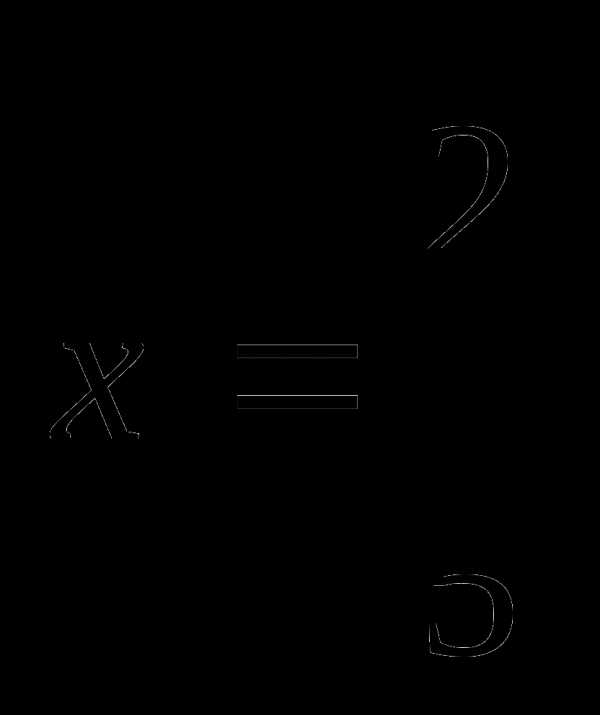 ;
; ;
; равно 1?
равно 1?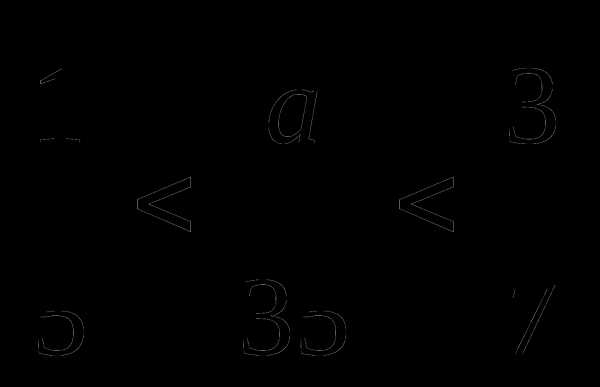 ?
? ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 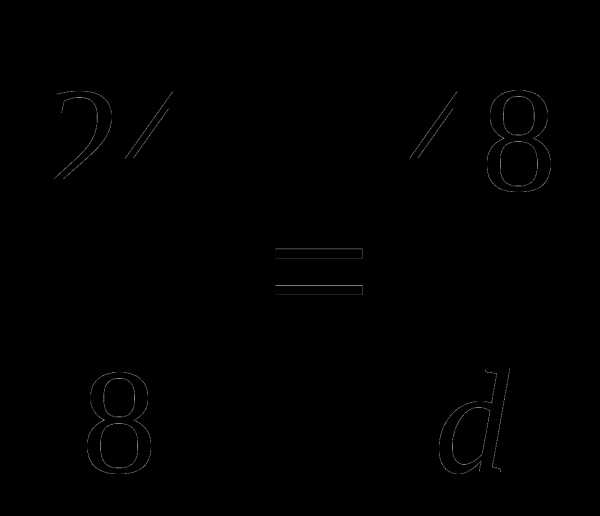 ?
? .
. ;
; ;
; ;
; ,
,  и
и  .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6)  ?
? .
.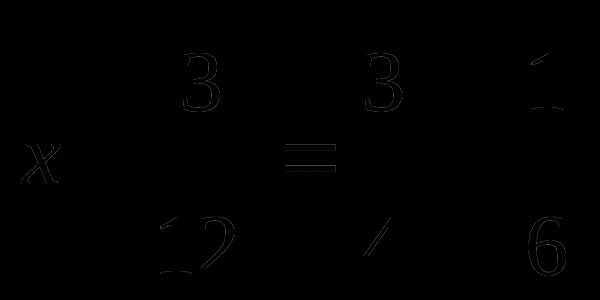 .
.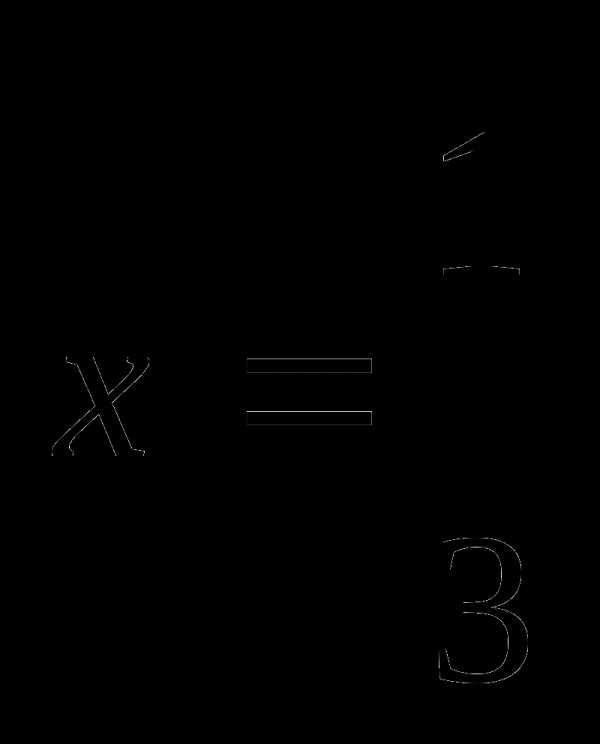 ;
;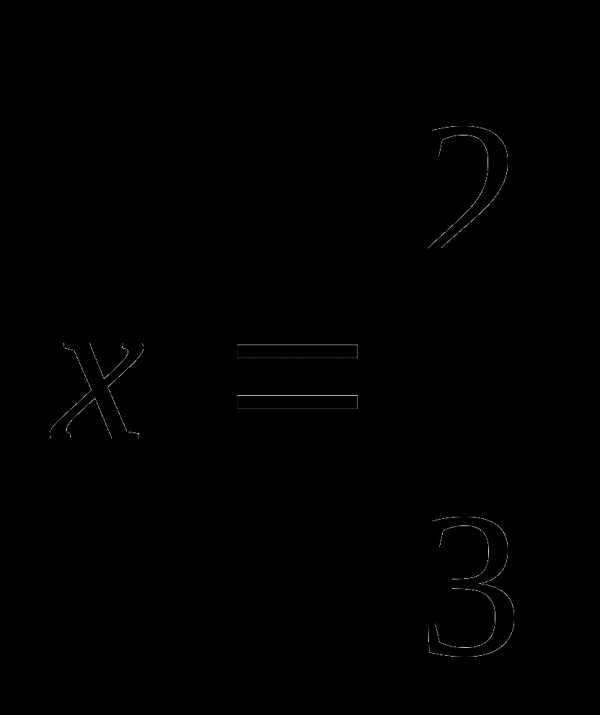 ;
;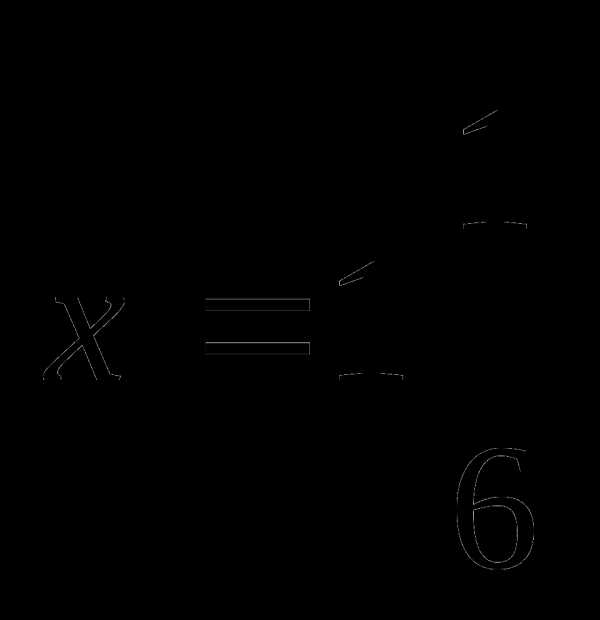 ;
; равно 2?
равно 2? ?
?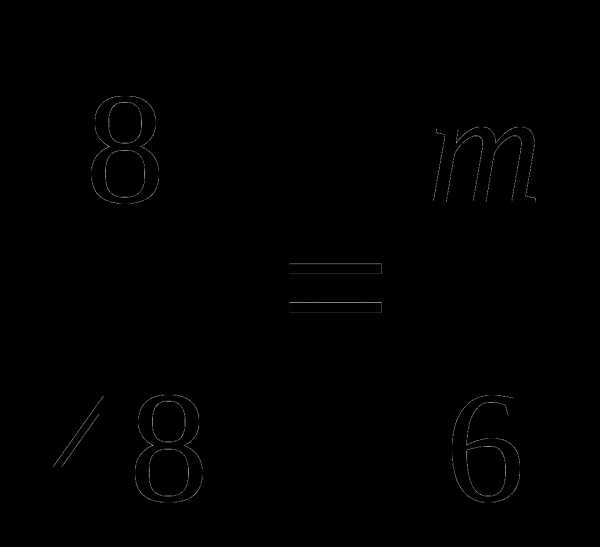 ; 2)
; 2) 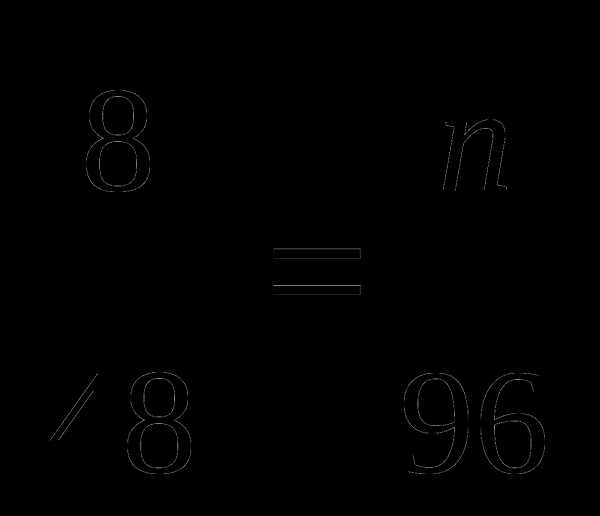 ; 3)
; 3) 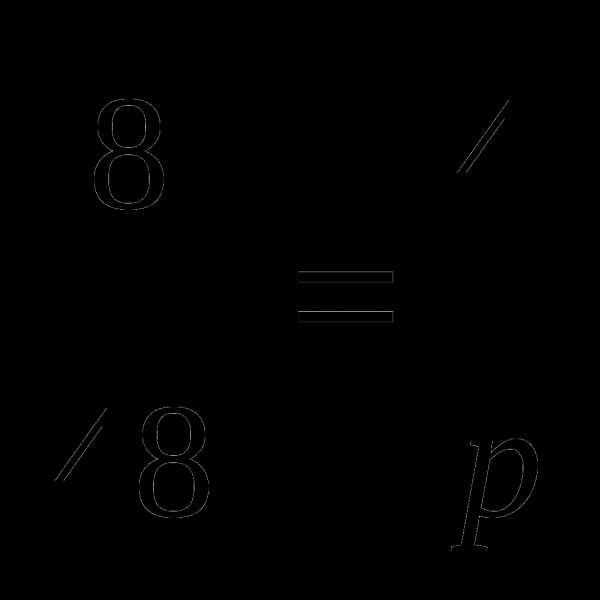 ; 4)
; 4)  ?
? .
. ;
; ;
; ,
,  .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6)  ?
?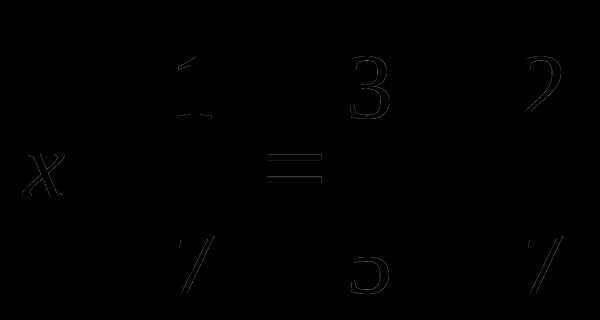 .
.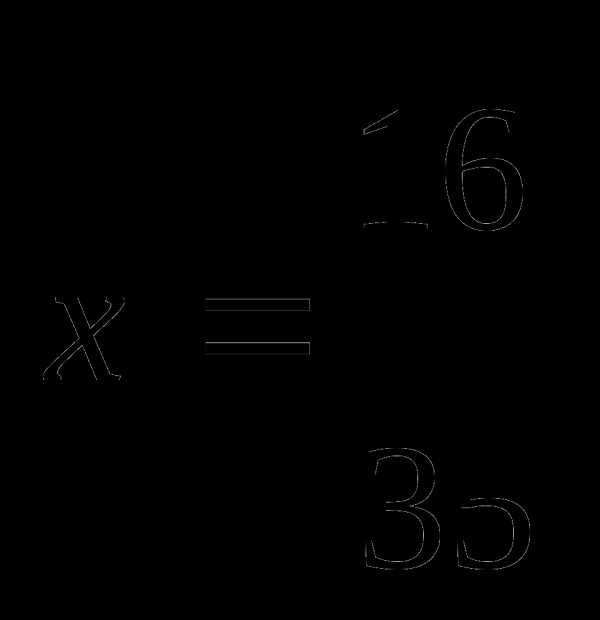 ;
;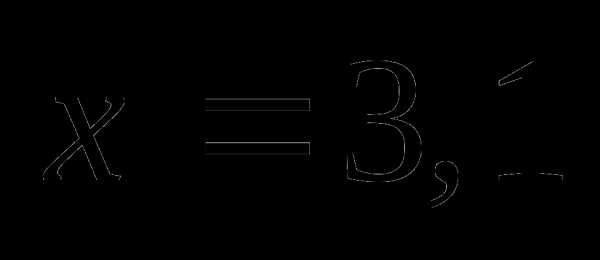 ;
;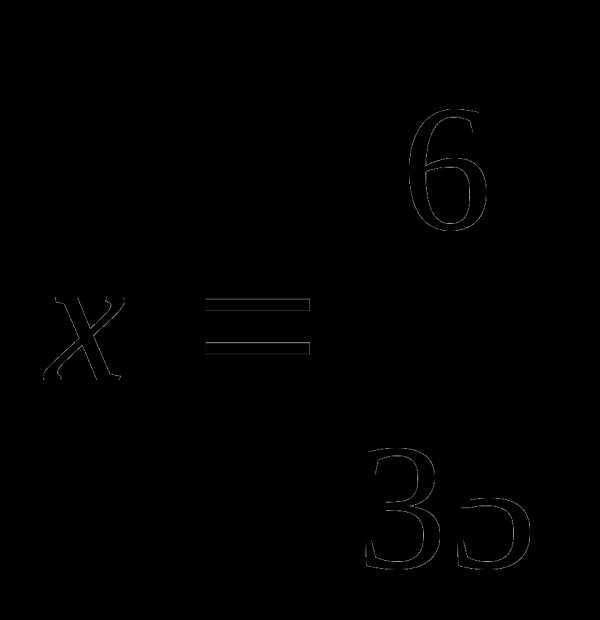 ;
; ;
; равно 6?
равно 6? ?
? —
—  равно: а)
равно: а)  ; в)
; в)  — (
— ( +
+  ) получится: а)
) получится: а)  ; б)
; б)  .
. расстояния между
расстояния между  этого расстояния. Какую часть всего
этого расстояния. Какую часть всего  ; б)
; б)  ; в)
; в)  .
. =
=  +
+  х равен:
х равен: ; в)
; в)  .
. — (
— ( +
+  ) получится: а)
) получится: а) 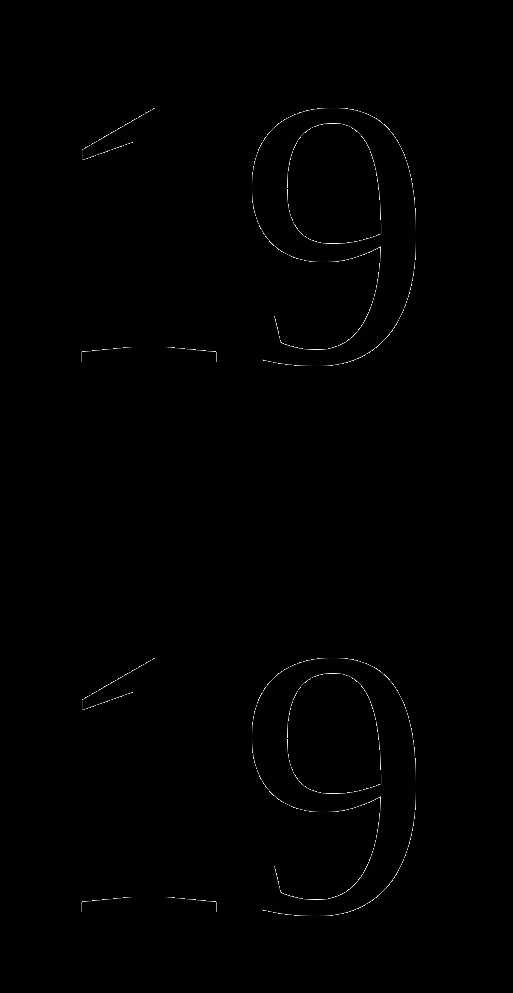 ; б)
; б) 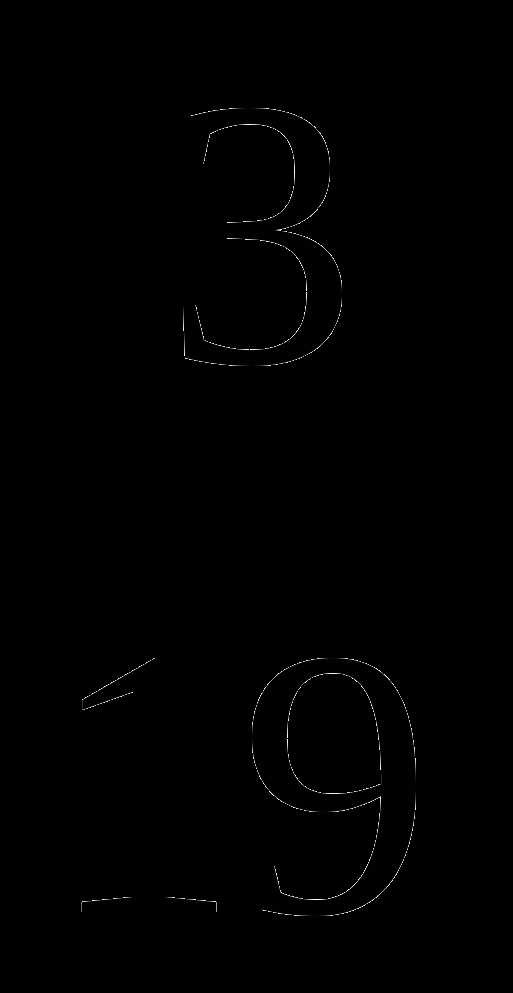 .
.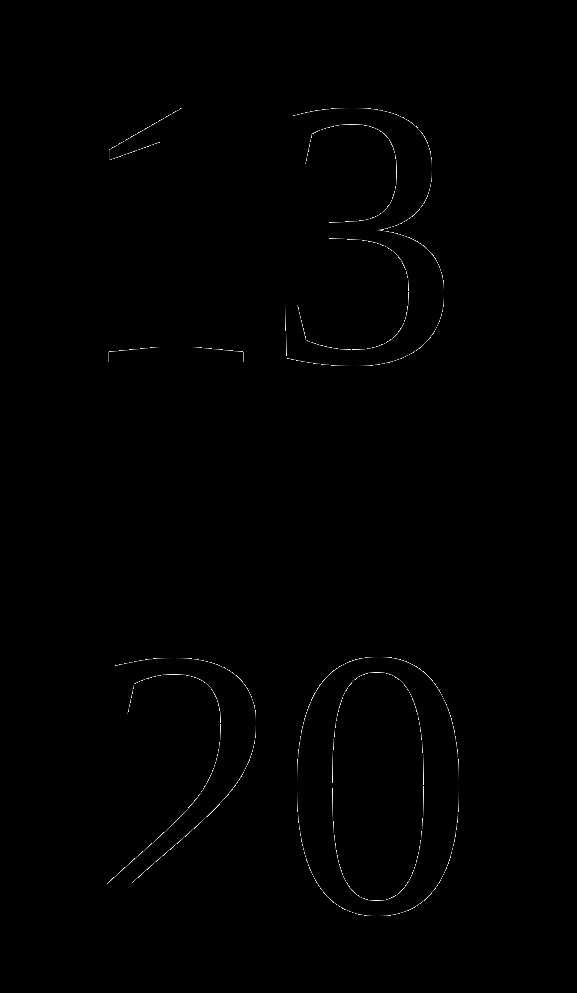 заказа, причем за первую неделю было выполнено
заказа, причем за первую неделю было выполнено 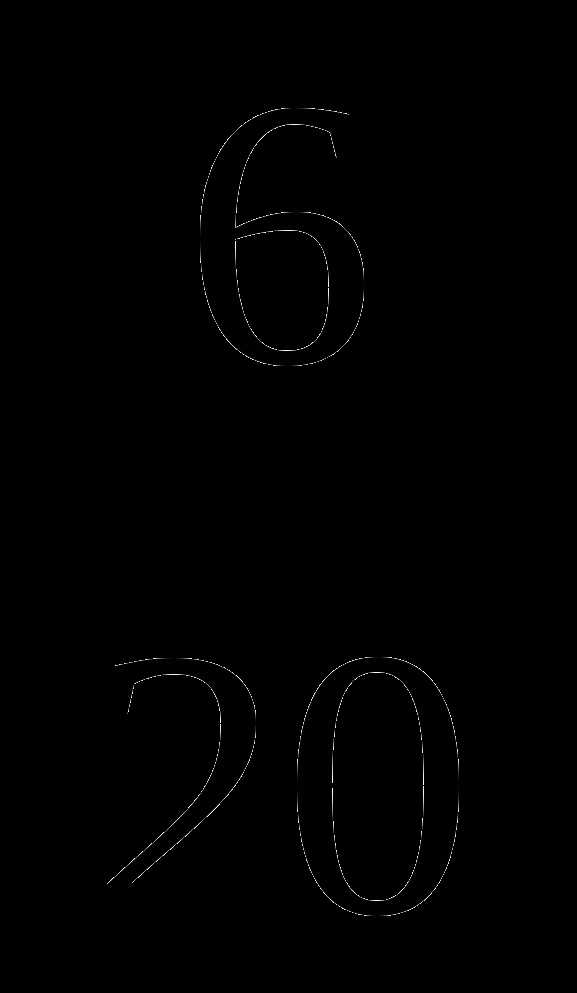 заказа. Какую часть заказа завод выполнил за вторую неделю?
заказа. Какую часть заказа завод выполнил за вторую неделю? ; б)
; б)  ; в)
; в)  .
. =
=  —
—  х равен:
х равен: ; в)
; в)  .
.