эконометрика — публикации с ключевым словом — Издательство «Креативная экономика»
Научные публикации (статьи и монографии) с ключевым словом эконометрика, выпущенные в Издательстве Креативная экономика (найдено: 4 за период c 2001 по 2019 год).
1. Беилин И.Л.
Инновационные подходы в цифровом моделировании региональных экономических процессов // Вопросы инновационной экономики. (№ 2 / 2019).
В статье впервые предлагается использование метода аналитической сегментации для формирования региональных инвестиционных портфелей малых инновационных предприятий, основанных на широком диапазоне собственных научно–исследовательских разработок. Это предприятия, созданные согласно № 209 ФЗ, на поддержку которых, в первую очередь, направленны программы Фонда содействия развитию малых форм предприятий в научно–технической сфере (Фонд содействия инновациям). К ним относятся программы «СТАРТ», «Развитие», «Коммерциализация», «Кооперация». Цифровая модель реализует возможности в «on–line» режиме корректирования сегментации и долей инвестирования портфелей региональных инновационных проектов в зависимости от изменений финансовых, экономических, технологических и эксплуатационных характеристик инновационного продукта. На основе методов сетевого планирования сформирована инновационная цифровая модель инвестирования малого инновационного предприятия, определен критический путь и резервы финансирования.
Беилин И.Л. Инновационные подходы в цифровом моделировании региональных экономических процессов // Вопросы инновационной экономики. – 2019. – Том 9. – № 2. – doi: 10.18334/vinec.9.2.40499.
2. Самышева Е.Ю.
Эконометрические методы в современной экономике // Российское предпринимательство. (№ 10 / 2010).
В статье анализируются особенности применения эконометрических методов в современной экономике страны. Оценка объектов и ситуаций, проверка гипотез, прогнозирование, принятие решений – это далеко не полный перечень задач, которые решаются с помощью статистических
методов. Подробнее об этом читайте в статье.
Самышева Е.Ю. Эконометрические методы в современной экономике // Российское предпринимательство. – 2010. – Том 11. – № 10. – с. 44-48. – url: https://creativeconomy.ru/lib/6338.
3. Орлова Л.А.
Эконометрика на промышленном предприятии // Российское предпринимательство. (№ 3 / 2003).
Многие авторы учебников по экономической теории статистический анализ экономических данных называют эконометрикой. Во многих странах эконометрические методы широко применяются для решения широкого спектра различных задач, возникающих на промышленных предприятиях. В соответствии с приведенным определением понятно, почему эконометрические методы часто называют статистическими. В нашей стране возможности эффективного применения эконометрики на промышленном предприятии еще недостаточно известны, поэтому вполне естественно начать с классификации эконометрических методов.
Орлова Л.А. Эконометрика на промышленном предприятии // Российское предпринимательство. – 2003. – Том 4. – № 3. – с. 79-84. – url: https://creativeconomy.ru/lib/920.
4. Орлов А.И.
Высокие статистические технологии и эконометрика в контроллинге // Российское предпринимательство. (№ 5 / 2001).
Высокие статистические технологии и эконометрика – неотъемлемая часть любой современной системы поддержки принятия решений. Используемые термины требуют пояснений. Согласно Энциклопедическому словарю, эконо-метрика – наука, изучающая конкретные количественные и качественные взаимосвязи экономических объектов и процессов с помощью математических и статистических методов и моделей.
Организованный в 1989 г. Институт высоких статистических технологий и эконометрики (ИВСТЭ) действует на базе кафедры «Экономика и организация производства» МГТУ им. Н.Э. Баумана. Институт на хоздоговорных и гос-бюджетных началах занимается развитием, изучением и внедрением высоких статистических технологий, т.е. наиболее современных технологий анализа технических, экономических, социологических, медицинских данных, ориенти-рованных на использование в условиях современного производства и экономики. Основной интерес представляют применение высоких статистических тех-нологий для анализа конкретных экономических данных., т.е. в эконометрике, прежде всего, в контроллинге.
Зачем нужны высокие статистические технологии? Разве недостаточно обычных статистических методов? Мы считаем и доказываем своими тео-ретическими и прикладными работами, что этого совершенно недостаточно.
Орлов А.И. Высокие статистические технологии и эконометрика в контроллинге // Российское предпринимательство. – 2001. – Том 2. – № 5. – с. 91-93. – url: https://creativeconomy.ru/lib/411.
Продолжить поиск в библиотеке по запросу «эконометрика»?
creativeconomy.ru
|
Поиск Лекций
Ресурсы по статистике и эконометрике Составители: Сергей Моргулис -Якушев и Петр Савельев.
Введение Эта страница призвана помочь слушателям программы дистанционного обучения Европейского Университета в Санкт-Петербурге разобраться в многообразии литературы по статистике и эконометрике, найти данные для обработки, подобрать наиболее подходящий для анализа данных статистический пакет. Страница может оказаться полезной также преподавателям и студентам экономических специальностей, экономистам-исследователям. Станица имеет следующую структуру. Вначале мы приводим краткий список некоторых известных нам учебных пособий по статистике и эконометрике, сопровождаемый краткими комментариями. Далее мы рассказываем об основных эконометрических пакетах, описываем целесообразность использования той или иной программы в зависимости от решаемой задачи, рассказываем о возможностях получения студенческих версий некоторых программ. Наконец, мы даем ссылки на базы данных, которые можно использовать как в учебных целях, так и для проведения исследований. Авторы будут очень признательны посетителям нашей страницы за конструктивные замечания и предложения. Ваши отзывы можно направлять любому из авторов по электронной почте. Учебные пособия по статистике и эконометрике. Нижеприведенный список учебных пособий не претендует на полноту, а комментарии к списку — на полное описание достоинств и недостатков данных пособий. Желая рассказать, прежде всего, о доступных нашим читателям источниках, мы намеренно сместили наше внимание от печатных изданий в сторону ресурсов Интернета и от англоязычных учебников — к русскоязычным.
Статьи и научные доклады по эконометрике
Различие между статьей и научным докладом следующее: научный доклад обычно представляет собой описание недавно проведенного исследования, обычно в авторской редакции. Научные доклады очень легко и быстро публикуются как в электронном, так и в печатном виде и дают представление о самых свежих научных результатах. Многие научные доклады после доработки публикуются журналами, т.е. превращаются в журнальные статьи. Ведущие западные экономические журналы являются рецензируемыми, т.е. публикуют статью только после того, как редактор журнала получит рецензию на статью от двух признанных специалистов по данной теме, причем рецензентам не известен автор статьи, а автору неизвестны рецензенты. Такая система, хотя и не является совершенной, в значительной степени снижает риск появления в журнале некачественных или неактуальных статей. По поводу научных докладов таких гарантий никто дать не может. В нерецензируемых журналах редактор принимает решение о публикации на основании собственного впечатления о статье. Поскольку редактор не может быть узким специалистом во многих областях, он вполне может пропустить некачественную статью. По нашим сведениям, среди российских экономических журналов, к сожалению, нет рецензируемых.
Некоторые журналы по эконометрике доступны в библиотечной базе JSTOR (Заметим, что статьи, интересные с точки зрения эконометрики, стоит искать не только в разделе Statistics, но и в разделах Economics и Finance). Хорошим источником научных докладов является база SSRN. Многие научные доклады из этой базы бесплатно доступны жителям бывшего Советского Союза и Восточной Европы. Много информации можно получить из Handbook of Econometrics. Handbook – это сборник обзоров оригинальных статей по достаточно узким темам. К такому источнику обычно обращаются уже после изучения базовых учебников. В сочетании со свежими журнальными статьями, не вошедшими в Handbook, и с научными докладами (working papers), этот источник дает практически полное представление о состоянии исследований в интересующей Вас узкой области знаний.
· Stata – мощный пакет для статистического и эконометрического анализа данных. Ориентирован, в первую очередь, на эконометристов. Компания Stata Corporation внимательно следит за развитием эконометрики и за нуждами исследователей и постоянно совершенствует пакет, добавляя в него все новые возможности для эконометрического анализа. Пакет особенно хорош для обработки пространственных данных (cross-section data), панельных (panel data) и данных по временам жизни (survival-time data). Интерфейс пакета предполагает программирование с помощью командного языка и минимум действий с помощью меню. Человеку, привыкшему работать с программой типа Microsoft Word, это может сначала показаться сложным и неудобным, но специфика работы с данными, на которые ориентирован пакет, показывает большие преимущества такого подхода. Освоить пакет достаточно легко, если обратиться к пособию «Прикладной эконометрический анализ в пакете Stata» С. Коленикова (см. разд. 2). Кроме того, пакет Stata имеет отличную систему встроенной подсказки. Пакет также имеет встроенный язык программирования.
Источники данных
Последнее обновление: май 2002 г. главная | макроэкономика | международная экономика | микроэкономика | эконометрика Рекомендуемые страницы: Поиск по сайту |
|
poisk-ru.ru
Эконометрика :: Федеральный образовательный портал
Опубликовано на портале: 28-10-2003
Николай Петрович Тихомиров, Елена Юрьевна Дорохина
|
Aннотация:
Цель курса — основной целью дисциплины “Эконометрика” является обучение студентов методологии и методике построения и применения эконо-метрических моделей для анализа состояния и для оценки законо-мерностей развития экономических и социальных систем в условиях взаимосвязей между их внутренними и внешними факторами.
Основные задачи курса:
расширение и углубление теоретических знаний о качественных особенностях экономических и социальных систем, количествен-ных взаимосвязях и закономерностях их развития;
овладение методологией и методикой построения и применения эконометрических моделей как для анализа состояния, так и для оценки закономерностей развития указанных систем;
изучение наиболее типичных моделей и получение навыков практической работы с ними. Программа включает содержание курса, темы лекций, списки основной и дополнительной литературы.
Разделы курса.
- Проблемы обоснования эконометрической модели;
- Методы оценки параметров линейных эконометрических моделей;
- Методы оценки коэффициентов эконометрической модели при коррелирующих или нестационарных ошибках;
- Модели с коррелирующими факторами;
- Модели с лаговыми зависимыми переменными;
- Линейные модели временных рядов;
- Модели финансовой эконометрики;
- Системы взаимозависимых эконометрических моделей;
- Модели с переменной структурой;
- Модели с дискретными зависимыми переменными;
- Методы оценки параметров нелинейных моделей;
- Использование эконометрических моделей в прогнозировании и анализе социальных и экономических процессов.
Ключевые слова
См. также:
Давид Львович Константиновский, Владимир Николаевич Шубкин
[Книга]
Марина Ивановна Либоракина
Полития. 2003. № 4. С. 225-237.
[Статья]
Blake LeBaron
Studies in Nonlinear Dynamics and Econometrics. 1997. Vol. 2. No. 2. P. 53-59.
[Статья]
Halbert L. White
Econometrica. 1980. Vol. 48. No. 4. P. 817-838.
[Статья]
John Aitchison, Samuel D. Silvey
Biometrika. 1957. Vol. 44. No. 1/2. P. 131-140.
[Статья]
Ray C. Fair
Journal of Political Economy. 1978. Vol. 86. P. 45-61.
[Статья]
Jerry Hausman
Econometrica. 1978. Vol. 46. No. 6. P. 1251-1272.
[Статья]
ecsocman.hse.ru
Статья по эконометрике на заказ
У большинства дни в университете подсознательно связываются с весельем и радостью. Но привычные радости буквально сразу после начала уроков в ВУЗе осложняются стрессовым учебным графиком, который никак не вписывается в планы студентов.
Рвение к освоению специальностью дается так тяжело, что не остается ни сил, ни желания для написания разного рода результирующих работ. Сумасшедший ритм студенческой жизни не дает в указанный срок выполнить такую работу, как научная статья по предмету «Эконометрика».
Научная статья на заказ как моментальное решение проблем
Именно для содействия и оказания посильной поддержки абитуриентам была создана наша компания, где каждый сможет смело заказать работу по любой дисциплине.
С нами вас ждет тишина и покой. А мы можем гарантировать вам ваше спокойствие. Вашу работу вы получите в указанный при оформлении период.
Почему нам верят миллионы клиентов?
- Абсолютная конфиденциальность. Вы можете рассчитывать, что поступившие к нам личные данные и тонкости заявки не подлежат разглашению.
- Надзор над процессом выполнения работы. Вы в любое время можете просмотреть свою работу на любом пункте его выполнения. Стоит только оформить заявку, как вы получаете персонального менеджера, который будет оперативно информировать вас о малейшем изменении в процессе выполнения заказа.
- Вспомогательное тестирование специалистами. Как только работа будет готова, она поступит к независимому специалисту, который проанализирует и выполнит проверку по новому, затем выдаст собственное заключение о ее соответствии тематике, указанным ранее требованиям и эталонам оформления.
- Высокая уникальность. Вы можете рассчитывать на работу, которая не один раз проверялась по программе «Антиплагиат», именно по этой причине уникальность работы будет превышать 70%.
- Поддержка всех заказов вплоть до сдачи. Если в момент проверки работы преподаватель сделает выговор, поправки и сдаст на доработку, мы сделаем эту доработку совершенно БЕСПЛАТНО! Достаточно будет лишь получить рецензию руководителя.
Для оформления заказа Вам вовсе нет нужды лично приходить в офис — хватит завершить заявку на выполнение на нашей страничке или позвонить нашим менеджерам по указанным телефонам.
fastfine.ru
Статьи и научные доклады по эконометрике
Слушатели должны понимать, что эконометрика является динамически развивающейся наукой, поэтому наиболее полную, а главное, свежую информацию можно получить только при прочтении эконометрических статей (articles, papers) и научных докладов (working papers). Статьи и научные доклады не дают систематических знаний, однако позволяют более глубоко познакомиться с тем или иным методом или результатом.
Различие между статьей и научным докладом следующее: научный доклад обычно представляет собой описание недавно проведенного исследования, обычно в авторской редакции. Научные доклады очень легко и быстро публикуются как в электронном, так и в печатном виде и дают представление о самых свежих научных результатах. Многие научные доклады после доработки публикуются журналами, т.е. превращаются в журнальные статьи.
Ведущие западные экономические журналы являются рецензируемыми, т.е. публикуют статью только после того, как редактор журнала получит рецензию на статью от двух признанных специалистов по данной теме, причем рецензентам не известен автор статьи, а автору неизвестны рецензенты. Такая система, хотя и не является совершенной, в значительной степени снижает риск появления в журнале некачественных или неактуальных статей. По поводу научных докладов таких гарантий никто дать не может. В нерецензируемых журналах редактор принимает решение о публикации на основании собственного впечатления о статье. Поскольку редактор не может быть узким специалистом во многих областях, он вполне может пропустить некачественную статью. По нашим сведениям, среди российских экономических журналов, к сожалению, нет рецензируемых.
Некоторые журналы по эконометрике доступны в библиотечной базе JSTOR(Заметим, что статьи, интересные с точки зрения эконометрики, стоит искать не только в разделе Statistics, но и в разделах Economics и Finance). Хорошим источником научных докладов является базаSSRN. Многие научные доклады из этой базы бесплатно доступны жителям бывшего Советского Союза и Восточной Европы.
Много информации можно получить из Handbook of Econometrics. Handbook – это сборник обзоров оригинальных статей по достаточно узким темам. К такому источнику обычно обращаются уже после изучения базовых учебников. В сочетании со свежими журнальными статьями, не вошедшими в Handbook, и с научными докладами (working papers), этот источник дает практически полное представление о состоянии исследований в интересующей Вас узкой области знаний.
Программное обеспечение (статистические пакеты)
Предлагаемый ниже обзор пакетов не является полным. Выбор пакетов связан с предпочтениями авторов сайта, поскольку мы писали только о тех пакетах, в которых сами работали. Любознательный читатель сможет расширить свои знания о многообразии эконометрических пакетов, если прочтет приложение ЭП в книге Магнус и др. (2001). Мы рекомендуем своим читателям осваивать такие профессиональные пакеты, как Stata (для анализа пространственных и панельных данных), EViews (для анализа временных рядов) и Gauss (для реализации нестандартных эконометрических методов).
Stata– мощный пакет для статистического и эконометрического анализа данных. Ориентирован, в первую очередь, на эконометристов. Компания Stata Corporation внимательно следит за развитием эконометрики и за нуждами исследователей и постоянно совершенствует пакет, добавляя в него все новые возможности для эконометрического анализа. Пакет особенно хорош для обработки пространственных данных (cross-section data), панельных (panel data) и данных по временам жизни (survival-time data). Интерфейс пакета предполагает программирование с помощью командного языка и минимум действий с помощью меню. Человеку, привыкшему работать с программой типа Microsoft Word, это может сначала показаться сложным и неудобным, но специфика работы с данными, на которые ориентирован пакет, показывает большие преимущества такого подхода. Освоить пакет достаточно легко, если обратиться к пособию «Прикладной эконометрический анализ в пакете Stata» С. Коленикова (см. разд. 2). Кроме того, пакет Stata имеет отличную систему встроенной подсказки. Пакет также имеет встроенный язык программирования.
EViews– очень хороший профессиональный пакет, ориентированный, в первую очередь, на анализ временных рядов. Имеет удобный, легко осваиваемый интерфейс с большим количеством меню, но возможно и программирование. Пакет широко используется как экономистами-исследователями, так и финансовыми аналитиками, специалистами в области макроэкономического прогнозирования, прогнозирования продаж и т.д. На сайте разработчика доступна студенческая версия программы. Отличная система подсказки пакета представляет собой, по существу, учебник по эконометрике, ориентированный на практическую работу. Пакет имеет встроенный язык программирования.
Gauss– профессиональный язык программирования, ориентированный на решение задач эконометрического анализа. Необходимость в программировании возникает, например, в случае, когда эконометрист пользуется нестандартными эконометрическими методами, которые не реализованы в статистических пакетах. Гаусс – излюбленная программа эконометристов-теоретиков. Ссылки, связанные с этим пакетом и домашние задания с использованием пакета можно найти, например, на сайтеСтанислава Анатольева. Одно из удобств этого языка программирования заключается в том, что переменная в нем по умолчанию является не скаляром, как в обычных языках, а матрицей. Например, для расчета оценки по МНК в Гауссе вместо организации двойных циклов для перемножения матриц и подпрограммы для обращения матрицы вы просто пишете знакомую формулу: b=INV(X’X)X’Y, и ответ готов! Для Гаусса существует обширная библиотека подпрограмм. Отрицательная сторона пакета – неразвитая диагностика ошибок.
SPSS– пакет анализа с развитым windows-интерфейсом и красивой графикой, особенно популярный среди социологов и маркетологов. Пакет ориентирован, главным образом, на анализ пространственных данных и на кластерный анализ. Удобной особенностью пакета является возможность написания программ. Однако встроенные модели и тесты для пространственных данных и для временных рядов заметно отстают от развития науки. Компания SPSS явно отдает предпочтение развитию качества графики перед развитием статистических возможностей пакета, что делает пакет идеальным для целей маркетинга, но малопривлекательным для современных эконометрических исследований.
Statistica– наиболее простой диалоговый пакет, позволяющий производить некоторые эконометрические расчеты с пространственными данными. Может быть полезен при начальном знакомстве с эконометрикой. Программа имеет удобный интерфейс. На сайте разработчика доступна студенческая версия программы.
PcGive– диалоговый пакет эконометрического моделирования. Позволяет проводить различные процедуры оценки и тесты, от метода наименьших квадратов до коинтеграционного анализа данных и оценки моделей одновременных уравнений. На сайте разработчика доступна студенческая версия программы.
studfiles.net
Статья — Основы эконометрики — Математика
Профессиональный Институт Управления
Факультет: Финансы и кредит
Специальность: Финансы и кредит
Курс: 5
Дисциплина: Эконометрика
Реферат на тему:
Основы эконометрики.
Студентки: Погосян Э.Т.
Группа: УФША-51/7-ВС
Проверил:_____________
Москва — 2009г.
Содержание
Введение……………………………………………………………………2
Основная часть:
1. Основные эконометрические модели………………………………….3
2. Структура современной эконометрики…………………………………4
3. Специфика и принципы эконометрики………………………………5-6
4. Эконометрические модели…………………………………………….7-8
Заключение…………………………………………………………………9
Список используемой литературы
Введение.
Эконометрика – это не то же самое, что экономическая статистика. Она отнюдь не идентична тому, что мы называем общей экономической теорией, хотя значительная доля этой теории носит определенно количественный характер. Также эконометрика не должна восприниматься как синоним применения математики в экономике. Опыт показывает, что статистика, и экономическая теория, и математика, взятые по отдельности, являются необходимыми, но не достаточными для действительного понимания количественных отношений в современной жизни. Именно объединение всех трех частей дает мощный эффект. И именно это составляет эконометрику.
С современных позиций эконометрику можно определить как науку о моделировании экономических явлений, позволяющем объяснять и прогнозировать их развитие, выявлять и измерять определяющие факторы.
Среди предпосылок возникновения эконометрики можно назвать разработку количественных методов в экономических исследованиях, накопление учетно-статистических данных, создание современной микро- и макроэкономики.
Особенно важным для развития количественного подхода был статистический анализ поведения цен на различные товары – отечественные и импортные. Появились исследования динамики цен на важнейшие товары, группы товаров, анализ региональных особенностей роста цен; уделялось внимание построению индексов цен, попыткам выявления цикличности в изменениях цен и связи с бизнес — циклами.
Исследования экономики с неизбежностью опирается на данные пассивного эксперимента, т.к. исследователь никак не может воздействовать на данные. Таковыми являются все реальные данные, которые нам предлагает официальная статистика, или учет, или специальное наблюдение.
1. Основные эконометрические модели.
Путь эконометрики в нашу страну был долгим и сложным. Первая попытка внедрить эконометрику в науку принадлежит Василию Сергеевичу Немчинову. Эта попытка привела к выделению экономико-математических методов и экономической кибернетики.
Применяемые в настоящее время эконометрические модели делят на:
· статистические и динамические – по характеру используемых данных. Промежуточное положение занимают модели панельных данных, основанные на данных по одной и той же совокупности за ряд лет;
· комплексные или некомплексные. Первые отличаются тем, что отражают связи между макроэкономическими показателями на всех стадиях процесса воспроизводства.
· аналитические, имитационные и прогностические. Деление по целям их применения.
Этапы построения эконометрической модели:
Первый: теоретический, в ходе которого формируется цель исследования, определяется круг участвующих в модели экономических характеристик, создается описание связей между ними.
Второй: информационный, когда осуществляется поиск требуемых данных, проверяется их достоверность, сопоставимость, осуществляются необходимые пересчеты, используются пространственные и временные данные.
Третий: спецификация модели, когда устанавливаются внешние и внутренние переменные, выявляются связи и соотношения.
Четвертый: идентификация модели, т.е. выявление условий корректного оценивания параметров модели на основе соотношения количества переменных и связей между ними.
Пятый: оценка параметров модели.
Шестой: проверка адекватности модели, делается вывод о том, какова точность расчетов на основе модели, получаемых прогнозных оценок, производится анализ остатков.
2. Структура современной эконометрики.
Термин «эконометрика» состоит из двух частей: «эконо-» — от «экономика» и «-метрика» — от «измерение». Эконометрика посвящена развитию и применению статистических методов в конкретной области науки и практики.
В эконометрике выделяют три вида научной и прикладной деятельности:
а) разработка и исследование эконометрических методов (методов прикладной статистики) с учетом специфики экономических данных;
б) разработка и исследование эконометрических моделей в соответствии с конкретными потребностями экономической науки и практики;
в) применение эконометрических методов и моделей для статистического анализа конкретных экономических данных.
Кратко рассмотрим виды научной и прикладной деятельности. Если работам соответствуют научные результаты, значимость которых оценивается по общеэконометрическим критериям, то для них основное — успешное решение задач конкретной области экономики. Прикладная статистика — курс математической статистики состоит в основном из доказательств теорем, как и соответствующие учебные пособия. Математическая статистика играет роль математического фундамента для прикладной статистики. Хотя статистические данные собираются и анализируются с незапамятных времен, современная математическая статистика как наука была создана сравнительно недавно — в первой половине ХХ в. Именно тогда были разработаны основные идеи и получены результаты, излагаемые ныне в учебных курсах математической статистики.
В результате специалист по математической статистике оказывается зачастую беспомощным при обработке реальных данных, а пакеты программ применяют лица, не имеющие необходимой теоретической подготовки.
3. Специфика и принципы эконометрики.
Чтобы продемонстрировать основные принципы эконометрики, рассмотрим пример из страхового бизнеса. Годовой пробег автомобиля — это важный фактор, но пользоваться им как оценочным затруднительно. Практическое решение состоит в определении ряда легко наблюдаемых факторов — мощности машины, возраста, географического положения, износа, каждый из которых имеет некоторую связь с истинным риском, в свою очередь определяющим фактический размер страховой премии.
Эконометрические методы строятся на синтезе трех областей знаний: экономики, математики и статистики. Основой является экономическая модель, под которой понимается схематическое представление экономического явления или процесса с помощью научной абстракции, отражения только характерных черт.
В эконометрике, как и в любой научной дисциплине, познание развивается в соответствии с общим научным методом, предполагающим:
— формулировку гипотезы с учетом соотношений между наблюдаемыми данными;
— сбор статистических данных и представление гипотезы в сжатой или математической форме;
— модификацию или улучшение гипотезы.
Таким образом, сердцевиной познания в экономике является эксперимент, предполагающий либо непосредственное наблюдение (измерение), либо математическое моделирование.
Область применения эконометрических моделей — все сферы экономической теории и практики, где есть возможность сбора и обработки статистических данных, прогнозирования их поведения.
Для анализа экономических данных могут применяться все разделы прикладной статистики, а именно:
· статистика случайных величин;
· многомерный статистический анализ;
· статистика временных рядов и случайных процессов;
· статистика объектов нечисловой природы, в том числе статистика интервальных данных.
Перечисленные четыре области выделены на основе математической природы элементов выборки: в первой из них это — числа, во второй — вектора, в третьей — функции, в четвертой — объекты нечисловой природы, т.е. элементы пространств, в которых нет операций сложения и умножения на число.
Есть два принципиально различных подхода к изучению поведения организаций и людей. Согласно первому из них вполне допустимо описывать действия человека в вероятностных терминах, например, считать его ответ на заданный вопрос случайной величиной. Сторонники второго подхода полагают, что поведение человека или организации является детерминированным, определяется теми или иными причинами, а случайность при анализе выборки возникает лишь из-за случайности при отборе лиц для опроса или предприятий для изучения. Если ответ на вопрос имеет вид «да» — «нет», то число ответов «да» при первом подходе, как известно, имеет биномиальное распределение, а при втором – гипергеометрическое.
Итак, специфика эконометрики проявляется не в перечне применяемых для анализа конкретных экономических данных статистических методов, а в частоте использования тех или иных методов.
4. Эконометрические модели.
Задача эконометрики — создание как более универсальных, так и специальных методов для обнаружения наиболее устойчивых характеристик в поведении реальных экономических показателей. Эконометрика разрабатывает методы подгонки формальной модели с целью наилучшего имитирования ею поведения.
Статистические и математические модели экономических явлений и процессов определяются спецификой той или иной области экономических исследований. Так, в экономике качества модели — используют как технические, так и экономические характеристики, а потому относятся к эконометрике, равно как и многие модели теории массового обслуживания.
К эконометрике качества относятся многие публикации научно-технического журнал «Заводская лаборатория». Этот журнал посвящен аналитической химии, физическим, математическим и механическим методам исследования, а также сертификации материалов. Он создан в 1932 г. и адресован специалистам черной и цветной металлургии, химической промышленности и др. Кроме сотрудников центральных заводских лабораторий, служб качества, надежности и других заводских подразделений, он ориентирован в основном на работников прикладных научно-исследовательских организаций. Технические и экономические вопросы обычно рассматриваются в неразрывном единстве.
Другой важный раздел эконометрики — теория и практика экспертных оценок. Экспертные оценки используют для решения ряда экономических задач, например, выбора оптимального направления инвестиций, или наилучшего образца определенного вида продукции для организации массового выпуска, или при прогнозировании развития экономической ситуации, или при распределении финансирования.
Менее полезными практически являются различные эконометрические модели, предназначенные для прогнозирования макроэкономических показателей. Они представляют собой систему линейных зависимостей между прошлыми и настоящими значениями переменных. В таких задачах оценивают как структуру модели. Структура такой модели — объект нечисловой природы, что и объясняет сложность соответствующей теории.
При анализе потоков платежей необходимо использовать эконометрические модели инфляционных процессов, поскольку без оценки индекса инфляции невозможно вычислить дисконт-функцию, а потому нельзя установить реальное соотношение авансовых и «итоговых» платежей. Прогнозирование сбора налогов может осуществляться с помощью системы временных рядов — на первом этапе по каждому одномерному параметру отдельно, а затем — с помощью некоторой линейной эконометрической системы уравнений, дающей возможность прогнозировать векторный параметр с учетом связей между координатами и лагов, т.е. влияния значений переменных в определенные прошлые моменты времени.
Заключение.
Подводя итоги сказанному выше, обратимся к вопросам подготовки кадров в области эконометрики. В настоящее время в классификаторах специальностей научных работников и специальностей, по которым идет подготовка студентов, эконометрика не представлена вообще, а статистика — двумя отдельными позициями: в специальности «теория вероятностей и математическая статистика» как часть математики и как одна из экономических специальностей. Такие практически важные области, как статистические методы в промышленности, в частности, статистические методы управления качеством и надежностью, технической диагностики, планирования эксперимента, а также статистические методы в менеджменте, в экологии, в химии, в геологии, в медицине и т.д., и т.п. вообще не представлены в рассматриваемых классификаторах. Можно сказать, что они существуют нелегально, потому что, например, научным работникам при защите диссертаций приходится «маскироваться» под другие специальности.
Поскольку кадры по статистическим методам и эконометрике не готовятся, то каждый специалист — самоучка, то общее их число на порядок меньше, чем в Великобритании. США и других странах, в которых науки «эконометрика» и «статистика» рассматривается в одном ряду с такими общепризнанными науками, как математикой, физикой, химией, биологией и др.
Очевидно, необходимы постоянные контакты между специалистами по социально-экономическим применениям статистических методов, с одной стороны, и математической статистике, с другой стороны. Эконометрика находится именно на этом стыке.
Список используемой литературы
1. Носко В.П. «Эконометрика для начинающих. Основные понятия,
элементарные методы, границы применимости, интерпретация
результатов» М. – 2000г.
2. Мардас А. Н. «Эконометрика». Краткий курс. М.- 2001г.
3. Учебное пособие. «Математические модели в экономике» М.- 2005г.
4. Давыдов С.Б. «Математическое моделирование экономических
систем». М.- 2002г.
ronl.org


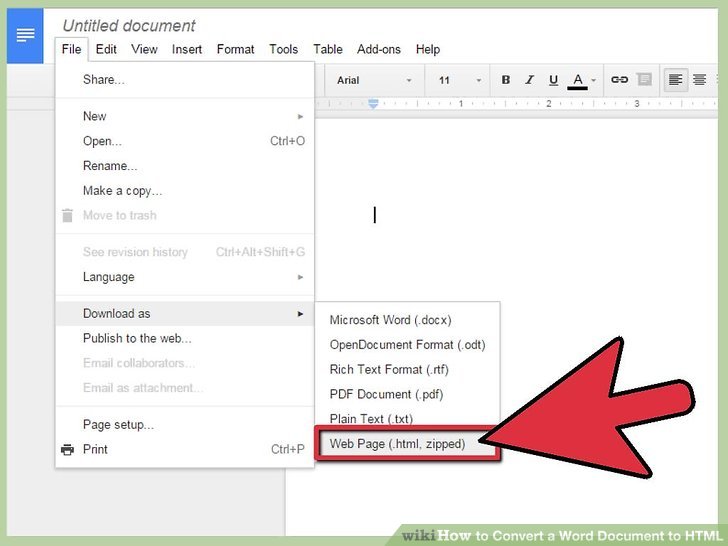

 ,
которую называютприсоединенной (взаимной, союзной):.
,
которую называютприсоединенной (взаимной, союзной):.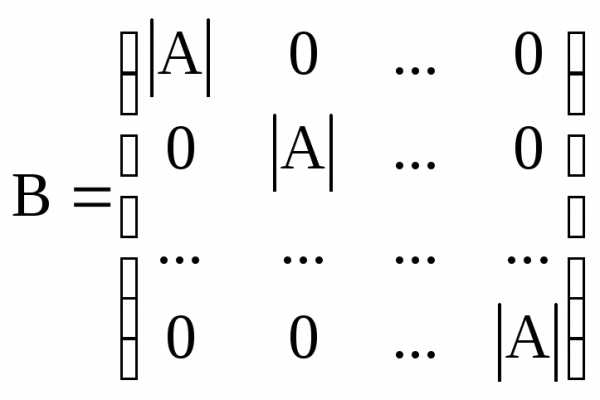
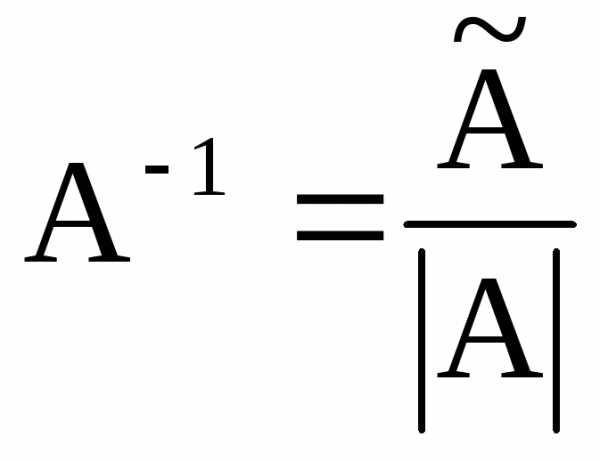 .
. .
. —
определитель матрицы, получаемой из
основной матрицы системы заменой её
—
определитель матрицы, получаемой из
основной матрицы системы заменой её -го
столбца столбцом свободных членов.
-го
столбца столбцом свободных членов.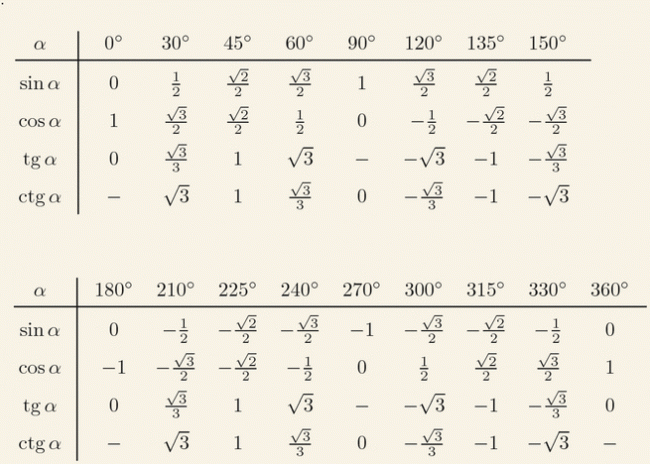









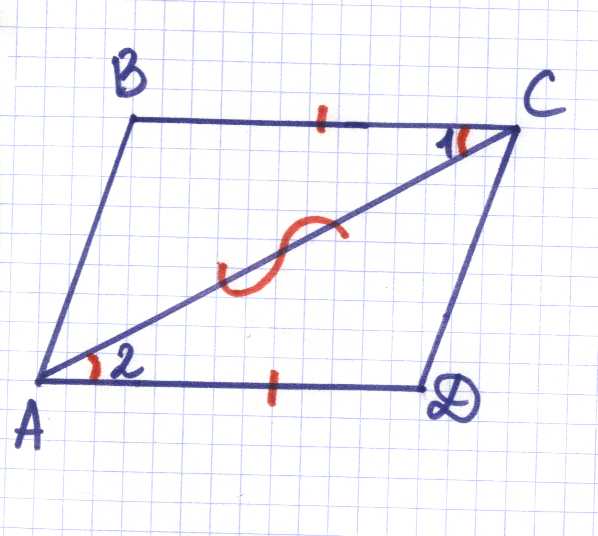
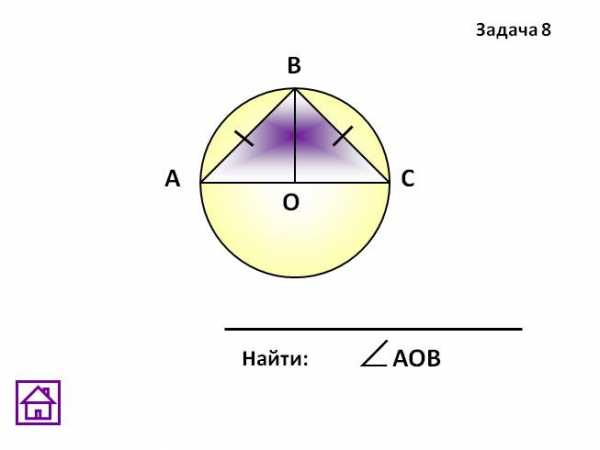
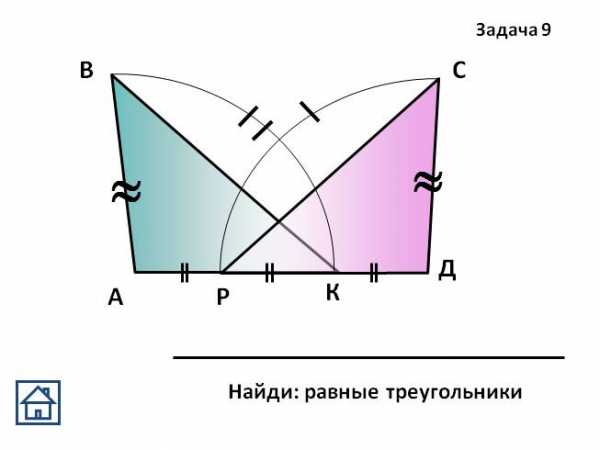
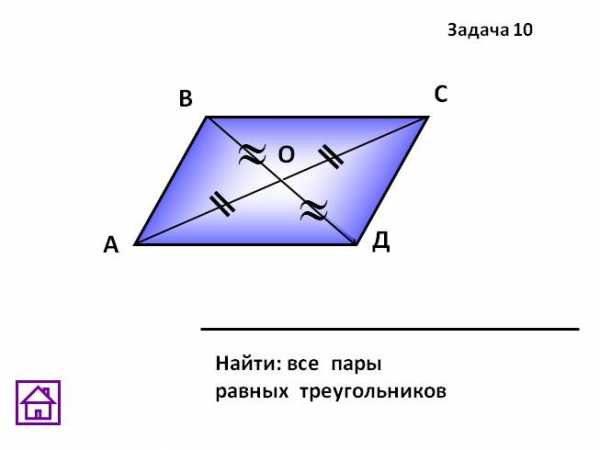
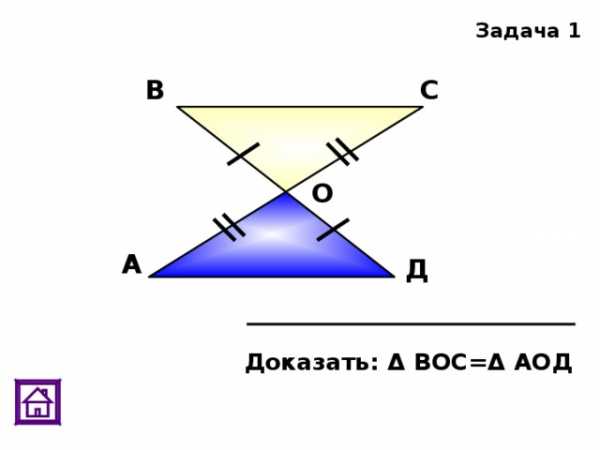
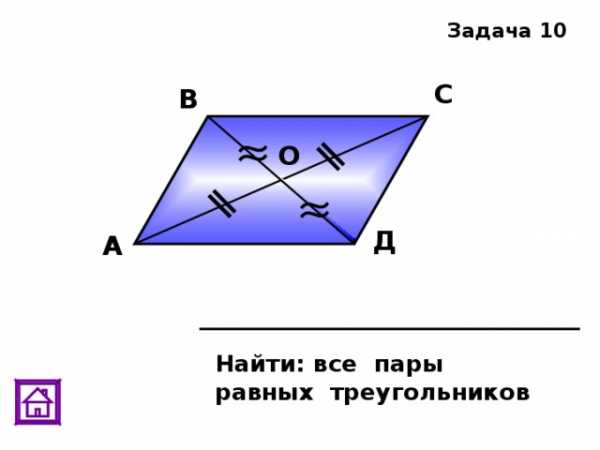
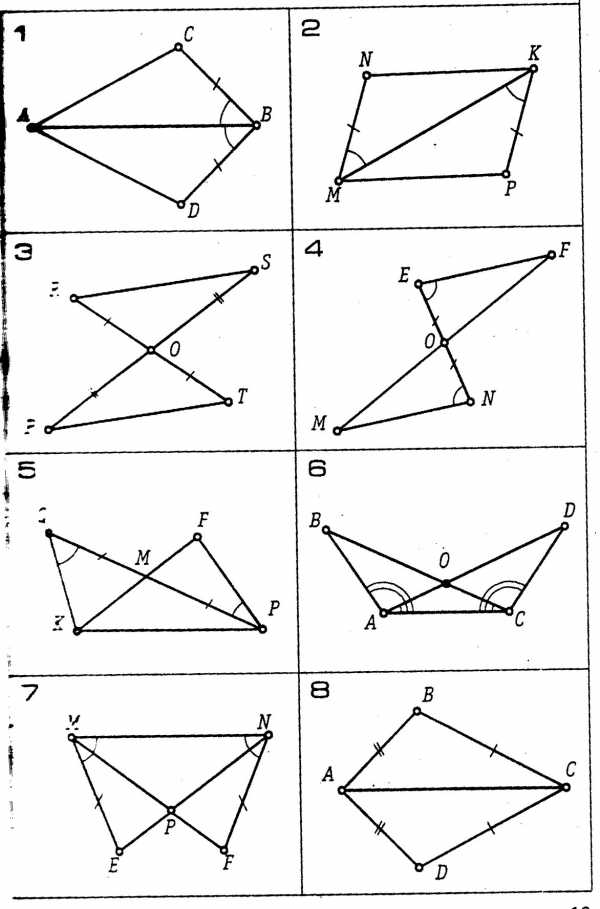 ) Дано:
) Дано:


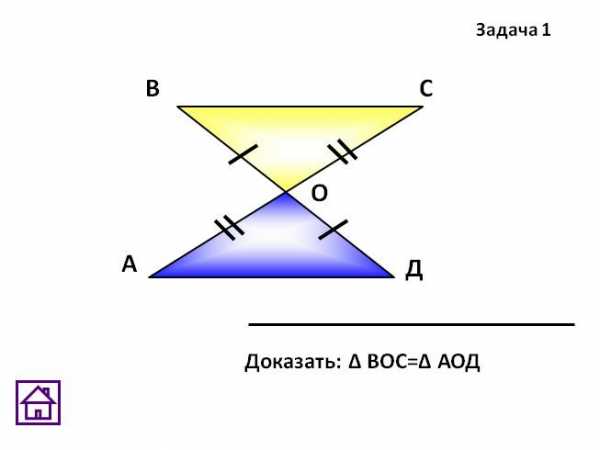







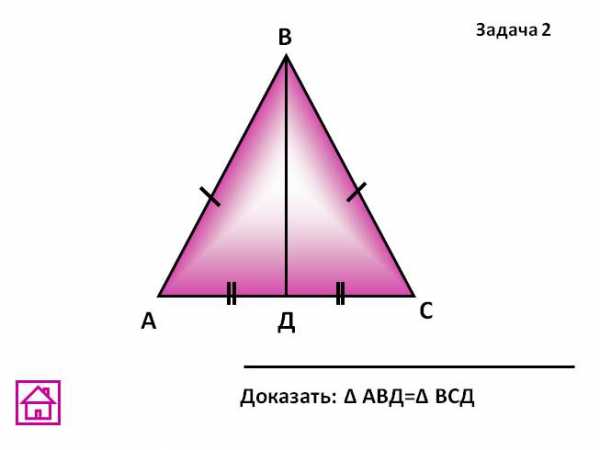

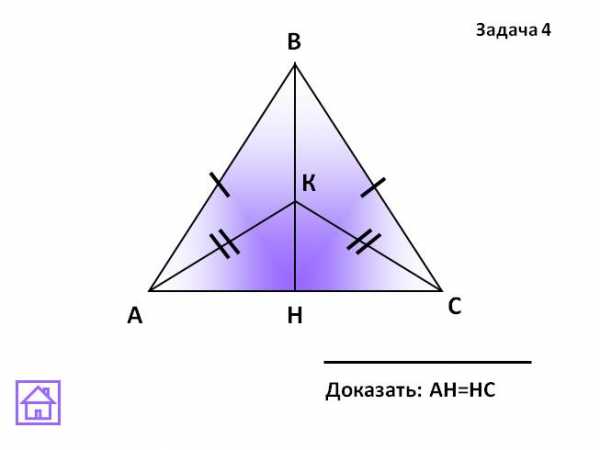
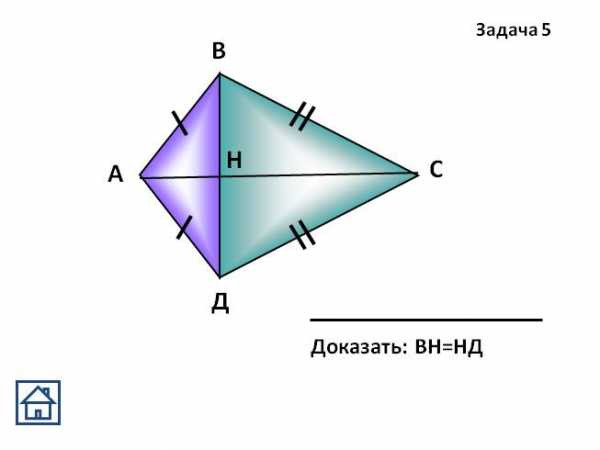

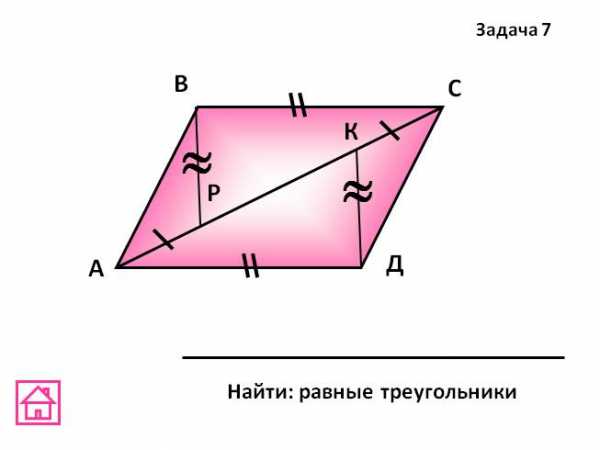





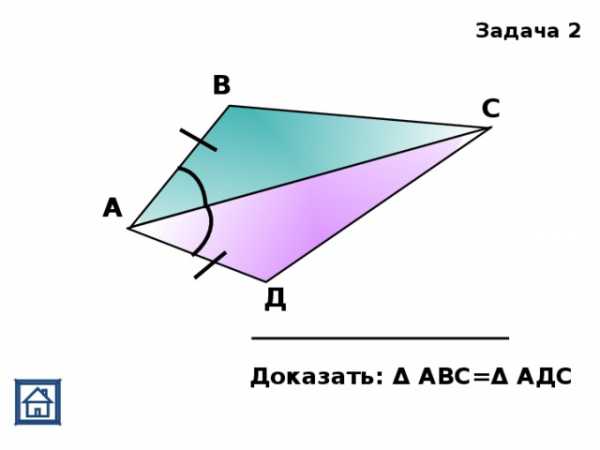
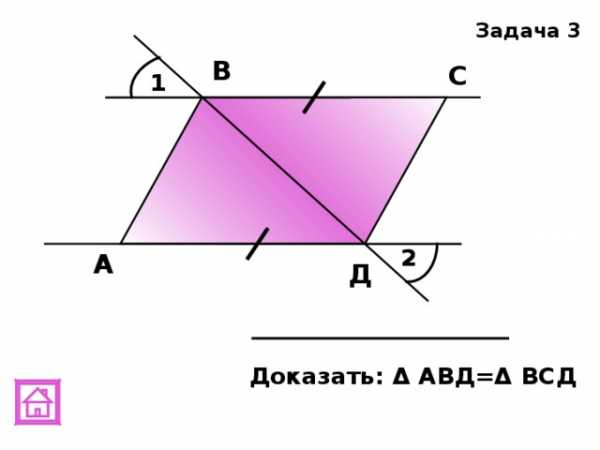
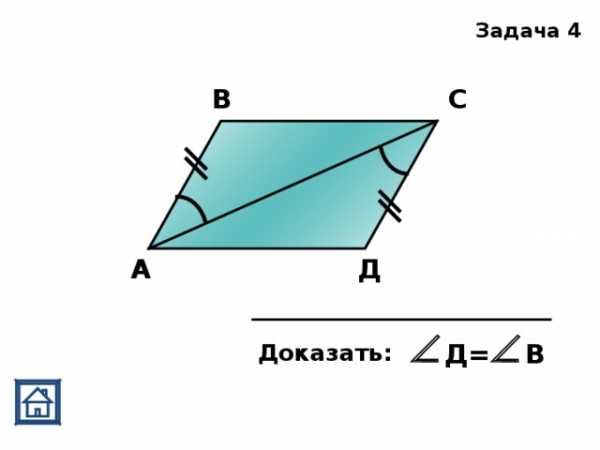

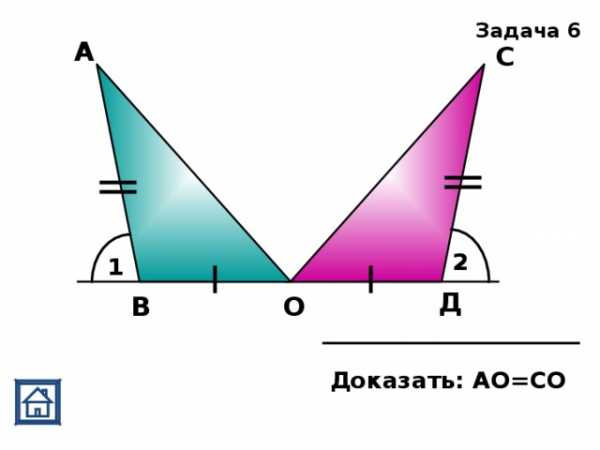






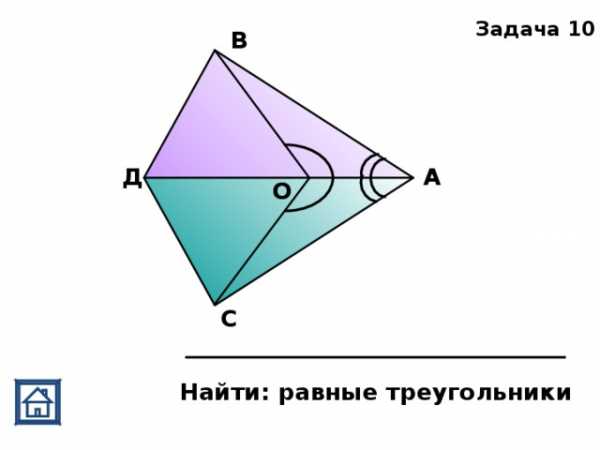


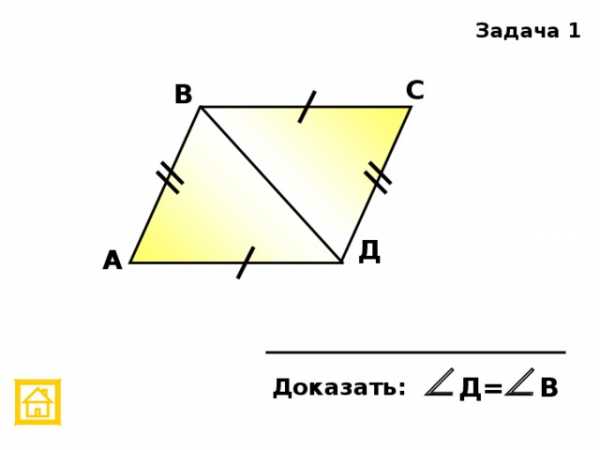
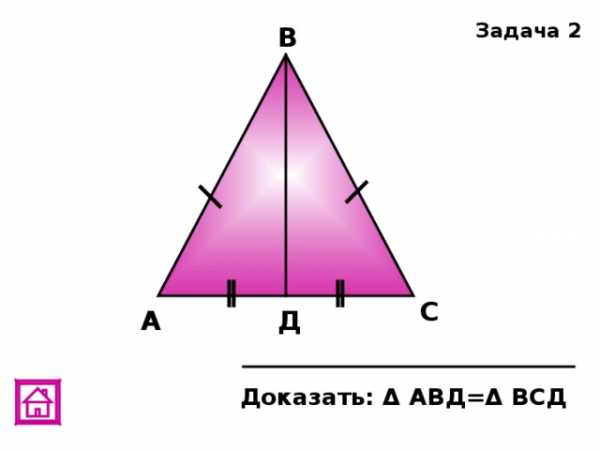
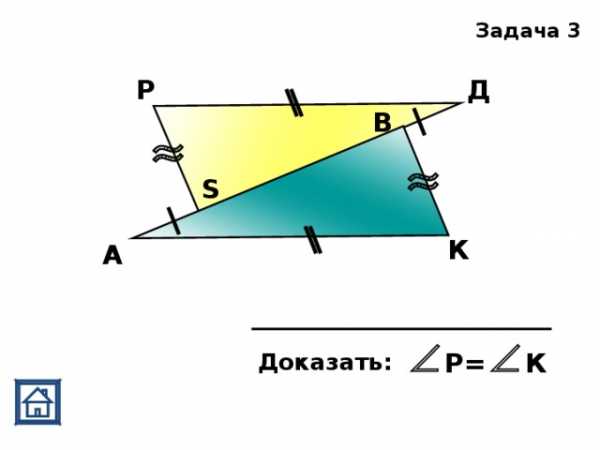




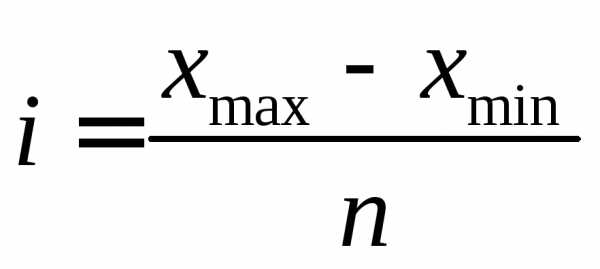

 ,
где
,
где ,
где
,
где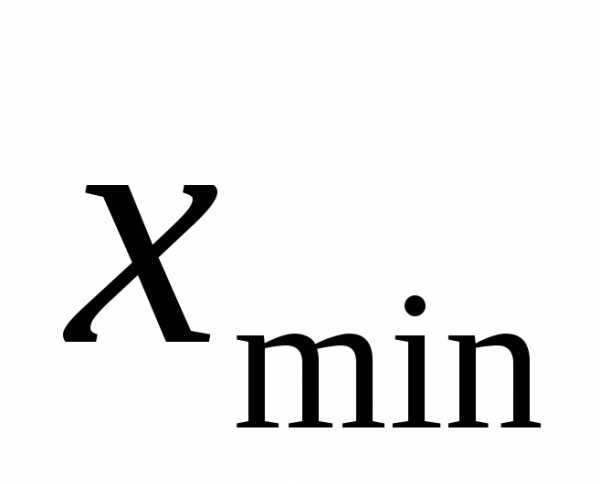 и наибольшее
и наибольшее значения.
значения.
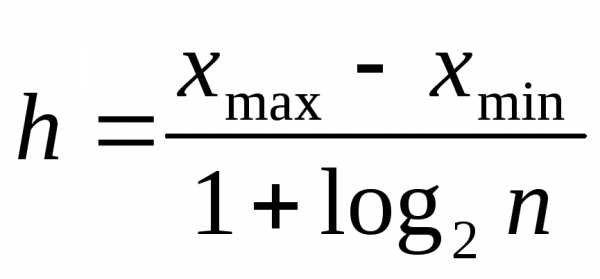 ,
где n – объем выборки – количество
данных в выборке; для вычислений берутlgn).
,
где n – объем выборки – количество
данных в выборке; для вычислений берутlgn).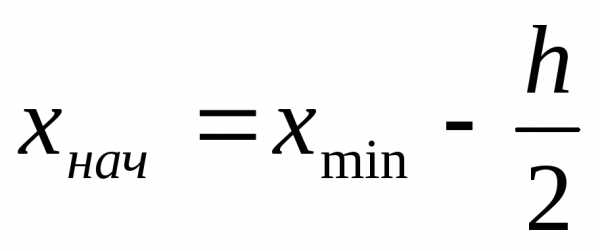 ;
;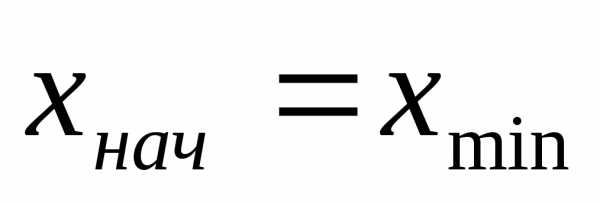 .
.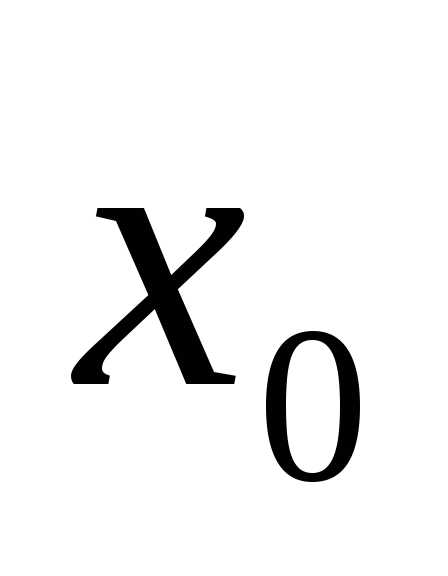 —
нижняя граница первого интервала. За
—
нижняя граница первого интервала. За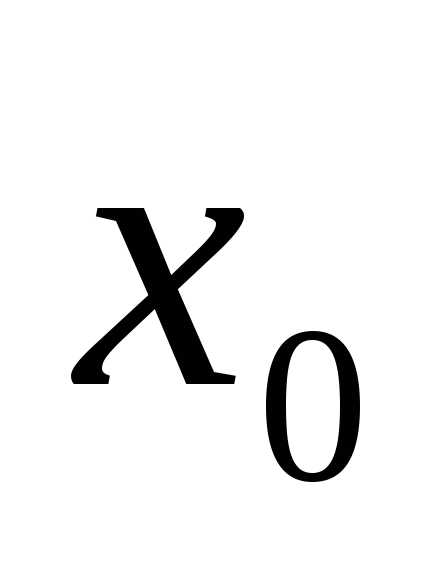 берется удобное число не большее
берется удобное число не большее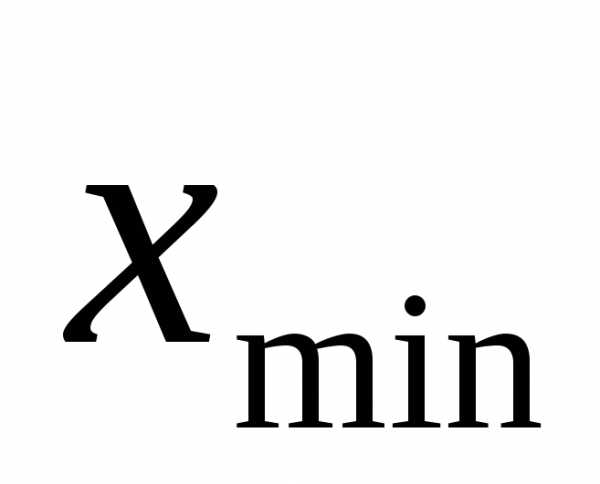 ,
верхняя граница последнего интервала
должна быть не меньше
,
верхняя граница последнего интервала
должна быть не меньше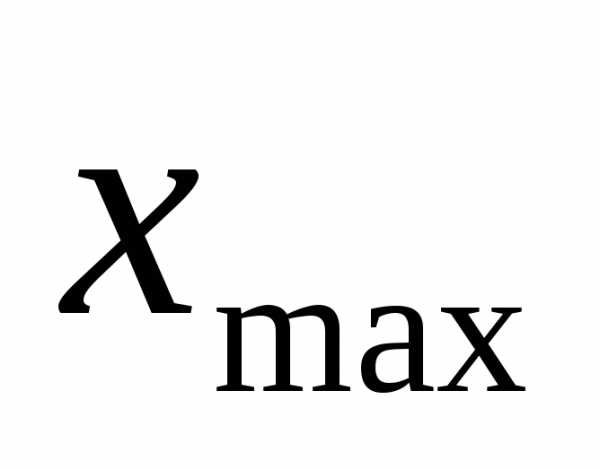 .
Рекомендуется, чтобы интервалы содержали
в себе исходные значения случайной
величины и выделять от5 до 20интервалов.
.
Рекомендуется, чтобы интервалы содержали
в себе исходные значения случайной
величины и выделять от5 до 20интервалов.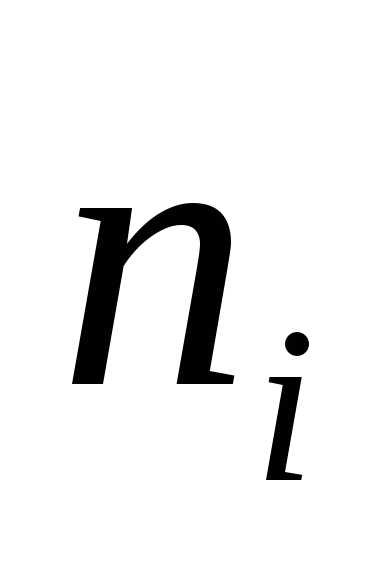 ,
то необходимо перегруппировать данные,
укрупняя интервалы (увеличивая шаг
,
то необходимо перегруппировать данные,
укрупняя интервалы (увеличивая шаг 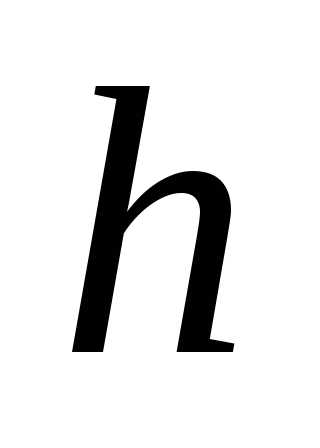 ).
).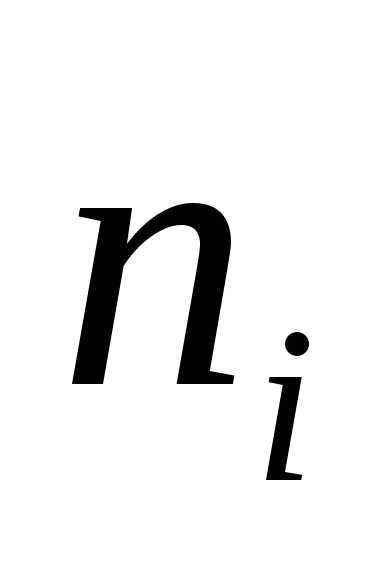 ,
— число студентов попавших в каждый из
полученных промежутков.
,
— число студентов попавших в каждый из
полученных промежутков.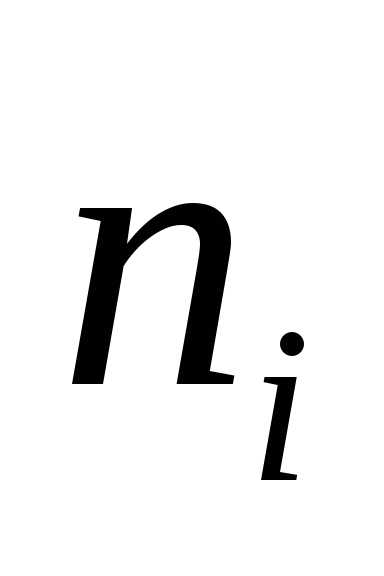 (частота)
(частота)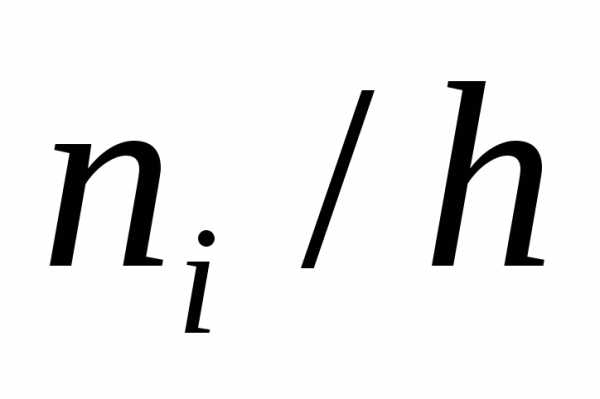 (плотность частоты).
(плотность частоты).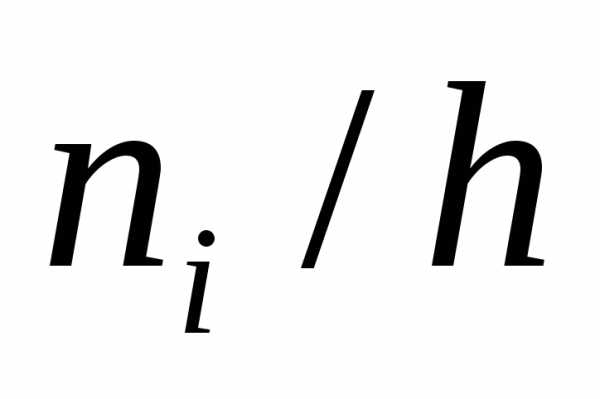 .
.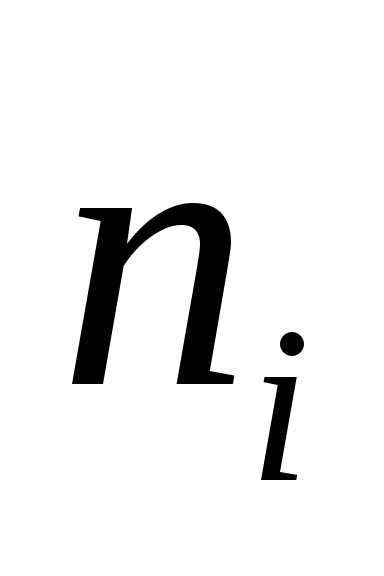 (частота)
(частота)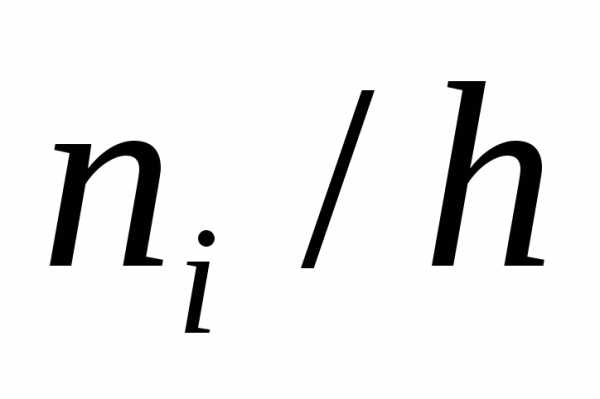
 ,определяет для каждого значения х
относительную частоту события Х <x.
,определяет для каждого значения х
относительную частоту события Х <x.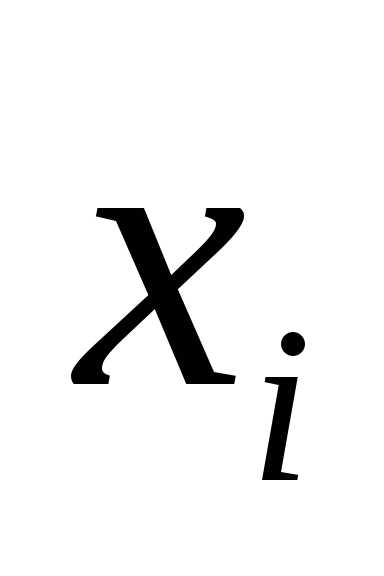 принимают середины частичных интервалов.
Частоты при этом не изменяются.
На оси 0х отмечают значения
принимают середины частичных интервалов.
Частоты при этом не изменяются.
На оси 0х отмечают значения 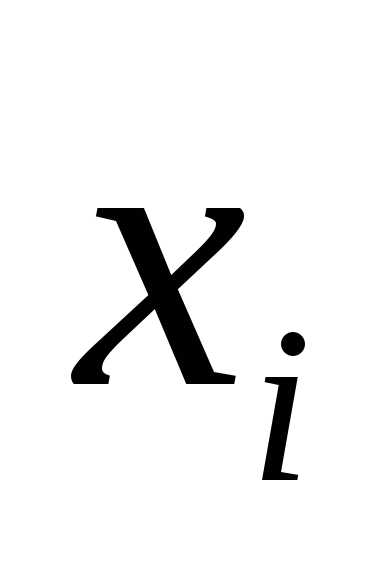 ,
на оси 0у – накопительные частоты.
,
на оси 0у – накопительные частоты.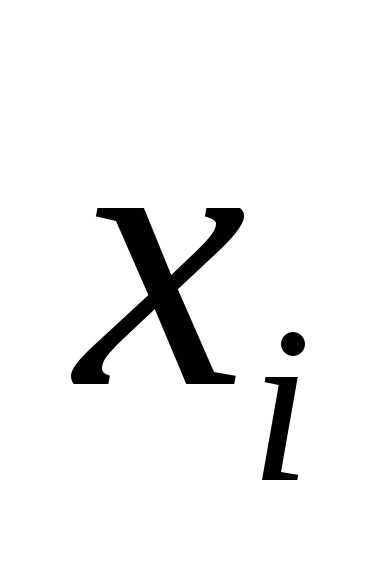 и запишем эти значения в первую
строку таблицы;
и запишем эти значения в первую
строку таблицы;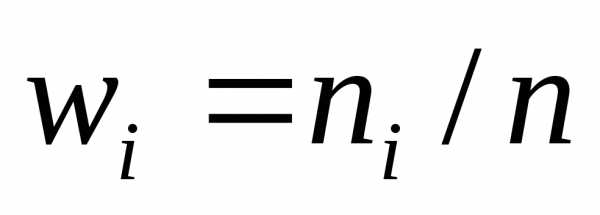 и запишем в третью строку таблицы;
и запишем в третью строку таблицы;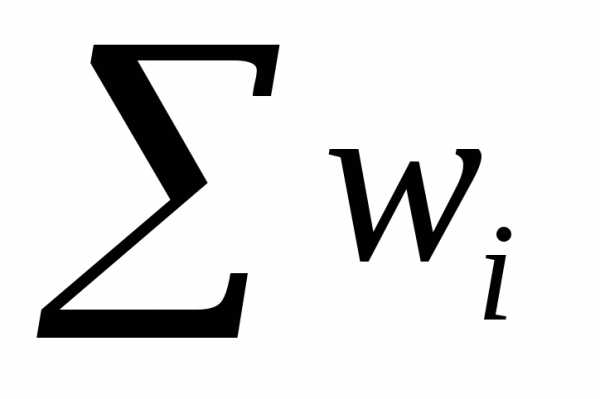 и запишем в четвертую строку таблицы.
и запишем в четвертую строку таблицы.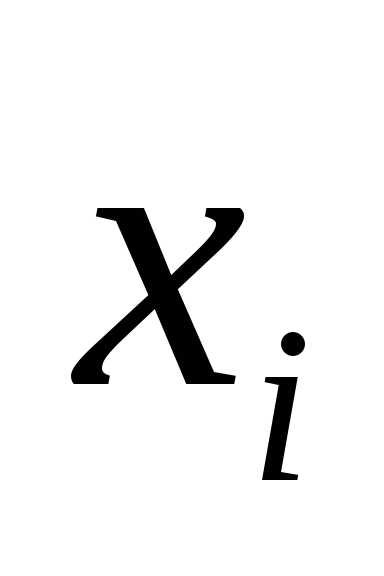 (середина интервала)
(середина интервала)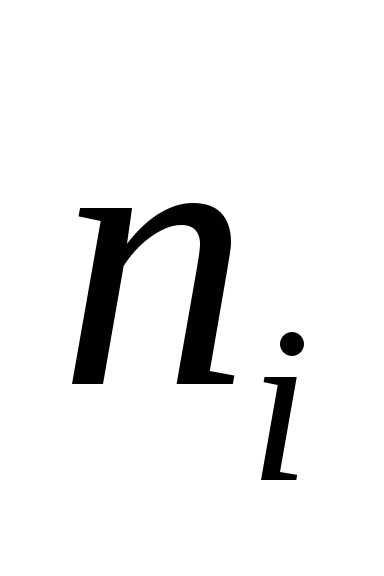 (частота)
(частота)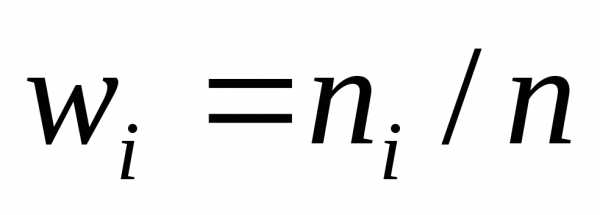
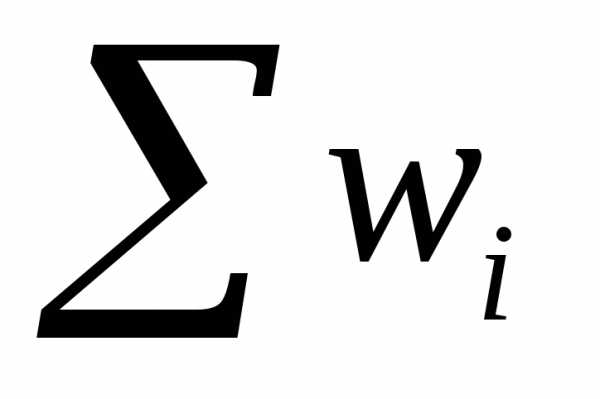
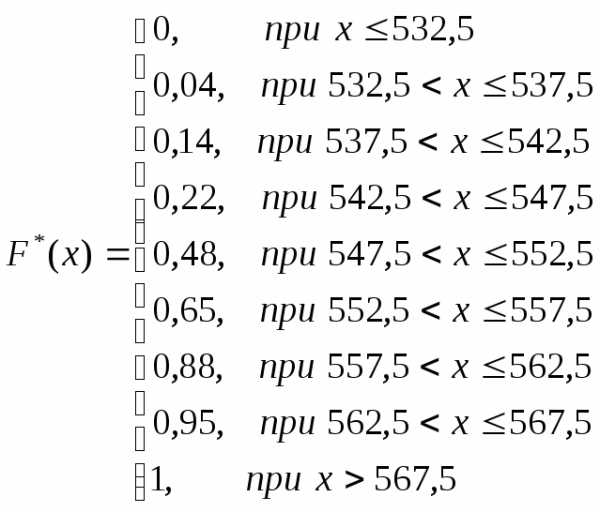
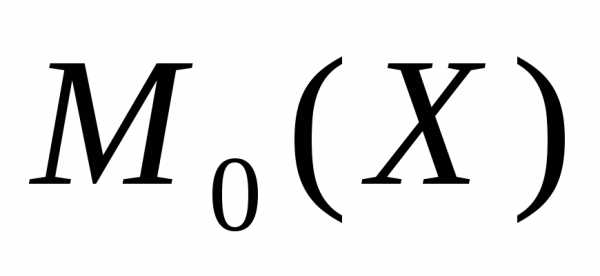 = 547,5.
= 547,5.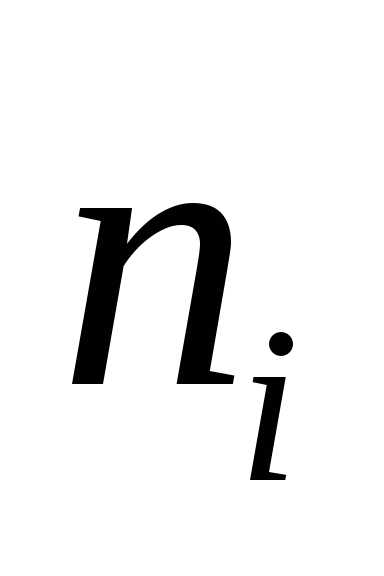 ;
(число одинаковых значений дискретной
случайной величины или число наблюдений
в i-м
интервале в случае непрерывной случайной
величины). Такое представление признака
и частот называется вариационным рядом.
;
(число одинаковых значений дискретной
случайной величины или число наблюдений
в i-м
интервале в случае непрерывной случайной
величины). Такое представление признака
и частот называется вариационным рядом. где
где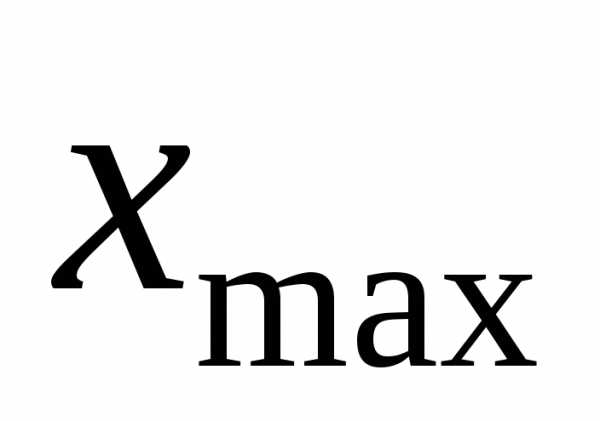 и
и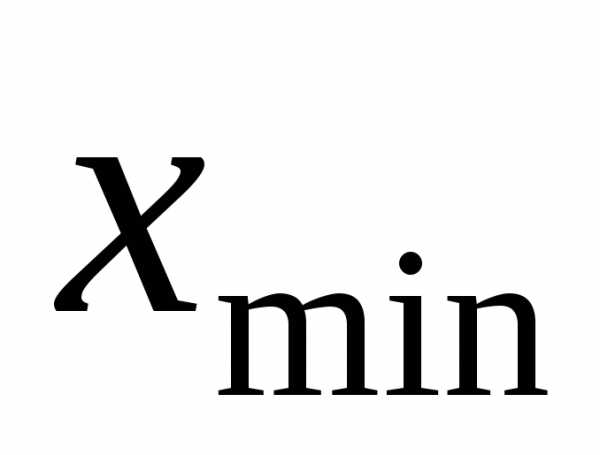 – соответственно максимальное и
минимальное значения признака
– соответственно максимальное и
минимальное значения признака 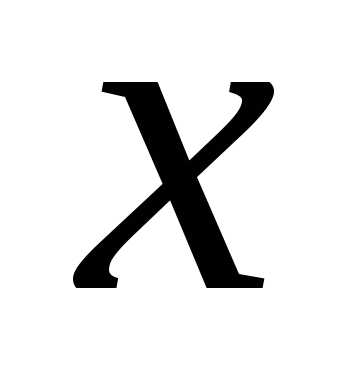 в выборке;l – количество
интервалов, причём в данной работе мы
будем использовать следующую формулу:
,
где n – объём
выборки.
в выборке;l – количество
интервалов, причём в данной работе мы
будем использовать следующую формулу:
,
где n – объём
выборки.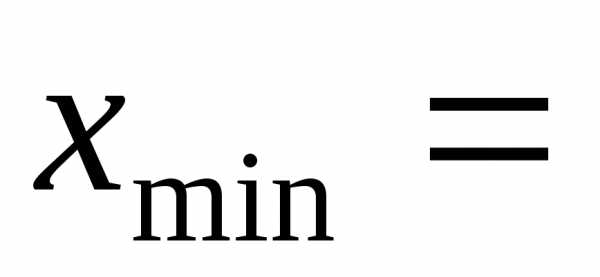 6,75,
6,75,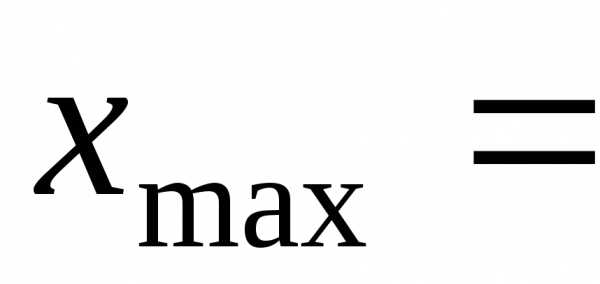 10,97
,
10,97
,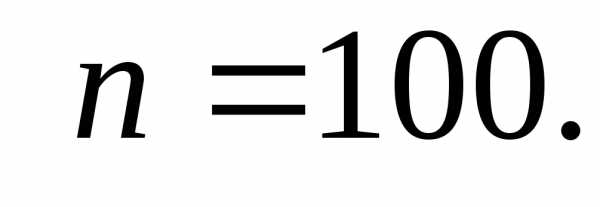
 (10,97–6,75)/10=0,422
(10,97–6,75)/10=0,422 0,43.
0,43.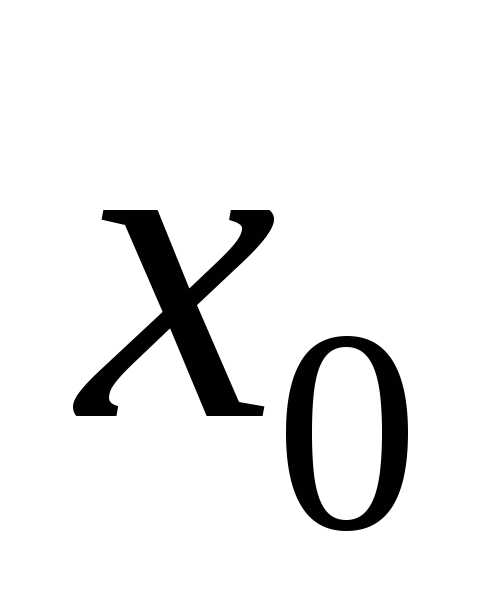 и длину интервала
и длину интервала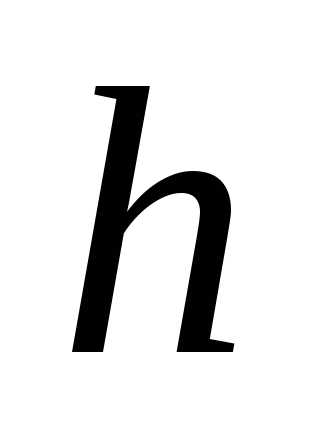 ,
построим весь интервальный ряд.
,
построим весь интервальный ряд.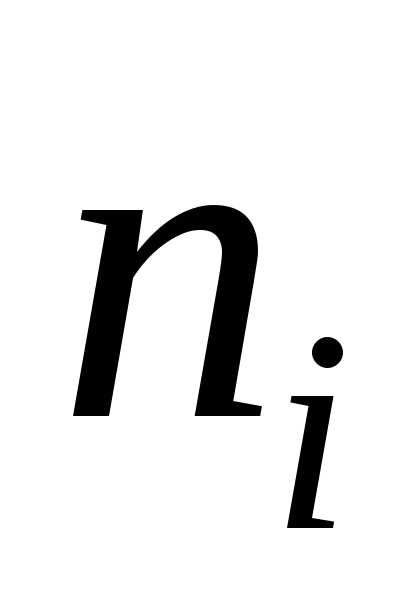 »
таблицы 1. Проведём проверку полученных
значений частот:
»
таблицы 1. Проведём проверку полученных
значений частот: .
.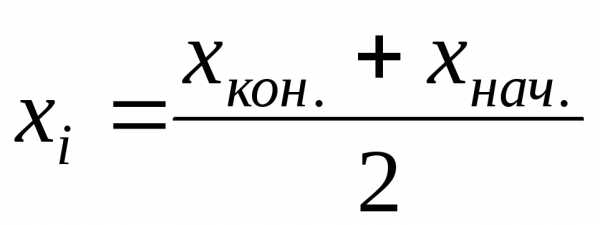 ,
где
,
где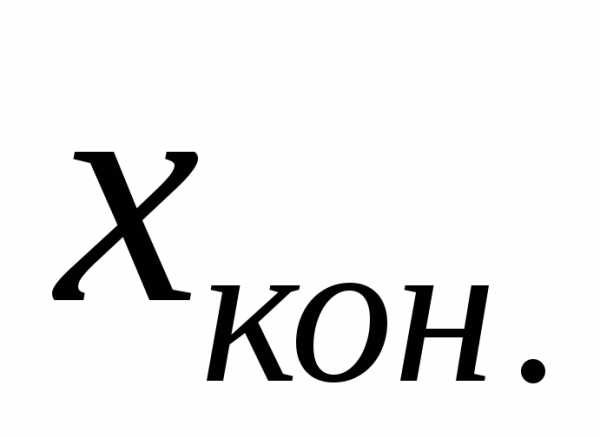 и
и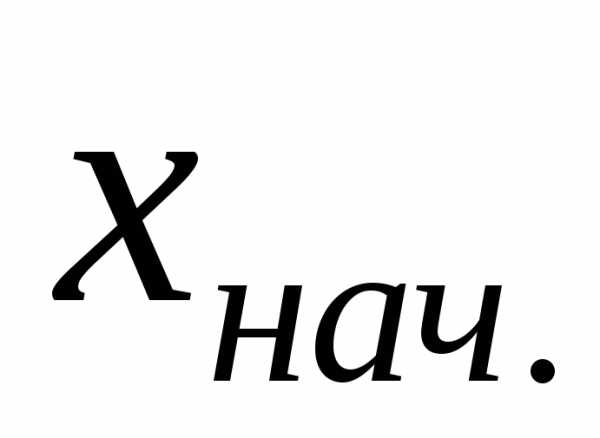 –
конечное и начальное значения определённого
интервала. Результаты занесем в таблицу
1.
–
конечное и начальное значения определённого
интервала. Результаты занесем в таблицу
1.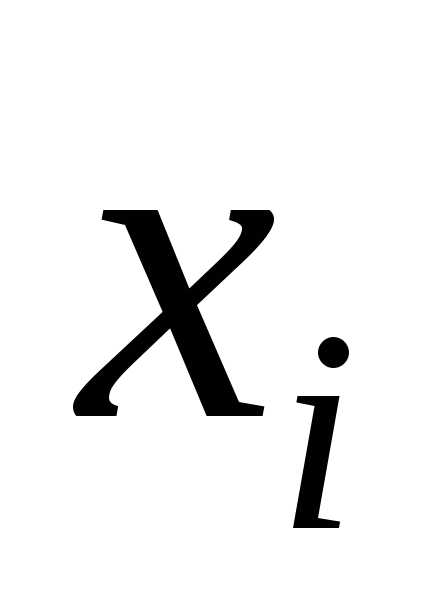

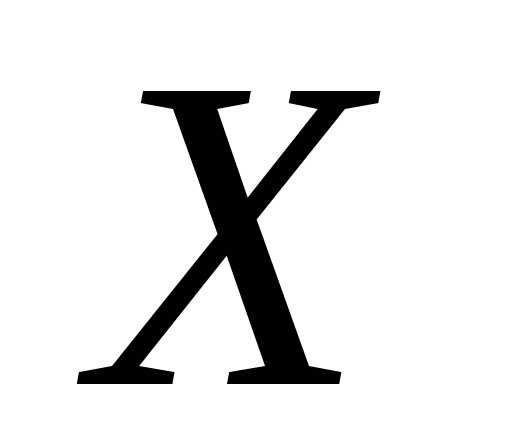 ,
на каждом из которых строим прямоугольник,
высота которого равна соответствующей
частоте интервала.
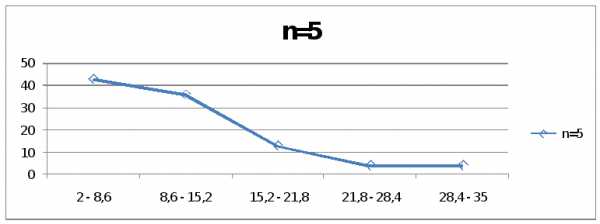
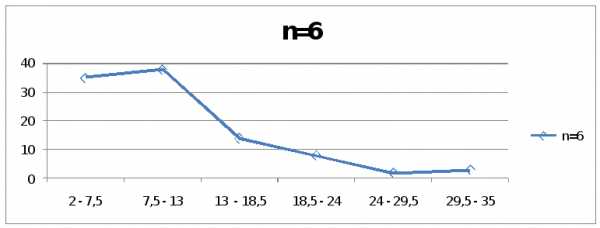
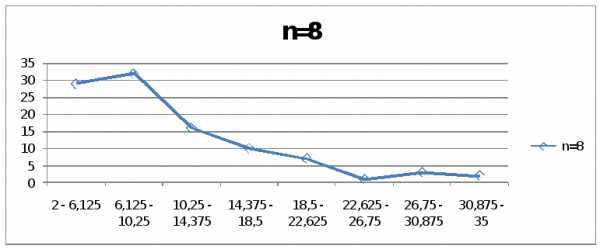
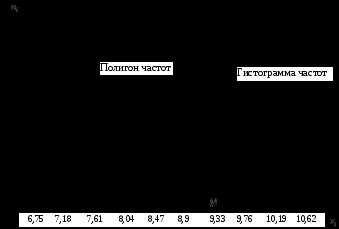
Если на гистограмме частот соединить
середины верхних сторон элементарных
прямоугольников, то полученная замкнутая
ломаная образует полигон распределения
частот (рис. 1). По гистограмме приближённо
определим моду (см. подраздел 5.1).
,
на каждом из которых строим прямоугольник,
высота которого равна соответствующей
частоте интервала.
Если на гистограмме частот соединить
середины верхних сторон элементарных
прямоугольников, то полученная замкнутая
ломаная образует полигон распределения
частот (рис. 1). По гистограмме приближённо
определим моду (см. подраздел 5.1).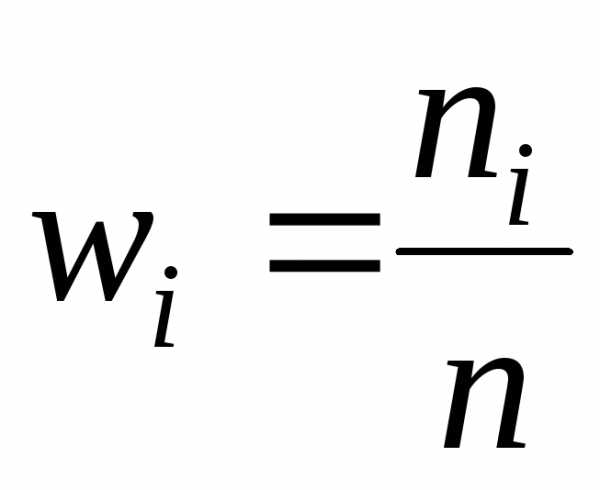 соответствует график функции плотности
распределения. По виду полигона делают
первоначальное предположение о законе
распределения исследуемой случайной
величины.
соответствует график функции плотности
распределения. По виду полигона делают
первоначальное предположение о законе
распределения исследуемой случайной
величины.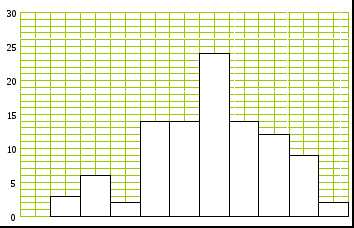
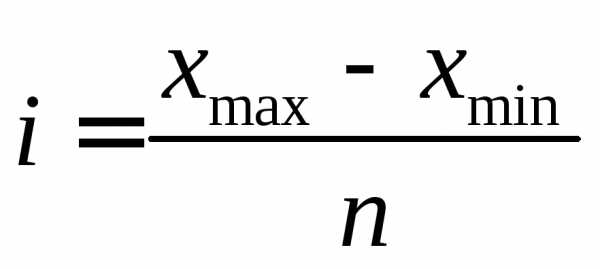
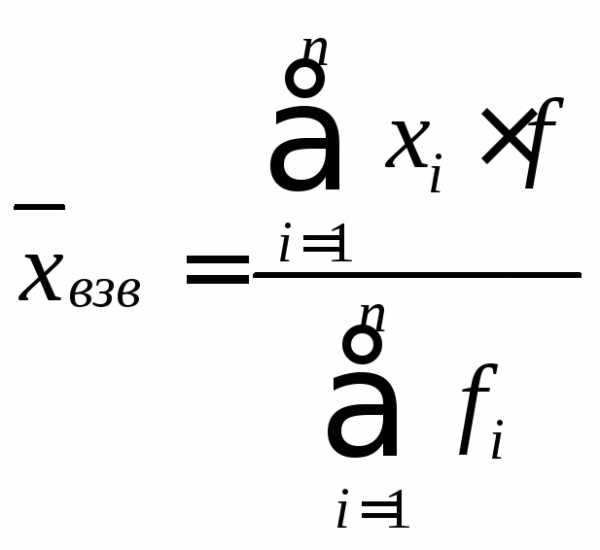 ,
где
,
где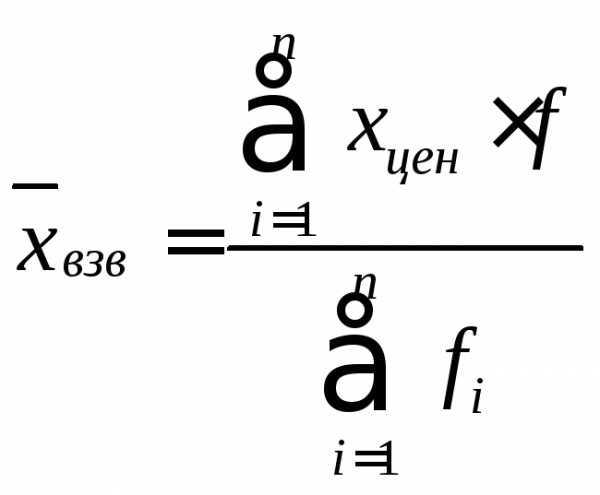 ,
где
,
где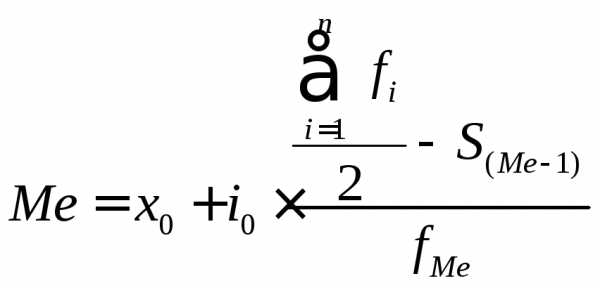 ,
где
,
где