градус в секунду [°/с] радиан в секунду [рад/с] • Механика • Конвертер угловой скорости и частоты вращения • Компактный калькулятор
Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисленияКонвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер паропроницаемости и скорости переноса параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
1 градус в секунду [°/с] = 0,0174532925199433 радиан в секунду [рад/с]
Общие сведения
Угловая скорость в спорте
Угловая скорость и хранение данных на оптических носителях
Угловая скорость в космосе
Потолочный вентилятор, вращающийся со скоростью 250 оборотов в минуту
Общие сведения
Угловая скорость — это векторная величина, определяющая скорость вращения тела относительно оси вращения. Этот вектор направлен перпендикулярно плоскости вращения и определяется с помощью правила буравчика. Угловую скорость измеряют как отношение между углом, на который переместилось тело, то есть угловым смещением, и временем, на это потраченным. В системе СИ угловое ускорение измеряют в радианах в секунду.
Угловая скорость в спорте
Угловая скорость часто используется в спорте. Например, спортсмены уменьшают или увеличивают угловую скорость движения клюшки для гольфа, биты или ракетки, чтобы улучшить результаты. Угловая скорость связана с линейной скоростью так, что из всех точек на отрезке, вращающемся вокруг точки на этом отрезке, то есть вокруг центра вращения, самая отдаленная точка от этого центра движется с самой высокой линейной скоростью. Так, например, если клюшка для гольфа вращается, то конец этой клюшки, больше всего удаленный от центра вращения двигается с самой высокой линейной скоростью. В то же время все точки на этом отрезке движутся с одинаковой угловой скоростью. Поэтому удлиняя клюшку, биту, или ракетку, спортсмен также увеличивает линейную скорость, а соответственно скорость удара, передающуюся мячу, так что он может пролететь на большее расстояние. Укорачивая ракетку или клюшку, даже перехватив ее ниже, чем обычно, наоборот замедляют скорость удара.
При первобытнообщинном строе главными охотниками были мужчины
Спортсменам с более длинными руками и ногами удается добиться бо́льшей угловой скорости
У высоких людей с длинными конечностями есть преимущество в отношении линейной скорости. То есть, передвигая ноги с одинаковой угловой скоростью, они двигают ступни с более высокой линейной скоростью. То же происходит и с их руками. Такое преимущество может быть одной из причин того, что в первобытных обществах мужчины занимались охотой чаще, чем женщины. Вероятно, что из-за этого также в процессе эволюции выиграли более высокие люди. Длинные конечности помогали не только в беге, но и во время охоты — длинные руки бросали копья и камни с большей линейной скоростью. С другой стороны, длинные руки и ноги могут быть неудобством. Длинные конечности имеют больший вес и для их перемещения нужна дополнительная энергия. Кроме этого, когда человек быстро бежит, длинные ноги быстрее двигаются, а значит, при столкновении с препятствием удар будет сильнее, чем у людей с короткими ногами, которые двигаются с той же линейной скоростью.
В гимнастике, фигурном катании и нырянии также используют угловую скорость. Если спортсмен знает угловую скорость, то легко вычислить количество переворотов и других акробатических трюков во время прыжка. Во время кувырков спортсмены обычно прижимают ноги и руки как можно ближе к корпусу, чтобы уменьшить инерцию и увеличить ускорение, а значит и угловую скорость. С другой стороны, во время ныряния или приземления, судьи смотрят, как ровно спортсмен приземлился. На высокой скорости трудно регулировать направление полета, поэтому спортсмены специально замедляют угловую скорость, немного вытягивая от корпуса руки и ноги.
Спортсмены, которые занимаются метанием диска или молота, тоже контролируют линейную скорость с помощью угловой. Если просто бросить молот, не вращая его по кругу на длинной стальной проволоке, увеличивающей линейную скорость, то бросок будет не таким сильным, поэтому молот сначала раскручивают. Олимпийские спортсмены поворачиваются вокруг своей оси от трех до четырех раз, чтобы увеличить угловую скорость до максимально возможной.
Угловая скорость и хранение данных на оптических носителях
Диски в накопителе на жестких магнитных дисках («винчестере») вращаются со скоростями от 4 200 оборотов в минуту на портативных устройствах с низким энергопотреблением до 15 000 оборотов в минуту на высокоэффективных серверах
Во время записи данных на оптических носителях, например на компакт дисках (CD), для измерения скорости записи и считывания данных в приводе также используются угловая и линейная скорости. Существует несколько способов записи данных, во время которых используют переменную или постоянную линейную или угловую скорость. Так, например, режим постоянной линейной скорости (по-английски — Constant Linear Velocity или CVL) — один из основных методов записи дисков, при котором данные записывают с одинаковой скоростью по всей поверхности диска. Во время записи в режиме зональной постоянной линейной скорости (по-английски — Zone Constant Linear Velocity или ZCLV) постоянная скорость поддерживается во время записи на определенной части, то есть зоне диска. В этом случае диск замедляет вращение при записи на внешних зонах. Режим частично постоянной угловой скорости (Partial Constant Angular Velocity или PCAV) позволяет осуществлять запись с постепенным увеличением угловой скорости, пока она не достигнет определенного порога. После этого угловая скорость становится постоянной.
Последний режим записи — режим постоянной угловой скорости (Constant Angular Velocity или CAV). В этом режиме во время записи по всей поверхности диска поддерживается одинаковая угловая скорость. При этом линейная скорость увеличивается по мере того, как записывающая головка перемещается все дальше и дальше к краю диска. Этот режим используется также при записи грампластинок и в компьютерных жестких дисках.
Угловая скорость в космосе
Геостационарная орбита
На расстоянии 35 786 километров (22 236 миль) от Земли находится орбита, на которой вращаются спутники. Это особенная орбита, потому что тела, вращающиеся на ней в одном направлении с Землей, проходят всю орбиту примерно за такое же время, которое требуется Земле, чтобы совершить полный круг вокруг своей оси. Это немного меньше 24 часов, то есть один сидерический день. Так как угловая скорость вращения тел на этой орбите равна угловой скорости вращения Земли, то наблюдателям с Земли кажется, что эти тела не движутся. Такая орбита называется геостационарной.
На эту орбиту обычно выводят спутники, которые отслеживают изменения погоды (метеорологические спутники), спутники, следящие за изменениями в океане и спутники связи, которые обеспечивают телевизионное и радиовещание, телефонную связь и спутниковый Интернет. Геостационарную орбиту часто используют для спутников потому, что антенны, один раз направленные на спутник, не нужно направлять вторично. С другой стороны, с их использованием связаны такие неудобства, как необходимость иметь прямое поле видимости между антенной и спутником. Кроме того, геостационарная орбита находится далеко от Земли и для передачи сигнала необходимо использовать более мощные передатчики, чем те, что используются для передачи с более низких орбит. Сигнал приходит с задержкой приблизительно в 0,25 секунды, что заметно для пользователей. Например, во время трансляции новостей корреспонденты в удаленных районах обычно связываются со студией по спутниковому каналу; при этом заметно, что когда телеведущий задает им вопрос, они отвечают с задержкой. Несмотря на это, спутники на геостационарной орбите широко используются. Например, до недавнего времени связь между континентами осуществлялась, главным образом, с помощью спутников. Сейчас ее в основном заменили межконтинентальные кабели, проложенные по океанскому дну; однако спутниковую связь до сих пор применяют в отдаленных районах. В последние двадцать лет спутники связи также обеспечивают доступ к интернету, особенно в отдаленных местах, где нет наземной инфраструктуры связи.
Спутниковые антенны
Срок службы спутника в основном определяется количеством топлива на борту, требуемым для периодической коррекции орбиты. Количество топлива в спутниках ограничено, поэтому когда оно заканчивается, спутники выводят из эксплуатации. Чаще всего их переводят на орбиту захоронения, то есть орбиту, намного выше геостационарной. Это — дорогостоящий процесс; однако если оставлять ненужные спутники на геостационарной орбите, это грозит вероятностью столкновений с другими спутниками. Место на геостационарной орбите ограничено, поэтому старые спутники, оставленные на орбите, будут занимать место, которое мог бы использовать новый спутник. В связи с этим во многих странах существуют нормы, требующие от владельцев спутников подписать договор о том, что в конце эксплуатации спутник будет выведен на орбиту захоронения.
Литература
Автор статьи: Kateryna Yuri
Unit Converter articles were edited and illustrated by Анатолий Золотков
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Расчеты для перевода единиц в конвертере «Конвертер угловой скорости и частоты вращения» выполняются с помощью функций unitconversion.org.
www.translatorscafe.com
оборотов в минуту [об/мин] градус в секунду [°/с] • Механика • Конвертер угловой скорости и частоты вращения • Компактный калькулятор
Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисленияКонвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер паропроницаемости и скорости переноса параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
1 оборотов в минуту [об/мин] = 6,00000000000002 градус в секунду [°/с]
Общие сведения
Угловая скорость в спорте
Угловая скорость и хранение данных на оптических носителях
Угловая скорость в космосе
Потолочный вентилятор, вращающийся со скоростью 250 оборотов в минуту
Общие сведения
Угловая скорость — это векторная величина, определяющая скорость вращения тела относительно оси вращения. Этот вектор направлен перпендикулярно плоскости вращения и определяется с помощью правила буравчика. Угловую скорость измеряют как отношение между углом, на который переместилось тело, то есть угловым смещением, и временем, на это потраченным. В системе СИ угловое ускорение измеряют в радианах в секунду.
Угловая скорость в спорте
Угловая скорость часто используется в спорте. Например, спортсмены уменьшают или увеличивают угловую скорость движения клюшки для гольфа, биты или ракетки, чтобы улучшить результаты. Угловая скорость связана с линейной скоростью так, что из всех точек на отрезке, вращающемся вокруг точки на этом отрезке, то есть вокруг центра вращения, самая отдаленная точка от этого центра движется с самой высокой линейной скоростью. Так, например, если клюшка для гольфа вращается, то конец этой клюшки, больше всего удаленный от центра вращения двигается с самой высокой линейной скоростью. В то же время все точки на этом отрезке движутся с одинаковой угловой скоростью. Поэтому удлиняя клюшку, биту, или ракетку, спортсмен также увеличивает линейную скорость, а соответственно скорость удара, передающуюся мячу, так что он может пролететь на большее расстояние. Укорачивая ракетку или клюшку, даже перехватив ее ниже, чем обычно, наоборот замедляют скорость удара.
При первобытнообщинном строе главными охотниками были мужчины
Спортсменам с более длинными руками и ногами удается добиться бо́льшей угловой скорости
У высоких людей с длинными конечностями есть преимущество в отношении линейной скорости. То есть, передвигая ноги с одинаковой угловой скоростью, они двигают ступни с более высокой линейной скоростью. То же происходит и с их руками. Такое преимущество может быть одной из причин того, что в первобытных обществах мужчины занимались охотой чаще, чем женщины. Вероятно, что из-за этого также в процессе эволюции выиграли более высокие люди. Длинные конечности помогали не только в беге, но и во время охоты — длинные руки бросали копья и камни с большей линейной скоростью. С другой стороны, длинные руки и ноги могут быть неудобством. Длинные конечности имеют больший вес и для их перемещения нужна дополнительная энергия. Кроме этого, когда человек быстро бежит, длинные ноги быстрее двигаются, а значит, при столкновении с препятствием удар будет сильнее, чем у людей с короткими ногами, которые двигаются с той же линейной скоростью.
В гимнастике, фигурном катании и нырянии также используют угловую скорость. Если спортсмен знает угловую скорость, то легко вычислить количество переворотов и других акробатических трюков во время прыжка. Во время кувырков спортсмены обычно прижимают ноги и руки как можно ближе к корпусу, чтобы уменьшить инерцию и увеличить ускорение, а значит и угловую скорость. С другой стороны, во время ныряния или приземления, судьи смотрят, как ровно спортсмен приземлился. На высокой скорости трудно регулировать направление полета, поэтому спортсмены специально замедляют угловую скорость, немного вытягивая от корпуса руки и ноги.
Спортсмены, которые занимаются метанием диска или молота, тоже контролируют линейную скорость с помощью угловой. Если просто бросить молот, не вращая его по кругу на длинной стальной проволоке, увеличивающей линейную скорость, то бросок будет не таким сильным, поэтому молот сначала раскручивают. Олимпийские спортсмены поворачиваются вокруг своей оси от трех до четырех раз, чтобы увеличить угловую скорость до максимально возможной.
Угловая скорость и хранение данных на оптических носителях
Диски в накопителе на жестких магнитных дисках («винчестере») вращаются со скоростями от 4 200 оборотов в минуту на портативных устройствах с низким энергопотреблением до 15 000 оборотов в минуту на высокоэффективных серверах
Во время записи данных на оптических носителях, например на компакт дисках (CD), для измерения скорости записи и считывания данных в приводе также используются угловая и линейная скорости. Существует несколько способов записи данных, во время которых используют переменную или постоянную линейную или угловую скорость. Так, например, режим постоянной линейной скорости (по-английски — Constant Linear Velocity или CVL) — один из основных методов записи дисков, при котором данные записывают с одинаковой скоростью по всей поверхности диска. Во время записи в режиме зональной постоянной линейной скорости (по-английски — Zone Constant Linear Velocity или ZCLV) постоянная скорость поддерживается во время записи на определенной части, то есть зоне диска. В этом случае диск замедляет вращение при записи на внешних зонах. Режим частично постоянной угловой скорости (Partial Constant Angular Velocity или PCAV) позволяет осуществлять запись с постепенным увеличением угловой скорости, пока она не достигнет определенного порога. После этого угловая скорость становится постоянной.
Последний режим записи — режим постоянной угловой скорости (Constant Angular Velocity или CAV). В этом режиме во время записи по всей поверхности диска поддерживается одинаковая угловая скорость. При этом линейная скорость увеличивается по мере того, как записывающая головка перемещается все дальше и дальше к краю диска. Этот режим используется также при записи грампластинок и в компьютерных жестких дисках.
Угловая скорость в космосе
Геостационарная орбита
На расстоянии 35 786 километров (22 236 миль) от Земли находится орбита, на которой вращаются спутники. Это особенная орбита, потому что тела, вращающиеся на ней в одном направлении с Землей, проходят всю орбиту примерно за такое же время, которое требуется Земле, чтобы совершить полный круг вокруг своей оси. Это немного меньше 24 часов, то есть один сидерический день. Так как угловая скорость вращения тел на этой орбите равна угловой скорости вращения Земли, то наблюдателям с Земли кажется, что эти тела не движутся. Такая орбита называется геостационарной.
На эту орбиту обычно выводят спутники, которые отслеживают изменения погоды (метеорологические спутники), спутники, следящие за изменениями в океане и спутники связи, которые обеспечивают телевизионное и радиовещание, телефонную связь и спутниковый Интернет. Геостационарную орбиту часто используют для спутников потому, что антенны, один раз направленные на спутник, не нужно направлять вторично. С другой стороны, с их использованием связаны такие неудобства, как необходимость иметь прямое поле видимости между антенной и спутником. Кроме того, геостационарная орбита находится далеко от Земли и для передачи сигнала необходимо использовать более мощные передатчики, чем те, что используются для передачи с более низких орбит. Сигнал приходит с задержкой приблизительно в 0,25 секунды, что заметно для пользователей. Например, во время трансляции новостей корреспонденты в удаленных районах обычно связываются со студией по спутниковому каналу; при этом заметно, что когда телеведущий задает им вопрос, они отвечают с задержкой. Несмотря на это, спутники на геостационарной орбите широко используются. Например, до недавнего времени связь между континентами осуществлялась, главным образом, с помощью спутников. Сейчас ее в основном заменили межконтинентальные кабели, проложенные по океанскому дну; однако спутниковую связь до сих пор применяют в отдаленных районах. В последние двадцать лет спутники связи также обеспечивают доступ к интернету, особенно в отдаленных местах, где нет наземной инфраструктуры связи.
Спутниковые антенны
Срок службы спутника в основном определяется количеством топлива на борту, требуемым для периодической коррекции орбиты. Количество топлива в спутниках ограничено, поэтому когда оно заканчивается, спутники выводят из эксплуатации. Чаще всего их переводят на орбиту захоронения, то есть орбиту, намного выше геостационарной. Это — дорогостоящий процесс; однако если оставлять ненужные спутники на геостационарной орбите, это грозит вероятностью столкновений с другими спутниками. Место на геостационарной орбите ограничено, поэтому старые спутники, оставленные на орбите, будут занимать место, которое мог бы использовать новый спутник. В связи с этим во многих странах существуют нормы, требующие от владельцев спутников подписать договор о том, что в конце эксплуатации спутник будет выведен на орбиту захоронения.
Литература
Автор статьи: Kateryna Yuri
Unit Converter articles were edited and illustrated by Анатолий Золотков
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Расчеты для перевода единиц в конвертере «Конвертер угловой скорости и частоты вращения» выполняются с помощью функций unitconversion.org.
www.translatorscafe.com
градус в секунду [°/с] оборотов в секунду [об/с] • Механика • Конвертер угловой скорости и частоты вращения • Компактный калькулятор
Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисленияКонвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер паропроницаемости и скорости переноса параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
1 градус в секунду [°/с] = 0,00277777777777777 оборотов в секунду [об/с]
Общие сведения
Угловая скорость в спорте
Угловая скорость и хранение данных на оптических носителях
Угловая скорость в космосе
Потолочный вентилятор, вращающийся со скоростью 250 оборотов в минуту
Общие сведения
Угловая скорость — это векторная величина, определяющая скорость вращения тела относительно оси вращения. Этот вектор направлен перпендикулярно плоскости вращения и определяется с помощью правила буравчика. Угловую скорость измеряют как отношение между углом, на который переместилось тело, то есть угловым смещением, и временем, на это потраченным. В системе СИ угловое ускорение измеряют в радианах в секунду.
Угловая скорость в спорте
Угловая скорость часто используется в спорте. Например, спортсмены уменьшают или увеличивают угловую скорость движения клюшки для гольфа, биты или ракетки, чтобы улучшить результаты. Угловая скорость связана с линейной скоростью так, что из всех точек на отрезке, вращающемся вокруг точки на этом отрезке, то есть вокруг центра вращения, самая отдаленная точка от этого центра движется с самой высокой линейной скоростью. Так, например, если клюшка для гольфа вращается, то конец этой клюшки, больше всего удаленный от центра вращения двигается с самой высокой линейной скоростью. В то же время все точки на этом отрезке движутся с одинаковой угловой скоростью. Поэтому удлиняя клюшку, биту, или ракетку, спортсмен также увеличивает линейную скорость, а соответственно скорость удара, передающуюся мячу, так что он может пролететь на большее расстояние. Укорачивая ракетку или клюшку, даже перехватив ее ниже, чем обычно, наоборот замедляют скорость удара.
При первобытнообщинном строе главными охотниками были мужчины
Спортсменам с более длинными руками и ногами удается добиться бо́льшей угловой скорости
У высоких людей с длинными конечностями есть преимущество в отношении линейной скорости. То есть, передвигая ноги с одинаковой угловой скоростью, они двигают ступни с более высокой линейной скоростью. То же происходит и с их руками. Такое преимущество может быть одной из причин того, что в первобытных обществах мужчины занимались охотой чаще, чем женщины. Вероятно, что из-за этого также в процессе эволюции выиграли более высокие люди. Длинные конечности помогали не только в беге, но и во время охоты — длинные руки бросали копья и камни с большей линейной скоростью. С другой стороны, длинные руки и ноги могут быть неудобством. Длинные конечности имеют больший вес и для их перемещения нужна дополнительная энергия. Кроме этого, когда человек быстро бежит, длинные ноги быстрее двигаются, а значит, при столкновении с препятствием удар будет сильнее, чем у людей с короткими ногами, которые двигаются с той же линейной скоростью.
В гимнастике, фигурном катании и нырянии также используют угловую скорость. Если спортсмен знает угловую скорость, то легко вычислить количество переворотов и других акробатических трюков во время прыжка. Во время кувырков спортсмены обычно прижимают ноги и руки как можно ближе к корпусу, чтобы уменьшить инерцию и увеличить ускорение, а значит и угловую скорость. С другой стороны, во время ныряния или приземления, судьи смотрят, как ровно спортсмен приземлился. На высокой скорости трудно регулировать направление полета, поэтому спортсмены специально замедляют угловую скорость, немного вытягивая от корпуса руки и ноги.
Спортсмены, которые занимаются метанием диска или молота, тоже контролируют линейную скорость с помощью угловой. Если просто бросить молот, не вращая его по кругу на длинной стальной проволоке, увеличивающей линейную скорость, то бросок будет не таким сильным, поэтому молот сначала раскручивают. Олимпийские спортсмены поворачиваются вокруг своей оси от трех до четырех раз, чтобы увеличить угловую скорость до максимально возможной.
Угловая скорость и хранение данных на оптических носителях
Диски в накопителе на жестких магнитных дисках («винчестере») вращаются со скоростями от 4 200 оборотов в минуту на портативных устройствах с низким энергопотреблением до 15 000 оборотов в минуту на высокоэффективных серверах
Во время записи данных на оптических носителях, например на компакт дисках (CD), для измерения скорости записи и считывания данных в приводе также используются угловая и линейная скорости. Существует несколько способов записи данных, во время которых используют переменную или постоянную линейную или угловую скорость. Так, например, режим постоянной линейной скорости (по-английски — Constant Linear Velocity или CVL) — один из основных методов записи дисков, при котором данные записывают с одинаковой скоростью по всей поверхности диска. Во время записи в режиме зональной постоянной линейной скорости (по-английски — Zone Constant Linear Velocity или ZCLV) постоянная скорость поддерживается во время записи на определенной части, то есть зоне диска. В этом случае диск замедляет вращение при записи на внешних зонах. Режим частично постоянной угловой скорости (Partial Constant Angular Velocity или PCAV) позволяет осуществлять запись с постепенным увеличением угловой скорости, пока она не достигнет определенного порога. После этого угловая скорость становится постоянной.
Последний режим записи — режим постоянной угловой скорости (Constant Angular Velocity или CAV). В этом режиме во время записи по всей поверхности диска поддерживается одинаковая угловая скорость. При этом линейная скорость увеличивается по мере того, как записывающая головка перемещается все дальше и дальше к краю диска. Этот режим используется также при записи грампластинок и в компьютерных жестких дисках.
Угловая скорость в космосе
Геостационарная орбита
На расстоянии 35 786 километров (22 236 миль) от Земли находится орбита, на которой вращаются спутники. Это особенная орбита, потому что тела, вращающиеся на ней в одном направлении с Землей, проходят всю орбиту примерно за такое же время, которое требуется Земле, чтобы совершить полный круг вокруг своей оси. Это немного меньше 24 часов, то есть один сидерический день. Так как угловая скорость вращения тел на этой орбите равна угловой скорости вращения Земли, то наблюдателям с Земли кажется, что эти тела не движутся. Такая орбита называется геостационарной.
На эту орбиту обычно выводят спутники, которые отслеживают изменения погоды (метеорологические спутники), спутники, следящие за изменениями в океане и спутники связи, которые обеспечивают телевизионное и радиовещание, телефонную связь и спутниковый Интернет. Геостационарную орбиту часто используют для спутников потому, что антенны, один раз направленные на спутник, не нужно направлять вторично. С другой стороны, с их использованием связаны такие неудобства, как необходимость иметь прямое поле видимости между антенной и спутником. Кроме того, геостационарная орбита находится далеко от Земли и для передачи сигнала необходимо использовать более мощные передатчики, чем те, что используются для передачи с более низких орбит. Сигнал приходит с задержкой приблизительно в 0,25 секунды, что заметно для пользователей. Например, во время трансляции новостей корреспонденты в удаленных районах обычно связываются со студией по спутниковому каналу; при этом заметно, что когда телеведущий задает им вопрос, они отвечают с задержкой. Несмотря на это, спутники на геостационарной орбите широко используются. Например, до недавнего времени связь между континентами осуществлялась, главным образом, с помощью спутников. Сейчас ее в основном заменили межконтинентальные кабели, проложенные по океанскому дну; однако спутниковую связь до сих пор применяют в отдаленных районах. В последние двадцать лет спутники связи также обеспечивают доступ к интернету, особенно в отдаленных местах, где нет наземной инфраструктуры связи.
Спутниковые антенны
Срок службы спутника в основном определяется количеством топлива на борту, требуемым для периодической коррекции орбиты. Количество топлива в спутниках ограничено, поэтому когда оно заканчивается, спутники выводят из эксплуатации. Чаще всего их переводят на орбиту захоронения, то есть орбиту, намного выше геостационарной. Это — дорогостоящий процесс; однако если оставлять ненужные спутники на геостационарной орбите, это грозит вероятностью столкновений с другими спутниками. Место на геостационарной орбите ограничено, поэтому старые спутники, оставленные на орбите, будут занимать место, которое мог бы использовать новый спутник. В связи с этим во многих странах существуют нормы, требующие от владельцев спутников подписать договор о том, что в конце эксплуатации спутник будет выведен на орбиту захоронения.
Литература
Автор статьи: Kateryna Yuri
Unit Converter articles were edited and illustrated by Анатолий Золотков
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Расчеты для перевода единиц в конвертере «Конвертер угловой скорости и частоты вращения» выполняются с помощью функций unitconversion.org.
www.translatorscafe.com
градус в секунду [°/с] градус в сутки [°/сутки] • Механика • Конвертер угловой скорости и частоты вращения • Компактный калькулятор
Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисленияКонвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер паропроницаемости и скорости переноса параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
1 градус в секунду [°/с] = 86399,9999999998 градус в сутки [°/сутки]
Общие сведения
Угловая скорость в спорте
Угловая скорость и хранение данных на оптических носителях
Угловая скорость в космосе
Потолочный вентилятор, вращающийся со скоростью 250 оборотов в минуту
Общие сведения
Угловая скорость — это векторная величина, определяющая скорость вращения тела относительно оси вращения. Этот вектор направлен перпендикулярно плоскости вращения и определяется с помощью правила буравчика. Угловую скорость измеряют как отношение между углом, на который переместилось тело, то есть угловым смещением, и временем, на это потраченным. В системе СИ угловое ускорение измеряют в радианах в секунду.
Угловая скорость в спорте
Угловая скорость часто используется в спорте. Например, спортсмены уменьшают или увеличивают угловую скорость движения клюшки для гольфа, биты или ракетки, чтобы улучшить результаты. Угловая скорость связана с линейной скоростью так, что из всех точек на отрезке, вращающемся вокруг точки на этом отрезке, то есть вокруг центра вращения, самая отдаленная точка от этого центра движется с самой высокой линейной скоростью. Так, например, если клюшка для гольфа вращается, то конец этой клюшки, больше всего удаленный от центра вращения двигается с самой высокой линейной скоростью. В то же время все точки на этом отрезке движутся с одинаковой угловой скоростью. Поэтому удлиняя клюшку, биту, или ракетку, спортсмен также увеличивает линейную скорость, а соответственно скорость удара, передающуюся мячу, так что он может пролететь на большее расстояние. Укорачивая ракетку или клюшку, даже перехватив ее ниже, чем обычно, наоборот замедляют скорость удара.
При первобытнообщинном строе главными охотниками были мужчины
Спортсменам с более длинными руками и ногами удается добиться бо́льшей угловой скорости
У высоких людей с длинными конечностями есть преимущество в отношении линейной скорости. То есть, передвигая ноги с одинаковой угловой скоростью, они двигают ступни с более высокой линейной скоростью. То же происходит и с их руками. Такое преимущество может быть одной из причин того, что в первобытных обществах мужчины занимались охотой чаще, чем женщины. Вероятно, что из-за этого также в процессе эволюции выиграли более высокие люди. Длинные конечности помогали не только в беге, но и во время охоты — длинные руки бросали копья и камни с большей линейной скоростью. С другой стороны, длинные руки и ноги могут быть неудобством. Длинные конечности имеют больший вес и для их перемещения нужна дополнительная энергия. Кроме этого, когда человек быстро бежит, длинные ноги быстрее двигаются, а значит, при столкновении с препятствием удар будет сильнее, чем у людей с короткими ногами, которые двигаются с той же линейной скоростью.
В гимнастике, фигурном катании и нырянии также используют угловую скорость. Если спортсмен знает угловую скорость, то легко вычислить количество переворотов и других акробатических трюков во время прыжка. Во время кувырков спортсмены обычно прижимают ноги и руки как можно ближе к корпусу, чтобы уменьшить инерцию и увеличить ускорение, а значит и угловую скорость. С другой стороны, во время ныряния или приземления, судьи смотрят, как ровно спортсмен приземлился. На высокой скорости трудно регулировать направление полета, поэтому спортсмены специально замедляют угловую скорость, немного вытягивая от корпуса руки и ноги.
Спортсмены, которые занимаются метанием диска или молота, тоже контролируют линейную скорость с помощью угловой. Если просто бросить молот, не вращая его по кругу на длинной стальной проволоке, увеличивающей линейную скорость, то бросок будет не таким сильным, поэтому молот сначала раскручивают. Олимпийские спортсмены поворачиваются вокруг своей оси от трех до четырех раз, чтобы увеличить угловую скорость до максимально возможной.
Угловая скорость и хранение данных на оптических носителях
Диски в накопителе на жестких магнитных дисках («винчестере») вращаются со скоростями от 4 200 оборотов в минуту на портативных устройствах с низким энергопотреблением до 15 000 оборотов в минуту на высокоэффективных серверах
Во время записи данных на оптических носителях, например на компакт дисках (CD), для измерения скорости записи и считывания данных в приводе также используются угловая и линейная скорости. Существует несколько способов записи данных, во время которых используют переменную или постоянную линейную или угловую скорость. Так, например, режим постоянной линейной скорости (по-английски — Constant Linear Velocity или CVL) — один из основных методов записи дисков, при котором данные записывают с одинаковой скоростью по всей поверхности диска. Во время записи в режиме зональной постоянной линейной скорости (по-английски — Zone Constant Linear Velocity или ZCLV) постоянная скорость поддерживается во время записи на определенной части, то есть зоне диска. В этом случае диск замедляет вращение при записи на внешних зонах. Режим частично постоянной угловой скорости (Partial Constant Angular Velocity или PCAV) позволяет осуществлять запись с постепенным увеличением угловой скорости, пока она не достигнет определенного порога. После этого угловая скорость становится постоянной.
Последний режим записи — режим постоянной угловой скорости (Constant Angular Velocity или CAV). В этом режиме во время записи по всей поверхности диска поддерживается одинаковая угловая скорость. При этом линейная скорость увеличивается по мере того, как записывающая головка перемещается все дальше и дальше к краю диска. Этот режим используется также при записи грампластинок и в компьютерных жестких дисках.
Угловая скорость в космосе
Геостационарная орбита
На расстоянии 35 786 километров (22 236 миль) от Земли находится орбита, на которой вращаются спутники. Это особенная орбита, потому что тела, вращающиеся на ней в одном направлении с Землей, проходят всю орбиту примерно за такое же время, которое требуется Земле, чтобы совершить полный круг вокруг своей оси. Это немного меньше 24 часов, то есть один сидерический день. Так как угловая скорость вращения тел на этой орбите равна угловой скорости вращения Земли, то наблюдателям с Земли кажется, что эти тела не движутся. Такая орбита называется геостационарной.
На эту орбиту обычно выводят спутники, которые отслеживают изменения погоды (метеорологические спутники), спутники, следящие за изменениями в океане и спутники связи, которые обеспечивают телевизионное и радиовещание, телефонную связь и спутниковый Интернет. Геостационарную орбиту часто используют для спутников потому, что антенны, один раз направленные на спутник, не нужно направлять вторично. С другой стороны, с их использованием связаны такие неудобства, как необходимость иметь прямое поле видимости между антенной и спутником. Кроме того, геостационарная орбита находится далеко от Земли и для передачи сигнала необходимо использовать более мощные передатчики, чем те, что используются для передачи с более низких орбит. Сигнал приходит с задержкой приблизительно в 0,25 секунды, что заметно для пользователей. Например, во время трансляции новостей корреспонденты в удаленных районах обычно связываются со студией по спутниковому каналу; при этом заметно, что когда телеведущий задает им вопрос, они отвечают с задержкой. Несмотря на это, спутники на геостационарной орбите широко используются. Например, до недавнего времени связь между континентами осуществлялась, главным образом, с помощью спутников. Сейчас ее в основном заменили межконтинентальные кабели, проложенные по океанскому дну; однако спутниковую связь до сих пор применяют в отдаленных районах. В последние двадцать лет спутники связи также обеспечивают доступ к интернету, особенно в отдаленных местах, где нет наземной инфраструктуры связи.
Спутниковые антенны
Срок службы спутника в основном определяется количеством топлива на борту, требуемым для периодической коррекции орбиты. Количество топлива в спутниках ограничено, поэтому когда оно заканчивается, спутники выводят из эксплуатации. Чаще всего их переводят на орбиту захоронения, то есть орбиту, намного выше геостационарной. Это — дорогостоящий процесс; однако если оставлять ненужные спутники на геостационарной орбите, это грозит вероятностью столкновений с другими спутниками. Место на геостационарной орбите ограничено, поэтому старые спутники, оставленные на орбите, будут занимать место, которое мог бы использовать новый спутник. В связи с этим во многих странах существуют нормы, требующие от владельцев спутников подписать договор о том, что в конце эксплуатации спутник будет выведен на орбиту захоронения.
Литература
Автор статьи: Kateryna Yuri
Unit Converter articles were edited and illustrated by Анатолий Золотков
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Расчеты для перевода единиц в конвертере «Конвертер угловой скорости и частоты вращения» выполняются с помощью функций unitconversion.org.
www.translatorscafe.com
градус в час [°/ч] радиан в секунду [рад/с] • Механика • Конвертер угловой скорости и частоты вращения • Компактный калькулятор
Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисленияКонвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер паропроницаемости и скорости переноса параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
1 градус в час [°/ч] = 4,84813681109536E-06 радиан в секунду [рад/с]
Общие сведения
Угловая скорость в спорте
Угловая скорость и хранение данных на оптических носителях
Угловая скорость в космосе
Потолочный вентилятор, вращающийся со скоростью 250 оборотов в минуту
Общие сведения
Угловая скорость — это векторная величина, определяющая скорость вращения тела относительно оси вращения. Этот вектор направлен перпендикулярно плоскости вращения и определяется с помощью правила буравчика. Угловую скорость измеряют как отношение между углом, на который переместилось тело, то есть угловым смещением, и временем, на это потраченным. В системе СИ угловое ускорение измеряют в радианах в секунду.
Угловая скорость в спорте
Угловая скорость часто используется в спорте. Например, спортсмены уменьшают или увеличивают угловую скорость движения клюшки для гольфа, биты или ракетки, чтобы улучшить результаты. Угловая скорость связана с линейной скоростью так, что из всех точек на отрезке, вращающемся вокруг точки на этом отрезке, то есть вокруг центра вращения, самая отдаленная точка от этого центра движется с самой высокой линейной скоростью. Так, например, если клюшка для гольфа вращается, то конец этой клюшки, больше всего удаленный от центра вращения двигается с самой высокой линейной скоростью. В то же время все точки на этом отрезке движутся с одинаковой угловой скоростью. Поэтому удлиняя клюшку, биту, или ракетку, спортсмен также увеличивает линейную скорость, а соответственно скорость удара, передающуюся мячу, так что он может пролететь на большее расстояние. Укорачивая ракетку или клюшку, даже перехватив ее ниже, чем обычно, наоборот замедляют скорость удара.
При первобытнообщинном строе главными охотниками были мужчины
Спортсменам с более длинными руками и ногами удается добиться бо́льшей угловой скорости
У высоких людей с длинными конечностями есть преимущество в отношении линейной скорости. То есть, передвигая ноги с одинаковой угловой скоростью, они двигают ступни с более высокой линейной скоростью. То же происходит и с их руками. Такое преимущество может быть одной из причин того, что в первобытных обществах мужчины занимались охотой чаще, чем женщины. Вероятно, что из-за этого также в процессе эволюции выиграли более высокие люди. Длинные конечности помогали не только в беге, но и во время охоты — длинные руки бросали копья и камни с большей линейной скоростью. С другой стороны, длинные руки и ноги могут быть неудобством. Длинные конечности имеют больший вес и для их перемещения нужна дополнительная энергия. Кроме этого, когда человек быстро бежит, длинные ноги быстрее двигаются, а значит, при столкновении с препятствием удар будет сильнее, чем у людей с короткими ногами, которые двигаются с той же линейной скоростью.
В гимнастике, фигурном катании и нырянии также используют угловую скорость. Если спортсмен знает угловую скорость, то легко вычислить количество переворотов и других акробатических трюков во время прыжка. Во время кувырков спортсмены обычно прижимают ноги и руки как можно ближе к корпусу, чтобы уменьшить инерцию и увеличить ускорение, а значит и угловую скорость. С другой стороны, во время ныряния или приземления, судьи смотрят, как ровно спортсмен приземлился. На высокой скорости трудно регулировать направление полета, поэтому спортсмены специально замедляют угловую скорость, немного вытягивая от корпуса руки и ноги.
Спортсмены, которые занимаются метанием диска или молота, тоже контролируют линейную скорость с помощью угловой. Если просто бросить молот, не вращая его по кругу на длинной стальной проволоке, увеличивающей линейную скорость, то бросок будет не таким сильным, поэтому молот сначала раскручивают. Олимпийские спортсмены поворачиваются вокруг своей оси от трех до четырех раз, чтобы увеличить угловую скорость до максимально возможной.
Угловая скорость и хранение данных на оптических носителях
Диски в накопителе на жестких магнитных дисках («винчестере») вращаются со скоростями от 4 200 оборотов в минуту на портативных устройствах с низким энергопотреблением до 15 000 оборотов в минуту на высокоэффективных серверах
Во время записи данных на оптических носителях, например на компакт дисках (CD), для измерения скорости записи и считывания данных в приводе также используются угловая и линейная скорости. Существует несколько способов записи данных, во время которых используют переменную или постоянную линейную или угловую скорость. Так, например, режим постоянной линейной скорости (по-английски — Constant Linear Velocity или CVL) — один из основных методов записи дисков, при котором данные записывают с одинаковой скоростью по всей поверхности диска. Во время записи в режиме зональной постоянной линейной скорости (по-английски — Zone Constant Linear Velocity или ZCLV) постоянная скорость поддерживается во время записи на определенной части, то есть зоне диска. В этом случае диск замедляет вращение при записи на внешних зонах. Режим частично постоянной угловой скорости (Partial Constant Angular Velocity или PCAV) позволяет осуществлять запись с постепенным увеличением угловой скорости, пока она не достигнет определенного порога. После этого угловая скорость становится постоянной.
Последний режим записи — режим постоянной угловой скорости (Constant Angular Velocity или CAV). В этом режиме во время записи по всей поверхности диска поддерживается одинаковая угловая скорость. При этом линейная скорость увеличивается по мере того, как записывающая головка перемещается все дальше и дальше к краю диска. Этот режим используется также при записи грампластинок и в компьютерных жестких дисках.
Угловая скорость в космосе
Геостационарная орбита
На расстоянии 35 786 километров (22 236 миль) от Земли находится орбита, на которой вращаются спутники. Это особенная орбита, потому что тела, вращающиеся на ней в одном направлении с Землей, проходят всю орбиту примерно за такое же время, которое требуется Земле, чтобы совершить полный круг вокруг своей оси. Это немного меньше 24 часов, то есть один сидерический день. Так как угловая скорость вращения тел на этой орбите равна угловой скорости вращения Земли, то наблюдателям с Земли кажется, что эти тела не движутся. Такая орбита называется геостационарной.
На эту орбиту обычно выводят спутники, которые отслеживают изменения погоды (метеорологические спутники), спутники, следящие за изменениями в океане и спутники связи, которые обеспечивают телевизионное и радиовещание, телефонную связь и спутниковый Интернет. Геостационарную орбиту часто используют для спутников потому, что антенны, один раз направленные на спутник, не нужно направлять вторично. С другой стороны, с их использованием связаны такие неудобства, как необходимость иметь прямое поле видимости между антенной и спутником. Кроме того, геостационарная орбита находится далеко от Земли и для передачи сигнала необходимо использовать более мощные передатчики, чем те, что используются для передачи с более низких орбит. Сигнал приходит с задержкой приблизительно в 0,25 секунды, что заметно для пользователей. Например, во время трансляции новостей корреспонденты в удаленных районах обычно связываются со студией по спутниковому каналу; при этом заметно, что когда телеведущий задает им вопрос, они отвечают с задержкой. Несмотря на это, спутники на геостационарной орбите широко используются. Например, до недавнего времени связь между континентами осуществлялась, главным образом, с помощью спутников. Сейчас ее в основном заменили межконтинентальные кабели, проложенные по океанскому дну; однако спутниковую связь до сих пор применяют в отдаленных районах. В последние двадцать лет спутники связи также обеспечивают доступ к интернету, особенно в отдаленных местах, где нет наземной инфраструктуры связи.
Спутниковые антенны
Срок службы спутника в основном определяется количеством топлива на борту, требуемым для периодической коррекции орбиты. Количество топлива в спутниках ограничено, поэтому когда оно заканчивается, спутники выводят из эксплуатации. Чаще всего их переводят на орбиту захоронения, то есть орбиту, намного выше геостационарной. Это — дорогостоящий процесс; однако если оставлять ненужные спутники на геостационарной орбите, это грозит вероятностью столкновений с другими спутниками. Место на геостационарной орбите ограничено, поэтому старые спутники, оставленные на орбите, будут занимать место, которое мог бы использовать новый спутник. В связи с этим во многих странах существуют нормы, требующие от владельцев спутников подписать договор о том, что в конце эксплуатации спутник будет выведен на орбиту захоронения.
Литература
Автор статьи: Kateryna Yuri
Unit Converter articles were edited and illustrated by Анатолий Золотков
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Расчеты для перевода единиц в конвертере «Конвертер угловой скорости и частоты вращения» выполняются с помощью функций unitconversion.org.
www.translatorscafe.com
градус в секунду [°/с] градус в минуту [°/мин] • Механика • Конвертер угловой скорости и частоты вращения • Компактный калькулятор
Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисленияКонвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер паропроницаемости и скорости переноса параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
1 градус в секунду [°/с] = 59,9999999999998 градус в минуту [°/мин]
Общие сведения
Угловая скорость в спорте
Угловая скорость и хранение данных на оптических носителях
Угловая скорость в космосе
Потолочный вентилятор, вращающийся со скоростью 250 оборотов в минуту
Общие сведения
Угловая скорость — это векторная величина, определяющая скорость вращения тела относительно оси вращения. Этот вектор направлен перпендикулярно плоскости вращения и определяется с помощью правила буравчика. Угловую скорость измеряют как отношение между углом, на который переместилось тело, то есть угловым смещением, и временем, на это потраченным. В системе СИ угловое ускорение измеряют в радианах в секунду.
Угловая скорость в спорте
Угловая скорость часто используется в спорте. Например, спортсмены уменьшают или увеличивают угловую скорость движения клюшки для гольфа, биты или ракетки, чтобы улучшить результаты. Угловая скорость связана с линейной скоростью так, что из всех точек на отрезке, вращающемся вокруг точки на этом отрезке, то есть вокруг центра вращения, самая отдаленная точка от этого центра движется с самой высокой линейной скоростью. Так, например, если клюшка для гольфа вращается, то конец этой клюшки, больше всего удаленный от центра вращения двигается с самой высокой линейной скоростью. В то же время все точки на этом отрезке движутся с одинаковой угловой скоростью. Поэтому удлиняя клюшку, биту, или ракетку, спортсмен также увеличивает линейную скорость, а соответственно скорость удара, передающуюся мячу, так что он может пролететь на большее расстояние. Укорачивая ракетку или клюшку, даже перехватив ее ниже, чем обычно, наоборот замедляют скорость удара.
При первобытнообщинном строе главными охотниками были мужчины
Спортсменам с более длинными руками и ногами удается добиться бо́льшей угловой скорости
У высоких людей с длинными конечностями есть преимущество в отношении линейной скорости. То есть, передвигая ноги с одинаковой угловой скоростью, они двигают ступни с более высокой линейной скоростью. То же происходит и с их руками. Такое преимущество может быть одной из причин того, что в первобытных обществах мужчины занимались охотой чаще, чем женщины. Вероятно, что из-за этого также в процессе эволюции выиграли более высокие люди. Длинные конечности помогали не только в беге, но и во время охоты — длинные руки бросали копья и камни с большей линейной скоростью. С другой стороны, длинные руки и ноги могут быть неудобством. Длинные конечности имеют больший вес и для их перемещения нужна дополнительная энергия. Кроме этого, когда человек быстро бежит, длинные ноги быстрее двигаются, а значит, при столкновении с препятствием удар будет сильнее, чем у людей с короткими ногами, которые двигаются с той же линейной скоростью.
В гимнастике, фигурном катании и нырянии также используют угловую скорость. Если спортсмен знает угловую скорость, то легко вычислить количество переворотов и других акробатических трюков во время прыжка. Во время кувырков спортсмены обычно прижимают ноги и руки как можно ближе к корпусу, чтобы уменьшить инерцию и увеличить ускорение, а значит и угловую скорость. С другой стороны, во время ныряния или приземления, судьи смотрят, как ровно спортсмен приземлился. На высокой скорости трудно регулировать направление полета, поэтому спортсмены специально замедляют угловую скорость, немного вытягивая от корпуса руки и ноги.
Спортсмены, которые занимаются метанием диска или молота, тоже контролируют линейную скорость с помощью угловой. Если просто бросить молот, не вращая его по кругу на длинной стальной проволоке, увеличивающей линейную скорость, то бросок будет не таким сильным, поэтому молот сначала раскручивают. Олимпийские спортсмены поворачиваются вокруг своей оси от трех до четырех раз, чтобы увеличить угловую скорость до максимально возможной.
Угловая скорость и хранение данных на оптических носителях
Диски в накопителе на жестких магнитных дисках («винчестере») вращаются со скоростями от 4 200 оборотов в минуту на портативных устройствах с низким энергопотреблением до 15 000 оборотов в минуту на высокоэффективных серверах
Во время записи данных на оптических носителях, например на компакт дисках (CD), для измерения скорости записи и считывания данных в приводе также используются угловая и линейная скорости. Существует несколько способов записи данных, во время которых используют переменную или постоянную линейную или угловую скорость. Так, например, режим постоянной линейной скорости (по-английски — Constant Linear Velocity или CVL) — один из основных методов записи дисков, при котором данные записывают с одинаковой скоростью по всей поверхности диска. Во время записи в режиме зональной постоянной линейной скорости (по-английски — Zone Constant Linear Velocity или ZCLV) постоянная скорость поддерживается во время записи на определенной части, то есть зоне диска. В этом случае диск замедляет вращение при записи на внешних зонах. Режим частично постоянной угловой скорости (Partial Constant Angular Velocity или PCAV) позволяет осуществлять запись с постепенным увеличением угловой скорости, пока она не достигнет определенного порога. После этого угловая скорость становится постоянной.
Последний режим записи — режим постоянной угловой скорости (Constant Angular Velocity или CAV). В этом режиме во время записи по всей поверхности диска поддерживается одинаковая угловая скорость. При этом линейная скорость увеличивается по мере того, как записывающая головка перемещается все дальше и дальше к краю диска. Этот режим используется также при записи грампластинок и в компьютерных жестких дисках.
Угловая скорость в космосе
Геостационарная орбита
На расстоянии 35 786 километров (22 236 миль) от Земли находится орбита, на которой вращаются спутники. Это особенная орбита, потому что тела, вращающиеся на ней в одном направлении с Землей, проходят всю орбиту примерно за такое же время, которое требуется Земле, чтобы совершить полный круг вокруг своей оси. Это немного меньше 24 часов, то есть один сидерический день. Так как угловая скорость вращения тел на этой орбите равна угловой скорости вращения Земли, то наблюдателям с Земли кажется, что эти тела не движутся. Такая орбита называется геостационарной.
На эту орбиту обычно выводят спутники, которые отслеживают изменения погоды (метеорологические спутники), спутники, следящие за изменениями в океане и спутники связи, которые обеспечивают телевизионное и радиовещание, телефонную связь и спутниковый Интернет. Геостационарную орбиту часто используют для спутников потому, что антенны, один раз направленные на спутник, не нужно направлять вторично. С другой стороны, с их использованием связаны такие неудобства, как необходимость иметь прямое поле видимости между антенной и спутником. Кроме того, геостационарная орбита находится далеко от Земли и для передачи сигнала необходимо использовать более мощные передатчики, чем те, что используются для передачи с более низких орбит. Сигнал приходит с задержкой приблизительно в 0,25 секунды, что заметно для пользователей. Например, во время трансляции новостей корреспонденты в удаленных районах обычно связываются со студией по спутниковому каналу; при этом заметно, что когда телеведущий задает им вопрос, они отвечают с задержкой. Несмотря на это, спутники на геостационарной орбите широко используются. Например, до недавнего времени связь между континентами осуществлялась, главным образом, с помощью спутников. Сейчас ее в основном заменили межконтинентальные кабели, проложенные по океанскому дну; однако спутниковую связь до сих пор применяют в отдаленных районах. В последние двадцать лет спутники связи также обеспечивают доступ к интернету, особенно в отдаленных местах, где нет наземной инфраструктуры связи.
Спутниковые антенны
Срок службы спутника в основном определяется количеством топлива на борту, требуемым для периодической коррекции орбиты. Количество топлива в спутниках ограничено, поэтому когда оно заканчивается, спутники выводят из эксплуатации. Чаще всего их переводят на орбиту захоронения, то есть орбиту, намного выше геостационарной. Это — дорогостоящий процесс; однако если оставлять ненужные спутники на геостационарной орбите, это грозит вероятностью столкновений с другими спутниками. Место на геостационарной орбите ограничено, поэтому старые спутники, оставленные на орбите, будут занимать место, которое мог бы использовать новый спутник. В связи с этим во многих странах существуют нормы, требующие от владельцев спутников подписать договор о том, что в конце эксплуатации спутник будет выведен на орбиту захоронения.
Литература
Автор статьи: Kateryna Yuri
Unit Converter articles were edited and illustrated by Анатолий Золотков
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Расчеты для перевода единиц в конвертере «Конвертер угловой скорости и частоты вращения» выполняются с помощью функций unitconversion.org.
www.translatorscafe.com

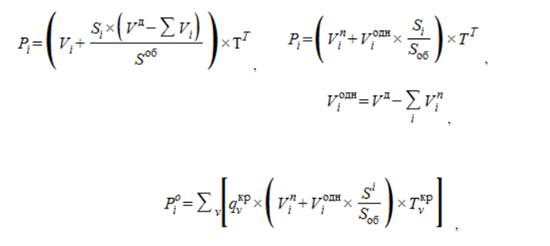
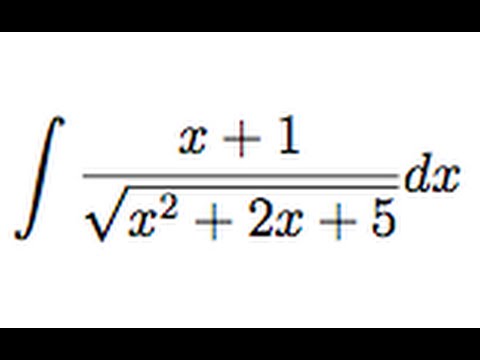

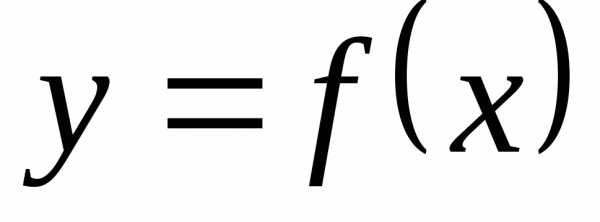 дифференцируема в некотором интервале.
Тогда её производная
дифференцируема в некотором интервале.
Тогда её производная 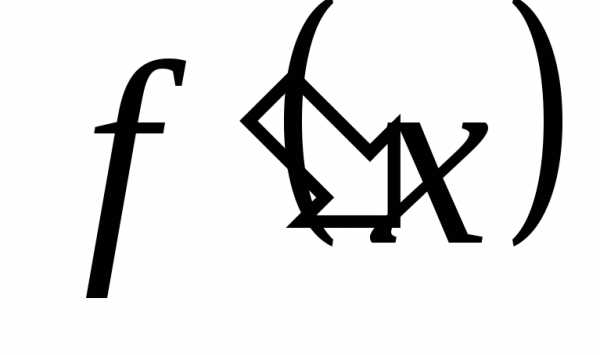 ,
вообще говоря, зависит отх , то есть
является функцией от х.
Следовательно, по отношению к ней снова
можно ставить вопрос о существовании
производной.
,
вообще говоря, зависит отх , то есть
является функцией от х.
Следовательно, по отношению к ней снова
можно ставить вопрос о существовании
производной.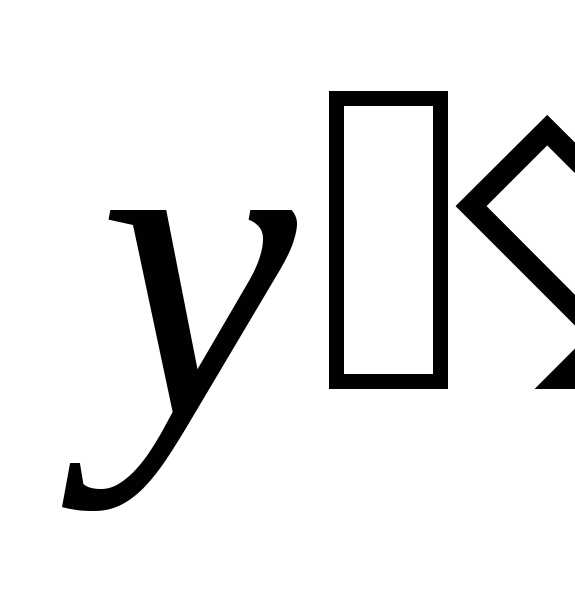 или
или ,
то есть
,
то есть .
. или
или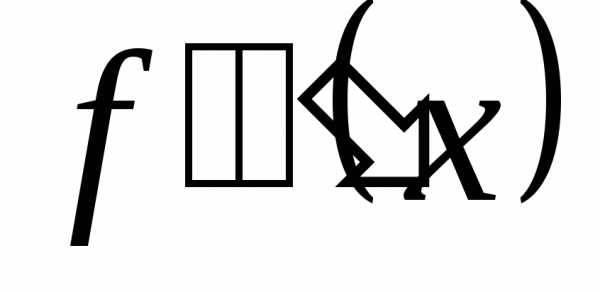 .
.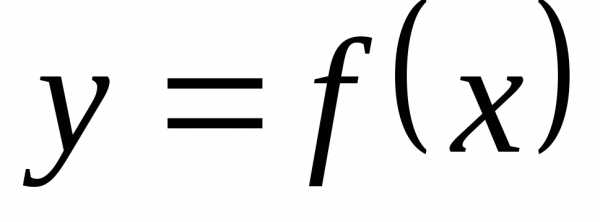 называется
первая производная от производной
(n-1)-го
порядка данной функции и обозначается
символом
называется
первая производная от производной
(n-1)-го
порядка данной функции и обозначается
символом  или
или :
: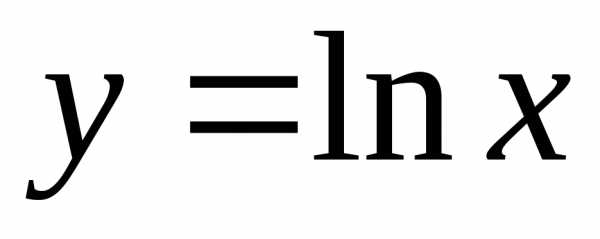 .
.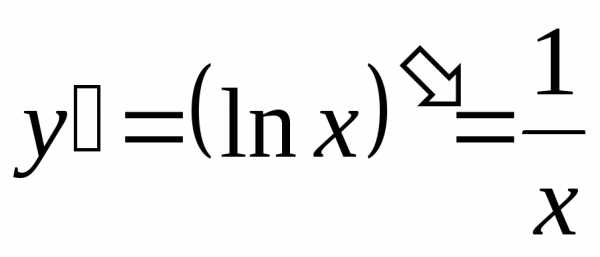 ,
, 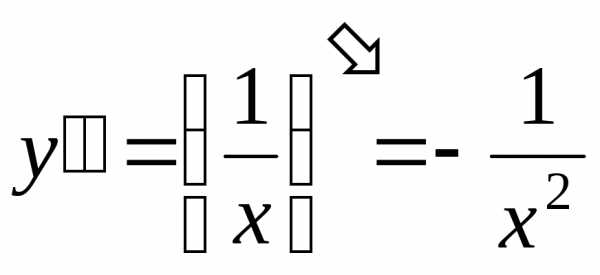 ,,
,,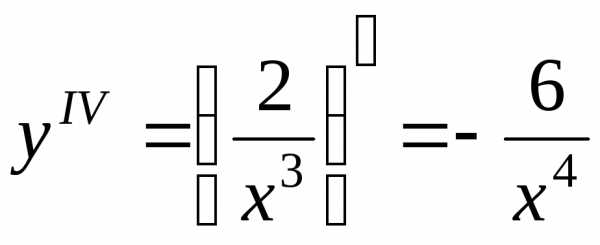 .
.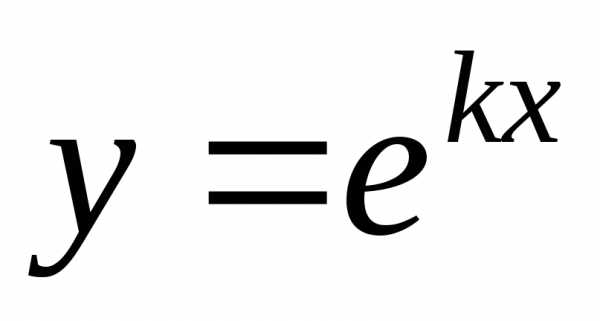 (k—const).
(k—const). ,.
,. .
.
 ,
, ,
, ,
, ,
,
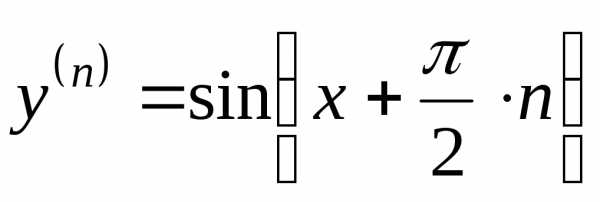 .
. Замечание.
Аналогично можно получить формулу n-ой
производной функции
:
Замечание.
Аналогично можно получить формулу n-ой
производной функции
: .
. Пример
5. Найти
производную n-ого
порядка для степенной функции
Пример
5. Найти
производную n-ого
порядка для степенной функции 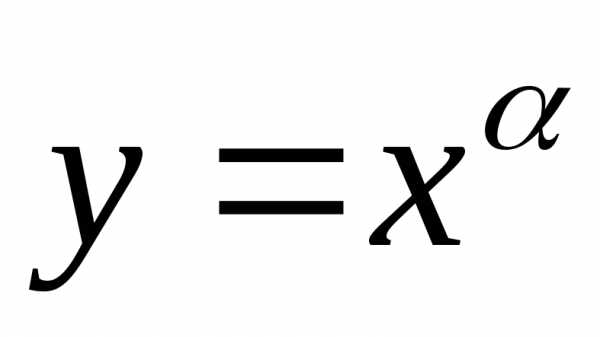 , где
, где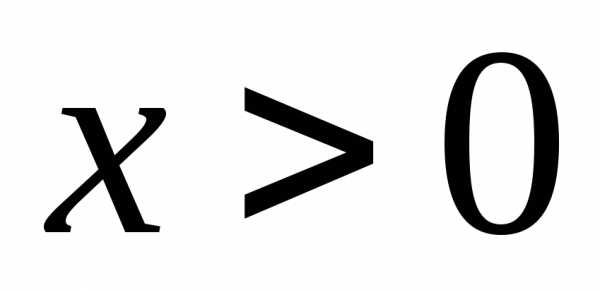 и
и — любое вещественное число.
— любое вещественное число. Решение.
Дифференцируя последовательно, получим:
Решение.
Дифференцируя последовательно, получим:
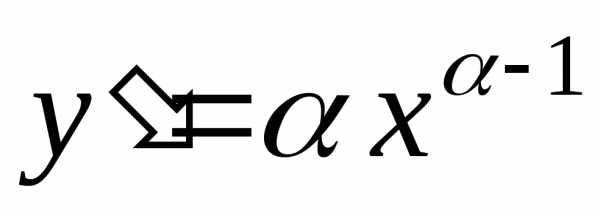 ,
,
,
, ,
, .
. ,
, 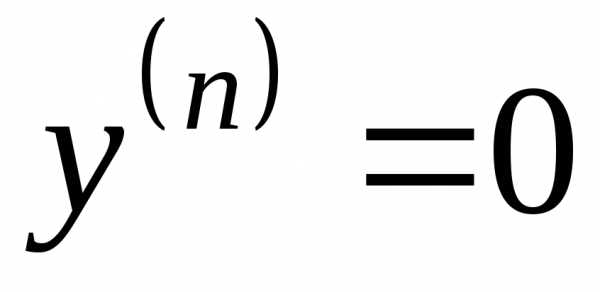 при
при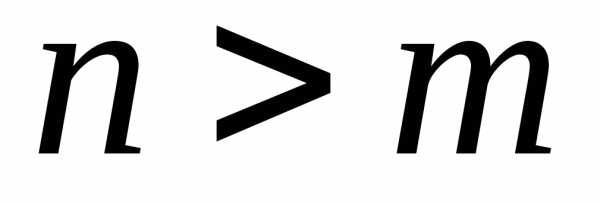 .
. Замечание. При строгом выводе формулы для производной n-ого
порядка следует применять метод
математической индукции.
Замечание. При строгом выводе формулы для производной n-ого
порядка следует применять метод
математической индукции.
 Вторая
производная параметрически заданной
функции
Вторая
производная параметрически заданной
функции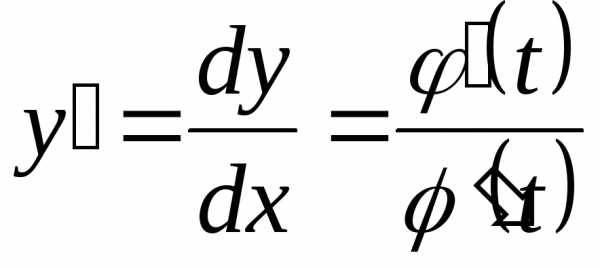 ,
то
,
то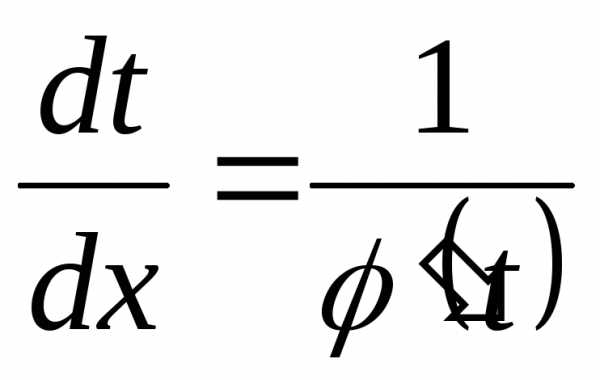 ,
,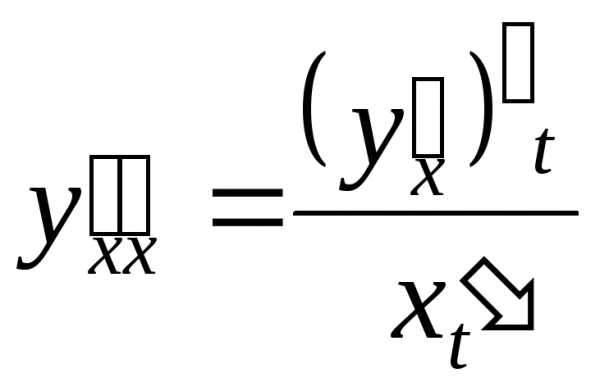 .
.
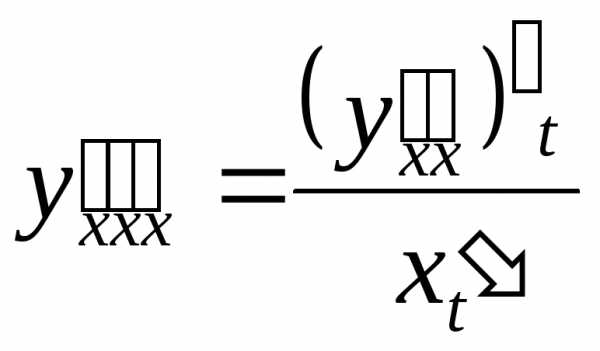 .
. ,
,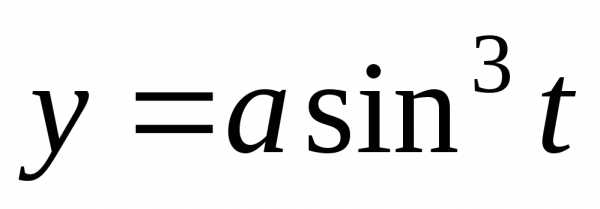 .
.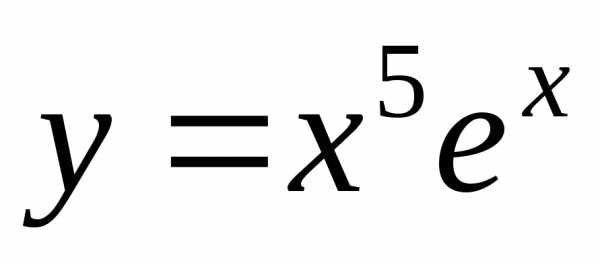 .
.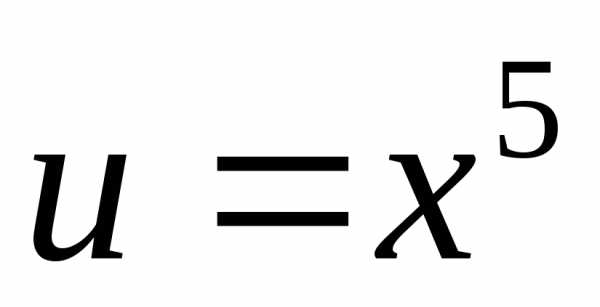 и
и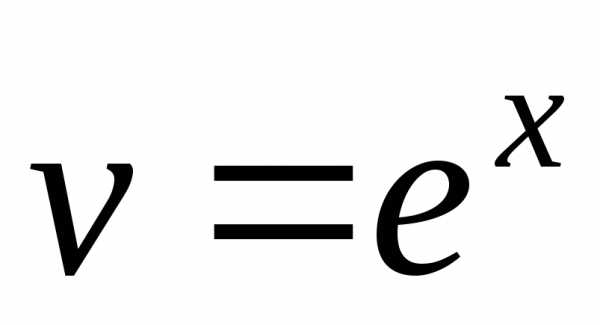 .
Найдем
.
Найдем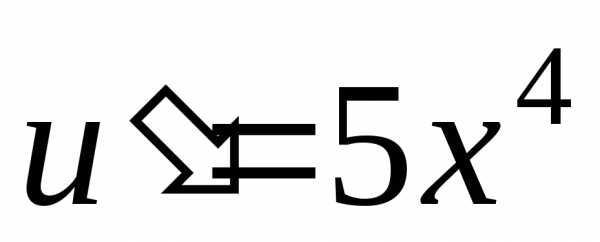 ,,,,;.
Подставляя эти выражения в формулу
Лейбница при
,,,,;.
Подставляя эти выражения в формулу
Лейбница при ,
получим
,
получим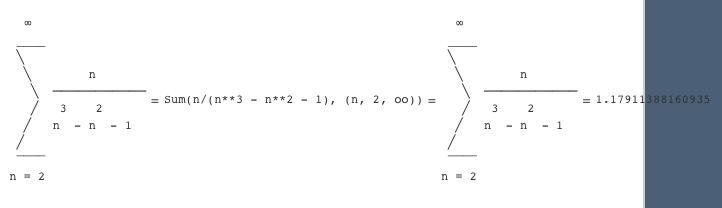

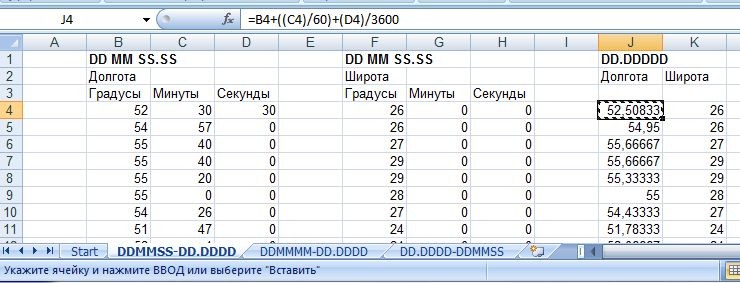







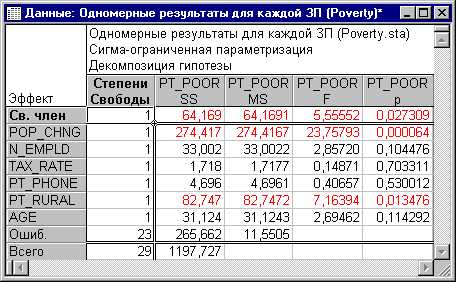
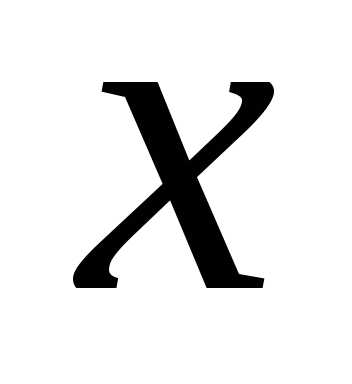 называютсякоэффициентами «чистой»
регрессии. Они характеризуют среднее
изменение результата с изменением
соответствующего фактора на единицу
при неизмененном значении других
факторов, закрепленных на среднем
уровне.
называютсякоэффициентами «чистой»
регрессии. Они характеризуют среднее
изменение результата с изменением
соответствующего фактора на единицу
при неизмененном значении других
факторов, закрепленных на среднем
уровне. от расчетных
от расчетных минимальна:
минимальна: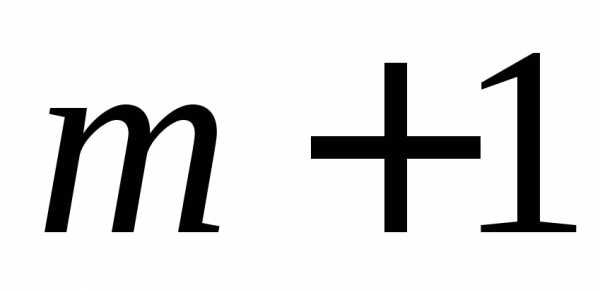 аргумента:
аргумента: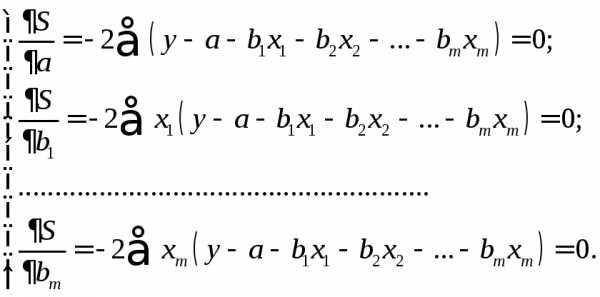
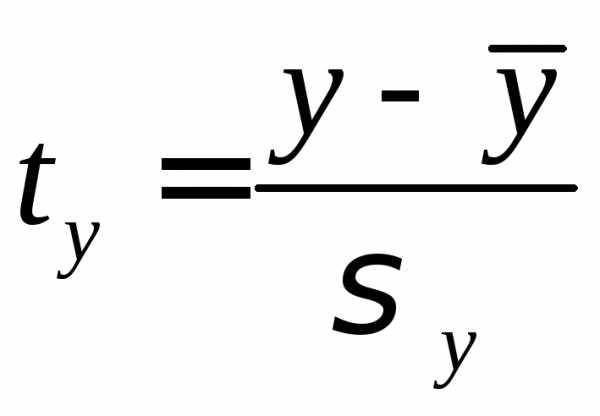 ,
,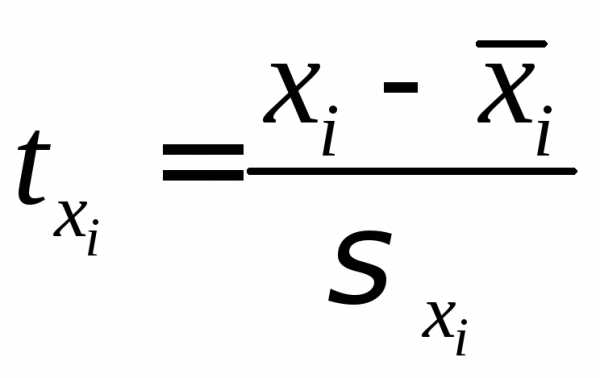 ,
для которых среднее значение равно
нулю:
,
для которых среднее значение равно
нулю: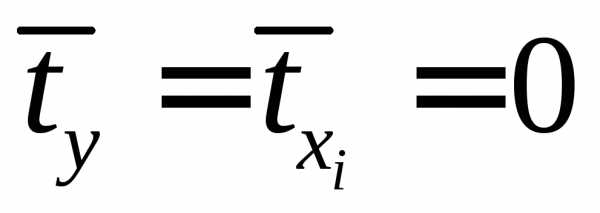 ,
а среднее квадратическое отклонение
равно единице:;
,
а среднее квадратическое отклонение
равно единице:; – стандартизированные коэффициенты
регрессии.
– стандартизированные коэффициенты
регрессии.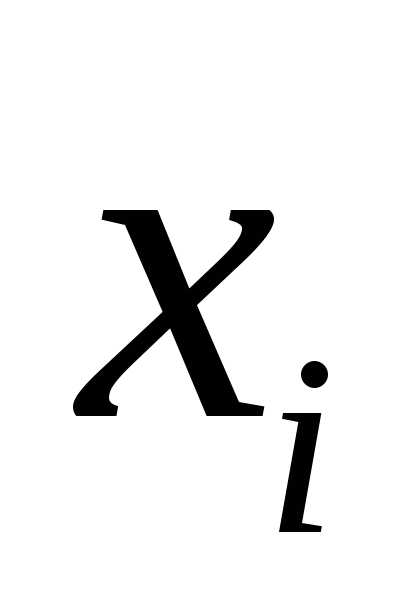 изменится на одну единицу при неизменном
среднем уровне других факторов. В силу
того, что все переменные заданы как
центрированные и нормированные,
стандартизованные коэффициенты регрессии
изменится на одну единицу при неизменном
среднем уровне других факторов. В силу
того, что все переменные заданы как
центрированные и нормированные,
стандартизованные коэффициенты регрессии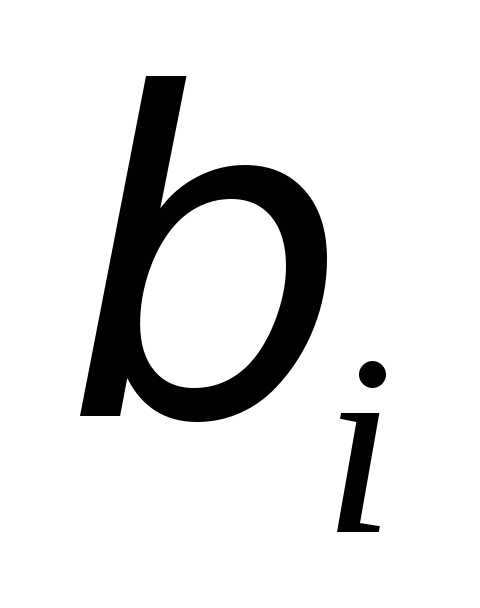 можно сравнивать между собой. Сравнивая
их друг с другом, можно ранжировать
факторы по силе их воздействия на
результат.В этом основное достоинство
стандартизованных коэффициентов
регрессии в отличие от коэффициентов
«чистой» регрессии, которые несравнимы
между собой.
можно сравнивать между собой. Сравнивая
их друг с другом, можно ранжировать
факторы по силе их воздействия на
результат.В этом основное достоинство
стандартизованных коэффициентов
регрессии в отличие от коэффициентов
«чистой» регрессии, которые несравнимы
между собой.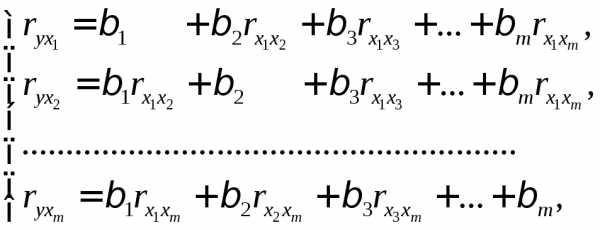 (1.28)
(1.28)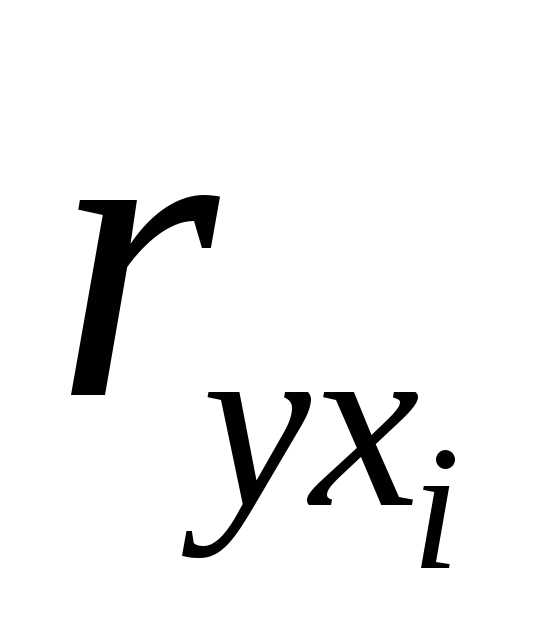 и
и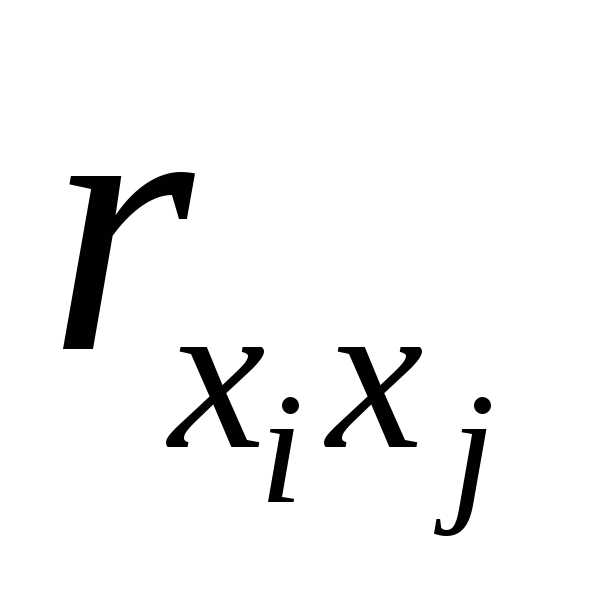 – коэффициенты парной и межфакторной
корреляции.
– коэффициенты парной и межфакторной
корреляции.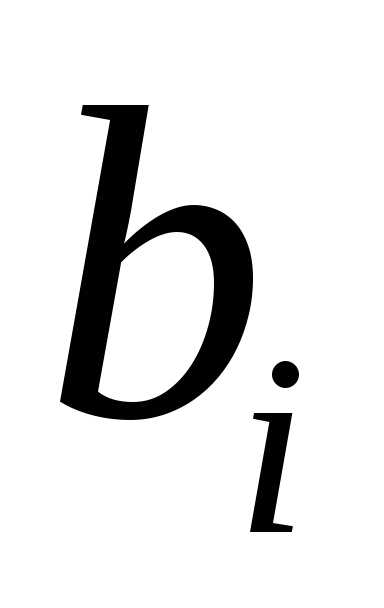 связаны со стандартизованными
коэффициентами регрессии
связаны со стандартизованными
коэффициентами регрессии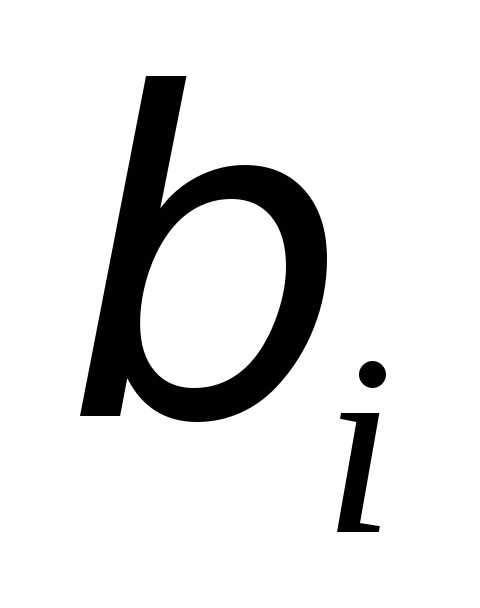 следующим образом:
следующим образом: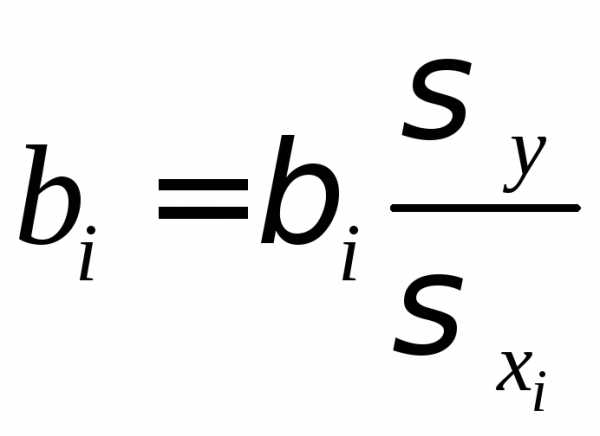 . (1.29)
. (1.29) определяется как
определяется как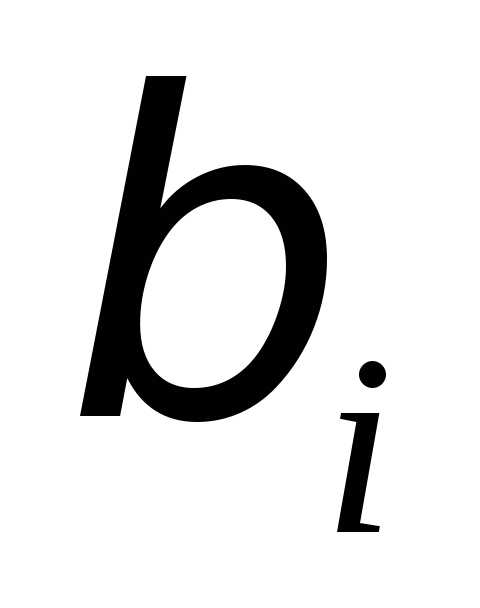 .
.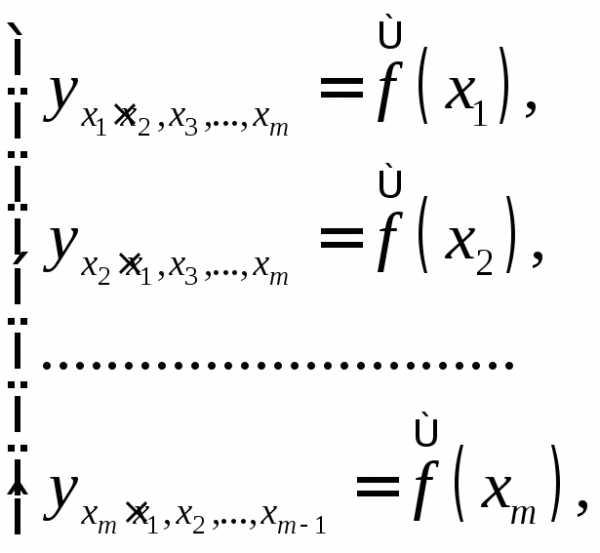 (1.31)
(1.31)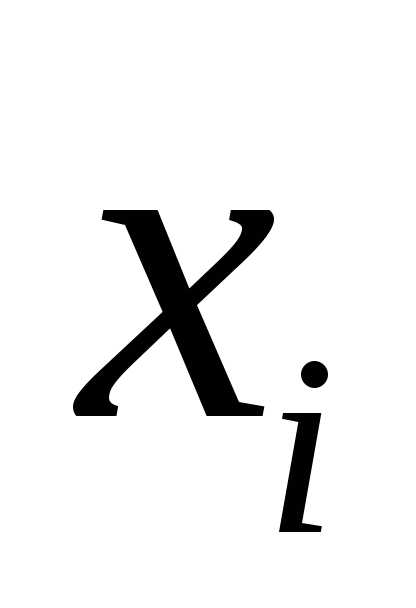 при закреплении остальных факторов на
среднем уровне. В развернутом виде
систему (1.31)
можно переписать в виде:
при закреплении остальных факторов на
среднем уровне. В развернутом виде
систему (1.31)
можно переписать в виде: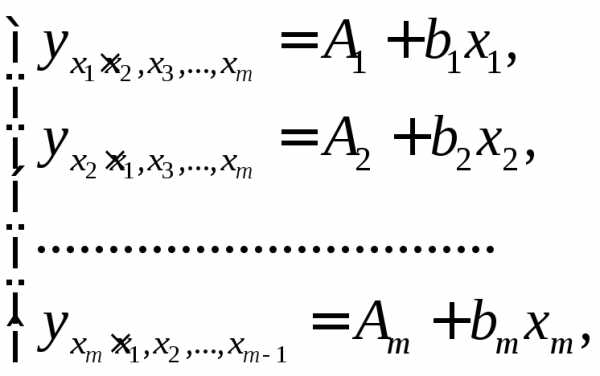 (1.32)
(1.32)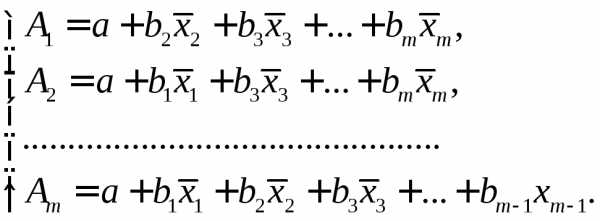
 – коэффициент регрессии для фактора
– коэффициент регрессии для фактора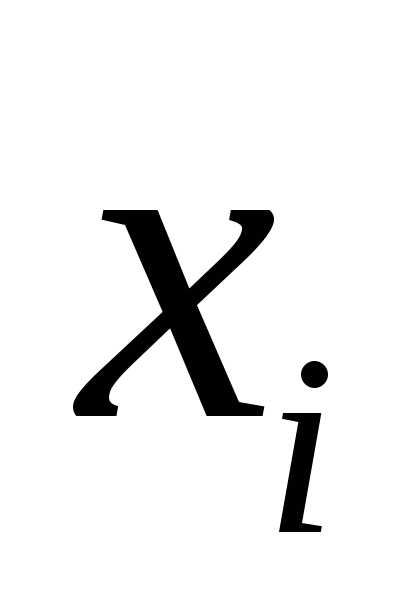 в уравнении множественной регрессии,– частное уравнение регрессии.
в уравнении множественной регрессии,– частное уравнение регрессии.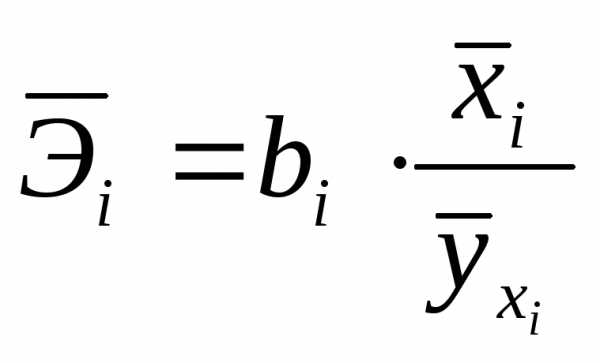 , (1.34)
, (1.34)