банк рефератов, дипломы, курсовые работы, шпаргалки
Онлайн сервис для студентов и авторов
5 000 пользователей, добавляющих рефераты регулярно
18 787 уникальных работ, прошедших модерацию
Минимум 50 новых и актуальных работ в день
Быстрый поиск по базе рефератов, контрольных, курсовых, дипломных, шпаргалок
Удобный каталог работ с разбивкой по дисциплинам, типу работ и алфавиту
Постоянно пополняемая база новыми бесплатными готовыми работами
Здесь эксперты помогают и консультируют студентов по учёбе без посредников
Все работы, представленные на сайте, загружены нашими пользователями, которые согласились с Пользовательским соглашением, с Открытой лицензией и обладают всеми необходимыми авторскими правами на данные работы. Скачивая работу вы соглашаетесь с тем, что она не будет выдана за свою, а будет использована исключительно как пример или первоисточник с обязательной ссылкой на авторство работы.
Новые события на сайте
Бесплатные рефераты
 Целью курсовой работы является разработка бизнес-плана создания предприятия. Достижение поставленной цели обуславливает решение следующих задач: исследование теоретических аспектов, анализ условий и предпосылок к разработке проекта, разработка проекта.
Раздел: Бесплатные рефераты по экономике организаций
Вид: Курсовая работа
Размер: 427.39K
Целью курсовой работы является разработка бизнес-плана создания предприятия. Достижение поставленной цели обуславливает решение следующих задач: исследование теоретических аспектов, анализ условий и предпосылок к разработке проекта, разработка проекта.
Раздел: Бесплатные рефераты по экономике организаций
Вид: Курсовая работа
Размер: 427.39K
 Целью расчетно-аналитической работы является анализ финансовой политики, выявление основных целей и проблем компании путем анализа денежных поток, а также дальнейшее их сопоставление с прибылью, структурой капитала и т.д.
Раздел: Бесплатные рефераты по управлению денежными потоками
Вид: Контрольная работа
Размер: 4.02M
Вуз: Финансовый Университет при Правительстве РФ
Целью расчетно-аналитической работы является анализ финансовой политики, выявление основных целей и проблем компании путем анализа денежных поток, а также дальнейшее их сопоставление с прибылью, структурой капитала и т.д.
Раздел: Бесплатные рефераты по управлению денежными потоками
Вид: Контрольная работа
Размер: 4.02M
Вуз: Финансовый Университет при Правительстве РФ  Цель курсовой работы заключается в разработке основ концепции понимания и следованию своего убеждения во всех возможных сущностях в правовом регулировании социальных отношений, складывающихся в современном российском обществе.
Раздел: Бесплатные рефераты по конституционному праву
Вид: Курсовая работа
Размер: 118.35K
Вуз: Хакасский государственный университет им. Н.Ф. Катанова
Цель курсовой работы заключается в разработке основ концепции понимания и следованию своего убеждения во всех возможных сущностях в правовом регулировании социальных отношений, складывающихся в современном российском обществе.
Раздел: Бесплатные рефераты по конституционному праву
Вид: Курсовая работа
Размер: 118.35K
Вуз: Хакасский государственный университет им. Н.Ф. Катанова  1. Фондовый рынок — это Ответ: рынок ценных бумаг 2. Первичный рынок ценных бумаг — это Ответ: продажа ценных бумаг нового выпуска их первым владельцам 3. Эффективный вторичный рынок характеризуется следующим Ответ: большое количество продавцов и покупателей, значительный объем заключаемых сделок 4. Укажите верное утверждение относительно соотношения риска и дохода Ответ: чем выше риск, тем выше должен быть ожидаемый доход
Раздел: Бесплатные рефераты по рынку ценных бумаг
Вид: Тест
Размер: 24.88K
1. Фондовый рынок — это Ответ: рынок ценных бумаг 2. Первичный рынок ценных бумаг — это Ответ: продажа ценных бумаг нового выпуска их первым владельцам 3. Эффективный вторичный рынок характеризуется следующим Ответ: большое количество продавцов и покупателей, значительный объем заключаемых сделок 4. Укажите верное утверждение относительно соотношения риска и дохода Ответ: чем выше риск, тем выше должен быть ожидаемый доход
Раздел: Бесплатные рефераты по рынку ценных бумаг
Вид: Тест
Размер: 24.88K
 Вопросы: 1. Сущность и содержание страхования. 2. Функции страхования, их проявление и использование в процессе хозяйствования. 3. Понятие риска. Материальное воплощение риска − ущерб и убытки. 4. Оценка риска для целей страхования. Селекция рисков, принимаемых на страхование. 5. Понятие андеррайтинга. Страховой максимум. Портфель рисков страховщика и его сбалансированность.
Раздел: Бесплатные рефераты по страхованию
Вид: Шпаргалка
Размер: 244.37K
Вопросы: 1. Сущность и содержание страхования. 2. Функции страхования, их проявление и использование в процессе хозяйствования. 3. Понятие риска. Материальное воплощение риска − ущерб и убытки. 4. Оценка риска для целей страхования. Селекция рисков, принимаемых на страхование. 5. Понятие андеррайтинга. Страховой максимум. Портфель рисков страховщика и его сбалансированность.
Раздел: Бесплатные рефераты по страхованию
Вид: Шпаргалка
Размер: 244.37K
studrb.ru
контрольные курсовые лабораторные аудиторные дипломные работы (ВКР) на заказ для студентов Финансового Университета при Правительстве РФ.
Мы — не официальный сайт Финансового Университета, официальный сайт бывшего ВЗФЭИ тут. Если нужно расписание, фамилии преподавателей, данные о поступлении, КОПРЫ, то вам туда, а не к нам.
Все виды студенческих работ, от рефератов на первых курсах, до сложных курсовых, от аудиторных и лабораторных до отчетов по практике и дипломных работ вы можете заказать на нашем неофициальном сайте ВЗФЭИ, созданном для помощи студентам Финансового Университета при Правительстве РФ (бывшего Всероссийского Заочного Финансово-Экономического Института).
Подробно о том, как заказать работу в ВЗФЭИ и реквизиты для оплаты.
Мы в ICQ 608-866-444 когда вам нужно быстрое решение проблемы. Позвонить нам можно по телефонам +7-499-638-57-48 и +7-919-163-12-54 в рабочее время по Москве.
Разумно было бы ознакомиться с отзывами о работе нашего ВЗФЭИ-сайта — читайте рубрику, открытую 14-го сентября 2011-го года.
Нужна скидка на неофициальном ВЗФЭИ? Можно выбрать «Методичку в обмен на 10% скидки»!
Напомним, что работы для вас пишут или бывшие, или действующие преподаватели ВЗФЭИ — посторонних людей у нас нет. Поэтому мы и назвали свой ресурс когда-то именно неофициальным сайтом Финансового Института.
Да, бесспорно, что приходя в тот или иной институт, а не только к нам, каждый (ну, если уж совсем честно — то большинство, а не каждый) отдает себе отчет в том, зачем он туда пришел.
Мы же в свое время столкнулись с тем, что взрослая жизнь частенько не дает возможности изучать в полном объеме то, что предлагают нам в нашем институте.
- иногда не удается убедить себя в том, что этот предмет мне действительно нужен — и не получается заставить самого себя писать по нему контрольную;
- иногда преподаватель откровенно неприятен или совершенно не умеет вести предмет так, чтобы он легко и с удовольствием усваивался — тогда уж, если нет времени на полностью самостоятельное изучения этой дисциплины с нуля и до курсовой — то опять же написать ту же самую курсовую достойно не сумеешь;
- иногда же личная жизнь настолько усложняется, что становится совершенно не до контрольных, рефератов, курсовых, лабораторных и аудиторными.
И большинство из тех, кто с нами работает (да и администрация этого проекта), когда-то в студенческие годы мечтали не раз о том, что если бы был такой проект, которому можно было бы доверить написание некоторых студенческих работ, то он был бы настоящей палочкой-выручалочкой. А если бы точно знать, что с какой бы просьбой ты не обратился, тебе всегда помогут, то, согласитесь, жизнь была бы намного свободнее и стабильней. Можно посоветоваться и на предмет методичек, и помогут с темой ВЗФЭИ шпоры к госам так же, как и другие задачи ВЗФЭИ неофициального — это важно.
Как утверждают, главным достоинством нашего проекта является то, что мы не продаем готовые работы, а ведь некоторые другие сайты для каждого экземпляра делают это по несколько раз.
Весь принцип сотрудничества неофициального сайта ВЗФЭИ с Вами заключается в выборе соответствующей методички, по которой потом и будет готовиться индивидуальная работа, которая к тому же может быть дополнительно отредактирована согласно вашим пожеланиям. Так что с нами вы получаете не субпродукт непонятного качества, а действительно качественную работу, которую наверняка лучшим образом оценят ваши преподаватели.
Если же они по той или иной причине не оценят нашу работу по достоинству, то мы всегда готовы переделать ее, пусть даже требования будут неадекватными. Подробнее о гарантиях качества наших работ вы можете прочитать с соответствующем разделе проекта ВЗФЭИ ОРГ.
Подготовив заказ, мы не продаем его таким, какой он получился, а доводим его до логического завершения, переделывая его столько, сколько это может потребоваться для Вашего успеха.
Материалы, представленные на сайте, поделены на два раздела. А именно:
- на работы по курсам;
- на работы по определенным категориям (рефераты, лабораторные, курсовые, дипломные и пр.).
Для того, чтобы оформить заказ, вам нужно просто отправить нам письмо на почту с темой и требованиями.
Предпочитаем заранее ответить на ряд вопросов, которые частенько возникают как у наших друзей, так и просто у сторонних наблюдателей. Не нарушаем ли мы чьих-то прав своим трудом? Нет, не нарушаем. Мы ничего здесь не продаем, ни учебных материалов, ни какой другой продукции сторонних лиц. Методички, которые вы можете скачать на нашем сайте, предоставляются исключительно в ознакомительных целях, и, скачивая их, за их дальнейшую судьбу Вы в ответе самостоятельно.
С введением деления на бакалавриат и магистратуру у нас возросла потребность в квалифицированных преподавателях, поэтому — вниманию авторов!
Номера счетов в электронных системах платежей для оплаты наших услуг:
- WebMoney R198456778409
- Яндекс.Деньги 41001274920394
Чтобы оформить заказ на студенческие работы какого-либо вида для студентов ВЗФЭИ, Вы можете обратиться по контактам, указанным ниже:
vzfei.org
Реферат — Взфэи фотография Фамилия Имя Отчество
Стандартная форма резюме для сотрудников ВЗФЭИ
Фотография
Фамилия Имя Отчество Андросова Людмила Дмитриевна
Степень, звание к.э.н., доцент
Должность во ВЗФЭИ доцент
Преподаваемые дисциплины Бюджетная система РФ, Финансово-бюджетное планирование и прогнозирование, Финансы, Финансы и кредит, Финансы, денежное обращение и кредит, Страхование
Педагогический стаж работы март 1976 года
Научная деятельность
СПИСОК
Научных и научно-методических работ
доцента кафедры финансов, бюджета и страхования,
кандидата экономических наук Андросовой Людмилы Дмитриевны
№
п/п
Наименование работы, ее вид
Форма работы
Выходные данные
Объем в п.л.
Соавторы
1
2
3
4
5
6
1
«Долгий ящик» валют-ной реформы
Печат.
«Новое время» № 49, 1975
0,5
2
Финансовые путы зависимости
Печат.
«Новое время» № 37
0,5
3
Подачки вместо помощи
Печат.
«Эконом. Газета» № 51, 1978
0,2
4
Состояние ликвидности в капиталистических странах
Печат.
БИКИ, № 20, 1977
0,5
5
Шаг на месте
Печат.
«Эконом. Газета» № 9, 1977
0,2
6
«Неликвидная» ликвидность
Печат.
«Эконом. Газета» № 27, 1977
0,5
7
Проблема международной ликвидности
Печат.
Материалы научной
Конференции Минфина СССР, М., Финансы, 1977
0,5
8
Кому и сколько задолжал Запад?
Печат.
Материалы лектору, про-пагандисту, № 5, 1978
0,5 0,25
Соавт. Лич. вклад
9
Специальные права за- имствования в совре-менной капиталисти-ческой валютной системе
Печат.
БИКИ, № 32, 1979
0,5
10
Ликвидные резервы капиталистических стран
Печат
БИКИ, № 97, 1979
0,5
11
Симптоматическая неудача
Печат.
«Экономич. газета» № 48, 1979
0,5
12
«Счет замещения» МВФ и перспективы его создания
Печат.
БИКИ, № 84, 1980
0,5
13
СДР и проблемы перес-тройки международной валютной системы
Печат.
Сборник науч-ных трудов ВЗФЭИ, 1980, вып. № 28
0,5
14
МВФ – МБРР. Кому дают кредиты?
Печат.
«Новое время» № 42, 1981
0,2
15
Бег на месте
Печат.
«Экономич. газета», № 47, 1981
0,2
16
Финансы и кредит СССР. Учебник под ред. Дробозиной Л.А. Глава 3, параграф 3; глава 8, параграфы 7, 8, 9.
Печат.
М., Финансы и статистика. 1982
1 0,75
Соав. Личн. вклад
17
Клещи кредитной зависимости
Печат.
«Новое время», № 42, 1983
0,3
18
Термины: «автомати-ческий бюджет», «бюд- жет-брутто», «бюджет- нетто», «бюджетная статистика», «бюджет-ный дефицит», «гарантированный кредит», «государст-венные банки», «дис-бурсменский счет»
Печат.
Финансово- кредитный словарь, т.1, М.: Финансы и статистика, 1984
0,5
19
Методическое письмо о подготовке к государст-венному экзамену по дисциплине «Финансы СССР»
Печат.
^ ВЗФЭИ, М. 1984
1,5 0,75
Соав. Личн. Вклад
20
Положение о социалис-тическом соревновании подразделений института
Печат.
^ ВЗФЭИ, М. 1984
2 1
Соав. Личн. Вклад
21
Методическое письмо о подготовке к государст- венному экзамену по дисципдине «Финансы СССР»
Печат.
^ ВЗФЭИ, М. 1985
2 0,5
Соав. Личн.вклад
22
Финансы и кредит СССР. Методические указания и темы курсовых работ
Печат
^ ВЗФЭИ, М. 1985
2 0,5
Соав. Личн. Вклад
23
Термины: «кассовые резервы», «ликвидность фирмы», «поземельные налоги», «отрицательный подоходный налог», «налоговая декларация», «кассовое исполнение бюджета», «консоли»
Печат.
Финансово – кредитный словарь. Т. 2, М. Финансы и стаистика. 1985
0,5
24
Экономия на нуждающихся
Печат.
«Экономичес-кая газета» № 27, 1987
0,3
25
О реформе и техничес-ком переоснащении Лондонской фондовой биржи
Печат.
БИКИ, № 77, 1987
0,5
26
Методическое письмо о подготовке к государст-венному экзамену по дисциплине «Финансы СССР»
Печат.
^ ВЗФЭИ, М. 1987
1,5 0,4
Соав. Личн. Вклад
27
Методическое письмо для преподавателей кафедры «Финансы» об использовании в учебном процессе материалов январского (1987г.) Пленума ЦК КПСС
Печат.
^ ФЗФЭИ, М. 1987
0,5
28
Термины: «покровите-льственные пошлины», «реконструктионная финансовая корпора-ция», «ройалти»
Печат.
Финансово- кредитный словарь, т. 3, М. Финансы и стаитсика. 1989
0,3
29
Финансы и кредит СССР. Учебник под ред. Дробозиной Л.А. Параг. «налоги с населения»
Печат.
М. Финансы и статистика. 1988
0,5
30
Методическое письмо о подготовке к государст-венному экзамену по дисциплине «Финансы СССР»
Печат.
^ ВЗФЭИ, М. 1988
1,5 0,5
Соав. Личн. Вклад
31
Финансы СССР. Методические указания и темы курсовых работ
Печат
^ ВЗФЭИ, М. 1988
2 0,5
Соав. Личн. Вклад
32
Новые явления в систе-ме государственного кредита Великобритании
Печат.
«Финансы СССР» № 1 1989
0,3
33
Об организации государственного кредитования
Печат.
«Финансы СССР» № 4 1991
0,5
34
Управление долгами
Печат.
Еженедельник «Финвест» № 3, 1991
0,2
35
Местные займы
Печат.
Еженедельник «Финвест» № 4, 1991
0,4
36
Приватизация: трудный путь
Печат.
Еженедельник «Финвест» № 5, 1991
0,3
37
Финансы предприятия
Печат.
М. Финвест, 1991
2
38
Ценные бумаги
Печат.
Еженедельник «Фнвест», № 7, 1991
1
39
Банковские реформы в Восточной Европе и России
Печат.
Еженедельник «Финвест», № 2, 1992
0,2
40
Вооружен и очень опасен? (Готов ли Центральный банк России к борьбе с инфляцией)
Печат.
Еженедельник «Финвест», № 19, 1992
0,5
41
Эта непростая финан-совая поддержка
Печат.
Еженедельник «Финвест», № 20, 1992
0,5
42
Банки и свободная конкуренция
Печат.
Еженедельник «Финвест», № 33, 1992
0,5
43
«Олимпия и Иорк» катастрофа мирового масштаба
Печат.
Еженедельник «Финвест», № 35, 1992
0,9
44
«Олимпия и Иорк». Агония
Печатный
Еженедельник «Финвест», № 36, 1992
0,9
45
Буря на валютных рынках
Печат
Еженедельник «Финвест», № 40, 1992
0,3
46
Пластиковые вместо деревянных
Печат.
Еженедельник «Финвест», № 42, 1992
0,4
47
Выбор источников финансирования: акции или облигации
Печат.
Еженедельник «Финвест», № 44, 1992
48
Форум банкиров
Печат.
Еженедельник «Финвест», № 49, 1992
0,3
49
Банкротство
Печат.
Еженедельник «Финвест», № 10, 1993
0,5
50
Общая теория финансов. Учебник под ред. Дробозиной Л.А. Глава 8. Государствен-ный кредит.
Печат.
М. Финансы и статистика. 1995
1
51
Настольная книга банкира. Банковская система России. Глава 11. О конкуренции в банковском деле
Печат.
М. ДЕКА. 1995
1
52
Финансы. Денежное обращение. Кредит. Учебник под ред. Дробозиной Л.А. Глава 8. Государственный кредит
Печат.
М. Юнити. 1996
0,5
53
Обучающая программа. Операции с ценными бумагами
Элект-ронный
Сбербанк Москвы. 1997
120 мгб4 п.л.
Соав. Личн.ввклад
54
Финансы. Учебник под ред. Дробозиной Л.А. Глава 8. Государствен-ный кредит как эконо-мическая категория
Печат.
^ М. ЮНИТИ, 1999
1
55
Финансы. Денежное обращение. Кредит. Учебник под ред. Поляка Г.Б. Главы 8, 18
Печат.
^ М. ЮНИТИ 2001
2,5
56
Программа по дисциплине «Финансы и кредит»
Печат.
^ ВЗФЭИ. М. 2002
1 0,5
Соав. Личн. Вклад
57
КОПР «Финансы». Глава 8.
Элект.
^ ВЗФЭИ. М. 2002
0,2
58
КОПР «Бюджет и бюджетная система»
Элект.
^ ВЗФЭИ. М. 2002
3 1,5
Соав. Л. Вкл
59
Финансы. Учебник под ред. Поляка Б.Г. Главы 7, 13
Печат.
^ М. ЮНИТИ. 2003
2,5
60
Финансы. Программа для студентов спец. 0604000, 060500.
Печат.
^ ВЗФЭИ. М. 2003
1,5 0,15
Соав. Л.вкл.
61
Проблемы совершенс-твования финансового контроля устойчивости банковской системы
Печат
Сбор. Научн труд.ВЗФЭИ 2004
0,5
62
Некоторые пути разви-тия контроля за финан-совой устойчивостью банковской системы России
Печат
Сбор.научн. трудов МИПК Плехановской Академии 2004
0,5
63
Финансы бюджетных организаций. Учебник под ред. Поляка Г.Б. Главы 1,9,10
Печат
Вузовский учебник 2005
3
64
Организация исполне-ния бюджета. Учебник под ред. Карчевского В.В. Глава 4
Печат
Вузовский учебник 2006
1
65
Бюджетная система. Учебник под ред Поляка Г.Б. Глава 14
Печат
ЮНИТИ, 2007
66
Финансы. Учебник под ред. Поляка Г.Б. Главы 7,13
Печат
ЮНИТИ. 2007
2
67
Финансы. Денежное об-ращение. Кредит. Учеб-ник под ред. Поляка Г.Б., главы 9, 18 п.19.1-19.3, 19.5, 19.7
Печат.
ЮНИТИ. 2007
3
68
Целевые бюджетные и внебюджетные фонды. Учебник под ред. Кар-чевского В.В., главы 3, 4, 5.
Печат
Вузовский учебник, 2008
3
69
«Финансы и кредит» метод.указан. для выполн. контрольных работ спец.080104, 080507
Печат
ВЗФЭИ, 2008
5,5
70
Финансы, денежное обращение и кредит. Программа. Спец. 080111
Печат
ВЗФЭИ, 2008
1
Поляк Г.Б.
71
Финансовый менеджмент. Учебник под ред. Поляка Г.Б., § 6.1-6.3
Печат.
М: Волтерс Клувер (Wolters Kluwer) 2009
72
Финансы и кредит. Программа. Спец. 521500.бакалавр
Печат
ВЗФЭИ, 2009
1
Егорычева И.Н.
73
Финансы и кредит. Методические указания по выпол.контр.работ. спе.521500, бакалавр
Печат
ВЗФЭИ, 2009
5
74
Финансы, денежное обращение и кредит.Метод. указ.по выпол.контр.работ. Спец.080615
Печат
ВЗФЭИ, 2009
5,75
75
Финансы бюджетных организаций. Учебник под ред. Поляка Г.Б.
Печат
^ ЮНИТИ –ДАНА, 2010
2
76
Финансы.и кредит. Учебник под ред Поляка ГюБ.
Печат
Волтерс Клувер, 2010
3
76
Бюджетная система.Учебник под ред. Поляка Г.Б.
Печат
ЮНИТИ- ДАНА,2011
2
Руководство аспирантами и докторантами 1
Инновационная образовательная деятельность: применение инновационного педагогического метода «Пресс-клуб»
Проекты прикладного характера, разработанные автором
Членство в организациях, почетные звания, награды
Координаты
Телефон 8(499) 144-85-12
e-mail fbno@ vzfei.ru
номер кабинет №411
ronl.org
Реферат — Курсовая взфэи — Разное
1657
Финансы
Особенности социальных внебюджетных фондов в РФ
Курсовая
ВЗФЭИ
57
2007
1000
Координаты: электронная почта [email protected], [email protected]
Icq 170552870, телефон 89168119086. www.wiseowl.ru
Содержание
ВВЕДЕНИЕ 2
3
^ ГЛАВА 1. СОЦИАЛЬНО-ЭКОНОМИЧЕСКАЯ СУЩНОСТЬ ВНЕБЮДЖЕТНЫХ ФОНДОВ 4
1.1. Необходимость социальных внебюджетных фондов 4
1.2. Особенности формирования и принципы функционирования социальных внебюджетных фондов 7
2.2. Пенсионная реформа
11
2.3. Состав и структура бюджета федерального Фонда обязательного медицинского страхования
13
2.4. Состав и структура доходов и расходов Фонда социального страхования РФ
16
^ ГЛАВА 3. СОВЕРШЕНСТВОВАНИЕ ДЕЯТЕЛЬНОСТИ ВНЕБЮДЖЕТНЫХ ФОНДОВ РФ СОЦИАЛЬНОГО НАЗНАЧЕНИЯ
19
3.1. Проблемы функционирования внебюджетных социальных фондов
19
3.2. Перспективы развития финансового механизма государственных внебюджетных социальных фондов
22
3.3. Размеры пособий
25
ЗАКЛЮЧЕНИЕ
28
БИБЛИОГРАФИЯ
31
ПРИЛОЖЕНИЯ 35
ВВЕДЕНИЕ
В мировой практике широко используются различные денежные фонды, как бюджетные, так и внебюджетные. Роль и значение последних постоянно меняются в зависимости от социально-экономической конъюнктуры. Дополнительные фонды возникли одновременно с образованием бюджетов, но наибольшего расцвета достигли в условиях рыночной экономики. Катализатором их развития, как правило, выступало обострение экономических противоречий между субъектами общества: государством и населением, государством и организациями, организациями и работниками, отдельными гражданами.
Цель фондов была в обособлении денежных средств из гласных, общепринятых финансовых потоков для защиты и реализации особых интересов.
Предметов работы выступают внебюджетные фонды.
Объектом исследования выступают доходы и расходы бюджетов социальных внебюджетных фондов РФ.
В условиях экономического кризиса в России, обусловившего дефицит финансовых ресурсов, у органов власти возникает необходимость ранжировать общественные потребности по степени важности и для удовлетворения наиболее насущных из них образовать целевые внебюджетные денежные фонды, тем самым ограждать эти потребности от значительного недофинансирования.
Внебюджетные фонды как субъект государственной финансовой системы не являются однородными и не обладают ни всеобщими преимуществами, ни недостатками в сравнении с бюджетной формой существования. Они могут возникать и ликвидироваться лишь в связи с определенными условиями, их предопределяющими, или отсутствием таковых.
Всё вышесказанное подтверждает актуальность данной курсовой работы.
Целью данной работы является рассмотрение сущности государственных внебюджетных фондов и их места в бюджетной системе России.
Исходя из поставленной цели можно выделить следующие задачи:
— определение сущности и значения государственных внебюджетных фондов;
— анализ бюджетов государственных внебюджетных фондов;
— рассмотрение проблем и перспектив развития государственных внебюджетных фондов.
Практическая значимость работы заключается разработке предложений по совершенствованию деятельности внебюджетных Фондов РФ социального назначения.
В работе использованы источники таких авторов как: Парыгиной В.А., Александрова И.М., Седовой М.Л. и других, а также нормативная база, регулирующая деятельность социальных внебюджетных фондов РФ.
^
ГЛАВА 1. СОЦИАЛЬНО-ЭКОНОМИЧЕСКАЯ СУЩНОСТЬ ВНЕБЮДЖЕТНЫХ ФОНДОВ
1.1. Необходимость социальных внебюджетных фондов
Чем сложнее государственное устройство страны (федеративное, конфедеративное), тем больше в ней различных фондов. На количество фондов влияют три объективных фактора: 1) численность собственников; 2) размеры финансовых ресурсов; 3) потребности и среда.
Внебюджетные фонды (ВБФ) представляют собой характерный финансовый инструмент (так называемую «заначку»), суть которого состоит в обособлении субъектом (государством, физическим, юридическим лицом или другим владельцем) части общеизвестных денежных ресурсов для удовлетворения своих специфических потребностей.
Общими причинами образования внебюджетных фондов являются ограниченность жизненных ценностей и наличие товарно-денежных отношений; соответственно их экономическую основу составляет многообразие форм собственности (сочетание частной, коллективной, государственной и т.д.).
Цель внебюджетных фондов заключается в удовлетворении специфических потребностей субъектов.
Форма функционирования внебюджетных фондов — планомерность: фонды всегда создаются для конкретных целей, а поэтому существуют только в плановом порядке.
Функции внебюджетных фондов аналогичны функциям всех финансовых категорий. Главная из них — перераспределение финансовых потоков.
Как явление внебюджетные фонды выступают, с одной стороны, финансовой категорией, а с другой — субъективным стоимостным инструментом экономической деятельности.
Как финансовая категория внебюджетные фонды выражают совокупность экономических отношений между субъектами по поводу формирования и использования денежных ресурсов для удовлетворения специфических потребностей.
Соответственно видам субъектов различаются внебюджетные фонды физических лиц, юридических лиц, государства, а также межгосударственных субъектов.
Субъективный характер внебюджетных фондов заключается в том, что они функционируют через конкретную деятельность физических или юридических лиц в виде особых финансовых организаций. Эта особенность порождает новые функциональные свойства внебюджетных фондов — контрольную и стимулирующую (регулирующую) функции, которые призваны обеспечивать эффективное использование фондов.
Органическое единство объективного и субъективного содержания находит свое выражение во внебюджетной политике, направленной на защиту и реализацию материальных интересов одних субъектов в противовес идентичным интересам других. Реализуется политика через функциональный механизм в форме внебюджетного менеджмента.
Таковы основные теоретические положения внебюджетных фондов как важного финансового инструмента рыночной экономики. На практике значение и роль фондов зависят от множества ситуаций и факторов как объективного, так и субъективного характера.
В условиях становления рыночной экономики роль внебюджетных фондов резко возрастает, что требует особого, глубоко обоснованного подхода к управлению их функционированием.
В любом обществе есть нетрудоспособные люди, которые в силу объективных жизненных обстоятельств не в состоянии обеспечить свое существование, — дети, инвалиды, старики, люди, временно нетрудоспособные. В силу ограниченности жизненных ценностей и природного эгоизма от содержания многих из них отказываются не только окружающие, знакомые, коллеги, но даже и самые близкие родственники.
Поэтому материальная защита таких людей возлагается на государство, которое выполняет в связи с этим функцию социального страхования.
Социальное страхование может осуществляться государством открыто, гласно, прозрачно, но в рамках государственного (федерального) бюджета под особым контролем представительных органов власти и руководством высших исполнительных органов —правительства страны и министерства финансов.
Такая система существует в современных стабильных демократических странах, а также была в СССР. Но страхование может производиться и вне государственного бюджета, через специальные внебюджетные фонды, подконтрольные, как правило, узкому кругу властных должностных лиц исполнительных органов власти.
Россия избрала вторую систему — использование государственных социальных внебюджетных фондов [30, с.142].
Первоначально внебюджетные фонды появились в виде специальных фондов или особых счетов задолго до возникновения единого центрального денежного фонда государства — бюджета. Государственная власть с расширением своей деятельности нуждалась во все новых расходах, требовавших средства для своего покрытия. Эти средства концентрировались в особых фондах, предназначенных для специальных целей. Такие фонды носили временный характер, и с выполнением государством намеченных мероприятий они прекращали свое существование. В связи с этим количество фондов постоянно менялось: одни возникали, другие аннулировались.
Создание специальных фондов позволяло привлекать дополнительные средства для расширения сферы деятельности правительства в области всегда актуальных военных расходов, научных исследований, регулирования экономического развития страны, внешнеэкономической деятельности и социальных выплат населению. Правительство имело возможность за счет временно свободных средств, аккумулированных в специальных фондах, покрывать кассовые разрывы и дефицит бюджета, а также покрывать непредвиденные расходы. Расширение деятельности государства привело к созданию значительного количества специальных фондов, названия которых, как правило, объясняли и цель расходования средств. Такая множественность фондов усложняла деятельность государства, поэтому с укреплением централизованного государства начинается период унификации специальных фондов. На основе объединения различных фондов был создан государственный бюджет, который после рассмотрения и утверждения его парламентом превращается в закон, обязательный к исполнению. Однако многие внебюджетные фонды сохранили своё значение и самостоятельность и существовали наряду с государственным бюджетом [27, с.324].
Впервые социальные внебюджетные фонды были созданы в РФ в 1992 г.
При их образовании ставились задачи:
1) «разгрузить» бюджет от существенной доли социальных расходов;
2) вывести из-под контроля законодательных органов власти значительные финансовые ресурсы, предоставив их в полное распоряжение исполнительных органов власти.
Для решения этих задач внебюджетные фонды были законодательно выведены из бюджетной системы страны. Лишь в 1998 г. под влиянием общественности и давлением представительных органов власти был принят Бюджетный кодекс РФ, зафиксировавший государственные социальные внебюджетные фонды в качестве важнейшего составного элемента бюджетной системы [39, с.150]
^ 1.2. Особенности формирования и принципы функционирования социальных внебюджетных фондов
Вступивший в действие в 2000 г. Бюджетный кодекс РФ включил в состав бюджетной системы РФ бюджеты государственных внебюджетных фондов. При этом нельзя не отметить определенное смысловое противоречие между словами «бюджет» и «внебюджетный», содержащихся в данном словосочетании.
Определения, приведенные в начале ст. 6 БК РФ, разделяют понятия «бюджет» и «внебюджетный фонд» как разные формы организации денежных средств, находящихся в распоряжении органов государственной власти.
Если бюджет определяется как форма образования и расходования фонда денежных средств, предназначенных для финансового обеспечения задач и функций государства и местного самоуправления, то государственный внебюджетный фонд — форма организации денежных средств, образуемых вне федерального бюджета и бюджетов субъектов РФ [1].
Таким образом, привычное в теории многоаспектное рассмотрение термина «бюджет» (фонд денежных средств или форма формирования и использования финансовых ресурсов, финансовый план, правовой акт) не в полной мере подходит к понятию «бюджет внебюджетного фонда»; «бюджет» в словосочетании «бюджет государственного внебюджетного фонда» означает только финансовый план и правовой акт, но не фонд денежных средств.
Бюджетное законодательство определяет в составе государственных внебюджетных фондов Пенсионный фонд РФ, Фонд социального страхования РФ, а также Федеральный и территориальные фонды обязательного медицинского страхования, т.е. фонды, формирование и использование которых связано с социальным страхованием.
За счет средств внебюджетных фондов обычно финансируются мероприятия по обязательному социальному страхованию в отношении работающих граждан, а за счет средств бюджета – неработающих.
Внебюджетные фонды не подлежат непосредственно контролю со стороны законодательных органов власти, освобождены от уплаты налогов, сборов, пошлин. Они могут возникать и ликвидироваться лишь в связи условиями, определяющими потребность их существования [30,с.135].
………..
Расходование средств государственных внебюджетных фондов осуществляется исключительно на цели, определенные законодательством Российской Федерации, субъектов Российской Федерации, регламентирующим их деятельность, в соответствии с бюджетами указанных фондов.
Исполнение бюджетов государственных внебюджетных фондов осуществляется Федеральным казначейством Российской Федерации [1].
Таким образом, в настоящее время лишь отдельные элементы бюджетного устройства и бюджетного процесса касаются государственных внебюджетных фондов. А именно:
— группировка доходов, расходов бюджетов государственных внебюджетных фондов, источников финансирования бюджетного дефицита осуществляется на основе единой бюджетной классификации;
— проекты бюджетов Пенсионного фонда РФ, Фонда социального страхования РФ, Федерального фонда РФ рассматриваются в составе документов вместе с проектом закона о федеральном бюджете на соответствующий год и утверждаются в форме федерального закона, проекты бюджетов территориальных фондов обязательного медицинского страхования рассматриваются вместе с проектом закона о бюджете субъекта РФ и утверждаются в форме закона субъекта РФ. В законодательной форме также утверждаются отчеты об исполнении бюджетов соответствующих фондов;
………
В таблице 2 представим структуру доходов фонда, составленную на основании Приложения 1.
Таблица 2
Структура доходов Пенсионного фонда РФ, %
….
Представим диаграмму структуры доходов фонда за 2007 год на рис.2, чтобы наглядно проанализировать их состав.
Среди доходной части, формирующей Пенсионный фонд РФ, следует особо выделить поступления от страховых взносов – в размере 48,39% в 2005 году, в 2006 году удельный вес данной части доходов падает до 46%, в 2007 году бюджет утвержден с суммой страховых взносов, составляющих 47,21% от суммы всех доходов фонда.
Среди страховых взносов наибольший удельный вес занимают страховые взносы на обязательное пенсионное страхование, направляемые на выплату страховой части трудовой пенсии. Динамика доли данного вида доходов Пенсионного фонда сокращается на 2,6%, при этом в 2005 году доля страховых взносов на выплату трудовой части пенсии составляла 41,96%, в 2006 году – 39,39%, в 2007 – 40,86%
….
Страховые взносы на обязательное пенсионное страхование, направляемые на выплату накопительной части трудовой пенсии также сокращаются в динамике по доле в структуре доходов, однако всего на 0,2%.
Удельный вес данной категории доходов составляет порядка 6%.
Незначительное место занимают страховые взносы в виде фиксированного платежа, и по дополнительному тарифу для работодателей – организаций.
Сравнительно малую долю в доходной части Пенсионного фонда занимает единый минимальный налог, зачисляемый в бюджеты государственных внебюджетных фондов – порядка 0,14 % в 2007 году и доля данного показателя растет на 91,4%.
Неналоговые доходов бюджета Пенсионного фонда РФ не превышают 1% от суммы доходов, в то время как безвозмездные перечисления, представленные субвенциями от других бюджетов бюджетной системы РФ занимают более половины структурной части доходов фонда.
……..
^ 2.2. Пенсионная реформа
Ни для кого не секрет, что демографическая ситуация в России прогрессирует. О причинах сверх смертности населения ведутся дискуссии давно как на высшем уровне политической власти страны, так и на школьных уроках географии. Но стоит задуматься и о последствиях подобного темпа снижения численности страны. Люди, для которых сейчас слово «пенсия» ассоциируется исключительно с пожилым населением, в первую очередь могут почувствовать последствия демографической динамики. Согласно статистике, соотношение пенсионного населения к трудоспособному стремительно снижается, что, безусловно, приведет к невозможности обеспечения государством достойной пенсией будущих пенсионеров. Пенсионный фонд не будет обладать достаточными пенсионными накоплениями из-за отсутствия необходимого количества работающих граждан.
С появлением пенсионной реформы ПФР перешел от распределительной системы пенсионных накоплений к распределительно-накопительной. Таким образом, пенсия стала включать в себя три части – базовую, страховую и накопительную. У каждого гражданина появились пенсионные накопительные счета, с помощью которых отдельная часть пенсии накапливается в собственный пенсионный фонд. Это значит, что каждый гражданин начинает формировать собственную пенсию с началом трудовой деятельности [20, с.9].
Новая пенсионная система, по замыслу ее разработчиков, рассчитана на активное участие будущих пенсионеров в формировании собственной пенсии. Отныне на протяжении всей трудовой деятельности граждане должны следить за своими пенсионными накоплениями, выстраивая отношения, как с работодателем, так и с пенсионным фондом. Качество документов, представленных работником и работодателем в территориальный орган Пенсионного фонда России (ПФР), и правильность сведений индивидуального учета, на основании которых устанавливается пенсия, влияет на ее размер.
Переход к новой пенсионной системе был необходим. Несмотря на ее весьма недолгое существование, уже можно отметить, что проблем у этой системы, как правовых, так и экономических, предостаточно. За примерами далеко ходить не надо.
Размер страховой и накопительной частей пенсии зависит от заработной платы будущего пенсионера. Идеология страховой и накопительной системы такова: будущая пенсия людей, которые сейчас работают, будет зависеть не от заработной платы за избранные 2-5 лет, а от всей суммы его заработной платы за весь период трудового стажа, и даже не от самой заработной платы, а от того, какие пенсионные взносы с его заработной платы были перечислены в ПФР. Причем большая часть суммы этих взносов — виртуальная, ибо ее часть, поступив в 2003, 2005, 2010 и др. годах в ПФР, раздается в рамках распределительной системы людям преклонного возраста. Но когда человек выйдет в 2025 г. на пенсию, то размер его базовой части будет стандартным, а вот страховой — будет зависеть от того, сколько за него взносов пришло. Если при этом не будет ограничен предел максимального размера страховой пенсии, то это выгодно лишь для хорошо зарабатывающих людей — пенсия пропорциональна поступившим от них взносам [34, с.83].
Но в реальности на российском рынке труда далеко не та ситуация, когда работники могут жестко потребовать от работодателя добросовестно платить пенсионные взносы. Речь идет о заработной плате «в конвертах», через страховые или другие схемы, т.е. суммы, фактически полученные в виде заработной платы, не проходят официальную отчетность и не приносят пенсионных взносов. Речь идет и о заработной плате, которая хотя и оформляется официально, но пенсионные взносы по каким-то причинам работодатель вдруг решил не заплатить. Или заплатил, но не дал для пенсионного фонда достаточной документации, чтобы их удалось персонифицировать.
Согласно ч.2 ст.7 Закона об обязательном пенсионном страховании право на пенсионное страхование реализуется лишь в случае уплаты страховых взносов. Уплата страховых взносов возлагается, как известно, на работодателя. Следовательно, за невыполнение этой обязанности должен нести ответственность работодатель, а не работник. Именно так и решалась многие годы эта проблема в страховом законодательстве — практически со дня принятия первого правового акта о социальном страховании. Кодекс законов о труде 1971 г. (ч. 3 ст. 237) подтверждал, что «неуплата работодателем взносов на государственное социальное страхование не лишает работника права на обеспечение за счет средств социального страхования» [3].
………
^ 2.3. Состав и структура бюджета федерального Фонда обязательного медицинского страхования
Фонд обязательного медицинского страхования РФ (ФОМС) образованный в соответствии с Законом РСФСР «О медицинском страховании граждан в РСФСР» (от 28 июня 1991 г), является правовой, экономической и организационной основой медицинского страхования, направленного на усиление заинтересованности и ответственности как самого застрахованного, так и государства, предприятия, учреждения, организации в охране здоровья работников.
Основными задачами Федерального фонда являются:
1) финансовое обеспечение установленных законодательством Российской Федерации прав граждан на медицинскую помощь за счет средств обязательного медицинского страхования в целях, предусмотренных Законом Российской Федерации «О медицинском страховании граждан в Российской Федерации»;
2) обеспечение финансовой устойчивости системы обязательного медицинского страхования и создание условий для выравнивания объема и качества медицинской помощи, предоставляемой гражданам на всей территории Российской Федерации в рамках базовой программы обязательного медицинского страхования;
3) аккумулирование финансовых средств Федерального фонда для обеспечения финансовой стабильности системы обязательного медицинского страхования [32, с. 39].
Финансовые средства Федерального фонда образуются за счет:
1) части страховых взносов (отчислений) хозяйствующих субъектов и иных организаций на обязательное медицинское страхование в размерах, устанавливаемых федеральным законом;
2) ассигнований из федерального бюджета на выполнение федеральных целевых программ в рамках обязательного медицинского страхования;
3) добровольных взносов юридических и физических лиц;
4) доходов от использования временно свободных финансовых средств;
5) нормированного страхового запаса Федерального фонда;
6) поступлений из иных источников, не запрещенных законодательством Российской Федерации.
Страховые взносы (отчисления) в Федеральный фонд перечисляются хозяйствующими субъектами и иными организациями в соответствии с установленным порядком [16].
Отразим данные за три года по деятельности федерального фонда обязательного медицинского страхования в таблице 4 (Приложение 3, 4).
Таблица 4
Доходы и расходы федерального Фонда обязательного медицинского страхования
……
Также значимое место занимают поступления от единого социального налога (в соответствии с законодательством в размере налоговой ставки 1,1% от ставки налога 26%).
Единый социальный налог занимает 40% в 2005 году, при этом его доля растет в 2006 году до 48% и падает до 46,9% в 2007 году, однако в суммовом выражении сумма поступлений от ЕСН увеличивается.
В доходы бюджета федерального фонда обязательного медицинского страхования зачисляются также и такие налоги:
Налоги на совокупный доход
Единый налог, взимаемый в связи с применением упрощенной системы налогообложения
Единый налог на вмененный доход для отдельных видов деятельности
Единый сельскохозяйственный налог
Однако доля данных видов доходов незначительна.
Таблица 6
Структура расходов Федерального фонда обязательного медицинского страхования РФ, %
……..
А именно на дотации на выполнение территориальных программ обязательного медицинского страхования в рамках базовой программы обязательного медицинского страхования порядка 30%.
Нормированный страховой запас ФФОМС в структуре расходов бюджета занимает примерно 4,5%.
Мероприятия в области здравоохранения, спорта и физической культуры, туризма – в размере 0,3% составляют расходную часть бюджета фонда.
Остальные расходы относятся к содержанию аппарата органов управления государственных внебюджетных фондов – примерно 0,1%; переподготовка и повышение квалификации кадров, и другие вопросы в области культуры, кинематографии, средств массовой информации.
^ 2.4. Состав и структура доходов и расходов Фонда социального страхования РФ
Фонд социального страхования Российской Федерации управляет средствами государственного социального страхования Российской Федерации.
Основными задачами Фонда являются:
обеспечение гарантированных государством пособий по временной нетрудоспособности, беременности и родам, женщинам, вставшим на учет в ранние сроки беременности, при рождении ребенка, по уходу за ребенком до достижения им возраста полутора лет, а также социального пособия на погребение или возмещение стоимости гарантированного перечня ритуальных услуг, санаторно-курортное обслуживание работников и их детей;
участие в разработке и реализации государственных программ охраны здоровья работников, мер по совершенствованию социального страхования;
осуществление мер, обеспечивающих финансовую устойчивость Фонда;
разработка совместно с Министерством труда и социального развития Российской Федерации и Министерством финансов Российской Федерации предложений о размерах тарифа страховых взносов на государственное социальное страхование;
организация работы по подготовке и повышению квалификации специалистов для системы государственного социального страхования, разъяснительной работы среди страхователей и населения по вопросам социального страхования;
сотрудничество с аналогичными фондами (службами) других государств и международными организациями по вопросам социального страхования [14].
Отразим данные за три года по деятельности Фонда социального страхования РФ в таблице (на основании Приложения 5, 6).
Таблица 7
Доходы и расходы Фонда социального страхования РФ
…….
Рис. 6. Анализ деятельности фонда социального страхования РФ
Исходя из представленных данных видно, что деятельность фонда социального страхования, в отличие от остальных внебюджетных социальных фондов отражает дефицит, который растет за исследуемый период.
Рассмотрим причины роста дефицита бюджета фонда, проанализировав доходную и расходную часть бюджета.
Таблица 8
Структура доходов Фонда социального страхования РФ, %
……..
Страховые взносы на обязательное социальное страхование от несчастных случаев на производстве и профессиональных заболеваний занимают 18,2%, 17,1%, 16,8% соответственно в 2005,2006 и 2007 годах.
Среди налоговых формирований доходной части также присутствуют налоги на совокупный доход, доля которых составляет в 2007 году – 2,7 %, то есть рост доли происходит на 74,6% за исследуемый период.
Единый налог, взимаемый в связи с применением упрощенной системы налогообложения и единый налог на вмененный доход для отдельных видов деятельности занимают каждый чуть более 1% в структуре доходов.
Среди неналоговых доходов можно отметить наиболее значимые это доходы от размещения временно свободных средств ФСС.
Субвенции Фонду социального страхования Российской Федерации составляли в 2005 году всего 9%, тогда как к 2006 году достигает уровень данного вида доходов в размере 15,4%, и 17,3 % в 2007 году.
Таким образом, основной удельный вес занимает единый социальный налог в структуре доходов фонда социального страхования.
Рассмотрим структуру расходов фонда в таблице 9.
Таблица 9
Структура расходов Фонда социального страхования РФ, %
……
За прошедшие годы произошли существенные изменения в источниках финансирования государственных внебюджетных фондов. Если первоначально основным источником были страховые взносы, в том числе уплачиваемые работниками в Пенсионный фонд Российской Федерации, то в результате замены с 2001 года страховых взносов в государственные внебюджетные фонды единым социальным налогом, основным источником доходов этих фондов стали налоговые поступления.
^ ГЛАВА 3. СОВЕРШЕНСТВОВАНИЕ ДЕЯТЕЛЬНОСТИ ВНЕБЮДЖЕТНЫХ ФОНДОВ РФ СОЦИАЛЬНОГО НАЗНАЧЕНИЯ
3.1. Проблемы функционирования внебюджетных социальных фондов
Формирование основной части доходов государственных внебюджетных фондов в рамках существующей налоговой системы приводит к дефициту и угрозе дестабилизации финансовой обеспеченности системы обязательного социального страхования за счет следующих факторов:
1) определения ставки единого социального налога без должного актуарного обоснования, только исходя из взаимосвязей внутри налоговой системы (в частности, с учетом ставки налога на прибыль организаций) и потребности снижения налоговой нагрузки на работодателя, когда в расчет не принимаются вопросы собственно социального страхования – уровни страхового замещения заработной платы, покупательные способности пенсий и пособий;
2) введения регрессивной шкалы ставок единого социального налога;
3) развития специальных налоговых режимов, налоговые базы которых не корреспондируются с базой для исчисления основных видов страхового возмещения по обязательному социальному страхованию, а налоговые ставки (в части отчислений в государственные внебюджетные фонды) также не имеют актуарного обоснования.
Наличие указанных факторов обусловлено коренным различием между налогами и страховыми взносами (индивидуальной безвозмездностью налогов и возмездным характером страховых взносов) и отсутствием в сформировавшейся на основе ЕСН системе финансового обеспечения государственных внебюджетных фондов целевой ориентации по видам расходов. Действие этих факторов привело к формированию скрытого дефицита государственных внебюджетных фондов, который выражался в низком уровне пенсий, изменении порядка обеспечения по обязательному социальному страхованию, ограничению количества статей расходов, финансируемых за счет средств обязательного медицинского страхования.
Указанные выше факторы финансовой дестабилизации обязательного социального страхования в среднесрочной перспективе будут действовать в сторону увеличения дефицита, сократить который возможно с помощью увеличения налоговой базы, то есть за счет роста заработной платы. Однако эти ресурсы, в рамках действующей системы регулирования социально-экономических отношений, представляются крайне ограниченными в силу сведения к минимуму функций государства по регулированию заработной платы, давления иностранной рабочей силы на рынок труда, состояния основных фондов и других факторов, не позволяющих обеспечить быстрый рост производительности труда [38, с.8].
Современная отечественная система социальной защиты населения совершенно не решает стоящие перед ней задачи. Можно выделять много проблем, обусловивших скудный размер выплачиваемых пенсий, пособий и низкое качество бесплатной медицины, выливающихся в негативное отношение россиян к отечественной системе социального страхования.
Основные недостатки российской системы социального страхования следует искать в неэффективной системе формирования доходов внебюджетных фондов, являющихся материальной базой социального страхования. Среди причин, препятствующих полноте формирования доходов российской социальной системы, главной является низкая налоговая культура россиян, большинство из которых стремится уклониться от уплаты обязательных платежей. Базой для исчисления обязательный платежей во внебюджетные фонды России являются доходы населения, масштабы сокрытия которых в нашей стране очень велики – реально, полноту уплаты налоговых платежей с доходов физических лиц можно ожидать только в государственной сфере, где налогоплательщик не извлекает особую выгоду с неуплаченных налоговых сумм; в сфере же частного бизнеса практика занижения доходов очень распространена, основная часть заработка наемным работникам негосударственного сектора выплачивается неофициально, выпадая тем самым из-под налогообложения [24, с.48].
Органы управления государственными внебюджетными фондами сталкиваются с проблемой, когда при единой бюджетной классификации РФ и единой инструкции по бюджетному учету возникает необходимость в дополнении данных документов, чтобы запланировать и учесть все операции, связанные с формированием и использованием средств государственных внебюджетных фондов. В настоящее время есть расхождения в классификации расходов на содержание органов управления государственными внебюджетными фондами: если в бюджетах Пенсионного фонда РФ и Фонда социального страхования РФ эти расходы отражаются по разд. 10 «Социальная политика», то в бюджете Федерального фонда обязательного медицинского страхования — в разд. 01 «Общегосударственные вопросы».
Серьезной проблемой также на данный момент является необходимость дополнительной группировки доходов и расходов для анализа операций, связанных с формированием и использованием средств государственных внебюджетных фондов. Например, такая дополнительная группировка необходима для того, чтобы разделить операции по социальному страхованию на случай общего заболевания и операции по социальному страхованию от несчастных случаев на производстве и профессиональных заболеваний по Фонду социального страхования РФ [35, с.34].
В настоящее время в структуре расходов федерального бюджета по функциональной классификации первое место занимает раздел «Межбюджетные трансферты», в том числе и потому, что к таким трансфертам относится перечисление средств федерального бюджета в государственные внебюджетные фонды. При этом принципы организации межбюджетных трансфертов между федеральным бюджетом и бюджетами государственных внебюджетных фондов, между бюджетами субъектов РФ и бюджетами территориальных фондов обязательного медицинского страхования совершенно иные, чем межбюджетные трансферты между федеральным бюджетом, бюджетами субъектов РФ и местными бюджетами, поскольку речь не идет о достижении сбалансированности нижестоящего бюджета, передачи государственных полномочий с одного уровня на другой. В конечном счете, это создало курьезную ситуацию, когда средства, выделяемые из федерального бюджета на покрытие дефицита бюджета Пенсионного фонда РФ, отражаются не в источниках финансирования дефицита бюджета Пенсионного фонда РФ, а в доходах бюджета Пенсионного фонда РФ.
…….
Подводя итог, следует отметить, что попытка распространить все правовые нормы формирования и использования средств федерального бюджета, бюджетов субъектов РФ и местных бюджетов на формирование и использование средств государственных внебюдж
ronl.org
Реферат — Курсовая взфэи — Разное
2279
Управленческий учет
Директ-костинг
Курсовая
ВЗФЭИ
51
2007
1000
Содержание
Введение 1
Заключение 2
Список использованных источников 4
Введение
На данный момент в России идет становление и развитие рыночных отношений. С каждым годом на рынке появляется все большее количество успешных предприятий, все острее становится конкуренция между ними. Чтобы выдержать конкуренцию, руководству предприятия необходимо обладать полной, адекватной информацией о деятельности фирмы и о ее финансовых результатах. Одним из наиболее важных показателей, на котором основывается конкурентная борьба, является себестоимость производимой продукции, которая определяет возможности для снижения цены.
Себестоимость можно рассчитать несколькими различными методами, одним из подобных методов является мало известный в нашей стране «direct-costing», который рассмотрен в данной работе. Этот метод основан на расчете себестоимости по усеченным затратам, что принципиально отличает его от всех ранее существовавших методов. Как и любой метод, «direct-costing» имеет ряд преимуществ и недостатков, но во многих случаях он дает более объективную оценку ситуации, нежели методы, основанные на учете полных издержек. В данной работе проведен анализ того, в каких случаях это происходит, а также когда наиболее выгодно применять именно данный метод планирования учета и калькулирования себестоимости.
Целью работы является анализ системы «Директ-костинг» с точки зрения принятия управленческих решений.
Задачи работы:
раскрыть сущность и необходимость управленческого учета в современных условиях
проанализировать особенности учета затрат по системе «Директ – костинг»
рассмотреть возможности совершенствования управленческого учета на основе системы «Директ – костинг»
Объектом исследования работы выступает ОАО «НЭТА».
Предметом исследования является организация управленческого учета затрат предприятия по системе «Директ – костинг».
Теоретической и методологической базой исследования послужили научные труды ведущих отечественных и зарубежных специалистов в области управленческого учета, менеджмента.
Заключение
В условиях развивающихся рыночных отношений эффективное управление производственной деятельностью предприятия все более зависит от уровня его информационного обеспечения. Мировой опыт свидетельствует об эффективности использования маржинального метода бухгалтерского учета — системы учета «Директ-костинг».
Система «директ — костинг» — это подход, когда в разрезе объектов калькулирования планируется и учитывается неполная, ограниченная себестоимость. Себестоимость может включать только прямые затраты; только переменные, то есть зависящие от изменения объемов производства, затраты; она может калькулироваться на основе только производственных расходов, связанных с изготовлением данной продукции, выполнением работ или оказанием услуг, даже если они носят косвенный характер. Но, несмотря на различную полноту включения в себестоимость объекта калькулирования различных видов расходов, общим для этого подхода является то, что другие виды затрат, которые также по своей экономической сущности составляют часть текущих издержек, не включаются в калькуляцию, а возмещаются единой суммой из выручки (или валовой прибыли).
Особенностью системы директ-костинг является, во-первых, разделение затрат на постоянные и переменные. Переменные расходы прямо зависят от объема и ассортимента выпускаемой продукции и с незначительными отклонениями колебания их величины синхронны с колебаниями объема выпуска. Напротив, постоянные расходы не зависят от изменений объема продукции. Их величина зависит только от длительности отчетного периода. Несмотря на некоторую условность деления затрат на постоянные и переменные, ценность такого разделения в упрощении учета и повышении оперативности получения данных о прибыли.
Вторая особенность системы директ-костинг — соединение производственного и финансового учета. По системе директ-костинг учет и отчетность на предприятиях организованы таким образом, что появляется возможность регулярного контроля данных по схеме «затраты — объем -прибыль».
В работе были показаны преимущества применения учета затрат методом «direct-costing». Так как он определяет себестоимость только по переменным затратам, а постоянные затраты списывает из прибыли того периода в котором они были произведены, то при его использовании не возникает несоответствий истинной прибыли предприятия и изложенных на бумаге расчетов.
По итогам работы можно сделать следующие выводы:
1. Система учета себестоимости «директ-костинг» позволяет получить данные о себестоимости единицы продукции, не искаженные разнесением косвенных затрат, как происходит при применении метода учета полной себестоимости.
2. Информация, полученная с помощью использования метода учета неполной производственной себестоимости («директ-костинг») позволяет установить взаимосвязи между выручкой, постоянными и переменными расходами и объемом производства.
Проанализировав все примеры можно посоветовать применять «direct-costing» на производстве, где имеется много цехов или отделов, где производится широкий ассортимент продукции, который к тому же часто меняется, где нет постоянных объемов выпуска, и где используют складирование непроданной в данный период продукции. Если же у этого предприятия к тому же не полностью загружены производственные мощности, и перед ним стоит дилемма, производить самому или же покупать какой-то из компонентов необходимых в дальнейшем производстве, а также оно сталкивается с рядом ограничивающих факторов, учитывая которые надо сформировать ассортимент, то в данном случае «direct-costing» просто необходим.
^ Список использованных источников
Вахрушина М.А. Бухгалтерский управленческий учет. — М.: ЗАО “Финстатинформ”, 1999.- 356 с.
Власова В.М. Основы предпринимательской деятельности: финансовый менеджмент. — М.: Финансы и статистика, 1999. — 128 с.
Врублевский Н.Д. Построение системы счетов управленческого учета // Бухгалтерский учет. 2000. С. 63-68.
Друри К. Введение в управленческий и производственный учет.- М.: АУДИТ, 1994. – 546 с.
Ивашкевич В.Б. Управленческий учет в информационной системе предприятия // Бухгалтерский учет. 1999. С. 97-102.
Касьянова Г.Ю., Колесников С.Н. Управленческий учет по формуле «три в одном». — М.: Статус-Кво-97, 1999. — 328 с.
Карпова Т. П. Управленческий учет. — М.: Аудит, Юнити, 1998. — 350 с.
Комментарий к главе 25 Налогового кодекса РФ «Налог на прибыль организаций». — 2-е изд., перераб. и доп. — М.: Современная экономика и право; Юрайт-М, 2002. — 280 с.
Мишин Ю.А. Система управленческого учета на современном предприятии // Менеджмент в России и за рубежом. — №3, 2001. – с. 35 – 38.
Методические рекомендации по оценке эффективности инвестиционных проектов. — М.: Экономика, 2000. — 422 с.
Николаева С.А. Особенности учета затрат в условиях рынка: система «директ-костинг». — М.: Финансы и статистика, 1993. — 128 с.
Николаева О., Шишкова Т. Управленческий учет. — Эдиториал УРСС, 2000. — 368 с.
Организация управленческого учета по системе «Директ – костинг» // Корпоративный менеджмент, № 2, 2001.
Палий В.Ф. Основы калькулирования.- М.: Финансы и статистика, 2001. – 289 с.
Пашигорева Г.И., Савченко О.С. Цели и задачи управленческого учета // Бухгалтерский учет. 2000. С. 63-65.
Росс С., Вестерфилд Р., Джордан Б. Основы корпоративных финансов. Ключ к успеху коммерческой организации — финансовое планирование и управление. — Лаборатория базовых знаний, 2000. — 720 с.
Русак Н.А., Русак В.А. Финансовый анализ субъекта хозяйствования: Справочное пособие. – Минск: Высш. шк., 2001. – 412 с.
Савицкая Г.В. Анализ хозяйственной деятельности предприятия: 4-е изд., перераб. и доп. – Минск: ООО «Новое знание», 2000. – 344 с.
Ткач В.И., Ткач М.В. Управленческий учет: международный опыт. — М.: Финансы и статистика, 1994. — 144 с.
Управленческий учет по формуле «три в одном»/Касьянова Г.Ю., Колесников С.Н. — М.: Издательско-консультационная компания «Статус-Кво97», 1999. — 328 с.
Управленческий учет: Учебное пособие / Под редакцией А.Д. Шеремета — М.: ФБК-ПРЕСС, 1999. — 512 с.
Хорнгрен Ч.Т., Фостер Дж. Бухгалтерский учет: управленческий аспект. — М.: Финансы и статистика, 1995.- 410 с.
Шеремет А. Д., Негашев Е. В. Методика финансового анализа. — М.: Инфра-М, 2000. — 208 с.
Шим Дж.К., Сигел Джоэл Г. Методы управления стоимостью и анализа затрат. – М.: Филинъ, 2001. – 458 с.
ronl.org
Реферат ВЗФЭИ
скачатьРеферат на тему:
План:
- Введение
- 1 Краткая характеристика
- 2 История института
- 3 Рейтинг института
- 4 Факультеты
- 5 Кафедры
- 6 Курсы ВЗФЭИ
- 7 Центр дополнительного профессионального образования
- 8 Филиалы
- 9 Дополнительные сведения Примечания
Введение
Всероссийский заочный финансово-экономический институт (ВЗФЭИ; англ. All-Russian Distance Institute of Finance and Economics) — основан 14 мая 1930 года.
1. Краткая характеристика
Крупнейший в России государственный и единственный специализированный заочный экономический вуз. Институт подготовил свыше 300 тысяч высококвалифицированных специалистов: учёных; руководителей финансовой и банковской систем; ведущих экономистов и главных бухгалтеров; руководителей различных звеньев управления народным хозяйством. Научные исследования проводят крупные учёные-экономисты, авторы известных в стране монографий, учебников, учебных пособий.
Преподаватели института участвуют в работе центральных органов власти и управления по подготовке законодательных актов и нормативных документов, в проведении экспертных оценок подготавливаемых проектов и экономических расчетов.
Институт является учебно-методическим центром страны по заочному экономическому образованию, а также одним из крупнейших в Российской Федерации научно-исследовательским центром.
В 2001 году ВЗФЭИ занял 7 место в рейтинге экономических вузов по России по итогам 2000 года.
Институт имеет государственную аккредитацию и лицензию на образовательную деятельность № 24Г-1144 от 11.09.2000 г.
2. История института
Институт основан 14 мая 1930 года под названием Центральный заочный институт финансово-экономических наук[1]. Позже, после слияния с другими вузами, получил название Всесоюзный заочный финансово-экономический институт[1].
Всероссийский заочный финансово-экономический институт является одним из самых крупных учебных заведений России. В настоящее время в нем обучается более 40 тысяч человек.
В 2000 году институту исполнилось 70 лет. За эти годы из его стен вышло около 300 тыс. специалистов с высшим экономическим образованием.
3. Рейтинг института
Рейтинг ВЗФЭИ на основе данных Минобразования РФ по состоянию на июль 2003 г. по профилю «Экономические вузы» занимал 7 строчку.
По данным мониторинга экономических вузов Федерального агентства по образованию за 2007 г. ВЗФЭИ занимает 14 строчку.
4. Факультеты
- Финансово-кредитный;
- Учетно-статистический;
- Менеджмента и маркетинга;
- Непрерывного обучения.
5. Кафедры
- Автоматизированных информационных систем;
- Аудита;
- Банковских технологий;
- Бухгалтерского учета и анализа хозяйственной деятельности;
- Высшей математики;
- Денег, кредита и ценных бумаг;
- Иностранных языков;
- Истории экономики, политики и культуры;
- Маркетинга;
- Менеджмента;
- Налогов и налогообложения;
- Права;
- Прикладной информатики;
- Региональной экономики и управления;
- Статистики;
- Философии и социологии;
- Финансов, бюджета и страхования;
- Финансового менеджмента;
- Экономики труда и управления персоналом;
- Экономики предприятий и предпринимательства;
- Экономико-математических методов и моделей;
- Экономической теории.
6. Курсы ВЗФЭИ
7. Центр дополнительного профессионального образования
8. Филиалы
Имеет филиалы в городах:
|
|
|
9. Дополнительные сведения
ВЗФЭИ является одним из учредителей Некоммерческого партнёрства «Институт социально-экономического развития Центрального федерального округа»
Примечания
- ↑ 12 История института — www.vzfei.ru/rus/about/ins_history.htm на официальном сайте.
wreferat.baza-referat.ru
Реферат — Всероссийский заочный финансово-экономический институт
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
Финансовое право
Методические указания по написанию реферата (эссе) для самостоятельной работы студентов II курса, обучающихся по направлению 521500 (080500.68) «Магистр менеджмента»
Факультет менеджмента и маркетинга
Кафедра «Право»
Москва 2009
^ Методические указания разработали:
Доктор социологических наук, доцент М.В.Кибакин
Кандидат юридических наук, доцент А.М.Фатхутдинова
Методические указания обсуждены на заседании кафедры “Право”
Зав. кафедрой А.Г.Чепурной
Программа одобрена на заседании Научно- методического Совета ВЗФЭИ
Председатель НМС, профессор Д.М. Дайитбегов
^ Финансовое право. Методические указания по написанию рефератов (эссе) работ для самостоятельной работы студентов II курса, обучающихся по направлению 521500 (080500.68) «Магистр менеджмента» – М.: ВЗФЭИ, 2009.
ББК ____.___-__
© Всероссийский заочный
финансово-экономический
институт (ВЗФЭИ), 2009
1. Общие методические рекомендации по написанию реферата (эссе)
Самостоятельная работа студентов при изучении дисциплины «Финансовое право» предполагает активное изучение современных проблем и тенденций развития высшего образования в России, его содержания, технологий обучения, методов, формирования системного профессионального мышления.
В процессе подготовки реферата или эссе студентами осуществляется научно-исследовательская деятельность по изучению современных особенностей правового регулирования управленческой деятельности, сущности и особенности правоотношений в данной сфере, порядок закрепления и реализации прав и ответственности руководителя, работников, собственников и иных субъектов правоотношений.
Подготовка реферата (эссе) является важным видом самостоятельного изучения студентами курса «Финансовое право» и является одной из форм текущего контроля знаний. Для ее успешного выполнения необходимо систематически работать с учебной, справочной и научной литературой.
Назначение реферативной работы — углубить знания студентов по основным проблемам современного права, выявить умение анализировать правоотношения, способность понимания современных проблем юридической теории и практики. При написании работы студент должен использовать современную учебную и научную литературу, обратиться к аналитическим исследованиям, обзорам и проблемным работам по вопросам современного права в сфере профессиональной деятельности.
Реферат — теоретическая работа магистранта, в которой излагаются различные точки зрения (в том числе и критические) на рассматриваемую проблему. Реферат может не включать собственных аналитических и практических исследований магистранта, но наличие обобщений и выводов магистранта по рассматриваемой проблеме является обязательным. Стандартная форма реферата: название темы — план — введение — основная часть (может включать несколько вопросов) — заключение — список литературы. Объем реферата — 10-25 страниц.
Эссе — это краткое изложение собственной позиции, собственных размышлений или собственной точки зрения магистранта по какой-либо проблеме. Оно может не включать обзора точек зрения других авторов по данной проблеме, но при сопоставлении собственного видения проблемы с другими позициями, эти позиции в очень краткой форме могут присутствовать.
Стандартная форма эссе: название проблемы — изложение собственного видения проблемы автором (может включать 1-3 вопроса) — выводы автора краткий список литературы (если есть ссылки на другие позиции). Объем эссе — 3-10 страниц.
Рефераты (эссе) оформляются на стандартных листах бумаги формата А-4 с одной стороны. Размер шрифта 14 пунктов, название шрифта: Times New Roman. Текст работы отпечатывается через полтора интервала, абзац составляет 1,25см (5 знаков). При этом соблюдаются следующие размеры полей: левое — 35мм, правое – 15мм, верхнее и нижнее – не менее 20мм. Работа должна иметь титульный лист, в верхней части которого указывается наименование ВЗФЭИ, под ним полное название кафедры, в центре листа указывается «Реферат» либо «Эссе» и название работы, в нижнем правом углу печатается Ф.И.О. магистранта, номер группы, номер курса и номер задания. Нумерация страниц сквозная, в верхнем правом колонтитуле.
^ 1.1. Порядок выполнения работ
Начинать работу над выбранной темой реферата (эссе) следует с программы курса «Финансовое право», которая позволит определить место избранной темы во всем курсе и выбрать необходимую для исследования темы литературу.
Настоящие методические рекомендации по выполнению реферативной работы предлагают примерный план анализа темы, не ограничивающий магистранта в выборе собственных подходов к освещению избранной проблемы. По согласованию с преподавателем допустимо самостоятельно сформулировать тему реферата (эссе), при условии, что она отражает проблемы, обозначенные в программе курса.
Тема реферата (эссе) должна раскрываться в соответствии с планом, который выносится на вторую страницу реферата (эссе). План определяет логику изложения материала. Анализ рекомендованной литературы позволит магистранту определить, какие именно аспекты проблемы будут им рассматриваться в реферате (эссе) и в какой последовательности.
Введение, обосновывающее актуальность рассматриваемой проблемы, должно предварять основное содержание реферата (эссе).
Текст реферата (эссе) должен содержать ссылки на монографии, материалы исследований, судебные обзоры, статьи и документы, анализируемые в реферативной работе. Недопустимы ссылки на интернет-сайты без указания автора.
Заключение является обязательным итоговым разделом реферата (эссе). В нем делаются выводы относительно тех положений, которые рассматривались в реферативной работе.
В конце реферата (эссе) следует привести список используемой литературы с указанием названия издательства и года выпуска.
Особое внимание следует обратить на правильное оформление работы. Необходимо выделить в тексте рассматриваемые проблемы в виде разделов или параграфов. Объем разделов реферата (эссе) должен быть соразмерен, так, недопустимо рассматривать проблему в одном параграфе на двух страницах, а в другом — на десяти. Приводимые в тексте имена авторов должны быть снабжены ссылками на источники.
Реферат (эссе) передаются на рецензирование. Ответы на замечания и вопросы рецензента нужно давать в письменной форме. Получение отрицательной рецензии предполагает необходимость доработки текста в соответствии с замечаниями и вторичное представление работы на рецензирование.
Работа должна быть подписана магистрантом с указанием даты ее написания. На титульном листе работы должна быть указана фамилия рецензента (преподавателя, читающего лекции на этом потоке).
По содержанию реферата (эссе) проводится устное собеседование.
Выбор темы реферата (эссе) производится следующим образом: студенты, фамилии которых начинаются от А до Д включительно, могут выбрать вариант с 1 по 4; от Е до К — вариант 5-9; от Л до О — вариант 10-13; от П до С до Я вариант 14 — 19. Форму работы (реферат или эссе) студент вправе выбирать самостоятельно.
Преподаватели могут по своему усмотрению вносить изменения в предлагаемые темы и рекомендовать магистрантам дополнительную литературу.
Работа сдаётся на кафедру на бумажном носителе и в электронном формате [email protected]
Примерные темы и
методические рекомендации по подготовке и написанию рефератов (эссе)
Темы рефератов (эссе).
Финансовая деятельность государства: понятие, содержание, задачи, методы, формы.
Правовое регулирование финансового контроля.
Бюджетное устройство и бюджетная система Российской Федерации.
Сущность, принципы и стадии бюджетного процесса в Российской Федерации.
Налоговые правонарушения и ответственность за их совершение.
Правовые основы страхования.
Правовые основы денежного обращения в Российской Федерации.
Финансовое право: понятие, система, особенности предмета и метода правового регулирования.
Финансово-правовые нормы и финансовые правоотношения.
Правовой статус, основные задачи и функции государственных органов, осуществляющих финансовую деятельность.
Правовое регулирование финансового контроля.
Понятие валюты и валютных ценностей. Валютные правоотношения.
Состав, структура и современное состояние банковской системы Российской Федерации.
Правовые основы страхования в Российской Федерации.
Понятие, значение государственного и муниципального кредита и его правовые основы.
Понятие, состав и основные признаки налоговых правонарушений.
Система налогов и сборов в Российской Федерации.
Стадия составления, рассмотрения, утверждения и исполнения бюджета.
Бюджетное право и бюджетные правоотношения.
^ 3. Методические рекомендации по написанию реферата
Тема 1. Финансовая деятельность государства: понятие, содержание, задачи, методы, формы
При рассмотрении темы обратите внимание на правовые основы финансовой деятельности государства. Дайте определение финансов в материальном и экономическом смысле, опишите функции финансов и отличие публичных финансов от частных.
Охарактеризуйте специфику функционирования отдельных государственных органов в процессе финансовой деятельности, уделив особое внимание характеристике деятельности различных ветвей власти.
Дайте определение и охарактеризуйте сущность финансового прогнозирования, финансового планирования, финансового регулирования, оперативного управления и финансового контроля.
Литература
Винницкий Д.В. Финансовое право в современных условиях: традиции и инновации // ФП. — 2006. — № 8.
Запольский С.В. О природе понятия «финансовая система России» // ФП. — 2006. — № 8.
Ивлиева М.Ф. Категории «финансы» и «финансовая деятельность государства» в науке финансовое право // ГП. — 2004. — № 7.
Казанцев И.М. Институты финансового права // ЖРП. — 2005. — № 9.
Ялбулганов А.А. Федеральные источники финансового права: вопросы систематизации и классификации // ФП. — 2007. — № 2.
Тема 2. Правовое регулирование финансового контроля
При рассмотрении темы обратите внимание на правовые основы финансового контроля. Дайте определение финансового контроля и опишите отдельные его виды (государственный, муниципальный, общественный, аудиторский). Опишите формы финансового контроля и методы его осуществления (ревизия, проверка, анализ, обследование, наблюдение, мониторинг)
Охарактеризуйте специфику отдельных видов контроля и их правовую основу, уделив особое внимание характеристике Парламентского контроля, а также деятельности по контролю, отдельных подразделений Министерства финансов РФ, Центрального банка РФ.
Дайте определение и охарактеризуйте сущность валютного контроля.
Литература
Варфоломеева Ю.А. Правовые основы финансового контроля // ФП. — 2005. — № 12.
Махмутова Э.Х. Система формализации финансового контроля в кредитной сфере: Банк России — правовой аспект // Банковское право. — 2005. — № 3.
Степанов М.В. Ревизия как основной метод финансового контроля и ведущая форма деятельности Счетной палаты Российской Федерации // СП. — 2004. — № 7.
Степашин С.В. Государственный финансовый контроль в России: прошлое, настоящее и будущее // Государственная власть и местное самоуправление. — 2006. — № 5.
Тема 3. Бюджетное устройство и бюджетная система
Российской Федерации
При рассмотрении темы обратите внимание на правовые основы бюджетной деятельности государства. Дайте определение бюджета в материальном, экономическом и юридическом смысле, опишите функции бюджета (распределительная, контрольная).
Охарактеризуйте специфику отдельных видов бюджетов (федеральный, региональный, местный, консолидированный, национальный, дефицитный, профицитный и др.) Опишите стадии бюджетного процесса и полномочия его участников.
Опишите и выделите особенности внебюджетных фондов
Дайте краткую характеристику налоговых и неналоговых поступлений бюджетов различных уровней.
Литература
Галкин А. Разграничение расходов между уровнями бюджетной системы // Законность. — 2004. — № 2.
Новикова Н.И. Понятие бюджетного федерализма в Российской Федерации: сравнительно-правовой аспект // ФП. — 2005. — № 8.
Порошин Е.А. К вопросу о бюджетном финансировании нормативных правовых актов // Банковское право. — 2006. — № 5.
Степашин С.В. Новая редакция бюджетного кодекса: достоинства и недостатки // ЖРП. —2007. — № 3.
Хужин А.М. Бюджетное право и бюджетный процесс в Российской Федерации: Лекция. — Нижний Новгород: Нижегородская академия МВД России, 2002.
Тема 4. Сущность, принципы и стадии бюджетного процесса
в Российской Федерации
При рассмотрении темы обратите внимание на правовые основы бюджетной деятельности государства. Дайте определение бюджета в материальном, экономическом и юридическом смысле, опишите функции бюджета (распределительная, прогностическая, контрольная).
Охарактеризуйте специфику отдельных видов бюджетов (федеральный, региональный, местный, консолидированный, национальный, дефицитный, профицитный и др.) Опишите стадии бюджетного процесса и полномочия его участников.
Дайте краткое описание отдельных принципов бюджетного процесса (прозрачность, достоверность, адресность, сбалансированность, единство кассы). Опишите специфику их реализации в деятельности различных ветвей власти.
Охарактеризуйте различные стадии бюджетного процесса (составление бюджета, рассмотрение и его утверждение, исполнение и отчёт). Особое внимание уделите на характеристику деятельности отдельных участников бюджетного процесса в т.ч. Центрального Банка РФ
Литература
Евсеев П.И., Ялбулганов А.А. Проблемы правового регулирования полномочий субъектов Российской Федерации в сфере бюджетных отношений // РП. — 2005. — № 2.
Иванова М.С. Правовое регулирование исполнения бюджета в зарубежных странах // Законодательство и экономика. — 2005. — № 1.
Иванова М.С. О реформировании казначейского исполнения бюджетов // Законодательство и экономика. — 2004. — № 6.
Клишина М.А. Составление проекта бюджета: проблемы и перспективы // ФП. — 2006. — № 3.
Яковлев Д.И. Проблемы правового регулирования исполнения федерального бюджета // ФП. — 2006. — № 4.
Тема 5. Налоговые правонарушения и ответственность
за их совершение
При рассмотрении темы обратите внимание на теоретические основы юридической ответственности. Дайте определение правонарушения вообще и налогового правонарушения в частности. Определите отличие между налоговым преступлением и налоговым правонарушением.
Охарактеризуйте специфику и общественную опасность налоговых правонарушений. Опишите отдельные элементы состава налогового правонарушения.
Дайте краткую характеристику отдельных видов налоговых правонарушений с использованием действующих в настоящие время УК РФ, КоАП РФ, НК РФ, БК РФ, постановлений Конституционного Суда РФ, Пленума Верховного суда РФ и Высшего Арбитражного суда РФ.
Опишите специфику деятельности отдельных органов государственной власти по предупреждению налоговых правонарушений.
Охарактеризуйте основные направления взаимодействия отдельных государственных органов (ФНС, МВД, ФССП) по профилактике налоговых правонарушений.
Литература
Архипенко Т.В., Макаров А.В. Соотношение налоговой и административной ответственности // ФП. — 2004 — № 5.
Лущаев С.В. Становление законодательства о юридической ответственности за налоговые правонарушения // История государства и права. — 2006. — № 8.
Макаров А.В. Архипенко Т.В. Характеристика налоговой ответственности. Санкции за нарушение налогового законодательства // ФП. — 2005. — № 6.
Тема 6. Правовые основы страхования
При рассмотрении темы обратите внимание на теоретические основы страхования. Дайте определение договора страхования, охарактеризуйте его отдельные виды. Опишите правовое положение страхователя, страховщика и выгодоприобретателя. Определите существенные условия договора страхования.
Охарактеризуйте специфику и особенности различных видов договоров страхования (страхование имущества, страхование жизни и здоровья, страхование юридической ответственности, страхование внедоговорной ответственности, страхование предпринимательского риска).
Дайте краткую характеристику основных направлений деятельности Федеральной службы страхового надзора.
Литература
Ипатов А.Б. О финансово-правовой природе института страхования // ФП. — 2006. — № 6.
Мамсуров М.Б. К вопросу страхования предпринимательских рисков // Юридический мир. — 2006. — № 1.
Стрельников В.В. Финансово-правовые отношения в сфере страхования // ЖРП. — 2006. — № 2.
Тема 7. Правовые основы денежного обращения в Российской
Федерации
При рассмотрении темы обратите внимание на теоретические основы денежного обращения в Российской Федерации. Дайте классификацию денег по природно-функциональному признаку (товарные, полноценные, кредитные), по юридической природе (законное платёжное средство), по эмиссионному институту (банкноты, казначейские деньги). Опешите этапы создания законного платёжного средства.
Охарактеризуйте содержание фундаментальных полномочий государства в денежной сфере.
Дайте определение эмиссии как категории российского законодательства.
Опишите основные направления денежно-кредитной и валютной политики государства.
Охарактеризуйте основные виды правонарушений в сфере денежного обращения.
Литература
Бельский К.С. К вопросу о понятии денежной системе РФ // ФП. — 2005. — № 8.
Словарь финансово-банковских терминов / Сост. Р.М. Ахмедов. — Уфа: ОНиРИО УЮИ МВД России, 2003.
Чураков М.С. К вопросу о понятии и содержании системы безналичных расчетов // Банковское право. — 2007. — № 1.
Тема 8. Финансовое право: понятие, система, особенности предмета и
метода правового регулирования
При рассмотрении темы обратите внимание на теоретические основы понимания права вообще. Дайте определение финансового права»и его соотношения с другими отраслями Российского права. Определите отличие « Финансового права» как отрасли права, науки и учебной дисциплины.
Охарактеризуйте специфику финансового права. Опишите основные источники финансового права.
Дайте краткую характеристику предмету и методу финансового права, охарактеризуйте его отдельные элементы.
Опишите специфику отдельных видов норм финансового права
Охарактеризуйте основные направления совершенствования финансового законодательства.
Литература
Агапцов С.А. Правовое регулирование деятельности пенсионного фонда Российской Федерации // ФП. — 2005. — № 3.
Ашмарина Е.М. Современная финансовая система Российской Федерации // ГП. — 2004. — № 6.
Ашмарина Е.М. Структура финансового права Российской Федерации на современном этапе // ГП. — 2004. — № 9.
Лахтина Т.А. О сущности финансовой системы как элемента современного государства // ФП. — 2005. — № 4.
Лукашев А.А. К вопросу о методологии построения системы финансового права // ФП. — 2006. — № 7.
Тема 9. Финансово-правовые нормы и финансовые правоотношения
При рассмотрении темы обратите внимание на теоретические основы понимания нормы права. Дайте характеристику её отдельным элементам. Охарактеризуйте отдельные виды норм финансового права
Дайте определение правоотношения вообще и финансового правоотношения в частности. Опешите структуру правоотношения и дайте характеристику его отдельным элементам. Перечислите основания возникновения, изменения и прекращения финансовых отношений.
Охарактеризуйте специфику финансовых отношений и особенности правового положения отдельных участников финансовых правоотношений.
Дайте краткую характеристику отдельных видов финансовых отношений.
Литература
Ашмарина Е.М. Специфика содержания некоторых финансово-правовых норм // ГП. — 2005. — № 2.
Запольский С.В. К вопросу о природе финансовых правоотношений: информационная составляющая // ФП. — 2007. — № 8.
Карасева М.В. Деньги — объект имущественных финансовых правоотношений // Законодательство и экономика. — 2006. — № 11.
Орлов М.Ю. Особенности норм налогового права // ФП. — 2007. — № 2.
Ручкин О.Ю. Общепризнанные принципы и нормы международного права и международные договоры как источники финансового права // Международное публичное и частное право. — 2005. — № 4.
Титов А.С. Противоречия и перспективы развития налоговых правоотношений // ФП. — 2006. — № 1.
Тема 10. Правовой статус, основные задачи и функции
государственных органов, осуществляющих
финансовую деятельность
При рассмотрении темы обратите внимание на различные основания классификации субъектов финансовых отношений, в том числе публично-территориальные образования, коллективные субъекты и т.д. Дайте краткую характеристику отдельным субъектам. Охарактеризуйте отдельные виды норм финансового права
Опишите правовое положение Министерства финансов, РФ обратив особое внимание его структурные подразделения такие как, Федеральная налоговая служба, Федеральная служба страхового надзора, Федеральная служба финансово-бюджетного надзора, Федеральное казначейство, Федеральную службу по финансовому мониторингу.
Охарактеризуйте финансовые органы субъектов Федерации и муниципальных образований.
Литература
Асадов А.М. Правовое обеспечение организации финансовой деятельности государства //СП. — 2005. — № 3.
Ашмарина Е.М. Финансовая деятельность современного государства // ГП. — 2004. — №3.
Винницкий Д.В. Категория «финансовая деятельность государства» в науке российского финансового права // ГП. — 2003. — № 2.
Ивлева М.Ф. Категории «финансы» и «финансовая деятельность государства» в науке финансового права // ГП. — 2004. — № 4.
Тема 11. Правовое регулирование финансового контроля
При рассмотрении темы обратите внимание на правовые основы финансового контроля. Дайте определение финансового контроля и опишите отдельные его виды (государственный, муниципальный, общественный, аудиторский). Опишите формы финансового контроля и методы его осуществления (ревизия, проверка, анализ, обследование, наблюдение, мониторинг)
Охарактеризуйте специфику отдельных видов контроля и их правовую основу, уделив особое внимание характеристике Парламентского контроля, а также деятельности по контролю, отдельных подразделений Министерства финансов, Центрального банка РФ.
Дайте определение и охарактеризуйте сущность валютного контроля.
Литература
Варфоломеева Ю.А. Правовые основы финансового контроля // ФП. — 2005. — № 12.
Конюхова Т.В. «Проблемы совершенствования законодательства о финансовом контроле в Российской Федерации» // ЖРП. — 2008. — № 2.
Косолапов С.В. Контрольно-ревизионная деятельность Счетной палаты Российской Федерации // ФП. — 2007. — № 5.
Коробкина Л.М. Федеральная служба финансово-бюджетного надзора как орган государственного финансового контроля // ФП. — 2007. — № 5.
Махмутова Э.Х. Система формализации финансового контроля в кредитной сфере: Банк России — правовой аспект // БП. — 2005. — № 3.
Степашин С.В. Государственный финансовый контроль в России: прошлое, настоящее и будущее // Государственная власть и местное самоуправление. — 2006. — № 5.
Тема 12. Понятие валюты и валютных ценностей. Валютные
правоотношения
При рассмотрении темы обратите внимание на правовые основы валютного регулирования и валютного контроля. Перечислите основные источники нормативно-правового регулирования валютных отношений в РФ. Дайте определение валюты в экономическом и юридическом смысле, опишите её отдельные виды.
Дайте определение валютного регулирования как направления валютной политики государства и как процесс установления валютно-правового режима.
Перечислите валютные ограничения и дайте определение «репатриация валюты»
Охарактеризуйте специфику правого положения отдельных участников валютных отношений (резидент, нерезидент).
Перечислите и охарактеризуйте отдельные виды валютных операций и их содержание.
Охарактеризуйте объекты валютных отношений и их соотношение с валютными ценностями.
Дайте определение и охарактеризуйте сущность валютного контроля.
Литература
Борисов А.Н. Комментарий к федеральному закону о валютном регулировании и валютном контроле: постатейный. — М.: Юстицинформ, 2004.
Рачиков Р.С. Становление и развитие института валютных ценностей в России IX-XXI вв.: учебное пособие, Красноярск: Сибирский юридический институт МВД России, 2006.
Сапожников Н.В. Правовой режим валютных операций // Закон. — 2005. — № 4.
Смирникова Ю.Л. Валютно-правовой статус резидентов и нерезидентов // БП. — 2006. — № 5.
Филипенко Е.Д. О полномочиях налоговых органов в сфере валютного контроля // Современное право. — 2007. — № 8.
Тема 13. Состав, структура и современное состояние банковской
системы Российской Федерации
При рассмотрении темы обратите внимание на правовые основы функционирования банковской системы. Дайте описание различных уровней банковской системы. Опишите принципы банковского кредита и основные цели деятельности Банка России.
Дайте развёрнутую характеристику основным функциям Банка России. Охарактеризуйте правовое положение кредитных организаций, их правоспособность и дееспособность.
Опишите порядок государственной регистрации и лицензирования деятельности кредитных организаций. Перечислите основания отзыва лицензии на осуществление банковских операций.
Литература
Бельский К.С. К вопросу о понятии денежной системе РФ // ФП. — 2005. — № 8.
Глушко А.В. Правовая природа центральных банков // ФП. — 2007. — № 4.
Горбунова О.Н., Денисов Е.Р. Некоторые вопросы финансово-правового регулирования денег и денежного оборота в Российской Федерации // ФП. — 2007. — № 8.
^ 4. Методические рекомендации по подготовке эссе
Тема 14. Правовые основы страхования в Российской Федерации
При рассмотрении темы обратите внимание на теоретические основы страхования. Дайте определение договора страхования, охарактеризуйте его отдельные виды. Опишите правовое положение страхователя, страховщика и выгодоприобретателя. Определите существенные условия договора страхования.
Охарактеризуйте специфику и особенности различных видов договоров страхования (страхование имущества, страхование жизни и здоровья, страхование юридической ответственности, страхование внедоговорной ответственности, страхование предпринимательского риска).
Дайте краткую характеристику основных направлений деятельности Федеральной службы страхового надзора.
Литература
Ипатов А.Б. О финансово-правовой природе института страхования // ФП. — 2006. — № 6.
Мамсуров М.Б. К вопросу страхования предпринимательских рисков // Юридический мир. — 2006. — № 1.
Стрельников В.В. Финансово-правовые отношения в сфере страхования // ЖРП. — 2006. — № 2.
Рогозин С.Н. Страхование ответственности: историко-правовой аспект // История государства и права. — 2007. — № 19.
Третьякова Е.Н. Влияние обязательного страхования гражданской ответственности владельцев транспортных средств на состояние аварийности // Административное право и процесс. — 2007.№ 3.
Тема 15.Понятие, значение государственного и муниципального
кредита и его правовые основы
При рассмотрении темы обратите внимание на теоретические основы кредитования. Дайте определение кредитного договора, охарактеризуйте его отдельные виды. Опишите правовое положение кредитора, должника и поручителя. Определите существенные условия кредитования.
Охарактеризуйте специфику и особенности различных видов публичного кредита (государственный, муниципальный).
Опишите основные принципы публичного кредита и особенности их проявления в деятельности государственных и муниципальных органов.
Дайте краткую характеристику основных форм публичного кредита (финансовый, нефинансовый, целевой, бюджетный) и государственных и муниципальных гарантий
Охарактеризуйте цели и методы управления публичным долгом, дайте характеристику отдельным видам государственных и муниципальных ценных бумаг.
Литература
Грачева И.В. Государственные гарантии как способ обеспечения исполнения обязательств: финансово-правовой аспект // Юридический мир. — 2007. — № 1.
Кошлина М. Проблемы правового регулирования предоставления гарантий субъектов Российской Федерации // Государственная власть и местное самоуправление. — 2006. — № 10.
Крохина Ю.А. Государственный кредит и государственный долг: политические причины и правовые последствия // ФП.—2003— № 2.
Тема 16. Понятие, состав и основные признаки налоговых
правонарушений
При рассмотрении темы обратите внимание на теоретические основы юридической ответственности. Дайте определение правонарушения вообще и налогового правонарушения в частности. Укажите отличия между налоговым преступлением и налоговым правонарушением.
Охарактеризуйте специфику и общественную опасность налоговых правонарушений. Опишите отдельные элементы состава налогового правонарушения.
Дайте краткую характеристику отдельных видов налоговых правонарушений с использованием действующих в настоящие время УК РФ, КоАП РФ, НК РФ, БК РФ, постановлений Конституционного Суда РФ, Пленума Верховного суда РФ и Высшего Арбитражного суда РФ.
Опишите специфику деятельности отдельных органов государственной власти по предупреждению налоговых правонарушений.
Охарактеризуйте основные направления взаимодействия отдельных государственных органов (ФНС, МВД, ФССП) по профилактике налоговых правонарушений.
Литература
Архипенко Т.В., Макаров А.В. Соотношение налоговой и административной ответственности // ФП. — 2004 — № 5.
Лущаев С.В. Становление законодательства о юридической ответственности за налоговые правонарушения // История государства и права. — 2006. — № 8.
Макаров А.В. Архипенко Т.В. Характеристика налоговой ответственности. Санкции за нарушение налогового законодательства // ФП. — 2005. — № 6.
Ялбулганов А.А., Кинсбурская В.А. Судебный порядок взыскания налоговой санкции // Закон. — 2007. — № 9.
Тема 17. Система налогов и сборов в Российской Федерации
При рассмотрении темы обратите внимание на теоретические основы системы налогообложения. Дайте определение налогов и сборов
Опишите основные элементы налоговой системы. Охарактеризуйте принципы построения и функционирования налоговой системы (единство налоговой системы, налоговый федерализм, справедливость налогообложения, стабильность налогов и сборов и их определённость эластичность налогообложения). Опишите отдельные функции налога (фискальную, распределительную, регулирующую, контрольную)
Дайте краткую характеристику отдельных элементов налога (ст. 17 НК РФ).
Опишите специфику деятельности отдельных органов государственной власти по предупреждению налоговых правонарушений.
Охарактеризуйте основные направления взаимодействия отдельных государственных органов (ФНС, МВД, ФССП) по профилактике налоговых правонарушений.
Литература
Затулина Т.Н. Конституционно-правовой статус участников налоговых отношений // Современное право. — 2007. — № 4.
Иконникова О.А. Правовое обеспечение государственных реформ в сфере налогообложения взаимозависимых организаций // ЖРП. — 2008. — № 3.
Назаров В.Н. Конституционные основы защиты прав налогоплательщика // ФП. — 2007. — № 9.
Науменко А.М., Хильченко Е.Н. Налоговый сбор: юридические признаки // ФП. — 2007. — № 7.
Орлов М.Ю. Особенности норм налогового права // ФП. — 2007. — № 2
Тема 18. Стадия составления, рассмотрения, утверждения и
исполнения бюджета
При рассмотрении темы обратите внимание на теоретические основы бюджетного процесса. Дайте определение бюджета в материальном, экономическом и юридическом смысле, опишите функции бюджета (распределительная, прогностическая, контрольная).
Охарактеризуйте специфику отдельных видов бюджетов (федеральный, региональный, местный, консолидированный, и др.) Опишите стадии бюджетного процесса и полномочия его участников.
Дайте краткое описание отдельных принципов бюджетного процесса (прозрачность, достоверность, адресность, сбалансированность, единство кассы). Опишите специфику их реализации в деятельности различных ветвей власти.
Охарактеризуйте различные стадии бюджетного процесса (составление бюджета, рассмотрение и его утверждение, исполнение и отчёт). Особое внимание уделите на характеристику деятельности отдельных участников бюджетного процесса в том числе Центрального Банка РФ.
Литература
Евсеев П.И., Ялбулганов А.А. Проблемы правового регулирования полномочий субъектов Российской Федерации в сфере бюджетных отношений // РП. — 2005. — № 2.
Иванова М.С. Правовое регулирование исполнения бюджета в зарубежных странах // Законодательство и экономика. — 2005. — № 1.
Иванова М.С. О реформировании казначейского исполнения бюджетов // Законодательство и экономика. — 2004. — № 6.
Карасева М. В. Согласительные процедуры в федеральном бюджетном законодательстве // ЖРП. — 2003. — № 1.
Клишина М.А. Составление проекта бюджета: проблемы и перспективы // ФП. — 2006. — № 3.
Макух О.В. Правовое регулирование контроля в бюджетном процессе // Юрист. — 2006. — № 7.
Тема 19. Бюджетное право и бюджетные правоотношения
При рассмотрении темы обратите внимание на правовые основы бюд
ronl.org


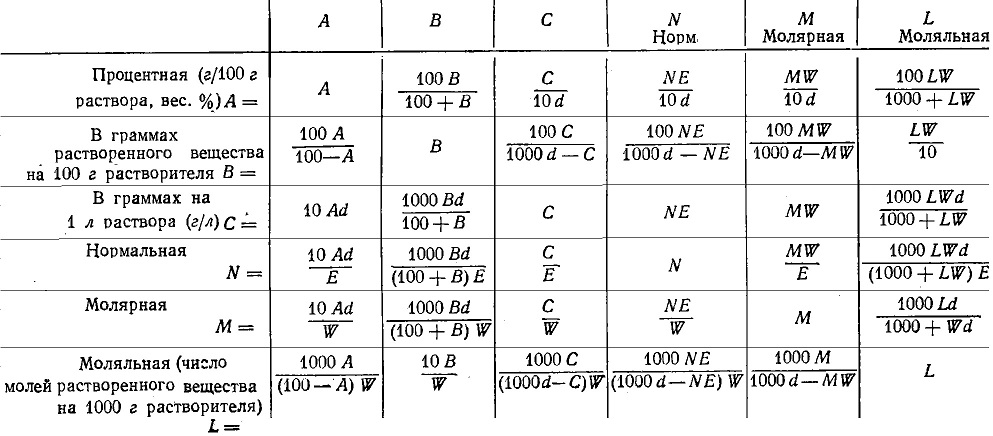
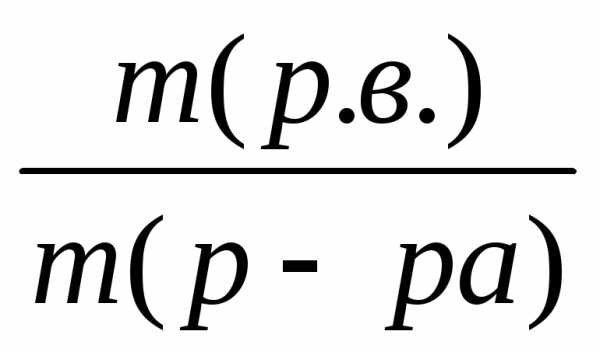 ,
(1)
,
(1)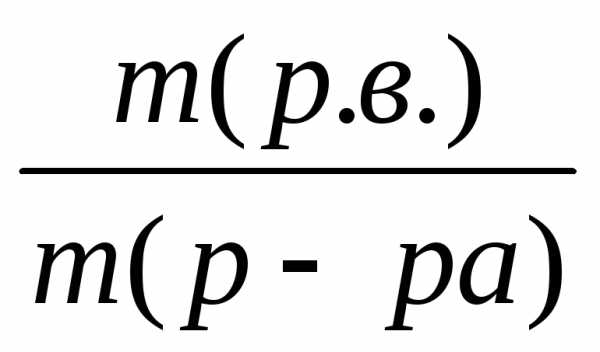 ∙ 100%
(2)
∙ 100%
(2)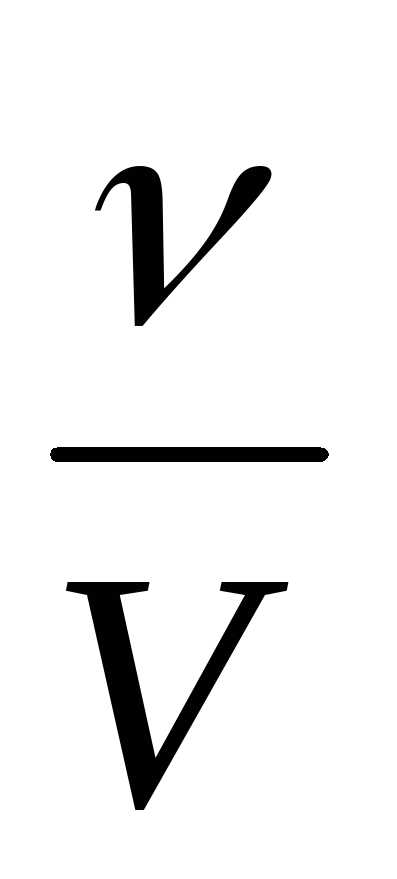 ,
(3)
,
(3)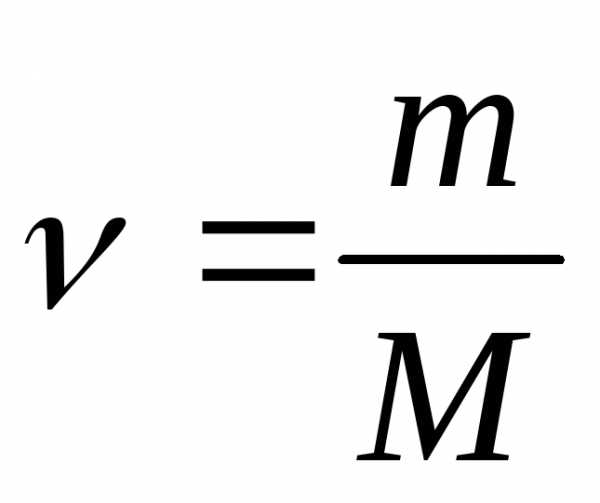 ,
(4)
,
(4)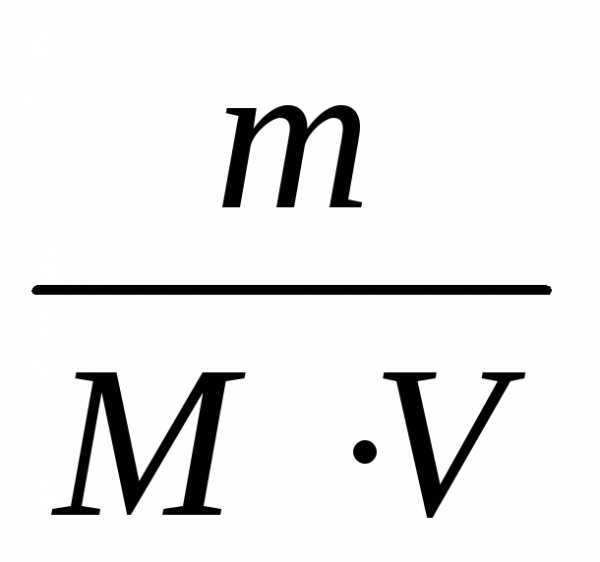 (5)
(5)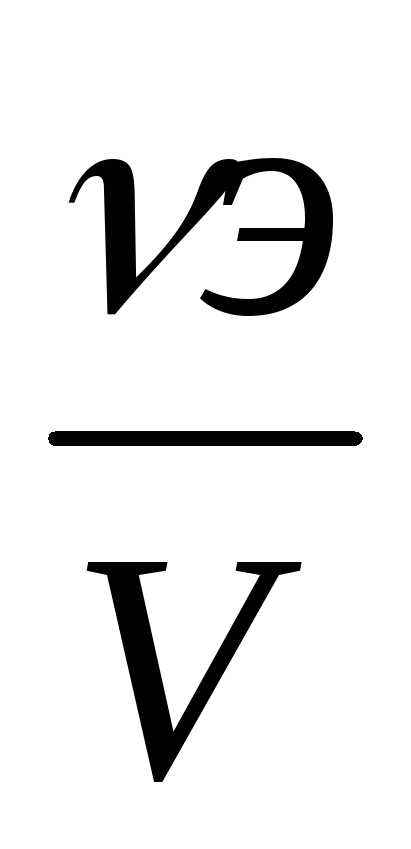 ,
(6)
,
(6)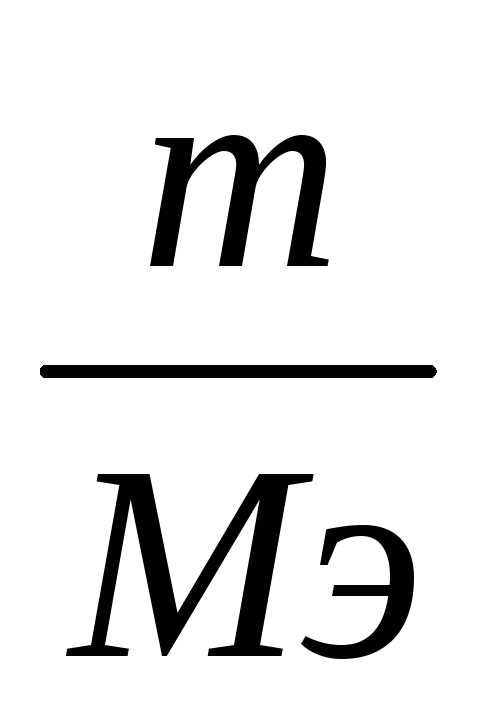 ,
то Сэ =
,
то Сэ =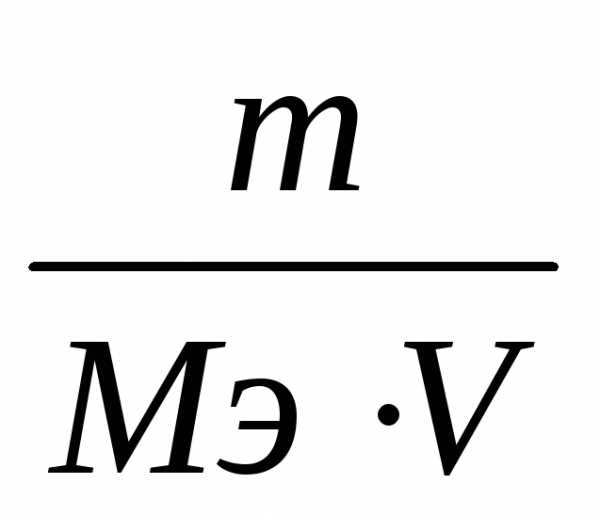 , (7)
, (7) , (8)
, (8) , (9)
, (9) ,
,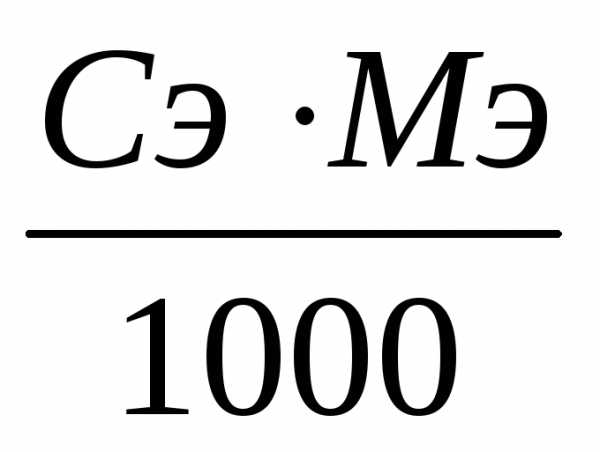 ,
(10)
,
(10) В хроматографических методах исследования используются объемные проценты, то есть вместо граммов содержание вещества указывается в миллилитрах. Молярная концентрация раствора также является распространенным приемом расчета. Ее суть заключается в выражении содержания вещества в молях на 1 л. В аналитической химии часто используется такое понятие, как нормальная концентрация. Она обозначает количество эквивалентов вещества, содержащихся в растворе. Например, если в качестве вещества используется серная кислота (H2SO4), то нормальность в данном случае означает двукратное уменьшение молярной концентрации, так как в одной молекуле содержится два атома водорода. В случае соляной кислоты (HCl), оба способа выражения будут равны.
В хроматографических методах исследования используются объемные проценты, то есть вместо граммов содержание вещества указывается в миллилитрах. Молярная концентрация раствора также является распространенным приемом расчета. Ее суть заключается в выражении содержания вещества в молях на 1 л. В аналитической химии часто используется такое понятие, как нормальная концентрация. Она обозначает количество эквивалентов вещества, содержащихся в растворе. Например, если в качестве вещества используется серная кислота (H2SO4), то нормальность в данном случае означает двукратное уменьшение молярной концентрации, так как в одной молекуле содержится два атома водорода. В случае соляной кислоты (HCl), оба способа выражения будут равны. В данное понятие вкладывается количество вещества, в частности его атомов, молекул, равное таковому, содержащемуся в 12 г углерода, а именно его стабильного изотопа 12С. Количество вещества рассчитывается делением его веса на молекулярную массу, которую можно рассчитать, исходя из атомного состава. В таблице Менделеева по каждому элементу есть показатель его массы, равный 1 молю.
В данное понятие вкладывается количество вещества, в частности его атомов, молекул, равное таковому, содержащемуся в 12 г углерода, а именно его стабильного изотопа 12С. Количество вещества рассчитывается делением его веса на молекулярную массу, которую можно рассчитать, исходя из атомного состава. В таблице Менделеева по каждому элементу есть показатель его массы, равный 1 молю. Другой причиной является применение кислот в реакциях по нейтрализации, которые, например, могут пригодиться в методах титриметрического анализа для определения концентрации щелочи. Здесь также активно используется нормальность. Проще говоря, серной кислоты для нейтрализации гидроксида калия нужно в 2 раза меньше, чем соляной, так как она содержит больше атомов водорода.
Другой причиной является применение кислот в реакциях по нейтрализации, которые, например, могут пригодиться в методах титриметрического анализа для определения концентрации щелочи. Здесь также активно используется нормальность. Проще говоря, серной кислоты для нейтрализации гидроксида калия нужно в 2 раза меньше, чем соляной, так как она содержит больше атомов водорода.
 Метод необходим также при расчете процесса электролиза солей. Последний достаточно активно применяется в практической деятельности. Например, для извлечения руд тяжелых металлов. С использованием данного метода получают фтор, хлор, очищают металлы. Сущность электролиза заключается в том, что при прохождении постоянного тока через раствор электролита с использованием отрицательного и положительного электрода (катода и анода), анионы и катионы движутся к противоположным зарядам и окисляются (или восстанавливаются).
Метод необходим также при расчете процесса электролиза солей. Последний достаточно активно применяется в практической деятельности. Например, для извлечения руд тяжелых металлов. С использованием данного метода получают фтор, хлор, очищают металлы. Сущность электролиза заключается в том, что при прохождении постоянного тока через раствор электролита с использованием отрицательного и положительного электрода (катода и анода), анионы и катионы движутся к противоположным зарядам и окисляются (или восстанавливаются). Взвешивание. Если необходимо приготовить 100 мл смеси, то делается навеска вещества, равная его проценту. При необходимости сделать меньший или больший объем жидкости пересчет осуществляется пропорцией или долями. Например, нужно сделать 50 мл 2% раствора вещества. Для определения количества навески в данном случае достаточно процент разделить на 2 раза, то есть получится 1 г вещества. После взвешивания можно всегда сделать перерасчет на молярную концентрацию.
Взвешивание. Если необходимо приготовить 100 мл смеси, то делается навеска вещества, равная его проценту. При необходимости сделать меньший или больший объем жидкости пересчет осуществляется пропорцией или долями. Например, нужно сделать 50 мл 2% раствора вещества. Для определения количества навески в данном случае достаточно процент разделить на 2 раза, то есть получится 1 г вещества. После взвешивания можно всегда сделать перерасчет на молярную концентрацию. Вещества с равными молярными концентрациями содержат одинаковое количество молекул. Именно эта концентрация позволяет четко определить нужный объем вещества для реакции. Массовая доля является скорее вспомогательной, упрощая некоторые процессы. Ее часто применяют микробиологи для получения определенного соотношения бактериальной биомассы со средой. Связано это с тем, что данные ученые исследуют высокомолекулярные соединения, и им удобнее выражать соотношение веществ в массе. Для химиков и физиков молярная концентрация растворов является основной. Числовые характеристики содержания вещества необходимы практически во всех естественных науках.
Вещества с равными молярными концентрациями содержат одинаковое количество молекул. Именно эта концентрация позволяет четко определить нужный объем вещества для реакции. Массовая доля является скорее вспомогательной, упрощая некоторые процессы. Ее часто применяют микробиологи для получения определенного соотношения бактериальной биомассы со средой. Связано это с тем, что данные ученые исследуют высокомолекулярные соединения, и им удобнее выражать соотношение веществ в массе. Для химиков и физиков молярная концентрация растворов является основной. Числовые характеристики содержания вещества необходимы практически во всех естественных науках.

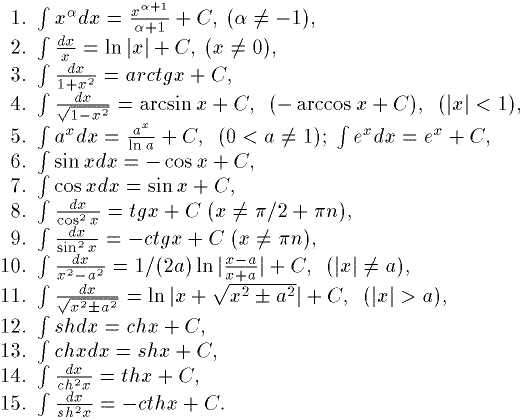 Теперь нужно запомнить самые основные свойства интегралов, приведенные ниже.
Теперь нужно запомнить самые основные свойства интегралов, приведенные ниже. 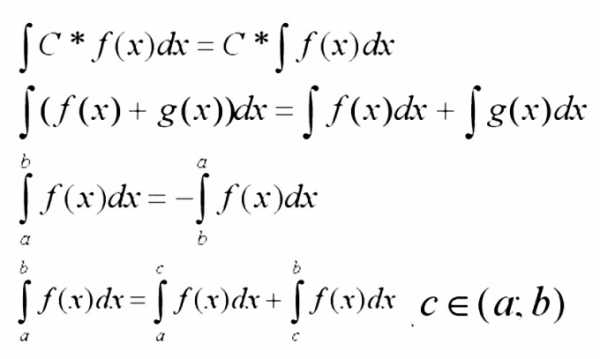 Интеграл от суммы функций лучше всего раскладывать на сумму интегралов. Это правило чаще всего применяется, когда слагаемые функции достаточно простые, если их можно найти при помощи таблицы интегралов.
Интеграл от суммы функций лучше всего раскладывать на сумму интегралов. Это правило чаще всего применяется, когда слагаемые функции достаточно простые, если их можно найти при помощи таблицы интегралов.

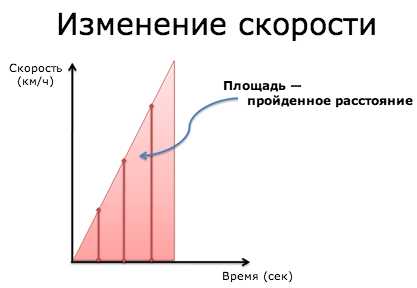
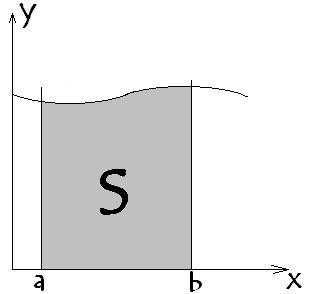
 Итак
ограниченная фигура прямоугольник.
Площадь прямоугольника равна произведению
длины на ширину. В наше случае длина 3,
ширина 1, площадь 3*1=3.
Попробуем решить
тоже самое не прибегая к построению,
используя интегрирование:Как
видите ответ получился тот же. Решение
интегралов – это собирание во едино
каких-либо элементарных частей. В случае
с площадью суммируются полоски бесконечно
малой ширины. Интегралы могут быть
определенными и неопределенными.
Решить
определенный интеграл значит найти
значение функции в заданных границах.
Решение неопределенного интеграла
сводиться к нахождению первообразной.F(x)
– первообразная. Дифференцируя
первообразую, мы получим исходное
подинтегральное выражение. Чтобы
проверить правильно ли мы решили
интеграл, мы дифференциируем полученный
ответ и сравниваем с исходным
выражением.
Основные функции и
первообразные для них приведены в
таблице:
Итак
ограниченная фигура прямоугольник.
Площадь прямоугольника равна произведению
длины на ширину. В наше случае длина 3,
ширина 1, площадь 3*1=3.
Попробуем решить
тоже самое не прибегая к построению,
используя интегрирование:Как
видите ответ получился тот же. Решение
интегралов – это собирание во едино
каких-либо элементарных частей. В случае
с площадью суммируются полоски бесконечно
малой ширины. Интегралы могут быть
определенными и неопределенными.
Решить
определенный интеграл значит найти
значение функции в заданных границах.
Решение неопределенного интеграла
сводиться к нахождению первообразной.F(x)
– первообразная. Дифференцируя
первообразую, мы получим исходное
подинтегральное выражение. Чтобы
проверить правильно ли мы решили
интеграл, мы дифференциируем полученный
ответ и сравниваем с исходным
выражением.
Основные функции и
первообразные для них приведены в
таблице: Основные
приемы решения интегралов:
Решить
интеграл, значит проинтегрировать
функцию по переменной. Если интеграл
имеет табличный вид, то можно сказать,
что вопрос, как решить интеграл, решен.
Если же нет, то основной задачей при
решении интеграла становиться сведение
его к табличному виду.
Сначала следует
запомнить основные свойства интегралов:
Основные
приемы решения интегралов:
Решить
интеграл, значит проинтегрировать
функцию по переменной. Если интеграл
имеет табличный вид, то можно сказать,
что вопрос, как решить интеграл, решен.
Если же нет, то основной задачей при
решении интеграла становиться сведение
его к табличному виду.
Сначала следует
запомнить основные свойства интегралов: 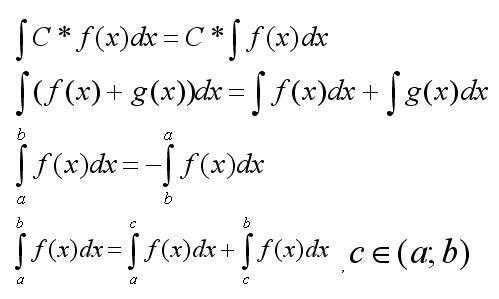
 Для
выполнения данного приема потребуется
хороший навык нахождения производных.
Для
выполнения данного приема потребуется
хороший навык нахождения производных.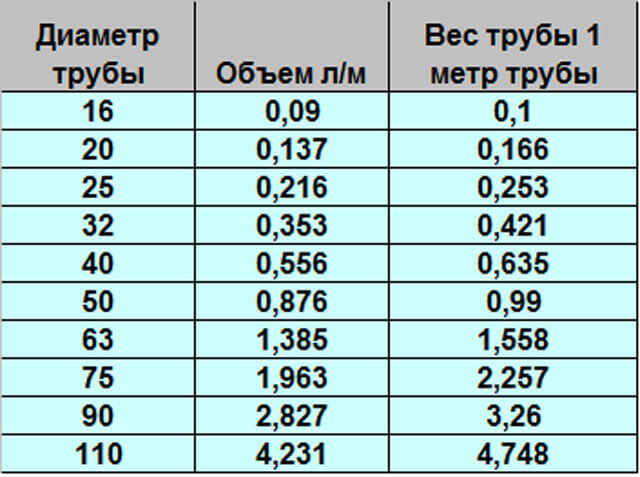

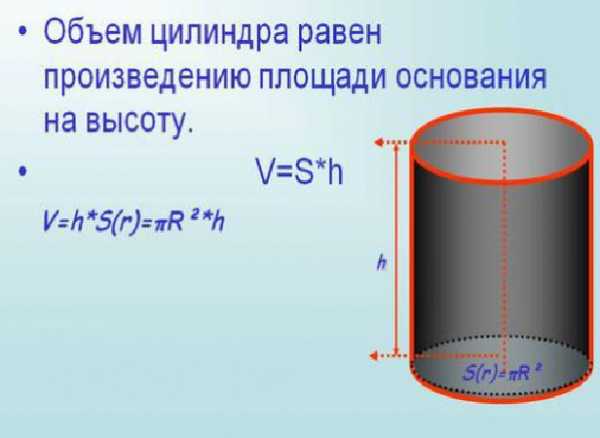


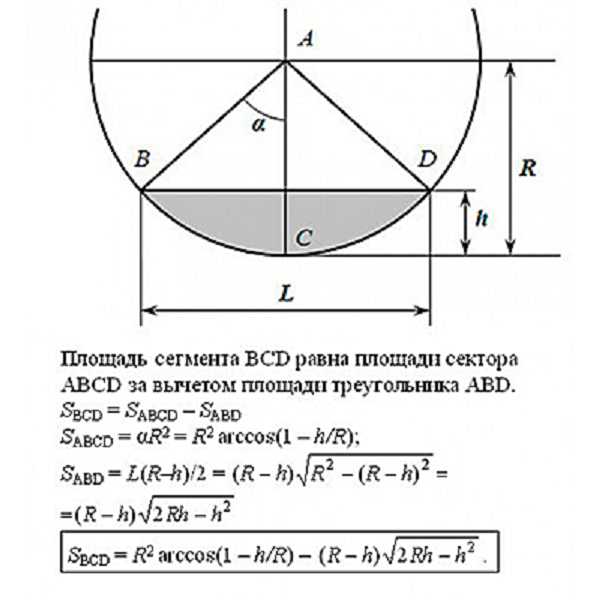
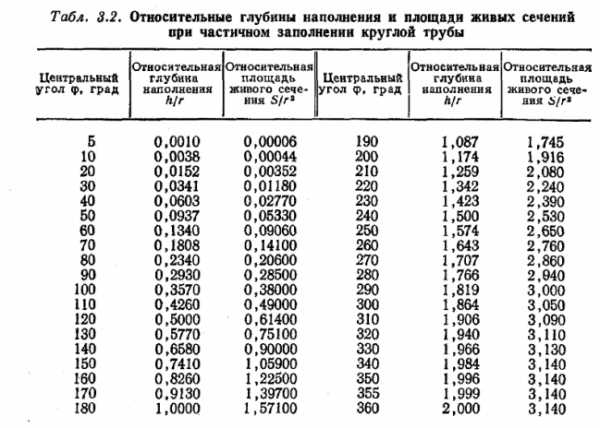

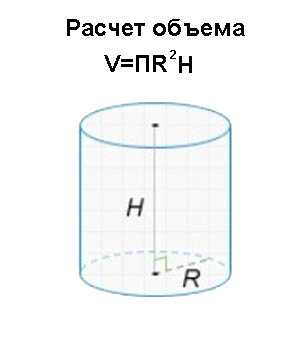



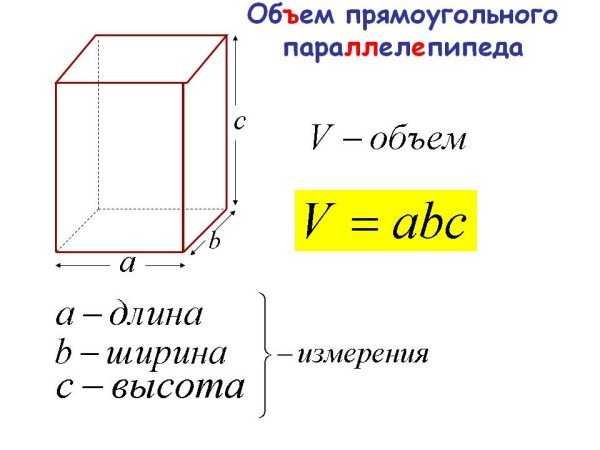

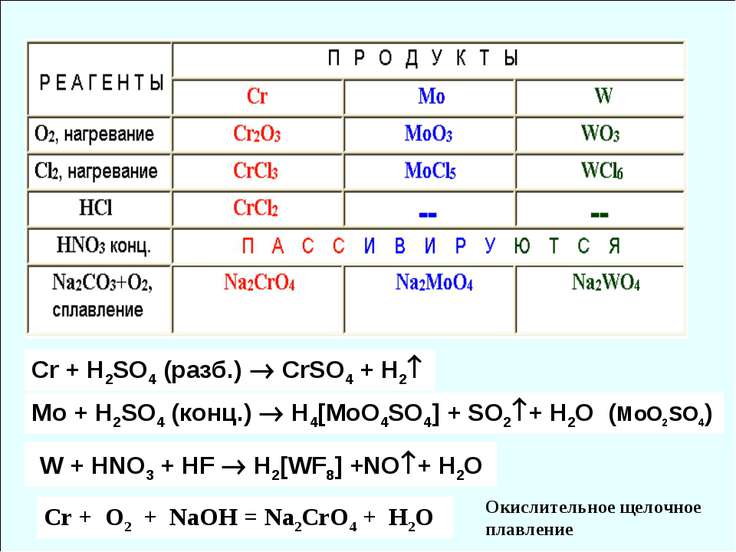













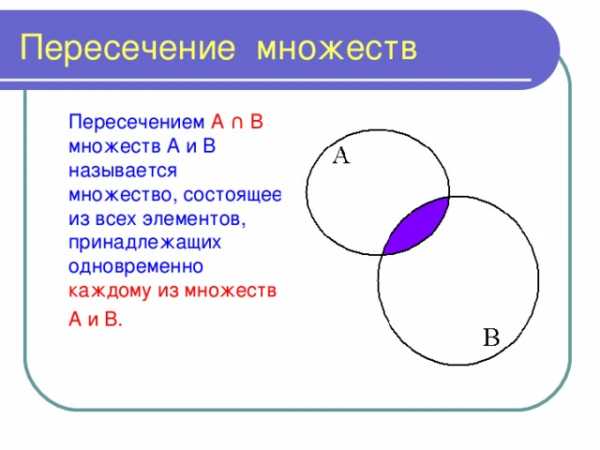
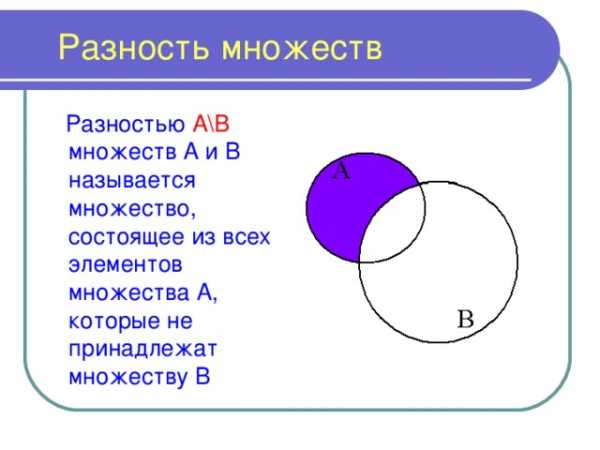

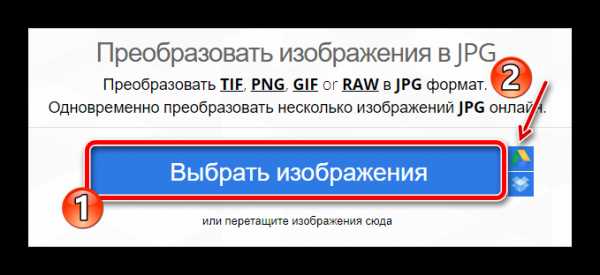

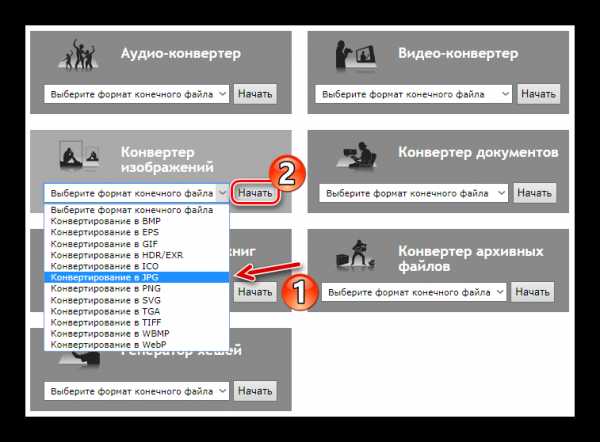


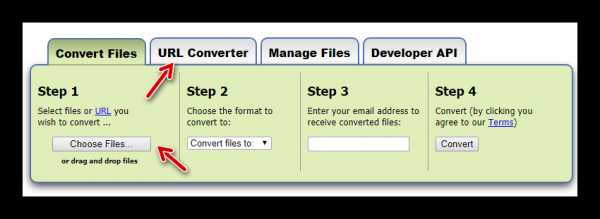
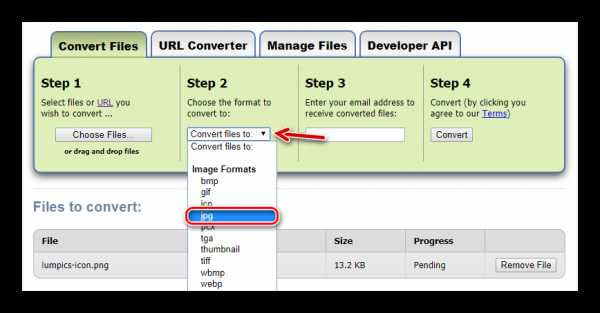
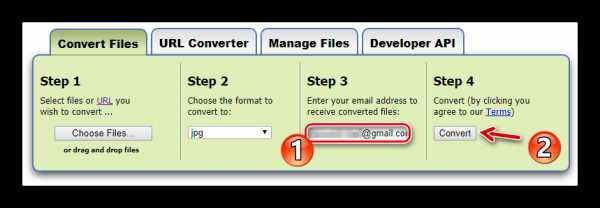
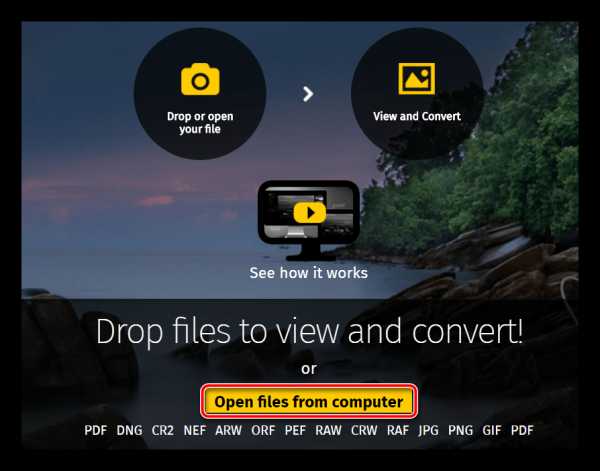
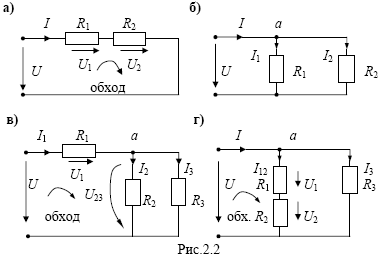

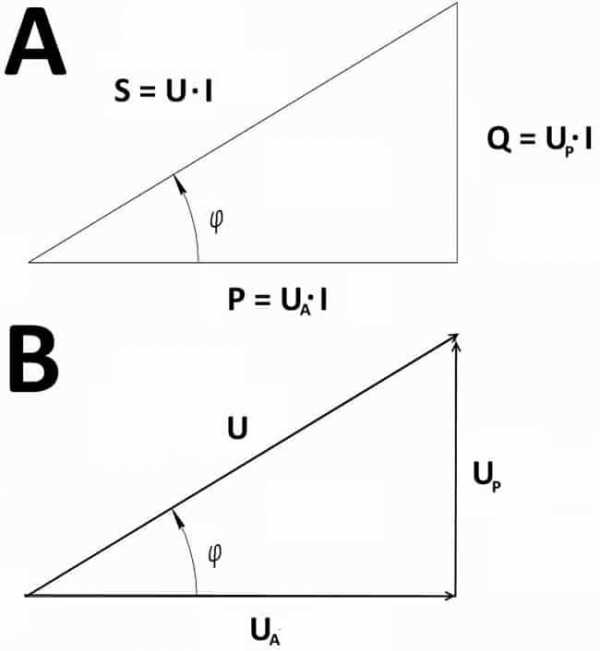 Треугольники мощности и напряжения
Треугольники мощности и напряжения Лабораторный ваттметр
Лабораторный ваттметр Щитовой ваттметр
Щитовой ваттметр Лабораторный фазометр
Лабораторный фазометр Щитовой фазометр
Щитовой фазометр