Отображение чисел в качестве дробей
Excel для Microsoft 365 Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Еще…Меньше
Используйте формат «Дроб», чтобы отображать или ввести числа как фактические дроби, а не в десятичных числах.
-
Выделите ячейки, которые нужно отформатировать.
-
На вкладке Главная нажмите кнопку вызова диалогового окна рядом с именем группы Число.
-
В списке Категория выберите

-
В списке Тип выберите нужный тип формата дроби.
|
Формат дроби |
В этом формате 123,456 отображается как |
|
Дробная часть с одной цифрой |
123 1/2, округление до ближайшего однозначного значения дроби |
|
Двузначная дробь |
123 26/57, округлизация до ближайшего двузначного значения дроби |
|
Трижды значок дроби |
123 57/125, округлизация до ближайшего трехзначного значения дроби |
|
Дробный в качестве дробей |
123 1/2 |
|
Дробный по кварталам |
123 2/4 |
|
Дробный в качестве частиц |
123 4/8 |
|
Дробные части в качестве шестнадцатых |
123 7/16 |
|
Дробный в качестве десятых |
123 5/10 |
|
Дробные части в качестве сотых |
123 46/100 |
Число в активной ячейке выбранного на этом сайте отображается в поле Образец, чтобы можно было просмотреть выбранные параметры форматирования.
-
После применения формата дроби к ячейке дробные числа, а также фактические дроби, которые вы в нее введите, будут отображаться как дроби. Например, если ввести 0,5 или 1/2, то при формате ячейки с типом дроби до одной цифры будет 1/2.
-
Если к ячейке не применен формат дроби и вы введите дробную часть, например
-
Если вам не нужно выполнять вычисления с дробями, перед тем как ввести в нее дробную часть, можно отформать ячейку как текст, щелкнув Текст в списке Категория.
 В этом случае дробные части не будут уменьшаться или преобразовываться в десятичных. Однако математические вычисления с дробями, которые отображаются как текст, выполнять нельзя.
В этом случае дробные части не будут уменьшаться или преобразовываться в десятичных. Однако математические вычисления с дробями, которые отображаются как текст, выполнять нельзя. -
Чтобы сбросить числовом формате, в диалоговом окне Категория(диалоговое окно Формат ячеек) или Числовом формате(вкладка
Главная, группа Число) нажмите кнопку Общий. В ячейках с форматом Общий форматирование к числам не применяется.
Десятичные дроби
Мы уже говорили, что дроби бывают обыкновенные и десятичные. На данный момент мы немного изучили обыкновенные дроби. Мы узнали, что обыкновенные дроби бывают правильные и неправильные. Также мы узнали, что обыкновенные дроби можно сокращать, складывать, вычитать умножать и делить. И ещё мы узнали, что бывают так называемые смешанные числа, которые состоят из целой и дробной части.
Мы ещё не до конца изучили обыкновенные дроби. Есть немало тонкостей и деталей, о которых следует поговорить, но уже сегодня мы начнём изучать десятичные дроби, поскольку обыкновенные и десятичные дроби достаточно часто приходится сочетать. То есть при решении задач приходиться работать с обоими видов дробей.
Этот урок возможно покажется сложным и непонятным. Это вполне нормально. Такого рода уроки требуют, чтобы их именно изучали, а не просматривали поверхностно.
Выражение величин в дробном виде
Иногда удобно бывает показать что-либо в дробном виде. Например, одна десятая часть дециметра записывается так:
Это выражение означает, что один дециметр был разделён на десять равных частей, и от этих десяти частей была взята одна часть. А одна часть из десяти в данном случае равна одному сантиметру:
Рассмотрим следующий пример. Пусть требуется показать 6 см и ещё 3 мм в сантиметрах в дробном виде.
Итак, 6 целых сантиметров у нас уже есть:
Но осталось еще 3 миллиметра. Как показать эти 3 миллиметра, при этом в сантиметрах? На помощь приходят дроби. Один сантиметр это десять миллиметров. Три миллиметра это три части из десяти. А три части из десяти записываются как см
Как показать эти 3 миллиметра, при этом в сантиметрах? На помощь приходят дроби. Один сантиметр это десять миллиметров. Три миллиметра это три части из десяти. А три части из десяти записываются как см
Выражение см означает, что один сантиметр был разделён на десять равных частей, и от этих десяти частей взяли три части.
В результате имеем шесть целых сантиметров и три десятых сантиметра:
Цифра 6 показывает число целых сантиметров, а дробь — число дробных. Эта дробь читается как «шесть целых и три десятых сантиметра».
Дроби, в знаменателе которых присутствуют числа 10, 100, 1000 можно записывать без знаменателя. Сначала пишут цéлую часть, а потом числитель дробной части. Целая часть отделяется от числителя дробной части запятой.
Например, запишем без знаменателя. Сначала записываем целую часть. Целая часть это 6
6
Целая часть записана. Сразу же после написания целой части ставим запятую:
6,
И теперь записываем числитель дробной части. В смешанном числе числитель дробной части это число 3. Записываем после запятой тройку:
В смешанном числе числитель дробной части это число 3. Записываем после запятой тройку:
6,3
Любое число, которое представляется в таком виде, называется десятичной дробью.
Поэтому показать 6 см и ещё 3 мм в сантиметрах можно с помощью десятичной дроби:
6,3 см
Выглядеть это будет следующим образом:
На самом деле десятичные дроби это те же самые обыкновенные дроби и смешанные числа. Особенность таких дробей заключается в том, что в знаменателе их дробной части содержатся числа 10, 100, 1000 или 10000.
Как и смешанное число, десятичная дробь имеет цéлую часть и дробную. Например, в смешанном числе целая часть это 6, а дробная часть это .
В десятичной дроби 6,3 целая часть это число 6, а дробная часть это числитель дроби , то есть число 3.
Бывает и так, что обыкновенные дроби в знаменателе которых числа 10, 100, 1000 даны без целой части. Например, дробь дана без целой части. Чтобы записать такую дробь как десятичную, сначала записывают 0, затем ставят запятую и записывают числитель дробной части. Дробь без знаменателя будет записана следующим образом:
Дробь без знаменателя будет записана следующим образом:
0,5
Читается как «ноль целых, пять десятых».
Перевод смешанных чисел в десятичные дроби
Когда мы записываем смешанные числа без знаменателя, мы тем самым перевóдим их в десятичные дроби. При переводе обыкновенных дробей в десятичные дроби нужно знать несколько моментов, о которых мы сейчас поговорим.
После того как записана целая часть, обязательно нужно посчитать количество нулей в знаменателе дробной части, поскольку количество нулей дробной части и количество цифр после запятой в десятичной дроби должно быть одинаковым. Что это значит? Рассмотрим следующий пример: перевести смешанное число в десятичную дробь.
Сначала записываем целую часть и ставим запятую:
3,
И можно бы сразу записать числитель дробной части и десятичная дробь готова, но обязательно нужно посчитать сколько нулей содержится в знаменателе дробной части.
Итак, посчитаем количество нулей в дробной части смешанного числа . Видим, что в знаменателе дробной части один ноль. Значит в десятичной дроби после запятой будет одна цифра и это цифра будет числитель дробной части смешанного числа , то есть число 2
Видим, что в знаменателе дробной части один ноль. Значит в десятичной дроби после запятой будет одна цифра и это цифра будет числитель дробной части смешанного числа , то есть число 2
3,2
Таким образом, смешанное число при переводе в десятичную дробь обращается в 3,2. Эта десятичная дробь читается так:
«Три целых, две десятых»
«Десятых» потому что в дробной части смешанного числа содержится число 10.
Пример 2. Перевести смешанное число в десятичную дробь.
Записываем цéлую часть и ставим запятую:
5,
И можно бы сразу записать числитель дробной части и получить десятичную дробь 5,3 но правило говорит, что после запятой должно быть столько цифр сколько нулей в знаменателе дробной части смешанного числа . А мы видим, что в знаменателе дробной части два нуля. Значит в нашей десятичной дроби после запятой должно быть две цифры, а не одна.
В таких случаях числитель дробной части нужно немного видоизменить: добавить ноль перед числителем, то есть перед числом 3
Теперь можно довести дело до конца. Записываем после запятой числитель дробной части:
Записываем после запятой числитель дробной части:
5,03
Видим, что количество цифр после запятой и количество нулей в знаменателе дробной части смешанного числа одинаково.
Десятичная дробь 5,03 читается так:
«Пять целых, три сотых»
«Сотых» потому что в знаменателе дробной части смешанного числа содержится число 100.
Пример 3. Перевести смешанное число в десятичную дробь.
Из предыдущих примеров мы узнали, что для успешного перевода смешанного числа в десятичную дробь, количество цифр в числителе дробной части и количество нулей в знаменателе дробной части должно быть одинаковым.
Перед переводом смешанного числа в десятичную дробь, его дробную часть нужно немного видоизменить, а именно сделать так, чтобы количество цифр в числителе дробной части и количество нулей в знаменателе дробной части было одинаковым.
В первую очередь смóтрим на количество нулей в знаменателе дробной части. Видим, что там три нуля:
Наша задача организовать в числителе дробной части три цифры. Одна цифра у нас уже есть — это цифра 2. Осталось добавить ещё две цифры. Ими будут два нуля. Добавим их перед цифрой 2. В результате количество нулей в знаменателе и количество цифр в числителе станет одинаковым:
Одна цифра у нас уже есть — это цифра 2. Осталось добавить ещё две цифры. Ими будут два нуля. Добавим их перед цифрой 2. В результате количество нулей в знаменателе и количество цифр в числителе станет одинаковым:
Теперь можно заняться переводом этого смешанного числа в десятичную дробь. Записываем сначала цéлую часть и ставим запятую:
3,
и сразу записываем числитель дробной части
3,002
Видим, что количество цифр после запятой и количество нулей в знаменателе дробной части смешанного числа одинаково.
Десятичная дробь 3,002 читается так:
«Три целых, две тысячных»
«Тысячных» потому что в знаменателе дробной части смешанного числа содержится число 1000.
Перевод обыкновенных дробей в десятичные дроби
Обыкновенные дроби, у которых в знаменателе числа 10, 100, 1000 или 10000, тоже можно перевести в десятичные дроби. Поскольку у обыкновенной дроби целая часть отсутствует, сначала записывают 0, затем ставят запятую и записывают числитель дробной части.
Здесь также количество нулей в знаменателе и количество цифр в числителе должно быть одинаковым. Поэтому следует быть внимательным.
Пример 1. Перевести обыкновенную дробь в десятичную дробь.
Целая часть отсутствует, значит сначала записываем 0 и ставим запятую:
0,
Теперь смóтрим на количество нулей в знаменателе. Видим, что там один ноль. И в числителе одна цифра. Значит можно спокойно продолжить десятичную дробь, записав после запятой цифру 5
0,5
В полученной десятичной дроби 0,5 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.
Десятичная дробь 0,5 читается так:
«Ноль целых, пять десятых»
Пример 2. Перевести обыкновенную дробь в десятичную дробь.
Целая часть отсутствует. Записываем сначала 0 и стáвим запятую:
0,
Теперь смóтрим на количество нулей в знаменателе. Видим, что там два нуля. А в числителе только одна цифра. Чтобы сделать количество цифр и количество нулей одинаковым, добавим в числителе перед цифрой 2 один ноль. Тогда дробь примет вид . Теперь количество нулей в знаменателе и количество цифр в числителе одинаково. Значит можно продолжить десятичную дробь:
Чтобы сделать количество цифр и количество нулей одинаковым, добавим в числителе перед цифрой 2 один ноль. Тогда дробь примет вид . Теперь количество нулей в знаменателе и количество цифр в числителе одинаково. Значит можно продолжить десятичную дробь:
0,02
В полученной десятичной дроби 0,02 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.
Десятичная дробь 0,02 читается так:
«Ноль целых, две сотых».
Пример 3. Перевести обыкновенную дробь в десятичную дробь.
Записываем 0 и стáвим запятую:
0,
Теперь посчитаем количество нулей в знаменателе дроби . Видим, что там пять нулей, а в числителе только одна цифра. Чтобы сделать количество нулей в знаменателе и количество цифр в числителе одинаковым, нужно в числителе перед цифрой 5 дописать четыре нуля:
Теперь можно продолжить десятичную дробь. Записываем после запятой числитель дроби
0,00005
В полученной десятичной дроби 0,00005 количество цифр после запятой и количество нулей в знаменателе дроби одинаково.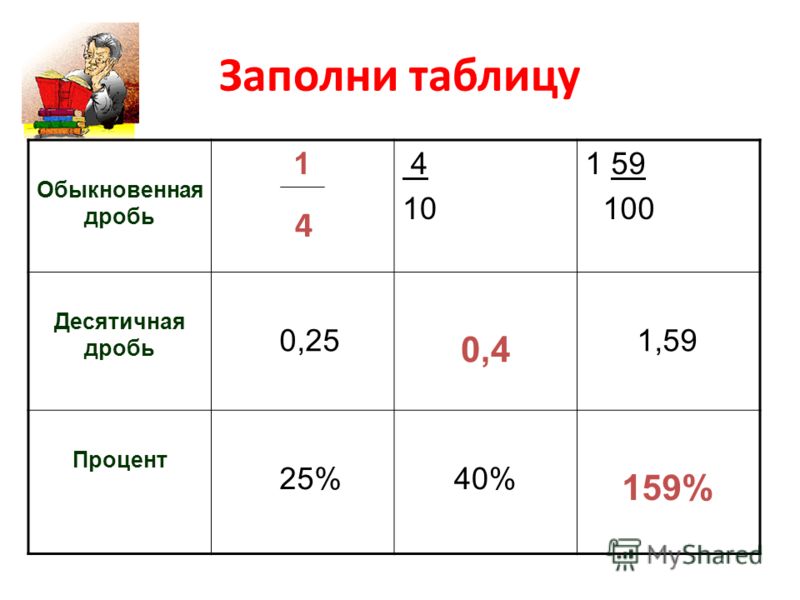 Значит дробь переведена правильно.
Значит дробь переведена правильно.
Десятичная дробь 0,00005 читается так:
«Ноль целых, пять стотысячных».
Перевод неправильных дробей в десятичную дробь
Неправильная дробь это дробь, у которой числитель больше знаменателя.
Бывают неправильные дроби, у которых в знаменателе содержатся числа 10, 100, 1000 или 10000. Такие дроби можно переводить в десятичные. Но перед переводом в десятичную дробь, у таких дробей необходимо выделять цéлую часть.
Пример 1. Перевести неправильную дробь в десятичную.
Дробь является неправильной. Чтобы перевести такую дробь в десятичную, нужно в первую очередь выделить у нее цéлую часть. Вспоминаем, как выделять целую часть у неправильных дробей. Если забыли, советуем вернуться к этой теме и хорошенько изучить её.
Итак, выделим целую часть в неправильной дроби . Напомним, что дробь означает деление — в данном случае деление числа 112 на число 10. Деление нужно выполнить с остатком:
Посмóтрим на этот рисунок и соберём новое смешанное число, подобно детскому конструктору. Частное 11 будет целой частью, остаток 2 — числителем дробной части, делитель 10 — знаменателем дробной части:
Частное 11 будет целой частью, остаток 2 — числителем дробной части, делитель 10 — знаменателем дробной части:
Мы получили смешанное число . Его и переведём в десятичную дробь. А как переводить такие числа в десятичные дроби мы уже знаем. Сначала записываем целую часть и ставим запятую:
11,
Теперь посчитаем количество нулей в знаменателе дробной части. Видим, что там один ноль. И в числителе дробной части одна цифра. Значит количество нулей в знаменателе дробной части и количество цифр в числителе дробной части одинаково. Это даёт нам возможность сразу записать после запятой числитель дробной части:
11,2
Значит, неправильная дробь при переводе в десятичную обращается в 11,2
Десятичная дробь 11,2 читается так:
«Одиннадцать целых, две десятых».
Пример 2. Перевести неправильную дробь в десятичную дробь.
Это неправильная дробь, поскольку числитель больше знаменателя. Но её можно перевести в десятичную дробь, поскольку в знаменателе содержится число 100.
В первую очередь выделим целую часть этой дроби. Для этого разделим уголком 450 на 100:
Соберём новое смешанное число — получим . Теперь переведём его в десятичную дробь. Записываем целую часть и ставим запятую:
4,
Теперь посчитаем количество нулей в знаменателе дробной части и количество цифр в числителе дробной части. Видим, что количество нулей в знаменателе и количество цифр в числителе одинаково. Это даёт нам возможность сразу записать числитель дробной части после запятой:
4,50
Значит неправильная дробь при переводе в десятичную обращается в 4,50
При решении задач, если в конце десятичной дроби оказываются нули, их можно отбросить. Давайте и мы отбросим ноль в нашем ответе. Тогда мы получим 4,5
Это одна из интересных особенностей десятичных дробей. Она заключается в том, что нули которые стоят в конце дроби, не придают этой дроби никакого веса. Другими словами, десятичные дроби 4,50 и 4,5 равны и между ними можно поставить знак равенства:
4,50 = 4,5
Возникает вопрос «а почему так происходит?» Ведь на вид 4,50 и 4,5 разные дроби. Весь секрет кроется в основном свойстве дроби, котором мы изучали ранее. Мы попробуем доказать, почему равны десятичные дроби 4,50 и 4,5, но после изучения следующей темы, которая называется «перевод десятичной дроби в смешанное число».
Весь секрет кроется в основном свойстве дроби, котором мы изучали ранее. Мы попробуем доказать, почему равны десятичные дроби 4,50 и 4,5, но после изучения следующей темы, которая называется «перевод десятичной дроби в смешанное число».
Перевод десятичной дроби в смешанное число
Любая десятичная дробь может быть обратно переведена в смешанное число. Для этого достаточно уметь читать десятичные дроби.
Например, переведём 6,3 в смешанное число. 6,3 это шесть целых и три десятых. Записываем сначала шесть целых:
6
и рядом три десятых:
Пример 2. Перевести десятичную дробь 3,002 в смешанное число
3,002 это три целых и две тысячных. Записываем сначала три целых
3
и рядом записываем две тысячных:
3
Пример 3. Перевести десятичную дробь 4,50 в смешанное число
4,50 это четыре целых и пятьдесят сотых. Записываем четыре целых
4
и рядом пятьдесят сотых:
Кстати, давайте вспомним последний пример из предыдущей темы. Мы сказали, что десятичные дроби 4,50 и 4,5 равны. Также мы сказали, что ноль можно отбросить. Докажем, что десятичные 4,50 и 4,5 равны. Для этого переведем обе десятичные дроби в смешанные числа.
Мы сказали, что десятичные дроби 4,50 и 4,5 равны. Также мы сказали, что ноль можно отбросить. Докажем, что десятичные 4,50 и 4,5 равны. Для этого переведем обе десятичные дроби в смешанные числа.
После перевода в смешанное число десятичная дробь 4,50 обращается в , а десятичная дробь 4,5 обращается в
Имеем два смешанных числа и . Переведём эти смешанные числа в неправильные дроби:
Теперь имеем две дроби и . Теперь вспоминаем основное свойство дроби, которое говорит о том, что при умножении (или делении) числителя и знаменателя дроби на одно и то же число, значение дроби не меняется.
Давайте разделим числитель и знаменатель первой дроби на число 10
Получили , а это есть вторая дробь. Значит и равны между собой и равны одному и тому же значению:
=
Попробуйте на калькуляторе разделить сначала 450 на 100, а затем 45 на 10. Забавная штука получится.
Перевод десятичной дроби в обыкновенную дробь
Любая десятичная дробь может быть обратно переведена в обыкновенную дробь. Для этого опять же достаточно уметь читать десятичные дроби. Например, переведём 0,3 в обыкновенную дробь. 0,3 это ноль целых и три десятых. Записываем сначала ноль целых:
Для этого опять же достаточно уметь читать десятичные дроби. Например, переведём 0,3 в обыкновенную дробь. 0,3 это ноль целых и три десятых. Записываем сначала ноль целых:
0
и рядом три десятых 0 . Ноль по традиции не записывают, поэтому окончательный ответ будет не 0, а просто .
Пример 2. Перевести десятичную дробь 0,02 в обыкновенную дробь.
0,02 это ноль целых и две сотых. Ноль не записываем, поэтому сразу записываем две сотых
Пример 3. Перевести 0,00005 в обыкновенную дробь
0,00005 это ноль целых и пять сто тысячных. Ноль не записываем, поэтому сразу записываем пять сто тысячных
Пример 4. Перевести 3,5 в обыкновенную дробь
Сначала переведём данную десятичную дробь в смешанное число:
Теперь смешанное число переведём в неправильную (обыкновенную) дробь:
Пример 5. Перевести 1,25 в обыкновенную дробь
Сначала переведём данную десятичную дробь в смешанное число:
Теперь смешанное число переведём в неправильную (обыкновенную) дробь:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Охотничья Дробь 4 Буквы — ответ на кроссворд и сканворд
Решение этого кроссворда состоит из 4 букв длиной и начинается с буквы Ш Ниже вы найдете правильный ответ на Охотничья дробь 4 буквы, если вам нужна дополнительная помощь в завершении кроссворда, продолжайте навигацию и воспользуйтесь нашей функцией поиска.
ответ на кроссворд и сканворд
Среда, 26 Июня 2019 Г.
ШРОТ
предыдущий следующий
ты знаешь ответ ?
ответ:
связанные кроссворды
- Шрот
- Измельченные семена масличных растений после извлечения жира, хороший корм
- Отход производства растительного масла
- Шрот
- Отход производства растительного масла 4 буквы
- Отход 4 буквы
- Побочный продукт обработки масличных растений 4 буквы
- Побочный продукт 4 буквы
похожие кроссворды
- Крупная охотничья дробь 7 букв
- Мелкая дробь, которая употребляется при стрельбе мелких птиц
- Самая мелкая дробь
- Крупная дробь для охотничьего ружья 7 букв
- Сам пустой, голос густой, дробь отбивает, ребят созывает (загадка) 7 букв
- Пуля (или дробь) с зарядом и капсюлем, заключенные в гильзе 6 букв
- Пуля или дробь с зарядом и капсулем, заключенные в гильзе 6 букв
- Пуля или дробь с пороховым зарядом и капсюль с воспламенителем 6 букв
- Ружейная дробь самого мелкого калибра 5 букв
- Самая мелкая дробь 5 букв
- Чугунная или свинцовая пуля; крупная дробь для охотничьих ружей 9 букв
- Колокольная «дробь» 5 букв
- Крупная ружейная дробь
- «пищевая дробь» 5 букв
- Дробь, но не в патроне 5 букв
- Дробь на карте 7 букв
- Крупная дробь для охотничьего ружья
- Чугунная или свинцовая пуля; крупная дробь для охотничьих ружей
Дроби — как объяснить ребенку действия с дробями
Тема дробей — одна из самых непростых для школьников. Понять их неподготовленному ребенку, а тем более выполнять с ними операции, может быть достаточно сложно. Но даже самая трудная задача может стать простой и понятной, если правильно к ней подойти. Для детей нужно использовать фантазию, наглядность и элементы игры. А также – сохранять спокойствие и терпеливо объяснять, даже если это потребуется сделать много раз.
Понять их неподготовленному ребенку, а тем более выполнять с ними операции, может быть достаточно сложно. Но даже самая трудная задача может стать простой и понятной, если правильно к ней подойти. Для детей нужно использовать фантазию, наглядность и элементы игры. А также – сохранять спокойствие и терпеливо объяснять, даже если это потребуется сделать много раз.
Как объяснить суть дробей ребенку?
Слово «дробь» будто говорит само за себя — оно означает дробление, деление. В школьной программе к изучению дробей приступают только в 5 классе, освоив все действия с целыми числами. Но знакомство с ними целесообразно начинать заранее, еще в старшем дошкольном возрасте. Это формирует пространственные представления у детей и тренирует логическое мышление.
Для начала нужно объяснить ребенку понятие долей. Это очень легко сделать на наглядных повседневных примерах. Самый простой и доступный — еда. Например, пирог — целый. Разделить его можно на несколько одинаковых частей. Один кусочек такого пирога и будет называться одной долей из всех возможных. Поделив пирог на четыре части, один кусочек называют одной четвертой частью.
Один кусочек такого пирога и будет называться одной долей из всех возможных. Поделив пирог на четыре части, один кусочек называют одной четвертой частью.
Таким образом делить можно все, что угодно: яблоки, апельсины, плитки шоколада, конфеты в коробке и т. д. Еще один прекрасный наглядный материал для изучения дробей — кубики конструктора Lego. С их помощью можно поделить целое на равные части очень легко. Дети быстро запоминают форму кубиков, и им не требуется постоянно пересчитывать количество выступающих элементов на них.
Если ребенок увидит практическое применение дробей и востребованность их в реальной жизни, ему будет проще понять их и осознать важность получения математических знаний и навыков.
Что нужно знать о дробях?
1. Дробь — число нецелое, оно обозначает количество долей целого.
2. Дробь меньше целого.
3. Чем на большее число долей поделено целое, тем эти доли меньше и наоборот — чем долей меньше, тем они, соответственно, больше.
Для обозначения долей в математике используют понятие обыкновенная дробь. С ее помощью можно записать абсолютно любое необходимое количество долей.
С ее помощью можно записать абсолютно любое необходимое количество долей.
Обыкновенная дробь представляет собой две части, именуемые числителем и знаменателем. Записываются они разделенными горизонтальной чертой либо наклонной вправо линией. Знаменатель пишется внизу либо справа от дробной черты, он показывает общее количество частей от целого, на которое оно было поделено. А числитель пишется вверху или слева от дробной черты и показывает, сколько долей целого сейчас взяли.
Вернемся к нашему пирогу. Очевидно, что разделить его реально на сколько угодно равных частей. В зависимости от того, на сколько частей его разделили, меняется и знаменатель дроби. У пирога, разделенного одной прямой линией на две части, знаменатель будет равен 2, у разделенного на три части — 3 и т. д. Числитель же, в свою очередь, показывает, сколько частей сейчас взято. Если взяли только одну часть из двух, то получится дробь 1/2, только две из трех — 2/3 и т. д.
Что такое смешанные дроби?
В математике выделяют дроби правильные и неправильные. Правильные — те, у которых числитель меньше знаменателя. Например: 1/3, 2/5, 4/12. Но бывает и так, что числитель становится больше знаменателя. Если объяснять предметно, то взято больше частей пирога, чем было тех, на которые он поделен. Такое вполне возможно и в жизни, и в математике.
Правильные — те, у которых числитель меньше знаменателя. Например: 1/3, 2/5, 4/12. Но бывает и так, что числитель становится больше знаменателя. Если объяснять предметно, то взято больше частей пирога, чем было тех, на которые он поделен. Такое вполне возможно и в жизни, и в математике.
У таких дробей можно отделить целую часть и оставшуюся после этого дробную. То есть будет видно, сколько взято целых пирогов и плюс определенное количество его частей. Нужно хорошо представить себе описанное, или даже проверить на практике, а не просто заучивать формулы. Тогда сокращение дробей будет выполняться ребенком осмысленно и безошибочно.
Для того чтобы трансформировать неправильную дробь в смешанное число, следует сперва числитель поделить на знаменатель. В результате почти всегда получим целое число и какой-то остаток. Целое число и нужно записать, как целую часть. А остаток — отправить в числитель дробной части. Неизменным остается только знаменатель.
Неправильными называют и дроби с одинаковым числом над и под дробной чертой: 6/6, 12/12 и т. д. Очевидно, что превратить их можно в 1. Наглядно это взято столько кусочков пирога, на сколько он и был поделен, т. е. целый пирог.
Примеры:
- 14/5 = (5*2+4) / 5 = 2 4/5
- 21/6 = (6*3+ 3) / 6 = 3 3/6
Задание:
Выделите целую часть из неправильных дробей:
- 15/4,
- 22/12,
- 30/7.
Можно провести противоположную процедуру — превратить смешанное число в неправильную дробь. Эта операция часто применяется в математических вычислениях, поэтому будет полезным узнать о ней. Для этого нужно сперва умножить целую часть и знаменатель. Затем получившееся число прибавить к числителю, а знаменатель оставить прежним.
Примеры:
- 3 1/8 = (3*8+1) / 8 = 25/8
- 7 4/9 = (7*9+4) / 9 = 67/9
Задание:
1. Преобразовать в смешанное число неправильную дробь:
Преобразовать в смешанное число неправильную дробь:
- 27/4,
- 18/5,
- 45/7.
2. Выполнить обратную первой задачу — смешанное число превратить в неправильную дробь:
- 3 4/5;
- 12 7/11.
Десятичные дроби
Дроби, в знаменателях которых есть числа, кратные десяти — 10, 100, 1000 и т. д. — в математике можно обозначать следующим образом. Сначала пишется целая часть, а потом числитель из дробной части, отделенный запятой.
Например, 5 4/10 попробуем записать в виде десятичной дроби. Пишем целую часть (5), ставим запятую и далее пишем числитель дробной части (4). Получаем: 5,4. Читается эта дробь так: «пять целых и четыре десятых». Число, представленное в таком виде, именуется десятичной дробью.
Существуют также десятичные дроби без целой части. Например: 7/100. Как быть в таком случае? Чтобы записать подобную дробь, пишут ноль, ставят запятую и далее записывают числитель дроби — 0,07. Такая дробь читается как «ноль целых, семь сотых».
Такая дробь читается как «ноль целых, семь сотых».
Десятичные дроби очень удобны, они используются в точных вычислениях. Десятичная система исчисления применяется человечеством с самых древних времен. Она интуитивна понятна и проста.
Задание:
Преобразовать следующие дроби в десятичные:
- 8/10,
- 4/100,
- 7/1000.
Сокращение дробей
Сокращение дробей выполняют для того, чтобы их упростить. Если числитель и знаменатель дроби таковы, что делятся на одно и то же число (имеют общий делитель), то можно просто разделить их на это число, упростив тем самым дробь. Эта математическая операция называется сокращением дробей. Чтобы разобраться с этим, рассмотрим пару таких примеров.
Пример 1. Сократить дробь 8/12
Решение будет следующим. Наибольшее число, на которое делятся и 8, и 12, — это 4. Поэтому, чтобы сократить дробь, просто поделим ее числитель и знаменатель на 4:
8/12 = 8:4 / 12:4 = 2/3
Пример 2.
 Сократить дробь 10/25
Сократить дробь 10/25Решение. Наибольшее число, на которое делятся и 10, и 25, — это 5. Потому, чтобы сократить дробь, поделим ее числитель и знаменатель на 5:
10/25 = 10:5 / 25:5 = 2/5
Несократимой называется дробь, у которой числитель и знаменатель имеют только один общий делитель — единицу.
Задание:
Сократите следующие дроби:
- 6/18,
- 20/40;
- 7/21.
Сложение дробей
Сначала разберем сложение дробей с одинаковыми знаменателями. В этом случае операция предельно простая. Складываются числители дробей, а знаменатель остается прежним.
Примеры:
- 1/7 + 2/7 = 3/7
- 3/8 + 5/8 = 8/8 = 1
Задание:
Выполни сложение дробей с одинаковыми знаменателями:
Но все усложняется, если нужно сложить дроби с разными знаменателями. В этом случае необходимо привести дроби к наименьшему общему знаменателю. Чтобы это сделать, необходимо найти наименьшее общее кратное. Это такое число, которое делится на оба эти числа без остатка. Например: 3/7 + 2/6. Наименьшее общее кратное для чисел 7 и 6 будет 42.
Это такое число, которое делится на оба эти числа без остатка. Например: 3/7 + 2/6. Наименьшее общее кратное для чисел 7 и 6 будет 42.
Далее ищем дополнительные множители для каждой из дробей. Для этого найденное на предыдущем этапе наименьшее общее кратное делим по очереди на знаменатель каждой из дробей:
- 42 / 7 = 6 — это будет дополнительный множитель для 3/7;
- 42 / 6 = 7 — это, соответственно, дополнительный множитель для 2/6.
Обе части каждой из наших дробей, и числитель и знаменатель, умножаем на свой, определенный выше, множитель:
- 3*6 / 7*6 = 18/42;
- 2*7 / 6*7 = 14/42.
Складываем полученные дроби аналогичным образом, как уже разобранные выше дроби с одинаковыми знаменателями:
- 18/42 + 14/42 = 32/42
Если это возможно, то дробь сокращают. Если дробь получилась неправильная, то следует целую часть из нее выделить.
Задание:
Выполни сложение дробей с разными знаменателями:
Вычитание дробей
Эта операция проводится аналогично сложению. Чтобы вычесть две дроби с одинаковыми знаменателями, нужно найти разность их числителей, а знаменатель оставить тем же.
Чтобы вычесть две дроби с одинаковыми знаменателями, нужно найти разность их числителей, а знаменатель оставить тем же.
Пример:
7/9 — 2/9 = (7-2) / 9 = 5/9
Задание:
Выполни вычитание дробей с одинаковыми знаменателями:
Для дробей с разными знаменателями также придется найти наименьшее общее кратное и дополнительные множители. Затем, по аналогии со сложением, произвести вычитание.
Пример:
6/7 — 8/10 = (6*10-8*7) / 70 = (60-56) / 70 = 4/70
Задание:
Выполни вычитание дробей с разными знаменателями:
Умножение дробей
Существует два варианта умножения дробей. Рассмотрим каждый из них в деталях.
Умножение обыкновенных дробей
В этом случае числители обеих дробей перемножаются — это будет новый числитель. Знаменатели обеих дробей также перемножаются — это будет новый знаменатель.
Пример:
2/5 * 3/4 = (2*3) / (5*4) = 6/20 = 3/10
Если это возможно, то следует сократить дроби перед перемножением. Это облегчит дальнейшие действия.
Это облегчит дальнейшие действия.
Пример:
24/35 * 25/36 = (24*25) / (35*36) = (2*5) / (7*3) = 10/21
Умножение смешанных дробей
Чтобы это сделать, необходимо превратить дроби в неправильные и далее действовать по алгоритму, приведенному в первом пункте.
Пример:
4 2/7 * 5 3/5 = 30/7 * 28/5 = (30*28) / (7*5) = (6*4) / (1*1) = 24/1 = 24
Задание:
Выполните умножение дробей:
- 5/7 * 6/8;
- 6/11 * 2/3;
- 2 3/7 * 4 5/9;
- 4 6/7 * 7 9/10.
Деление дробей
Освоив умножение, с делением также можно справиться легко. Правило деления дробей заключается в следующем: при делении одной дроби на другую нужно первую перемножить на обратную (перевернутую) вторую дробь. Или, иными словами, числитель первой умножить на знаменатель второй (это будет новый числитель), а знаменатель первой умножить на числитель второй (это будет новый знаменатель).
Пример:
4/7 : 2/5 = 4/7 * 5/2 = 20/14 = 10/7 = 1 3/7
Бывают ситуации, когда дробь нужно разделить на целое число. В этом случае следует представить дробь как неправильную. Числителем у нее будет это целое число, а знаменателем просто единица. Далее действовать нужно по уже знакомому правилу деления дробей из предыдущего случая.
В этом случае следует представить дробь как неправильную. Числителем у нее будет это целое число, а знаменателем просто единица. Далее действовать нужно по уже знакомому правилу деления дробей из предыдущего случая.
Пример:
5/9 : 2 = 5/9 : 2/1 = (5*1) / (9*2) = 5/18
Задание:
Выполните деление дробей:
- 6/11 : 3;
- 7/15 : 2;
- 9/12 : 4.
Сравнение дробей
Если сравниваются дроби с одинаковыми знаменателями, то очевидно, что большей будет та, числитель у которой больше.
Пример:
1/5 < 4/5, так как знаменатели одинаковы, а в числителе 1 меньше 5.
Если сравниваются дроби с одинаковыми числителями, то большей будет та, знаменатель у которой меньше.
Пример:
1/2 > 1/8, так как числители одинаковы, а в знаменателе 8 больше 2.
Дроби же с разными знаменателями так просто не сравнишь. Нужно сперва определить их общий знаменатель и привести к нему обе дроби. Правила этой операции были приведены выше. Получим дроби, сравнить которые можно очень легко.
Правила этой операции были приведены выше. Получим дроби, сравнить которые можно очень легко.
Пример:
Сравниваем дроби 2/5 и 1/10. Для этого приводим их к общему знаменателю — 10. Получаем 4/10 и 1/10. Теперь сравниваем дроби, уже имеющие одинаковые знаменатели: 4/10 > 1/10.
Есть один секрет, который нужно запомнить. Если одна из сравниваемых дробей неправильная, то она всегда больше правильной. Если подумать и вспомнить свойства дробей, то все становится понятно. Ведь неправильная дробь всегда будет больше единицы, тогда как правильная, наоборот, всегда будет меньше.
Задание:
Определите, какие дроби изображены на рисунке, и сравните их:
Итак, мы рассмотрели дроби, правила всех действий с ними. Надеемся, что наши объяснения и рекомендации будут очень полезны. Начинайте знакомить детей с дробями еще до школы. Хорошо усвоив эти понятия, ребенок без труда справится затем и с записью дробей, и с действиями с ними.
Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате
узнать подробнее
Читайте также:
- Таблица умножения для детей
- Как объяснить ребенку состав числа?
Какой будет 4/5 в виде дроби? – Обзоры Вики
Таблица преобразования десятичных и дробных чисел
| Доля | Эквивалентные дроби | Десятичная дробь |
|---|---|---|
| 3/5 | 6/10 | .6 |
| 4/5 | 8/10 | .8 |
| 1/6 | 2/12 | .166 |
| 5/6 | 10/12 | .833 |
Аналогично, как вычитать дроби? Есть 3 простых шага для вычитания дробей
- Убедитесь, что нижние числа (знаменатели) совпадают.

- Вычтите верхние числа (числители). Поместите ответ в тот же знаменатель.
- Упростите дробь (при необходимости).
Сколько будет 3/4 минус 1 3 в дроби? На практике достаточно найти общий знаменатель (не обязательно наименьший) путем умножения знаменателей: 4 × 3 = 12. На следующем промежуточном этапе он не может еще больше упростить результат дроби путем сокращения. Другими словами – три четверти минус одна треть = пять двенадцатых.
Во-вторых, что такое 4/5 как целое число? Число 4.5 является смешанным десятичным числом. Это никогда не может быть выражено в целом число, потому что оно имеет дробную часть. Чай . 5 представляет 1/2.
Что такое 4/5 в виде десятичной дроби?
Ответ: 4/5 в виде десятичной дроби 0.8.
тогда что такое 5 4 как смешанное число? 5/4 неправильная дробь, 1 1/4 — его представление смешанных чисел.
Как умножать дроби? Есть 3 простых шага для умножения дробей
- Умножьте верхние числа (числители).
- Умножьте нижние числа (знаменатели).
- При необходимости упростите дробь.
Как найти 4/5 числа?
Чтобы найти одну пятую числа, мы делим число на пять. Затем, чтобы найти четыре пятых числа, мы сначала находим одну пятую от этого числа, а затем умножьте это на четыре.
Что такое дробь? Таблица преобразования десятичных дробей в дробные
| Десятичная дробь | Доля |
|---|---|
| 0.6 | 3/5 |
| 0.625 | 5/8 |
| 0.66666667 | 2/3 |
| 0.7 | 7/10 |
Как найти 4/5 числа?
Чтобы найти одну пятую числа, мы делим число на пять. Затем, чтобы найти четыре пятых числа, мы сначала находим одну пятую этого числа, а затем умножьте это на четыре.
Как упростить неправильную дробь? Чтобы упростить неправильную дробь, начните с превратить его в смешанное число, разделив числитель на знаменатель. Затем превратите остаток в дробь, поместив его над знаменателем исходной дроби. При необходимости упростите последнюю дробь, чтобы получить ответ.
Затем превратите остаток в дробь, поместив его над знаменателем исходной дроби. При необходимости упростите последнюю дробь, чтобы получить ответ.
Как упростить смешанные дроби?
Как превратить неправильные дроби в смешанные дроби?
Ответ: Чтобы преобразовать неправильную дробь в смешанную дробь, разделите числитель на знаменатель, запишите частное как целое число, а остаток как числитель поверх того же знаменателя. Давайте посмотрим на пример этого преобразования. Пояснение: Преобразуйте 23/4 в смешанную дробь.
Как упростить дроби?
Как уменьшить дроби
- Запишите множители для числителя и знаменателя.

- Определите наибольший общий фактор между ними.
- Разделите числитель и знаменатель на наибольший общий множитель.
- Запишите уменьшенную дробь.
Что такое 1 пятая как дробь? Пятая часть – это одна из пяти равных частей. Его также можно записать как 20% или 0.2.
Как найти дробь дроби?
Что такое дробь для детей?
Фракция — это часть целого числа, и способ разбить число на равные части. Оно записывается как количество подсчитываемых равных частей, называемое числителем, по отношению к количеству частей в целом, называемым знаменателем. Эти числа разделены линией.
Как вы представляете дробь? Десятичные числа можно записывать в виде дробей. Чтобы преобразовать десятичную дробь в дробь, поместите десятичное число над его числовым значением. Например, в 0.6 шестерка находится на месте десятых, поэтому мы ставим 6 над 10, чтобы получить эквивалентную дробь, 6/10.
Чтобы преобразовать десятичную дробь в дробь, поместите десятичное число над его числовым значением. Например, в 0.6 шестерка находится на месте десятых, поэтому мы ставим 6 над 10, чтобы получить эквивалентную дробь, 6/10.
Что такое 4/5 как оценка?
Ответ: 4 из 5 можно записать как 4/5 и равно 80%.
Что такое форма неправильной дроби? Неправильная дробь это дробь, числитель которой больше или равен знаменателю. Например, 9/4, 4/3 — неправильные дроби. … С другой стороны, смешанная дробь — это дробь, которая записывается как комбинация натурального числа и правильной дроби. Это упрощенная форма неправильной дроби.
Как вычесть смешанные дроби?
Как вычитать дроби со смешанными дробями?
Калькулятор дробей
Этот калькулятор выполняет основные и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражения с дробями:
Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т. е. 1,45 .
е. 1,45 .
Math Symbols
| Symbol | Symbol name | Symbol Meaning | Example | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| + | plus sign | addition | 1/2 + 1/3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| — | знак минус | вычитание | 1 1/2 — 2/3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| * | asterisk | multiplication | 2/3 * 3/4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| × | times sign | multiplication | 2 /3 × 5/6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| : | division sign | division | 1/2 : 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| / | division slash | division | 1/3 / 5 1/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
more math problems »
Равные дроби для 4/5Калькулятор эквивалентных дробей
Вот ответ на вопросы типа: 4/5 или Какие числа эквивалентны 4/5? Этот калькулятор эквивалентных дробей шаг за шагом покажет вам эквивалентные дроби для любой введенной вами дроби. См. ниже пошаговое решение, как найти эквивалентные дроби. Как найти эквивалентные дроби? Две дроби эквивалентны, если они обе равны при записи в наименьшем выражении. Важно: 45 выглядит как дробь, но на самом деле это неправильная дробь.
получить одно и то же значение, показывающее, что они эквивалентны. Если данная дробь не приводится к наименьшему члену, вы можете найти другие эквивалентные дроби, разделив числитель и знаменатель на одно и то же число. Что такое эквивалентная дробь? Как узнать, равны ли две дроби?Нахождение эквивалентных дробей может быть легким, если вы используете это правило: Определение эквивалентных дробей: две дроби ab и cd эквивалентны, только если произведение (умножение) числителя (a) первой дроби и знаменателя (d ) другой дроби равно произведению знаменателя (b) первой дроби на числитель (c) другой дроби. Другими словами, если вы перемножите (ab и cd) равенство останется, т. е. a.d = b.c. Итак, вот несколько примеров:
Таблица/таблица эквивалентных дробейЭта таблица/диаграмма эквивалентных дробей содержит общепринятые практические дроби. Вы можете легко конвертировать дроби в десятичные, а также из долей дюймов в миллиметры.
Ссылка:
эквивалентные фракции — образцы
8/10208 Equivel Fractment для Фракции |
DisclaimerWhile every effort сделано для обеспечения точности информации, представленной на этом веб-сайте, ни этот веб-сайт, ни его авторы не несут ответственности за какие-либо ошибки или упущения. Поэтому содержимое этого сайта не подходит для любого использования, связанного с риском для здоровья, финансов или имущества.
ДробиСколько равных частей целого Разрежьте пиццу, и мы получим дроби:
Верхнее число говорит, сколько у нас срезов. Попробуйте сами:Эквивалентные дробиНекоторые дроби могут выглядеть по-разному, но на самом деле они одинаковы, например:
Обычно лучше всего показывать ответ, используя самую простую дробь (в данном случае 1 / 2 ). Это называется Упрощение или Сокращение Дробь Числитель / Знаменатель Мы называем верхнее число Числитель , это количество частей у нас . Числитель Знаменатель Вам просто нужно запомнить эти имена! (Если вы забыли, просто подумайте «Down»-знаменатель) Сложение дробейЛегко складывать дроби с тем же знаменателем (то же самое нижнее число):
Одна четверть плюс одна четверть равно двум четвертям, равно половине Другой пример:
Пять восьмых плюс одна восьмая равно шести восьмым, равно трем четвертям Сложение дробей с разными знаменателями Но что делать, если знаменатели (нижние числа) не совпадают?
Три восьмых плюс одна четвертая равно… чему? Надо как-то сделать знаменатели одинаковыми. В данном случае это легко, потому что мы знаем, что 1 / 4 то же, что 2 / 8 :
Три восьмых плюс две восьмых равно пяти восьмым.0009 :
(Они оба работают хорошо, используйте тот, который вам больше нравится.) Другие действия, которые мы можем делать с дробямиМы также можем:
Посетите указатель фракций, чтобы узнать больше.
Освежите свою математику: дробиОсвежите свою математику: дробиЧто такое дробь?До сих пор мы имели дело с целыми числами или целыми числами, найденными путем подсчета. Дробь – это одно целое число, деленное на другое.
Мы записываем дроби как одно число над другим,
с горизонтальной линией между ними, например: Дробь – это одно целое число, деленное на другое.
Мы записываем дроби как одно число над другим,
с горизонтальной линией между ними, например: 3 или в строке текста как одно число с косой чертой или косой чертой, а затем другое число, вот так: 3/4. Дробь 3/4 или три четверти означает 3 части из 4. Верхнее число 3 называется числителем, а нижнее число 4 — знаменателем. Чтобы вычислить долю чего-либо, умножить на числитель и разделить на знаменатель. Например, 3/4 от 12 равно 9: 3 Упражнение: дробиЧто такое половина как дробь? Сколько будет четыре пятых от 20? Проверьте ответ на упражнение с дробями. Упрощение дробейИногда числитель и знаменатель имеют общий множитель. Мы можем упростить дробь, разделив верхнюю и нижнюю часть на множитель. Например: 15 3 × 5 3 потому что общий делитель 15 и 20 равен 5. Упражнение: упрощение дробейУпрощение 27/30. Проверьте ответ на упражнение по упрощению дробей. Неправильные дробиДроби от 0 до 1 называются правильными дробями. Неправильные дроби – это те, которые больше 1. Например, 7/4 — неправильная дробь. Мы также можем выразить это как целое число и правильную дробь: 1¾. Упражнение: неправильные дробиПредставьте пять и две трети в виде неправильной дроби. Выражать 17 в виде целой и правильной дроби. Проверьте ответ на упражнение с неправильными дробями. ВзаимныеОбратная величина числа равна единице, деленной на число. Обратная величина 2 равна ½. И наоборот, величина, обратная ½, равна 2. Чтобы найти обратную дробь, переворачиваем ее,
чтобы числитель стал знаменателем и
знаменатель становится числителем. 4 5 Мы можем преобразовать это в целое число и правильную дробь как 1¼. Упражнение: обратные связиКаковы обратные числа 4 и 5/6? Проверьте ответ на взаимное упражнение. Умножение дробейЧтобы умножить две дроби, мы просто умножаем их числители, умножьте их знаменатели и при необходимости упростите: 2 1
2 × 1
2
1 Упражнение: умножение дробейУмножьте четыре пятых на три четверти. Проверьте ответ на упражнение на умножение дробей. Сложение и вычитание дробейЕсли мы хотим сложить две дроби с одинаковыми знаменателями, мы просто добавляем числители: 2 1
2 + 1
3 Если мы хотим сложить две дроби с разными знаменателями,
мы должны сначала привести их к одному знаменателю. 2 5
2 × 2 5 × 3
4 15
4 + 15
19 Мы также можем записать 19/18 как 1 1/18. Чтобы вычесть дроби, мы делаем то же самое, за исключением того, что мы вычитаем числители после нахождения наименьшего общего знаменателя: 5 1
5 × 2 1 × 3
10 3
10 – 3
7 Упражнение: сложение и вычитание дробей Добавьте 3/4 и 2/3, затем вычтите 1/6. Проверьте ответ на упражнение на сложение и вычитание дробей. Вернуться к главному меню «Освежить математику». Мартину Бланду, получившему степень магистра наук. индекс. На домашнюю страницу Мартина Блэнда. Эта страница поддерживается Мартином Бландом. Назад к началу. Что такое дробь? — Определение, факты и примерыЧто такое дробь?Фракции представляют собой части целого или набора объектов. Дробь состоит из двух частей. Число в верхней части строки называется числителем. Он сообщает, сколько равных частей целого или набора взято. Число под чертой называется знаменателем. Он показывает общее количество равных частей, на которые делится целое, или общее количество одинаковых объектов в коллекции. Доля целого Когда целое делится на равные части, количество частей, которые мы берем, составляет дробь. Если торт разделить на восемь равных частей и один кусок торта положить на тарелку, то говорят, что на каждой тарелке есть $\frac{1}{8}$ торта. Читается как «одна восьмая» или «1 на 8». Доля набора объектовВсего 5 детей. 3 из 5 девочек. Итак, доля девушек составляет три пятых ( $\frac{3}{5}$ ). 2 из 5 мальчиков. Итак, доля мальчиков составляет две пятых ( $\frac{2}{5}$ ). Равные и неравные частиЧтобы определить дробь, нужно разделить целое на равные части. Представление дробиДробь может быть представлена тремя способами: в виде дроби, в процентах или в виде десятичной дроби. Рассмотрим каждую из трех форм представления. Дробное представление,Первая и наиболее распространенная форма представления дроби — это форма ab. Здесь, a называется числителем, а b называется знаменателем. И числитель, и знаменатель разделяются чертой. Пример: Дробь $\frac{3}{4}$ можно понять следующим образом. Числитель: 3 Знаменатель: 4 Дробь представляет собой три части, когда целое делится на четыре равные части. Десятичное представлениеВ этом формате дробь представляется в виде десятичного числа. Пример: Дробь $\frac{3}{4}$ можно представить в виде десятичной дроби, разделив числитель (3) на знаменатель (4). $\frac{3}{4}$ = 0,75. Таким образом, в десятичном представлении $\frac{3}{4}$ записывается как 0,75. Процентное представлениеВ этом представлении дробь умножается на 100, чтобы преобразовать ее в проценты. Пример: Если мы хотим представить в процентах, мы должны умножить $\frac{3}{4}$ на 100. $\frac{3}{4}$ x 100 = 0,75 x 100 = 75. Таким образом, мы можем представить $\frac{3}{4}$ как 75%. Дроби в числовой строкеДроби могут быть представлены в числовой строке, как показано ниже. Типы дробей Основными частями дроби являются числитель и знаменатель. Смешанные дроби в неправильные дробиСмешанные дроби можно преобразовать в неправильные дроби, умножив целое число на знаменатель и прибавив его к числителю. Он становится новым числителем, а знаменатель остается неизменным. Пример: 8$\frac{2}{3}$ = $\frac{(8 \times 3) + 2}{3}$ = $\frac{26}{3}$ ЗаключениеСамый простой способ научить детей этой теме — помочь им визуализировать дроби. Это можно сделать с помощью вырезок из бумаги или интерактивных онлайн-игр, подобных тем, которые доступны на https://www.splashlearn.com/fraction-games. Посетите веб-сайт Splashlearn, чтобы узнать больше о таких увлекательных способах изучения различных математических концепций. Решенные примеры1. Преобразовать смешанное число 4$\frac{3}{5}$ в неправильную дробь. Решение: 4$\frac{3}{5}$ = $\frac{(4 ✕ 5) + 3}{5}$ = $\frac{20 + 3}{5}$ = $\ frac{23}{5}$ 2. Решение: Простейшая форма $\frac{14}{20}$ = $\frac{7}{10}$ Простейшая форма $\frac{7}{10}$ = $\ frac{7}{10}$ Поскольку простейшей формой обеих дробей является $\frac{7}{10}$, мы можем сказать, что две дроби эквивалентны. 3. Из следующих дробей отделить правильную и неправильную дробь $\frac{9}{2}$, $\frac{4}{11}$, $\frac{16}{16}$, $\frac {2}{3}$, $\frac{7}{9}$, $\frac{5}{6}$ Решение: Правильная дробь: $\frac{4}{11}$ , $\frac{2}{3}$, $\frac{7}{9}$, $\frac{5}{6}$ Неправильная дробь: $\frac{9}{2}$, $ \frac{16}{16}$ 4. Преобразовать $\frac{2}{5}$ в процентах. Решение: $\frac{2}{5} \times 100%$ = 40% Практические задачи$\frac{3}{10}$ $\frac{7}{16}$ $\frac{10}{11}$ $\frac{12}{17 }$ Правильный ответ: $\frac{10}{11}$ 0,5 0,75 0,80 0,375 Правильный ответ: 0,375 2 9 6 8 Правильный ответ: 9 Правильная дробь Единичная дробь Неправильная дробь Смешанная дробь Правильный ответ: правильный Дробь Часто задаваемые вопросыКак проще всего определить, можно ли преобразовать число в смешанную дробь? Самый простой способ определить это — сравнить числитель со знаменателем. Если числитель больше знаменателя, дробь неправильная и может быть преобразована в смешанную дробь. Есть ли реальные примеры использования дробей? Дроби очень распространены в повседневной жизни. |


 В этом случае дробные части не будут уменьшаться или преобразовываться в десятичных. Однако математические вычисления с дробями, которые отображаются как текст, выполнять нельзя.
В этом случае дробные части не будут уменьшаться или преобразовываться в десятичных. Однако математические вычисления с дробями, которые отображаются как текст, выполнять нельзя.

 Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  Отсюда шесть пар синих, три пары коричневых, две черных и две белых. Какая часть носков Макса коричневого или черного цвета?
Отсюда шесть пар синих, три пары коричневых, две черных и две белых. Какая часть носков Макса коричневого или черного цвета? У трех из них нет ластика на конце. Какая часть карандашей не имеет ластика на конце?
У трех из них нет ластика на конце. Какая часть карандашей не имеет ластика на конце? Например:
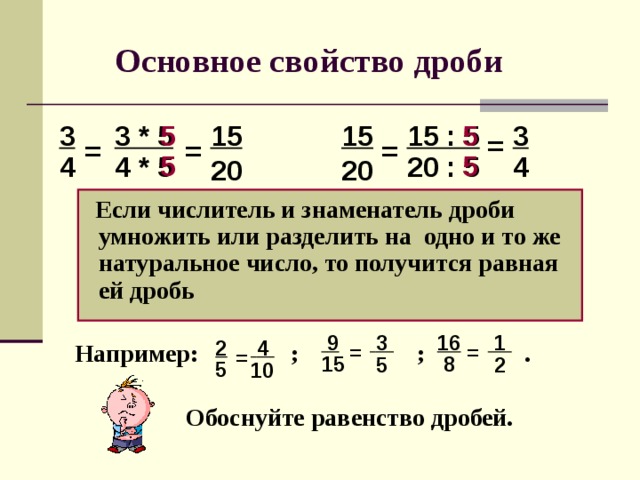
Например: Дробь 810 равна 45 при сокращении до наименьших членов. Чтобы найти равнозначные дроби, нужно просто умножить числитель и знаменатель той сокращенной дроби (45) на одно и то же натуральное число, т. е. умножить на 2, 3, 4, 5, 6…
Дробь 810 равна 45 при сокращении до наименьших членов. Чтобы найти равнозначные дроби, нужно просто умножить числитель и знаменатель той сокращенной дроби (45) на одно и то же натуральное число, т. е. умножить на 2, 3, 4, 5, 6…
 191
191 144
144 319
319 097
097 875
875 653
653 034
034 813
813
 02+17.19
02+17.19

 Делим верх и низ на 5.
Делим верх и низ на 5.
 Мы делаем это, находя наименьшее общее кратное знаменателей.
Мы называем это наименьшим общим знаменателем.
Для дробей 2/9 и 5/6 наименьший общий знаменатель равен 18.
Чтобы получить это, мы находим множители 6 и 9.
Делители 6 равны 1, 2, 3 и 6.
Делители 9 равны 1, 3 и 9.
Наибольший общий делитель равен 3.
6/3 = 2 и 9/3 = 3.
Таким образом, наименьшее общее кратное равно 3 × 2 × 3 = 18.
Затем мы умножаем верх и низ каждой дроби на коэффициент, который
сделает нижнюю часть наименьшим общим знаменателем:
Мы делаем это, находя наименьшее общее кратное знаменателей.
Мы называем это наименьшим общим знаменателем.
Для дробей 2/9 и 5/6 наименьший общий знаменатель равен 18.
Чтобы получить это, мы находим множители 6 и 9.
Делители 6 равны 1, 2, 3 и 6.
Делители 9 равны 1, 3 и 9.
Наибольший общий делитель равен 3.
6/3 = 2 и 9/3 = 3.
Таким образом, наименьшее общее кратное равно 3 × 2 × 3 = 18.
Затем мы умножаем верх и низ каждой дроби на коэффициент, который
сделает нижнюю часть наименьшим общим знаменателем:

 На их основе можно определить различные типы фракций. Давайте рассмотрим некоторые распространенные типы дробей.
На их основе можно определить различные типы фракций. Давайте рассмотрим некоторые распространенные типы дробей. Эквивалентны ли дроби $\frac{14}{20}$ и $\frac{7}{10}$?
Эквивалентны ли дроби $\frac{14}{20}$ и $\frac{7}{10}$?
