| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | сфера (4) | | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | ||
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | 3/9 | ||
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
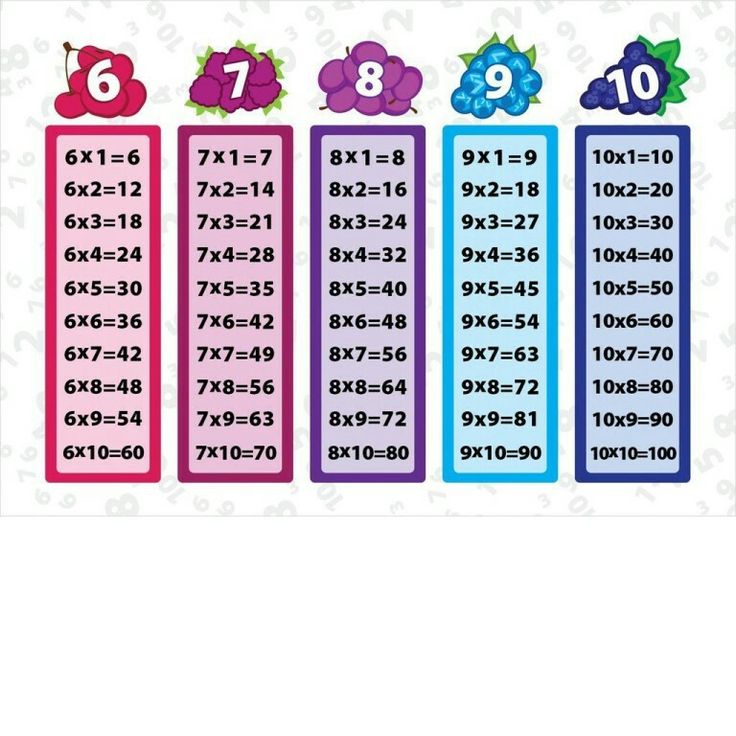
Таблица умножения на 6, 7, 8 и 9 на пальцах
?Previous Entry | Next Entry
Летом Арина должна выучить таблицу умножения.
До 5 она уже знает, а дальше набор цифр немного сложнее. Сегодня мы обнаружили любопытный метод умножения на пальцах. Разобрались. Арина в восторге, да и я несколько удивлена, почему в школе об этом не знали! Делюсь.
Поверните кисти ладонями к себе и присвойте каждому пальцу цифры от 6 и до 10 начиная с мизинца.
Теперь попробуем умножить, например, 7х8. Для этого соедините палец №7 на левой руке с пальцем №8 на правой.
А теперь считаем пальцы: количество пальцев под соединенными — это десятки.
А пальцы левой руки, оставшиеся сверху, умножаем на пальцы правой — это и будут наши единицы (3х2=6). Итоге равен 56.
Иногда бывает так, что при умножении «единиц» результат получается больше 9. В таких случаях нужно плюсовать оба результата в столбик.
Например, 7х6. В этом случае получается, что «единицы» равны 12 (3х4). В десятки равны 3.
3 (десятки)
+
12 (единицы)
________
42
Умножение на 9
Снова поверните кисти ладонями к себе, но теперь нумерация пальцев будет идти по порядку с лева на право, то есть от 1 до 10.
Теперь умножаем, например, 2х9. Все то, что идет до пальца №2 — это десятки (то есть 1 в этом случае). А все то, что остается после пальца №2 — единицы (то есть 8). В итоге получаем 18.
из интернета
И тем не менее, мы пришли к выводу, что учить таблицу необходимо, а этот метод можно использовать в том случае, если что-то позабудется.
Вы помните всю таблицу умножения?
| October 2022 | ||||||
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 | |||||
- mertingero : (no subject) [+0]
- interv : (no subject) [+0]
- winged_crocodil : (no subject) [+1]
- gera544 : (no subject) [+0]
- shatff : (no subject) [+0]
- grushenka : (no subject) [+0]
- remch_ch : (no subject) [+0]
- demkristo : (no subject) [+0]
- voxpop_66 : (no subject) [+0]
- minskblog : (no subject) [+0]
- slavikap : (no subject) [+0]
- bass7013 : Таблица умножения на 6, 7, 8 и 9 на пальцах [+0]
- hroft_clone3 : (no subject) [+2]
- think_head : (no subject) [+0]
- stetson_hat : (no subject) [+0]
- tinaword : (no subject) [+0]
- prof61 : (no subject) [+0]
Дизайн журнала: — от harmful_viki
Powered by LiveJournal.
com
| 1 | Найти том | сфера (5) | | |
| 2 | Найти площадь | круг (5) | | |
| 3 | Найдите площадь поверхности | сфера (5) | | |
| 4 | Найти площадь | круг (7) | | |
| 5 | Найти площадь | круг (2) | | |
| 6 | Найти площадь | круг (4) | | |
| 7 | Найти площадь | круг (6) | | |
| 8 | Найти том | сфера (4) | | |
| 9 | Найти площадь | круг (3) | | |
| 11 | Найти простую факторизацию | 741 | ||
| 12 | Найти том | сфера (3) | | |
| 13 | Оценить | 3 квадратный корень из 8*3 квадратный корень из 10 | ||
| 14 | Найти площадь | круг (10) | | |
| 15 | Найти площадь | круг (8) | | |
| 16 | Найдите площадь поверхности | сфера (6) | | |
| 17 | Найти простую факторизацию | 1162 | ||
| 18 | Найти площадь | круг (1) | | |
| 19 | Найдите окружность | круг (5) | | |
| 20 | Найти том | сфера (2) | | |
| 21 | Найти том | сфера (6) | | |
| 22 | Найдите площадь поверхности | сфера (4) | | |
| 23 | Найти том | сфера (7) | ||
| 24 | Оценить | квадратный корень из -121 | ||
| 25 | Найти простую факторизацию | 513 | ||
| 26 | Оценка | квадратный корень из 3/16* квадратный корень из 3/9 | ||
| 27 | Найти том | коробка (2)(2)(2) | | |
| 28 | Найдите окружность | круг (6) | | |
| 29 | Найдите окружность | круг (3) | | |
| 30 | Найдите площадь поверхности | сфера (2) | | |
| 31 | Оценить | 2 1/2÷22000000 | ||
| 32 | Найдите Том | коробка (5)(5)(5) | | |
| 33 | Найти том | коробка (10)(10)(10) | | |
| 34 | Найдите окружность | круг (4) | | |
| 35 | Преобразование в проценты | 1,7 | ||
| 36 | Оценить | (5/6)÷(4/1) | ||
| 37 | Оценить | 3/5+3/5 | ||
| 38 | Оценить | ф(-2) | 92 | |
| 40 | Найти площадь | круг (12) | | |
| 41 | Найти том | коробка (3)(3)(3) | | |
| 42 | Найти том | коробка (4)(4)(4) | 92-4*-1+2||
| 45 | Найти простую факторизацию | 228 | ||
| 46 | Оценить | 0+0 | ||
| 47 | Найти площадь | круг (9) | | |
| 48 | Найдите окружность | круг (8) | | |
| 49 | Найдите окружность | круг (7) | | |
| 50 | Найти том | сфера (10) | | |
| 51 | Найдите площадь поверхности | сфера (10) | | |
| 52 | Найдите площадь поверхности | сфера (7) | | |
| 53 | Определить, является простым или составным | 5 | ||
| 60 | Преобразование в упрощенную дробь | 2 1/4 | ||
| 61 | Найдите площадь поверхности | сфера (12) | | |
| 62 | Найти том | сфера (1) | | |
| 63 | Найдите окружность | круг (2) | | |
| 64 | Найти том | коробка (12)(12)(12) | | |
| 65 | Добавить | 2+2= | ||
| 66 | Найдите площадь поверхности | коробка (3)(3)(3) | | |
| 67 | Оценить | корень пятой степени из 6* корень шестой из 7 | ||
| 68 | Оценить | 7/40+17/50 | ||
| 69 | Найти простую факторизацию | 1617 | ||
| 70 | Оценить | 27-(квадратный корень из 89)/32 | ||
| 71 | Оценить | 9÷4 | ||
| 72 | Оценка 92 | |||
| 74 | Оценить | 1-(1-15/16) | ||
| 75 | Преобразование в упрощенную дробь | 8 | ||
| 76 | Оценка | 656-521 | 9-2 | |
| 79 | Оценить | 4-(6)/-5 | ||
| 80 | Оценить | 3-3*6+2 | ||
| 81 | Найдите площадь поверхности | коробка (5)(5)(5) | | |
| 82 | Найдите площадь поверхности | сфера (8) | | |
| 83 | Найти площадь | круг (14) | | |
| 84 | Преобразование в десятичное число | 5 ноября | ||
| 85 9-2 | ||||
| 88 | Оценить | 1/2*3*9 | ||
| 89 | Оценить | 4/4-17/-4 | ||
| 90 | Оценить | 11. 02+17.19 | ||
| 91 | Оценить | 3/5+3/10 | ||
| 92 | Оценить | 4/5*3/8 | ||
| 93 | Оценить | 6/(2(2+1)) | ||
| 94 | Упростить | квадратный корень из 144 | ||
| 95 | Преобразование в упрощенную дробь | 725% | ||
| 96 | Преобразование в упрощенную дробь | 6 1/4 | ||
| 97 | Оценить | 7/10-2/5 | ||
| 98 | Оценить | 6÷3 | ||
| 99 | Оценить | 5+4 | ||
| 100 | Оценить | квадратный корень из 12- квадратный корень из 192 |
7 раз 8 равно 54: Призыв к запоминанию математики | Джеймс Тантон | КЭД
Во время интервью Radio Five Live в 1998 году министра школьных стандартов Великобритании Стивена Байерса спросили: сколько будет 7 умножить на 8? Он дал ответ 54.
Его ошибочный ответ вызвал личные насмешки в национальных СМИ и подтолкнул настроения к тому, чтобы заучивание таблицы умножения 12 x 12 к девяти годам стало стандартом английской школы.
Несомненно, существуют веские психологические причины для неправильных ответов на простые вопросы под давлением. Но давайте представим, что у министра Байерса была возможность и средства подумать, прежде чем ответить. В качестве гипотетического упражнения, вот четыре возможных ответа, которые он мог бы дать. Кто из них, по вашему мнению, мог внушить ему чувство уверенности в своих силах?
а) «54»
б) «Это сложно. Но я помню, как меня учили мнемонике «5 6 7 8». Итак, 7×8 — это 56 дюймов.
c) «Это хитрый вопрос. Но я держу в голове, что 7×7 — это 49, так что 7×8 на семь больше, чем это: 56».
d) «56»
Возможно, многие люди скажут, что ответ d) внушает наибольшее доверие: «Просто знайте свои математические факты».
Если ваш единственный опыт и ожидание от математики — это вычисления и вычислительные факты, то скорость — ключ к успеху для такого взгляда на математику: «Давайте не будем лишать наших девятилетних мальчиков и девочек возможности добиться успеха». Многие люди также утверждают, что практика запоминания, среди прочего, способствует нейронной пластичности, и, кажется, есть доказательства того, что запоминание арифметических фактов для удобства влияет на гиппокампальную область мозга, область, ответственную за запоминание фактов.0951
Итак, если вычисления — это ваш основной взгляд на математику, а запоминание, необходимое для достижения успеха, происходит с радостью, легкостью и удовольствием — регулярная практика, тогда дерзайте. Просто держите его радостным, я говорю! И есть много приятных способов помочь юным ученикам развить понимание чисел и иметь под рукой арифметические факты. На самом деле все хорошо и хорошо, несмотря на яростные споры о «механическом заучивании» в интернете.
Опять же, мой единственный совет/пожелание: Всегда имейте в виду радость.
Ну, до определенного момента все хорошо.
Эти дебаты, кажется, встроены в контекст математики в младших классах — в частности, о запоминании таблиц умножения — с заявленной целью улучшения возможностей для элементарных арифметических алгоритмов и разбрызгивания арифметики, которая может возникнуть даже в более поздних классах. . Кажется, мы забываем, что наши юные ученики находятся в тринадцатилетнем путешествии по математике, то есть от К до 12 лет. И основная часть тех лет будет , а не , должны быть ориентированы на арифметические вычисления. (Математика для старших классов не предназначена для решения исключительно длинных задач на умножение.)
Вот моя позиция по поводу дебатов о запоминании в отношении математики старших классов для 8–12 классов, а также математики в колледже:
Я бы больше всего впечатлен, если министр Байерс ответит c).
Я говорю, что возиться можно.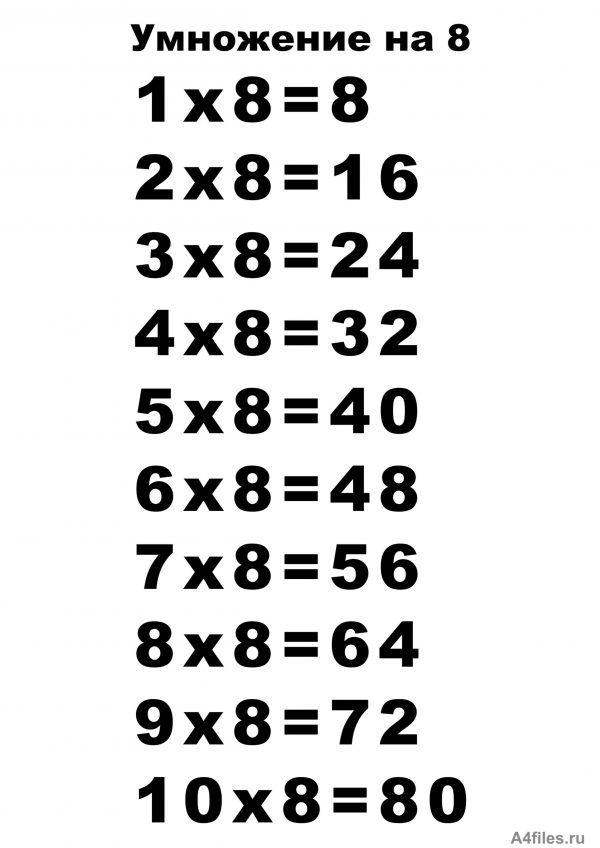
Иметь уверенность, чтобы попытаться оправиться от нащупывания и добиться успеха, это замечательно! Ответ в) сказал бы мне, что министр, спустя столько лет после окончания школы, сохранил ловкость в игре с числами и мыслит как математик. Математика, по сути, вполне может быть определена как изучение структуры и игра со структурой, и, следовательно, в) демонстрирует именно искусство и практику выполнения математических действий. Это математика, которую я практикую как математик, и математика, с которой сталкиваются студенты средних школ и колледжей.
***
В школьной программе слишком много материала для запоминания. (Ну, некоторые студенты стараются запомнить все это, но я не уверен, что такой подход доставляет удовольствие.) Возьмем, к примеру, тригонометрию, синус, косинус и тангенс углов.
На уроке математики начинают играть с тригонометрическими тождествами. А их там много! Вот двадцать пять , с которыми, скорее всего, столкнется ваш ребенок , и они пугают! (Одно уравнение — это на самом деле три связанных вместе.
)
Конечно, я как учитель средней школы не хочу, чтобы ученики запоминали все эти правила (да и мне, как математику, они не нужны в моей голове: они некрасивы и трудны!)
Ну и что делать Я хочу, чтобы мои студенты делали, и что я лично делаю как математик?
Проводим инвентаризацию. То есть мы подводим итоги того, что у нас уже есть в запасе, и смотрим, что мы можем создать из того, что у нас есть. Не случайно слова инвентарь и инвент связаны вместе.
На следующей диаграмме показано, как учащиеся могут сократить задачу «запоминания» этого списка до
Пять идентичностей уже «в наличии», а также три определения и две идентичности, необходимые для заполнения недостающих частей.а) распознать пять формул как уже имеющиеся в наличии — они являются явным следствием нашего представления о том, что такое тригонометрия,
б) распознать, что основная часть формул в списке является следствием трех определений и всего двух тождеств.
909:50 Существует множество тригонометрических тождеств, намного больше двадцати пяти. И после обсуждения в классе, подобного приведенному выше, я был бы уверен, что мои старшеклассники смогут справиться с ранее невидимыми личностями. Точно так же я надеюсь, что если бы Стивен Байерс ответил c) на факт умножения 7 x 8 = 56, у него хватило бы сообразительности и уверенности в себе, чтобы увидеть, почему 7 ½ x 7 ½ очень близко к 56. (Насколько близко?) Или мы должны заставить учащихся запомнить их дробные таблицы умножения?Значит, было бы неуместно помогать ученикам средней школы готовиться к такому типу мышления старшей школы?
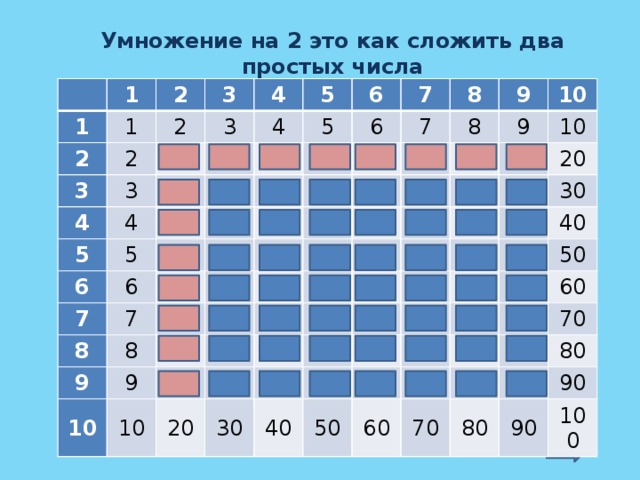
Предположим, во время оживленной дискуссии в классе мы нарисовали на доске таблицу умножения 10 x 10 и попросили учащихся
а) обвести кружком все факты умножения, которые они считают простыми и уже имеют в голове (кратные 1 , числа, кратные 10, 3 умноженные на 3 и т. д.)
б) обратите внимание, что, поскольку таблица симметрична, нужно отсортировать только 55, а не 100 фактов умножения.
Фу!
c) обсудить стратегии быстрого доступа к фактам умножения, которые им кажутся трудными, и обсудить то, что кажется им трудным.
Фу!Возможно, в таком обсуждении хитрые продукты тоже могли бы начать прилипать.
***
Все разговоры требуют контекста. Обсуждение уровня математических фактов, необходимого для хорошего математического изобретения, также требует контекста. Изобретение для какой математики? Какой взгляд на математику? Какие уровни? Наши учащиеся испытают полный спектр математических структур в своих путешествиях K-12 — вычисления и арифметика, геометрия, алгебра, моделирование, анализ и исчисление — каждая из которых требует изменения математической зрелости для работы с задействованными концепциями. Можем ли мы помнить об этом?
Но, возможно, споры о запоминании касаются не математики как таковой , а преимуществ заучивания как такового, поскольку урок математики является всего лишь одной из площадок в школе для этого: повторите все 144 факта умножения на уроке математики, все 50 столиц штатов на уроках обществознания, отрывки из Макбета на уроках английского и так далее.
Или, возможно, это сочетание обоих мотивов: развитие мгновенного запоминания фактов умножения заставляет наших детей практиковать навыки запоминания, создавая, по крайней мере, некоторый мысленный перечень фактов вычисления К-5. Беспроигрышный вариант, если хотите.
Мне трудно расшифровать мотивацию многих статей, которые я прочитал в Интернете о запоминании на уроках математики. Обычно я не могу комментировать просто потому, что не знаю основного контекста аргумента.
Но как бы ни обстояло дело с определенными математическими практиками, все будет хорошо, если мы позаботимся о том, чтобы практика соответствовала математике, учитывала всю историю математики и, самое главное, проводилась с радостью для всех и каждого. . Отжимания могут быть необходимы время от времени, и это нормально, если мы немного поиграли с математикой и знаем, почему мы хотим отжиматься. мы просто не можем позволить упражнения станут единственным определяющим математическим опытом для наших студентов.
(Многие, как и я, обеспокоены тем, что «учебный» подход к запоминанию попадет в эту ловушку.)
Как и когда мы ожидаем, что ученики узнают или вычислят, что 7 x 8 равно 56, всегда будет предметом споров, я уверен. Надеюсь, в будущих разговорах мы сможем быть ясными и ясными о том, о каких аспектах математического пути K-12 мы говорим. И когда мы размышляем о системе образования, давайте также обязательно отметим работу, которую уже проделали наши педагоги. Прямо сейчас они усердно работают, чтобы донести до наших учеников смысл, актуальность и радость математики — удивление, благоговение, практическое применение, отжимания и все такое. Их таланты замечательны, они стремятся к лучшему для наших учеников, и все во благо.
Три заключительных примечания
1. Просто чтобы завершить мои мысли. Ответ а) тоже возмутил бы меня, если бы министр после некоторого размышления остановился на этом ответе. И ответ б) разочаровал бы меня. Конечно, милые мнемоники действительно милы, но они поверхностны и обычно не обращают внимания ни на какие вопросы структуры или смысла.