Бинарные числа: двоичная система счисления
Бинарные числа — это числа из двоичной системы счисления, имеющей основание 2. Она непосредственно реализована в цифровой электронике, используется в большинстве современных вычислительных устройств, включая компьютеры, мобильные телефоны и разного рода датчики. Можно сказать, что все технологии нашего времени построены на бинарных числах.
Запись чисел
Любое число, сколь бы большим оно ни было, в двоичной системе записывается посредством двух символов: 0 и 1. Например цифра 5 из всем знакомой десятичной системы в двоичной будет представлено как 101. Бинарные числа могут быть обозначены префиксом 0b или амперсандом (&), например: &101.
Во всех системах счисления, исключая десятичную, символы читаются по одиночке, то есть взятое в пример 101 читается как «один ноль один».
Перевод из одной системы в другую
Программисты, постоянно работающие с двоичной системой счисления, на ходу могут перевести бинарное число в десятичное.
Это действительно можно сделать и без всяких формул, особенно если человек имеет представление о том, как работает самая малая часть компьютерного «мозга» — бит.
Цифра ноль так же обозначает 0, а цифра один в двоичной системе тоже будет единицей, но что делать дальше, когда цифры закончились? Десятичная система «предложила» бы в таком случае ввести термин «десяток», а в бинарной системе это будет называться «двойка».
Если 0 это &0 (амперсанд — обозначение двоичной системы), 1 = &1, то 2 будет обозначаться как &10. Тройку тоже можно записать в двух разрядах, она будет иметь вид &11, то есть одна двойка и одна единица. Возможные комбинации исчерпаны, и в десятичной системе на этом этапе вводятся сотни, а в двоичной — «четверки». Четыре — это &100, пять — &101, шесть — &110, семь — &111. Следующая, более крупная единица счета — это восьмерка.
Можно заметить особенность: если в десятичной системе разряды умножаются на десять (1, 10, 100, 1000 и так далее), то в двоичной, соответственно, на два: 2, 4, 8, 16, 32.
Это соответствует размеру флеш-карт и прочих накопителей, использующихся в компьютерах и других устройствах.
Что такое бинарный код
Числа, представленные в двоичной системе счисления, называются бинарными, однако в таком виде можно представить и не числовые значения (буквы и символы). Таким образом, в цифрах можно закодировать слова и тексты, правда вид они будут иметь не столь лаконичный, ведь для записи всего одной буквы потребуется несколько нолей и единиц.
Но каким образом компьютерам удается считывать такое количество информации? На самом деле все проще, чем кажется. Люди, привыкшие к десятичной системе счисления, сначала переводят двоичные числа в более привычные, и только потом производят с ними какие-либо манипуляции, а в основе компьютерной логики изначально лежит бинарная система чисел. Единице в технике соответствует высокое напряжение, а нулю — низкое, либо для единицы напряжение есть, а для ноля вообще отсутствует.
Бинарные числа в культуре
Ошибкой будет считать, что двоичная система счисления — это заслуга современных математиков.
Хотя бинарные числа и являются основополагающими в технологиях нашего времени, использовались они уже очень давно, причем в разных уголках планеты. Используются длинная линия (единица) и прерывистая (ноль), кодирующие восемь символов, означающих восемь стихий: небо, землю, гром, воду, горы, ветер, огонь и водоем (массу воды). Этот аналог 3-битных цифр описывался в классическом тексте книги Перемен. Триграммы составляли 64 гексаграммы (6-битные цифры), порядок которых в книге Перемен был расположен в соответствии с двоичными цифрами от 0 до 63.
Этот порядок был составлен в одиннадцатом веке китайским ученым Шао Юном, хотя нет доказательств того, что он действительно понимал двоичную систему счисления в целом.
В Индии еще до нашей эры тоже применялись бинарные числа в математической основе для описания поэзии, составленные математиком Пингалой.
Узелковая письменность инков (кипу) считается прообразом современных баз данных. Именно они впервые применили не только бинарный код числа, но и не числовые записи в двоичной системе.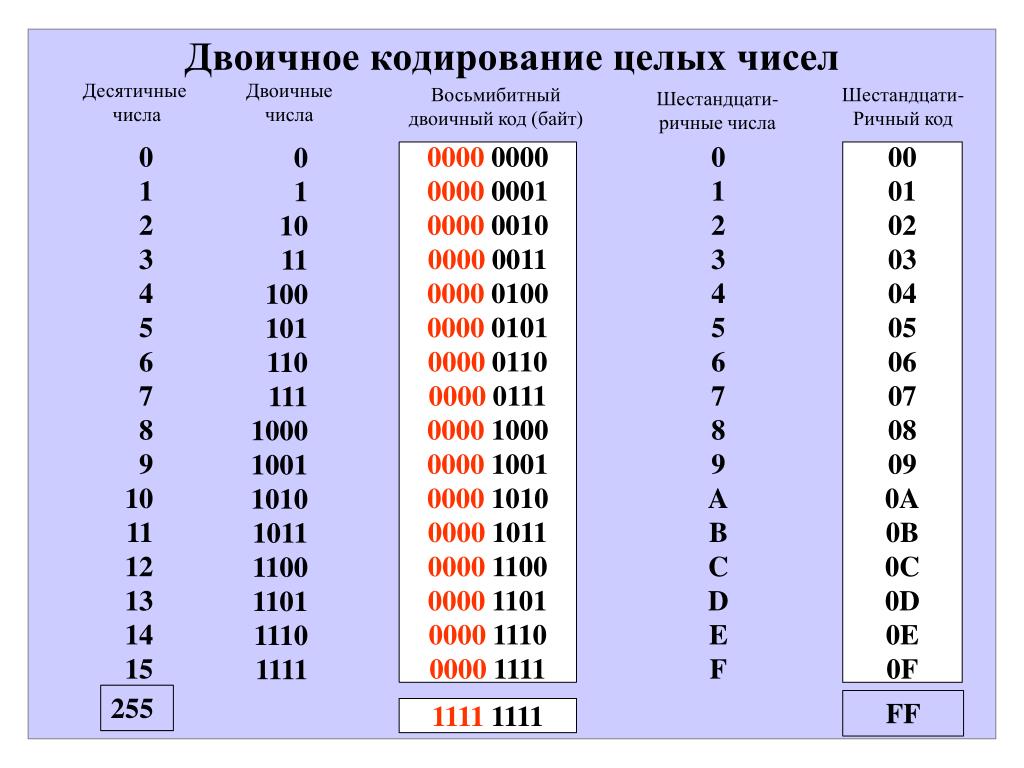
Узелковое письмо кипу характерно не только первичными и дополнительными ключами, но и использованием позиционных чисел, кодированием с помощью цвета и сериями повторений данных (циклами). Инки впервые применили способ ведения бухгалтерского учета, называемый двойной записью.
Первый из программистов
Двоичную систему счисления, основанную на цифрах 0 и 1, описал и знаменитый ученый, физик и математик, Готфрид Вильгельм Лейбниц. Он увлекался древней китайской культурой и, изучая традиционные тексты книги Перемен, заметил соответствие гексаграмм бинарным числам от 0 до 111111. Он восхитился свидетельствам подобных достижений в философии и математике для того времени. Лейбница можно назвать первым из программистов и информационных теоретиков. Именно он обнаружил, что если записать группы двоичных чисел вертикально (одно под другим), то в получившихся вертикальных столбцах чисел будут регулярно повторяться ноли и единицы. Это позвонило ему предположить, что возможно существование совершенно новых математических законов.
Лейбниц понял и то, что бинарные числа оптимальны для применения в механике, основой которой должна быть смена пассивных и активных циклов. На дворе был 17 век, а этот великий ученый изобрел на бумаге вычислительную машину, работавшую на основе его новых открытий, однако быстро понял, что цивилизация еще не достигла такого технологического развития, и в его время создание такой машины будет невозможным.
Бинарные коды – rentamatic
Add to Wishlist
Категория: Абсолютные энкодеры
- Описание
- Отзывы (0)
Термин «бинарный» по смыслу – состоящий из двух частей, компонентов. Таким образом бинарные коды это коды которые состоят только из двух символьных состояний например черный или белый, светлый или темный, проводник или изолятор. Бинарный код в цифровой технике это способ представления данных (чисел, слов и других) в виде комбинации двух знаков, которые можно обозначить как 0 и 1.
Знаки или единицы БК называют битами. Одним из обоснований применения БК является простота и надежность накопления информации в каком-либо носителе в виде комбинации всего двух его физических состояний, например в виде изменения или постоянства светового потока при считывании с оптического кодового диска.
Двоичный код
В цифровой технике способ представления данных (чисел, слов и других) в виде комбинации двух знаков, которые можно обозначить как 0 и 1. Знаки или единицы ДК называют битами.
Одним из обоснований применения ДК является простота и надежность накопления информации в каком-либо носителе в виде комбинации всего двух его физических состояний, например в виде изменения или постоянства магнитного потока в данной ячейке носителя магнитной записи.
Наибольшее число, которое может быть выражено двоичным кодом, зависит от количества используемых разрядов, т.е. от количества битов в комбинации, выражающей число.
Например, для выражения числовых значений от 0 до 7 достаточно иметь 3-разрядный или 3-битовый код:
| числовое значение | двоичный код |
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | |
| 6 | 110 |
| 7 | 111 |
Отсюда видно, что для числа больше 7 при 3-разрядном коде уже нет кодовых комбинаций из 0 и 1.
Переходя от чисел к физическим величинам, сформулируем вышеприведенное утверждение в более общем виде: наибольшее количество значений m какой-либо величины (температуры, напряжения, тока и др.), которое может быть выражено двоичным кодом, зависит от числа используемых разрядов n как m=2n. Если n=3, как в рассмотренном примере, то получим 8 значений, включая ведущий 0.
Двоичный код является многошаговым кодом. Это означает, что при переходе с одного положения (значения) в другое могут изменятся несколько бит одновременно. Например число 3 в двоичном коде = 011. Число же 4 в двоичном коде = 100. Соответственно при переходе от 3 к 4 меняют свое состояние на противоположное все 3 бита одновременно. Считывание такого кода с кодового диска привело бы к тому, что из-за неизбежных отклонений (толеранцев) при производстве кодового диска изменение информации от каждой из дорожек в отдельности никогда не произойдет одновременно. Это в свою очередь привело бы к тому, что при переходе от одного числа к другому кратковременно будет выдана неверная информация.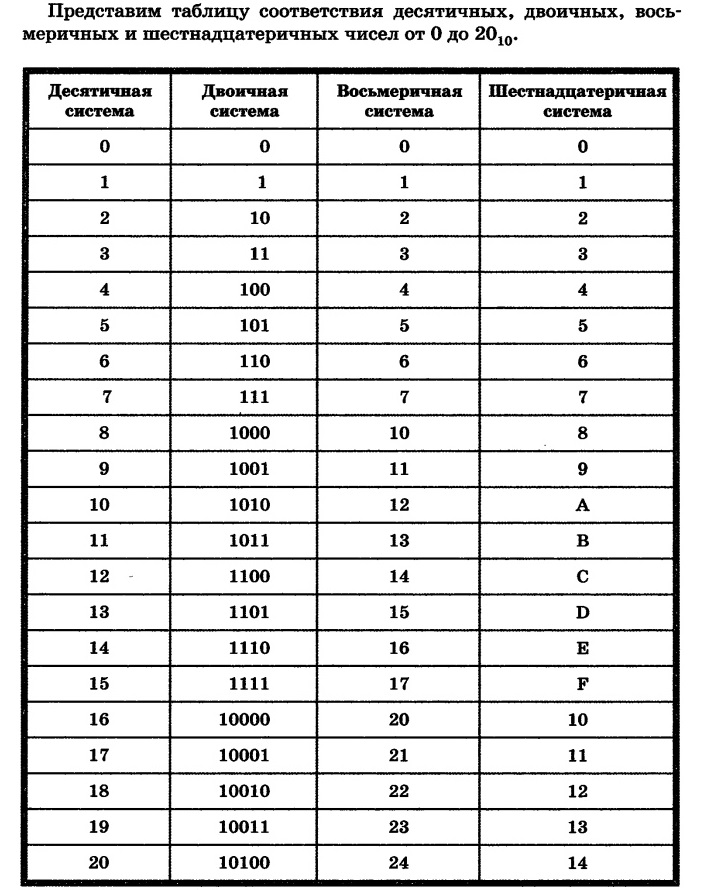
Грей-код является так называемым одношаговым кодом, т.е. при переходе от одного числа к другому всегда меняется лишь какой-то один из всех бит информации. Погрешность при считывании информации с механического кодового диска при переходе от одного числа к другому приведет лишь к тому, что переход от одного положения к другом будет лишь несколько смещен по времени, однако выдача совершенно неверного значения углового положения при переходе от одного положения к другому полностью исключается.
Преимуществом Грей-кода является также его способность зеркального отображения информации. Так инвертируя старший бит можно простым образом менять направление счета и таким образом подбирать к фактическому (физическому) направлению вращения оси.
Изменение направления счета таким образом может легко изменяться управляя так называемым входом ” Complement “. Выдаваемое значение может таким образом быть возврастающим или спадающим при одном и том же физическом направлении вращения оси.
Соответствие десятичных чисел в диапазоне от 0 до 15 двоичному коду и коду Грея
| Двоичное кодирование | Кодирование по методу Грея | ||||
| Десятичный код | Шестнадц. значение | Десятичный код | Двоичное значение | Шестнадц. значение | |
| 0 | 0000 | 0h | 0 | 0000 | 0h |
| 1 | 0001 | 1h | 1 | 0001 | 1h |
| 2 | 0010 | 2h | 3 | 0011 | 3h |
| 3 | 0011 | 3h | 2 | 2h | |
| 4 | 0100 | 4h | 6 | 0110 | 6h |
| 5 | 0101 | 5h | 7 | 0111 | 7h |
| 6 | 0110 | 6h | 5 | 0101 | 5h |
| 7 | 0111 | 7h | 4 | 0100 | 4h |
| 8 | 1000 | 8h | 12 | Ch | |
| 9 | 1001 | 9h | 13 | 1101 | Dh |
| 10 | 1010 | Ah | 15 | 1111 | Fh |
| 11 | 1011 | Bh | 14 | 1110 | Eh |
| 12 | 1100 | Ch | 10 | 1010 | Ah |
| 13 | 1101 | Dh | 11 | 1011 | Bh |
| 14 | 1110 | Eh | 9 | 1001 | 9h |
| 15 | 1111 | Fh | 8 | 1000 | 8h |
Преобразование кода Грея в привычный бинарный код можно осуществить используя простую схему с инверторами и логическими элементами “исключающее или” как показано ниже:
Код Gray-Excess
Обычный одношаговый Грей-код подходит для разрешений, которые могут быть представлены в виде числа возведенного в степень 2.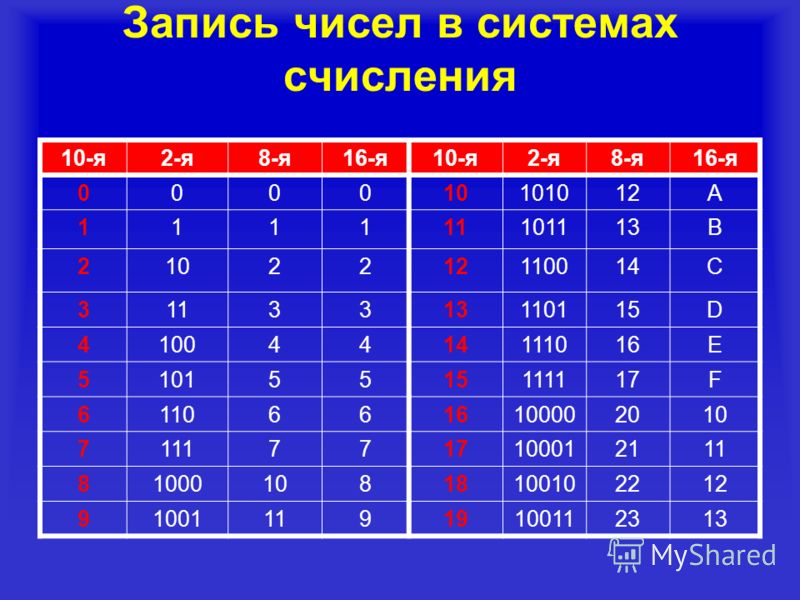
В случаях где надо реализовать другие разрешения из обычного Грей-кода вырезается и используется средний его участок. Таким образом сохраняется «одношаговость» кода. Однако числовой диапазон начинается не с нуля, а смещяется на определенное значение. При обработке информации от генерируемого сигнала отнимается половина разницы между первоначальным и редуцированным разрешением. Такие разрешения как например 360? для выражения угла часто реализируются этим методом. Так 9-ти битный Грей-код равный 512 шагов, урезанный с обеих сторон на 76 шагов будет равен 360°.
Двоичная система счисления | Информатика
В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, десятичная двойка является основанием двоичной системы счисления, аналогично тому, как в десятичной системе основанием является число десять.
Чтобы научиться считать в двоичной системе счисления, рассмотрим, как формируются числа в привычной для нас десятичной.
В десятичной системе счисления мы располагаем десятью знаками-цифрами: от 0 до 9.
Когда счет достигает числа 9, вводится новый более старший разряд – десятки. При этом разряд единиц обнуляется и счет в этом разряде опять начинается с нуля. После числа 19 разряд десятков увеличивается на 1, а разряд единиц снова обнуляется. Получается число 20. Когда десятки дойдут до 9, впереди них появится третий разряд – сотни.
Формирование каждого последующего числа в двоичной системе счисления аналогично тому, как это происходит в десятичной за исключением того, что используются всего-лишь две цифры: 0 и 1. Как только разряд достигает своего предела, то есть единицы, появляется новый разряд, а старый обнуляется.
0 1 10 11 100 101 110 111
Итак, число три в двоичной системе записывается как 11, в десятичной – как 3. Количественно это одинаковые числа. Это одно и то же число, выраженное в различных системах счисления. Если есть вероятность неоднозначной трактовки числа, к нему приписывается нижний индекс в десятичной системе счисления, обозначающий, в какой системе счисления выражено данное число:
112 = 310
Индекс для числа, выраженного в десятичной системе, обычно опускается.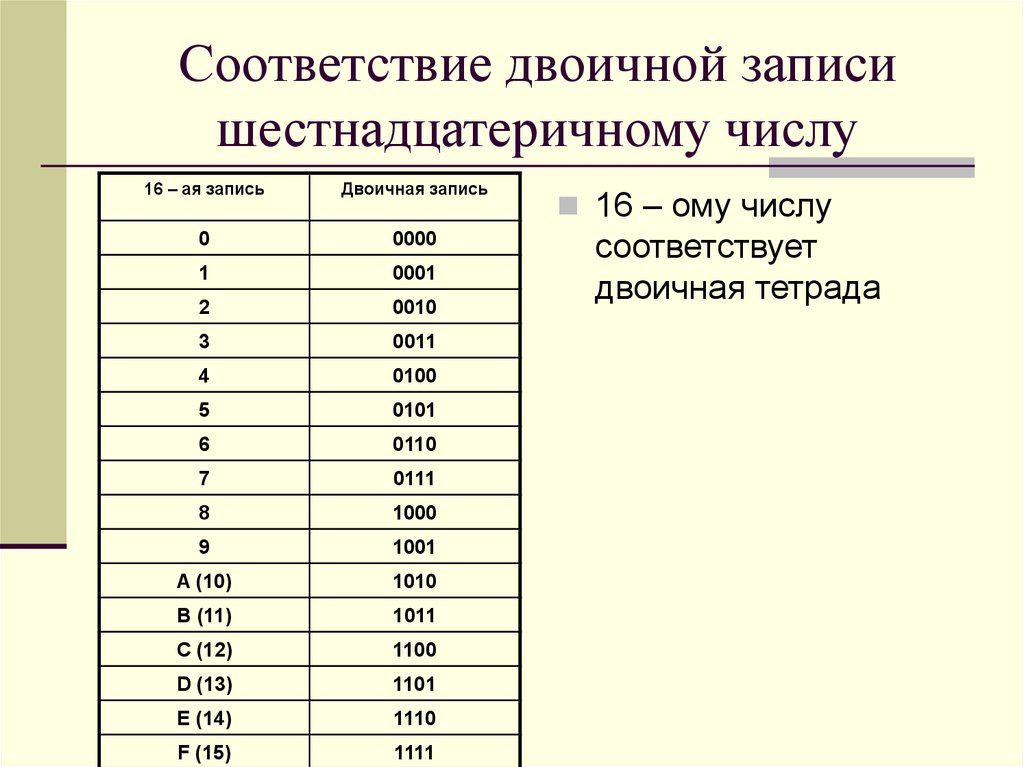
Перевод чисел из двоичной системы счисления в десятичную
В двоичной системе счисления с увеличением значения количество разрядов растет очень быстро. Как определить, что значит двоичное число 10001001? Нам сложно понять, сколько это, мы привыкли мыслить в десятичной системе. Поэтому часто используется перевод двоичных чисел в десятичные.
В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и так далее. Например:
5476 = 5000 + 400 + 70 + 6
Можно пойти еще дальше и разложить число, используя основание системы счисления, возводимое в показатель степени, равный разряду цифры, уменьшенному на единицу:
5476 = 5 * 103 + 4 * 102 + 7 * 101 + 6 * 100
После равенства числа 5, 4, 7 и 6 – это набор цифр из которых состоит число 5476. Все эти цифры умножаются на десять, возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.
Так, например, 6 находится в первом разряде, поэтому она умножается на 10(1-1). Натуральное число в нулевой степени равно единице. Таким образом, мы умножаем 6 на 1.
Точно также производится разложение числа в двоичной системы счисления, кроме того, что основанием выступает двойка, а не десятка. Здесь до знака равенства число представлено в двоичной системе счисления, после «равно» запись идет в десятичной:
10001001 = 1 * 27 + 0 * 26 + 0 * 25 + 0 * 24 + 1 * 23 + 0 * 22 + 0 * 21 + 1 * 20
Результат вычислений дает десятичное число, количественно равное двоичному 10001001:
1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20 =
= 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137
То есть число 10001001 по основанию 2 равно числу 137 по основанию 10:
100010012 = 13710
Почему двоичная система счисления так распространена?
Дело в том, что двоичная система счисления – это язык современной вычислительной техники.
Когда любые данные сохраняются на компьютере, они кодируются числами. С числами же компьютер выполняет операции, изменяя эти данные.
Допустим, у нас есть десятичное число 14, которое требуется сохранить в компьютерной памяти. Мы задействуем участок памяти, в данном случае состоящий как минимум из двух элементов, отводимых под разряды. В одном из разрядов мы сохраняем десятичное число 1, в другом – число 4.
Элемент памяти – это физическое устройство. Если проектировать его для хранения десятичной цифры, потребуется создать такое устройство, которое может находиться в десяти разных физических состояниях и способно переключаться между ними. Каждое из этих состояний будет соответствовать числу от 0 до 9.
Создать такой элемент памяти возможно, однако сложнее и дороже, чем создать элемент, способный находиться только в двух состояниях. Одно состояние сопоставить нулю, второе – единице. Кроме того, подобное хранение данных является более надежным.
Поэтому оказалось проще перевести число 14 в двоичную систему счисления, получив число 1110, и именно его сохранить в памяти.
И пусть даже при этом будут задействованы не два, а четыре разряда, то есть четыре элементарных единиц памяти.
Перевод десятичного числа в двоичное
Одним из алгоритмов перевода десятичного числа в двоичное является деление нацело на два с последующим «сбором» двоичного числа из остатков. Переведем таким образом число 14 в двоичное представление.
14 / 2 = 7, остаток 0 7 / 2 = 3, остаток 1 3 / 2 = 1, остаток 1 1 / 2 = 0, остаток 1
Собирать остатки надо с конца, то есть с последнего деления. Получаем 1110.
Выполним то же самое для числа 77:
77 / 2 = 38, остаток 1 38 / 2 = 19, остаток 0 19 / 2 = 9, остаток 1 9 / 2 = 4, остаток 1 4 / 2 = 2, остаток 0 2 / 2 = 1, остаток 0 1 / 2 = 0, остаток 1
Собираем остатки вместе, начиная с конца: 1001101.
Проверим, выполнив обратный перевод:
1001101 = 1*26 + 0*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77
Двоичная система счисления — Схема, преобразование и операции
Двоичная система счисления используется для определения числа в двоичной системе.
Двоичная система используется для представления числа только двумя числами, 0 и 1. Двоичная система счисления обычно используется компьютерными языками, такими как Java, C++. Поскольку компьютер понимает только двоичный язык, равный 0 или 1, все входные данные, поступающие на компьютер, декодируются им в серии нулей или единиц для дальнейшей обработки. В этом уроке мы узнаем, как преобразовать десятичное число в его двоичное число и преобразовать двоичное число в десятичное число.
| 1. | Что такое двоичная система счисления? |
| 2. | Таблица двоичной системы счисления |
| 3. | Преобразование двоичного кода в десятичный |
| 4. | Преобразование десятичного числа в двоичное |
| 5. | Операции с двоичными числами |
| 6. | Часто задаваемые вопросы о двоичной системе счисления |
Что такое двоичная система счисления?
«Би» в двоичном формате означает «два».
Следовательно, это возвращает линию к представлению числа только с точки зрения 0 и 1. Можно легко выразить десятичные числа в терминах двоичной системы счисления. Десятичные числа и двоичные числа имеют разные обозначения. Десятичное число представлено с основанием 10, а двоичное число представлено с основанием 2. Например, 2 в десятичной записи представлено как \((2)_{10}\). Двоичное число для 2 представлено как \((10)_{2}\). Следовательно, 10 — это двоичное представление числа 2.
Таблица двоичной системы счисления
Числа от 1 до 10 могут быть выражены в двоичной системе счисления следующим образом:
Преобразование двоичного кода в десятичный
Двоичное число можно преобразовать в десятичное число, представив каждую цифру как произведение заданного числа 1 или 0 в соответствующей степени двойки. Если двоичное число состоит из n цифр, B = \(a_{n-1 }…a_{3}a_{2}a_{1}a_{0}\), десятичное число для него задается как, D = (a 0 × 2 0 ) + (а 1 × 2 1 ) + (а 2 × 2 2 ) + .
..
Давайте разберемся в этом на примере.
Мы можем преобразовать 10101 в десятичную форму следующим образом:
Двоичное число 10101 выражается как \((10101)_{2}\) = (1 × 2 4 ) + (0 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 ) = \((21)_{10}\). Таким образом, двоичное число 10101 выражается как \((21)_{10}\).
Преобразование десятичного числа в двоичное
Десятичное число можно преобразовать в двоичное путем деления данного числа на 2, пока мы не получим частное, равное 1. Числа записываются снизу вверх.
Давайте разберемся в этом на примере.
Мы можем преобразовать 30 в двоичную форму следующим образом:
Десятичное число 30 выражается как \((30)_{10}\) = \((11110)_{2}\).
Операции с двоичными числами
Двоичное сложение
Складываем двоичные числа поразрядно и получаем ответ на сложение. При сложении двух двоичных чисел важно помнить приведенную ниже таблицу.
Двоичное вычитание
Двоичные числа вычитаются цифра за цифрой и получается ответ. Приведенная ниже таблица учитывается при вычитании двух двоичных чисел.
Двоичное умножение
Правила умножения любых двух двоичных чисел задаются следующим образом:
Дополнение до 1 и 2 двоичного числа
- Дополнение до 1 двоичного числа получается путем инвертирования цифр двоичного числа. Например, дополнением \((101)_{2}\) до 1 является \((010)_{2}\).
- Дополнение до 2 двоичного числа получается путем инвертирования цифр двоичного числа и добавления 1 к младшему значащему биту. Например, дополнение 2 к \((111)_{2}\) равно \((001)_{2}\), которое получается путем взятия дополнения 1 к \((111)_{2}\) и добавления 1 до младшего значащего бита.
Советы, которые следует помнить
Вот несколько важных моментов, которые следует помнить о двоичной системе счисления:
- Двоичное число состоит из двух чисел 0 и 1.
- Двоичные числа представлены цифрой 2 в основании. Например, \((101)_{2}\).
- Каждая цифра двоичного числа называется битом. Например, \((111)_{2}\) — трехбитная двоичная система.
- Двоичное сложение также называется операцией «И».
- Двоичное умножение также называется операцией «ИЛИ».
- Двоичное вычитание можно выполнить, взяв 1 и 2 в дополнении к двоичному числу.
- Старшая цифра в двоичном числе представляет знак двоичного числа, который используется для выполнения двоичных операций со знаком. 1 представляет отрицательный знак, а 0 представляет положительный знак.
Темы, относящиеся к двоичной системе счисления
- 32 в двоичной системе счисления
- 128 в двоичном формате
- 255 в двоичном формате
- Двоично-десятичный калькулятор
- Двоичный калькулятор
- Двоично-десятичная формула
Примеры двоичной системы счисления
Пример 1: Преобразование десятичного числа \((162)_{10}\) в двоичное.
Решение: Чтобы получить двоичное число для 162, мы можем непрерывно делить его на 2.
Частное Остаток 81 0 40 1 20 0 10 0 5 0 2 1 1 0 0 1
\(\следовательно\) Двоичное число для \((162)_{10}\) равно \((10100010)_{2}\).Пример 2: Преобразование двоичного числа \((100101)_{2}\) в десятичное число.
Решение: Двоичное число \((100101)_{2}\) = (1 × 2 0 ) + (0 × 2 1 ) + (1 × 2 2 ) + (0 × 2 3 ) + (0 × 2 4 ) + (1 × 2 5 ) = \((37)_{10}\)
\(\следовательно\) Двоичное число \((100101)_{2}\) равно \((37)_{10}\).Пример 3: Докажите, что двоичное число \((1000100)_{2}\) можно преобразовать в десятичное число \((68)_{10}\).
Решение: Двоичное число \((1000100)_{2}\) = (0 × 2 0 ) + (0 × 2 1 ) + (1 × 2 2 ) + (0 × 2 3 ) + (0 × 2 4 ) + (0 × 2 5 ) + (1 × 2 6 ) = 64 + 4 = \((68)_{10}\)
\(\следовательно\) Двоичное число \((1000100)_{2}\) можно преобразовать в двоичное число \((68)_{10}\).
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами
Записаться на бесплатный пробный урок
Практические вопросы по двоичной системе счисления
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о двоичной системе счисления
Что такое двоичная система счисления?
Система представления, в которой число может быть выражено только двумя цифрами (0 и 1) с основанием 2, называется двоичной системой счисления.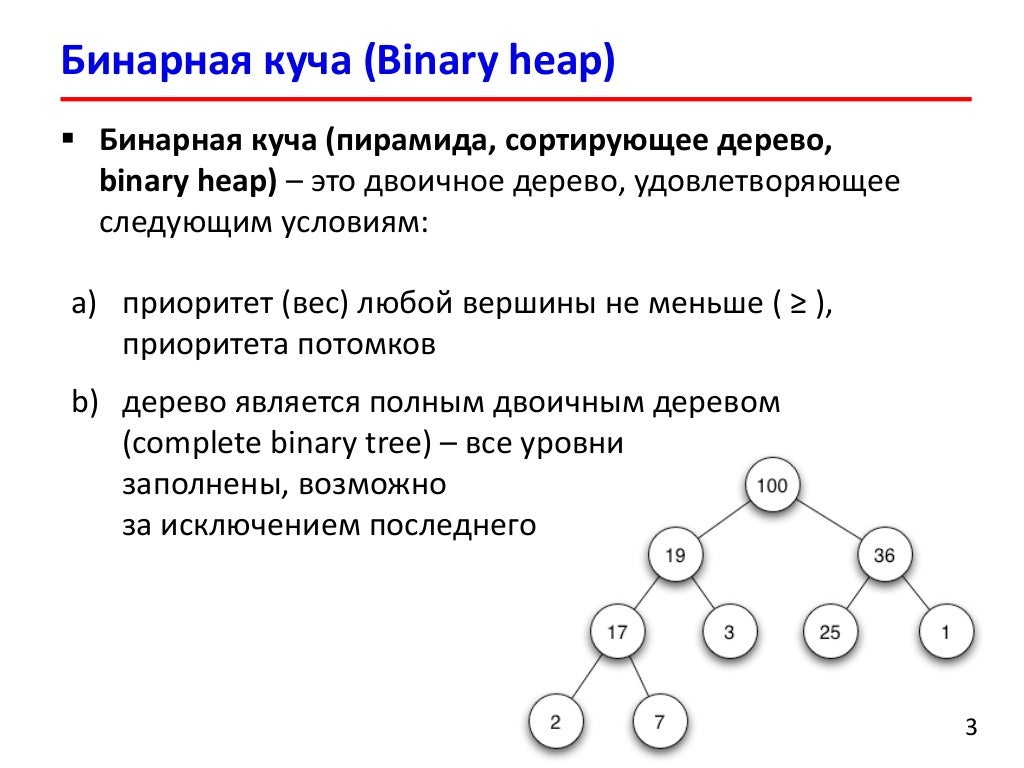
Почему в компьютерах используется двоичная система счисления?
Компьютерные системы всегда обрабатывают заданные инструкции, используя 0 или 1, поскольку они существуют либо во включенном, либо в выключенном состоянии. Это позволяет им быстрее обрабатывать информацию.
Что означает 10101 в двоичной системе счисления?
10101 означает 21 в двоичной системе счисления.
Как преобразовать десятичное число в двоичную систему счисления?
Десятичное число можно преобразовать в двоичную систему счисления, разделив данное число на 2, пока мы не получим частное, равное 1. Числа записываются снизу вверх.
Как преобразовать двоичное число в десятичное число?
Мы можем преобразовать двоичное число в десятичное число, выражая каждую цифру как произведение заданного числа 1 или 0 в соответствующей степени 2. Если двоичное число имеет n цифр, B = \((a)_{n -1}\).. \((а)_{3}\) \((а)_{2}\) \((а)_{1}\) \((а)_{0}\ ), десятичное число для него дается как, D = ( \((a)_{0}\)×2 0 ) + ( \((a)_{1}\)×2 1 ) + ( \((a)_{2}\)×2 2 ) + .
..
Что означает 1011 означает в двоичной системе счисления?
1011 означает 11 в двоичной системе счисления как 1 × 2 0 + 1 × 2 1 + 0 × 2 2 + 1 × 2 3 = 1+ 2+ 0 + 8 = 11.
. 
10.2021, автор: Computer Hope
Таким образом, числа физически представлены внутри вычислительного устройства, что позволяет выполнять вычисления. Эта концепция более подробно объясняется в нашем разделе о том, как читать двоичные числа.
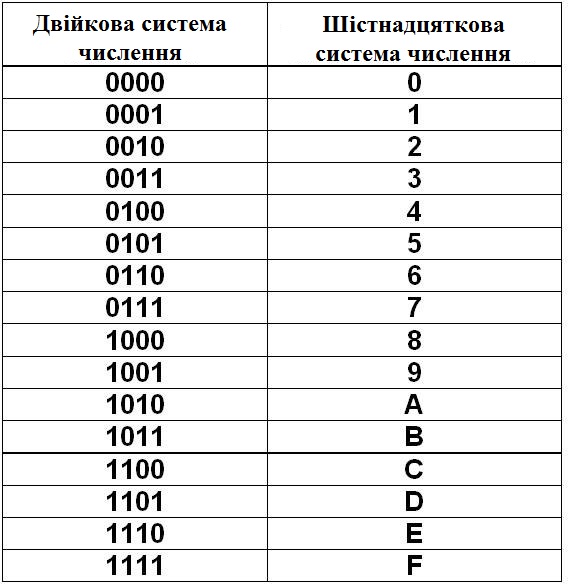
Каждый столбец представляет число два, возведенное в степень, причем значение этой степени увеличивается на единицу при перемещении по каждой из восьми позиций. Чтобы получить итог этого примера, прочитайте диаграмму от справа налево и добавьте значение каждого столбца к предыдущему столбцу: (8+32+64) = 104. Как видите, мы не считаем биты с 0, потому что они «выключены».| Показатель степени: | 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
| Значение: | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| ВКЛ/ВЫКЛ: | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
Следующий пример — 11111111 в двоичном формате, максимальное 8-битное значение 255.
Опять же, читая справа налево, мы имеем 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 = 255.
| Значение: | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| ВКЛ/ВЫКЛ: | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Примечание
Счет на компьютере обычно начинается с «0» вместо «1». Следовательно, подсчет всех битов равен 255, но если начать с 0, получится 256.
Когда у вас восемь бит, это равно одному байту. Если вы возьмете двоичный код из первого примера (01101000), что в сумме составляет «104», и поместите его в ASCII, получится строчная буква «h». Чтобы написать слово «привет», вам нужно добавить двоичный код для буквы «i», то есть 01101001. Соединив эти два кода, мы получим 0110100001101001 или 104 и 105, что представляет «привет».
Дополнительную информацию о преобразовании двоичного кода в ASCII можно найти по следующей ссылке.
- Как компьютер преобразует текст в двоичный код или в 0 и 1?
Как добавить в двоичный файл
Сложение в двоичном формате очень похоже на сложение в десятичном формате. Например, если бы у нас был двоичный файл 01101011 (107) и мы хотели добавить 10000111 (135), мы бы выполнили следующие шаги.
| + | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Начиная с правой стороны, мы должны добавить 1+1, чтобы получить «2». Поскольку в двоичном формате нет числа два, мы будем использовать двоичное значение «10» и перенести «1» в следующий столбец.
В следующем столбце мы добавили бы «1», которую мы перенесли в следующий столбец, и добавили бы 1+1+1, чтобы получить «3».
В двоичном формате нет числа «3», поэтому мы используем «11» (3 в двоичном формате), ставим 1 и переносим 1 в следующий столбец.
Затем мы снова добавляем «1», которая была перенесена, и добавляем 1+0+1, чтобы получить «10» (2 в двоичном формате).
| 0 | 1 | 0 |
Мы повторяем этот же процесс для всех восьми цифр, чтобы получить следующий результат 11110010 (242).
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 |
Что такое сдвиг влево и вправо?
Сдвиг влево — это когда каждый бит в двоичном числе сдвигается (перемещается) влево, чтобы удвоить двоичное значение или умножить его на два. Например, двоичное число «00000011» равно трем, а при сдвиге влево оно становится «00000110», что равно шести. Другой пример: двоичное число «00111110» равно 62, а сдвиг битов влево дает «01111100» или 124.
A правый сдвиг похож на сдвиг влево, за исключением того, что биты сдвигаются вправо, чтобы разделить число на два. Например, двоичное число «00001010» равно десяти, а при сдвиге вправо оно становится «00000101» или пятью.
Что такое префикс «0b»?
Во избежание путаницы при записи двоичного числа оно может иметь префикс «0b» (ноль и b). Например, 0b0100 представляет «0100» в двоичном формате. Используя этот префикс, читатель знает, что это не «100» в десятичном виде.
Бинарный юмор
Изображение является примером бинарного юмора (шутки) с помощью известного высказывания на многих футболках гиков. Те, кто умеет читать в двоичном формате, понимают, что эта цитата на самом деле говорит: «В мире есть только 90 774 двух 90 775 типов людей: те, кто понимает двоичный код, и те, кто не понимает». В двоичной системе 10 равно два , а не число десять .
Преобразовать текст в двоичный
Следующий инструмент преобразует любой текст в двоичный.