Деление в столбик ➗ примеры и правила, как научиться
Как правильно делить в столбик
Делить столбиком проще, чем высчитывать в уме. Этот способ наглядный, помогает держать во внимании каждый шаг и запомнить алгоритм, который впоследствии будет срабатывать автоматически.
Рассмотрим пример деления трёхзначного числа на однозначное 322:7. Для начала определимся с терминами:
- 322 — делимое или то, что необходимо поделить;
- 7 — делитель или то, на что нужно поделить:
- частное — результат действия.
Шаг 1. Слева размещаем делимое 322, справа делитель 7, между ставим уголок, а частное посчитаем и запишем под делителем.
Шаг 2. Смотрим на делимое слева направо и находим ту часть, которая больше делителя. 3, 32 или 322? Нам подходит 32. Теперь нужно определить сколько раз наш делитель 7 содержится в числе 32. Похоже, что четыре раза. Проверяем 4*7=28, 28<32 все верно. Пишем 4 под чертой — это первая цифра частного. Между 32 и 28 ставим знак «минус», вычитаем по правилам и результат записываем под чертой.
Результат вычитания должен быть меньше делителя. Если это не так, значит есть ошибка в расчете. Нужно увеличить выбранное число и выполнить действие еще раз.
Шаг 3. Остаток равен 4. Для продолжения решения его нужно увеличить. Мы сделаем это за счет следующей цифры делимого. Приписываем к четверке оставшуюся 2 и продолжаем размышлять.
Шаг 4. Сколько раз делитель 7 содержится в 42? Кажется, шесть раз. Проверяем 7*6=42, 42=42 все верно. Записываем полученное число к четверке справа — это вторая цифра частного. Делаем вычитание в столбик 42 из 42, в остатке получаем 0. Значит числа разделились нацело.
Мы закончили решать пример и в результате получили целое число 46.
Как выглядит деление в столбик с остатком
Это такое же деление, только в результате получается неровное число, как получилось в примере выше.
- Например, делим 19 на 5. Наибольшее число, делящееся на 5 до 19 это 15. Проверяем 5*3=15, 19-15=4. Ответ: 3 и остаток 4. Записываем так: 19:5=3(4).
- Еще пример: делим 29 на 6. Также определяем максимальное число, делящееся на 6 до 29. Подходит 24. Ответом будет: 4 и остаток 5. А записываем: 29:6=4(5).
Примеры на деление в столбик
Давайте закрепим знания на практике. Для этого разделите столбиком примеры ниже, а после проверьте полученные цифры — чур, не подглядывать!
|
Ответы:
- легкий уровень: 9; 12; 7; 8; 19;
- средний уровень: 18; 36; 63; 91; 95;
- сложный уровень: 159; 24; 54; 82; 73.
В детской школе Skysmart ученики решают примеры вместе с енотом Максом и его друзьями. Мы подобрали для вашего ребенка тысячи увлекательных заданий — от простых логических загадок до хитрых головоломок, над которыми интересно подумать. Все это поможет легче и быстрее справиться со школьной математикой. Запишите вашего ребенка на бесплатный вводный урок математики в Skysmart — мы покажем, что математика может быть увлекательным путешествием!
😃 Деление — правила, секретные примеры, упражнения, игры
Деление – одна из четырех основных математических операций (сложение, вычитание, умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Деление – интересная операция, в чем мы и убедимся с вами в этой статье!
Деление чисел
Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение. 3*3=9. Верно? Абсолютно.
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Деление с остатком
Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.
Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
Деление на 3 и 9
Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Найти сумму цифр делимого.
Поделить на 3 или 9 (в зависимости от того, что вам нужно).
Если ответ получается без остатка, то и число поделится без остатка.
Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.
Умножение и деление
Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение. В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление 3 класс
В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:
Задача 1. Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?
Задача 2. На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
Задача 3. Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?
Задача 4. Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг. Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг. Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг. Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг. Ставим точку под делителем.
5 шаг. После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:
6 шаг. Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг. Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг. Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг*. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3)(4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Деление натуральных чисел
Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление презентация
Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Презентация на тему «Деление»
Примеры на деление
Легкий уровень
28:4=
16:8=
27:3=
32:8=
64:8=
54:6=
42:6=
49:7=
40:8=
Средний уровень
225:15=
512:8=
144:9=
312:6=
315:7=
625:25=
392:4=
984:8=
Сложный уровень
5712:68=
1035:23=
1121:59=
2352:49=
1610:35=
6300:75=
875:35=
297000:270=
385000:11=
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Играть сейчас
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Играть сейчас
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Играть сейчас
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Играть сейчас
Игра «Копилка»
Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Играть сейчас
Игра «Быстрое сложение перезагрузка»
Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Играть сейчас
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать.
После прохождения курса ребенок сможет:
- В 2-5 раз лучше запоминать тексты, лица, цифры, слова
- Научится запоминать на более длительный срок
- Увеличится скорость воспоминания нужной информации
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Как улучшить память и развить внимание
Бесплатное практическое занятие от advance.
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Деление / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Деление
В этом разделе познакомимся с делением и узнаем, что деление – это математическая операция, обратная умножению.
Умножение – это последовательное сложение чисел, а деление – это последовательное вычитание чисел.
В математике существует знак для умножения — это точка ( • ) посередине строки между числами, которые нужно перемножить, а для деления существует особый знак — это две точки ( : ) между числами, которые нужно поделить между собой.
Как ёжикам поделить между собой яблоки поровну?
Нужно воспользоваться действием деления и узнать, сколько раз по 3 содержится в 6.
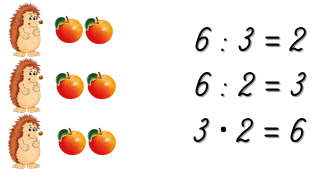
1) 6 : 3 = 2 (яб.) — мы узнали, сколько яблок получит каждый ёжик.
2) 6 : 2 = 3 (ёж.) — мы узнали, сколько ёжиков получат по 2 яблока.
3) 2 • 3 = 6 (яб.) — мы узнали, сколько яблок нужно, чтобы у каждого из трёх ёжиков было по 2 яблока.
Любой пример на умножение можно представить двумя примерами на деление.
Например, для выражения 6 • 4 = 24 есть два обратных выражения:
24 : 4 = 6 — нужно из 24 вычесть число 4 ровно 6 раз.
24 : 6 = 4 — нужно из 24 вычесть число 6 ровно 4 раз.
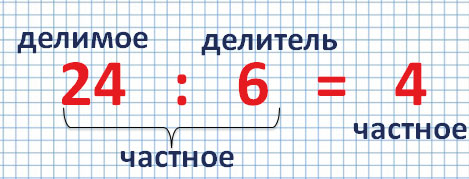
Числа при делении
При делении, как и при другом математическом действии, каждое число имеет свое название.
Число, которое делят, называется делимое.
Число, на которое делят, называется делитель.
Результат деления называется частное.
Чтение числовых выражений
24 : 6 = 4
Этот пример можно прочитать по-разному.- 24 разделить на 6 равняется 4.
- 24 уменьшить в 6 раз – получится 4.
- Делимое – 24, делитель – 6, частное – 4.
- Частное от деления числа 24 на 6 равно 4.
Деление на 1
4 : 1 = 4
23 : 1 = 23

Деление на 0

Деление числа само на себя
Связь деления и умножения

Чётные и нечётные числа
Числа, которые делятся на 2 без остатка, называются чётными, а числа, которые не делятся на 2 без остатка, называются нечётными.
Чётные: 6, 22 44, 60, 74, 82, 96
Нечётные: 7, 13, 21, 37, 45, 97
В несколько раз меньше
Для примера решим задачу:
В магазине было 8 котят, а лисичек
составим схему:
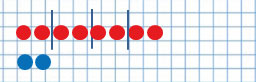
Значит, чтобы узнать, сколько было лисичек, нужно 8 : 4 = 2 (л.)
Вывод: Если в задаче есть слова «в … раз меньше», то задача решается делением.
Во сколько раз больше? Во сколько раз меньше?
Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?

Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?
8 : 2 = 4 (раза)
Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Табличное деление
Внетабличное деление
Деление с остатком
Деление суммы на число
Деление на однозначное число
Деление чисел, оканчивающихся нулями
Свойства деления
Правило встречается в следующих упражнениях:
2 класс
Страница 58. Вариант 1. № 1, Моро, Волкова, Проверочные работы
Страница 66, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 72, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 74, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 75, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 78, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 79, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 84, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 65, Моро, Волкова, Рабочая тетрадь, 2 часть
Страница 72, Моро, Волкова, Рабочая тетрадь, 2 часть
3 класс
Страница 21, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 108, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 20. Вариант 1. Тест 1, Моро, Волкова, Проверочные работы
Страница 37. Вариант 2. № 4, Моро, Волкова, Проверочные работы
Страница 55. Вариант 2. Тест 2, Моро, Волкова, Проверочные работы
Страница 61. Вариант 2. Тест 2, Моро, Волкова, Проверочные работы
Страница 82, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 99, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 105, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 59, Моро, Волкова, Рабочая тетрадь, 2 часть
4 класс
Страница 5, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 20, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 66, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 82, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 90, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 24, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 55, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 58, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 89, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 47, Моро, Волкова, Рабочая тетрадь, 2 часть
5 класс
Задание 441, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 673, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 818, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Упражнение 36, Мерзляк, Полонский, Якир, Учебник
Упражнение 1, Мерзляк, Полонский, Якир, Учебник
Упражнение 520, Мерзляк, Полонский, Якир, Учебник
Упражнение 656, Мерзляк, Полонский, Якир, Учебник
Упражнение 657, Мерзляк, Полонский, Якир, Учебник
Упражнение 673, Мерзляк, Полонский, Якир, Учебник
Упражнение 1050, Мерзляк, Полонский, Якир, Учебник
© budu5.com, 2020
Пользовательское соглашение
Copyright
примеры на умножение и деление, сложение и вычитание
Ваш ребенок еще только учится в начальной школе, а вы уже задумываетесь о его дальнейшей учебе, развитии и будущем? Это очень похвально. А думали ли вы над тем, что успеваемость ребенка можно улучшить, если заниматься с ним ежедневно по математике всего лишь 15 минут в день дополнительно? И это не выдумки. В материалах этой статьи мы приведем примеры и задачи для школьников начальной школы по математике, а именно, для третьеклассников. (Для удобства решения приведенные ниже задания вы можете распечатать).
Как учить ребенка учиться
Умеет ли ваш ребенок учиться? Уверена, что многих родителей этот вопрос поставил в тупик. А действительно, что значит «уметь учиться»? Когда ваш юный школьник только пошел в школу, после занятий, возможно, он бежал домой и очень хотел сразу же делать уроки. Так бывает, когда дети очень ждут поступления в 1 класс. Но со временем интересы к своевременному выполнению домашнего задания ослабевают и «домашка» становится скучным времяпровождением.
А ведь именно нежелание выполнять домашние задания, готовиться к школьным рефератам, семинарам и викторинам, становится основной причиной того, что ребенок вначале не хочет, а после и не умеет учиться. Пробелы в знаниях могут накапливаться словно снежный ком, снижая успеваемость школьника и убивая в нем желание учиться.
Чтобы школьник учился этой сложной и ответственной науке – учиться – родители должны всячески помогать ему: составить распорядок дня, учить ребенка выполнять домашнее задание наперед, прорешивать или прописывать дополнительные упражнения, чтобы тренировать и руку для письма, и мозг для устного счета. Математике дается детям начального звена сложнее всего, именно поэтому мы и подготовили для школьников 3 класса этот материал.
Примеры по математике на умножение и деление
Еще во втором классе дети выучили таблицу умножения. Если вы сейчас находитесь в полном заблуждении, как выучить с ребенком таблицу умножения, то рекомендуем к ознакомлению следующий материал по ссылке. На протяжении второго класса школьники постепенно осваивали простые примеры и задачи, используя таблицу умножения, а в третьем классе они оттачивают навыки умножения и сложения.
Задание 1
Заменить сложение вычитанием в тех примерах, в которых от замены знака ответ не изменится:
5 + 5 + 5 =
1 + 1 + 1 + 1 =
0 + 0 + 0 + 0 + 0 =
8 + 8 + 8 + 8 =
7 + 7 — 7 + 7 =
7 + 7 + 7 — 7 =
14 + 14 =
61 + 61 =
Подсказка:
5 + 5 + 5 = 15, если заменить знак «+» на знак «•», то получится
5 • 5 • 5 = 125. 15 не равно 125. Значит, в первом равенстве заменить знак «+» на знак «•» нельзя.
По аналогии решаем стальные равенства и делаем выводы о возможной или невозможной замене знака «+» на знак «•».
Задание 2
Какие выражения нельзя заменить суммой, чтобы ответ не изменился:
0 • 4 =
1 • 0 =
1 • 1 =
1 • 6 =
0 • 9 =
7 • 0 =
5 • 2 =
2 • 2 =
Подсказка:
Вспомните, каким правилом следует пользоваться при умножении на ноль.
Задание 3
Решите примеры:
45 : 5 + 1 =
45 : 5 • 1 =
543 — 5 • 1 =
(543 — 5) • 1 =
423 + 7 • 0 =
(423 + 7) • 1 =
10 — 0 + 4 =
10 • 0 + 4 =
Задание 4
Из каждого выражения на умножение составьте выражения на деление:
6 • 8 =
7 • 1 =
4 • 0 =
0 • 3 =
4 • 9 =
Подсказка
6 • 8 = 48
48 : 8 = 6
48 : 8 = 6
Задание 5
Какое значение имеют следующие выражение:
а : а =
а : 1 =
0 : а =
а : 0 =
Задание 6
Решите примеры:
(596 + 374) • 1 =
596 + 374 • 1 =
(596 + 374) • 0 =
596 + 374 + 0 =
0 • 320 : 1 =
0 + 320 : 1 =
Обязательно повторите с ребенком правила умножения и деления числа на единицу и умножения или деления числа на ноль, а также особенности деления ноля на любое число. Часто именно в этих примерах дети делают ошибки, которые влекут за собой дальнейшее неправильное решение примеров, выражений и задач.
Задание 7 (задача)
В оздоровительный лагерь привезли фрукты: 7 ящиков винограда и 5 ящиков персиков. Масса привезенных персиков составляет 40 килограммов. Какая масса винограда, если ящик винограда на 1 килограмм весит больше, чем ящик персиков.
Решение
Найдем, сколько весит один ящик персиков. Известно, что общая масса персиков составляет 40 кг, а всего ящиков – 5.
Первое действие:
40 : 5 = 8 (кг) весит один ящик персиков.
Теперь найдем, сколько весит один ящик винограда, если известно, что он тяжелее на 1 кг, чем ящик персиков.
Второе действие:
8 + 1 = 9 (кг) весит один ящик винограда.
Теперь находим общую массу всего винограда, если известно, что один ящик весит 9 кг, а всего винограда – 7 ящиков.
Третье действие:
9 • 7 = 63 (кг) – общая масса винограда.
Ответ: масса привезенного винограда составляет 63 кг.
Задание 8
Сосна может расти 600 лет, береза – 350 лет. А ива – в 6 раз меньше от сосны. Что может расти дольше береза или ива? И насколько лет?
Решение
Вначале рассчитаем, сколько лет может расти ива, если известно, что она растет в 6 раз меньше, чем сосна.
Первое действие:
600 : 6 = 100 (лет) может расти ива.
Теперь, когда известно, что ива может расти 100 лет, сравним продолжительность «жизни» березы и ивы. Известно, что береза растет 350 лет, а ива – 100. 350 больше чем 100, значит береза может расти дольше ивы. Чтобы рассчитать, на сколько береза может расти дольше ивы, решаем равенство.
Второе действие:
350 — 100 = 250 (лет) – на столько береза может расти дольше ивы
Ответ: береза может расти дольше ивы на 250 лет.
Важно! Если задачу можно решить несколькими способами, обязательно сообщите об этом ребенку. Пусть потренирует логику и начертит все возможные схем решения задачи, т.е. составить схематическое условие. Ведь правильно составленное условие задачи – это 90% успешного решения.
Задание 9
В понедельник гусеница начала ползти вверх по дереву высотой 9 метров. За день она поднялась вверх на 5 метров, а за ночь – опустилась на 2 метра. На какой день гусеница достигнет верхушки дерева?
Решение
Для начала рассчитаем, на сколько метров поднимается гусеница вверх за один день, с учетом того, что ночью на опускается.
Первое действие:
5 — 2 = 3 (м) гусеница проползает за сутки вверх.
Теперь найдем количеств дней, необходимых на преодоление расстояния 9 метров вверх по дереву.
Второе действие:
9 : 3 = 3 (дня) нужно гусенице, чтобы достичь вершины дерева.
Ответ: 3 дня нужно гусенице, чтобы достичь вершины дерева.
Задание 10
В коробке было 18 килограммов печенья. Сначала из нее взяли 13 килограммов печенья, потом досыпали в 4 раза больше, чем оставалось. Сколько килограммов печенья стало в коробке.
Решение
Сначала найдем, сколько килограммов печенья осталось в коробке, после того, как из нее забрали 13 килограммов.
Первое действие:
18 — 13 = 5 (кг) печенья осталось в коробке
Теперь рассчитаем сколько килограммов печенья досыпали в коробку.
Второе действие:
5 • 4 = 20 (кг) досыпали
Сложим тот вес, который оставался в коробке, и тот, который досыпали, чтобы найти, сколько килограммов печения стало в коробке.
Третье действие:
5 + 20 = 25 (кг) стало
Ответ: 25 килограммов печения стало в коробке.
Задание 11
За лето хозяйка вырастила 208 домашних птиц. Кур и уток было 129, а уток и гусей – 115. Сколько кур, уток и гусей вырастила хозяйка за лето?
Решение
Известно, что кур и уток было 129, а всего птиц – 208. Значит, можно найти количество гусей.
Первое действие:
208 (птиц) – 129 (уток + кур) = 79 гусей
Также известно, что уток и гусей всего 115, значит мы можем найти, сколько было кур.
Второе действие:
208 (птиц) – 115 (уток + гусей) = 93 кур
Теперь, когда мы знаем количество гусей и кур, а также общее количество домашних птиц, мы можем найти количество уток.
Третье действие:
208 — (79 + 93) = 36 уток
Ответ: за лето хозяйка вырастила 79 гусей, 93 кур и 36 уток.
Второй вариант решения
Известно, что кур и уток было 129, а всего птиц – 208. Значит, можно найти количество гусей.
Первое действие:
208 (птиц) – 129 (уток + кур) = 79 гусей
Также известно, что уток и гусей всего 115, значит мы можем найти, сколько было уток
Второе действие:
115 (уток + гусей) – 79 (гусей) = 36 уток
Теперь, когда мы знаем количество гусей и уток по отдельности, а также общее количество домашних птиц, мы можем найти количество кур.
Третье действие:
208 – (79 + 36) = 208 – 115 = 93 кур
Ответ: за лето хозяйка вырастила 79 гусей, 93 кур и 36 уток.
Примеры и задачи по математике на сложение и вычитание
Основной задачей заданий и примеров по математике на сложение и вычитание в третьем классе является популяризация математических знаний и идей, поддержка и развитие математических знаний школьников, стимулирование и мотивация учеников в изучении естественно-математический предметов.
Задание 1
Реши уравнения:
Х – 40 = 60
Х + 4 = 61
Х – 16 = 25
Х + 25 = 84
Х – 45 = 251
Х + 56 = 106
Х + 78 = 301
Задание 2
Расставьте скобки так, чтобы ответом выражения в первом случае было 6, а в втором – 2:
12 : 2 + 2 • 2 =
Подсказка
12 : (2 + 2) • 2 = 6
12 : (2 + 2 • 2) = 2
Важно! Некоторые условия составлены таким образом, чтобы ребенок включал логическое мышление. Прорешивая такие задания он мыслит, делает предположения, размышляет, и находит правильное решение задания.
Задание 3
Перевести в одну систему измерения и решить выражения:
1 м – 5 дм =
1 м – 5 см =
6 м 5 дм – 8 дм =
5 см + 5 см =
15 см + 5 дм =
3 дм – 6 см =
3 дм 5 см – 15 см =
1 дм 2 см – 3 см =
1 м 6 дм – 8 дм =
Задание 4
Из каждого выражения произведения отнять 15 и записать новые выражение и решить их:
7 • 3 =
7 • 6 =
7 • 9 =
8 • 6 =
8 • 4 =
3 • 9 =
4 • 4 =
5 • 7 =
Подсказка
Если 7 • 3 = 21, то 21 – 15 = 6
Задание 5
Решить примеры:
7 • 6 + 7 • 4 =
21 : 3 – 6 =
(35 – 28) • 5 =
(68 – 26) : 7 =
7 + (6 : 2) =
3 – 14 : 2 =
60 – 63 : 7 =
81 – 56 : 7 =
50 + 42 : 7 =
Задание 6 (задача)
В шести одинаковых бочонках 24 литра воды. Сколько литров воды в сети таких же бочонках, на сколько литров больше во втором случае, чем в первом?
Решение
Вначале найдем, сколько воды вмещается в один бочонок.
Первое действие:
24 : 6 = 4 (л) в одном бочонке
Теперь рассчитаем, сколько воды в семи одинаковых бочонках
Второе действие:
4 • 7 = 28 (л) в сети одинаковых бочонках
Найдем ответ на главный вопрос задачи, на сколько литров больше во втором случае, чем в первом.
Третье действие:
28 – 24 = 4 (л) на столько литров больше во втором случае, чем в первом
Ответ: на 4 литра воды больше во втором случае, чем в первом
Задание 7
Отец и сын купили на рынке картошку в 6 одинаковых сетках. Отец принес домой 4 сетки, а сын 2. Всего получилось 18 килограммов картошки. Сколько килограммов принес отец? Сколько килограммов принес сын? На сколько больше килограммов картошки принес отец?
Решение
Рассчитаем, сколько картошки было в одной сетке, если известно, то всего принести 18 килограммов в 6 одинаковых сетках.
Первое действие:
18 : 6 = 3 (кг) в одной сетке.
Теперь узнаем сколько килограммов принес отец и сколько килограммов принес сын.
Второе действие:
3 • 4 = 12 (кг) принес отец
Третье действие:
3 • 2 = 6 (кг) принес сын
Найдем искомую разницу.
Четвертое действие:
12 – 6 = 6 (кг) на столько больше принес отец.
Ответ: Отец принес на 6 килограммов больше картошки, чем сын.
Задание 8
За 5 часов работы двигателя было израсходовано 30 литров бензина. Сколько бензина будет израсходовано за 8 часов работы двигателя. На сколько больше двигатель израсходует бензина за разницу во времени?
Решение
Рассчитаем, сколько бензина расходует двигатель за час своей работы.
Первое действие:
30 : 5 = 6 (л) за один час работы
Рассчитаем, сколько составляет разница во времени?
Второе действие:
8 – 5 = 3 (ч) разница во времени
Теперь можно рассчитать, сколько бензина израсходовано за оставшиеся 3 часа.
Третье действие:
3 • 6 = 18 (л) потрачено за 3 часа.
Ответ: за 3 часа двигатель истратил 18 литров бензина
Второй способ решения
Рассчитаем, сколько бензина расходует двигатель за час своей работы.
Первое действие:
30 : 5 = 6 (л) за один час работы
Рассчитаем, сколько бензина будет израсходовано за 8 часов работы двигателя.
Второе действие:
8 • 6 = 48 (л) израсходовано за 8 часов работы двигателя
Теперь можно рассчитать разницу потраченного топлива.
Третье действие:
48 – 30 = 18 (л) разница потраченного топлива
Ответ: за 3 часа двигатель истратил 18 литров бензина
Важно! Задания на сложение и вычитание не исключают в своем условии или решении возможность других математических действий, например, умножения или деления. Ученик третьего класса уже должен уметь различать в условии требования к сложению и умножению, делению и вычитанию. Именно потому задания по математике для этого класса часто носят смешанный характер.
Задание 9
В двух прудах плавало 56 уток. Когда из первого пруда во второй перелетело 7 уток, то в нем осталось 25. Сколько уток с самого начала плавало во втором пруду?
Решение
Известно, что после того, как из первого пруда улетело 7 уток, в нем осталось 25. Находим количество уток в первом пруду с самого начала.
Первое действие:
7 + 25 = 32 (утки) было в первом пруду.
Теперь можем найти, сколько уток плавало во втором пруду с самого начала.
Второе действие:
56 – 32 = 24 (утки) было во втором пруду.
Ответ: с самого начала во втором пруду было 24 утки.
Задание 10
С первого куста собрали 9 килограммов ягод. Со второго куста собрали на 3 килограммов больше, чем с первого, а с третьего – на 2 килограммов больше, чем со второго. Сколько килограммов ягод собрали с третьего куста? Сколько всего ягод собрали?
Решение
Вначале найдем, сколько килограммов ягод собрали со второго куста.
Первое действие:
9 + 3 = 12 (кг) ягод со второго куста
Теперь определяем, сколько килограммов ягод собрали с третьего куста
Второе действие:
12 + 2 = 14 (кг) год с третьего куста
Когда все составляющие известны, находим ответ на главный вопрос задачи.
Третье действие:
9 + 12 + 14 = 35 (кг) ягод всего
Ответ: всего собрали 35 килограммов ягод.

Вместо заключения
Уделяйте математике достаточно внимания уже с начальной школы. Этот предмет не только тренируем мозг в устном счете, но и умении логически мыслить, развивать смекалку. Постепенно привыкая к выполнению дополнительных и основных заданий, ребенок учится учиться, выполнять требования учителя, грамотно планировать свое время, распределять время для учебы и досуга.
Математические задания для третьеклассников моно составлять самостоятельно по приведенным нами аналогии, это не составит особого труда. Зато ваш ученик сможет больше тренироваться в математике, выполнять задания на каникулах и выходных, а также заниматься дополнительно после школы.
Материал по математике (3 класс) на тему: Примеры табличного умножения и деления, 3 класс (карточка).
8 * 3 7 * 4 56 : 8 6 * 9 3 * 4 56 : 7
5 * 6 9 * 7 24 : 4 5 * 7 8 * 4 24 : 3
3 * 9 6 * 6 35 : 5 4 * 6 7 * 7 25 : 5
2 * 8 4 * 9 18 : 9 9 * 5 2 *9 16 : 8
7 * 6 8 * 4 64 : 8 8 * 6 5 * 6 42 : 6
8 * 3 7 * 4 56 : 8 6 * 9 3 * 4 56 : 7
5 * 6 9 * 7 24 : 4 5 * 7 8 * 4 24 : 3
3 * 9 6 * 6 35 : 5 4 * 6 7 * 7 25 : 5
2 * 8 4 * 9 18 : 9 9 * 5 2 *9 16 : 8
7 * 6 8 * 4 64 : 8 8 * 6 5 * 6 42 : 6
8 * 3 7 * 4 56 : 8 6 * 9 3 * 4 56 : 7
5 * 6 9 * 7 24 : 4 5 * 7 8 * 4 24 : 3
3 * 9 6 * 6 35 : 5 4 * 6 7 * 7 25 : 5
2 * 8 4 * 9 18 : 9 9 * 5 2 *9 16 : 8
7 * 6 8 * 4 64 : 8 8 * 6 5 * 6 42 : 6
8 * 3 7 * 4 56 : 8 6 * 9 3 * 4 56 : 7
5 * 6 9 * 7 24 : 4 5 * 7 8 * 4 24 : 3
3 * 9 6 * 6 35 : 5 4 * 6 7 * 7 25 : 5
2 * 8 4 * 9 18 : 9 9 * 5 2 *9 16 : 8
7 * 6 8 * 4 64 : 8 8 * 6 5 * 6 42 : 6
8 * 3 7 * 4 56 : 8 6 * 9 3 * 4 56 : 7
5 * 6 9 * 7 24 : 4 5 * 7 8 * 4 24 : 3
3 * 9 6 * 6 35 : 5 4 * 6 7 * 7 25 : 5
2 * 8 4 * 9 18 : 9 9 * 5 2 *9 16 : 8
7 * 6 8 * 4 64 : 8 8 * 6 5 * 6 42 : 6
8 * 3 7 * 4 56 : 8 6 * 9 3 * 4 56 : 7
5 * 6 9 * 7 24 : 4 5 * 7 8 * 4 24 : 3
3 * 9 6 * 6 35 : 5 4 * 6 7 * 7 25 : 5
2 * 8 4 * 9 18 : 9 9 * 5 2 *9 16 : 8
7 * 6 8 * 4 64 : 8 8 * 6 5 * 6 42 : 6
8 * 3 7 * 4 56 : 8 6 * 9 3 * 4 56 : 7
5 * 6 9 * 7 24 : 4 5 * 7 8 * 4 24 : 3
3 * 9 6 * 6 35 : 5 4 * 6 7 * 7 25 : 5
2 * 8 4 * 9 18 : 9 9 * 5 2 *9 16 : 8
7 * 6 8 * 4 64 : 8 8 * 6 5 * 6 42 : 6
Внетабличное деление / Деление / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Деление
- Внетабличное деление
Внетабличное деление на однозначное число
99 : 9 = ?
Рассуждай так:
В числе 99 – 9 десятков и 9 единиц; делю 9 десятков на 9, получаю 1 десяток, или это число 10; далее делю 9 единиц на 9 и получаю число 1. Теперь к 10 прибавляю 1 и получаю 11. Тогда,
99 : 9 = 11
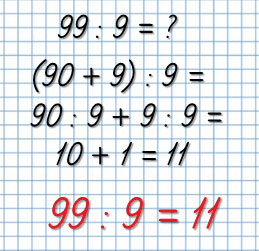
84 : 4 = ?
Рассуждай так:
В числе 84 – 8 десятков и 4 единицы; делю 8 десятков на 4, получаю 2 десятка, или это число 20; далее делю 4 единицы на 4 и получаю число 1. Теперь к 20 прибавляю 1 и получаю 21. Тогда,
84 : 4 = 11
Нахождение частного подбором
87 : 29 = ?
Пробуем в частном 2 и проверяем: 29 • 2 = 58, 58 < 87, число 2 не подходит.
Пробуем в частном 3 и проверяем: 29 • 3 = 87, 87 = 87, значит, 87 : 29 = 3.
Внетабличное деление на двузначное число
Если ты еще не умеешь решать такие примеры столбиком, то можно решать при помощи умножения.
Рассуждай так:
Деление суммы на число
Чтобы разделить сумму на число, можно вычислить сумму и разделить её на число или разделить на число каждое слагаемое и полученные результаты сложить.
Случай 1:
(15 + 25) : 5 = ?
Рассуждай так:
Способ 1:
Нахожу сумму чисел 15 и 25, получаю 40. Теперь 40 делю на 5 и получаю 8.
Записываю так:
(15 + 25) : 5 = 40 : 5 = 8
Способ 2:
Каждое из слагаемых делю на 5 и результат складываю. Сначала делю первое слагаемое 15 на 5, получу 3, потом на 5 разделю второе слагаемое 25, получу 5, теперь полученные результаты 3 и 5 сложу и получу 8. Запишу так:
(15 + 25) : 5 = 15 : 5 + 25 : 5 = 3 + 5 = 8
Значит, (15 + 25) : 5 = 8
Случай 2:
36 : 2 = ?
Рассуждай так:
Число 36 представлю в виде суммы слагаемых, которые легко делятся на 2, например, 20 и 16. Эту сумму надо разделить на 2.
32 : 2 = (20 + 16) : 2 = ?
Сначала делю первое слагаемое 20 на 2, получу 10, потом на 2 разделю второе слагаемое 16, получу 8, теперь полученные результаты 10 и 8 сложу и получу 18.
32 : 2 = (20 + 16) : 2 = 20 : 2 + 16 : 2 = 10 + 8 = 18
Значит, 36 : 2 = 18
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Табличное деление
Деление с остатком
Деление суммы на число
Деление на однозначное число
Деление чисел, оканчивающихся нулями
Свойства деления
Деление
Правило встречается в следующих упражнениях:
3 класс
Страница 55. Вариант 2. Тест 2, Моро, Волкова, Проверочные работы
Страница 18, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 25, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 30, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 32, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 34, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 45, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 99, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 102, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 40, Моро, Волкова, Рабочая тетрадь, 2 часть
4 класс
Страница 79, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 91, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 20, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 36, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 39, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 26, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 81, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 94, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 114, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 70, Моро, Волкова, Рабочая тетрадь, 2 часть
5 класс
Упражнение 242, Мерзляк, Полонский, Якир, Учебник
Упражнение 254, Мерзляк, Полонский, Якир, Учебник
Упражнение 264, Мерзляк, Полонский, Якир, Учебник
Упражнение 291, Мерзляк, Полонский, Якир, Учебник
Упражнение 5, Мерзляк, Полонский, Якир, Учебник
Упражнение 316, Мерзляк, Полонский, Якир, Учебник
Упражнение 317, Мерзляк, Полонский, Якир, Учебник
Упражнение 318, Мерзляк, Полонский, Якир, Учебник
Упражнение 362, Мерзляк, Полонский, Якир, Учебник
Упражнение 365, Мерзляк, Полонский, Якир, Учебник
© budu5.com, 2020
Пользовательское соглашение
Copyright
Задачи деление на равные части и по содержанию. Задачи по математике 3 класс.
Задачи по математике для 3 класса
Задача 1
На склад привезли 3 ящика мандарин, одинаковых повесу, всего 27 килограмма. Сколько мандарин было в каждом ящике?
Решение:
- 1) 27 : 3 = 9
- Ответ: 9
Задача 2
36 чашек поставили на 4 стола. Сколько чашек поставили на каждый стол?
Решение:
- 1) 36 : 4 = 9
- Ответ: 9
Задача 3
20 яблок разделили поровну между 5 детьми. Сколько яблок досталось каждому ребенку?
Решение:
- 1) 20 : 5 = 4
- Ответ: 4
Задача 4
Ученикам раздали 21 учебник по 7 учебников каждому. Скольким детям раздали учебники?
Решение:
- 1) 21 : 7 = 3
- Ответ: 3
Задача 5
9 порций мороженого разделили поровну между 3 детьми. Сколько порций мороженого получил каждый ребенок?
Решение:
- 1) 9 : 3 = 3
- Ответ: 3
Задача 6
40 тетрадей разложили поровну на 5 стопок. Сколько тетрадей в каждой стопке?
Решение:
- 1) 40 : 5 = 8
- Ответ: 8
Задача 7
28 яблок разложили в 4 корзины поровну. Сколько яблок положили в каждую корзину?
Решение:
- 1) 28 : 4 = 7
- Ответ: 7
Задача 8
В 3 дворах 15 лавочек поровну. Сколько лавочек в одном таком дворе?
Решение:
- 1) 15 : 3 = 5
- Ответ: 5
Задача 9
40 килограмм картошки разложили поровну в 2 мешка. Сколько картошки положили в каждый мешок?
Решение:
- 1) 40 : 2 = 20
- Ответ: 20
Дивизион
Дивизия разбивается на равные части или группы.
Это результат «честного обмена».
Пример: есть 12 шоколадных конфет, и 3 друга хотят ими поделиться, как они делят шоколадные конфеты?
12 конфет
12 шоколадных конфет, разделенных на 3
Ответ: 12 разделить на 3 равно 4. Каждый получает 4.
Символы
÷ /
Мы используем символ ÷ или иногда символ / для обозначения деления:
Давайте использовать здесь оба символа, чтобы мы к ним привыкли.
Другие примеры
Вот еще несколько примеров:
Противоположность умножению
Деление — это , противоположное умножению . Когда мы знаем факт умножения, мы можем найти факт деления:
Пример: 3 × 5 = 15, поэтому 15/5 = 3.
Также 15/3 = 5.
Почему? Что ж, подумайте о числах в строках и столбцах, как на этой иллюстрации:
| Умножение… | … Подраздел | |
|---|---|---|
| 3 группы по 5 штук составляют 15 … | … 15 разделить на 3 будет 5 | |
а также: | ||
| 5 групп по 3 человека составляют 15… | … 15 разделить на 5 равно 3. | |
Итак, четыре связанных факта :
- 3 × 5 = 15
- 5 × 3 = 15
- 15/3 = 5
- 15/5 = 3
Знание таблицы умножения может помочь вам с делением!
Пример: что такое 28 ÷ 7?
Обыскивая таблицу умножения, мы обнаруживаем, что 28 равно 4 × 7, поэтому 28, разделенное на 7, должно быть равно 4.
Ответ: 28 ÷ 7 = 4
Имена
Для каждого числа в дивизионе есть специальные названия:
делимое ÷ делитель = частное
Пример: в 12 ÷ 3 = 4:
- 12 — это дивиденд
- 3 — делитель
- 4 — частное
Но иногда он не работает идеально!
Иногда мы не можем точно разделить вещи… может быть что-то осталось.
Пример: Есть 7 костей, которые можно разделить с 2 детенышами.
Но 7 нельзя разделить точно на 2 группы,
так что каждый щенок получает 3 кости,
, но останется 1 над :
Мы называем это остатком .
Подробнее об этом см. Раздел и остатки
Упражнения
Попробуйте эти листы деления.
.Рабочие листыDivision | K5 Обучение
Рабочие листы > Математика > Математика по теме > Дивизион
Таблицы деления на 3-6 классы
Наши рабочие листы бесплатного деления начинаются с практики простых фактов деления (например, 10 ÷ 2 = 5) и переходят к полному делению с делителями до 99. Включены упражнения с остатками и без остатков, а также с пропущенными делителями или дивидендами. Эти бесплатные рабочие листы организованы по классам; логин не требуется.
Выберите свою оценку / тему:
Рабочие листы 3-го класса
Рабочие листы 4-го класса
Листы с длинным делением для 4-го класса
Рабочие листы 5-го класса
Рабочие листы 6-го класса
Карточки дивизиона
Темы включают:
- Значение предложений деления и деления
- Равные группы
- Деление на 2 или 3, 4 или 5, 6 или 7, 8 или 9
- Практика отдела фактов (таблицы 1-10)
- Практика отдела фактов (таблицы 1-12)
- Семейства фактов умножения и деления
- Факты деления с пропущенными дивидендами или делителями
- Делим на 10
- Делим на 100
- Разделить на 10
- Разделить на целые сотни
- Разделите трех- или четырехзначные числа на однозначные числа (без остатков)
- Деление с остатками (1-100)
- Деление в длину: факты о делении (1-100), без остатка
- Длинное деление: Факты деления (1-100) с остатком
- Проблемы с разделением слов
- Факты отдела (таблицы 1-10, 1-12)
- Факты деления с пропущенным дивидендом или делителем
- Разделить на 10 или 100
- Разделить на целые десятки или сотни
- Разделите целые десятки или сотни на однозначные числа
- Деление чисел до 1000 на однозначные числа
- Дивизия с остатками (1-1,000)
- Разделить на 10 или 100, с остатком
- Смешанные задачи умножения и деления слов
- Проблемы со словами, состоящие из 4 смешанных операций
- Разделение фактов в длинной форме
- Двухзначные числа, разделенные на однозначные числа, с остатками или без остатка
- Трехзначные числа, разделенные на однозначные числа, с остатками или без остатка
- 4-значные числа, разделенные на 1-значные числа, с остатком или без остатка
- Разделите в уме трех- или четырехзначные числа на однозначные числа
- Дивизия с остатками 1-100, 1-1,000
- Деление на целые десятки или сотни с остатком
- Деление в столбик с однозначными делителями, без остатка
- Деление в столбик с однозначными делителями, с остатком
- Деление в столбик с 2-значными делителями (10-25, 10-99)
- Отсутствуют проблемы с дивидендами или делителями
- Проблемы с отсутствующим множителем (решите в столбик)
- Смешанные 4 операции слова задачи
- 1–10 000 разделить на однозначные числа, без остатка
- 1–100 000 разделить на однозначные числа, остаток
- Деление в столбик на двузначные делители
- Отсутствуют проблемы с дивидендами или делителями
- Проблемы с отсутствующим множителем (решите в столбик)
Связанные темы
Рабочие листы умножения
Рабочие листы с дробями

Образец рабочего листа
.Рабочие листы отдела
Добро пожаловать на страницу рабочих листов по разделению на Math-Drills.com! Пожалуйста, уделите нам безраздельное внимание, пока мы представляем эту страницу. Наши рабочие листы для разделения помогут вам научить студентов очень важной концепции разделения. Если учащиеся хорошо помнят факты умножения, учить фактам деления не составит труда. Если вы хотите, чтобы ваши ученики добились успеха в обучении разделению, убедитесь, что они знают свои факты умножения на 81, как умножать на 0 и как умножать на 10.Если они этого не знают, это займет намного больше времени.
На этой странице вы найдете множество рабочих листов деления, включая факты деления и длинное деление с остатками и без них. Мы начнем с некоторых фактов деления, которые, как вы знаете, являются просто фактами умножения, выраженными по-другому. Основное отличие состоит в том, что нельзя разделить на 0 и получить действительное число. Если вы действительно хотите, чтобы ваши ученики производили впечатление, скажем, за обеденным столом, когда родители спрашивают их, что они узнали сегодня, вы можете научить их, что деление на ноль не определено.
Остальная часть страницы посвящена длинному делению, которое по некоторым причинам не нравится некоторым представителям населения. Деление в столбик является наиболее сложной задачей, когда учащиеся не знают фактов умножения, поэтому сначала убедитесь, что они их знают. О, мы это уже сказали. А как насчет алгоритма деления в столбик … может быть, тот, который вы, или ваши родители, или ваши бабушка и дедушка изучили? Мы твердо говорим: да! Причина, по которой вы и ваши предки использовали его, заключается в том, что это эффективный и красивый алгоритм, который позволит вам решить некоторые из самых сложных проблем деления, которые не могли коснуться даже базовые десять блоков.Он одинаково хорошо работает с десятичными и целыми числами. Деление в столбик на самом деле не так уж и сложно.
Самые популярные рабочие листы дивизиона на этой неделе
Информационные листы отдела
Таблицы фактов разделения, включая таблицы делений, факты деления и рабочие листы с фактами отдельных делений.
Таблицы фактов отдела

Факты о горизонтальном делении рабочих листа
Манипуляторы могут помочь учащимся «понять» понятие деления.Например, ученики могут перегруппировать базовые десять блоков в блоки, а затем разделить блоки на стопки. Например, 81 ÷ 9 будет 9 стопок по 9 единиц.
Отдел, по сути, задает вопрос: «Сколько _____ в _____?» На вопрос 81 ÷ 9 подсказка будет звучать так: «Сколько девяток в 81?» Эта подсказка пригодится учащимся, которые изучают математику позже, когда у них есть более сложные концепции, такие как деление десятичных знаков или дробей. «Сколько третей в четырех?» или еще лучше, сколько третьих чашек в четырех чашках? При необходимости достаньте мерные чашки.
Факты о вертикальном делении рабочих листа
Факты о горизонтальном делении рабочих листа с номерами фокусировки
Факты о делении рабочих листа с комбинациями чисел фокусировки
Длинные листы деления
Рабочие листы для деления в столбик для отработки различных стратегий деления в столбик, включая вопросы без остатков, остатков и десятичных частных.
Длинное деление рабочих листа без остатков
Нужен более простой способ делить большие числа? Попробуйте этот метод, используя степень десяти. Чтобы успешно использовать этот метод, учащиеся должны уметь умножать на десять и вычитать. Студенты вычитают дивиденд, умноженный на убывающую степень десяти, пока не получат ноль или остаток. Пример: 1458 ÷ 54. Примечание 54 × 1 = 54, 54 × 10 = 540 (больше ничего не требуется).1458 — 540 — 540 = 378. Обратите внимание, что 540 было вычтено дважды, поэтому количество раз, когда 54 «переходит» в 1458, составляет 20 раз. Продолжая, 378 — 54 — 54 — 54 — 54 — 54 — 54 — 54 = 0. Поскольку 54 было вычтено семь раз, частное увеличивается на семь, в сумме получается 27. Другими словами, 54 «переходит в» 1458, 27 раз.
Мы могли бы также упомянуть, что этот метод может быть еще более сложным, если использовать кратные степени десяти. В приведенном выше примере
.синтетический Примеры деления (стр. 2 из 4) Разделы: Введение, Рабочие примеры, Нахождение нулей, Факторинг полиномы
Для этого первого упражнения Я покажу весь процесс синтетического деления шаг за шагом.
В этом упражнении никогда не говорилось что-либо о многочленах, множителях или нулях, но это деление говорит что, если разделить 2 x 4 3 x 3 5 x 2 + 3 x + 8 по x 2, то остаток будет 2, и, следовательно, x 2 не является коэффициент 2 x 4 3 x 3 5 x 2 + 3 x + 8, и x = 2 не является нулем (что есть, корень или x -перехват) исходного полинома.Авторские права Элизабет Стапель 2002-2011 Все права защищены
Этот вопрос задает меня, по сути, преобразовать «неправильную» полиномиальную «дробь» в полиномиальное «смешанное число». То есть меня спрашивают сделать что-то похожее на преобразование неправильной дроби 17 / 5 к смешанному номеру 3 2 / 5 , что на самом деле является сокращением для выражения сложения «3 + 2 / 5 ». Чтобы преобразовать полином разделение на требуемый формат «смешанных чисел», я должен сделать деление; Я покажу большинство шагов.
Как видите, остаток 68.Так как я начал с многочлена степени 3 а затем разделить на x 3 (то есть по многочлен степени 1), У меня остался многочлен степени 2. Тогда нижняя строка представляет собой многочлен 3 x 2 + 7 х + 24 с остатком 68. Поместив этот результат в требуемый формат «смешанных чисел», Я получаю ответ: Это всегда правда, когда вы используете синтетическое деление, ваш ответ (в нижней строке) будет быть на один уровень меньше, чем вы начали, потому что вы разделили из линейного фактора.Вот откуда я узнал, что мой ответ, обозначенный «3 7 24 дюймов нижний ряд обозначал квадратичный, поскольку я начал с кубического. << Предыдущая Вверх | 1 | 2 | 3 | 4 | Вернуться к указателю Далее >>
|

