Свойства математического ожидания
1) Размерность математического ожидания равна размерности случайной величины.
2) Математическое ожидание может быть любым действительным числом: положительным, равным 0, отрицательным.
3) Математическое ожидание постоянной величины равно этой постоянной:
4) Математическое ожидание суммы независимых случайных величин равно сумме математических ожиданий:
5) Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий:
6) Постоянный множитель можно вынести за знак математического ожидания:
Например:
Пусть в результате экспериментов получено следующее распределение случайной величины
2(X) } $$Свойства дисперсии
1) Размерность дисперсии равна квадрату размерности случайной величины.
2) Дисперсия может быть любым неотрицательным действительным числом.
3) Дисперсия постоянной величины равна нулю:
4) Дисперсия суммы независимых случайных величин равна сумме дисперсий:
5) Постоянный множитель можно вынести за знак дисперсии:
Например:
Продолжим исследование и найдём дисперсию для распределения случайной величины X – числа появления белых шаров. Составим расчётную таблицу:
xi
0
1
2
3
4
5
Σ
pi
0,0074
0,0618
0,2060
0,3433
0,2861
0,0954
1
x ip1
0
0,0618
0,4120
1,0300
1,1444
0,4768
3,125
\(\mathrm{x_i^2}\)
0
1
4
9
16
25
–
\(\mathrm{x_i^2p_i}\)
0
0,0618
0,8240
3,0899
4,5776
2,3842
10,9375
Получаем: D(X) = 10,9375 – 3,1252 ≈ 1,1719.
п.4. Среднее квадратичное отклонение
Среднее квадратичное отклонение (СКО) дискретной случайной величины X = {xi} – это корень квадратный от дисперсии: $$ \mathrm{ \sigma(X)=\sqrt{D(X)} } $$ СКО характеризует степень отклонения случайной величины от среднего значения.
Свойства СКО
1) Размерность СКО равна размерности случайной величины.
2) СКО может быть любым неотрицательным действительным числом.
3) СКО постоянной величины равно нулю:
4) Постоянный множитель можно вынести за знак СКО:
п.5. Правило трёх сигм
Большое количество случайных величин, измеряемых в экспериментах (например, в школьных лабораторных работах), имеет так называемое нормальное распределение.
В частности, при больших n, биномиальное распределение можно с хорошей точностью описывать как нормальное с M(X) = np и \(\mathrm{\sigma(X)=\sqrt{npq}}\).
График плотности нормального распределения p(x) похож на колокол, с максимумом, соответствующим M(X) = Xcp – среднему значению измеряемой величины.
Величина СКО σ(X) характеризует степень отклонения X от среднего значения M(X).
Если величина X имеет нормальное распределение, то в пределах
±σ лежит 68,26% значений, принимаемых этой величиной
±2σ лежит 95,44% значений, принимаемых этой величиной
±3σ лежит 99,72% значений, принимаемых этой величиной
Вероятность того, что нормально распределённая величина примет значение, отклоняющееся от среднего больше, чем на «три сигмы», равна 0,28%, т.е. пренебрежимо мала.
п.6. Примеры
Пример 1. Найдите математическое ожидание, дисперсию и СКО при бросании кубика.
Закон распределения величины X – очки на верхней грани при бросании кубика и расчётная таблица:
xi
1
2
3
4
5
6
Σ
pi
1/6
1/6
1/6
1/6
1/6
1/6
1
xip1
1/6
1/3
1/2
2/3
5/6
1
3,5
\(\mathrm{x_i^2}\)
1
4
9
16
25
36
–
\(\mathrm{x_i^2p_i}\)
\(\mathrm{\frac16}\)
\(\mathrm{\frac23}\)
\(\mathrm{1\frac12}\)
\(\mathrm{2\frac23}\)
\(\mathrm{4\frac16}\)
6
\(\mathrm{15\frac16}\)
Получаем: \begin{gather*} \mathrm{ M(X)=\sum_{i=1}^6 x_ip_i=3,5 }\\ \mathrm{ D(X)=\sum_{i=1}^6 x_i^2p_i-M^2(X)=15\frac16-3,5^3=2\frac{11}{12} }\\ \mathrm{ \sigma(X)=\sqrt{D(X)}=\sqrt{2\frac{11}{12}}\approx 1,7 } \end{gather*} Ответ: \(\mathrm{M(X)=3,5;\ D(X)=2\frac{11}{12};\ \sigma(X)\approx 1,7}\).
2=p(1-p)=pq}\)
По свойству дисперсии суммы независимых событий: \begin{gather*} \mathrm{ D(X)=D(X_1+X_2+…+X_n)=D(X_1)+D(X_2)+…+D(X_n)= }\\ \mathrm{=\underbrace{pq+pq+…+pq}_{n\ \text{раз}}=npq } \end{gather*} Что и требовалось доказать.
Пример 4. 100 канцелярских кнопок высыпали на стул. Вероятность, что кнопка упала острием вверх, равна 0,4. Найдите среднее количество, дисперсию и СКО для числа кнопок, упавших острием вверх. Найдите интервал оценки для количества этих кнопок по правилу «трёх сигм».
По условию n = 100, p = 0,4.
Для каждой кнопки может быть два исхода: упасть острием вверх или вниз.
Таким образом, это испытание Бернулли с биномиальным распределением случайной величины. \begin{gather*} \mathrm{ M(X)=np=100\cdot 0,4=40 }\\ \mathrm{D(X)=npq=100\cdot 0,4\cdot 0,6=24 }\\ \mathrm{\sigma(X)=\sqrt{D(X)}=\sqrt{24}\approx 4,9} \end{gather*} Интервал оценки «три сигмы»: \begin{gather*} \mathrm{ M(X)-3\sigma(X)\lt X\lt M(X)+3\sigma(X) }\\ \mathrm{40-3\cdot 4,9\lt X\lt 40+3\cdot 4,9 }\\ \mathrm{25,3\lt X\lt 54,7}\\ \mathrm{26\leq X\leq 54} \end{gather*} Скорее всего (99,7%), от 26 до 54 кнопок будут острием вверх.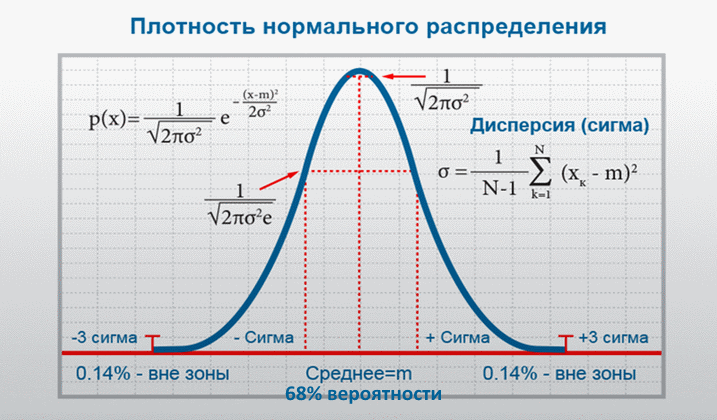
2\cdot p_i}\)
Получаем: \begin{gather*} \mathrm{ M(X)=\sum_{i=0}^{10} x_ip_i=2,5 }\\ \mathrm{ D(X)=\sum_{i=0}^{10} x_i^2p_i-M^2(X)=8,125=2,5^2=1,875 }\\ \mathrm{ \sigma(X)=\sqrt{D(X)}=\sqrt{1,875}\approx 1,37 } \end{gather*}
Интервал оценки «три сигмы»: \begin{gather*} \mathrm{ M(X)-3\sigma(X) \lt X\lt M(X)+3\sigma(X) }\\ \mathrm{ 2,5-3\cdot 1,37\lt X \lt 2,5+3\cdot 1,37 }\\ \mathrm{ -1,61\lt X\lt 6,61 }\\ \mathrm{ 0\leq X\leq 6 } \end{gather*} Скорее всего (по расчетам – 99,65%), вы угадаете от 0 до 6 ответов.
{4}{p_i} \right)\approx 1-(0,0563+0,1877+…+0,1460)=0,0781 }\end{gather*} Шансов мало – 7,81%. Т.е. «средний балл» при сдаче тестов мало достижим методом научного тыка.
Вероятность угадать все 10 ответов: p10≈ 0,000001. Шанс – один из миллиона.
Рейтинг пользователей
за неделю
- за неделю
- один месяц
- три месяца
Помогай другим
Отвечай на вопросы и получай ценные призы каждую неделю
См. подробности
Экспоненциальное распределение и Центральная предельная теорема
Статья посвящена краткому исследованию экспоненциального (показательного) распределения с использованием языка программирования R с целью проверки центральной предельной теоремы.
Параметры экспоненциального распределения
Плотность вероятности экспоненциальной случайной величины \(X\) имеет вид: \[f(x;\lambda) = \lambda e^{-\lambda x} (x > 0),\] где \(\lambda\) > 0 — параметр экспоненциального распределения.
2}.\] Для нашего распределения с параметром \(\lambda\) = 0.2 математическое ожидание равно 5, дисперсия равна 25.
Распределение средних значений экспоненциальных случайных величин
Возьмем несколько экспоненциальных случайных величин (к примеру, 40 штук) и найдем их среднее значение. Повторим это 1000 раз. В результате получим распределение средних значений сорока экспоненциальных случайных величин. Построим гистограмму распределения.
mns = NULL
for (i in 1:n) mns = c(mns, mean(rexp(40, lambda)))
data_means <- data.frame(x = mns)
m <- mean(data_means$x)
ggplot(data_means, aes(x = x)) + ylab("") +
geom_histogram(aes(y=..density..), binwidth=0.2, colour="black", fill="white") +
geom_density(alpha = 0.2, fill = "#FF6666") +
ggtitle("Распределение средних значений") +
stat_function(fun=dnorm, colour="red", args = list(mean = 5, sd = 1)) +
geom_vline(aes(xintercept=m), linetype="dashed", size=1, color="blue")Из рисунка видно, что распределение средних визуально похоже на нормальное распределение — мы добавили его для наглядности на график (красная линия).
2/n\) = 25/40 = 0.625.
R код ниже генерирует три распределения средних значений различного числа экспоненциальных случайных величин (10, 40 и 100) и строит их гистограммы.
cfunc <- function(x, n) sqrt(n) * (mean(x) - 5) / 5
dat <- data.frame(
x = c(apply(matrix(rexp(n * 10, lambda), n), 1, cfunc, 10),
apply(matrix(rexp(n * 40, lambda), n), 1, cfunc, 40),
apply(matrix(rexp(n * 100, lambda), n), 1, cfunc, 100)
),
size = factor(rep(c(10, 40, 100), rep(n, 3))))
ggplot(dat, aes(x = x, fill = size)) + ylab("") +
geom_histogram(alpha = .20, binwidth=.3, colour = "black", aes(y = ..density..)) +
stat_function(fun = dnorm, colour="red") +
facet_grid(. ~ size, scales = "free")Видно, что при увеличении \(n\) закон распределения средних приближается к нормальному распределению (красная линия).
Заключение
В результате исследования распределения средних значений 40 экспоненциальных случайных величин мы показали, что и среднее значение, и дисперсия данного распределения достаточно близки к теоретическим значениям.
Кроме того, исследуемое распределение приближается к нормальному распределению при увеличении размера выборки.
6.4: Ожидаемое значение и дисперсия дискретной функции распределения вероятностей
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 20890
- Морис А. Герати
- Колледж Де Анза
Ранее мы описали, как вычислить выборочное среднее и выборочную дисперсию как меры центра и разброса для выборочных данных. Для вероятностных моделей популяций мы можем рассчитать ожидаемое значение как параметр, описывающий центр данных, и дисперсию популяции как параметр , описывающий разброс.
Определение: параметр и статистика
Параметр — это величина, описывающая совокупность.
{2}\) (произносится как сигма-квадрат). 9{2} \cdot P(x)\)Стандартное отклонение совокупности: \(\sigma=\sqrt{\operatorname{Var}(x)}\)
Пример: тест с множественным выбором
Учащимся предлагается экзамен с множественным выбором из 4 вопросов. Найдите ожидаемое значение и дисперсию генеральной совокупности случайной величины с заданным распределением вероятностей:
| \(x\) | \(Р(х)\) |
|---|---|
| 0 | 0,1 |
| 1 | 0,1 |
| 2 | 0,2 |
| 3 | |
| 4 | 0,2 |
Решение
Чтобы найти ожидаемое значение \(X\), взвесьте каждое значение \(X\) по вероятности, затем сложите их.
| \(х\) | \(Р(х)\) | \(х \cточка Р(х)\) |
|---|---|---|
| 0 | 0,1 | 0,0 |
| 1 | 0,1 | 0,1 |
| 2 | 0,2 | 0,4 |
| 3 | 0..4 | 1,2 |
| 4 | 0,2 | 0,8 |
| Итого | 1,0 | \(\му\) = 2,5 |
Ожидаемое количество правильных ответов 2,5.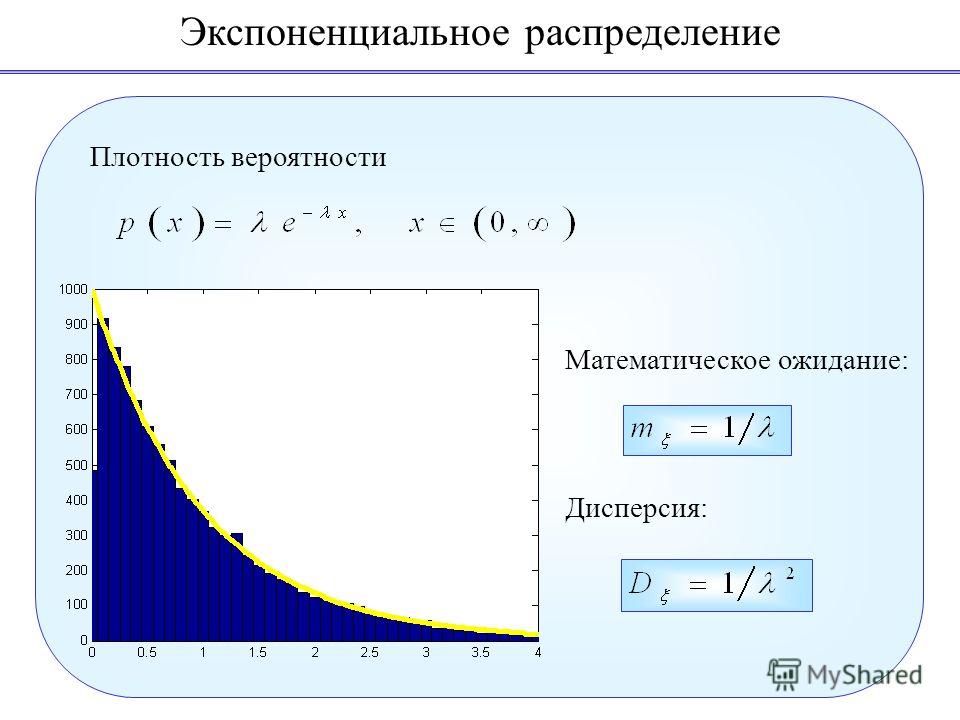
{2} \cdot P(x)\)»> 0,450
Дисперсия населения составляет 1,45, а стандартное отклонение населения равно \(\sqrt{1,45}=1,20\) правильных ответов.
Пример: крупные атлантические ураганы
Исторически в течение года в Атлантическом океане было от нуля до восьми крупных ураганов. На основе этих данных мы можем создать дискретную функцию распределения вероятностей X для количества крупных атлантических ураганов в году 65 :
| \(x\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| \(Р(х)\) | 0,187 | 0,290 | 0,271 | 0,090 | 0,054 | 0,054 | 0,036 | 0,012 | 0,006 |
Найдите математическое ожидание и дисперсию генеральной совокупности этой случайной величины.
{2}\)»> 9{2}\)
Ожидаемое количество крупных атлантических ураганов в любой год составляет 1,936. Дисперсия населения составляет 2,919, а стандартное отклонение населения составляет 1,709 крупных ураганов в год.
Эта страница под заголовком 6.4: Ожидаемое значение и дисперсия дискретной функции распределения вероятностей распространяется под лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Морисом А. Джерати посредством исходного содержимого, которое было отредактировано для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Морис А.
Джерати
- Лицензия
- CC BY-SA
- Версия лицензии
- 4,0
- Теги
- источник@http://nebula2.deanza.edu/~mo/holisticInference.html
- источник@https://professormo.com/holistic/HolisticStatisticsRev180817.pdf
ДжератиОценка дисперсии
Марко Табога, доктор философии
Оценка дисперсии статистический задача вывода, в которой выборка используется для получения точечная оценка дисперсия неизвестного распределения.
Проблема обычно решается с помощью выборочная дисперсия как оценка дисперсии населения.
В этой лекции мы приводим два примера, касающихся:
Образцы IID из нормального распределения среднее значение которого известно;
Выборки IID из нормального распределения, среднее значение которого неизвестно.
Для каждого из этих двух случаев мы получаем ожидаемое значение, распределение и асимптотические свойства оценщика дисперсии.
СОДЕРЖАНИЕ
Нормальные образцы IID — известное среднее значение
Выборка
Оценка
Ожидаемое значение
- 11111111111111111111111111111111111110
- 111111111111111010.0003
Distribution of the estimator
Risk of the estimator
Consistency of the estimator
Normal IID samples — Unknown mean
The sample
The estimator
Ожидаемое значение оценщика
Дисперсия оценщика
Распределение оценщика
Риск оценщика
Консистенция оценки
Решенные упражнения
Упражнение 1
УПРАЖНЕНИЕ 2
НОМЕР.
В этом примере оценки дисперсии мы делаем предположения, подобные
те, которые мы сделали в средней оценке
нормальные образцы IID.Образец
Образец изготовлен из независимых рисует из нормального распределения.
В частности, мы наблюдаем реализацию независимые случайные величины , …, , все имеющие
известное среднее значение ;
неизвестная дисперсия .
Оценщик
Мы используем следующую оценку дисперсия:
Ожидаемое значение оценщика
Ожидаемое значение оценщика равна истинной дисперсии :
Доказательство
Это можно доказать, используя линейность ожидал значение:
Следовательно, оценщик является беспристрастным.
Дисперсия оценщика
Дисперсия оценщика is
Proof
Это можно доказать, используя тот факт, что для нормальное распределение и формула дисперсии независимого сумма:
Таким образом, дисперсия оценки стремится к нулю по мере увеличения размера выборки. стремится к бесконечности.
Распределение оценщика
Оценщик имеет гамма-распределение с параметрами и .
Доказательство
Оценщик можно написать как где переменные являются независимыми стандартными нормальными случайными величинами и , представляет собой сумму квадратов независимые стандартные нормальные случайные величины, имеет распределение хи-квадрат с степеней свободы (см. лекцию под названием Распределение хи-квадрат для более подробной информации). Умножение случайной величины хи-квадрата на степеней свободы по получается гамма-случайная величина с параметрами и (см. лекцию Гамма-распределение Больше подробностей).
Риск оценщика
Среднеквадратическая ошибка оценщик
Непротиворечивость оценщика
оценщикможет рассматривать как выборочное среднее последовательности где общий член последовательности это
Поскольку последовательность
является последовательностью IID с конечным средним, она удовлетворяет условиям
Усиленный закон больших Колмогорова
Числа.
Таким образом, выборочное среднее значение почти наверное сходится к истинному среднему :
Другими словами, оценщик сильно последователен.
Он также слабо непротиворечив, потому что сходимость почти наверняка подразумевает сходимость в вероятность:
Нормальные образцы IID — Неизвестное среднее
Этот пример оценки дисперсии аналогичен предыдущему. Единственный отличие состоит в том, что мы ослабляем предположение о том, что среднее значение распределения известен.
Образец
Выборка состоит из независимых выборок из нормального распределения.
В частности, мы наблюдаем реализацию независимые случайные величины , …, , все имеют нормальное распределение с:
неизвестное среднее ;
неизвестная дисперсия .
Оценщик
В этом примере также необходимо определить среднее значение распределения, поскольку оно неизвестно. по оценкам.
Он оценивается с выборочным средним :
Мы используем следующие оценки дисперсии:
нескорректированная выборка дисперсия:
скорректированная выборка дисперсия:
Ожидаемое значение оценщика
Ожидаемое значение нескорректированной выборочной дисперсии is
Proof
Это можно доказать как следует: Но когда (так как и независимы, когда — см. Взаимная независимость через ожидания). Следовательно,
Таким образом, нескорректированная выборочная дисперсия является необъективной оценкой истинного дисперсия .
Скорректированная выборочная дисперсия , напротив, является несмещенной оценкой дисперсия:
Доказательство
Это можно доказать как следует:
Таким образом, когда также среднее
оценивается, нам нужно разделить на
а не по
получить несмещенную оценку.
Интуитивно, рассматривая квадраты отклонений от среднего значения выборки, скорее чем квадраты отклонений от истинного среднего, мы недооцениваем истинное изменчивость данных.
На самом деле сумма квадратов отклонений от истинного среднего всегда больше чем сумма квадратов отклонений от выборочного среднего.
Деление на а не по точно исправляет это предубеждение. Число на которое мы делим называется числом степеней свободы и он равен количеству точек выборки () минус количество других оцениваемых параметров (в нашем случае , истинное значение ).
Коэффициент, на который нам нужно умножить смещенную оценку для получения несмещенной оценки это
Этот коэффициент известен как корректировка степеней свободы .
объясняет, почему
называется нескорректированной выборочной дисперсией и
называется скорректированной выборочной дисперсией.
Дисперсия оценщика
Дисперсия нескорректированной выборочной дисперсии
Доказательство
Это доказывается в следующем подразделе. (распределение оценщика).
Дисперсия скорректированной выборочной дисперсии is
Proof
Это также доказывается в следующем подраздел (распределение оценщика).
Следовательно, как дисперсия и дисперсия сходятся к нулю как размер выборки стремится к бесконечности.
Обратите внимание, что нескорректированная выборочная дисперсия , несмотря на смещение, имеет меньшую дисперсию, чем скорректированная дисперсия выборки , который вместо этого беспристрастен.
Распределение оценщика
Нескорректированная выборочная дисперсия имеет гамма-распределение с параметрами и .
Доказательство
Чтобы доказать этот результат, нам нужно использовать некоторые
факты о квадратичных формах с нормальными случайными величинами, которые
представлено в лекции под названием
Нормальное распределение —
Квадратичные формы. Чтобы понять это доказательство, вам нужно сначала прочитать, что
лекция, в частности раздел, озаглавленный
Выборочная дисперсия
как квадратичная форма. Определите
матрицагде
является
матрица идентичности и
это
вектор единиц.
симметрична и идемпотентна. Обозначим через
в
случайный вектор, чьи
-й
запись равна
.
Случайный вектор
имеет многомерное нормальное распределение со средним
и ковариационная матрица
.
Используя тот факт, что матрица симметрична и идемпотентна, нескорректированная выборочная дисперсия может быть записана как
Используя тот факт, что случайный
векторимеет
стандартное многомерное нормальное распределение и
факт, что
,
мы можем переписать
В
другие слова,
пропорциональна квадратичной форме стандартного нормального случайного вектора
()
а квадратичная форма включает симметричную идемпотентную матрицу, след которой
равно
. Следовательно, квадратичная форма
имеет распределение хи-квадрат с
степени свободы. Наконец, мы можем
напиши это
является,
представляет собой случайную величину хи-квадрат, деленную на количество степеней свободы
и умножается на
.
Таким образом,
представляет собой гамма-случайную величину с параметрами
и
(см. лекцию Гамма-распределение
для объяснения). Кроме того, по свойствам гамма-случайных величин его
ожидаемое значение
остров
его дисперсия
Скорректированная выборочная дисперсия имеет гамма-распределение с параметрами и .
Доказательство
Доказательство этого результата аналогично доказательство нескорректированной выборочной дисперсии, найденное выше. Его также можно найти в лекция под названием «Нормальный распределение — Квадратичные формы. Здесь мы просто замечаем, что , являющийся гамма-случайной величиной с параметрами и , ожидал стоимость и дисперсия
Риск оценщика
Среднеквадратическая ошибка нескорректированная выборочная дисперсия is
Proof
Это можно доказать как следует:
Среднеквадратическая ошибка скорректированной выборочной дисперсии is
Proof
Это можно доказать как следует:
Следовательно, среднеквадратическая ошибка нескорректированной выборочной дисперсии всегда равна меньше, чем среднеквадратическая ошибка скорректированной выборки дисперсия:
Непротиворечивость оценщика
И нескорректированная, и скорректированная выборочные дисперсии
непротиворечивые оценки
неизвестная дисперсия
.
Доказательство
Нескорректированный образец
дисперсия
быть написанным
как где
у нас есть
определено
две последовательности
и
являются образцом средств
и
соответственно. Последние оба удовлетворяют условиям
Усиленный закон больших чисел Колмогорова
(они образуют последовательности IID с конечными
означает), из чего следует, что их выборка означает
и
почти наверняка сходятся к своим истинным
означает: так как
в
функция
непрерывный и почти
уверен, что сходимость сохраняется непрерывными преобразованиями, мы
получитьПоэтому
оценщик
сильно последователен. это
также слабо согласован, потому что
сходимость почти наверняка подразумевает сходимость в
вероятность:
скорректированная выборочная дисперсия
можно написать
как
соотношение
можно рассматривать как постоянную случайную величину
определяется как
следует: какой
сходится почти наверное к
. Следовательно,
куда
оба
и
почти наверное сходятся. Так как произведение является непрерывной функцией и
почти наверняка сходимость сохраняется при непрерывном преобразовании, мы
Таким образом,
также
сильно последователен.
Решенные упражнения
Ниже вы можете найти несколько упражнений с поясненными решениями.
Упражнение 1
Вы наблюдаете три независимых извлечения из нормального распределения с неизвестными иметь в виду и неизвестная дисперсия . Их значения 50, 100 и 150.
Используйте эти значения для получения несмещенной оценки дисперсии распределение.
Раствор
Среднее значение выборки Ан несмещенная оценка дисперсии обеспечивается скорректированной выборкой дисперсия:
Упражнение 2
Машина (лазерный дальномер) используется для измерения расстояния между сама машина и заданный объект.
При измерении расстояния до объекта, расположенного на расстоянии 10 м друг от друга, измерение
ошибки, совершаемые машиной, нормально и независимо распределяются и
в среднем равны нулю.
Дисперсия погрешностей измерений составляет менее 1 квадратного сантиметра, но его точное значение неизвестно и требует оценки.
Чтобы оценить его, мы повторно проводим одно и то же измерение и вычисляем выборочная дисперсия ошибок измерения (которую мы также можем вычислить потому что мы знаем истинное расстояние).
Сколько измерений нам нужно провести, чтобы получить оценку дисперсии со стандартным отклонением менее 0,1 квадратных сантиметров?
Решение
Обозначим ошибки измерения через , …, . Используется следующая оценка дисперсии: дисперсия этой оценки Так Мы необходимо обеспечить то или что безусловно проверено ifor
Как цитировать
Пожалуйста, указывайте как:
Taboga, Marco (2021). «Оценка дисперсии», Лекции по теории вероятностей и математической статистике. Прямая публикация Kindle. Онлайн приложение. https://www.statlect.com/fundamentals-of-statistics/variance-estimation.