Вычислить площадь круга без пи
Germany.ru → Форумы → Архив Досок→ Образование
Вычислить площадь круга без пи
1174 1 2 3 все
tuljakпрохожий07.07.08 18:13
07.07.08 18:13
Дочери в школе дали задание : как можно точнее вычислить площадь круга без применения пи. Что-то не сообразим никак. Помогите bitte!
#1
akoyaпрохожий07.07.08 18:26
NEW 07.07.08 18:26
в ответ tuljak 07.07.08 18:13
3/4*(r*2)*(r*2)
#2
Кот Дивуарстарожил07.07.08 18:43
NEW 07.07.08 18:43
в ответ tuljak 07.07.08 18:13
Непонятно, что значит без пи? Если нельзя использовать само число пи, то можно взять 22/7 или 355/113, они почти равны пи.
#3
Кот Дивуарстарожил07.07.08 18:45
NEW 07.07.08 18:45
в ответ Кот Дивуар 07.07.08 18:43
А можно даже 1570796327/500000000, еще точнее будет В общем, можно любую точность обеспечить 🙂
#4
AndreasWollmannзнакомое лицо07.07.08 19:24
NEW 07.07.08 19:24
в ответ tuljak 07.07.08 18:13, Последний раз изменено 07.07.08 19:27 (AndreasWollmann)
В какой класс ходит девочка?
Если ещё не знакома с интегралами, то схема примерно такая:
1 круг делиться точно на 4 четвертинки.
одну четвертинку можно представить в качестве большого количества прямоугольников разной высоты, которые стоят плотно друг к дружке.
на подобие http://www.scribd.com/doc/262068/- страницы 22, 21.

Что-бы улучшить точность можно взять трапецию заместо прямоугольника.
формула описывающая круг, центр которого лежит в середине системы координат: r*r = x*x + y*y
т.е. переставив на y имеем: y = квадратный корень из (радиус в квадрате минус х-координата в квадрате)
при r = 1 ( Einheitsradius)
y = квадратный корень из ( 1 минус х-координата в квадрате)
Как Вы уже догадались, «y» являться высотой прямоугольника.
#5
Кот Дивуарстарожил07.07.08 21:49
NEW 07.07.08 21:49
в ответ AndreasWollmann 07.07.08 19:24
Еще можно взять лист бумаги, нарисовать на нем круг и бросать на лист что-нибудь мелкое — зернышки, семечки и т.п. Потом посчитать отношение количества зернышек упавших в круг к общему количеству зернышек. Площадь листа посчитать легко. Оттуда можно посчитать площадь круга. Чем больше зернышек бросить, тем точнее будет результат.
#6
Кот Дивуарстарожил07.07.08 21:51
NEW 07.07.08 21:51
в ответ akoya 07.07.08 18:26
В ответ на:
3/4*(r*2)*(r*2)
Непонятная формула. Двойки с четверкой сокращаются, получается квадрат радиуса помноженный на 3.
#7
akoyaпрохожий07.07.08 22:03
NEW 07.07.08 22:03
в ответ Кот Дивуар 07.07.08 21:51
(3*d*d)/4
d это диаметр или 2r. 4r*r это площадь описаного квадрата. 3/4 этой площади занимает вписаный почти круг.
#8
Кот Дивуарстарожил07.07.08 22:06
NEW 07.07.08 22:06
в ответ akoya 07.07.08 22:03
Это очень приблизительно. Погрешность почти 5%.
#9
akoyaпрохожий08. 2 а значит предётся сначала одну из них диференцировать (субституция). потом всё что получится умножить на 4 и найти разницу с 4r*r (площадь квадрата со стороной в 2r) получится то что внутри круга теоретически.
2 а значит предётся сначала одну из них диференцировать (субституция). потом всё что получится умножить на 4 и найти разницу с 4r*r (площадь квадрата со стороной в 2r) получится то что внутри круга теоретически.
#10
jekapar02Я хороший мальчик08.07.08 13:50
NEW 08.07.08 13:50
в ответ tuljak 07.07.08 18:13
Взять стакан с диаметром данного круга (если под рукой). Налить отмерянный объём воды в стакан. Померять высоту воды. Объём разделить на высоту. Получаем площадь круга.
Рассмеши Богов, и они непременно рассмешат тебя в ответ
#11
sitnikпостоялец08.07.08 14:07
NEW 08.07.08 14:07
в ответ tuljak 07.07.08 18:13
Вопрос в том, что она уже умеет. Можно «Поинтегрировать» :). Впишите в круг n-угольник. На его сторонах постройте треугольники. Они равнобедренные. Дальше очевидно. Ну и чем больше n?\, тем точнее. 🙂
Они равнобедренные. Дальше очевидно. Ну и чем больше n?\, тем точнее. 🙂
#12
yana_arhзнакомое лицо09.07.08 09:17
NEW 09.07.08 09:17
в ответ tuljak 07.07.08 18:13, Последний раз изменено 09.07.08 09:18 (yana_arh)
Можно попробовать вычислить через прощадь сектора:
S=п*r2(квадрат)*n/360 = l/2(r2(квадрат)*α(альфа),
где
l — длина дуги, ограничивающей сектор
n — градусная мера соответствующего угла
α(альфа) — радианная мера угла
чтобы вычислить l :
l=r*α(альфа)
1 рад = 57.2957795╟
т.е, в нашем случае, для площади круга берем угол равный 360╟, а это равняется: 360╟/ 57.2957795╟ = 6,283185 радиан
#13
Кот Дивуарстарожил09.07.08 09:29
NEW 09.07.08 09:29
в ответ yana_arh 09.07.08 09:17
Формально тут числа пи нет, но в действительности есть.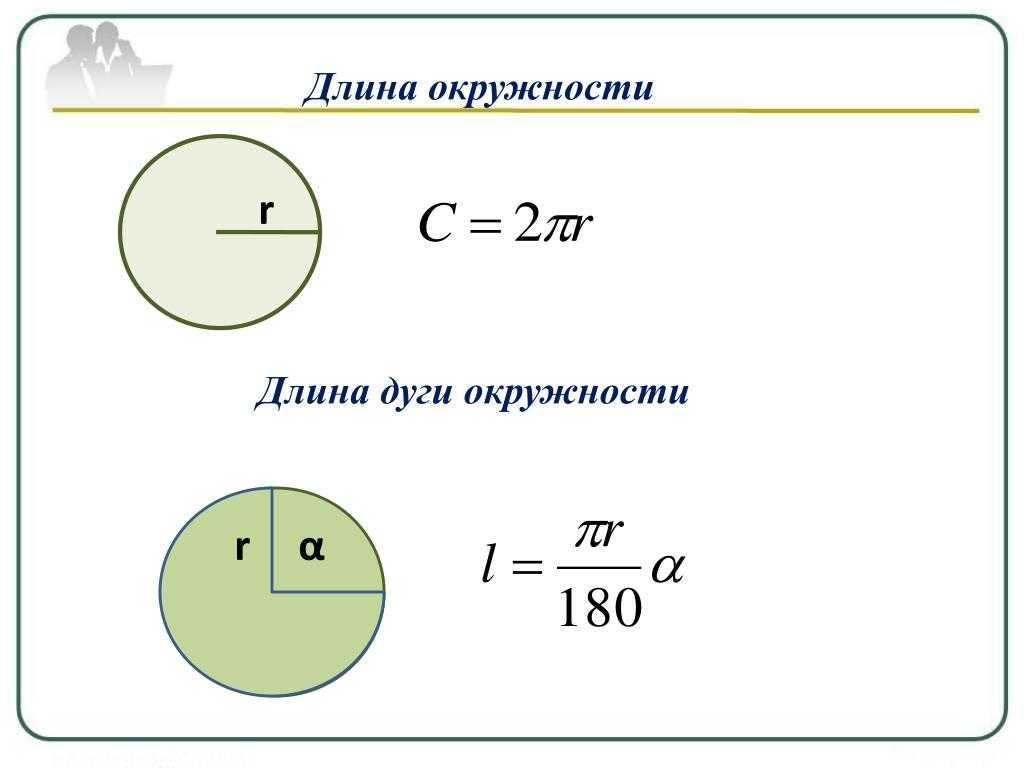 Радианная мера угла как раз через пи и определяется.
Радианная мера угла как раз через пи и определяется.
#14
NEW 09.07.08 11:06
в ответ tuljak 07.07.08 18:13
Хм. Если будет любой круг с известной площадью, то на основе его можно вычислить площадь любого другого круга.
#15
nrw1979коренной житель09.07.08 11:10
NEW 09.07.08 11:10
в ответ nrw1979 09.07.08 11:06
Я не думаю что всякое интегрирование и прочее здесь применимо. Об этом нужно забыть — не школьный уровень.
Встраивание многоугольников — попахивает численными методами, тоже не то.
Это как в задачах на построение — все должно быть очень просто и в то же время оригинально.
#16
nrw1979коренной житель09.
NEW 09.07.08 11:12
в ответ yana_arh 09.07.08 09:17
В ответ на:
1 рад = 57.2957795╟
т.е, в нашем случае, для площади круга берем угол равный 360╟, а это равняется: 360╟/ 57.2957795╟ = 6,283185 радиан
Т.е. 2*pi ? Так нужно же без пи, превращение буквы пи в число с длинющим хвостом не проходит.
#17
nrw1979коренной житель09.07.08 11:20
NEW 09.07.08 11:20
в ответ nrw1979 09.07.08 11:06
Ну я продолжу. Не совсем ясно из условия что вообще МОЖНО делать.
Первый вариант я уже описал. Имея круг с известной площадью при помощи пропорции можно вычислить площадь любого другого круга.
Вопрос в том где взять круг с известной площадью.
Можно попробовать так:
1. Берем круглый стакан.
2. Меряем ниточкой длину окружности по краешку. L=2 pi R
 2. S/L = R/2 => S=LR/2
2. S/L = R/2 => S=LR/2#18
nrw1979коренной житель09.07.08 11:22
NEW 09.07.08 11:22
в ответ jekapar02 08.07.08 13:50
В ответ на:
Взять стакан с диаметром данного круга (если под рукой). Налить отмерянный объём воды в стакан. Померять высоту воды. Объём разделить на высоту. Получаем площадь круга.
Нужно найти еще ровный стакан. А то они по большей части кривые.
#19
Кот Дивуарстарожил09.07.08 11:50
NEW 09.07.08 11:50
в ответ nrw1979 09.07.08 11:20
Так ты от числа пи никуда не ушел. Площадь первого круга все равно через пи считаешь.
#20
3 метода как вычислить площадь круга на Python с примерами
В этом уроке мы покажем, как пользователь может вычислить площадь круга, используя Python с заданным радиусом данного круга.
Чтобы понять формат ввода-вывода кода, пользователь должен обратить внимание на следующее:
- Входные данные кода состоят из целого числа «R», которое представляет радиус круга.
- На выходе кода будет напечатана область круга.
Алгоритм вычисления площади
Ниже приведены шаги, которые мы будем использовать для вычисления площади данного круга:
- Шаг 1. Мы должны передать ввод с помощью функции input(). Вход будет соответствовать радиусу данного круга.
- Шаг 2: Площадь круга будет рассчитана по формуле: Площадь = πR2.
Площадь круга = π * R * R
Где π(PI) = 3.14
R = радиус круга
D или(2R) = Диаметр круга, (R + R).
- Шаг 3: Распечатаем вывод кода, то есть площадь данного круга.
Методы поиска площади заданного круга с помощью Python
- Метод 1. Найти площадь данного круга с помощью математического модуля.
import math as M
Radius = float(input("Please enter the radius of the given circle: "))
area_of_the_circle = M. pi* Radius * Radius
print(" The area of the given circle is: ", area_of_the_circle)
pi* Radius * Radius
print(" The area of the given circle is: ", area_of_the_circle)
Выход:
Please enter the radius of the given circle: 3 The area of the given circle is: 28.274333882308138
- Метод 2. Вычислить площадь данного круга с помощью π.
π = 3.14
Radius = float(input("Please enter the radius of the given circle: "))
area_of_the_circle = π * Radius * Radius
print(" The area of the given circle is: ", area_of_the_circle)
Выход:
Please enter the radius of the given circle: 3 The area of the given circle is: 28.259999999999998
- Метод 3. Вычислить площадь данного круга с помощью функции.
import math
def area_of_the_circle(Radius):
area = Radius** 2 * math.pi
return area
Radius = float(input("Please enter the radius of the given circle: "))
print(" The area of the given circle is: ", area_of_the_circle(Radius))
Выход:
Please enter the radius of the given circle: 3 The area of the given circle is: 28.274333882308138
Заключение
В этом уроке мы показали три метода вычисления площади данного круга. Чтобы ее вычислить, пользователь должен знать радиус или диаметр данного круга. Из трех методов первый – самый простой и точный.
Михаил Русаков
Изучаю Python вместе с вами, читаю, собираю и записываю информацию опытных программистов.
Еще для изучения:
Вычисление площади круга
Все математические ресурсы GMAT
22 Диагностические тесты 693 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
GMAT Math Help » Проблемные вопросы » Геометрия » Круги » Радиус » Вычисление площади круга
Круг имеет радиус . Вычислите площадь круга.
Возможные ответы:
Правильный ответ:
Объяснение:
Используя формулу площади круга, мы можем подставить заданное значение его радиуса и вычислить наше решение:
Сообщить об ошибке
Какова площадь круга диаметром ?
Возможные ответы:
Правильный ответ:
Объяснение:
Площадь круга определяется как , где это радиус круга. Нам дан диаметр круга, который в два раза больше длины .
Нам дан диаметр круга, который в два раза больше длины .
Если , то
Тогда, найдя:
Сообщить об ошибке
Окружность на координатной плоскости определяется уравнением . Какова площадь круга?
Возможные ответы:
Недостаточно информации.
Правильный ответ:
Объяснение:
Уравнение окружности с центром в начале координатной плоскости: , где – радиус окружности.
Площадь круга, в свою очередь, определяется уравнением .
Поскольку у нас есть уравнение , мы можем вывести то и то .
Сообщить об ошибке
Какова площадь круга диаметром ?
Возможные ответы:
Недостаточно информации.
Правильный ответ:
Объяснение:
Площадь круга определяется как , где это радиус круга. Нам дан диаметр круга, который в два раза больше длины .
Если , то
Следовательно:
Сообщить об ошибке
Квадрат вписан в круг .
Какова площадь области внутри круга, но не внутри квадрата?
Возможные ответы:
Правильный ответ:
Объяснение:
Нашим первым шагом будет проведение двух радиусов от центра круга к двум соседним вершинам квадрата, образуя треугольник, третья сторона которого является краем квадрата. Поскольку эти радиусы делят пополам прямые углы квадрата, мы можем определить, что треугольник, который мы нарисовали, равен 45˚ — 45˚ — 90˚ прямоугольный треугольник. Из-за правил, регулирующих эти равнобедренные прямоугольные треугольники, мы можем определить, что, поскольку два катета треугольника равны 5 (радиус = 5), гипотенуза (сторона квадрата) должна быть равна .
Из-за правил, регулирующих эти равнобедренные прямоугольные треугольники, мы можем определить, что, поскольку два катета треугольника равны 5 (радиус = 5), гипотенуза (сторона квадрата) должна быть равна .
Теперь мы можем найти площадь квадрата:
и площадь круга:
Наконец, мы вычитаем площадь квадрата из площади круга:
Инженер проектирует штриховку
4 Сообщить об ошибке
4 для подводной лодки. Если окружность люка должна быть равна , какова будет его площадь? Возможные ответы:
Правильный ответ:
Пояснение:
Инженер проектирует круглый люк для подводной лодки. Если окружность люка должна быть равна , какова будет его площадь?
Чтобы найти площадь, нам понадобится радиус. Мы можем найти радиус, используя следующую формулу:
Итак, подставьте и решите для r
Затем используйте формулу площади, чтобы найти площадь:
Итак, у нас есть ответ!
Сообщить об ошибке
и являются площадью и диаметром одного и того же круга.
.
Какое из следующих утверждений верно?
Возможные ответы:
изменяется обратно пропорционально четвертой степени .
изменяется прямо как квадрат .
изменяется обратно пропорционально квадрату .
изменяется прямо как четвертая степень .
изменяется прямо как квадратный корень из .
Правильный ответ:
изменяется обратно пропорционально четвертой степени .
Объяснение:
Площадь и диаметр круга связаны Формулой
Заместительство:
IF, то
,
и изменяются по сравнению с четвертой силой.
Сообщить об ошибке
Круг имеет радиус . Укажите его площадь.
Возможные ответы:
Правильный ответ:
Объяснение:
Площадь круга обнаружена с использованием следующей формулы:
Набор:
Отчет о ошибке
, если растение кувшина Sarracenia purpure 6 дюймов, какова площадь отверстия?
Возможные ответы:
Правильный ответ:
Пояснение:
Если растение-кувшин Sarracenia purpurea имеет круглое отверстие с окружностью 6 дюймов, какова площадь отверстия?
Нам нужно работать в обратном направлении от окружности, чтобы найти площадь.
Окружность можно найти следующим образом:
Используйте это, чтобы найти «r», которое мы будем использовать для нахождения площади:
Далее, площадь поиска с использованием следующей:
Отчет о ошибке
← Предыдущий 1 2 3 Далее →
Уведомление об копирном правом
Все GMAT Math Resources
22.
693 практических теста
Вопрос дня
Карточки
Обучение по понятиям
Площадь круга
Упражнение 12.1
Оборудование: Для этого вам понадобится компас, ножницы, линейка и транспортир.
Мероприятия.
Цель: Открыть формулу для
площадь круга.
Шаг 1: Используя циркуль, начертите круг радиусом 7 см.
Затем отметьте центр круга и нарисуйте его радиус.
Шаг 2: Поместите центр транспортира в центр
круг и нулевая линия по радиусу. Затем отметьте каждые 30 вокруг
круг.
Затем отметьте каждые 30 вокруг
круг.
Шаг 3: Используя линейку и карандаш, нарисуйте линии, соединяющие каждый
30 отметок до центра круга, чтобы образовалось 6 диаметров. Диаграмма
полученный таким образом будет иметь 12 частей, как показано ниже.
Шаг 4: Раскрасьте детали, как показано ниже.
Шаг 5: Вырежьте круг, а затем разрежьте по диаметру так, чтобы
что все части (т.е. сектора) разделены.
Шаг 6: Расположите все сектора так, чтобы получилась форма,
аппроксимирует параллелограмм, как показано ниже.
Шаг 7: С помощью линейки измерьте основание и высоту
приблизительный параллелограмм, полученный на шаге 6.
Вопросы: 1. Рассчитайте площадь фигуры на шаге 6 по формуле:
2. Какова площадь круга, нарисованного на шаге 1?
3. Оказывается, существует формула для расчета площади
круг. Сможете ли вы обнаружить это?
Из приведенного выше действия видно, что, упорядочивая секторы
круг как параллелограмм, который:
Помните: Площадь круга A определяется по следующей формуле, где r — радиус круга:
Пример 8 Решение:
Итак, площадь 616 м 2 .
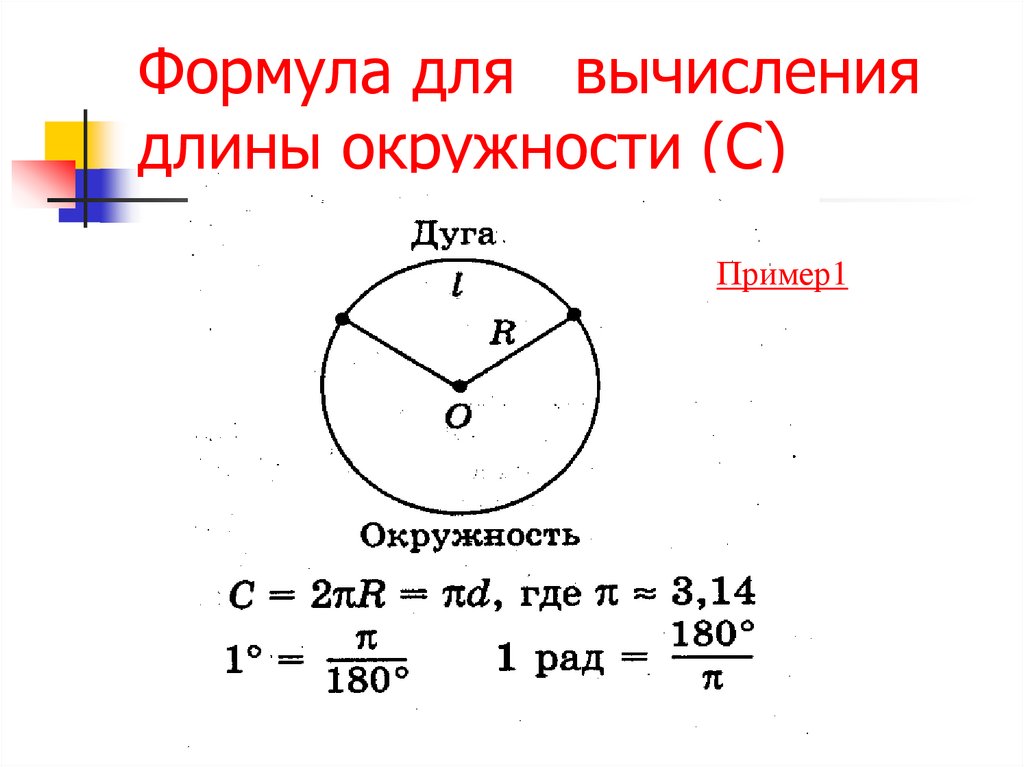

Цель: Открыть формулу для площадь круга.
 Затем отметьте каждые 30 вокруг
круг.
Затем отметьте каждые 30 вокруг
круг.


 pi* Radius * Radius
print(" The area of the given circle is: ", area_of_the_circle)
pi* Radius * Radius
print(" The area of the given circle is: ", area_of_the_circle)
 274333882308138
274333882308138