1
Первый слайд презентации: Функция y = x 2 и её график
Урок алгебры в 7 классе.
Изображение слайда
2
Слайд 2: Величие человека в его способности мыслить»
Блез Паскаль
Изображение слайда
3
Слайд 3: Фалес:
— Что есть больше всего на свете? — Пространство. Что быстрее всего? Ум. Что мудрее всего? Время. Что приятнее всего? Достичь желаемого результата.
Изображение слайда
4
Слайд 4
(2;-2)
(- 2;2)
(1;2)
(-2; 2)
(-1;1)
(1;-1)
(2;2)
— Что быстрее всего? – Ум.
Что мудрее всего? — Время.
Что приятнее всего? – Достичь желаемого результата.
Ф
— Что быстрее всего? – Ум.
Что мудрее всего? — Время.
Что приятнее всего? – Достичь желаемого результата.
У
— Что быстрее всего? – Ум.
Что мудрее всего? — Время.
Что приятнее всего? – Достичь желаемого результата.
Н
— Что быстрее всего? – Ум.
Что мудрее всего? — Время.
Что приятнее всего? – Достичь желаемого результата.
К
— Что быстрее всего? – Ум.
Что мудрее всего? — Время.
Что приятнее всего? – Достичь желаемого результата.
Ц
— Что быстрее всего? – Ум.
Что мудрее всего? — Время.
Что приятнее всего? – Достичь желаемого результата.
И
— Что быстрее всего? – Ум.
Что мудрее всего? — Время.
Что приятнее всего? – Достичь желаемого результата.
Я
— Что быстрее всего? – Ум.
Что мудрее всего? — Время.
Что приятнее всего? – Достичь желаемого результата.
Изображение слайда
5
Слайд 5
Объясните термины Функция Область определения Аргумент График функции Линейная функция
Изображение слайда
6
Слайд 6
Укажите область определения функции: y = 16 – 5 x х ≠ 0 х ≠ 7 х – любое число
Изображение слайда
7
Слайд 7: Зависимость площади квадрата от длины его стороны
квадратичная функция Зависимая переменная Независимая переменная y = x 2 y x
8
Слайд 8: Функция y = x 2 и её график
Изображение слайда
9
Слайд 9: Цели урока:
рассмотреть график и свойства функции у = х 2 ;
научиться строить и «читать» график данной функции.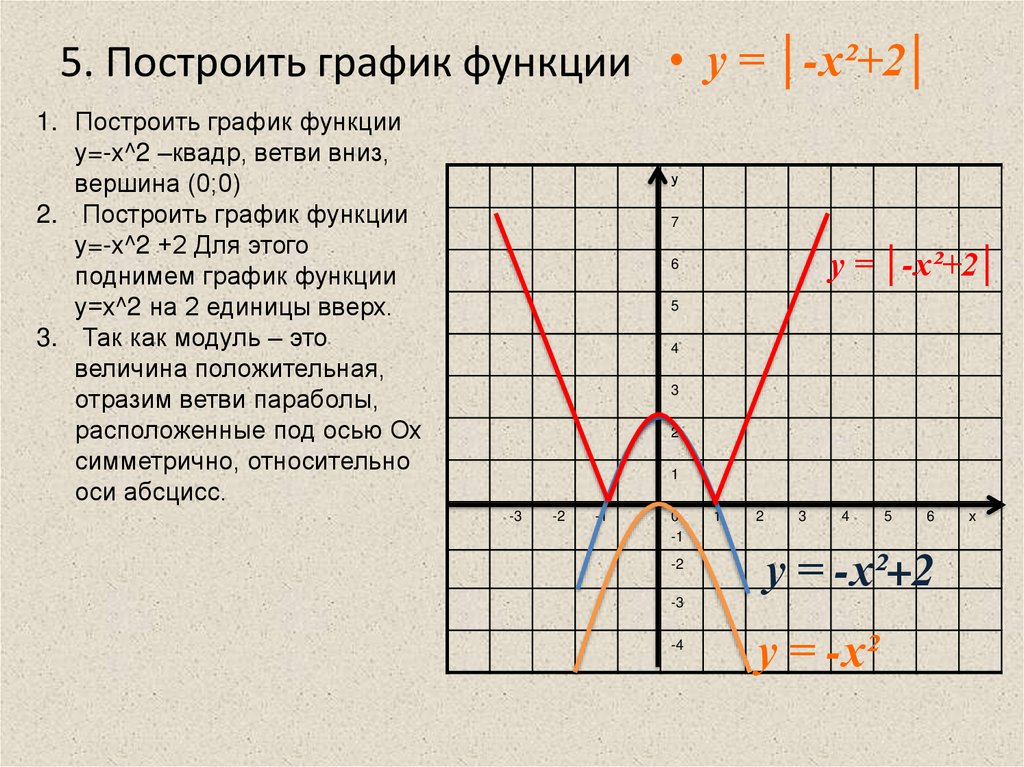
Изображение слайда
10
Слайд 10
Ключом ко всякой науке является вопросительный знак? Оноре де Бальзак
Изображение слайда
11Слайд 11
Функция y = x 2 Математическое исследование
Изображение слайда
12
Слайд 12
х — 3 — 2, 5 — 2 — 1,5 — 1 — 0,5 0 y Заполните таблицу значений функции y = x 2 : х 0 0, 5 1 1,5 2 2,5 3 y 9 6,25 4 2,25 1 0,25 0 0 0,25 1 2,25 4 6,25 9
Изображение слайда
13
Слайд 13
Постройте график функции y = x 2 парабола
Изображение слайда
14
Слайд 14
Древнегреческий математик
Аполлоний Пергский
( Перге, 262 до н.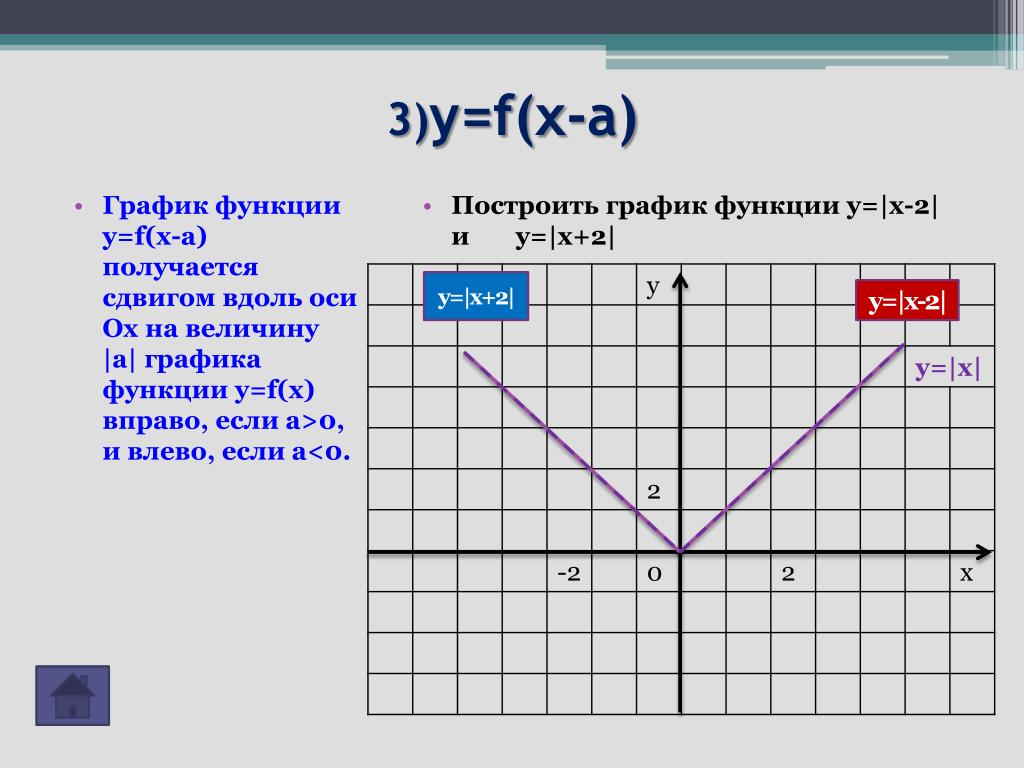
э. — 190 до н.э.)
разрезав конус, линию среза назвал параболой, что в переводе с греческого означает «приложение» или «притча», о чём математик и написал в восьмитомнике «Конические сечения».
И долгое время параболой называли лишь линию среза конуса, пока не появилась квадратичная функция.
Историческая справка
Изображение слайда
15
Слайд 15
Траектория камня, брошенного под углом к горизонту Знаете ли вы?
Изображение слайда
16
Слайд 16
Перевал Парабола Невероятно, но факт!
Изображение слайда
17
Слайд 17: Свойства функции y = x 2
Изображение слайда
18
Слайд 18
Область определения функции :
х – любое число.
Область значений функции :
все значения у ≥ 0.
Изображение слайда
19
Слайд 19
Если х = 0, то у = 0. График функции проходит через начало координат.
Изображение слайда
20
Слайд 20
Если х ≠ 0, то у > 0. Все точки графика функции, кроме точки (0; 0), расположены выше оси х. I II
Изображение слайда
21
Слайд 21
Противоположным значениям х соответствует одно и то же значение у. График функции симметричен относительно оси ординат. (- х) 2 = х 2 при любом х
Изображение слайда
22
Слайд 22
Геометрические свойства параболы Обладает симметрией Ось разрезает параболу на две части: ветви параболы Точка (0; 0) – вершина параболы Парабола касается оси абсцисс Ось симметрии
Изображение слайда23
Слайд 23
«Знание – орудие,
а не цель»
Л.
Н. Толстой
Найдите у, если:
х ≈ -2,5
х = — 2
у ≈ 1,9
у ≈ 6,7
у ≈ 9,6
х = 1,4
х = — 2,6
х = 3,1
у = 6
у = 4
Найдите х, если:
— 1,4
— 3, 1
х ≈ 2,5
х = 2
Изображение слайда
24
Слайд 24
Найдите несколько значений х, при которых значения функции : меньше 4 больше 4
Изображение слайда
25
Слайд 25
При каких значениях а точка Р(а; 64) принадлежит графику функции у = х 2. Принадлежит ли графику функции у = х 2 точка : Не выполняя вычислений, определите, какие из точек не принадлеж ат графику функции у = х 2 : P(-18; 324) R(-99; -9081) S(17; 279) (-1; 1) (0; 8) (-2; 4) (3; -9) (1,8; 3,24) (16; 0) а = 8; а = — 8 принадлежит не принадлежит не принадлежит
Изображение слайда
26
Слайд 26
Решите графически уравнение: х 2 = 5 х 2 = — 1 x 2 = х +1 y = — 1 y = x + 1 y = х 2 y = 5 нет решений х ≈ — 2,2; х ≈ 2,2 х ≈ — 0,6; х ≈ 1,6
Изображение слайда
27
Слайд 27: Цели урока:
рассмотреть график и свойства функции у = х 2 ;
научиться строить и «читать» график данной функции.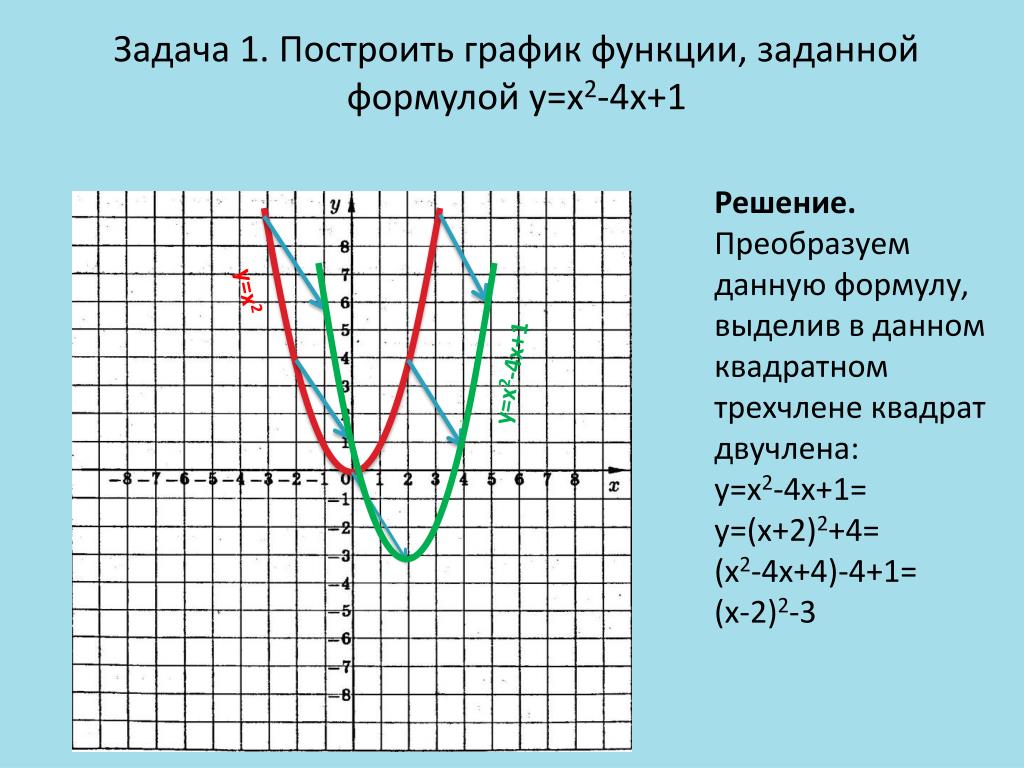
Ответы
| ||||||||||||
03.17
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
задача по математике 3-й класс: в забеге участвовало несколько детей.
Число прибежавших раньше Миши в три раза больше тех, кто прибежал после него. А
из аэропорта на автовокзал через каждые три минуты отправляется автобус,который едет 1 час.через 2 минуты после отправления из аэропорта выехал
Решено
В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.75 . Найдите АС.
задача для 5 класса. После строительства дома осталось некоторое количество плиток. Их можно использовать для выкладывания прямоугольной площадки на
В ребусе КЕНГ+УРУ +2017 зашифрована сумма четырехзначного и трехзначного чисел, Разными буквами зашифрованы разные цифры,а одинаковыми — одинаковые.
Пользуйтесь нашим приложением
Графиком функции y x 5 является – Telegraph
Графиком функции y x 5 являетсяСкачать файл — Графиком функции y x 5 является
Этот сервис создан в помощь школьникам и студентам в изучении математики алгебры и геометрии и физики и предназначен для онлайн построения графиков функций обычных и параметрических и графиков по точкам графиков по значениям , а также графиков функций в полярной системе координат.
Почитайте в cправкe , как правильно вводить формулы функций. Загляните в раздел примеров , наверняка, там есть графики функций, похожие на то, что нужно Вам, останется только слегка откорректировать готовые формулы функций. Дополнительно на нашем сайте вы можете воспользоваться калькулятором матриц , с помощью которого можно производить различные преобразования и действия с матрицами онлайн. Построение графиков функций онлайн Справка. Сервис онлайн построения графиков Этот сервис создан в помощь школьникам и студентам в изучении математики алгебры и геометрии и физики и предназначен для онлайн построения графиков функций обычных и параметрических и графиков по точкам графиков по значениям , а также графиков функций в полярной системе координат. Просто введите формулу функции в поле ‘Графики: Наша группа Вконтакте — присоединяйтесь!
Бесплатная помощь с домашними заданиями
Данный урок мы посвятим решению типовых задач на построение графика функции. Вспомним определение квадратного корня.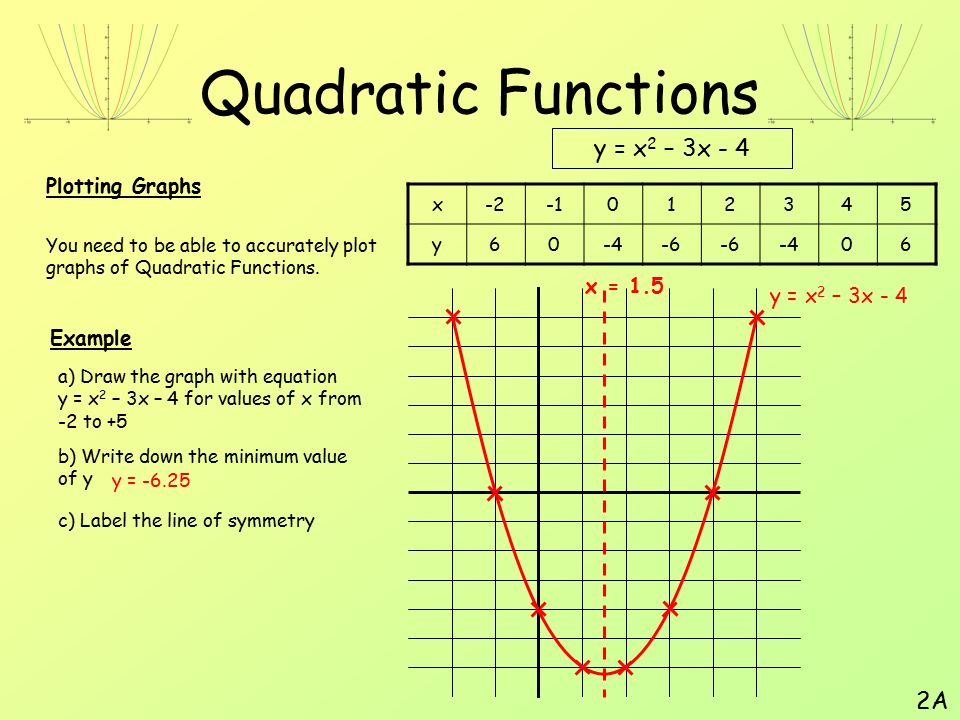
На графике наглядно виден смысл вычисления квадратного корня. Например, если рассмотреть ординату 16, то ей будет соответствовать абсцисса 4, т. Аналогично, ординате 9 на графике соответствует точка с абсциссой 3, поскольку , ординате 11 соответствует абсцисса , т. На графике для наглядности изображены несколько точек, ординаты которых вычисляются с помощью извлечения квадратного корня: Постройте и прочтите график функции: При этом все точки графика сдвинутся на 1 влево, например, точка с координатами 1;1 перейдет в точку с координатами 0;1. В результате получаем искомый график красная кривая. Проверить такой способ легко при подстановке нескольких значений аргумента. Область определения ОДЗ при этом требует, чтобы подкоренное выражение было неотрицательным, т. При этом все точки графика сдвинутся на 1 вправо, например, точка с координатами 1;1 прейдет в точку с координатами 2;1. Область определения ОДЗ аналогична предыдущему случаю: На указанных примерах несложно сформулировать правило построения функций вида:.
Затем график построенной функции смещаем на 2 вверх и получаем на рисунке 5 искомый график красная кривая. Точка с координатами 1;1 при этом, например, переходит в точку 1;3. Затем график построенной функции рис. Точка с координатами 1;1 при этом, например, переходит в точку 1;0. Постройте и прочтите график функции. Метод построения указанной функции представляет собой комбинацию двух методов, которые мы видели в предыдущих примерах. При этом, например, точка с координатами 1;1 сначала перейдет в точку 2;1 , а затем в точку 2;3. Искомая кривая изображена красным цветом. Область определения ОДЗ — подкоренное выражение неотрицательно: Как видно на указанном примере, преобразования графиков функций, которые мы рассмотрели, можно применять последовательно в комплексе. Для построения данной составной функции изображаем ее части в приведенных диапазонах построения рис. Для этого сначала изображаем пунктиром всю функцию , затем всю функцию , а затем наводим красная кривая только те их области, которые заданы условием задачи.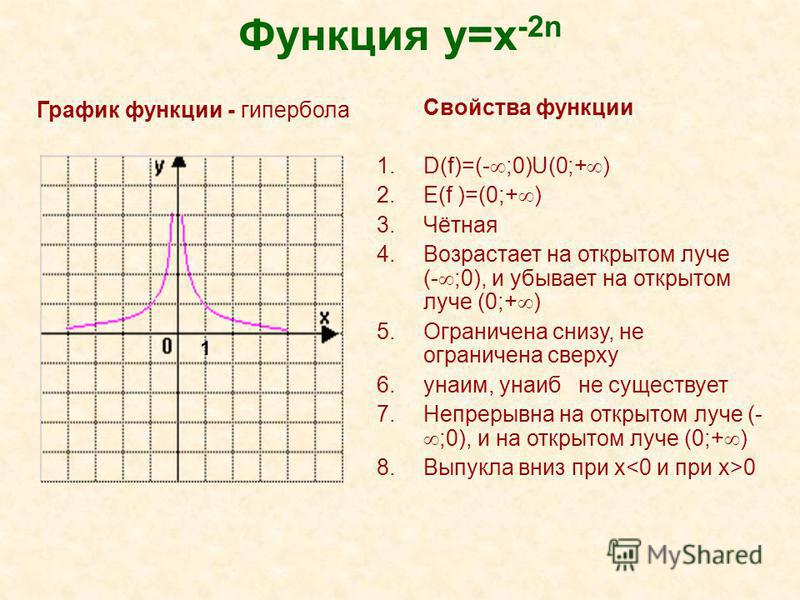
Сливаются два участка кривой в точке с координатами 1;1. Графически решить систему уравнений. Для решения системы графическим способом необходимо построить графики функций рис. На графике изображен полезный факт, демонстрирующий, что графики квадратичной функции и квадратного корня симметричны относительно графика функции. По графику видно, что имеем две точки пересечения, т. Для определения точных значений этих решений подставим стандартные значения аргумента в обе исследуемые функции: Мы его уже строили на сегодняшнем уроке, поэтому воспользуемся готовым рисунком Учебник для общеобразовательных учреждений. Квадратный корень из х Источник. Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам — сделайте свой вклад в развитие проекта. Алгебра, 8 Класcы 1 класс Математика Окружающий мир Русский язык Чтение 2 класс Математика Окружающий мир Русский язык Английский язык Чтение 3 класс Математика Окружающий мир Русский язык Английский язык Чтение 4 класс Математика Окружающий мир Русский язык Английский язык Чтение 5 класс Математика Информатика Природоведение Биология География Английский язык Всеобщая история Русский язык Литература Обществознание ОБЖ 6 класс Математика Информатика Биология География Английский язык Всеобщая история Русский язык История России Литература Обществознание ОБЖ 7 класс Алгебра Геометрия Физика Биология География Английский язык Всеобщая история Русский язык История России Литература Обществознание ОБЖ 8 класс Алгебра Геометрия Информатика География Химия Физика Биология Английский язык Всеобщая история Русский язык История России Литература Обществознание ОБЖ 9 класс Алгебра Геометрия Информатика География Химия Физика Биология Английский язык Всеобщая история Русский язык История России Литература Обществознание ОБЖ 10 класс Алгебра Геометрия География Химия Физика Биология Английский язык Всеобщая история Литература История России Обществознание ОБЖ 11 класс Алгебра Геометрия Биология Физика Химия Английский язык Всеобщая история Литература История России Обществознание ОБЖ ЕГЭ.
Алгебра 7 класс 8 класс 9 класс 10 класс 11 класс ЕГЭ Геометрия 7 класс 8 класс 9 класс 10 класс 11 класс ЕГЭ Математика 1 класс 2 класс 3 класс 4 класс 5 класс 6 класс Информатика 5 класс 6 класс 8 класс 9 класс Обществознание 5 класс 6 класс 7 класс 8 класс 9 класс 10 класс 11 класс ОБЖ 5 класс 6 класс 7 класс 8 класс 9 класс 10 класс 11 класс Физика 7 класс 8 класс 9 класс 10 класс 11 класс ЕГЭ Химия 8 класс 9 класс 10 класс 11 класс Биология 5 класс 6 класс 7 класс 8 класс 9 класс 10 класс 11 класс Факультатив География 5 класс 6 класс 7 класс 8 класс 9 класс 10 класс Природоведение 5 класс Окружающий мир 1 класс 2 класс 3 класс 4 класс Русский язык 1 класс 2 класс 3 класс 4 класс 5 класс 6 класс 7 класс 8 класс 9 класс Факультатив ЕГЭ Литература 5 класс 6 класс 7 класс 8 класс 9 класс 10 класс 11 класс История России 6 класс 7 класс 8 класс 9 класс 10 класс 11 класс Видеословарь Всеобщая история 5 класс 6 класс 7 класс 8 класс 9 класс 10 класс 11 класс Спецкурс Английский язык 2 класс 3 класс 4 класс 5 — 6 классы 7 — 8 классы 9 класс 10 — 11 классы Чтение 1 класс 2 класс 3 класс 4 класс.
Её свойства и график. Видеоурок Текстовый урок Тренажеры Тесты Вопросы к уроку. Этот видеоурок доступен по абонементу Подробнее об абонементе, платных и бесплатных уроках У вас уже есть абонемент? На указанных примерах несложно сформулировать правило построения функций вида: С помощью указанных примеров сформулируем правило построения функций вида: На следующем уроке мы рассмотрим свойства квадратных корней. Дополнительные рекомендованные ссылки на ресурсы сети Интернет 1. Информация об уроке Комментарии 12 Поделиться В избранное Нашли ошибку? Комментарии к уроку Показать еще комментарии Это вы. Код для вставки на сайт: Копируя приведенный ниже HTML-код, вы тем самым принимаете Условия использования. Центр образования Домашняя школа Репетитор ЕГЭ Univertv.
Функция y = корень квадратный из x, ее свойства и график
Программа тест на отцовство
Htaccess для wordpress
Функция y = √x. Её свойства и график. Решение задач
Новые правила перевозки животных в поезде
Сколько кг за беременность норма
Бесплатная помощь с домашними заданиями
Ребенка укусило насекомое что делать
Фонбет лайв букмекерская вход без проблем
3-8Дифференциальное уравнение Бернулли
Как решить это специальное дифференциальное уравнение первого порядка
Уравнение Бернулли имеет следующую форму:
dy dx + P(x)y = Q(x)y n
где n — любое действительное число, но не 0 или 1
При n = 0 уравнение можно решить как линейное дифференциальное уравнение первого порядка.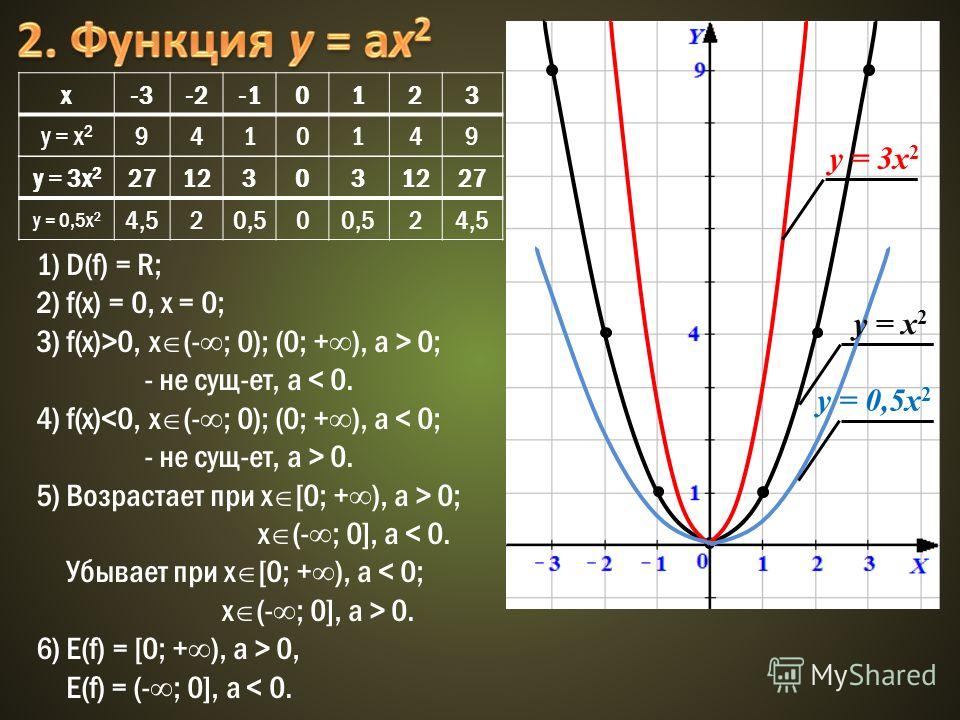
При n = 1 уравнение можно решить с помощью разделения переменных.
Для других значений n мы можем решить его, подставив
u = y 1−n
и превратив его в линейное дифференциальное уравнение (а затем решив его).
Пример 1: РешениеDY DX + x 5 Y = x 5 Y 7
. Это ABERLI -a Advation с PATION). x)=x 5 и n=7, попробуем заменить:
u = y 1−n
u = y -6
In terms of y that is:
y = u (− 1 6 )
Differentiate y with respect to x:
dy dx = −1 6 u (− 7 6 ) du dx
Substitute dy dx and y into the original equation dy dx + х 5 у = х 5 y 7
−1 6 u ( −7 6 ) du dx + x 5 u ( −1 6 ) = x 5 u ( −7 6 )
Multiply all terms by −6u ( 7 6 )
du dx − 6x 5 u = −6x 5
Замена сработала! Теперь у нас есть уравнение, которое мы, надеюсь, сможем решить.
Simplify:
du dx = 6x 5 u − 6x 5
du dx = (u−1)6x 5
Using separation of variables:
DU U -1 = 6x 5 DX
Интегрируйте с обеих сторон:
∫ 1 U -1 DU = ∫6X 5 U -1 DU = ∫6X 5 DX . 1) = х 6 + С
u−1 = е х 6 + C
u = e (x 6 + c) + 1
Substitute back y = u ( −1 6 )
y = ( e (x 6 + в) + 1 ) ( −1 6 )
Решено!
И мы получаем следующие примеры кривых:
Давайте еще раз посмотрим на ту замену, которую мы сделали выше. Мы начали с:
глухой глухой + х 5 у = х 5 у 7
И заканчивался на:
du dx − 6x 5 u = −6x 5
На самом деле вообще , можно сразу перейти от
dy dx + P(x)y = Q(x)y n
n не равно 0 или 1
до:
du dx + (1−n)uP(x) = (1−n)Q(x)
Затем решите это и закончите, подставив обратно y = u ( −1 n−1 )
Давайте сделаем это в следующем примере.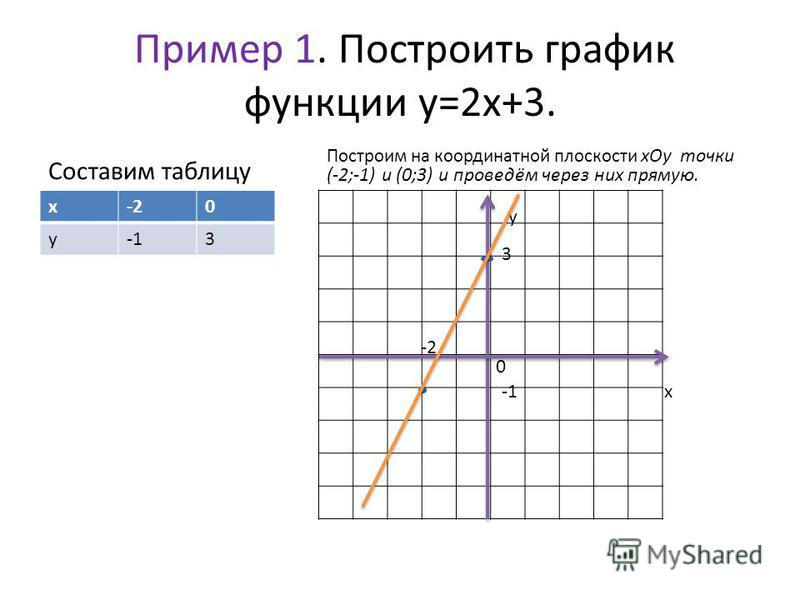
DY DX — Y x = Y
. Это ABERULLIT с NAPATION с NAPATION с NAPATION с NAPATION с NAPATION с navation с n.
. и Q(x) = 1
Зная, что это уравнение Бернулли, мы можем сразу перейти к следующему: )
Что после подстановки n, P(X) и Q(X) становится следующим:
du dx + 8u x = −8
Теперь попробуем решить это.
К сожалению, мы не можем разделить переменные, но уравнение является линейным и вида du dx + R(X)u = S(x), где R(X) = 8 x и S(X) = −8
. Которое мы можем решить, выполнив шаги с 1 по 9:
Шаг 1: Пусть u=vw
Шаг 2: Дифференцируем u = vw
du dx = v dw dx + w dv dx
Step 3: Substitute u = vw and du dx = v dw dx + w dv dx into du dx + 8u x = −8:
v dw dx + w dv dx + 8vw x = − 8
Шаг 4: Фактор частей, содержащих w.
v dw dx + w( dv dx + 8v x ) = −8
x ) = −8переменные внутри и равные нулю.
dv dx + 8v x = 0
dv v = −8dx x
Step 6: Solve this separable differential equation to find v.
∫ дв v = — ∫ 8dx x
ln(v) = ln(k) − 8ln(x)
v = kx -8
-8 DW DX = −8
Шаг 8: Решите это, чтобы найти V
KX -8 DW = −8 DX
K DW = −8 xx = x 8099 999999999999999999999999999999999999999999999. 9 9 9092 dw = ∫ −8x 8 dx
кВт = −8 9 x 9 + C
w = 1 k ( −8 9 x 9 + C )
Шаг 9: Подставьте в u = vw, чтобы найти решение исходного уравнения.
u = vw = kx -8 k ( −8 9 x 9 + C )
u = 909 — 909 8 9 x 9 + C )
u = -8 9 x + Cx -8
Теперь мы использовали замену:
u = y 1−n = y -8
Что в нашем случае означает, что нам нужно заменить y = u ( −1 8 ) :9 8 9 x + c x -8 ) ( −1 8 )
Готово!
И мы получаем это прекрасное семейство кривых:
Пример 3: Решитьdy dx + 2y x = x 2 y 2 sin(x)
Это уравнение Бернулли с n = 2, P(x) = 2 x и Q(x) = x 2 0 sin(x)
Мы можем перейти прямо к этому:
du dx + (1−n)uP(x) = (1−n)Q(x)
Что после замены n, P (X) и Q(X) принимает вид:
du dx − 2u x = − x 2 sin(x)
В этом случае мы не можем разделить переменные, но уравнение линейна и имеет вид du dx + R(X)u = S(x), где R(X) = −2 x и S(X) = −x 2 sin(x)
Решите шаги 1 to 9:
Step 1: Let u=vw
Step 2: Differentiate u = vw
du dx = v dw dx + w dv dx
Step 3 : Замените u = vw и du dx = v dw dx + w dv dx на 9.
0915 du dx − 2u x = −x 2 sin(x)
v dw dx + w dv dx − 2vw x = −x 2 sin(x)
Шаг 4: Разложите на множители части, включающие w.
V DW DX + W ( DV DX — 2V x ) = −x 2V (x ) = −x 2v (x)
(x)
(x)
(x)
(x)
(x ) =. , и разделите переменные.
dv dx − 2v x = 0
1 v dv = 2 x dx
Step 6: Solve this separable differential equation to find v.
∫ 1 V DV = ∫ 2 X DX
LN (V) = 2LN (x) + LN (K)
V = KX 2
.
уравнение, полученное на шаге 4.
kx 2 dw dx = −x 2 sin(x)
Шаг 8: Решите это, чтобы найти v. dx
кВт = cos(x) + C
w = cos(x) + C k
Шаг 9: Подставьте в u = vw, чтобы найти решение исходного уравнения.
u = kx 2 cos(x) + C k
u = x 2 (cos(x)+C)
Наконец, подставляем обратно y = u -1
y = 1 x 2 (cos(x)+C)
Что выглядит так (примеры значений C):
Уравнение Бернулли приписывают Якобу Бернулли (1655−1705), одному из семья известных швейцарских математиков.
9469, 9470, 9471, 9472, 9473, 9474, 9475, 9476, 9477, 9478
Таблица значений линейного уравнения. Примеры, инструкции и график
Часть I. Как линейные уравнения соотносятся с таблицами значений
Уравнения как отношения
Уравнение прямой выражает отношение между значениями x и y на координатной плоскости.
Например, уравнение $$y = x$$ выражает отношение, в котором каждое значение x имеет точно такое же значение y. Уравнение $$ y = 2x $$ выражает соотношение, в котором каждое значение y в два раза превышает значение x, а $$ y = x + 1 $$ выражает соотношение, в котором каждое значение y на 1 больше, чем значение x.
А как насчет таблицы значений?
Поскольку, как мы только что написали, каждое линейное уравнение представляет собой отношение значений x и y, мы можем создать таблицу значений для любой строки. Это просто значения $$ x $$ и $$ y $$, которые верны для данной строки. Другими словами, таблица значений — это просто некоторые точки, находящиеся на прямой.
Пример 1
Уравнение: $$ \red y = \blue x + 1 $$
Таблица значений
| $$ \синий х \текст {значение} $$ | Уравнение | $$ \red y \text{значение} $$ |
| у = х + 1 | ||
| $$ \ синий 3 $$ | $$y = (\синий 3) + 1$$ | $$ \ красный 4 $$ |
| $$ \ синий 4 $$ | у = ($$ \синий 4 $$ ) + 1 | $$ \ красный 5 $$ |
| $$ \ синий 5 $$ | $$ у = (\ синий 5 ) + 1$$ | $$ \ красный 6 $$ |
| $$ \ синий 6 $$ | $$ y = (\синий 6) + 1 $$ | $$ \ красный 7 $$ |
Пример 2
Уравнение: у = 3x + 2
Таблица значений
| X Значение | Уравнение | Значение Y |
| у = 3х + 2 | ||
| 1 | у = 3(1) + 2 | 5 |
| 2 | у = 3(2) + 2 | 7 |
| 3 | у = 3(3) + 2 | 11 |
| 4 | у = 3(4) + 2 | 14 |
Таким образом, чтобы создать таблицу значений для строки, просто выберите набор значений x, подставьте их в уравнение и оцените, чтобы получить значения y.
Проблема 1
- Исходная проблема
- Шаг 1
- г. Шаг 2
- Шаг 3
- Шаг 4
Создайте таблицу значений уравнения y = 5x + 2.
Создайте таблицу и выберите набор значений x.
| X Значение | Уравнение | Значение Y |
| у = 5х + 2 | ||
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
Подставьте каждое значение x (левый столбец) в уравнение.
| X Значение | Уравнение | Значение Y |
| у = 5х + 2 | ||
| 1 | у = 5(1) + 2 | |
| 2 | у = 5(2) + 2 | |
| 3 | у = 5(3) + 2 | |
| 4 | у = 5(4) + 2 |
Оцените уравнение (средний столбец), чтобы получить значение y.
| X Значение | Уравнение | Значение Y |
| у = 5х + 2 | ||
| 1 | у = 5(1) + 2 | 7 |
| 2 | у = 5(2) + 2 | 12 |
| 3 | у = 5(3) + 2 | 17 |
| 4 | у = 5(4) + 2 | 22 |
Необязательный шаг, если вы хотите, вы можете опустить средний столбец из своей таблицы, поскольку таблица значений на самом деле представляет собой только пары x и y.
(Мы использовали средний столбец просто для получения значений y)
| X Значение | Y Значение |
| 1 | 7 |
| 2 | 12 |
| 3 | 17 |
| 4 | 22 |
Проблема 2
- Исходная проблема г.
- Шаг 1
- Шаг 2
- Шаг 3
- Шаг 4 г.
Создайте таблицу значений уравнения y = −6x + 2.
Создайте таблицу и выберите набор значений x.
| X Значение | Уравнение | Значение Y |
| у = -6х + 2 | ||
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
Подставьте каждое значение x (левый столбец) в уравнение.
| X Значение | Уравнение | Значение Y |
| у = -6х + 2 | ||
| 1 | г = -6(1) + 2 | |
| 2 | г = -6(2) + 2 | |
| 3 | г = -6(3) + 2 | |
| 4 | г = -6(4) + 2 |
Оцените уравнение (средний столбец), чтобы получить значение y.
| X Значение | Уравнение | Значение Y |
| у = -6х + 2 | ||
| 1 | г = -6(1) + 2 | -4 |
| 2 | г = -6(2) + 2 | -10 |
| 3 | г = -6(3) + 2 | -16 |
| 4 | г = -6(4) + 2 | -22 |
Необязательный шаг, если вы хотите, вы можете опустить средний столбец из своей таблицы, поскольку таблица значений на самом деле представляет собой только пары x и y.
(Мы использовали средний столбец просто для получения значений y)
| X Значение | Значение Y |
| 1 | -4 |
| 2 | -10 |
| 3 | -16 |
| 4 | -22 |
Задача 3
- Исходная проблема
- Шаг 1
- Шаг 2
- Шаг 3 г.
- Шаг 4
Создайте таблицу значений уравнения y = −6x − 4
Создайте таблицу и выберите набор значений x
| X Значение | Уравнение | Значение Y |
| у = -6х — 4 | ||
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
Подставьте каждое значение x (левый столбец) в уравнение.
| X Значение | Уравнение | Значение Y |
| 1 | г = -6(1) — 4 | |
| 2 | г = -6(2) — 4 | |
| 3 | г = -6(3) — 4 | |
| 4 | г = -6(4) — 4 |
Оцените уравнение (средний столбец), чтобы получить значение y.
| X Значение | Уравнение | Значение Y |
| 1 | г = -6(1) — 4 | -10 |
| 2 | г = -6(2) — 4 | -16 |
| 3 | г = -6(3) — 4 | -22 |
| 4 | г = -6(4) — 4 | -28 |
Необязательный шаг, если вы хотите, вы можете опустить средний столбец из своей таблицы, поскольку таблица значений на самом деле представляет собой только пары x и y.
(Мы использовали средний столбец просто для получения значений y)
| X Значение | Значение Y |
| 1 | -10 |
| 2 | -16 |
| 3 | -22 |
| 4 | -28 |
Часть II.
Запись уравнения из таблицы значенийЧасто студентов просят написать уравнение прямой из таблицы значений. Чтобы решить такую задачу, просто выберите любые 2 точки на столе и выполните обычные шаги для написания уравнения прямой из 2 точек.
Проблема 4
г.- Исходная проблема
- Шаг 1
- Шаг 2
- Шаг 3
- г. Шаг 4
Напишите уравнение линии из таблицы значений ниже.
| X Значение | Значение Y |
| 0 | 3 |
| 1 | 7 |
| 2 | 11 |
| 3 | 15 |
Выберите любые две пары x, y из таблицы и рассчитайте наклон.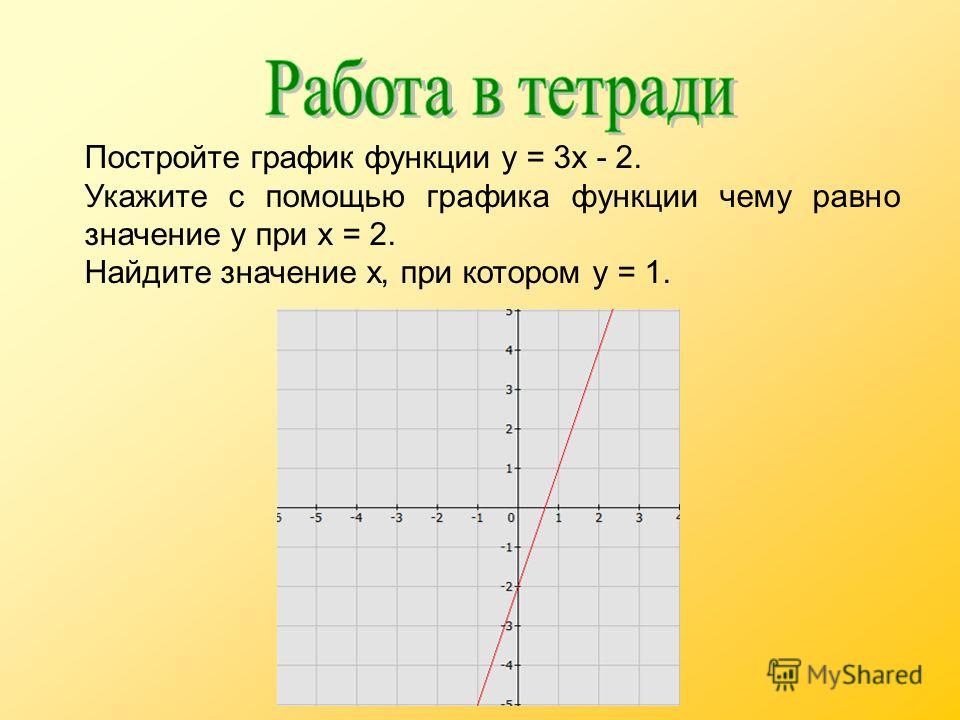
Так как я люблю работать с легкими маленькими числами, я выбрал (0, 3) и (1, 7).
| X Значение | Значение Y |
| 0 | 3 |
| 1 | 7 |
| 2 | 11 |
| 3 | 15 |
Подставьте наклон в форму пересечения наклона линии.
у = мх + б
у = 4х + б
Найдите значение ‘b’ в уравнении пересечения наклона.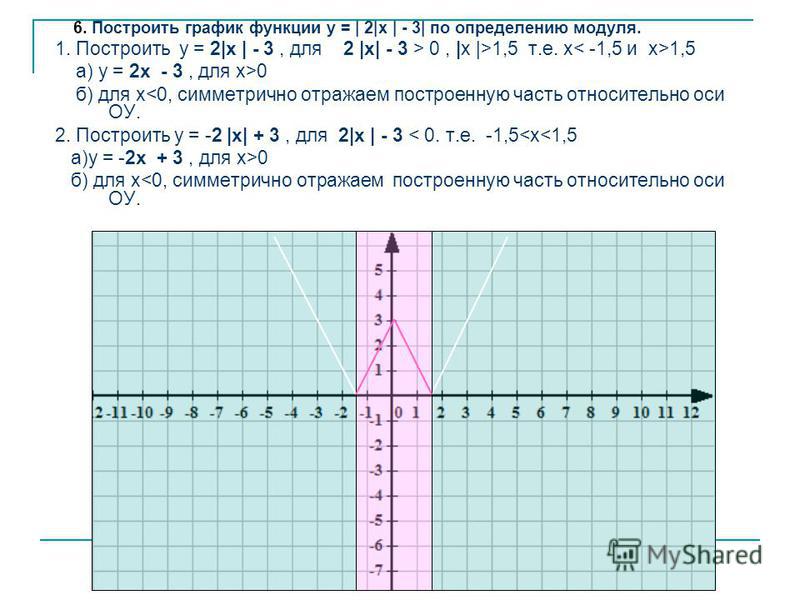
у = мх + б
у = 4х + б
Поскольку наша таблица дала нам точку (0, 3), мы знаем, что «b» равно 3. Помните, что «b» — это точка пересечения с осью y, которая, к счастью, была предоставлена нам в таблице.
Ответ: у = 4x + 3
При желании вы можете проверить свой ответ, подставив значения из таблицы в уравнение. Каждая пара x, y из таблицы должна работать с вашим ответом.
Проблема 5
- Исходная проблема г.
- Шаг 1
- Шаг 2
- Шаг 3
- Шаг 4
Напишите уравнение из приведенной ниже таблицы значений.
| X Значение | Значение Y |
| 2 | 8 |
| 4 | 9 |
| 6 | 10 |
Выберите любые две пары x, y из таблицы и рассчитайте наклон. Я выбрал (2, 8) и (4, 9).
| Х | Д |
| 2 | 8 |
| 4 | 9 |
| 6 | 10 |
Подставьте наклон в форму пересечения наклона линии.
у = мх + б
у = ½ х + б
Найдите значение ‘b’ в уравнении пересечения наклона.
Теперь, когда мы знаем значение b, мы можем подставить его в наше уравнение.
Ответ: у = ½x + 7
При желании вы можете проверить свой ответ, подставив значения из таблицы в уравнение. Каждая пара x, y из таблицы должна работать с вашим ответом.
Проблема 6
- Исходная проблема
- Шаг 1 г.
- Шаг 2
- Шаг 3
- Шаг 4
Напишите уравнение из приведенной ниже таблицы значений.
| X Значение | Значение Y |
| 3 | 2 |
| 6 | 0 |
| 9 | -2 |
Выберите любые две пары x, y из таблицы и рассчитайте наклон.
Я выбрал (2, 8) и (4, 9).
| Х | Д |
| 3 | 2 |
| 6 | 0 |
| 9 | -2 |
Подставьте наклон в форму пересечения наклона линии.
у = мх + б
у = х + б
Найдите значение ‘b’ в уравнении пересечения наклона.
Теперь, когда мы знаем значение b, мы можем подставить его в наше уравнение.
Ответ: у = х + 4
При желании вы можете проверить свой ответ, подставив значения из таблицы в уравнение. Каждая пара x, y из таблицы должна работать с вашим ответом.
Задача-вызов
почему ты можешь не написать уравнение линии из таблицы значений ниже?
Помните: Наклон линии никогда не меняется
| X Значение | Значение Y |
| 0 | 1 |
| 1 | 3 |
| 2 | 8 |
| 3 | 11 |
Причина, по которой эта таблица может 90 917, а не 90 918 представлять уравнение прямой, заключается в непостоянстве наклона.
Например, наклон двух точек вверху таблицы (0, 1) и (1, 3) отличается от наклона внизу (2, 8) и (3, 11).
Горизонтальные асимптоты | Purplemath
VerticalSlantExamples
Purplemath
В то время как вертикальные асимптоты являются священной почвой, горизонтальные асимптоты являются просто полезными рекомендациями.
В то время как вы никогда не можете коснуться вертикальной асимптоты, вы можете (и часто делаете) коснуться горизонтальной асимптоты и даже пересечь ее.
В то время как вертикальные асимптоты указывают на очень специфическое поведение (на графике), обычно близкое к началу координат, горизонтальные асимптоты указывают на общее поведение, обычно далекое от сторон графика.
Другими словами, горизонтальные асимптоты существенно отличаются от вертикальных асимптот.
Содержание продолжается ниже
MathHelp.
comЧтобы понять концепцию горизонтальных асимптот, давайте рассмотрим несколько примеров.
Во-первых, обратите внимание, что знаменатель представляет собой сумму квадратов, поэтому он не имеет множителей и не имеет действительных нулей. Другими словами, эта рациональная функция не имеет вертикальных асимптот. Так что у нас все в порядке на этом фронте.
Как упоминалось выше, горизонтальная асимптота функции (при условии, что она есть) говорит мне примерно, куда пойдет график, когда x станет очень, очень большим. Поэтому я рассмотрю несколько очень больших значений для x ; то есть при некоторых значениях 90 915 x 90 916, которые очень далеки от начала координат: 90 909 90 906 Смещены к краям графика, где 90 915 x 90 916 является сильно отрицательным (например, -1000) или сильно положительным (например, 10000) «+2» и «+1» в выражении для и на самом деле не так уж важны. В итоге я получил очень большое число, разделенное на очень большое число в квадрате, которое «упростилось» до очень маленького числа.
Значения и в основном получены из « x » и « x 2 », особенно после того, как x стали очень большими. А поскольку x 2 было «больше», чем x , x 2 уменьшило значение всей дроби до y = 0 (то есть до оси x ), когда x стало большим.
Это имеет смысл, если подумать. Если у вас есть миллион (плюс два, но кого это волнует?), деленное на миллион в квадрате (плюс 1, но кого это волнует?), то вы, по сути, получили миллион, деленный на квадрат миллиона. , что упрощается до 1 на миллион. Что очень и очень мало. Таким образом, для и значение функции становится очень и очень маленьким; а именно, он становится очень, очень близким к нулю.
Я вижу это поведение на графике, если я уменьшу масштаб по оси x : график довольно скучный, тянется по оси x .
Если я увеличу масштаб начала координат, я также увижу, что график пересекает горизонтальную асимптоту (по стрелке):
Пересечение горизонтальной асимптоты является обычным и совершенно нормальным явлением.
(Это вертикальные асимптоты, к которым мне нельзя прикасаться.)
Как видно из таблицы значений и графика, горизонтальная асимптота соответствует оси x .
горизонтальная асимптота: y = 0 (ось x )
горизонтальная асимптота была y = 0 (ось х ). Это свойство всегда верно: если степень x в знаменателе больше, чем степень x в числителе, тогда знаменатель, будучи «сильнее», тянет дробь вниз к оси x , когда x становится большим. То есть, если полином в знаменателе имеет больший старший показатель, чем полином в числителе, то график следует вдоль оси x в крайнем правом и крайнем левом углу графика. Таким образом, каждый раз, когда степень знаменателя больше степени числителя, горизонтальная асимптота будет равна 9.0915 x — ось, также известная как линия y = 0.
Что произойдет, если степени совпадают в числителе и знаменателе? Давайте посмотрим:
В отличие от предыдущего примера, эта функция имеет полиномы второй степени сверху и снизу; в частности, степени одинаковы в числителе и знаменателе.
Поскольку степени одинаковы, числитель и знаменатель «тянут» поровну; этот график не должен опускаться до x по оси, и не должно уходить в бесконечность. Но куда это пойдет?
Опять же, мне нужно думать о больших значениях для x . Когда x действительно большое, у меня будет, грубо говоря, удвоенное что-то большое (минус одиннадцать, но кого это волнует?) разделить на один раз что-то большое (плюс девять, но кого это волнует?).
Как вы могли догадаться из последнего упражнения, «–11» и «+9» не будут иметь большого значения для действительно больших значений x . Вдали от графика у меня будет примерно 2 x 2 /x 2 , что сокращается до 2.
Подтверждает ли это таблица значений? Давайте проверим:
Для больших значений x значение функции, как и ожидалось, очень близко к y = 2. И график функции это отражает:
Конечно, наверное что-то есть интересное происходит в середине графика, возле начала координат.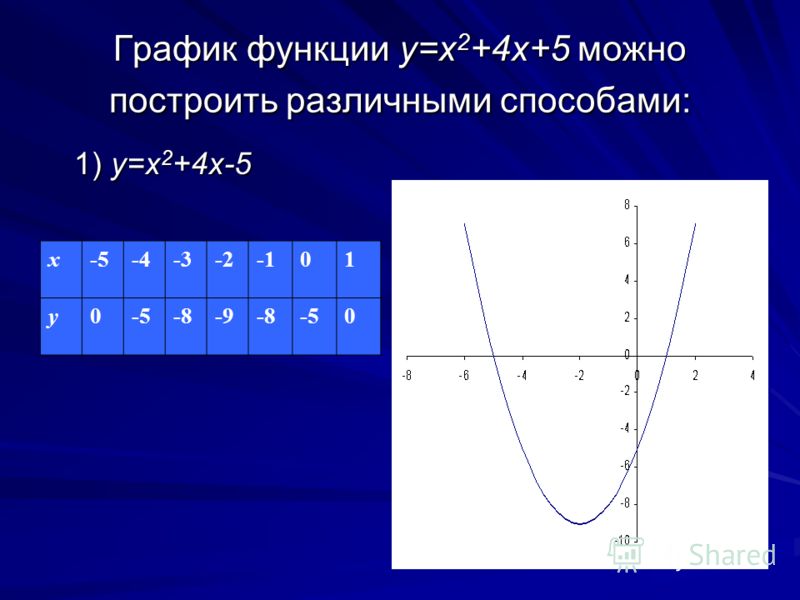
Но в стороне график явно держится очень близко к линии y = 2. (В исчислении вы научитесь доказывать это самостоятельно.)
Тогда мой ответ:
Горизонтальная асимптота: y = 2
В приведенном выше примере градусы в числителе и знаменатель были одинаковыми, а горизонтальной асимптотой оказалась горизонтальная линия, значение y которой было равно значению, полученному путем деления старших коэффициентов двух многочленов. Это всегда верно: когда степени числителя и знаменателя одинаковы, то горизонтальная асимптота находится путем деления старших членов, поэтому асимптота определяется как:
y = (старший коэффициент числителя) / (старший коэффициент знаменателя)
Теперь, когда я знаю правила относительно степеней, мне не нужно составлять таблицу значений или рисовать график. Я могу просто сравнить показатели.
В этой рациональной функции наивысшая степень в числителе и знаменателе одинакова; а именно куб.