График арифметическая прогрессия: Онлайн калькулятор: Арифметическая прогрессия

Содержание

Открытая Математика. Функции и Графики. Геометрическая прогрессия

Геометрическая прогрессия

Числовую последовательность {b_n}, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же число q ≠ 0, называют геометрической прогрессией:

b_{n + 1} = b_n · q.

Важно отметить, что число q, которое называется знаменателем прогрессии, отлично от нуля. Так как bn-1=bnq, то bn+1bn-1=bn2. Верна и обратная теорема.

Последовательность {b_n} является геометрической тогда и только тогда, когда для любого n > 1 выполняется соотношение bn2=bn+1 bn-1, где bn≠0 при всех n. Тем не менее, важно понимать, что формула bn=bn+1bn-1 справедлива только для геометрической прогрессии с положительными членами, а предыдущее соотношение верно для произвольной геометрической прогрессии.

Каждый член геометрической прогрессии {b_n} определяется формулой b_n = b₁ · q^{n – 1}.

Докажем это пользуясь методом математической индукции. Легко убедиться, что при n = 1 данная формула верна. Пусть эта формула верна для n = k. Докажем ее справедливость для n = k + 1. Имеем b_{k + 1} = b_k · q = b₁ · q^{k – 1} · q = b₁ · q^k. Теорема доказана.

Банковский счет

Сумма n первых членов геометрической прогрессии {b_n} равна Sn=b1qn-1q-1 при q ≠ 1 и S_n = n · b₁ при q = 1.

Эти формулы также доказываются методом математической индукции. Докажите их самостоятельно.

При |q| < 1 limn→∞bn=0, поэтому в этом случае геометрическая прогрессия называется бесконечно убывающей.

Суммой бесконечно убывающей геометрической прогрессии называется число S=limn→∞Sn, где S_n – сумма n первых членов геометрической прогрессии.

Сумма бесконечно убывающей геометрической прогрессии (|q| < 1) равна S=b11-q.

Для доказательства достаточно заметить, что S=limn→∞Sn=limn→∞b1qn-1q-1=b1q-1limn→∞qn-1=b11-q. В предпоследнем переходе использовались свойства пределов последовательностей.

Ахиллес и черепаха

Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ «Облако знаний».

1. Арифметическая прогрессия

2. Арифметический квадратный корень

3.

Биссектриса

4. Вписанная окружность

5. Выпуклый четырёхугольник

6. Геометрическая прогрессия

7. Длина окружности, площадь

8. Дроби

9. Исследование функции

10. Значения обратных тригонометрических функций

11. Исследование графика функции

12. Касательная, секущая

13. Квадрат

14. Квадратная функция

15. Квадратное уравнение

16. Конус

17. Куб

18. Линейная функция

19. Линейное уравнение

20. Логарифм

21. Медиана

22. Метод интервалов

23. Модуль: уравнения и неравенства

24. Модуль

25. Неравенства

26. Область определения функции

27. Обратные тригонометрические функции

28. Описанная окружность

29. Определение тригонометрических функций

30. Основные соотношения в треугольнике

31. Основные тригонометрические формулы

32. Периодическая дробь

33. Площадь треугольника

34.

Правильная пирамида

35. Правильный многоугольник

36. Преобразование графика функции

37. Произвольный выпуклый многоугольник

38. Призма

39. Признаки делимости чисел

40. Производные элементарных функций

41. Проценты

42. Прямоугольный параллелепипед

43. Прямоугольный треугольник

44. Равнобедренный треугольник

45. Равносильные уравнения

46. Равносторонний треугольник

47. Ромб

48. Свойства прямых и плоскостей

49. Свойства тригонометрических функций

50. Свойства элементарных функций

51. Сектор

52. Среднее арифметическое, геометрическое

53. Средняя линия

54. Степень

55. Таблица значений тригонометрических функций

56. Теорема Виета

57. Теорема косинусов, синусов

58. Трапеция

59. Углы на плоскости

60. Универсальная подстановка

61. Уравнение движения

62. Уравнения с косинусом

63.

Уравнения с синусом

64. Уравнения с тангенсом и котангенсом

65. Усеченная пирамида

66. Усеченный конус

67. Формула дополнительного угла

68. Формулы двойного аргумента

69. Формулы обратных тригонометрических функций

70. Формулы половинного аргумента

71. Формулы произведения функций

72. Формулы сокращенного умножения

73. Формулы суммы аргументов

74. Формулы суммы функций

75. Функция корень

76. Функция модуль

77. Хорда

78. Центральный, вписанный угол

79. Цилиндр

80. Четность-нечетность функций

81. Шар

82. Шаровой сектор, сегмент

1. Арифметическая прогрессия

Определение: Последовательность, у которой задан первый член

a1, а каждый следующий равен предыдущему, сложенному с

одним и тем же числом d, называется арифметической

прогрессией:

an+1 = an + d, где d – разность прогрессии.

Длина окружности, площадь

17. Куб

18. Линейная функция

y = kx + b,

k – угловой коэффициент, b – свободный

член

Дроби

28. Описанная окружность

-Центр окружности, описанной около треугольника, лежит на

пересечении серединных перпендикуляров к его трем сторонам.

-Центр окружности, описанной около прямоугольного

треугольника, лежит на середине гипотенузы.

-Около трапеции можно описать окружность только тогда, когда

трапеция равнобочная.

-Если окружность описана около произвольного

четырехугольника, тогда попарные суммы противолежащих

углов равны между собой:



29. Определение тригонометрических функций

19. Линейное уравнение:

Исследование функции

20. Логарифм

10. Значения обратных тригонометрических функций

21. Медиана

11. Исследование графика функции

30. Основные соотношения в треугольнике

Неравенство треугольника:

a + b > c; a + c > b; b + c > a

Сумма углов: 

Против большей стороны лежит больший угол, и обратно,

против большего угла лежит большая сторона.

Против равных сторон лежат равные углы, и обратно, против

равных углов лежат равные стороны.

22. Метод интервалов

31. Основные тригонометрические формулы

12. Касательная, секущая

Касательная – прямая, имеющая с окружностью одну общую

точку.

Секущая – прямая, имеющая с окружностью две общие точки.

Арифметический квадратный корень

23. Модуль: уравнения и неравенства

32. Периодическая дробь

13. Квадрат

Прямоугольник, у которого все стороны равны, называется

квадратом.

24. Модуль

Биссектриса

33. Площадь треугольника

14. Квадратная функция

Биссектриса – отрезок, выходящий из вершины треугольника и

делящий угол пополам.



Биссектриса делит противолежащую сторону на части ,

пропорциональные прилежащим сторонам: ab : ac = b : c



Биссектриса делит площадь треугольника, пропорционально

прилежащим сторонам.

4. Вписанная окружность

Центр окружности, вписанной в треугольник, лежит на

пересечении биссектрис треугольника.

Если окружность вписана в произвольный четырехугольник,

тогда попарные суммы противолежащих сторон равны между

собой: a + b = c + d

25. Неравенства

Определения:

Неравенством называется выражение вида:

a < b (a b),

a > b (a b)

34. Правильная пирамида

26. Область определения функции

35. Правильный многоугольник

Правильным многоугольником называется многоугольник, у

которого все стороны и углы равны между собой.

Около всякого правильного многоугольника можно описать

окружность и в него вписать окружность, причём центры этих

окружностей совпадают.

Выпуклый четырёхугольник

15. Квадратное уравнение

36. Преобразование графика функции

27. Обратные тригонометрические функции

6. Геометрическая прогрессия

Определение: Последовательность, у которой задан первый член

b1 0, а каждый следующий равен предыдущему, умноженному

на одно и то же число q 0, называется геометрической

прогрессией:

bn+1 = bn q, где q – знаменатель прогрессии.

16. Конус

37. Произвольный выпуклый многоугольник

47. Ромб

Параллелограмм, все стороны которого равны называется

ромбом.

Диагональ ромба является его осью симметрии. Диагонали

взаимно перпендикулярны. Диагонали являются биссектрисами

углов.

59. Углы на плоскости

48. Свойства прямых и плоскостей

38. Призма

60. Универсальная подстановка

73. Формулы суммы аргументов:

74. Формулы суммы функций

75. Функция корень

49. Свойства тригонометрических функций

61. Уравнение движения

76. Функция модуль

50. Свойства элементарных функций

39. Признаки делимости чисел:

Признак

На 2 Числа, оканчивающиеся нулём или четной цифрой

Числа, у которых две последние цифры нули или

На 4

выражают число, делящееся на 4.

Числа, у которых три последние цифры нули или

На 8

выражают число, делящееся на 8.

На 3 Числа, сумма цифр которых делится на 3.

На 9 Числа, сумма цифр которых делится на 9.

На 5 Числа, оканчивающиеся нулём или цифрой 5.

Числа, у которых две последние цифры нули или

На 25

выражают число, делящееся на 25.

На 10 Числа, оканчивающиеся нулём.

40. Производные элементарных функций

Пример

…….6

……12

…..104

570612

359451

…….5

……75

……0

63. Уравнения с синусом

62. Уравнения с косинусом

77. Хорда

Хорда – отрезок, соединяющий две точки окружности.

51. Сектор

64. Уравнения с тангенсом и котангенсом

Диаметр, делящий хорду пополам, перпендикулярен хорде.

В окружности равные хорды равноудалены от центра

окружности.

Отрезки пересекающихся хорд связаны равенством:

41. Проценты

Процентом называется сотая часть от числа.

65. Усеченная пирамида

1%A = 0,01A

78. Центральный, вписанный угол

Основные типы задач на проценты:

Сколько процентов составляет число A от числа B?

B —

100%

A —

52. Среднее арифметическое, геометрическое

Среднее арифметическое:



Сложные проценты.

Число A увеличилось на 20%, а затем полученное число

уменьшили на 25%.

Как, в итоге, изменилось исходное число?

1) A1 = (100% + 20%)A = 120%A = 1,2A

2) A2 = (100% — 25%)A1=75%A1 = 0,75A1 = 0,751,2A = 0,9A =

90%A

3) A1 – A = 90%A – 100%A = -10%A

Ответ:

уменьшилось на 10%.

Изменение величины.

Как изменится время, если скорость движения увеличится на

25%?

t

1 S

t1 



0,8 80%t

v1 1,25v 1,25 v

x 100%

a1 a2 a3 … an

Среднее геометрическое:

a1 a2 … ak

66. Усеченный конус

79. Цилиндр

53. Средняя линия

Средняя линия – отрезок, соединяющий середины двух сторон

треугольника.



Средняя линия параллельна третьей стороне и равна её

половине:

nb b



Средняя линия отсекает подобный треугольник, площадь

которого равна одной четверти от исходного.



Ответ:

уменьшится на 20%

67. Формула дополнительного угла

80. Четность-нечетность функций

Определение:

Функция y = f(x) называется четной, если:

Функция y = f(x) называется нечетной, если:

Примеры:

четные функций:

нечетные функций:

arcsinx, arctgx

68. Формулы двойного аргумента

42. Прямоугольный параллелепипед

f(-x) = f(x)

f(-x )= — f(x)

54. Степень

y = x, y = x2, y = cosx

y = 1/x, y = x3, y = sinx, tgx, ctgx,

43. Прямоугольный треугольник

69. Формулы обратных тригонометрических функций

Свойства:

График четной функции симметричен относительно оси Oy.

График нечетной функции симметричен относительно начала

системы координат О.

81. Шар

55. Таблица значений тригонометрических функций

70. Формулы половинного аргумента

82. Шаровой сектор, сегмент

44. Равнобедренный треугольник

треугольник, у которого две стороны равны.

56. Теорема Виета

Приведенное квадратное уравнение:

x1 + x2 = — p

x1 x2 = q

Углы, при основании треугольника, равны

Высота, проведенная из вершины, является биссектрисой и

медианой.

45. Равносильные уравнения

57. Теорема косинусов, синусов

x2 + px + q = 0

71. Формулы произведения функций

72. Формулы сокращенного умножения

Квадрат

суммы

(a + b)2 = a2 + 2ab + b2

Квадрат

разности

(a — b)2 = a2 — 2ab + b2

46. Равносторонний треугольник

треугольник, у которого все стороны равны.

Все углы равны 600.

Каждая из высот является одновременно биссектрисой и

медианой.

Центры описанной и вписанной окружностей совпадают.

Радиусы окружностей:

58. Трапеция

Четырёхугольник, у которого две стороны параллельны, а другие

не параллельны, называется трапецией.

Разность

квадратов

a2 – b2 = (a + b)(a – b)

Куб

суммы

Куб

разности

(a + b)3 = a3 + 3a2b + 3ab2 + b3

r



Площадь

a 3

; R

(a — b)3 = a3 — 3a2b + 3ab2 — b3

S

a2 3

Сумма

кубов

Разность

кубов

a3 + b3 = (a + b)( a2 — ab + b2)

a3 – b3 = (a – b)( a2 + ab + b2)

Курс математики | Кафедра математики

Body

Университет штата Огайо предлагает более 100 различных математических курсов для студентов. Приведенная ниже информация поможет ориентироваться в прохождении математических курсов бакалавриата в OSU. Список всех математических курсов OSU, описание курсов и информацию о том, в какие семестры они преподаются, см. Математические курсы.

Чтобы получить доступ к математическим курсам, необходимым для вашей специальности, см. раздел «Требования к математике по специальностям » и обратитесь к своему научному консультанту, чтобы узнать, какой курс математики подходит именно вам.

Чтобы понять последовательность исчисления в OSU, см.: Последовательности исчисления

Продвинутый уровень

Текст

Переход к серии исчисления

Математика 1050 Pre-College Mathematics
Математика 1075 Довузовская математика II
Математика 1148 Высшая алгебра
Математика 1149 Тригонометрия
Математика 1151 Исчисление I или Математика 1156 Исчисление для биологических наук

Затем учащийся может продолжить изучение математики 1152, 1157 или 1172 и получить предварительные условия для курсов старших классов.

Переход к бизнес-вычислениям

Математика 1050 Довузовская математика I
Математика 1075 Довузовская математика II
Математика 1130 Колледж Алгебра для бизнеса
Математика 1131 Исчисление для бизнеса

Переход к математике 1116

Математика 1050 Довузовская математика I
Математика 1075 Pre-College Mathematics II или Math 1060 Supplementary Pre-College Mathematics
Математика 1116 Экскурсии по математике

Текст

Переход к серии исчислений

Математика 1075 Предвузовская математика II
Математика 1148 Высшая алгебра
Математика 1149 Тригонометрия
Математика 1151 Исчисление I или Математика 1156 Исчисление для биологических наук

Переход к бизнес-анализу

Математика 1075 Pre-College Mathematics II
Математика 1130 Колледж Алгебра для бизнеса
Математика 1131 Исчисление для бизнеса

Переход к математике 1116

Математика 1075 Предварительный курс математики II
Математика 1116 Экскурсии по математике

Текст

ПРИМЕЧАНИЕ: Только для специальностей, связанных с STEM, с консультацией академического совета

Переход к серии исчислений

Математика 1120 Предварительное исчисление с обзором I — часть первая из двух частей серии для специальностей STEM, только NFYS
Математика 1121 Предварительное исчисление с обзором II

Эти два курса в сочетании с эквивалентны курсам от 1075 до 1150. Затем учащийся может продолжить изучение математики 1151 и получить предварительные условия для курсов старших классов.

Текст

Переход к серии 9 исчисления0016

Математика 1148 Колледж алгебры
Математика 1149 Тригонометрия
Математика 1151 Исчисление I или Математика 1156 Исчисление для биологических наук

Переход к бизнес-вычислениям

Математика 1148 Колледж алгебры
Математика 1131 Исчисление для бизнеса

Текст

Переход к серии вычислений

Математика 1150 Предварительное исчисление
Математика 1151 Исчисление I или Математика 1156 Исчисление для биологических наук

Переход к бизнес-вычислениям

Математика 1150 Предварительное исчисление
Математика 1131 Исчисление для бизнеса

Текст

Переход к серии исчислений

Математика 1140 Исчисление с обзором I — часть первая из двух частей серии для специальностей STEM, только NFYS
Математика 1141 Исчисление с обзором II

Эти два курса эквивалентны курсу «Математика 1151». Затем учащийся может перейти к курсу «Математика 1152» или 1172 и получить предварительные условия для курсов старшего уровня.

Текст

Математика 1131 Исчисление для бизнеса

Это завершающий курс, который не используется в качестве обязательного.

Текст

Математика 1151 Исчисление I или математика 1156 Исчисление для биологических наук

Текст

Следующая блок-схема представляет собой изображение прогрессии младших курсов математики. Пожалуйста, используйте раскрывающиеся меню, представленные выше, для интерпретации блок-схемы.

Математика 1152
Математика 1172

Текст

Базовая математика

Математика 1152 Исчисление II
Математика 2153 Исчисление III
Математика 2568 Линейная алгебра
Математика 3345 Основы математики
Математика 4530 Вероятность
Math 2255 Дифференциальные уравнения и их приложения
Математика 4557 Уравнения с частными производными
Математика 3618 Теория процента
Математика 5632 Финансовая экономика для актуариев
Математика 4350 Количественная неврология

Математика 2153 и последующие курсы являются обязательными для многих математических курсов старших классов.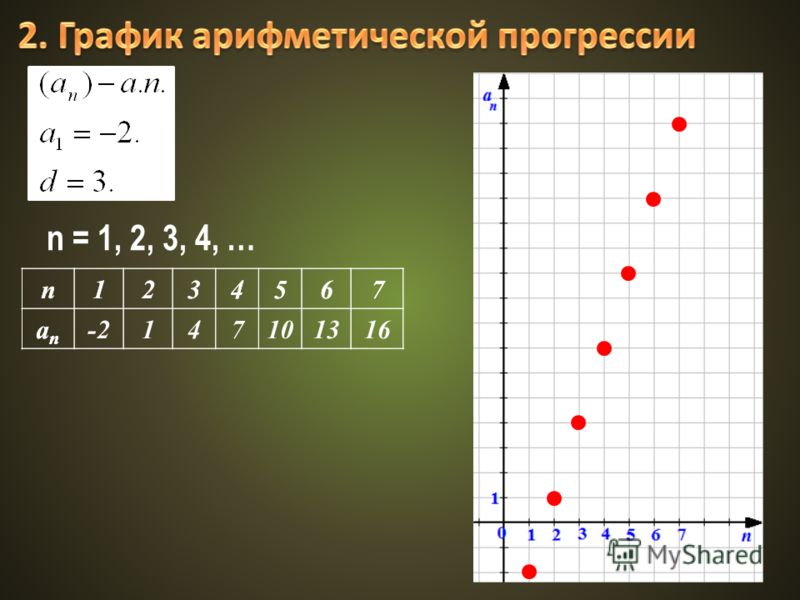 Дополнительную информацию см. на странице курса математики.

Text

Engineering Pathways

Вариант 1

Math 1172 Engineering Mathematics A
Математика 2173 Инженерная математика B
Математика 2174 Линейная алгебра и дифференциальные уравнения для инженеров

Вариант 2

Математика 1172 Инженерная математика A
Математика 2177 Математические темы для инженеров

Вариант 3

Математика 1172 Инженерная математика A
Математика 2568 Линейная алгебра
Математика 2415 Обыкновенные уравнения и уравнения с частными производными

Математика 1172 также является обязательным условием для изучения математики 2153 и требует дополнительной курсовой работы для старших классов. Дополнительную информацию см. на страницах курса математики.

Текст

Следующая таблица иллюстрирует возможный курс математики старших классов.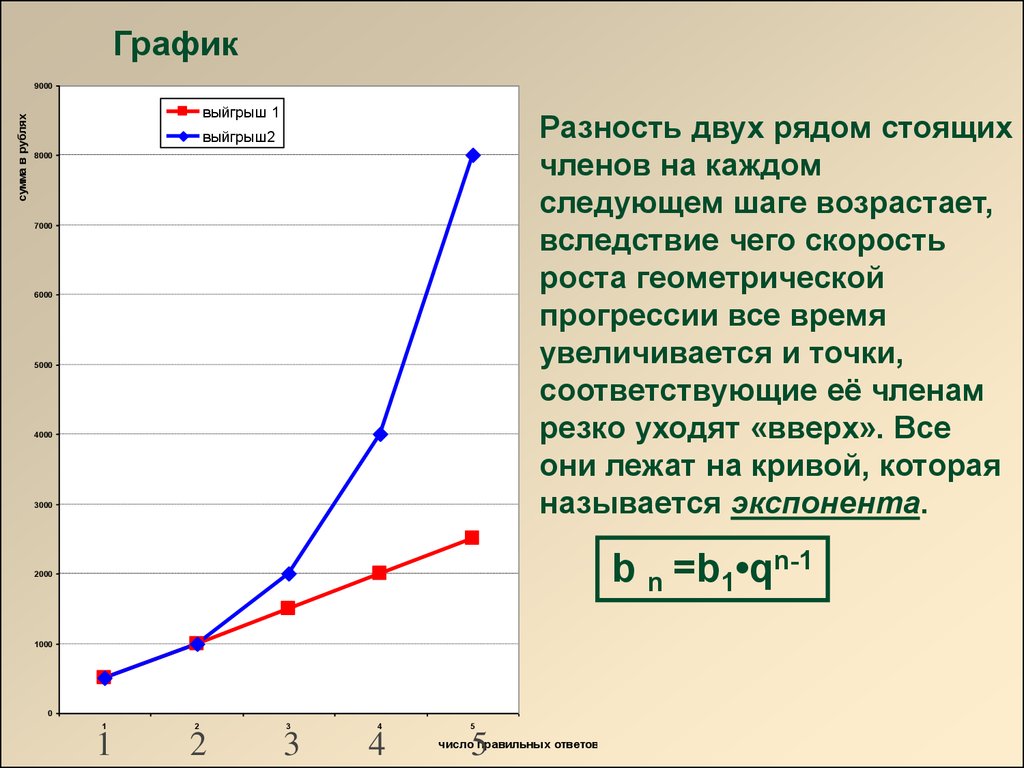 Описание курсов и предварительных условий предлагается на вкладках выше. Пожалуйста, поработайте со своим научным руководителем, чтобы интерпретировать математический путь, предназначенный для вашей специальности. Список всех математических курсов OSU, описание курсов и информацию о том, в какие семестры они преподаются, см. Математические курсы.

Текст

Следующая таблица иллюстрирует возможный курс инженерной математики. Описание курсов и предварительных условий предлагается на вкладках выше. Пожалуйста, поработайте со своим научным руководителем, чтобы интерпретировать математический путь, предназначенный для вашей специальности.

Text

Следующая диаграмма иллюстрирует возможный поток курсов для специальностей образования в Колледже образования и экологии человека. Пожалуйста, поработайте со своим научным руководителем, чтобы интерпретировать математический путь, предназначенный для вашей специальности. Список всех математических курсов OSU, описание курсов и информацию о том, в какие семестры они преподаются, см. Математические курсы.

Math Sequence Chart — Домашнее обучение для кредита колледжа

Опубликовано 11 марта 2022 г. 30 ноября 2022 г. Дженнифер Кук-ДеРоса, М.С.

Эта простая диаграмма показывает, когда ваша математическая последовательность может приносить баллы колледжа наряду с баллами средней школы.

Типичная математическая прогрессия

Арифметика (k-8 классы)
Предварительная алгебра (6-9 классы)
Алгебра 1 (8-10 классы)
Геометрия (9-10 классы)*
Алгебра 2 (10-12 классы)
Тригонометрия/Предварительный исчисление (10-12 классы)
Математика (10-12 классы)

*геометрия может помещаться между алгеброй 1 и 2, после алгебры 2, внутри курса алгебры или полностью опущена. Каждый издатель учебных программ по математике рассматривает этот предмет немного по-своему .

Дублирование времени и усилий

Мы часто думаем, что занятия в колледже значительно сложнее или более продвинуты, чем занятия в старшей школе, но в математической последовательности, как только ваш подросток достигает определенного уровня, он уже занимается той же математикой что они будут делать в колледже. Поскольку математика в средней школе никогда не стоит зачета в колледже, подросткам часто приходится пересдавать предмет, который они уже выучили. Это удваивает их время, усилия и деньги! Если вы хотите упростить процесс, вы можете использовать математику на уровне колледжа в старшей школе, когда они достигают этой точки в типичной математической последовательности.

Подробнее о каждом пути

4-летняя степень, не связанная с STEM: Студенты, получающие 4-летнюю степень по специальностям, не связанным с естественными науками, технологиями, инженерией или математикой (STEM), часто не предъявляют требований по математике. Большинство специальностей, не связанных с STEM, не предъявляют математических требований. Требование «общее образование» будет включать какой-то тип математики, но при желании вы можете поискать колледжи с низким уровнем математики. Требование «общее образование» колледжа будет минимальным для всех в для каждой специальности , так что неспециалисты, не относящиеся к STEM, могут по-прежнему иметь высшее общее образование по математике, если вы учитесь в «математическом» колледже. Всегда смотрите на требования целевого колледжа к «общему образованию». Поскольку в большинстве колледжей требуется только 1 общеобразовательный курс математики, вы можете найти требования по математике в вашем целевом колледже в таблице выше и посмотреть, сколько математики требуется для этого. Число обычно указывает на уровень сложности. Например, MATh205 должен быть проще, чем MATh221, но это скорее рекомендация, чем правило.

4-летняя степень STEM: Учащиеся, получающие 4-летнюю степень по специальности STEM (или бизнесу), будут иметь математические требования, выходящие за рамки «общего образования», и многие из них будут служить предварительными условиями для других классов. (пример: кредит по исчислению 1 может быть обязательным условием для регистрации на курс общей физики) Иногда математика на специальность STEM «начинается» с исчисления 1, поэтому более низкая математика, такая как предварительный исчисление, может не «засчитываться» для их степени, но это низко висит фрукты. Всегда хватайте низко висящие плоды! Я встречал сотни людей, которые сменили специальность или сменили колледж, так что никогда не помешает иметь дополнительный кредит по математике «в банке».

Другое: Если ваш учащийся хочет получить краткосрочное обучение, двухгодичную степень, лицензию, стажировку, профессиональную программу или что-то другое, кроме 4-летней степени, его математические требования могут сильно отличаться от приведенной выше таблицы. ! Многие профессии требуют специальной математики . Когда вы заметите другой предлагаемый курс обучения, вы захотите обратить внимание на предлагаемую последовательность. Студенту, готовящемуся стать сварщиком или слесарем-трубопроводчиком, необходимы навыки объемной геометрии. Чем больше вы знаете об их целевом занятии, тем лучше вы будете подготовлены к их руководству. В другом сценарии у подростка, который посещает школу косметологии, может вообще не быть требований к математике, но бухгалтерия и бизнес-математика — отличный выбор для студента, который однажды может открыть собственный салон.

Введите адрес электронной почты…

Вы также можете прочитать…

Math Success 4 Math Averse

Итак, если вы уже чувствуете, что начинаете реагировать на заголовок, этот пост не для вас. Как и во всем, в чем вы хороши, вы не можете себе представить, что другие люди не могут «стать» в этом тоже… если бы только у них было лучшее отношение, другая учебная программа, лучший учитель и т. д. Области STEM (наука, технология , инженерное дело и математика) сейчас в моде — в большинстве университетов количество специальностей STEM за последние несколько лет увеличилось вдвое, поэтому […]

Нравится:

Нравится Загрузка.