| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. |
|
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) |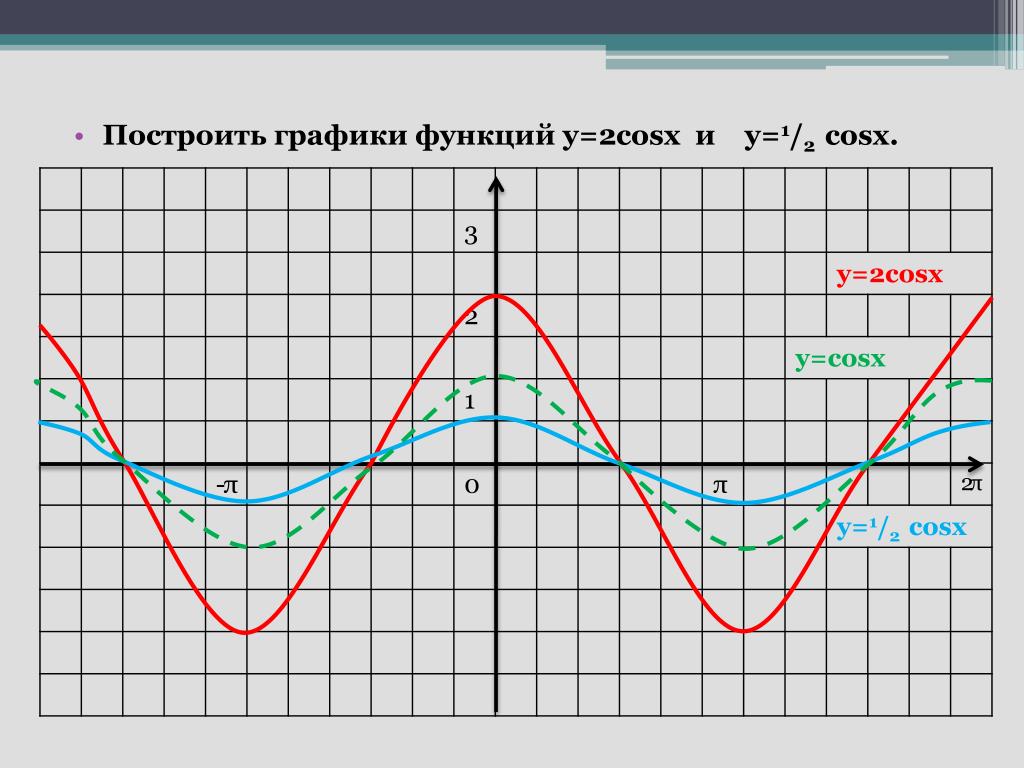
|
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) |
|
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) |
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) |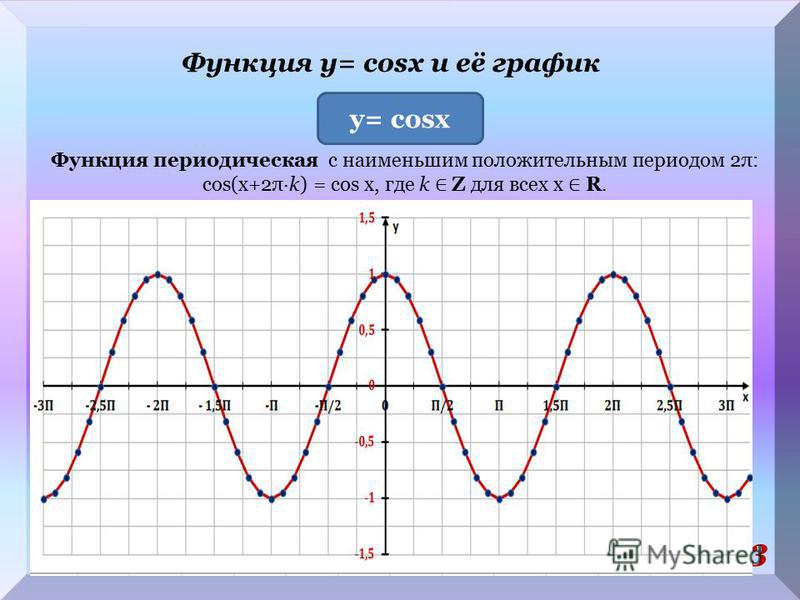
|
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) |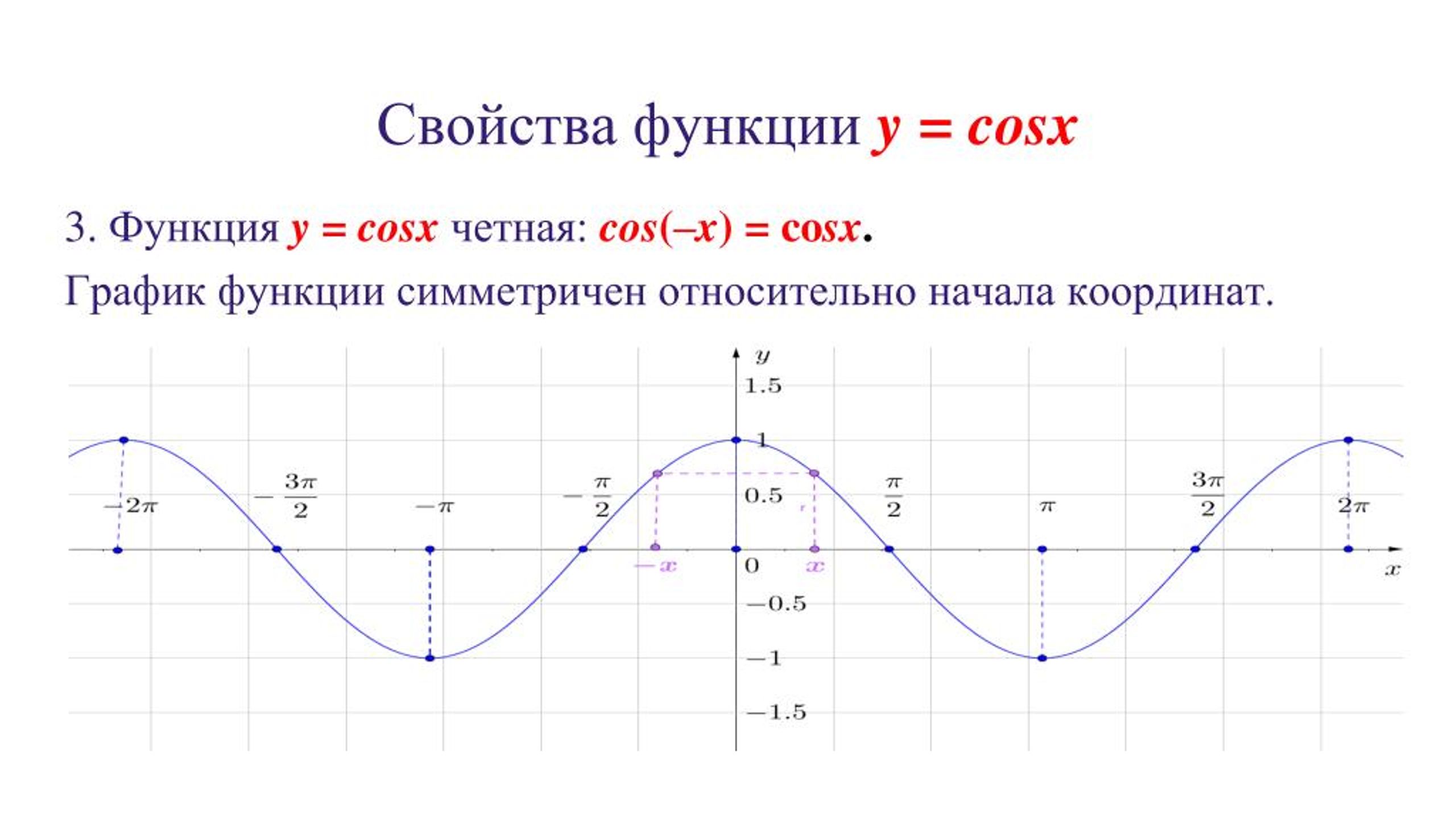
|
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) |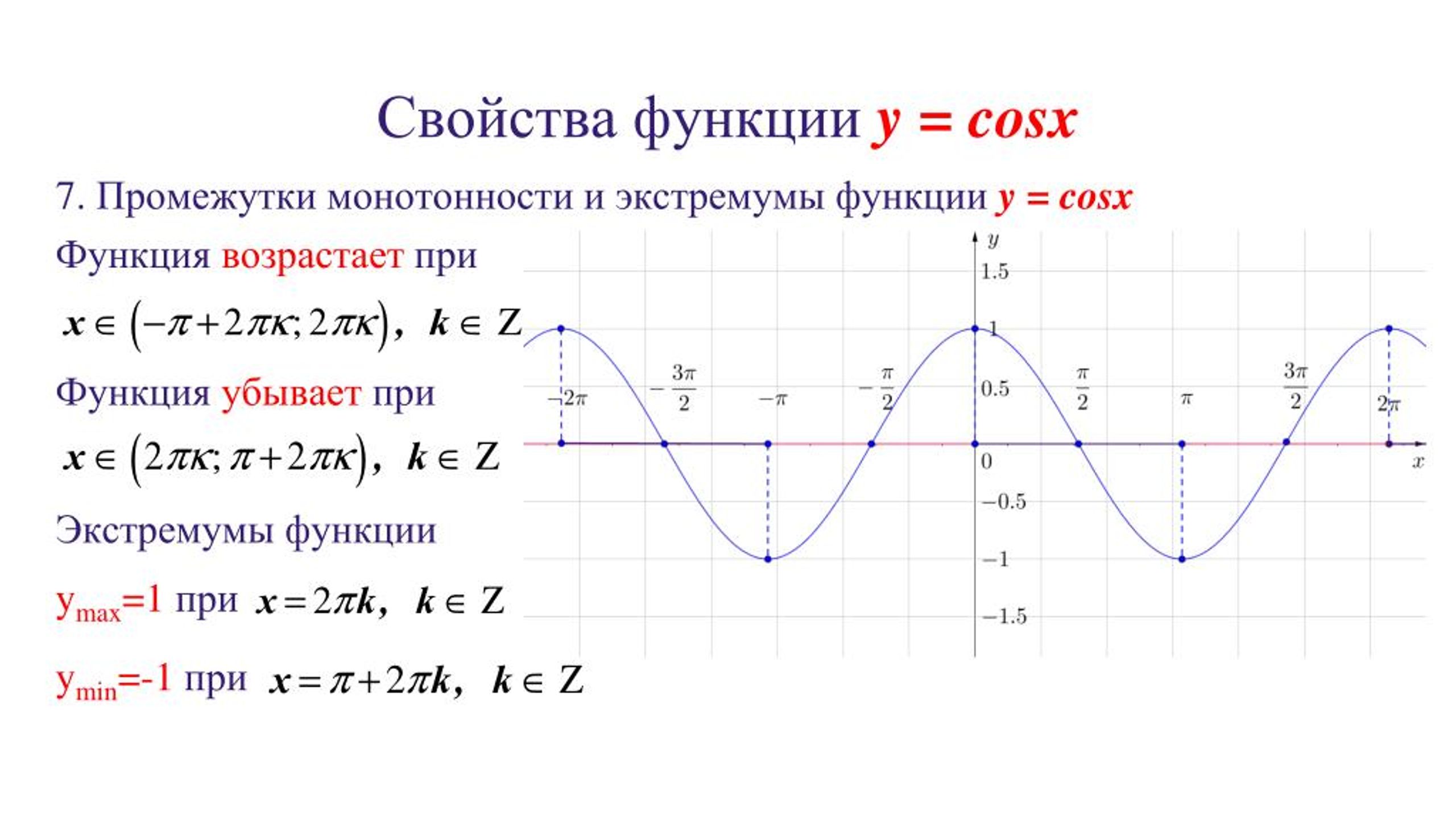
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) |
|
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Функция y = cos x, свойства и график косинуса с примерами
- Развертка абсциссы движения точки по числовой окружности в функцию от угла
- Свойства функции y=cosx
- Примеры
п.
1. Развертка ординаты движения точки по числовой окружности в функцию от углаРазвертка абсциссы движения точки по числовой окружности в функцию от угла (см. §2 данного справочника).
Рассмотрим, как изменяется косинус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=cosx на этом отрезке.
Если мы продолжим движение по окружности для углов x > 2π, кривая продолжится вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x<0, кривая продолжится влево.
В результате получаем график y=cosx для любого \(x\in\mathbb{R}\).
График y=cosx называют косинусоидой.
Часть косинусоиды для –π≤x≤π называют волной косинусоиды.
Часть косинусоиды для \(-\frac\pi2\leq x\leq\frac\pi2\) называют полуволной или аркой косинусоиды.
Заметим, что термин «косинусоида» используется достаточно редко.
Обычно, и в случае косинуса, говорят о «синусоиде».
п.2. Свойства функции
y=cosx1. Область определения \(x\in\mathbb{R}\) — множество действительных чисел.
2. Функция ограничена сверху и снизу $$ -1\leq cosx\leq 1 $$ Область значений \(y\in[-1;1]\)
3. Функция чётная $$ cos(-x)=cosx $$
4. Функция периодическая с периодом 2π $$ cos(x+2\pi k)=cosx $$
5. Максимальные значения \(y_{max}=1\) достигаются в точках $$ x=2\pi k $$ Минимальные значения \(y_{min}=-1\) достигаются в точках $$ x=\pi+2\pi k $$ Нули функции \(y_{0}=cosx_0=0\) достигаются в точках \(x=\frac\pi2 +\pi k\)
6. Функция возрастает на отрезках $$ -\pi+2\pi k\leq x\leq 2\pi k $$ Функция убывает на отрезках $$ 2\pi k\leq x\leq\pi+2\pi k $$
7. Функция непрерывна.
п.3. Примеры
Пример 1.Найдите наименьшее и наибольшее значение функции y=cosx на отрезке:
a) \(\left[\frac\pi6; \frac{3\pi}{4}\right]\) $$ y_{min}=cos\left(\frac{3\pi}{4}\right)=-\frac{\sqrt{2}}{2},\ \ y_{max}=cos\left(\frac\pi6\right)=\frac{\sqrt{3}}{2} $$ б) \(\left[\frac{5\pi}{6}; \frac{5\pi}{3}\right]\) $$ y_{min}=cos(\pi)=-1,\ \ y_{max}=cos\left(\frac{5\pi}{3}\right)=\frac12 $$
Пример 2.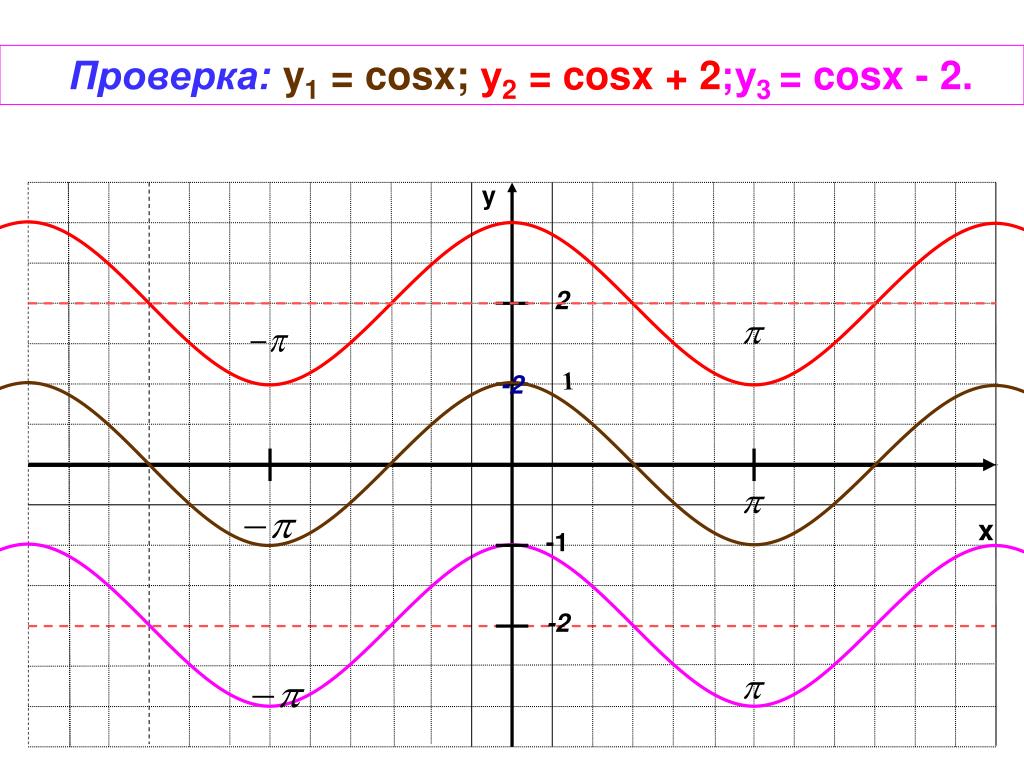
2}{4}\right)\) (см. §29 справочника для 8 класса)
Два корня: \(x_{1,2}=\pm\frac\pi2\)
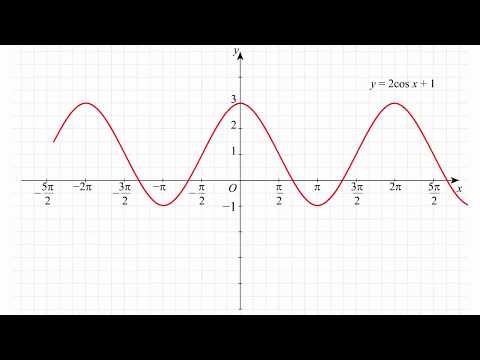
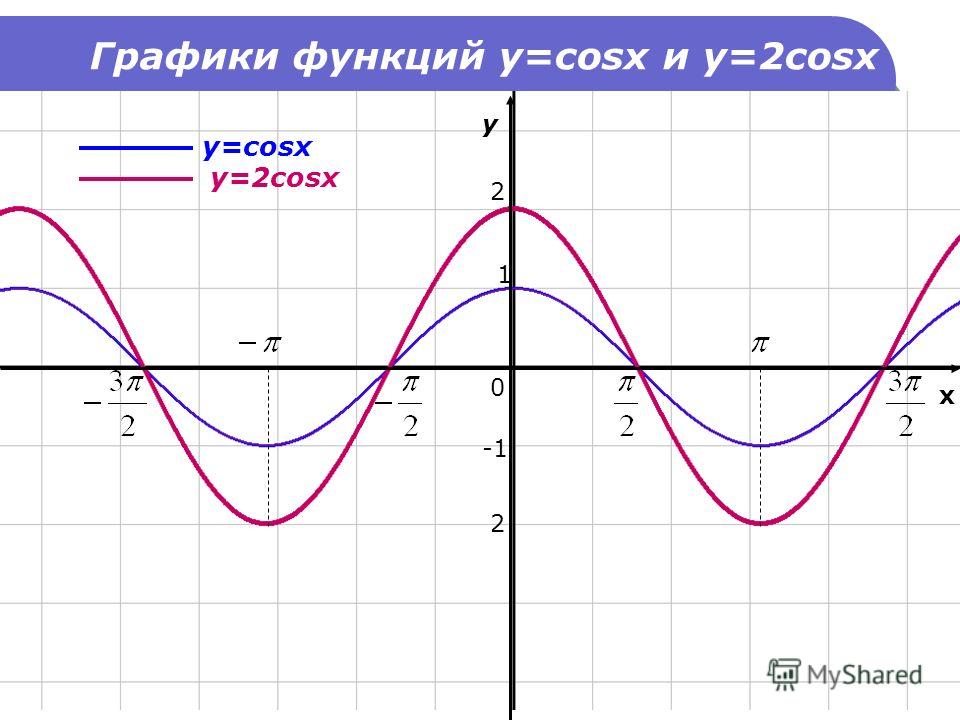
Пример 3. Постройте в одной системе координат графики функций $$ y=cosx,\ \ y=-cosx,\ \ y=2cosx,\ \ y=cosx-2 $$
\(y=-cosx\) – отражение исходной функции \(y=cosx\) относительно оси OX. Область значений \(y\in[-1;1]\).
\(y=2cosx\) – исходная функция растягивается в 2 раза по оси OY. Область значений \(y\in[-2;2]\).
\(y=cosx-2\) — исходная функция опускается вниз на 2. Область значений \(y\in[-3;-1]\).
Пример 4. Постройте в одной системе координат графики функций $$ y=cosx,\ \ y=cos2x,\ \ y=cos\frac{x}{2} $$
Амплитуда колебаний у всех трёх функций одинакова, область значений \(y\in[-1;1]\).
Множитель под косинусом изменяет период колебаний.
\(y=cosx\) – главная арка косинуса соответствует отрезку \(-\frac\pi2\leq x\leq\frac\pi2\)
\(y=cos2x\) — период уменьшается в 2 раза, главная арка укладывается в отрезок \(-\frac\pi4\leq x\leq\frac\pi4\).
\(y=cos\frac{x}{2}\) — период увеличивается в 2 раза, главная арка растягивается в отрезок \(-\pi \leq x\leq \pi\).
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 |
|
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
График функции косинуса
Горячая математика
тригонометрические отношения
также можно рассматривать как функции переменной, являющейся мерой угла.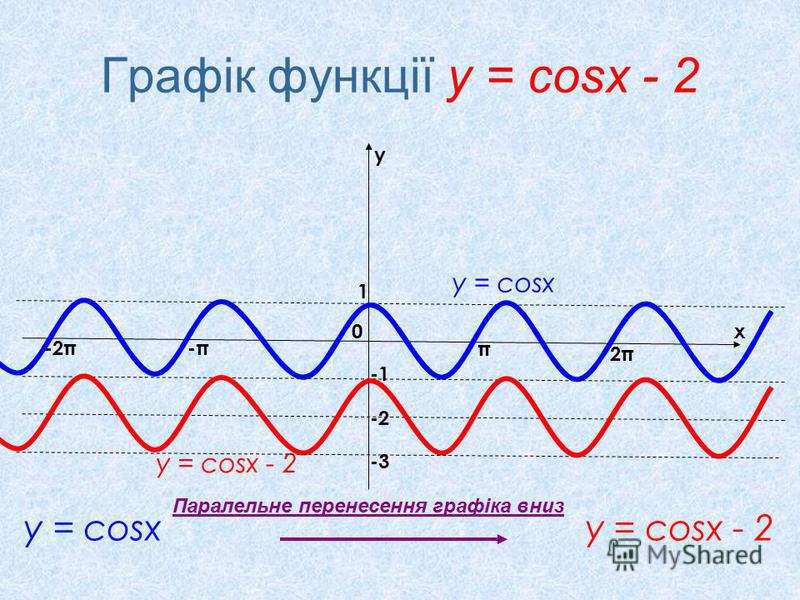
Эта угловая мера может быть либо задана в
градусов
или
радианы
. Здесь мы будем использовать радианы.
График косинус функция у «=» потому что ( Икс ) выглядит так:
Свойства функции косинуса, у «=» потому что ( Икс ) .
Домен : ( − ∞ , ∞ )
Диапазон : [ − 1 , 1 ] или − 1 ≤ у ≤ 1
у -перехват : ( 0 , 1 )
Икс
-перехват
:
(
н
π
2
,
0
)
, где
н
является целым числом.
Период: 2 π
Непрерывность: непрерывно вкл. ( − ∞ , ∞ )
Симметрия: у -ось (четная функция)
Максимальное значение у «=» потому что ( Икс ) происходит, когда Икс «=» 2 н π , где н является целым числом.
Минимальное значение у «=» потому что ( Икс ) происходит, когда Икс «=» π + 2 н π , где н является целым числом.
Амплитуда и период функции косинуса
Амплитуда графика
у
«=»
а
потому что
(
б
Икс
)
это величина, на которую она изменяется выше и ниже
Икс
-ось.
Амплитуда = | а |
Период функции косинуса – это длина кратчайшего интервала на Икс -ось, по которой повторяется график.
Период = 2 π | б |
Пример:
Нарисуйте графики у «=» потому что ( Икс ) и у «=» 2 потому что ( Икс ) . Сравните графики.
Для функции
у
«=»
2
потому что
(
Икс
)
, график имеет амплитуду
2
. С
б
«=»
1
, график имеет период
2
π
.
Таким образом, он циклически повторяется один раз из
0
к
2
π
с одним максимумом
2
, и один минимум
−
2
.