079. Линейные и квадратные неравенства
Линейными неравенствами с одной переменной называются неравенства вида ; ; ; .
Пример 1. Решите неравенство .
Решение. Раскроем скобки и сделаем необходимые преобразования:
.
Решением исходного неравенства будет открытый интервал от «минус» бесконечности до сорока третьих.
Ответ. .
Пример 2. Решите неравенство .
Решение. Умножим обе части неравенства на 3 и сделает преобразования:
.
Ответ. .
Неравенства вида или , где называются Квадратными неравенствами или неравенствами второй степени.
Если есть неравенство, где , то можно умножить обе части неравенства на и изменить знак неравенства на противоположный. Тогда получим неравенство, равносильное данному, где .
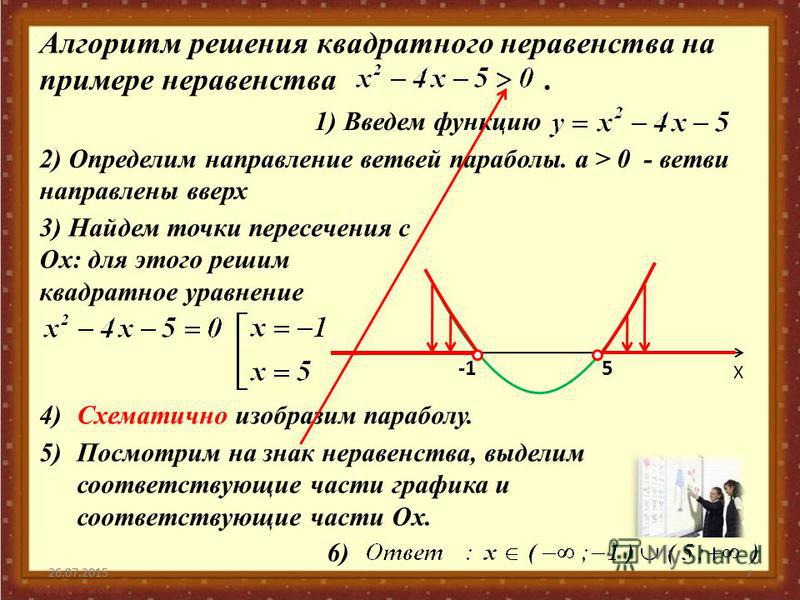
На основании вышесказанного, рассмотрим только решение неравенств вида , и , где . При решении квадратных неравенств учитывают свойства квадратной функции, графиком которой является парабола.
Рассмотрим три случая.
I. Если , , то неравенство верно при всех (парабола расположена выше оси ), а неравенство не имеет решений (парабола расположена ниже оси ), т. е. .
Пример 3. Решите неравенство .
Решение. Найдем значение дискриминанта данного квадратного уравнения: Так как , то выражение имеет положительные значения на всей числовой оси, т. е. .
Ответ. .
II. А) Если , и тогда это неравенство можно записать в виде:
.
(Парабола пересекает ось в двух точках и , ее ветви направлены вверх. Решением данного неравенства будут интервалы, на которых парабола расположена выше оси ).
Б) Если , и тогда это неравенство можно записать в виде:
(Парабола пересекает ось в двух точках и , ее ветви направлены вверх. Решением данного неравенства будут интервалы, на которых парабола расположена ниже оси ).
Пример 4. Решите неравенство .
Решение.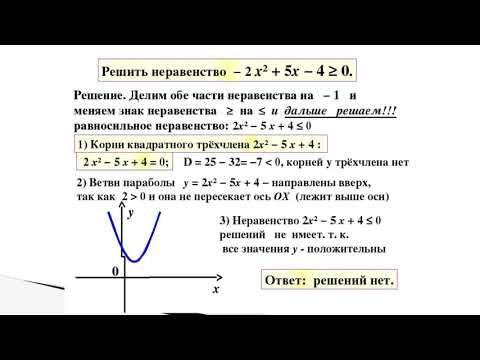
Рассмотрим квадратный трехчлен у которого ; , тогда его корни Представим левую часть неравенства в виде произведения
Ответ.
III. А) Если , и тогда это неравенство можно записать в виде:
.
(Парабола имеет с осью одну общую точку , ее ветви направлены вверх. Решением данного неравенства будет вся числовая ось , за исключением общей точки ).
Б) Если , и тогда это неравенство можно записать в виде:
.
(Парабола имеет с осью одну общую точку , ее ветви направлены вверх. Так как левая часть неравенства может принимать только неотрицательные значения, то решений нет).
Пример 5. Решите неравенство .
Решение. Умножим обе части неравенства на получим: Тогда:
Поэтому .
Ответ. .
| < Предыдущая | Следующая > |
|---|
§ 1. Линейные и квадратные неравенства
Класс
1 класс
2 класс
- Английский язык
- Математика
3 класс
- Русский язык
- Английский язык
- Математика
4 класс
- Русский язык
- Английский язык
- Математика
5 класс
- Русский язык
- Английский язык
- Математика
- Биология
6 класс
- Русский язык
- Английский язык
- Математика
- Биология
7 класс
- Русский язык
- Английский язык
- Математика
- Биология
- Физика
- Химия
8 класс
- Русский язык
- Английский язык
- Математика
- Биология
- Физика
- Химия
9 класс
- Русский язык
- Английский язык
- Математика
- Биология
- Физика
- Химия
10 класс
- Английский язык
- Биология
- Физика
- Химия
11 класс
- Английский язык
- Биология
- Химия
9 КЛАСС
§ 1.
2-4acОбе части неравенства можно умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный
D>0 - два корня, D=0 - один корень, D<0 - нет корней
Любой член неравенства можно перенести из одной части неравенства в другую с противоположным знаком, не меняя при этом знак неравенства
Любой член неравенства можно перенести из одной части неравенства в другую с противоположным знаком, не меняя при этом знак неравенства
Любой член неравенства можно перенести из одной части неравенства в другую с противоположным знаком, не меняя при этом знак неравенства
Вопросники:
Вопрос:
Вопрос:
Вопрос:
Линейные и квадратные неравенства | Примеры
В этой статье мы собираемся изучить концепцию линейных неравенств и квадратных неравенств. Поскольку вопросы о неравенстве часто появляются на экзаменах, рекомендуется тщательно понять и осветить тему. Здесь мы будем обсуждать линейные и квадратные неравенства.
Предлагаемое действие
БЕСПЛАТНЫЕ живые мастер-классы от нашего звездного факультета с более чем 20-летним опытом. Зарегистрируйтесь сейчас
Что такое неравенство?
В алгебре неравенство имеет алгебраические выражения, включающие переменные и постоянные члены, так что одно выражение либо меньше, либо больше другого выражения.
Основные правила действий над неравенством:
- Вы можете прибавлять или вычитать одно и то же число из обеих частей неравенства, не меняя истинности неравенства. Если a > b, то a+k > b+k, например. Если 7 > 5, то 7 + 3 > 5 + 3, а если 10 < 5, то 10 - 3 < 5 - 3
- Вы можете умножить или разделить обе части неравенства на одно и то же положительное число. Это не изменит знак неравенства. Если a>b, то ak > bk; k > 0 например. 8 > 6 => 8 × 4 > 6 × 4
- Если умножить или разделить обе части неравенства на одно и то же отрицательное число, то знак неравенства изменится.
Если a > b, то ak < bk; k<0 например 9 > 5 => 9 × (-3) < 5 × (-3)
Если a > b, то ak < bk; k<0 например 9 > 5 => 9 × (-3) < 5 × (-3)Приведенные выше правила являются основными, которые будут использоваться при решении неравенств.
Решение линейных неравенств
Неравенства могут быть разных типов, например, линейные неравенства, квадратные неравенства. Давайте обсудим методы решения этих неравенств один за другим.
- Линейные неравенства Линейные неравенства — это те неравенства, в которых наивысшая степень переменной равна 1. Это простые неравенства, которые нужно решить. Для их решения требуется знание некоторых основных алгебраических правил. Возьмем пример.
Пример 1: Решить неравенство; (3x+2/-3)< Решение: Имеем (3x+2/-3)< => 3x + 2 > — 15 (Знак неравенства изменился, так как оно умножено на — 3) 3x > — 17 => x >(-17/3) является решением данного неравенства.
Знайте, где вы находитесь в неравенстве. Пройдите этот тест сейчас.
Решение квадратных неравенств
Квадратных неравенств:
Квадратными неравенствами называются такие неравенства, в которых наибольшая степень переменной равна 2.
Теперь для решения таких неравенств выполните следующие шаги:
- Приравняйте правую часть неравенства к нулю, переставив члены (если они есть) из левой части.
- Разложите выражение в левой части на множители и убедитесь, что коэффициент при ‘x’ в каждом множителе положителен.
- Приравняйте к нулю оба фактора, чтобы получить критические точки. Нанесите эти точки на числовую прямую. На числовой прямой будет три области, и крайняя правая область даст вам положительное неравенство, средняя область даст вам отрицательное неравенство, а самая левая часть снова даст вам положительное неравенство. Вы поймете это из следующего примера.
Пример 2: Решить неравенство x 2 + x — 28 < 2.
Решение : Имеем x 2 + x — 28 < 2
Шаг I 6 Правая рука:5 сторона равна нулю, получаем x 2 + x — 30 < 0 Шаг II: Факторизируем уравнение, получаем x
Примечание: Если исходное неравенство равно x 2 +x — 30 > 0, то решение будет следовать тем же шагам, что и выше, и решение неравенства будет (- ∞, — 6) U ( 5,∞), то есть все значения, для которых на графике показаны положительные значения.
Пройдите этот тест сейчас, чтобы проверить свое понимание неравенства.
Изучите все концепции линейных и квадратных неравенств, посмотрев это видео Achievers о линейных и квадратных неравенствах
Предлагаемое действие:
Начните подготовку с БЕСПЛАТНОГО доступа к 25+ макетам, 75+ видео и 100+ тестам по главам. Зарегистрируйтесь сейчас решить неравенства. Обычно эта тема считается сложной, но если у вас есть ясные основы, то она очень проста. В случае квадратичных неравенств просто следуйте приведенным выше шагам, и решение будет следовать.
Если у вас все еще есть какие-либо сомнения относительно какого-либо правила или метода, описанного в статье, не стесняйтесь опубликовать их в качестве комментария в разделе ниже.
Решение квадратных и линейных неравенств
Решение квадратных и линейных неравенств — Mr-Mathematics.com30 августа 2021 г.
На этом уроке учащиеся узнают, как решать квадратные и линейные неравенства с помощью нарисованного графика.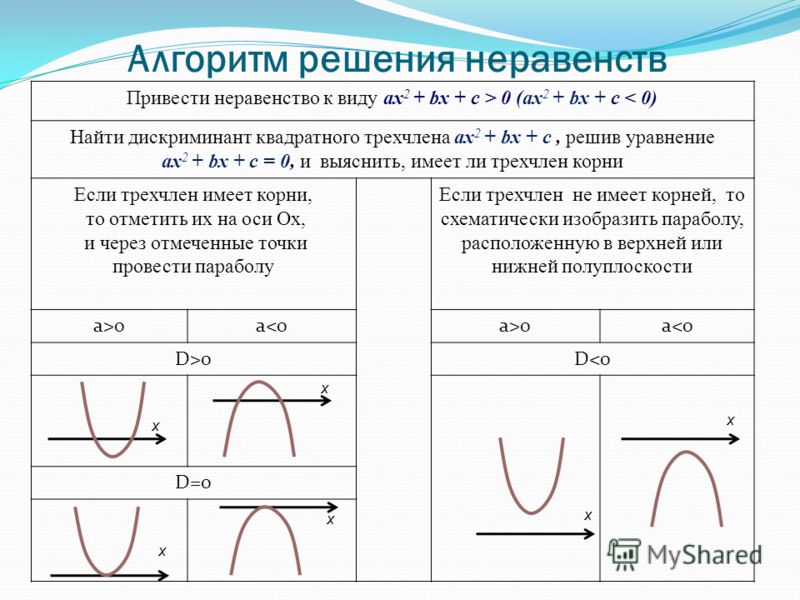
Позже, по мере обучения, учащимся предлагается решить пару квадратных неравенств.
Начальный урок повторяет решение квадратных неравенств, которые ученики изучили на предыдущем уроке.
Чтобы напомнить учащимся о процессе, я показываю, как решить x 2 – 2x – 15 > 0 с помощью факторизации. Затем я делаю набросок графика и спрашиваю класс, рассматриваем ли мы точки выше или ниже оси x.
Затем я прошу учащихся сопоставить оставшиеся три квадратных неравенства с их решениями.
Решение квадратных и линейных неравенств Когда мы начинаем основную часть урока, я использую Autograph, чтобы быстро проиллюстрировать две рассматриваемые функции a).
Важно скрыть ось, иначе легко будут найдены две точки пересечения.
С незакрашенными осями я прошу учащихся поработать в парах, чтобы составить и решить уравнение, где две линии пересекаются. Повторив большую часть этого процесса в начальной части, учащиеся с легкостью решают остальную часть задачи.
По мере того, как мы отвечаем на следующие несколько вопросов, я продолжаю иллюстрировать графики на Autograph, чтобы класс мог решить оставшуюся часть задачи алгебраически.
Контрольный вопросКонтрольный вопрос занимает от 5 до 10 минут для большинства учащихся. Я ожидаю, что каждый нарисует две функции на графике и отметит координаты, в которых каждая линия пересекает оси. Это значительно упрощает определение точек пересечения.
Некоторые учащиеся пытаются найти корни квадратного числа при отрицательном -3x 2 term и другие перевернули график. Обе ошибки были легко устранены при обратной связи с доской.
Когда учащиеся правильно нарисовали две функции, все без особого труда решили задачу.