Калькулятор онлайн. Бесплатный калькулятор
Калькулятор онлайн — это незаменимый инструмент для широкого круга интернет-пользователей. Прямо на нашем сайте вы можете использовать мощный калькулятор онлайн, который на данный момент является одним из лучших. Предлагаемый калькулятор онлайн способен как на простые, так и на сложные вычисления: логарифмы, тригонометрические функции, извлечение корней, проценты и многое другое.
Еще одна его особенность — это возможность построения графиков, что может порадовать как школьников со студентами, так и людей занимающихся научной деятельностью. На самом деле представленный онлайн калькулятор рассчитан не только на учащихся и ученых, сервис может оказаться полезным и для бизнеса, бухгалтерии, сметчиков и для многих других направлений деятельности, которые сопряжены с частыми вычислениями.
В этом калькуляторе ещё есть конвертер величин для перевода различных физических величин — вес, расстояние, время, компьютерные единицы и др.
Основное преимущество онлайн сервиса — это доступ к калькулятору с любого компьютера или мобильного устройства в любое удобное для вас время! Можете использовать его круглосуточно. Нужен только выход в интернет! Еще одним бесспорным плюсом является то, что сервис предоставляет этот калькулятор бесплатно и не требует регистрации пользователя.
Это достаточно простой калькулятор в освоении и использовании, с той лишь оговоркой, что в сервисе нет справочной информации на русском. Пожалуй, это единственный минус, который имеет предлагаемый онлайн калькулятор, — сервис на английском языке. В окне самого калькулятора размещен небольшой демонстрационный видеоролик. Он даёт только общее представление о том, как пользоваться калькулятором. Однако, для многих этого недостаточно.
Как показала практика, не все могут в полной мере использовать калькулятор инструкция к которому отсутствует.
В зависимости от сложности вычислений калькулятор использовать можно и как обычный калькулятор, выполняющий основные арифметические операции, и как инженерный калькулятор с дополнительными функциями. Теперь в вашем распоряжении и сам бесплатный калькулятор, и инструкция к нему.
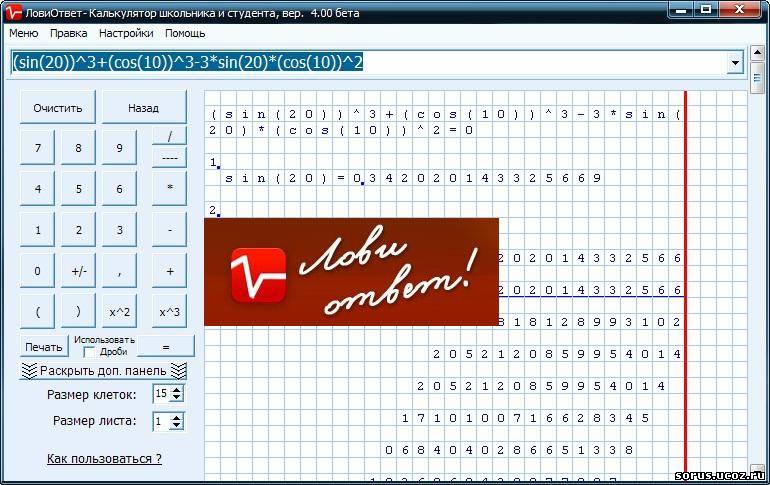
Для выполнения математических вычислений в кальуляторе укажите последовательность математического выражения в поле ввода и нажмите на кнопку со знаком равенства. Online калькулятор моментально произведет расчеты и выдаст результат. Вводить числа и знаки можно с помощью мышки, нажимая на кнопки самого калькулятора, или прямо с клавиатуры (при этом форма с онлайн калькулятором должна быть активна, для этого нужно поставить курсор в поле ввода данных).
возвести число в степень онлайн
Калькулятор степеней — это автоматизированный инструмент для выполнения соответствующих математических вычислений, которые заключается в перемножении числа на самого себя. Степень показывает сколько раз подряд следует умножить число. Допускается возведение в любую степень.
| В какую степень возвести: | ||
| Число которое надо возвести в степень: |
Пример арифметической операции
Чтобы возвести 4 в 3 предстоит выполнить 4*4*4. Решение — 64, поскольку 4*4=16, а 16*4=64.
Пример содержит:
Основание. В арифметике так называют множитель, которое необходимо умножить на самого себя, чтобы найти решение. Приведенное выше вычисление содержит основание — 4.
Степень. В арифметике данным показателем показывают сколько раз основание должно быть умножено.

Чтобы правильно записать операцию необходимо сначала написать основание, а затем справа в верхнем углу вторую часть выражения: 43. Данная запись позволяет экономить пространство и сокращает количество используемых символов. Итоговое значение пишется по стандартным правилам арифметики.
Использование множителей меньше нуля
Свойства множителей, которые предварительно были возведены в число меньше нуля считать очень легко. Надо:
Посчитать так, будто речь идет о положительной степени.
Разделить единицу на получившийся результат.
Чтобы не бояться отрицательных чисел можно привести простой пример: 4-3. Операция может записаться иначе: 1/(4*4*4*4) или 1/64. Решение — 0,015625.
Если оба числа выражения меньше нуля, действие проходит по аналогичным правилам. Решением может быть как отрицательный, так и положительный результат.
Если в выражении множитель меньше нуля, тогда в соответствии с правилами арифметики, четная отрицательная степень даст положительный результат. Нечетная отрицательная — результат меньше нуля.
Нечетная отрицательная — результат меньше нуля.
Преимущества сервиса
Самостоятельно выполнять эти операции не всегда удобно. К тому же, может не быть времени на это. В этом случае можно воспользоваться онлайн калькулятором умножения основания на само себя и получить готовый результат с решением.
Среди других преимуществ:
Простая работа даже с большими множителями.
Простое управление. Можно получить результат после заполнения онлайн формы.
Допускается проведение неограниченного количества действий.
Полезная информация
Существует таблица, в которой содержатся решения выполнения данных действий. Ее можно выучить, подобно тому, как в школе учатся правила умножения. Особенно таблица полезна людям, которые по роду своей деятельности связаны с математикой.
Остальным также будет интересно запомнить таблицу. Помимо того, что это поможет сэкономить время, тренировка памяти гарантированно развивает когнитивные способности.
Данные арифметические операции с основанием 2 активно применяются в IT и знакомы пользователям персональных компьютеров.
Чтобы воспользоваться приложением достаточно заполнить оба поля, после чего нажать кнопку «вычислить».
Калькулятор степени полинома — Онлайн калькулятор степени полинома
‘ Калькулятор степени полинома ‘ представляет собой онлайн-инструмент, который помогает вычислить степень заданного многочлена.
Что такое калькулятор степени полинома?
Онлайн-калькулятор степеней многочлена поможет вам вычислить степень заданного многочлена за несколько секунд.
Калькулятор степени полинома
ПРИМЕЧАНИЕ: Пожалуйста, вводите полином только с точки зрения «x».
Как пользоваться калькулятором степени полинома?
Чтобы найти степень многочлена, выполните следующие шаги:
- Шаг 1: Введите многочлен в указанное поле ввода.
- Шаг 2: Нажмите кнопку «Найти» , чтобы найти степень многочлена.

- Шаг 3: Нажмите кнопку «Сброс» , чтобы очистить поля и найти степень для различных полиномов
Как найти степень многочлена?
Степень полинома определяется как наибольшая экспоненциальная степень переменного члена в полиноме, указывающая степень этого полинома. Для проверки степени полинома учитываются только переменные, коэффициенты игнорируются.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Книга A Бесплатный пробный класс
Решенные примеры на калькуляторе полиномиальной степениПример 1:
Найдите степень полинома x 2 + 5x + 6
Решение:
9 9002 x 99Решение:
9 9002 x 999:
9 9002 x 99 . 2
2
5x имеет степень 1 (x имеет показатель 1)
Следовательно, наибольшая степень из них равна 2, поэтому полином имеет степень из 2.
Пример 2:
Найдите степень полинома X 5 — 5x 2 + 6
Решение:
x 5 имеет степень 5 (x имеет показатель 5)
.5x 2 имеет степень 2 (x имеет показатель степени 2)
Следовательно, наибольшая степень из них равна 5, поэтому полином имеет степень 5.
Пример 3:
Найти степень многочлена x 4 + 6x 3 — 2x + 5
Решение:
x 4 имеет степень 4 (x имеет показатель степени 4)
6x 3 имеет степень 3 (x ha степень 3
2x имеет степень 1 (x имеет показатель степени 1)
Следовательно, наибольшая степень из них равна 4, поэтому полином имеет степень 4.
Точно так же вы можете попробовать калькулятор, чтобы найти степень полинома для
а) 8x 3 + 2x 2 + x+ 1 б) 5x 2 + 7x + 9
☛ Статьи по теме:- Степень многочлена
- Многочлены
Калькулятор степеней и старших коэффициентов с решением
Используйте этот калькулятор степеней и старших коэффициентов, чтобы найти наивысшую степень, старший член и постоянное число, связанные с ним.
Продолжайте читать, чтобы ознакомиться с рассматриваемой концепцией.
9{3} + 17X + 8 = 0 $$Степень этого выражения равна 3, так как оно является наивысшим среди всех, содержащихся в данном алгебраическом предложении.
Как работает калькулятор степени и старшего коэффициента?
Результаты, отображаемые этим калькулятором степеней полинома, являются точными и генерируются мгновенно. Если вы также хотите наблюдать полином с помощью этого бесплатного калькулятора ведущего члена, ознакомьтесь с приведенным ниже руководством по использованию:
Если вы также хотите наблюдать полином с помощью этого бесплатного калькулятора ведущего члена, ознакомьтесь с приведенным ниже руководством по использованию:
Ввод:
- Введите полином и переменную в соответствующие поля
- Нажмите кнопку расчета
Вывод:
Калькулятор свободного нахождения степени полинома определяет:
- Степень полинома
- Начальный термин, используемый в выражении
- Старший коэффициент в выражении
Часто задаваемые вопросы:
Что такое 5-я степень многочлена?
Полиномам 3, 4 или 5 степени присвоены определенные имена. Они называются кубическими, квартиками и квинтиками соответственно. Но каким бы ни было выражение, вы можете определить его степень, используя этот калькулятор степени полинома.
Какова степень многочлена 7?
Для каждой константы, участвующей в алгебраическом предложении, степень постоянного члена всегда равна нулю, что также может быть проверено нашей свободной степенью полиномиального калькулятора.
Какова степень 0?
Нулевой полином — это тот, в котором нет ненулевого члена. Поэтому его степень не определена. Кроме того, вы можете перепроверить это, запустив калькулятор степени и ведущего коэффициента за считанные секунды.
Что такое многочлен первой степени?
Поскольку степень здесь равна 1, такой многочлен известен как выражение линейного полинома. Общее линейное выражение для такого предложения дается следующим образом:
$$ ax + b = 0 $$
Вывод:
Степени многочленов являются поставщиками решений. Они позволяют узнать, сколькими возможными способами полиномиальная функция может быть сведена к простому члену. Более того, это также означает каждый раз, когда функция пересекает независимую ось (ось x). Вот почему эта концепция широко используется экономистами, математиками и инженерами. А когда дело доходит до анализа любого номинального полинома с целью экономии времени, все они используют калькулятор полиномов наилучшей степени для точных и оперативных расчетов.