League of Legends Wiki:Lua | League of Legends Wiki
в: Статьи-наставления
Править код- Lua (лу́а, с порт. — «луна») — скриптовый язык программирования, разработанный в подразделении Tecgraf (Computer Graphics Technology Group) Католического университета Рио-де-Жанейро (Бразилия). Интерпретатор языка является свободно распространяемым, с открытыми исходными текстами на языке Си.[1]
В данной статье будут даны области применения языка Lua в League of Legends Вики. Для более подробного изучения языка и его синтаксиса читайте следующие статьи:
- Официальное руководство по фреймворку Scribunto (на англ. языке)
- Статья о Lua в Викии Вики
- Lua reference manual
Содержание
- 1 Введение
- 2 Структура Lua на сайте
- 3 Вызов
- 4 Примечания
Введение[]
Язык Lua стал вводиться в русскоязычном сегменте League of Legends Wiki с февраля 2019 года, когда был добавлен и частично локализован первый модуль Модуль:SkinData и хранилище SkinData/data, предназначенный для демонстрации образов чемпионов.
Лавинообразное увеличение роли Lua показе информации об игре произошло зимой 2020 г., когда были созданы Модуль:ChampionData и первый полностью самостоятельный проект Модуль:ItemData, которые переняли сведения о чемпионах и предметах LoL из Data-шаблонов.
Основной задачей при внедрении Lua было уменьшить единовременное число правок при выходе обновлений, а также упрощение получения доступа к различным данным о конкретном чемпионе или предмете. Также стоит отметить, что внешне Lua гораздо ближе к традиционным языкам программирования, чем функции парсера, хотя и не предоставляет практически никакого функционала, который не давали бы вторые (в этом основное отличие от используемого в проектах JavaScript, чьи функции могут быть опасны и посему должны быть обязательно отправляться на проверку перед выпуском в проекте).
Структура Lua на сайте[]
В целом все существующие Lua скрипты можно разделить на два вида по области применения: утилиты и хранилища. Утилиты содержат полезные функции, которые слишком сложно записывать при помощи функций парсера: перекрашивание текста по ключевым словам, вывод иконок и др.
Основные используемые скрипты-утилиты:
- Модуль:Feature — Общая библиотека стандартных программистских функций, например, сортировка массива, тернарный оператор, проверка на nil и прочее.
- Модуль:Filename — библиотека для вызова названий файлов
- Модуль:ImageLink — библиотека для вызова любых иконок игровых объектов.
- Модуль:Color — библиотека для перекрашивания текста по ключевым словам (используется в шаблоне {{As}})
- Модуль:Stats icon — библиотека для вызова иконок характеристик (используется в шаблоне {{Sti}})
- Модуль:RusLocalization — библиотека со специфическими функциями локализации
Модули-хранилища используются как базы данных об определенном классе игровых объектов: чемпионах, их образах, предметах, рассказах. Они состоят из 2 компонентов:
Они состоят из 2 компонентов:
- Таблица игровых объектов — просто огромный массив Lua, в котором перечисляются все однотипные объекты:
- Модуль:ChampionData/data — чемпионы
- Модуль:ItemData/data — предметы
- Модуль:UniverseData/data — объекты лора игры (регионы, рассказы, комиксы, сюжетные видеоролики)
- Модуль:UniverseData/skinlines — линейки образов
- Модуль:TFTUnitData/data — чемпионы TFT
- Модуль:TFTTraitData/data — чемпионы TFT
- Модуль:LoRData/data — карты LoR
- Модуль:RusLocalization/LittleLegends/data — Маленькие легенды
- Модуль с функциями, которые обеспечивают вывод хранимой информации в удобном виде, имитируя работу шаблонов.
- Модуль:ChampionData
- Модуль:ItemData
- Модуль:UniverseData
- Модуль:TFTUnitData
- Модуль:TFTTraitData
- Модуль:LoRData
(Для упрощения доступа также у некоторых хранилищ есть геттер (например, Модуль:ItemData/getter), с помощью которого можно получать конкретные поля объектов.
Вызов[]
Вызов многих модулей вставлен в шаблоны, чтобы упростить использование или избежать неверного указания параметров. У модулей практически нет «защиты от дурака» и при любой ошибке работа модуля будет приостановлена.
Основной код для вызова:
{{#invoke:''Название модуля''|Название функции}}- Пример
{{#invoke:ChampionData|getChampionTable}}Примечания[]
- ↑ Википедия о Lua
v · e
| Правила | Общие правила · Загрузка файлов · Нейтральность · Лицензирование · Статьи-заготовки · Категоризация · Запрещённые материалы · Вандализм · Деструктивное поведение · Удаление статей · Имена участников · Личные страницы |
|---|---|
| Рекомендации | Общие наставления · Шаблоны · Lua · Статьи о чемпионах (Новый чемпион · Новый образ · Категоризация · Умения) · Статьи о предмете · Статьи о руне · Статьи о лоре · Статьи о TFT · Статьи о LoR · Статьи о WR · Работа в исходном коде · FAQ |
| Прочее | Список задач (LoL · TFT · LoR) · Команда Вики |
Материалы сообщества доступны в соответствии с условиями лицензии CC-BY-SA, если не указано иное.
Синусы и косинусы… — Брянский Вольф тебе товарищ — LiveJournal
?
| ||||
| ||||||||||||||||||||||||||||||
Использование формул сложения синуса и косинуса для доказательства тождества. Задача 3
Вот особенно сложный, но интересный пример, в котором используются формулы синуса и косинуса разности. В задаче говорится: вывести тангенс разностной идентичности, что означает вывести тангенс тангенса альфа минус бета.
Теперь первое, что я знаю о тангенсе, это то, что тангенс представляет собой синус относительно косинуса, так что это синус альфа минус бета относительно косинуса альфа минус бета, и тогда я могу использовать синус и косинус наших формул разности, чтобы заполнить это. У меня есть синус, косинус, косинус, синус; синус альфа, косинус бета минус косинус альфа, синус бета больше и для косинуса у меня есть косинус, косинус, синус, синус. Косинус альфа, косинус бета упс и минус становится плюсом, синус альфа, синус бета.
Теперь это беспорядок, и для упрощения требуется хитрость, и хитрость заключается в том, чтобы умножить верх и низ на 1 на косинус альфа, косинус бета, 1 на косинус альфа, косинус бета, и это даст нам действительно хороший результат, смотреть, что здесь происходит. Таким образом, эта 1 над косинусом альфа и косинусом бета будет распределена по обоим этим терминам в числителе: синус альфа, косинус бета над косинусом альфа, косинус бета косинус бета отменит, и у меня будет синус альфа над косинусом альфа минус . Вот что происходит с первым сроком.
Вот что происходит с первым сроком.
Второй член, я получаю косинус-альфа, синус-бета над косинусом-альфа, косинус-бета, косинус-альфа отменяется, и у меня остается синус-бета над косинусом-бета, это хорошо. Первый член в знаменателе косинус альфа, косинус бета над косинусом альфа косинус бета 1 плюс и, наконец, синус альфа синус, синус бета над косинусом альфа, косинус бета. Синус альфа, синус бета ничто не отменяет здесь косинус альфа, косинус бета, но вот что мы получаем, это тангенс альфа, тангенс бета больше 1 плюс тангенс альфа умноженный на тангенс бета, и это наш тангенс формулы разности. Тангенс альфа минус бета равен тангенсу альфа минус тангенс альфа больше 1 плюс тангенс альфа тангенс бета.
Давайте воспользуемся этим на очень простом примере. Задача говорит найти тангенс 15 градусов? Итак, сначала вы хотите выразить 15 градусов как некоторую разницу, которая включает в себя хорошие углы, особые углы. Например, тангенс 45 минус 30. На самом деле позвольте мне пойти с 60 минус 45, позвольте мне сказать вам, почему.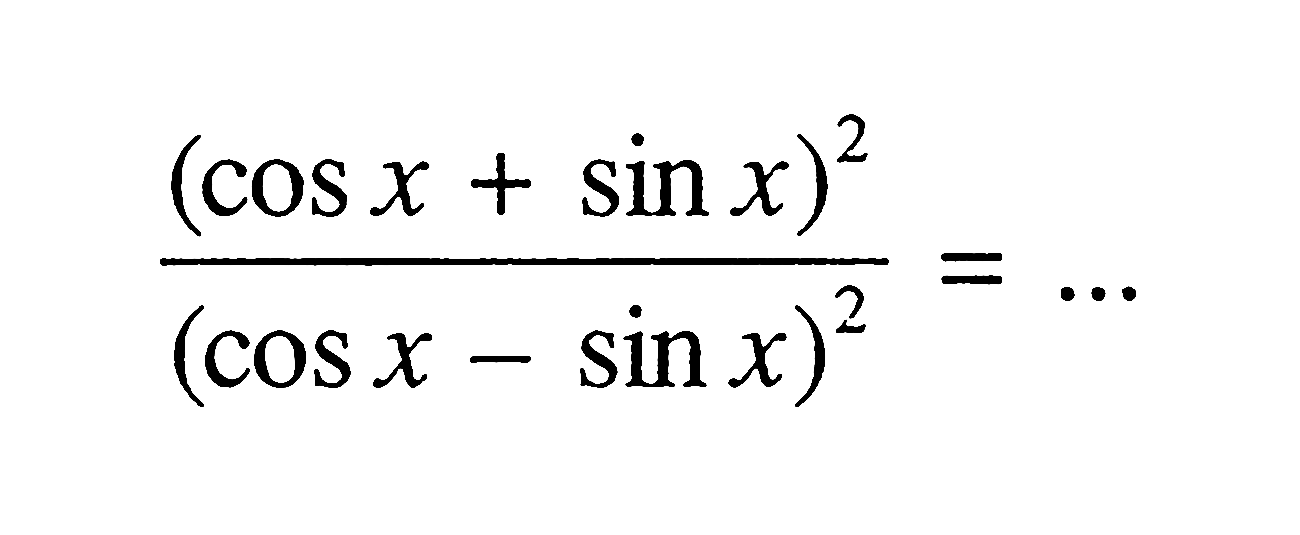 Если вы помните тангенс 30 градусов, это 1 над корнем 3, а тангенс 60 градусов это корень 3, я не хочу, чтобы в моих ответах была 1 над корнем 3, поэтому я собираюсь держаться подальше от этого, но даст мне немного более приятный ответ, так что это тангенс 60 градусов минус 45 градусов.
Если вы помните тангенс 30 градусов, это 1 над корнем 3, а тангенс 60 градусов это корень 3, я не хочу, чтобы в моих ответах была 1 над корнем 3, поэтому я собираюсь держаться подальше от этого, но даст мне немного более приятный ответ, так что это тангенс 60 градусов минус 45 градусов.
Теперь из формулы тангенс альфа минус тангенс бета так что тангенс 60 минус тангенс 45 на 1 плюс произведение двух, тангенс 60, тангенс 45 и это даст мне тангенс 60 это хорошо, это корень 3, тангенс 45 — это 1, 1 плюс, а затем корень 3 раза 1, а не bas, это довольно хороший ответ, но обычно нам не нравится иметь радикалы в знаменателе, поэтому давайте рационализируем это.
Итак, чтобы рационализировать знаменатель, вы помните прием умножения на сопряженное? Это то, что мы собираемся сделать здесь, за исключением того, что я собираюсь умножить в форме, давайте посмотрим 1 минус корень 3, 1 минус корень 3. В знаменателе я собираюсь получить 1² минус корень 3², это 1 минус 3. В числителе, и это то же самое, позвольте мне умножить его, я получаю корень 3 умножить на 1, корень 3 корень 3 раза отрицательный корень 3 минус 3, -1 умножить на 1, -1 и -1 умножить на отрицательный корень 3 плюс корень 3.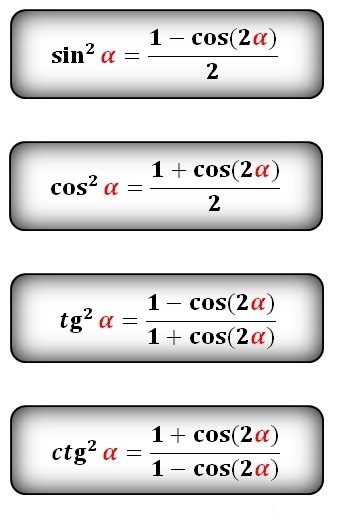 У меня внизу -2, а сверху два корня 3 минус 4. Если я разделю все это на -2, я получу отрицательный корень 3 плюс 2, и это мой ответ. 2 минус корень 3, это тангенс 15 градусов.
У меня внизу -2, а сверху два корня 3 минус 4. Если я разделю все это на -2, я получу отрицательный корень 3 плюс 2, и это мой ответ. 2 минус корень 3, это тангенс 15 градусов.
тригонометрия — Как $\cos (\alpha /\beta)$ выражается через $\cos\alpha$ и $\cos\beta$?
Спросил
Изменено 7 лет, 5 месяцев назад
Просмотрено 556 раз
$\begingroup$
Если возможно выразить $\cos n\alpha$ через $\cos\alpha$ в виде степенного ряда для целого числа $n$ …
Мне нравится видеть выражение для частного угла, которое очевидно подсчитывается, когда $ (\alpha , \beta) $ меняются местами.
EDIT1:
Что-то вроде:
$$ \cos (\alpha — \beta)= \cos \alpha \cos \beta + \sin \alpha \sin \beta $$
EDIT2:
Нравится знать, почему $\cos(\alpha/\beta)$ нельзя выразить через $\cos\alpha, \cos\beta$, но $\cos(\alpha+\beta)$ можно выразить через $ \cos\alpha$ и $\cos\beta.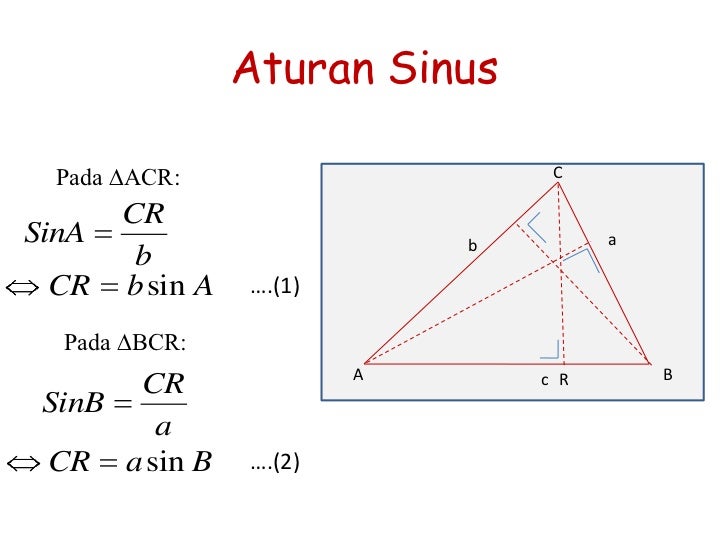

 Весьма неодобрительно относящегося к ученикам и прочим бездарям от учения. Чем-то похожим на Ивана Алексеевича Бунина, который под старость едко поучал молодых писателей как надо писать, сердито тряся тростью… Употребляющим старорежимные же выражения «Извольте работать, молодые люди!» либо «Потрудитесь объяснить, что это значит…»
Весьма неодобрительно относящегося к ученикам и прочим бездарям от учения. Чем-то похожим на Ивана Алексеевича Бунина, который под старость едко поучал молодых писателей как надо писать, сердито тряся тростью… Употребляющим старорежимные же выражения «Извольте работать, молодые люди!» либо «Потрудитесь объяснить, что это значит…» Никакого панибратства! Косинусы остаются друг с другом, синусы — отдельно. Никакой попытки братания! И плюс меняется на минус. Всё не соглашательски , а — наоборот!
Никакого панибратства! Косинусы остаются друг с другом, синусы — отдельно. Никакой попытки братания! И плюс меняется на минус. Всё не соглашательски , а — наоборот! В эпоху спама однозначно должен ассоциироваться с пенисом. 😉
В эпоху спама однозначно должен ассоциироваться с пенисом. 😉
 ..
.. ~)
~)