Предел функции
Предел функции Math Task
1.Предел функции.
|
|||||||||||||||||||||||||||||
| 6 7 8 9 10 11 12 13 14 | |||||||||||||||||||||||||||||
Пусть задана некая функция f(x). | f(x)– А | < ɛ
Иными словами, при подставлении любого числа х>р данное неравенство всегда будет выполняться.
lim f(x) = А |
Рис.1 |
||||||||||||||||||||||||||||
Геометрический смысл предела функции y=f(x) в бесконечности заключается в том, что при стремлении х к бесконечности, значение функции f(x) стремится к числу А. Таким образом, неравенство | f(x) – А | < ɛ равносильно двойному неравенству: А — ɛ < f(x) < А + ɛ и функция принимает значения в диапазоне шириной 2ɛ (рис. |
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
Примеры. |
|||||||||||||||||||||||||||||
| 6 7 8 9 10 11 12 13 14 | |||||||||||||||||||||||||||||
|
|
||
www. mathtask.ru mathtask.ru |
||
Техника вычисления пределов — презентация онлайн
Похожие презентации:
Предел функции. Непрерывность
Понятие предела функции в точке
Предел функции в точке
Предел функции
Понятие предела функции
Понятие предела функции. Бесконечно малая и бесконечно большая функции
Предел функции
Предел функции в точке и на бесконечности. Свойства пределов. Замечательные пределы
Теория пределов
Предел Бесконечно маленькая величина
1. ТЕХНИКА ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ
2. 1.Предел функции в точке.
lim f ( x)x a
3. 1.1. Предел многочлена.
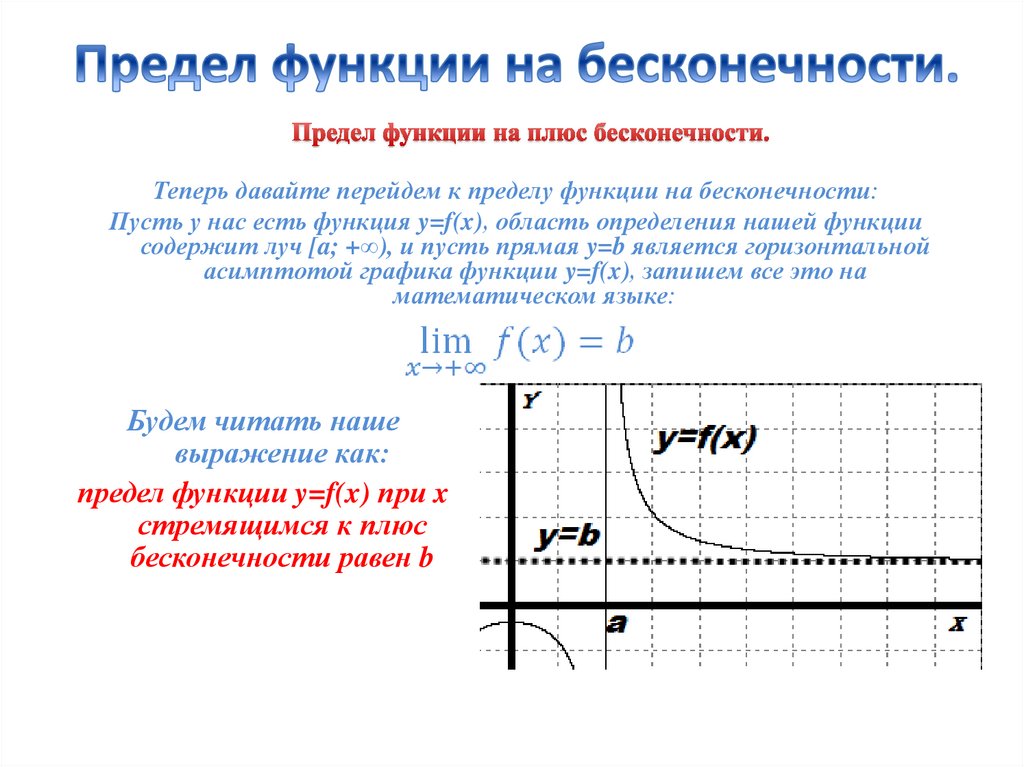 lim P( x) P(a)
lim P( x) P(a)x a
lim( x 5 x 4) 2 5 2 4 2
3
x 2
3
4. 1.2.Предел дробно-рациональной функции.
P( x)lim
x a R( x)
5. Раскрытие неопределенности
00
разложите числитель или (и)
знаменатель на множители,
сократите дробь,
вычислите предел.
6. Примеры:
x 2 0x 2
1) lim 2
lim
x 2 x 4
0 x 2 x 2 x 2
1
1
1
lim
lim
x 2 x 2
x 2 2 2
4
x 10 x 3
x 2 13 x 30 0
2) lim
lim
2
x 10
100 x
0 x 10 10 x 10 x
x 3
7
lim
0.35
x 10 10 x
20
7. 1.3. Предел иррациональной функции. Раскрытие неопределенности
1.3. Предел иррациональнойфункции.
0
Раскрытие неопределенности
0
домножить
числитель и знаменатель
дроби на выражение, сопряженное
числителю или (и) знаменателю,
упростить выражение и сократить дробь,
вычислить предел.
8. Примеры:
1 x 1 1 x 11 x 1 0
lim
lim
x 0
x
0 x 0
x 1 x 1
lim
x 0
1 x 1
x 1 x 1
x 0
x
x 1 x 1
1
lim
0.
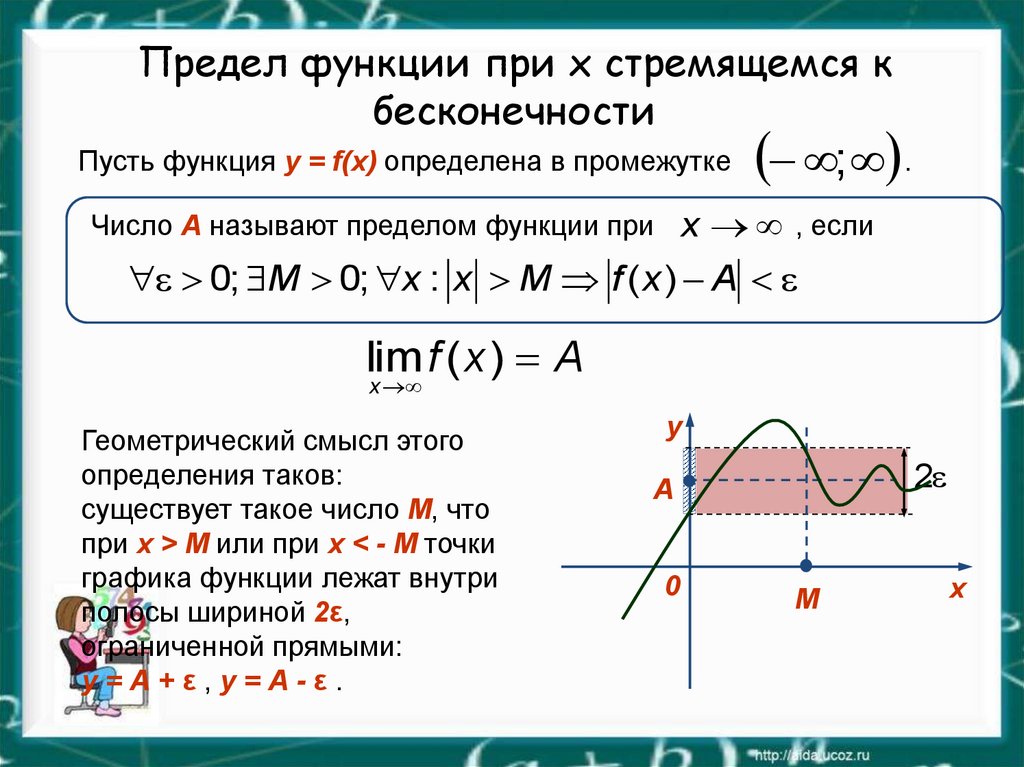 5
5x 0
1 1
1 x 1
1
lim
9. 2. Предел функции на бесконечности .
lim f ( x)x
10. 2.1.Раскрытие неопределенности
11. Примеры: большая степень числителя превышает большую степень знаменателя, следовательно, предел стремится к бесконечности.
x 7x / x 7/ x
1) lim 2
lim 2 3
3
x 5 x / x 4 / x
x 5 x 4
3
1 7 / x
3
3
3
1 0
1
lim
lim
lim
3
x
x 0 0
x 0
5/ x 4/ x
3
12. Примеры: большая степень числителя совпадает с большей степенью знаменателя, следовательно, предел — отличное от нуля число.
6 x3 3x 16 x 3 / x 3 3 x / x 3 1/ x 3
2) lim
lim
3
3
3
3
x
5x 2
5x / x 2 / x
x
6 3 / x 1/ x
2
lim
x
5 2/ x
3
3
6 0 0 6
lim
1.2
x
5 0
5
13. Примеры: большая степень числителя меньше большей степени знаменателя, следовательно, предел равен нулю.
3x 4 x3x / x 4 x / x
3) lim
lim
6
6
6
6
7 x 8 x 7 x / x 8 / x
x
3
3
3/ x 4/ x
3
lim
x
7 8/ x
3
5
6
0 0
lim
0
x 7 0
6
3.
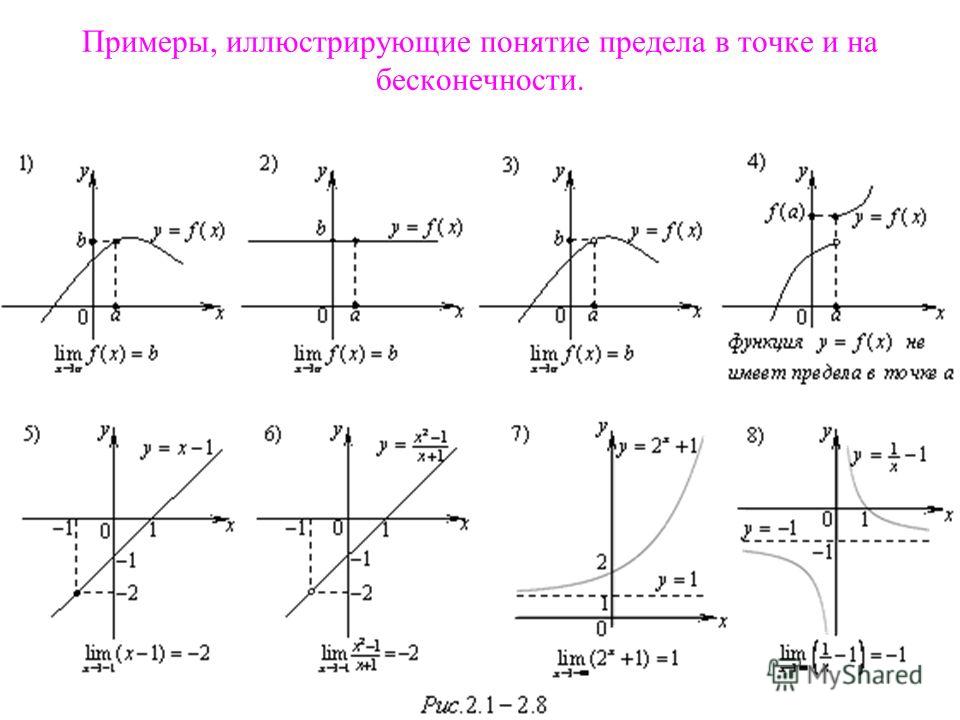 Замечательные
Замечательныепределы.
15. 3.1. Первый замечательный предел.
limx 0
lim
x 0
sin
sin
1
1
16. Примеры:
sin 5 x 0sin 5 x 5
1) lim
lim
x 0
x
5
0 x 0 x
sin 5 x 5
lim
1 5 5
x 0
5x 1
sin13x 0
sin13x 13
2) lim
lim
x 0 sin 8 x
8
0 x 0 sin 8 x
English Русский Правила
Исчисление— Докажите, что $\lim_{x\to\infty}\frac{f(x)}x=\lim_{x\to\infty}f'(x)$
Задай вопрос
спросил
Изменено 6 лет, 4 месяца назад
Просмотрено 953 раза
$\begingroup$
Я придумал теорему. (Возможно, это нельзя назвать теоремой, но я не знаю, как еще это назвать.
Если $$\lim_{x\to\infty}f'(x)$$ существует (конечно), тогда $$\lim_{x\to\infty}\frac{f(x)}x=\lim_{x \to\infty}f'(x)$$ Мне еще предстоит найти контрпример, и мне кажется, что он имеет смысл, но я не могу его доказать.
Эта «теорема» имеет решающее значение для ответа на вопрос, который меня попросили дать, но мой ответ не будет очень хорошим, если я не смогу доказать, почему он работает.
Что я пробовал:
Мне удалось доказать, что $f(x)$ имеет линейную асимптоту (думаю, моя терминология верна).
Если:
$$\lim_{x\to\infty}f(x)=\lim_{x\to\infty}mx+b$$
Тогда:
$$\lim_{x\to \infty}\frac{f(x)}x=\lim_{x\to\infty}\frac{mx+b}x=m$$
Но это не работает, если нет асимптоты. Возьмем, к примеру, $f(x)=\ln(x)$. $b$ в $mx+b$ было бы бесконечно.
- исчисление
- пределы
- производные
4
$\begingroup$
Строгий способ показать это — использовать аргументы $\varepsilon$-$M$.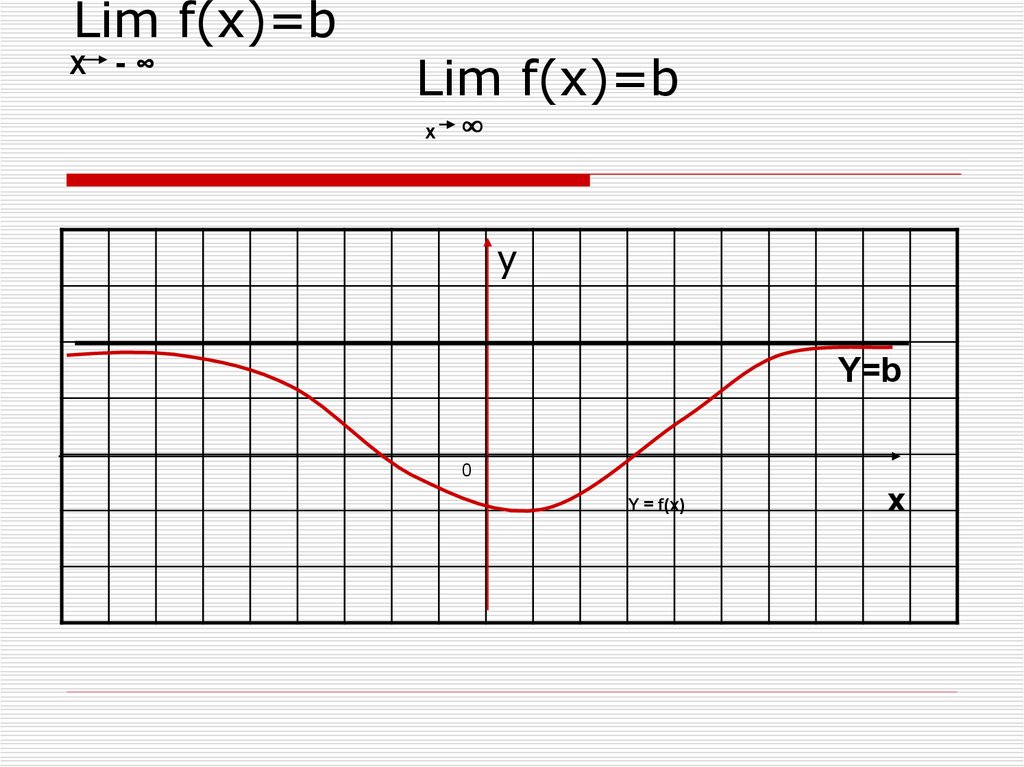 К
условие $c \equiv \lim_{x \to \infty} f'(x)$ существует и конечно, из чего следует, что для любого заданного $\varepsilon > 0$ существует $M > 0$ такое, что для всех $x \geq М$,
$$|f'(x) — с| < \varepsilon. \тег{1}$$
С другой стороны, по теореме о среднем значении для любого $x > M$ имеем
$$f(x) = f(M) + f'(\xi)(x — M)$$
для некоторого $\xi \in (M, x)$. Следовательно, для всех $x > M$ следует, что
\начать{выравнивать*}
& \left|\frac{f(x)}{x} — c\right| \\
= & \left|\frac{f(M) + f'(\xi)(x — M)}{x} — c\right| \\
= & \left|f'(\xi) — c + \frac{f(M) — f'(\xi)M}{x}\right| \\
\leq & |f'(\xi) — c| + \frac{|f(M) — f'(\xi)M|}{x} \\ < & \varepsilon + \varepsilon = 2\varepsilon.
\конец{выравнивание*}
На последнем шаге мы можем увеличить $x$ всякий раз, когда это необходимо, чтобы последний член был ограничен $\varepsilon$, это возможно, поскольку числитель ограничен фиксированным числом. Это завершает доказательство.
К
условие $c \equiv \lim_{x \to \infty} f'(x)$ существует и конечно, из чего следует, что для любого заданного $\varepsilon > 0$ существует $M > 0$ такое, что для всех $x \geq М$,
$$|f'(x) — с| < \varepsilon. \тег{1}$$
С другой стороны, по теореме о среднем значении для любого $x > M$ имеем
$$f(x) = f(M) + f'(\xi)(x — M)$$
для некоторого $\xi \in (M, x)$. Следовательно, для всех $x > M$ следует, что
\начать{выравнивать*}
& \left|\frac{f(x)}{x} — c\right| \\
= & \left|\frac{f(M) + f'(\xi)(x — M)}{x} — c\right| \\
= & \left|f'(\xi) — c + \frac{f(M) — f'(\xi)M}{x}\right| \\
\leq & |f'(\xi) — c| + \frac{|f(M) — f'(\xi)M|}{x} \\ < & \varepsilon + \varepsilon = 2\varepsilon.
\конец{выравнивание*}
На последнем шаге мы можем увеличить $x$ всякий раз, когда это необходимо, чтобы последний член был ограничен $\varepsilon$, это возможно, поскольку числитель ограничен фиксированным числом. Это завершает доказательство.
$\endgroup$
1
$\begingroup$
Правило Лопиталя не требует, чтобы числитель стремился к бесконечности.
На самом деле предел $\lim_{x\to \infty}f(x)$ даже не должен существовать . См. примечание ЗДЕСЬ, в котором упоминается интересующий случай.
Таким образом, если $f'(x)$ существует для некоторого интервала $(x_0,\infty)$ и существует $\lim_{x\to \infty}\frac{f'(x)}{1}$, то у нас есть
$$\lim_{x\to \infty}\frac{f(x)}{x}=\lim_{x\to \infty}f'(x)$$
$\endgroup$
8
$\begingroup$
Нижеследующее не является строгим ответом (хорошие ответы уже были опубликованы), а скорее примечанием об интуиции, лежащей в основе результата, в некоторой степени связанной с последней частью, которую вы отредактировали в вопросе.
Когда существует предел $\lim_{x\to\infty}f'(x) = L$, интуитивно $f(x)$ становится все ближе и ближе к линейной функции наклона $L$ по мере того, как $x\to \infty$ (которая может быть горизонтальной асимптотой, если $L = 0$, или наклонной в противном случае).
Теперь рассмотрим точку $P \equiv (x,y)$ на кривой $y = f(x)$. Прямая, проходящая через начало координат $O \equiv (0,0)$ и точку $P$, имеет наклон $y/x = f(x)/x$. При достаточно большом $x$ прямая $OP$ будет пересекать асимптоту $f(x)$ в окрестности $P$, которая становится все меньше и меньше по мере того, как $x$ растет к $\infty$, поскольку $f$ «приближается» к своей асимптоте. В пределе $x\to \infty$ сама точка пересечения стремится к бесконечности, то есть $OP$ стремится к прямой
$\endgroup$
исчисление — Доказательство того, что $\lim\limits_{x\to\infty}f'(x) = 0$, когда $\lim\limits_{x\to\infty}f(x)$ и $\lim\limits_ {x\to\infty}f'(x)$ существуют
спросил
Изменено 5 месяцев назад
Просмотрено 55 тысяч раз
$\begingroup$
Я пытался решить следующую задачу:
Предположим, что $f$ и $f’$ являются непрерывными функциями на $\mathbb{R}$ и что $\displaystyle\lim_{x\to\infty }f(x)$ и $\displaystyle\lim_{x\to\infty}f'(x)$ существуют. Покажите, что $\displaystyle\lim_{x\to\infty}f'(x) = 0$.
Покажите, что $\displaystyle\lim_{x\to\infty}f'(x) = 0$.
Я не совсем уверен, что делать. Поскольку информации не так много, я думаю, что тут мало что можно сделать. Я попытался использовать определение производной и показать, что она становится $0$, когда $x$ становится $\infty$, но на самом деле это не сработало. Теперь я думаю, что мне следует предположить $\displaystyle\lim_{x\to\infty}f'(x) = L \neq 0$ и попытаться получить противоречие, но я не уверен, откуда оно взялось. .
Может ли кто-нибудь указать мне правильное направление (например, определенную теорему или свойство, которое я должен использовать?) Спасибо
- исчисление
- реальный анализ
- пределы
- функции
- производные
2
3
$\begingroup$
Применить хитрый прием L’Hospital: $\, $, если $\rm\ f + f\,’\!\to L\ $ как $\rm\ x\to\infty\ $, то $\rm\ f \к L,\ f\,’\!\к 0,\, $ начиная с 9x}\, =\, \lim_{x\to\infty}\, (f(x)+f'(x))\qquad $$
Это применение правила Лопиталя получило некоторую известность, потому что проблема появилась в учебнике классического исчисления Харди Курс чистой математики , но с менее элегантным решением. Например, см. Ландау; Джонс: старая выносливая проблема, Math. Журнал 56 (1983) 230-232.
Например, см. Ландау; Джонс: старая выносливая проблема, Math. Журнал 56 (1983) 230-232.
$\endgroup$
11
$\begingroup$
Подсказка: если предположить, что $\lim _{x \to \infty } f'(x) = L \ne 0$, противоречие будет получено из теоремы о среднем значении (рассмотрите $f(x)-f(M )$ для фиксированного, но сколь угодно большого $M$, и пусть $x \to \infty$).
Объяснение: если предел $f(x)$ существует, то существует горизонтальная асимптота. Следовательно, когда функция приближается к бесконечности, она становится более линейной, и поэтому производная приближается к нулю.
$\endgroup$
11 9{‘}(х)=0$.
$\endgroup$
$\begingroup$
Чтобы немного расширить мой комментарий, поскольку $\lim_{x \to \infty} f(x) = L$, мы получаем
$$\lim_{x \to \infty} \frac{f(x )}{x} =0 \,. $$
$$
Но также, поскольку $\lim_{x \to \infty} f'(x)$ существует, по Лопиталю мы имеем
$$\lim_{x \to \infty} \frac{f(x)}{x}= \lim_{x \to \infty} f'(x) \,.$$
Обратите внимание, что использование MTV в основном такое же доказательство, поскольку вот как в этом случае доказывается L’H… 92}$ 😉
$\endgroup$
5
$\begingroup$
Это ответ на интересное наблюдение, сделанное Rhythmic Fistman в комментарии под моим (первым) ответом. Предположим, что $\lim _{x \to \infty } f'(x) = L$ для некоторого $L \in \mathbb{R}$. Тогда из определения производной
$$
L = \ mathop {\ lim} \ limit_ {x \ to \ infty} \ mathop {\ lim } \ limit_ {h \ to 0} \ frac {{f (x + h) — f (x)}} {h }.
$$
Как заметил Ритмический Кулак, наивное изменение порядка пределов приводит к равенству
$$
L знак равно \ mathop {\ lim } \ limit_ {h \ to 0} \ mathop {\ lim } \ limit_ {x \ to \ infty} \ frac {{f (x + h) — f (x)}} {h } = 0,
$$
где последнее равенство следует из предположения, что $\lim _{x \to \infty } f(x)$ существует (конечно).

 Тогда число А будет называться пределом функции y = f(x) при х стремящимся к бесконечности, если при всех х больше определенного числа р, разность между значением функции и числом А по модулю будет меньше любого, сколь угодно малого положительного числа ɛ>0. Т.е. верно неравенство:
Тогда число А будет называться пределом функции y = f(x) при х стремящимся к бесконечности, если при всех х больше определенного числа р, разность между значением функции и числом А по модулю будет меньше любого, сколь угодно малого положительного числа ɛ>0. Т.е. верно неравенство: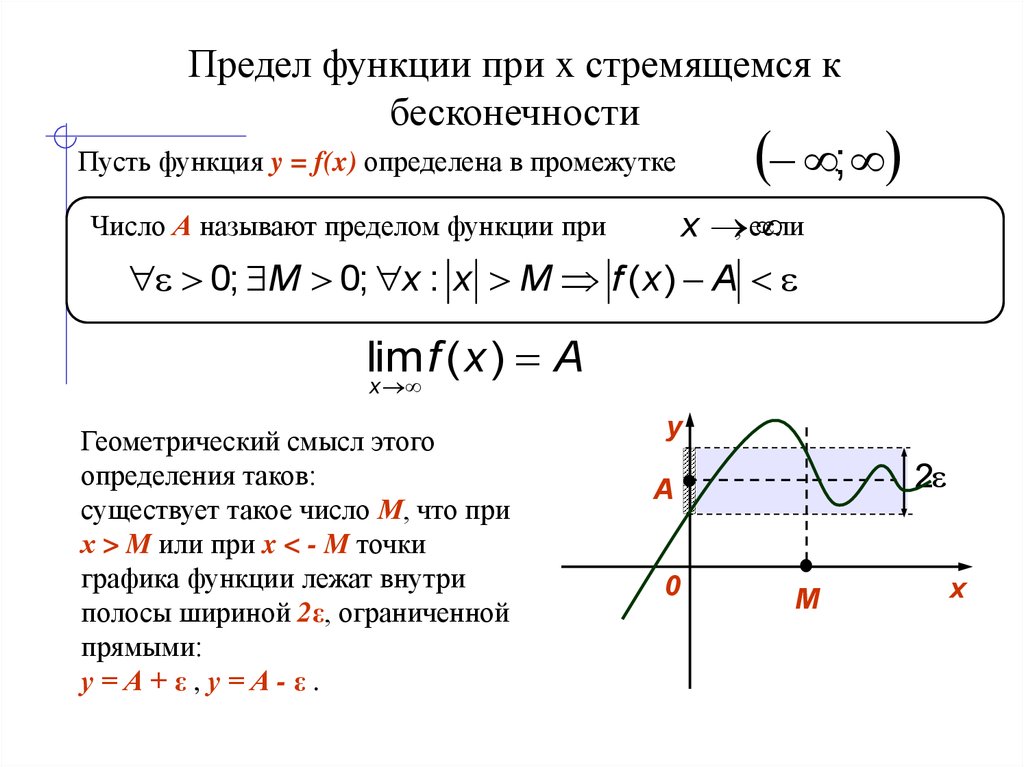 1).
1). На самом деле предел $\lim_{x\to \infty}f(x)$ даже не должен существовать . См. примечание ЗДЕСЬ, в котором упоминается интересующий случай.
На самом деле предел $\lim_{x\to \infty}f(x)$ даже не должен существовать . См. примечание ЗДЕСЬ, в котором упоминается интересующий случай.