| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | сфера (4) | | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | ||
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | 3/9 | ||
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Узнаем как найти радиус окружности: в помощь школьникам
Как найти радиус окружности? Этот вопрос всегда актуален для школьников, изучающих планиметрию.
Ниже мы рассмотрим несколько примеров того, как можно справиться с поставленной задачей.
В зависимости от условия задачи радиус окружности вы можете найти так.
Формула 1: R = Л / 2π, где Л – это длина окружности, а π – константа, равная 3,141…
Формула 2: R = √( S / π), где S – это величина площади круга.
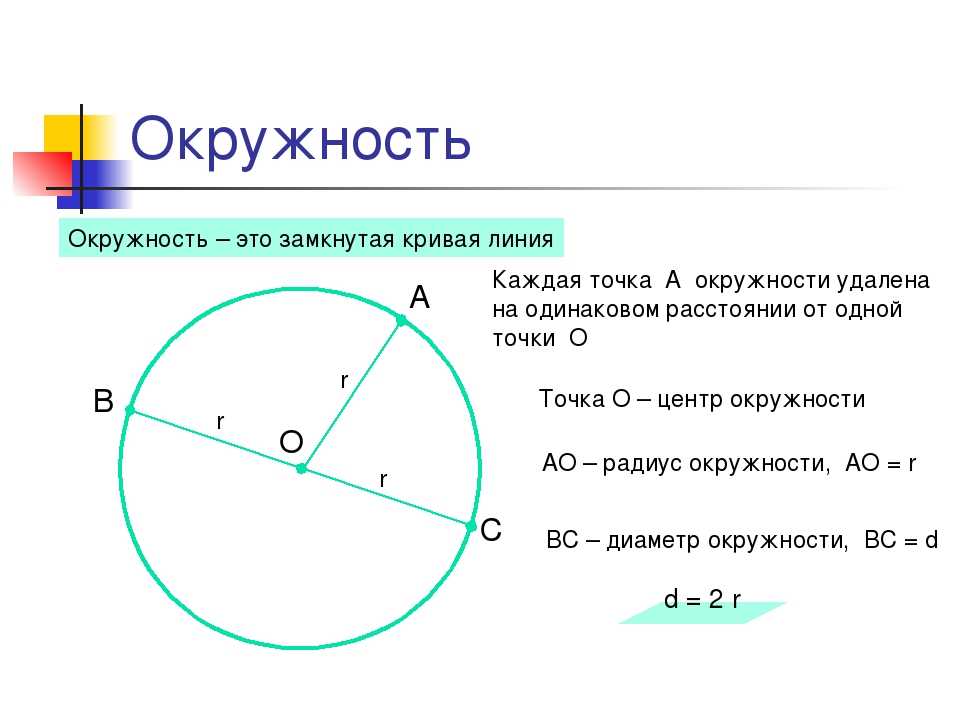
Формула 3: R = Д/2, где Д – это диаметр окружности, то есть длина того отрезка, который, проходя через центр фигуры, соединяет две максимально удаленные друг от друга точки.
Как найти радиус описанной окружности
Сначала давайте определимся с самим термином. Окружность называется описанной тогда, когда она касается всех вершин заданного многоугольника. При этом следует заметить, что описать окружность можно только вокруг такого многоугольника, стороны и углы которого между собой равны, то есть вокруг равностороннего треугольника, квадрата, правильного ромба и т.п. Для решения поставленной задачи необходимо найти периметр многоугольника, а также вымерить его стороны и площадь.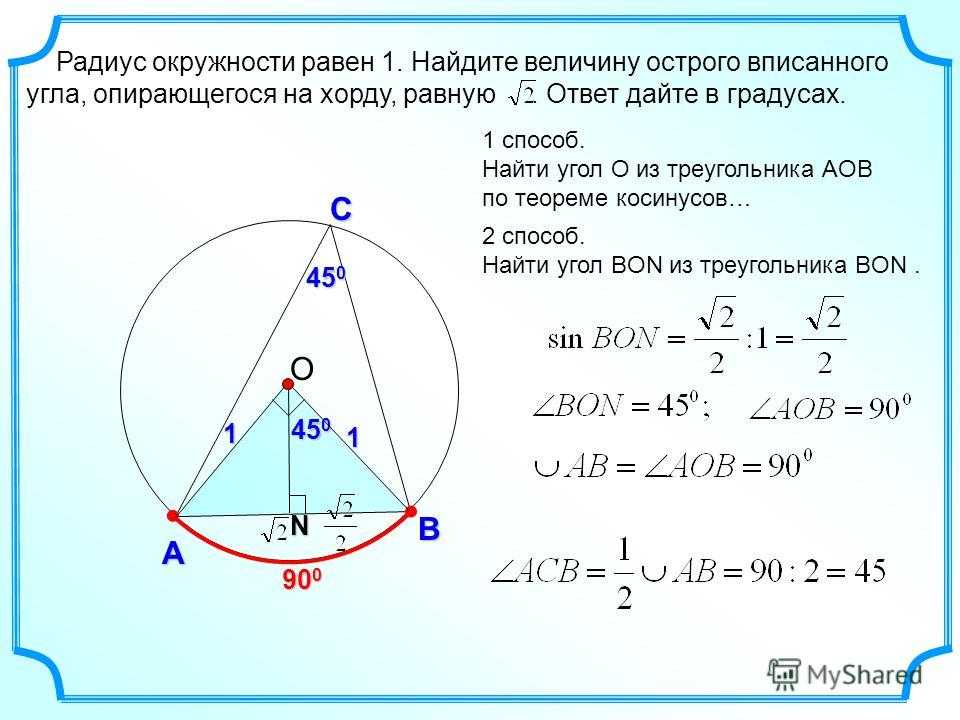
Поэтому вооружитесь линейкой, циркулем, калькулятором и тетрадкой с ручкой.
Как найти радиус окружности, если она описана вокруг треугольника
Формула 1: R = (А*Б*В) / 4S, где А, Б, В – длины сторон треугольника, а S – его площадь.
Формула 2: R = А / sin а, где А – длина одной из сторон фигуры, а sin а – высчитанное значение синуса противолежащего этой стороне угла.
Радиус окружности, которая описана вокруг прямоугольного треугольника.
Формула 1: R = В/2, где В – гипотенуза.
Формула 2: R = М*В, где В – гипотенуза, а М – медиана, проведенная к ней.
Как найти радиус окружности, если она описана вокруг правильного многоугольника
Формула: R = А / (2 * sin (360/(2*n))), где А – длина одной из сторон фигуры, а n – количество сторон в данной геометрической фигуре.
Как найти радиус вписанной окружности
Вписанной окружность называется тогда, когда она касается всех сторон многоугольника. Рассмотрим несколько примеров.
Формула 1: R = S / (Р/2), где – S и Р – площадь и периметр фигуры соответственно.
Формула 2: R = (Р/2 — А) * tg (а/2), где Р – периметр, А – длина одной из сторон, а – противолежащий этой стороне угол.
Как найти радиус окружности, если она вписана в прямоугольный треугольник
Формула 1:
Радиус окружности, которая вписана в ромб
Окружность можно вписать в любой ромб, как равносторонний, так и неравносторонний.
Формула 1: R = 2 * Н, где Н – это высота геометрической фигуры.
Формула 2: R = S / (А*2), где S – это площадь ромба, а А – длина его стороны.
Формула 3: R = √((S * sin А)/4), где S – это площадь ромба, а sin А – синус острого угла данной геометрической фигуры.
Формула 4: R = В*Г/(√(В² + Г²), где В и Г – это длины диагоналей геометрической фигуры.
Формула 5: R = В*sin (А/2), где В – диагональ ромба, а А – это угол в вершинах, соединяющих диагональ.
Радиус окружности, которая вписана в треугольник
В том случае, если в условии задачи вам даны длины всех сторон фигуры, то сначала высчитайте периметр треугольника (П), а затем полупериметр (п):
П = А+Б+В, где А, Б, В – длин сторон геометрической фигуры.
п = П/2.
Формула 1: R = √((п-А)*(п-Б)*(п-В)/п).
А если, зная все те же три стороны, вам дана еще и площадь фигуры, то можете рассчитать искомый радиус следующим образом.
Формула 2: R = S * 2(А + Б + В)
Формула 3: R = S/п = S / ( А+Б+В)/2), где – п – это полупериметр геометрической фигуры.
Формула 4: R = (п — А) * tg (А/2), где п – это полупериметр треугольника, А – одна из его сторон, а tg (А/2) – тангенс половины противолежащего этой стороне угла.
А ниже приведенная формула поможет отыскать радиус той окружности, которая вписана в равносторонний треугольник.
Формула 5: R =А * √3/6.
Радиус окружности, которая вписана в прямоугольный треугольник
Если в задаче даны длины катетов, а также гипотенуза, то радиус вписанной окружности узнается так.
Формула 1: R = (А+Б-С)/2, где А, Б – катеты, С – гипотенуза.
В том случае, если вам даны только два катета, самое время вспомнить теорему Пифагора, чтобы гипотенузу найти и воспользоваться вышеприведенной формулой.
С = √(А²+Б²).
Радиус окружности, которая вписана в квадрат
Окружность, которая вписана в квадрат, делит все его 4 стороны ровно пополам в точках касания.
Формула 1: R = А/2, где А – длина стороны квадрата.
Формула 2: R = S / (Р/2), где S и Р – площадь и периметр квадрата соответственно.
Нахождение длины окружности — Криста Кинг Математика
Формула длины окружности
Помните, что радиусом окружности является длина от ее центра до точки на окружности,
и что диаметр представляет собой особую хорду, проходящую через центр окружности. Диаметр всегда состоит из двух радиусов, так что ???d=2r???.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
И ???\пи??? это специальное число, ???\pi \приблизительно 3,14???, которое описывает соотношение между длиной окружности круга и длиной его диаметра.
Длина окружности – это расстояние по окружности (ее периметру), равное ???2???, умноженному на ???\pi??? и радиус, или просто ???\pi??? раз больше диаметра.
???C=2\pi r???
???С=\pi д???
Нахождение длины окружности по радиусу или диаметру
Пройти курс
Хотите узнать больше о геометрии? У меня есть пошаговый курс для этого. 🙂
Учить больше
Нахождение длины окружности по диаметру окружности
Пример
Какова длина окружности диаметром ???10\text{ дюймов}????
Формула для длины окружности, если мы знаем диаметр окружности: ???C=\pi d???. Мы знаем, что диаметр круга равен ???10\text{in}??? поэтому, когда мы подставляем это в формулу, мы получаем
???C=\pi \cdot 10???
???C=10\pi \text{in}???
???C\примерно 10(3.
14)\текст{in}???
???C\примерно 31,4\текст{in}???
Иногда вас могут попросить найти длину окружности части круга.
Длина окружности — это расстояние по окружности,
Нахождение длины окружности четверти окружности
Пример
Какова с точностью до сотых длина окружности дуги этой четверти окружности?
Формула для длины окружности, если известен радиус ???C=2\pi r???, а радиус равен ???7??? футов, поэтому длина окружности равна
???C=2\pi (7)\text{ футов}???
???C=14\pi \text{ футов}???
Это полная окружность, поэтому нам нужно разделить эту окружность на ???4??? найти длину дуги.
???\frac{C}{4}=\frac{14\pi \text{ футов}}{4}=3,5\pi \text{ футов}???
Обратите внимание, если бы нас попросили найти периметр фигуры, нам нужно было бы добавить длины радиусов к этой части окружности. Периметр будет
???P\приблизительно 10,99\текст{ футов} + 7 \текст{ футов}+7\текст{ футов}???
???P\приблизительно 24,99\текст {фут}???
Получить доступ к полному курсу геометрии
Начать
Учим математикуКриста Кинг математика, выучить онлайн, онлайн курс, онлайн математика, геометрия, окружность, длина окружности, окружность, радиус окружности, диаметр окружности, радиус, диаметр, дуга окружности , окружность четверти окружности, окружность полукруга, четверть окружности, полуокружность
0 лайковКак рассчитать и решить для периметра или длины окружности, радиуса и диаметра круга | The Calculator Encyclopedia
Изображение выше представляет собой круг.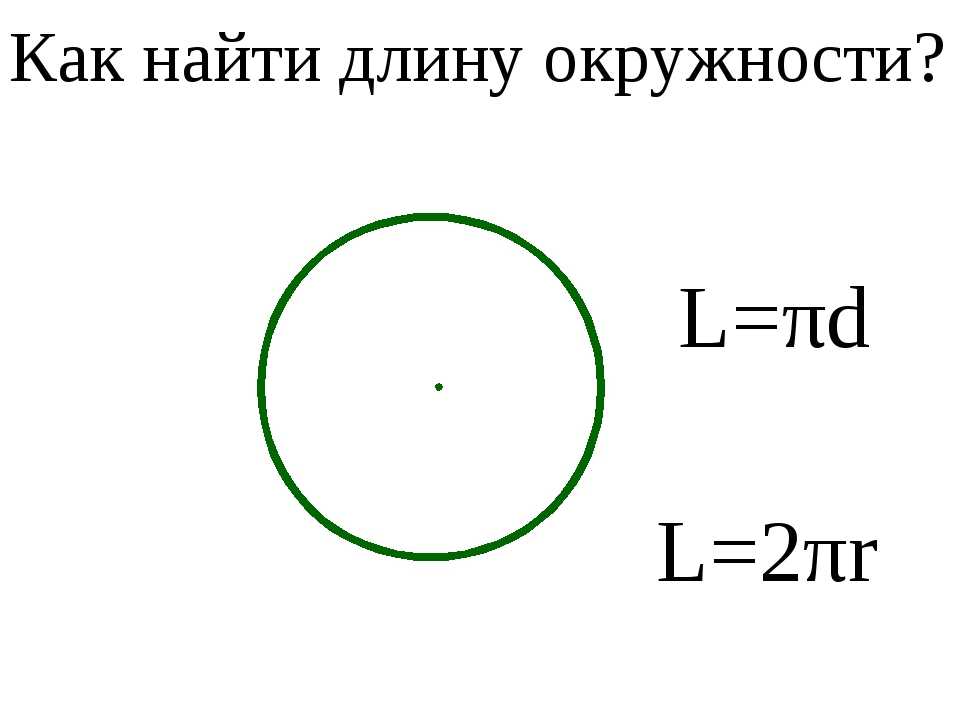
Чтобы вычислить периметр или длину окружности, необходим один важный параметр, а именно радиус окружности (r). Вы также можете использовать диаметр круга для вычисления площади круга (d).
Формула для расчета периметра или длины окружности:
P = 2πr
Где:
P = периметр или длина окружности
r = радиус окружности
Давайте решим пример:
Найдите периметр или длину окружности, где радиус окружности равен 8 см.
Это означает, что;
r = радиус круга = 8 см
P = 2πr
P = 2 x 3,142 x 8
P = 50,265
Следовательно, периметр или длина окружности составляет 50,265 см.
Вычисление площади круга с использованием диаметра круга.
Формула: P = πd
Где:
P = периметр или длина окружности
Давайте решим пример:
Найдите периметр или длину окружности, где диаметр круг 10 см.
Это означает, что;
d = диаметр круга = 10 см
P = πd
P = 3,142 x 10
P = 31,42
Следовательно, периметр или длина окружности с диаметром 31,42 см.
Как рассчитать радиус окружности, зная периметр или длину окружности
r = P / 2π
где;
r = радиус круга
P = периметр или длина окружности
Давайте решим пример:
Найдите радиус окружности, где периметр или длина окружности составляет 16 см.
Это означает, что;
P = периметр или окружность круга = 16 см
R = P / 2π
R = 16 / 6.284
R = 2,55
Следовательно, RAD15 RADIIM 9005. 2,55 см.
Как рассчитать диаметр окружности, зная периметр или длину окружности
d = P / π
где;
d = Диаметр окружности
P = периметр или длина окружности
Давайте решим пример;
Найдите диаметр круга, если периметр или длина окружности равны 20 см
Отсюда следует, что;
P = периметр или окружность круга = 20 см
D = P / π
D = 20 / π
D = 6,365
.
Следовательно, диаметм
D = 6,365
, диаметром
. 6,365 см.
Никзом Калькулятор – Энциклопедия калькулятора способна вычислить периметр или длину окружности.
Чтобы получить ответ и вычисления периметра или окружности круга, используйте Калькулятор Никзома – Энциклопедия калькуляторов. Во-первых, вам нужно получить приложение.
Вы можете получить это приложение любым из следующих способов:
Через Интернет – https://www.nickzom.org/calculator-plus
Чтобы получить доступ к профессиональной версии через Интернет, вам необходимо зарегистрируйте и подпишитесь на 1500 NGN на в год , чтобы иметь полный доступ ко всем функциям.
Вы также можете попробовать демо-версию через https://www.nickzom.org/calculator
Android (платная) – https://play.
google.com/store/apps/details?id=org .nickzom.nickzomcalculator
Android (бесплатно)
Apple (платно) – https://itunes.apple .com/us/app/nickzom-calculator/id1331162702?mt=8
Однажды, вы получили приложение Encyclopedia Calculator, перейдите к карте калькулятора , а затем нажмите на Mensuration под математикой Раздел
Теперь нажмите на Периметр 669
, нажмите Периметр 666. Измерение
На приведенном ниже снимке экрана показана страница или действие для ввода вашего значения, чтобы получить ответ для периметра или окружности круга в соответствии с соответствующим параметром, который является радиусом круга (r).
Теперь введите соответствующее значение для параметра, как того требует пример выше, где радиус окружности равен 8 см.