Проекция точки на прямую
|
|
|
|||||||||||||||||||||||||||||
Найти проекцию вектора онлайн калькулятор. Калькулятор онлайн.Вычисление проекции вектора на вектор
а на ось или какой-либо другой вектор существуют понятия ее геометрической проекции и числовой (или алгебраической) проекции. Результатом геометрической проекции будет вектор, а результатом алгебраической – неотрицательное действительное число. Но перед тем, как перейти к этим понятиям вспомним необходимую информацию.
Но перед тем, как перейти к этим понятиям вспомним необходимую информацию.
Предварительные сведения
Основное понятие – непосредственно понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.
Определение 2Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $\overline{a}$ (рис. 1).
Введем еще несколько понятий, связанных с понятием вектора.
Определение 3
Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой или на прямых, параллельных друг другу (рис. 2).
2).
Определение 4
Два ненулевых вектора будем называть сонаправленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они будут направлены в одну сторону (рис. 3).
Обозначение: $\overline{a}\overline{b}$
Определение 5
Два ненулевых вектора будем называть противоположно направленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они направлены в разные стороны (рис. 4).
Обозначение: $\overline{a}↓\overline{d}$
Определение 6
Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|\overline{a}|$
Перейдем к определению равенства двух векторов
Определение 7
Два вектора будем называть равными, если они удовлетворяют двух условиям:
- Они сонаправлены;
- Их длины равны (рис. 5).
Геометрическая проекция
Как мы уже сказали ранее, результатом геометрической проекции будет вектор.
Определение 8
Геометрической проекцией вектора $\overline{AB}$ на ось будем называть такой вектор, который получается следующим образом: Точка начала вектора $A$ проецируется на данную ось. Получаем точку $A»$ — начало искомого вектора. Точка конца вектора $B$ проецируется на данную ось. Получаем точку $B»$ — конец искомого вектора. Вектор $\overline{A»B»}$ и будет искомым вектором.
Рассмотрим задачу:
Пример 1
Постройте геометрическую проекцию $\overline{AB}$ на ось $l$, изображенные на рисунке 6.
Проведем из точки $A$ перпендикуляр к оси $l$, получим на ней точку $A»$. Далее проведем из точки $B$ перпендикуляр к оси $l$, получим на ней точку $B»$ (рис. 7).
Введение…………………………………………………………………………3
1. Значение вектора и скаляра………………………………………….4
2. Определение проекции, оси и координатой точки…………………5
3. Проекция вектора на ось………………………………………………6
4. Основная формула векторной алгебры……………………………. .8
.8
5. Вычисление модуля вектора по его проекциям……………………9
Заключение………………………………………………………………………11
Литература………………………………………………………………………12
Введение:
Физика неразрывно связана с математикой. Математика дает физике средства и приемы общего и точного выражения зависимости между физическими величинами, которые открываются в результате эксперимента или теоретических исследований.Ведь основной метод исследований в физике – экспериментальный. Это значит – вычисления ученый выявляет с помощью измерений. Обозначает связь между различными физическими величинами. Затем, все переводится на язык математики. Формируется математическая модель. Физика — есть наука, изучающая простейшие и вместе с тем наиболее общие закономерности. Задача физики состоит в том, чтобы создать в нашем сознании такую картину физического мира, которая наиболее полно отражает свойства его и обеспечивает такие соотношения между элементами модели, какие существуют между элементами.
Итак, физика создает модель окружающего нас мира и изучает ее свойства. Но любая модель является ограниченной. При создании моделей того или иного явления принимаются во внимание только существенные для данного круга явлений свойства и связи. В этом и заключается искусство ученого — из всего многообразия выбрать главное.
Физические модели являются математическими, но не математика является их основой. Количественные соотношения между физическими величинами выясняются в результате измерений, наблюдений и экспериментальных исследований и лишь выражаются на языке математики. Однако другого языка для построения физических теорий не существует.
1. Значение вектора и скаляра.
В физике и математике вектор — это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей. Их можно противопоставить другим величинам, таким, как масса, объем, давление, температура и плотность, которые можно описать обычным числом, и называются они «скалярами» .
Их можно противопоставить другим величинам, таким, как масса, объем, давление, температура и плотность, которые можно описать обычным числом, и называются они «скалярами» .
Они записываются либо буквами обычного шрифта, либо цифрами (а, б, t, G, 5, −7….). Скалярные величины могут быть положительными и отрицательными. В то же время некоторые объекты изучения могут обладать такими свойствами, для полного описания которых знание только числовой меры оказывается недостаточным, необходимо ещё охарактеризовать эти свойства направлением в пространстве. Такие свойства характеризуются векторными величинами (векторами). Векторы, в отличие от скаляров, обозначаются буквами жирного шрифта: a, b, g, F, С ….
Нередко вектор обозначают буквой обычного (нежирного) шрифта, но со стрелкой над ней:
Кроме того, часто вектор обозначают парой букв (обычно заглавных), причём первая буква обозначает начало вектора, а вторая — его конец.
Модуль вектора, то есть длину направленного прямолинейного отрезка, обозначают теми же буквами, как и сам вектор, но в обычном (не жирном) написании и без стрелки над ними, либо точно также как и вектор (то есть жирным шрифтом или обычным, но со стрелкой), но тогда обозначение вектора заключается в вертикальные черточки.
Вектор – сложный объект, который одновременно характеризуется и величиной и направлением.
Не бывает также положительных и отрицательных векторов. А вот равными между собой векторы быть могут. Это когда, например, aиb имеют одинаковые модули и направлены в одну сторону. В этом случае справедлива запись a = b. Надо также иметь в виду, что перед символом вектора может стоять знак минус, например, — с, однако, этот знак символически указывает на то, что вектор -с имеет такой же модуль, как и вектор с, но направлен в противоположную сторону.
Вектор -с называют противоположным (или обратным) вектору с.
В физике же каждый вектор наполнен конкретным содержанием и при сравнении однотипных векторов (например, сил) могут иметь существенное значение и точки их приложения.
2.Определение проекции, оси и координатой точки.
Ось – это прямая, которой придается какое–то направление.
Ось обозначается какой-либо буквой: X , Y , Z , s , t … Обычно на оси выбирается (произвольно) точка, которая называется началом отсчета и, как правило, обозначается буквой О. От этой точки отсчитываются расстояния до других интересующих нас точек.
От этой точки отсчитываются расстояния до других интересующих нас точек.
Проекцией точки на ось называется основание перпендикуляра, опущенного из этой точки на данную ось. То есть, проекцией точки на ось является точка.
Координатой точки на данной оси называется число, абсолютная величина которого равна длине отрезка оси (в выбранном масштабе), заключённого между началом оси и проекцией точки на эту ось. Это число берется со знаком плюс, если проекция точки располагается в направлении оси от ее начала и со знаком минус, если в противоположном направлении.
3.Проекция вектора на ось.
Проекцией вектора на ось называется вектор, который получается в результате перемножения скалярной проекции вектора на эту ось и единичного вектора этой оси. Например, если а x – скалярная проекция вектора а на ось X, то а x ·i — его векторная проекция на эту ось.
Обозначим векторную проекцию также, как и сам вектор, но с индексом той оси на которую вектор проектируется. Так, векторную проекцию вектора а на ось Х обозначим а x
(жирная буква, обозначающая вектор и нижний индекс названия оси) или
Так, векторную проекцию вектора а на ось Х обозначим а x
(жирная буква, обозначающая вектор и нижний индекс названия оси) или
(нежирная буква, обозначающая вектор, но со стрелкой наверху (!) и нижний индекс названия оси).
Скалярной проекцией вектора на ось называется число , абсолютная величина которого равна длине отрезка оси (в выбранном масштабе), заключённого между проекциями точки начала и точки конца вектора. Обычно вместо выражения скалярная проекция говорят просто – проекция . Проекция обозначается той же буквой, что и проектируемый вектор (в обычном, нежирном написании), с нижним (как правило) индексом названия оси, на которую этот вектор проектируется. Например, если на ось Х проектируется вектора, то его проекция обозначается а x . При проектировании этого же вектора на другую ось, если ось Y , его проекция будет обозначаться а y .
Чтобы вычислить проекцию вектора на ось (например, ось X) надо из координаты точки его конца вычесть координату точки начала, то есть
а x
= х к
− x н.
Проекция вектора на ось — это число. Причем, проекция может быть положительной, если величина х к больше величины х н,
отрицательной, если величина х к меньше величины х н
и равной нулю, если х к равно х н.
Проекцию вектора на ось можно также найти, зная модуль вектора и угол, который он составляет с этой осью.
Из рисунка видно, что а x = а Cos α
То есть, проекция вектора на ось равна произведению модуля вектора на косинус угла между направлением оси и направлением вектора . Если угол острый, то
Cos α > 0 и а x
> 0, а, если тупой, то косинус тупого угла отрицателен, и проекция вектора на ось тоже будет отрицательна.
Углы, отсчитываемые от оси против хода часовой стрелки, принято считать положительными, а по ходу — отрицательными. Однако, поскольку косинус – функция четная, то есть, Cos α = Cos (− α), то при вычислении проекций углы можно отсчитывать как по ходу часовой стрелки, так и против.
Чтобы найти проекцию вектора на ось надо модуль этого вектора умножить на косинус угла между направлением оси и направлением вектора.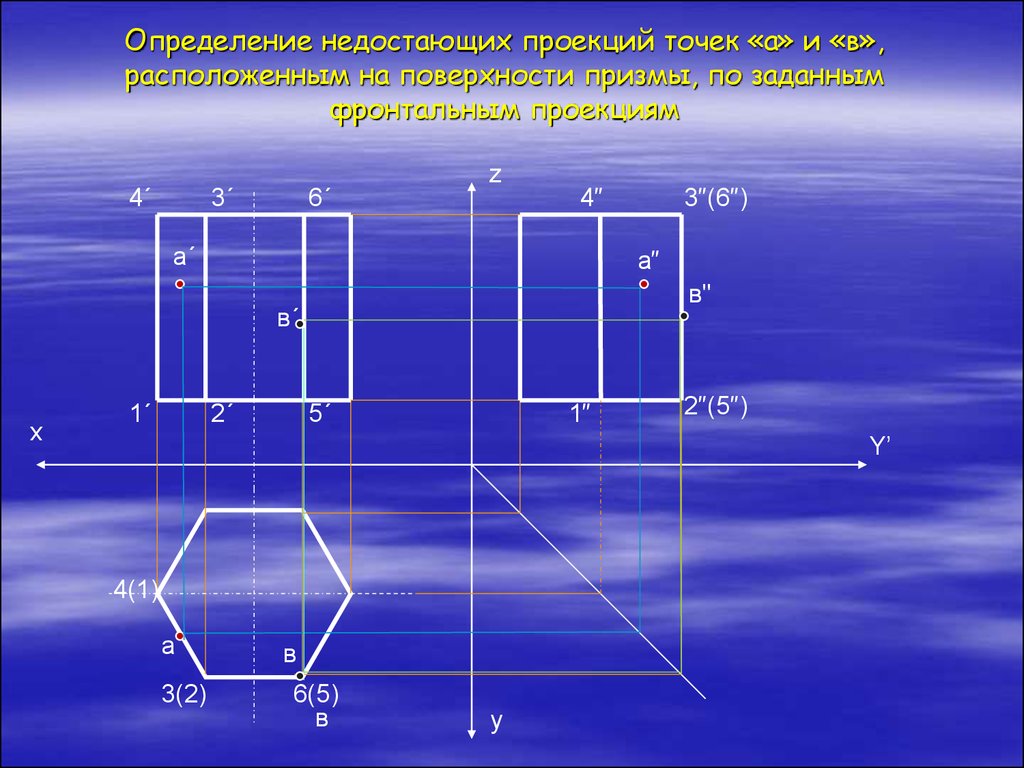
4. Основная формула векторной алгебры.
Спроектируемвектор а на оси Х и Y прямоугольной системы координат. Найдем векторные проекции вектора а на эти оси:
а x = а x ·i, а y = а y ·j.
Но в соответствии справилом сложения векторов
а = а x + а y .
а = а x ·i + а y ·j.
Таким образом, мы выразили вектор через его проекции и орты прямоугольной системы координат (или через его векторные проекции).
Векторные проекции а x и а y называютсясоставляющими или компонентами вектора а. Операция, которую мы выполнили, называется разложением вектора по осямпрямоугольной системы координат.
Если вектор задан в пространстве, то
а = а x ·i + а y ·j + а z ·k.
Эта формула называется основной формулой векторной алгебры. Конечно, ее можно записать и так.
Пусть в пространстве даны два вектора и . Отложим от произвольной точки O векторы и . Углом между векторами и называется наименьший из углов . Обозначается .
Рассмотрим ось l и отложим на ней единичный вектор (т.е. вектор, длина которого равна единице).
Под углом между вектором и осью l понимают угол между векторами и .
Итак, пусть l – некоторая ось и – вектор.
Обозначим через A 1 и B 1 проекции на ось l соответственно точек A и B . Предположим, что A 1 имеет координату x 1 , а B 1 – координату x 2 на оси l .
Тогда проекцией вектора на ось l называется разность x 1 – x 2 между координатами проекций конца и начала вектора на эту ось.
Проекцию вектора на ось l будем обозначать .
Ясно, что если угол между вектором и осью l острый, то x 2 > x 1 , и проекция x 2 – x 1 > 0; если этот угол тупой, то x 2 x 1
и проекция x 2 – x 1 l
, то x 2 = x 1 и x 2 – x 1 =0.
Таким образом, проекция вектора на ось l – это длина отрезка A 1 B 1 , взятая с определённым знаком. Следовательно, проекция вектора на ось это число или скаляр.
Аналогично определяется проекция одного вектора на другой. В этом случае находятся проекции концов даного вектора на ту прямую, на которой лежит 2-ой вектор.
Рассмотрим некоторые основные свойства проекций .
ЛИНЕЙНО ЗАВИСИМЫЕ И ЛИНЕЙНО НЕЗАВИСИМЫЕ СИСТЕМЫ ВЕКТОРОВ
Рассмотрим несколько векторов .
Линейной комбинацией данных векторов называется любой вектор вида , где — некоторые числа. Числа называются коэффициентами линейной комбинации. Говорят также, что в этом случае линейно выражается через данные векторы , т.е. получается из них с помощью линейных действий.
Например, если даны три вектора то в качестве их линейной комбинации можно рассматривать векторы:
Если вектор представлен как линейная комбинация каких-то векторов, то
говорят, что он разложен по этим
векторам.
Векторы называются линейно зависимыми , если существуют такие числа, не все равные нулю, что . Ясно, что заданные векторы будут линейно зависимыми, если какой-либо из этих векторов линейно выражается через остальные.
В противном случае, т.е. когда соотношение выполняется только при , эти векторы называются линейно независимыми .
Теорема 1. Любые два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
Доказательство :
Аналогично можно доказать следующую теорему.
Теорема 2. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.
Доказательство .
БАЗИС
Базисом называется совокупность отличных от нулей линейно независимых векторов. Элементы базиса будем обозначать .
В предыдущем пункте мы видели, что два неколлинеарных вектора на
плоскости линейно независимы. Поэтому согласно теореме 1, из предыдущего
пункта, базисом на плоскости являются любые два неколлинеарных вектора на этой
плоскости.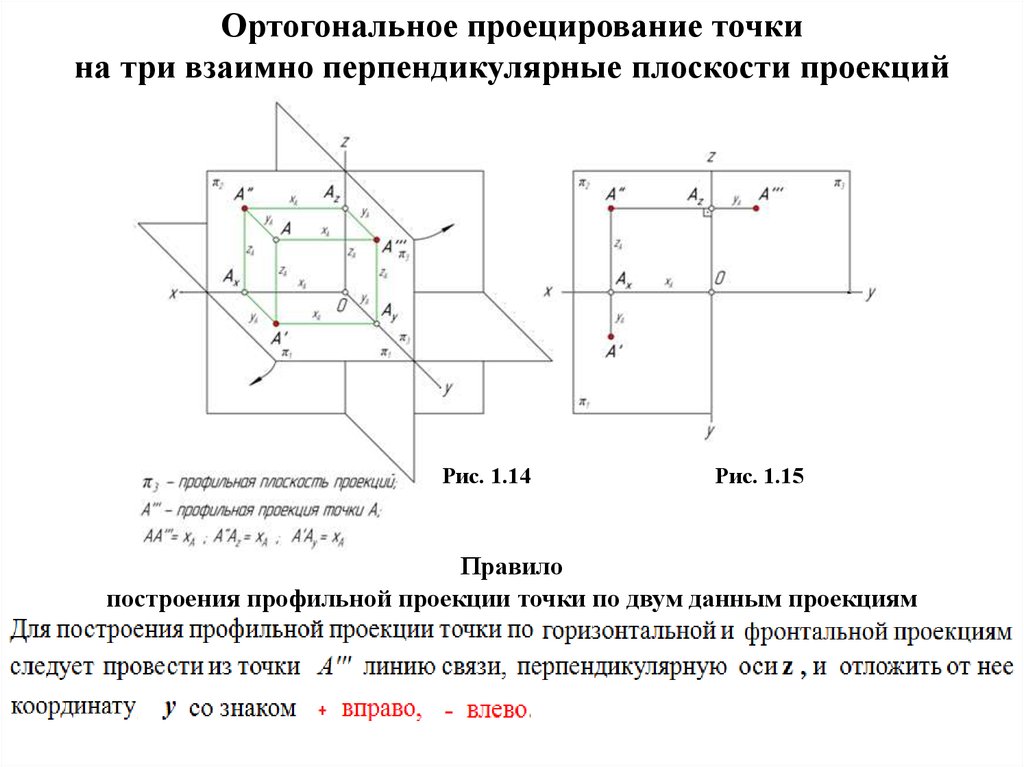
Аналогично в пространстве линейно независимы любые три некомпланарных вектора. Следовательно, базисом в пространстве назовём три некомпланарных вектора.
Справедливо следующее утверждение.
Теорема. Пусть в пространстве задан базис . Тогда любой вектор можно представить в виде линейной комбинации , где x , y , z – некоторые числа. Такое разложение единственно.
Доказательство .
Таким образом, базис позволяет однозначно сопоставить каждому вектору тройку чисел – коэффициенты разложения этого вектора по векторам базиса: . Верно и обратное, каждой тройке чисел x, y, z при помощи базиса можно сопоставить вектор, если составить линейную комбинацию .
Если базис и , то числа x, y, z называются координатами вектора в данном базисе. Координаты вектора обозначают .
ДЕКАРТОВА СИСТЕМА КООРДИНАТ
Пусть в пространстве задана точка O и три некомпланарных вектора .
Декартовой системой координат в пространстве (на плоскости) называется совокупность точки и базиса, т. е.
совокупность точки и трёх некомпланарных векторов (2-х неколлинеарных векторов), выходящих из этой точки.
е.
совокупность точки и трёх некомпланарных векторов (2-х неколлинеарных векторов), выходящих из этой точки.
Точка O называется началом координат; прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат – осью абсцисс, ординат и аппликат. Плоскости, проходящие через оси координат, называют координатными плоскостями.
Рассмотрим в выбранной системе координат произвольную точку M . Введём понятие координаты точки M . Вектор , соединяющий начало координат с точкой M . называется радиус-вектором точки M .
Вектору в выбранном базисе можно сопоставить тройку чисел – его координаты: .
Координаты радиус-вектора точки M . называются координатами точки M . в рассматриваемой системе координат. M(x,y,z) . Первая координата называется абсциссой, вторая – ординатой, третья – аппликатой.
Аналогично определяются декартовы координаты на плоскости.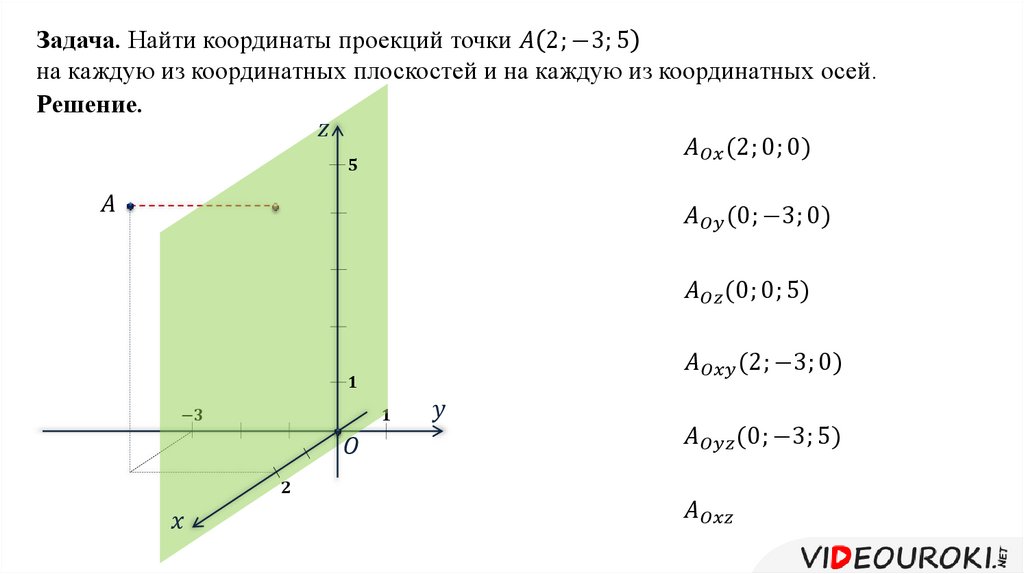 Здесь точка имеет только две координаты – абсциссу и ординату.
Здесь точка имеет только две координаты – абсциссу и ординату.
Легко видеть, что при заданной системе координат каждая точка имеет определённые координаты. С другой стороны, для каждой тройки чисел найдётся единственная точка, имеющая эти числа в качестве координат.
Если векторы, взятые в качестве базиса, в выбранной системе координат, имеют единичную длину и попарно перпендикулярны, то система координат называется декартовой прямоугольной.
Несложно показать, что .
Направляющие косинусы вектора полностью определяют его направление, но ничего не говорят о его длине.
Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:
Пр a b = |b|cos(a,b) или
Где a b — скалярное произведение векторов , |a| — модуль вектора a .
Инструкция
. Для нахождения проекции вектора Пp a b в онлайн режиме необходимо указать координаты векторов a и b .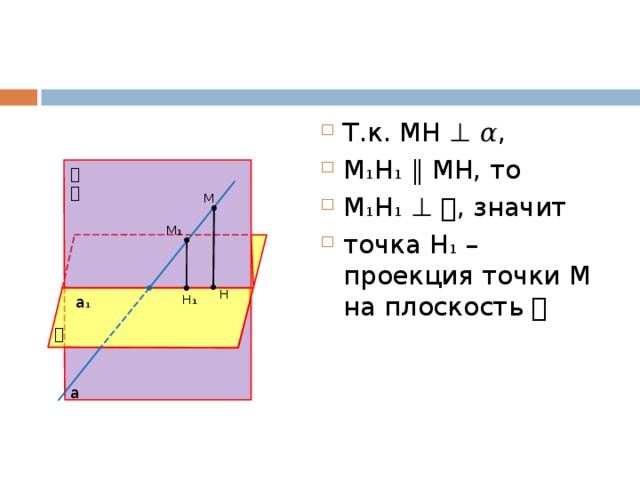 При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word
. Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор .
При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word
. Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор .
две координаты вектора
три координаты вектора
a: ; ;
b: ; ;
Классификация проекций вектора
Виды проекций по определению проекция вектора
Виды проекций по системе координат
Свойства проекции вектора
- Геометрическая проекция вектора есть вектор (имеет направление).
- Алгебраическая проекция вектора есть число.
Теоремы о проекциях вектора
Теорема 1 . Проекция суммы векторов на какую-либо ось равна проекции слагаемых векторов на ту же ось.
Теорема 2 . Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:
Пр a b = |b|cos(a,b)
Виды проекций вектора
- проекция на ось OX.

- проекция на ось OY.
- проекция на вектор.
| Проекция на ось OX | Проекция на ось OY | Проекция на вектор |
| Если направление вектора A’B’ совпадает с направлением оси OX, то проекция вектора A’B’ имеет положительный знак. | Если направление вектора A’B’ совпадает с направлением оси OY, то проекция вектора A’B’ имеет положительный знак. | Если направление вектора A’B’ совпадает с направлением вектора NM, то проекция вектора A’B’ имеет положительный знак. |
| Если направление вектора противоположно с направлением оси OX, то проекция вектора A’B’ имеет отрицательный знак. | Если направление вектора A’B’ противоположно с направлением оси OY, то проекция вектора A’B’ имеет отрицательный знак. | Если направление вектора A’B’ противоположно с направлением вектора NM, то проекция вектора A’B’ имеет отрицательный знак. |
Если вектор AB параллелен оси OX, то проекция вектора A’B’ равна модулю вектора AB. | Если вектор AB параллелен оси OY, то проекция вектора A’B’ равна модулю вектора AB. | Если вектор AB параллелен вектору NM, то проекция вектора A’B’ равна модулю вектора AB. |
| Если вектор AB перпендикулярен оси OX, то проекция A’B’ равна нулю (нуль-вектор). | Если вектор AB перпендикулярен оси OY, то проекция A’B’ равна нулю (нуль-вектор). | Если вектор AB перпендикулярен вектору NM, то проекция A’B’ равна нулю (нуль-вектор). |
1. Вопрос: Может ли проекция вектора иметь отрицательный знак. Ответ: Да, проекций вектора может быть отрицательной величиной. В этом случае, вектор имеет противоположное направление (см. как направлены ось OX и вектор AB)
2. Вопрос: Может ли проекция вектора совпадать с модулем вектора. Ответ: Да, может. В этом случае, векторы параллельны (или лежат на одной прямой).
3. Вопрос: Может ли проекция вектора быть равна нулю (нуль-вектор).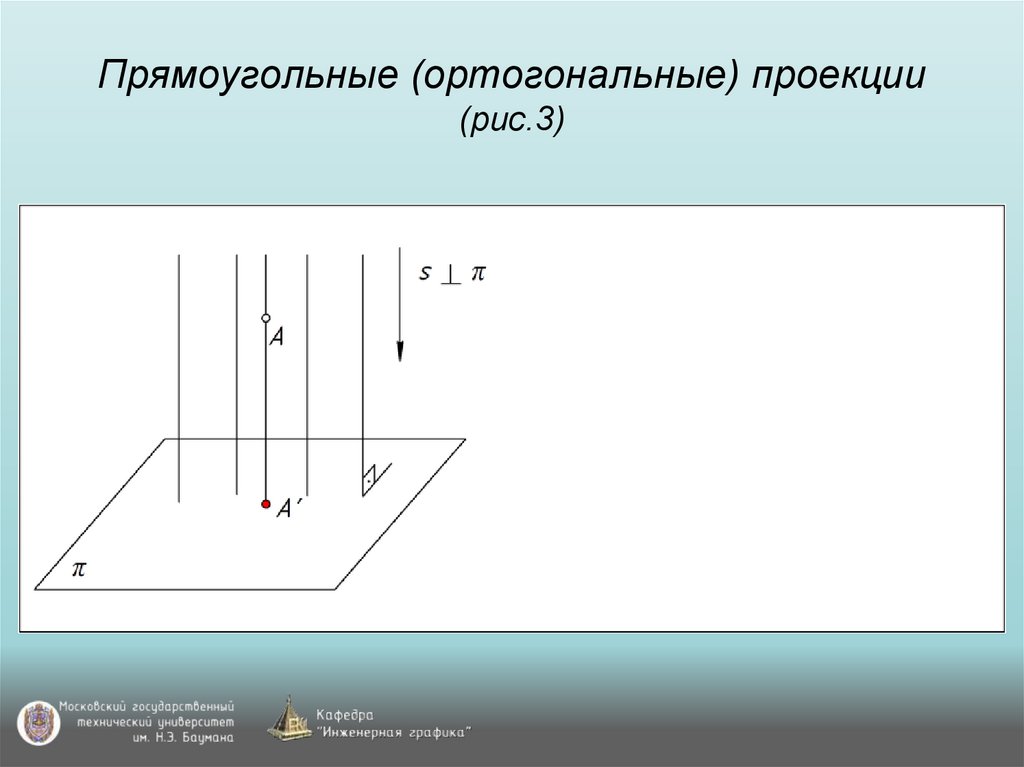 Ответ: Да, может. В этом случае вектор перпендикулярен соответствующей оси (вектору).
Ответ: Да, может. В этом случае вектор перпендикулярен соответствующей оси (вектору).
Пример 1
. Вектор (рис. 1) образует с осью OX (она задана вектором a) угол 60 о. Если OE есть единица масштаба, то |b|=4, так что .
Действительно, длина вектора (геометрической проекции b) равна 2, а направление совпадает с направлением оси OX.
Пример 2
. Вектор (рис. 2) образует с осью OX (с вектором a) угол (a,b) = 120 o . Длина |b| вектора b равна 4, поэтому пр a b=4·cos120 o = -2.
Действительно, длина вектора равна 2, а направление противоположно направлению оси.
Проектирование различных линий и поверхностей на плоскость позволяет построить наглядное изображение предметов в виде чертежа. Будем рассматривать прямоугольное проектирование, при котором проектирующие лучи перпендикулярны плоскости проекции. ПРОЕКЦИЕЙ ВЕКТОРА НА ПЛОСКОСТЬ считают вектор = (рис. 3.22), заключенный между перпендикулярами, опущенными из его начала и конца.
Рис.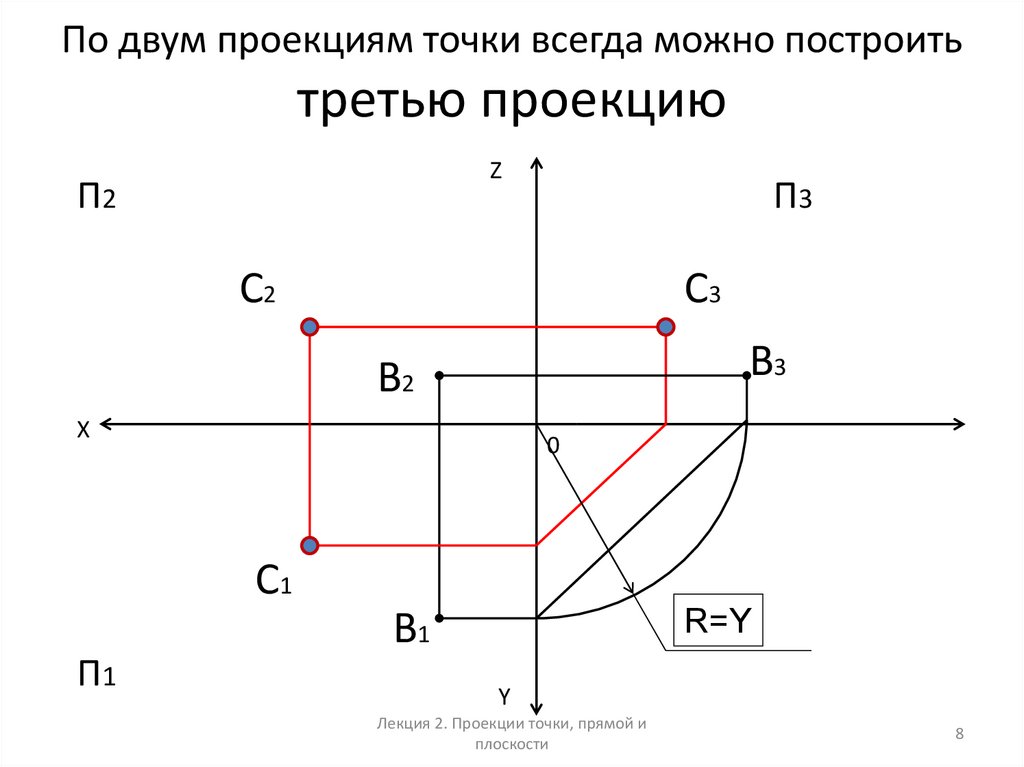 3.22. Векторная проекция вектора на плоскость.
3.22. Векторная проекция вектора на плоскость.
Рис. 3.23. Векторная проекция вектора на ось.
В векторной алгебре часто приходится проектировать вектор на ОСЬ, то есть на прямую, имеющую определенную ориентацию. Такое проектирование выполняется легко, если вектор и ось L лежат в одной плоскости (рис. 3.23). Однако задача усложняется, когда это условие не выполнено. Построим проекцию вектора на ось, когда вектор и ось не лежат в одной плоскости (рис. 3.24).
Рис. 3.24. Проектирование вектора на ось
в общем случае.
Через концы вектора проводим плоскости, перпендикулярные прямой L. В пересечении с этой прямой данные плоскости определяют две точки А1 и B1 — вектор , который будем называть векторной проекцией данного вектора. Задача нахождения векторной проекции может быть решена проще, если вектор приведен в одну плоскость с осью, что возможно осуществить, так как в векторной алгебре рассматриваются свободные векторы.
Наряду с векторной проекцией, существует и СКАЛЯРНАЯ ПРОЕКЦИЯ, которая равна модулю векторной проекции, если векторная проекция совпадает с ориентацией оси L, и равна величине, ей противоположной, если векторная проекция и ось L имеют противоположную ориентацию.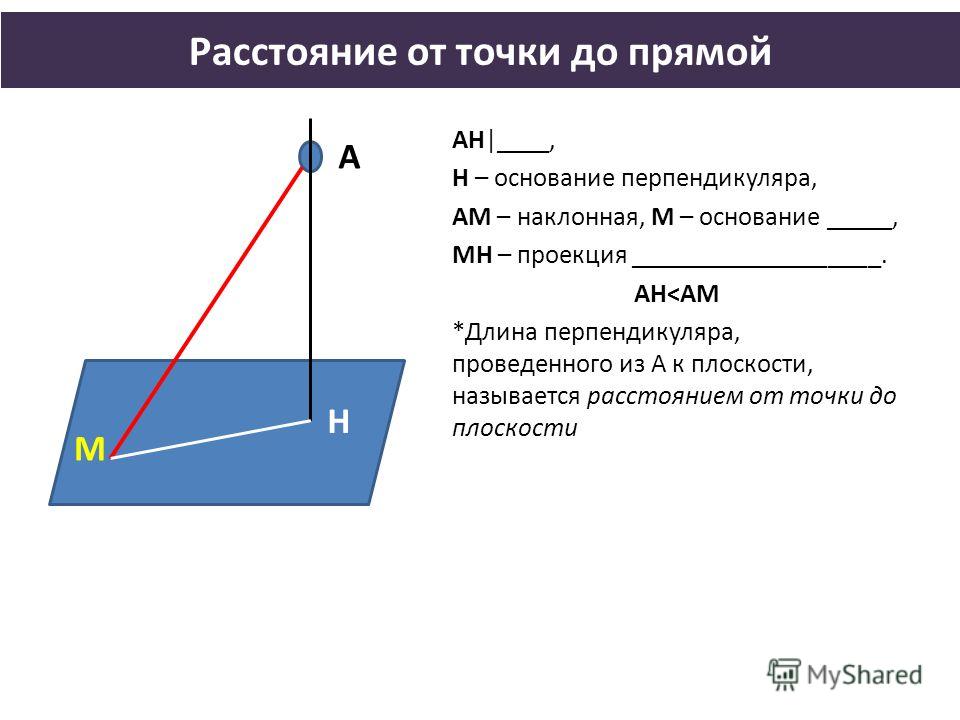 Скалярную проекцию будем обозначать:
Скалярную проекцию будем обозначать:
Векторная и скалярная проекции не всегда терминологически разделяются строго на практике. Обычно пользуются термином «проекция вектора», подразумевая под этим скалярную проекцию вектора. При решении же необходимо четко эти понятия различать. Следуя установившейся традиции, будем использовать термины «проекция вектора», подразумевая скалярную проекцию, и «векторная проекция» — в соответствии с установленным смыслом.
Докажем теорему, позволяющую вычислять скалярную проекцию заданного вектора.
ТЕОРЕМА 5. Проекция вектора на ось L равна произведению его модуля на косинус угла между вектором и осью, то есть
(3.5)
Рис. 3.25. Нахождение векторной и скалярной
Проекций вектора на ось L
( и ось L одинаково ориентированы).
ДОКАЗАТЕЛЬСТВО . Выполним предварительно построения, позволяющие найти угол G Между вектором и осью L. Для этого построим прямую MN, параллельную оси L и проходящую через точку О — начало вектора (рис. 3.25). Угол и будет искомым углом. Проведем через точки А и О две плоскости, перпендикулярные оси L. Получим:
3.25). Угол и будет искомым углом. Проведем через точки А и О две плоскости, перпендикулярные оси L. Получим:
Так как ось L и прямая MN параллельны.
Выделим два случая взаимного расположения вектора и оси L.
1. Пусть векторная проекция и ось L одинаково ориентированны (рис. 3.25). Тогда соответствующая скалярная проекция .
2. Пусть и L ориентированы в разные стороны (рис. 3.26).
Рис. 3.26. Нахождение векторной и скалярной проекций вектора на ось L ( и ось L ориентированы в противоположные стороны).
Таким образом, в обоих случаях справедливо утверждение теоремы.
ТЕОРЕМА 6. Если начало вектора приведено к некоторой точке оси L, и эта ось расположена в плоскости s, вектор образует с векторной проекцией на плоскость s угол , а с векторной проекцией на ось L — угол , кроме того сами векторные проекции образуют между собой угол , то
Как строить проекцию вектора. Калькулятор онлайн.Вычисление проекции вектора на вектор
Пусть в пространстве даны два вектора и . Отложим от произвольной точки O векторы и . Углом между векторами и называется наименьший из углов . Обозначается .
Отложим от произвольной точки O векторы и . Углом между векторами и называется наименьший из углов . Обозначается .
Рассмотрим ось l и отложим на ней единичный вектор (т.е. вектор, длина которого равна единице).
Под углом между вектором и осью l понимают угол между векторами и .
Итак, пусть l – некоторая ось и – вектор.
Обозначим через A 1 и B 1 проекции на ось l соответственно точек A и B . Предположим, что A 1 имеет координату x 1 , а B 1 – координату x 2 на оси l .
Тогда проекцией вектора на ось l называется разность x 1 – x 2 между координатами проекций конца и начала вектора на эту ось.
Проекцию вектора на ось l будем обозначать .
Ясно, что если угол между вектором и осью l острый, то x 2 > x 1 , и проекция x 2 – x 1 > 0; если этот угол тупой, то x 2 x 1
и проекция x 2 – x 1 l
, то x 2 = x 1 и x 2 – x 1 =0.
Таким образом, проекция вектора на ось l – это длина отрезка A 1 B 1 , взятая с определённым знаком. Следовательно, проекция вектора на ось это число или скаляр.
Аналогично определяется проекция одного вектора на другой. В этом случае находятся проекции концов даного вектора на ту прямую, на которой лежит 2-ой вектор.
Рассмотрим некоторые основные свойства проекций .
ЛИНЕЙНО ЗАВИСИМЫЕ И ЛИНЕЙНО НЕЗАВИСИМЫЕ СИСТЕМЫ ВЕКТОРОВ
Рассмотрим несколько векторов .
Линейной комбинацией данных векторов называется любой вектор вида , где — некоторые числа. Числа называются коэффициентами линейной комбинации. Говорят также, что в этом случае линейно выражается через данные векторы , т.е. получается из них с помощью линейных действий.
Например, если даны три вектора то в качестве их линейной комбинации можно рассматривать векторы:
Если вектор представлен как линейная комбинация каких-то векторов, то
говорят, что он разложен по этим
векторам.
Векторы называются линейно зависимыми , если существуют такие числа, не все равные нулю, что . Ясно, что заданные векторы будут линейно зависимыми, если какой-либо из этих векторов линейно выражается через остальные.
В противном случае, т.е. когда соотношение выполняется только при , эти векторы называются линейно независимыми .
Теорема 1. Любые два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
Доказательство :
Аналогично можно доказать следующую теорему.
Теорема 2. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.
Доказательство .
БАЗИС
Базисом называется совокупность отличных от нулей линейно независимых векторов. Элементы базиса будем обозначать .
В предыдущем пункте мы видели, что два неколлинеарных вектора на
плоскости линейно независимы. Поэтому согласно теореме 1, из предыдущего
пункта, базисом на плоскости являются любые два неколлинеарных вектора на этой
плоскости.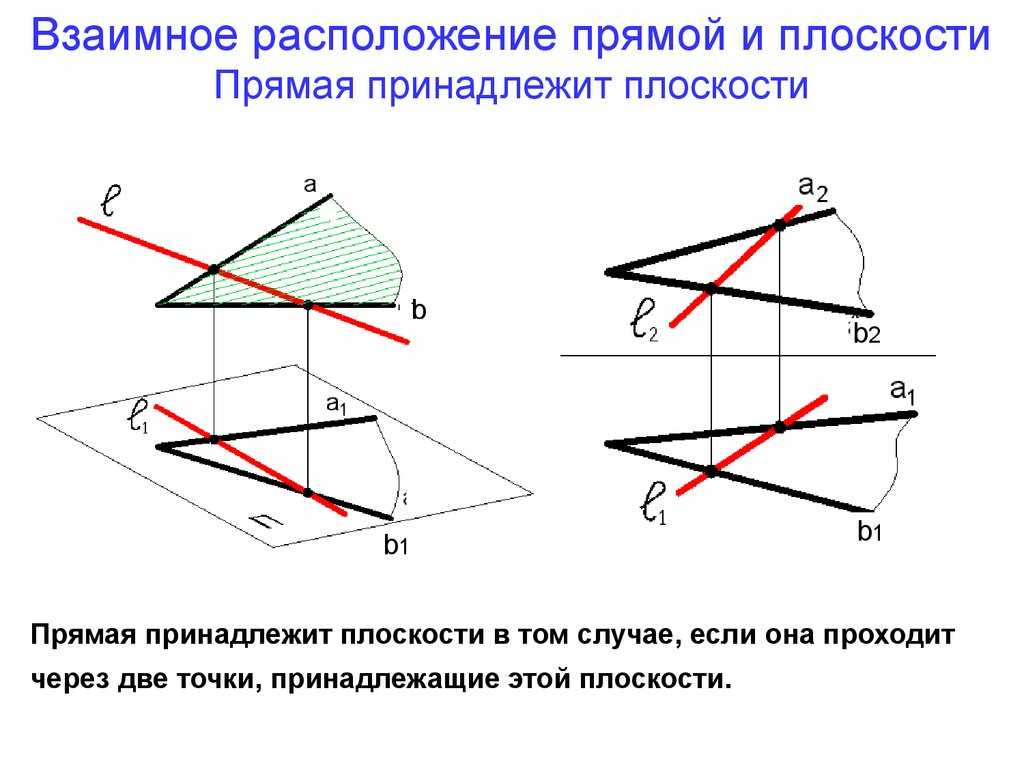
Аналогично в пространстве линейно независимы любые три некомпланарных вектора. Следовательно, базисом в пространстве назовём три некомпланарных вектора.
Справедливо следующее утверждение.
Теорема. Пусть в пространстве задан базис . Тогда любой вектор можно представить в виде линейной комбинации , где x , y , z – некоторые числа. Такое разложение единственно.
Доказательство .
Таким образом, базис позволяет однозначно сопоставить каждому вектору тройку чисел – коэффициенты разложения этого вектора по векторам базиса: . Верно и обратное, каждой тройке чисел x, y, z при помощи базиса можно сопоставить вектор, если составить линейную комбинацию .
Если базис и , то числа x, y, z называются координатами вектора в данном базисе. Координаты вектора обозначают .
ДЕКАРТОВА СИСТЕМА КООРДИНАТ
Пусть в пространстве задана точка O и три некомпланарных вектора .
Декартовой системой координат в пространстве (на плоскости) называется совокупность точки и базиса, т.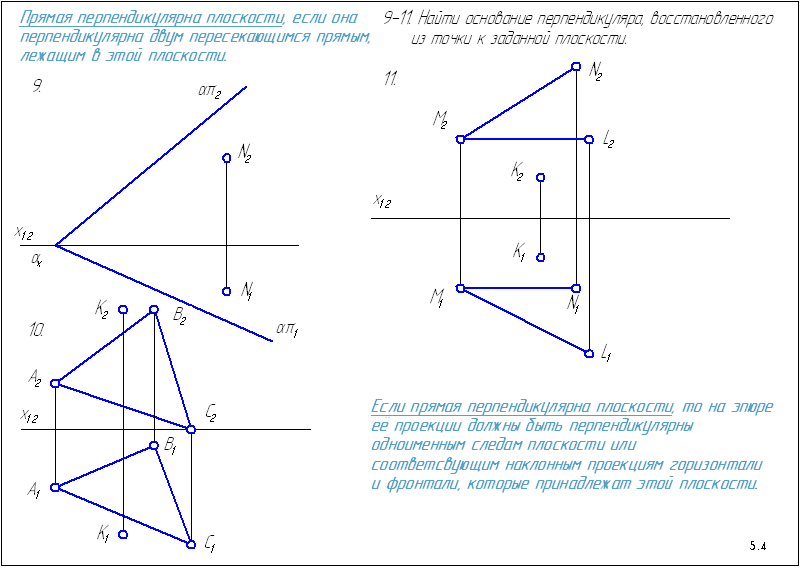 е.
совокупность точки и трёх некомпланарных векторов (2-х неколлинеарных векторов), выходящих из этой точки.
е.
совокупность точки и трёх некомпланарных векторов (2-х неколлинеарных векторов), выходящих из этой точки.
Точка O называется началом координат; прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат – осью абсцисс, ординат и аппликат. Плоскости, проходящие через оси координат, называют координатными плоскостями.
Рассмотрим в выбранной системе координат произвольную точку M . Введём понятие координаты точки M . Вектор , соединяющий начало координат с точкой M . называется радиус-вектором точки M .
Вектору в выбранном базисе можно сопоставить тройку чисел – его координаты: .
Координаты радиус-вектора точки M . называются координатами точки M . в рассматриваемой системе координат. M(x,y,z) . Первая координата называется абсциссой, вторая – ординатой, третья – аппликатой.
Аналогично определяются декартовы координаты на плоскости. Здесь точка имеет только две координаты – абсциссу и ординату.
Здесь точка имеет только две координаты – абсциссу и ординату.
Легко видеть, что при заданной системе координат каждая точка имеет определённые координаты. С другой стороны, для каждой тройки чисел найдётся единственная точка, имеющая эти числа в качестве координат.
Если векторы, взятые в качестве базиса, в выбранной системе координат, имеют единичную длину и попарно перпендикулярны, то система координат называется декартовой прямоугольной.
Несложно показать, что .
Направляющие косинусы вектора полностью определяют его направление, но ничего не говорят о его длине.
Введение…………………………………………………………………………3
1. Значение вектора и скаляра………………………………………….4
2. Определение проекции, оси и координатой точки…………………5
3. Проекция вектора на ось………………………………………………6
4. Основная формула векторной алгебры……………………………..8
5. Вычисление модуля вектора по его проекциям………………….
 ..9
..9Заключение………………………………………………………………………11
Литература………………………………………………………………………12
Введение:
Физика неразрывно связана с математикой. Математика дает физике средства и приемы общего и точного выражения зависимости между физическими величинами, которые открываются в результате эксперимента или теоретических исследований.Ведь основной метод исследований в физике – экспериментальный. Это значит – вычисления ученый выявляет с помощью измерений. Обозначает связь между различными физическими величинами. Затем, все переводится на язык математики. Формируется математическая модель. Физика — есть наука, изучающая простейшие и вместе с тем наиболее общие закономерности. Задача физики состоит в том, чтобы создать в нашем сознании такую картину физического мира, которая наиболее полно отражает свойства его и обеспечивает такие соотношения между элементами модели, какие существуют между элементами.
Итак, физика создает модель окружающего нас мира и изучает ее свойства. Но любая модель является ограниченной. При создании моделей того или иного явления принимаются во внимание только существенные для данного круга явлений свойства и связи. В этом и заключается искусство ученого — из всего многообразия выбрать главное.
Но любая модель является ограниченной. При создании моделей того или иного явления принимаются во внимание только существенные для данного круга явлений свойства и связи. В этом и заключается искусство ученого — из всего многообразия выбрать главное.
Физические модели являются математическими, но не математика является их основой. Количественные соотношения между физическими величинами выясняются в результате измерений, наблюдений и экспериментальных исследований и лишь выражаются на языке математики. Однако другого языка для построения физических теорий не существует.
1. Значение вектора и скаляра.
В физике и математике вектор — это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей. Их можно противопоставить другим величинам, таким, как масса, объем, давление, температура и плотность, которые можно описать обычным числом, и называются они «скалярами» .
Они записываются либо буквами обычного шрифта, либо цифрами (а, б, t, G, 5, −7….). Скалярные величины могут быть положительными и отрицательными. В то же время некоторые объекты изучения могут обладать такими свойствами, для полного описания которых знание только числовой меры оказывается недостаточным, необходимо ещё охарактеризовать эти свойства направлением в пространстве. Такие свойства характеризуются векторными величинами (векторами). Векторы, в отличие от скаляров, обозначаются буквами жирного шрифта: a, b, g, F, С ….
Нередко вектор обозначают буквой обычного (нежирного) шрифта, но со стрелкой над ней:
Кроме того, часто вектор обозначают парой букв (обычно заглавных), причём первая буква обозначает начало вектора, а вторая — его конец.
Модуль вектора, то есть длину направленного прямолинейного отрезка, обозначают теми же буквами, как и сам вектор, но в обычном (не жирном) написании и без стрелки над ними, либо точно также как и вектор (то есть жирным шрифтом или обычным, но со стрелкой), но тогда обозначение вектора заключается в вертикальные черточки.
Вектор – сложный объект, который одновременно характеризуется и величиной и направлением.
Не бывает также положительных и отрицательных векторов. А вот равными между собой векторы быть могут. Это когда, например, aиb имеют одинаковые модули и направлены в одну сторону. В этом случае справедлива запись a = b. Надо также иметь в виду, что перед символом вектора может стоять знак минус, например, — с, однако, этот знак символически указывает на то, что вектор -с имеет такой же модуль, как и вектор с, но направлен в противоположную сторону.
Вектор -с называют противоположным (или обратным) вектору с.
В физике же каждый вектор наполнен конкретным содержанием и при сравнении однотипных векторов (например, сил) могут иметь существенное значение и точки их приложения.
2.Определение проекции, оси и координатой точки.
Ось – это прямая, которой придается какое–то направление.
Ось обозначается какой-либо буквой: X , Y , Z , s , t … Обычно на оси выбирается (произвольно) точка, которая называется началом отсчета и, как правило, обозначается буквой О. От этой точки отсчитываются расстояния до других интересующих нас точек.
От этой точки отсчитываются расстояния до других интересующих нас точек.
Проекцией точки на ось называется основание перпендикуляра, опущенного из этой точки на данную ось. То есть, проекцией точки на ось является точка.
Координатой точки на данной оси называется число, абсолютная величина которого равна длине отрезка оси (в выбранном масштабе), заключённого между началом оси и проекцией точки на эту ось. Это число берется со знаком плюс, если проекция точки располагается в направлении оси от ее начала и со знаком минус, если в противоположном направлении.
3.Проекция вектора на ось.
Проекцией вектора на ось называется вектор, который получается в результате перемножения скалярной проекции вектора на эту ось и единичного вектора этой оси. Например, если а x – скалярная проекция вектора а на ось X, то а x ·i — его векторная проекция на эту ось.
Обозначим векторную проекцию также, как и сам вектор, но с индексом той оси на которую вектор проектируется. Так, векторную проекцию вектора а на ось Х обозначим а x
(жирная буква, обозначающая вектор и нижний индекс названия оси) или
Так, векторную проекцию вектора а на ось Х обозначим а x
(жирная буква, обозначающая вектор и нижний индекс названия оси) или
(нежирная буква, обозначающая вектор, но со стрелкой наверху (!) и нижний индекс названия оси).
Скалярной проекцией вектора на ось называется число , абсолютная величина которого равна длине отрезка оси (в выбранном масштабе), заключённого между проекциями точки начала и точки конца вектора. Обычно вместо выражения скалярная проекция говорят просто – проекция . Проекция обозначается той же буквой, что и проектируемый вектор (в обычном, нежирном написании), с нижним (как правило) индексом названия оси, на которую этот вектор проектируется. Например, если на ось Х проектируется вектора, то его проекция обозначается а x . При проектировании этого же вектора на другую ось, если ось Y , его проекция будет обозначаться а y .
Чтобы вычислить проекцию вектора на ось (например, ось X) надо из координаты точки его конца вычесть координату точки начала, то есть
а x
= х к
− x н.
Проекция вектора на ось — это число. Причем, проекция может быть положительной, если величина х к больше величины х н,
отрицательной, если величина х к меньше величины х н
и равной нулю, если х к равно х н.
Проекцию вектора на ось можно также найти, зная модуль вектора и угол, который он составляет с этой осью.
Из рисунка видно, что а x = а Cos α
То есть, проекция вектора на ось равна произведению модуля вектора на косинус угла между направлением оси и направлением вектора . Если угол острый, то
Cos α > 0 и а x
> 0, а, если тупой, то косинус тупого угла отрицателен, и проекция вектора на ось тоже будет отрицательна.
Углы, отсчитываемые от оси против хода часовой стрелки, принято считать положительными, а по ходу — отрицательными. Однако, поскольку косинус – функция четная, то есть, Cos α = Cos (− α), то при вычислении проекций углы можно отсчитывать как по ходу часовой стрелки, так и против.
Чтобы найти проекцию вектора на ось надо модуль этого вектора умножить на косинус угла между направлением оси и направлением вектора.
4. Основная формула векторной алгебры.
Спроектируемвектор а на оси Х и Y прямоугольной системы координат. Найдем векторные проекции вектора а на эти оси:
а x = а x ·i, а y = а y ·j.
Но в соответствии справилом сложения векторов
а = а x + а y .
а = а x ·i + а y ·j.
Таким образом, мы выразили вектор через его проекции и орты прямоугольной системы координат (или через его векторные проекции).
Векторные проекции а x и а y называютсясоставляющими или компонентами вектора а. Операция, которую мы выполнили, называется разложением вектора по осямпрямоугольной системы координат.
Если вектор задан в пространстве, то
а = а x ·i + а y ·j + а z ·k.
Эта формула называется основной формулой векторной алгебры. Конечно, ее можно записать и так.
Обозначим через а угол между вектором и осью проекции и перенесем вектор
так, чтобы его начало совпало с какой-нибудь точкой оси. Если направления составляющей вектора и оси одина ковы, то угол а будет острым и, как видно из рис. 24, а,
24, а,
где а — модуль вектора а. Если же направления вектора и оси противоположны, то, учитывая знак проекции, будем иметь-(см. рис. 24, б)
т. е. предыдущее выражение (нужно помнить, что в данном случае угол а тупой и
Таким образом, проекция вектора на ось равна произведению модуля вектора на косинус угла между вектором и осью:
Кроме этой имеющей исключительно важное значение формулы, для проекции вектора на ось можно дать еще одну очень простую формулу. Установим на оси начало отсчета и выберем масштаб, общий с масштабом векторов. Как известно, координатой точки называется число, выражающее в выбранном масштабе расстояние от начала отсчета оси до проекции данной точки на ось, причем это число берется со знаком плюс, если проекция точки удалена от начала отсчета в сторону направления оси, и со знаком минус в противном случае. Так, например, координатой точки А (рис. 23, б) будет взятое со знаком число, выражающее длину отрезка а координатой точки В будет взятое со знаком — число, определяющее длину отрезка (мы не останавливаемся на этом
подробнее, считая, что читатель знаком с понятием координат точки из курса элементарной математики).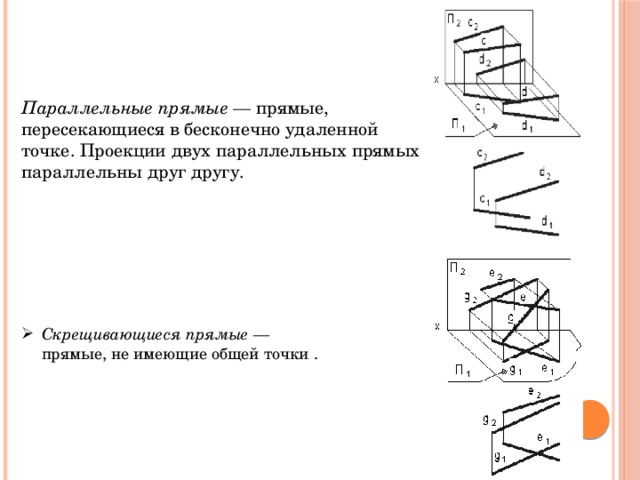
Обозначим через координату начала, а через координату конца вектора на ось х. Тогда, как видно из рис. 23, а, будем иметь
Проекция вектора на ось х будет равна
или, учитывая предыдущие равенства,
Легко видеть, что эта формула имеет общий характер и не зависит от расположения вектора относительно оси и начала отсчета. Действительно, рассмотрим случай, изображённый на рис. 23, б. Из определения координат точек и проекции вектора последовательно получим
(читатель легко проверит справедливость формулы и и при другом расположении вектора относительно оси и начала отсчета).
Из (6.11) следует, что проекция вектора на ось равна разности координат конца и начала вектора.
Вычисление проекции вектора на ось встречается весьма часто в самых различных вопросах. Поэтому необходимо выработать твердые навыки вычисления проекций. Можно указать некоторые приемы, облегчающие процесс вычисления проекций.
1. Знак проекции вектора на ось, как правило, можно определить непосредственно из чертежа, а модуль проекции можно вычислить по формуле
где — острый угол между вектором и осью проекций — если а если Этом прием, не внося ничего принципиально нового, несколько
облегчает вычисление проекции, так как не требует тригонометрических преобразований.
2. Если требуется определить проекции вектора на две взаимноперпендикулярные оси х и у (предполагается, что вектор лежит в плоскости этих осей) и — острый угол между вектором и осью х, то
(знак проекций определяется из чертежа).
Пример. Найти проекции на оси координат х и у силы изображенной на рис. 25. Из чертежа видно, что обе проекции будут отрицательны. Следовательно,
3. Иногда применяется правило двойного проектирования, состоящее в следующем. Пусть дан вектор и ось лежащая в плоскости Опустим из конца вектора перпендикуляры на плоскость и прямую и соединим затем основания перпендикуляров отрезком прямой линии (рис. 26). Обозначим угол между вектором и плоскостью через угол между и через и угол между вектором и осью проекций через а. Так как угол прямой (по построению), то
а на ось или какой-либо другой вектор существуют понятия ее геометрической проекции и числовой (или алгебраической) проекции. Результатом геометрической проекции будет вектор, а результатом алгебраической – неотрицательное действительное число.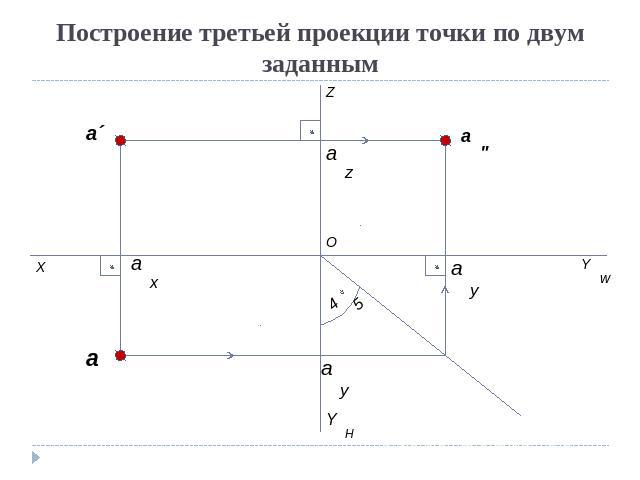 Но перед тем, как перейти к этим понятиям вспомним необходимую информацию.
Но перед тем, как перейти к этим понятиям вспомним необходимую информацию.
Предварительные сведения
Основное понятие – непосредственно понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $\overline{a}$ (рис. 1).
Введем еще несколько понятий, связанных с понятием вектора.
Определение 3
Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой или на прямых, параллельных друг другу (рис.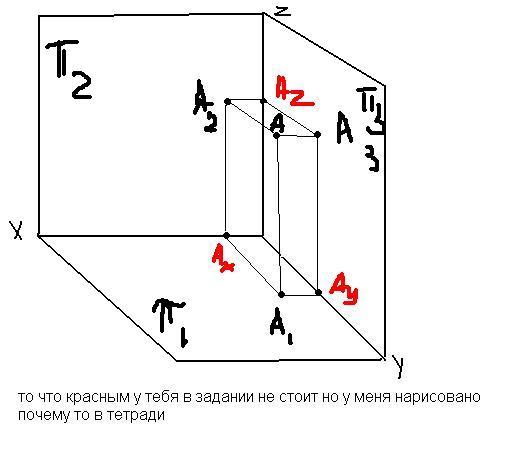 2).
2).
Определение 4
Два ненулевых вектора будем называть сонаправленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они будут направлены в одну сторону (рис. 3).
Обозначение: $\overline{a}\overline{b}$
Определение 5
Два ненулевых вектора будем называть противоположно направленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они направлены в разные стороны (рис. 4).
Обозначение: $\overline{a}↓\overline{d}$
Определение 6
Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|\overline{a}|$
Перейдем к определению равенства двух векторов
Определение 7
Два вектора будем называть равными, если они удовлетворяют двух условиям:
- Они сонаправлены;
- Их длины равны (рис. 5).
Геометрическая проекция
Как мы уже сказали ранее, результатом геометрической проекции будет вектор.
Определение 8
Геометрической проекцией вектора $\overline{AB}$ на ось будем называть такой вектор, который получается следующим образом: Точка начала вектора $A$ проецируется на данную ось. Получаем точку $A»$ — начало искомого вектора. Точка конца вектора $B$ проецируется на данную ось. Получаем точку $B»$ — конец искомого вектора. Вектор $\overline{A»B»}$ и будет искомым вектором.
Рассмотрим задачу:
Пример 1
Постройте геометрическую проекцию $\overline{AB}$ на ось $l$, изображенные на рисунке 6.
Проведем из точки $A$ перпендикуляр к оси $l$, получим на ней точку $A»$. Далее проведем из точки $B$ перпендикуляр к оси $l$, получим на ней точку $B»$ (рис. 7).
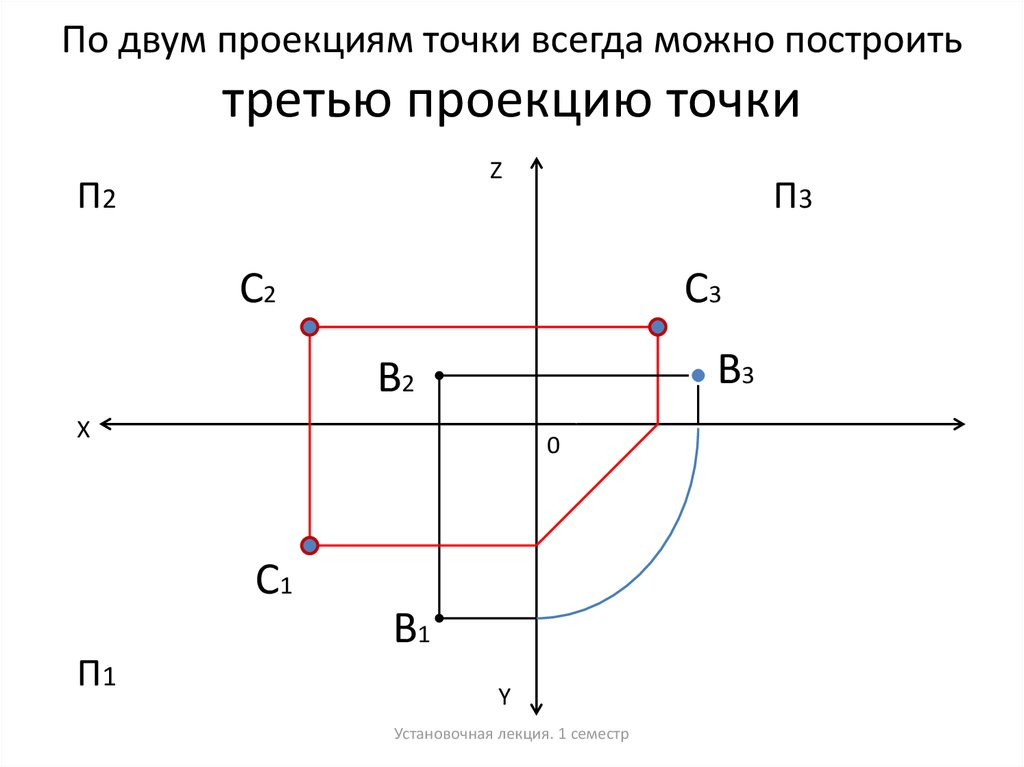
На чертежах изображения геометрических тел строятся при использовании метода проекции. Но для этого одного изображения недостаточно, необходимо минимум две проекции. С помощью них и определяются точки в пространстве. Следовательно, нужно знать, как найти проекцию точки.
Проекция точки
Для этого потребуется рассмотреть пространство двугранного угла, с расположенной внутри точкой (А). Здесь используются горизонтальная П1 и вертикальная П2 плоскости проекций. Точка (А) проецируется на проекционные плоскости ортогонально. Что касается перпендикулярных проецирующих лучей, то они объединяются в проецирующую плоскость, перпендикулярную плоскостям проекций. Таким образом, при совмещении горизонтальной П1 и фронтальной П2 плоскостей путем вращения по оси П2 / П1, получаем плоский чертеж.
Здесь используются горизонтальная П1 и вертикальная П2 плоскости проекций. Точка (А) проецируется на проекционные плоскости ортогонально. Что касается перпендикулярных проецирующих лучей, то они объединяются в проецирующую плоскость, перпендикулярную плоскостям проекций. Таким образом, при совмещении горизонтальной П1 и фронтальной П2 плоскостей путем вращения по оси П2 / П1, получаем плоский чертеж.
Затем перпендикулярно оси показывается линия с расположенными на ней точками проекции. Так получается комплексный чертеж. Благодаря построенным отрезкам на нем и вертикальной линии связи, легко можно определять положение точки относительно проекционных плоскостей.
Чтобы было проще понять, как найти проекцию, необходимо рассмотреть прямоугольный треугольник. Его короткая сторона является катетом, а длинная – гипотенузой. Если выполнить на гипотенузу проекцию катета, то она поделится на два отрезка. Для определения их величины, нужно выполнить расчет набора исходных данных. Рассмотрим на данном треугольнике, способы расчета основных проекций.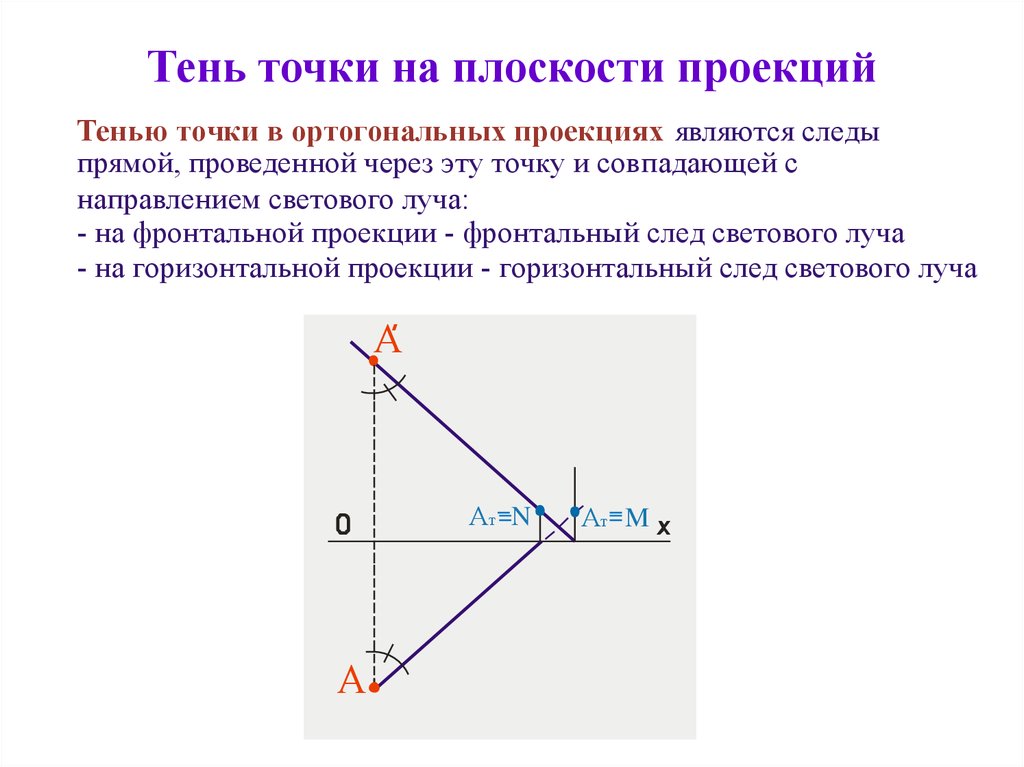
Как правило, в данной задаче указывают длину катета N и длину гипотенузы D, чью проекцию и требуется найти. Для этого узнаем, как найти проекцию катета.
Рассмотрим способ нахождения длины катета (А). Учитывая, что среднее геометрическое от проекции катета и длины гипотенузы равняется искомой нами величине катета: N = √(D*Nd).
Как найти длину проекции
Корень из произведения можно найти возведением в квадрат значения длины искомого катета (N), а затем поделенного на длину гипотенузы: Nd = (N / √ D)² = N² / D. При указании в исходных данных значений только катетов D и N, длину проекции следует находить при помощи теоремы Пифагора.
Найдем длину гипотенузы D. Для этого нужно воспользоваться значениями катетов √ (N² + T²), а затем подставить полученное значение в следующую формулу нахождения проекции: Nd = N² / √ (N² + T²).
Когда в исходных данных указаны данные о длине проекции катета RD, а также данные о величине гипотенузы D, следует вычислять длину проекции второго катета ND при помощи простой формулы вычитания: ND = D – RD.
Проекция скорости
Рассмотрим, как найти проекцию скорости. Для того чтобы заданный вектор представлял описание движения, его следует разместить в проекции на координатные оси. Различают одну координатную ось (луч), две координатные оси (плоскость) и три координатные оси (пространство). При нахождении проекции необходимо из концов вектора опустить перпендикуляры на оси.
Для того чтобы уяснить значения проекции, необходимо узнать, как найти проекцию вектора.
Проекция вектора
При движении тела перпендикулярно относительно оси, проекция будет представлена в виде точки, и иметь значение равное нулю. Если же движение осуществляется параллельно координатной оси, то проекция будет совпадать с модулем вектора. В случае, когда тело движется таким образом, что вектор скорости направлен под углом φ относительно оси (х), проекция на данную ось будет являться отрезком: V(x) = V cos(φ), где V – это модель вектора скорости.Когда направления вектора скорости и координатной оси совпадают, то проекция является положительной, и наоборот. 2).
2).
Проекция точки на плоскость уравнение. Проецирование точки
Проекция точки на плоскость является частным случаем общей задачи нахождения проекции точки на поверхность. В силу простоты вычисления проекции точки на касательную к поверхности плоскость используется в качестве нулевого приближения при решении общей задачи.
Рассмотрим задачу проецирования точки на плоскость, заданную радиус-вектором
Будем считать, что векторы не коллинеарные. Допустим, что в общем случае векторы не ортогональны и имеют не единичную длину. Плоскость проходит через точку в которой параметры равны нулю, а векторы определяют параметрические направления. Заданная точка имеет единственную проекцию на плоскость (4.6.1). Построим единичную нормаль к плоскости
Рис. 4.6.1. Проекция точки на плоскость s(u, v)
Вычислим радиус-вектор проекции точки на плоскость как разность радиус-вектора проецируемой точки и составляющей вектора параллельной нормали к плоскости,
(4. 6.4)
6.4)
На рис. 4.6.1 показаны векторы плоскости ее начальная точка и проекция заданной точки.
Параметры и длины проекций связаны уравнениями
где косинус угла между векторами определяется по формуле (1.7.13).
Из системы этих уравнений найдем параметры проекции точки на плоскость
(4.6.6)
где — коэффициенты первой основной квадратичной формы плоскости (1.7.8), они же ковариантные компоненты метрического тензора поверхности, — контравариантные компоненты метрического тензора поверхности. Если векторы ортогональные, то формулы (4.6.6) и (4.6.7) примут вид
Расстояние от точки до ее проекции на плоскость в общем случае вычисляется как длина вектора . Расстояние от точки до ее проекции на плоскость можно определить, не вычисляя проекцию точки, а вычислив проекцию вектора на нормаль к плоскости
(4.6.8)
Частные случаи.
Проекции точки на некоторые аналитические поверхности могут быть найдены без привлечения численных методов. Например, чтобы найти проекции точки на поверхность кругового цилиндра, конуса, сферы или тора, нужно перевести проецируемую точку в местную систему координат поверхности, где легко найти параметры проекций. Аналогично могут быть найдены проекции на поверхности выдавливания и вращения. В некоторых частных случаях положения проецируемой точки ее проекции могут быть легко найдены и на другие поверхности.
Аналогично могут быть найдены проекции на поверхности выдавливания и вращения. В некоторых частных случаях положения проецируемой точки ее проекции могут быть легко найдены и на другие поверхности.
Общий случай.
Рассмотрим задачу проецирования точки на поверхность в общем случае. Пусть требуется найти все проекции точки на поверхность . Каждая искомая точка поверхности удовлетворяет системе двух уравнений
Система уравнений (4.6.9) содержит две неизвестные величины — параметры u и v. Эта задача решается так же, как и задача нахождения проекций заданной точки на кривую.
На первом этапе определим нулевые приближения параметров поверхности для проекций точки, а на втором этапе найдем точные значения параметров, определяющие проекции заданной точки на поверхность
Пройдем по поверхности с шагами вычисляемыми по формулам (4.2.4) и (4.2.5), описанным выше способом движения по параметрической области. Обозначим параметры точек, через которые мы пройдем, через . В каждой точке будем вычислять скалярные произведения векторов
(4. 6.10)
6.10)
Если искомое решение лежит вблизи точки с параметрами , то будут иметь разные знаки, а также и будут иметь разные знаки. Смена знаков скалярных произведений говорит о том, что рядом находится искомое решение. За нулевое приближение параметров примем значения Начиная с нулевого приближения параметров, одним из методов решения нелинейных уравнений найдем решение задачи с заданной точностью. Например, в методе Ньютона на итерации приращения параметров проекции найдутся из системы линейных уравнений
где частные производные радиус-вектора по параметрам. Следующее приближение параметров проекции точки равны . Процесс уточнения параметров закончим, когда на очередной итерации выполнятся неравенства , где — заданная погрешность. Таким же образом найдем все остальные корни системы уравнений (4.6.9).
Если требуется найти только ближайшую проекцию заданной точки на поверхность, то можно пройти по тем же точкам геометрического объекта и выбрать из них ближайшую к заданной точке. Параметры ближайшей точки и следует выбрать в качестве нулевого приближения решения задачи.
Параметры ближайшей точки и следует выбрать в качестве нулевого приближения решения задачи.
Проекция точки на поверхность в заданном направлении.
В определенных случаях возникает задача определения проекции точки на поверхность не по нормали к ней, а вдоль заданного направления. Пусть направление проецирования задано вектором единичной длины q. Построим прямую линию
(4.6.12)
проходящую через заданную точку и имеющую направление заданного вектора. Проекции точки на поверхность в заданном направлении определим как точки пересечения поверхности с прямой (4.6.12), проходящей через заданную точку в заданном направлении.
Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:
Пр a b = |b|cos(a,b) или
Где a b — скалярное произведение векторов , |a| — модуль вектора a .
Инструкция
. Для нахождения проекции вектора Пp a b в онлайн режиме необходимо указать координаты векторов a и b .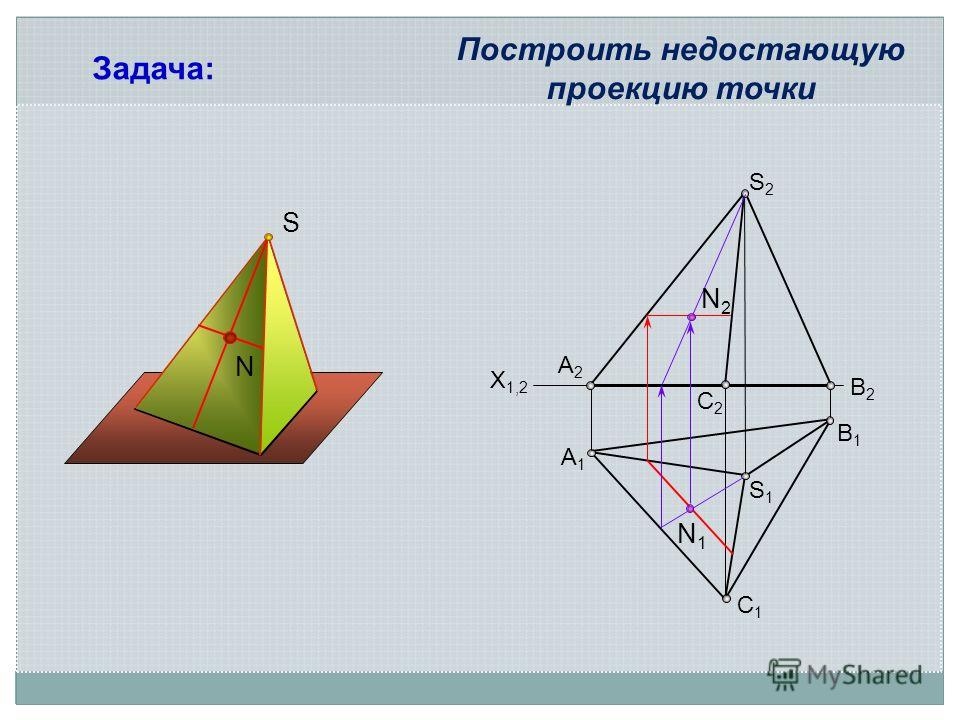 При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word
. Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор .
При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word
. Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор .
Классификация проекций вектора
Виды проекций по определению проекция вектора
- Геометрическая проекция вектора AB на ось (вектор) называется вектор A»B» , начало которого A’ есть проекция начала A на ось (вектор), а конец B’ – проекция конца B на ту же ось.
- Алгебраическая проекция вектора AB на ось (вектор) называется длина вектора A»B» , взятая со знаком + или — , в зависимости от того, имеет ли вектор A»B» то же направление, что и ось (вектор).
Виды проекций по системе координат
Свойства проекции вектора
- Геометрическая проекция вектора есть вектор (имеет направление).
- Алгебраическая проекция вектора есть число.
Теоремы о проекциях вектора
Теорема 1
. Проекция суммы векторов на какую-либо ось равна проекции слагаемых векторов на ту же ось.
Проекция суммы векторов на какую-либо ось равна проекции слагаемых векторов на ту же ось.
AC» =AB» +B»C»
Теорема 2 . Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:
Пр a b = |b|·cos(a,b)
Виды проекций вектора
- проекция на ось OX.
- проекция на ось OY.
- проекция на вектор.
| Проекция на ось OX | Проекция на ось OY | Проекция на вектор |
| Если направление вектора A’B’ совпадает с направлением оси OX, то проекция вектора A’B’ имеет положительный знак. | Если направление вектора A’B’ совпадает с направлением оси OY, то проекция вектора A’B’ имеет положительный знак. | Если направление вектора A’B’ совпадает с направлением вектора NM, то проекция вектора A’B’ имеет положительный знак. |
Если направление вектора противоположно с направлением оси OX, то проекция вектора A’B’ имеет отрицательный знак.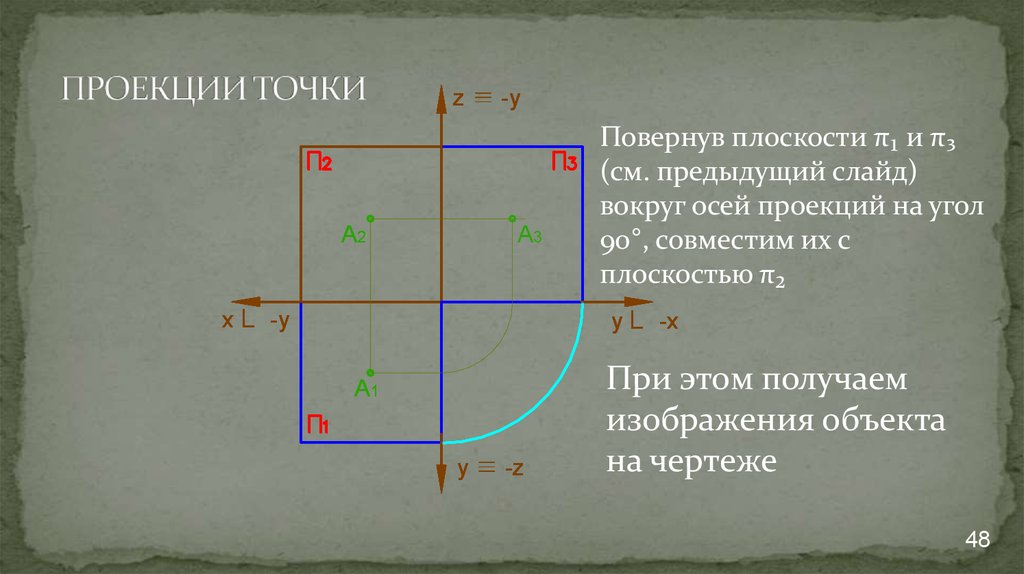 | Если направление вектора A’B’ противоположно с направлением оси OY, то проекция вектора A’B’ имеет отрицательный знак. | Если направление вектора A’B’ противоположно с направлением вектора NM, то проекция вектора A’B’ имеет отрицательный знак. |
| Если вектор AB параллелен оси OX, то проекция вектора A’B’ равна модулю вектора AB. | Если вектор AB параллелен оси OY, то проекция вектора A’B’ равна модулю вектора AB. | Если вектор AB параллелен вектору NM, то проекция вектора A’B’ равна модулю вектора AB. |
| Если вектор AB перпендикулярен оси OX, то проекция A’B’ равна нулю (нуль-вектор). | Если вектор AB перпендикулярен оси OY, то проекция A’B’ равна нулю (нуль-вектор). | Если вектор AB перпендикулярен вектору NM, то проекция A’B’ равна нулю (нуль-вектор). |
1. Вопрос: Может ли проекция вектора иметь отрицательный знак. Ответ: Да, проекций вектора может быть отрицательной величиной. В этом случае, вектор имеет противоположное направление (см. как направлены ось OX и вектор AB)
В этом случае, вектор имеет противоположное направление (см. как направлены ось OX и вектор AB)
2. Вопрос: Может ли проекция вектора совпадать с модулем вектора. Ответ: Да, может. В этом случае, векторы параллельны (или лежат на одной прямой).
3. Вопрос: Может ли проекция вектора быть равна нулю (нуль-вектор). Ответ: Да, может. В этом случае вектор перпендикулярен соответствующей оси (вектору).
Пример 1
. Вектор (рис. 1) образует с осью OX (она задана вектором a) угол 60 о. Если OE есть единица масштаба, то |b|=4, так что .
Действительно, длина вектора (геометрической проекции b) равна 2, а направление совпадает с направлением оси OX.
Пример 2
. Вектор (рис. 2) образует с осью OX (с вектором a) угол (a,b) = 120 o . Длина |b| вектора b равна 4, поэтому пр a b=4·cos120 o = -2.
Действительно, длина вектора равна 2, а направление противоположно направлению оси.
При решении геометрических задач в пространстве часто возникает проблема определения расстояния между плоскостью и точкой. В некоторых случаях это необходимо для комплексного решения. Эту величину можно вычислить, если найти проекцию на плоскость точки. Рассмотрим этот вопрос подробнее в статье.
В некоторых случаях это необходимо для комплексного решения. Эту величину можно вычислить, если найти проекцию на плоскость точки. Рассмотрим этот вопрос подробнее в статье.
Уравнение для описания плоскости
Перед тем как перейти к рассмотрению вопроса касательно того, как найти проекцию точки на плоскость, следует познакомиться с видами уравнений, которые задают последнюю в трехмерном пространстве. Подробнее — ниже.
Уравнением общего вида, определяющим все точки, которые принадлежат данной плоскости, является следующее:
A*x + B*y + C*z + D = 0.
Первые три коэффициента — это координаты вектора, который называется направляющим для плоскости. Он совпадает с нормалью для нее, то есть является перпендикулярным. Этот вектор обозначают n¯(A; B; C). Свободный коэффициент D однозначно определяется из знания координат любой точки, принадлежащей плоскости.
Понятие о проекции точки и ее вычисление
Предположим, что задана некоторая точка P(x 1 ; y 1 ; z 1) и плоскость.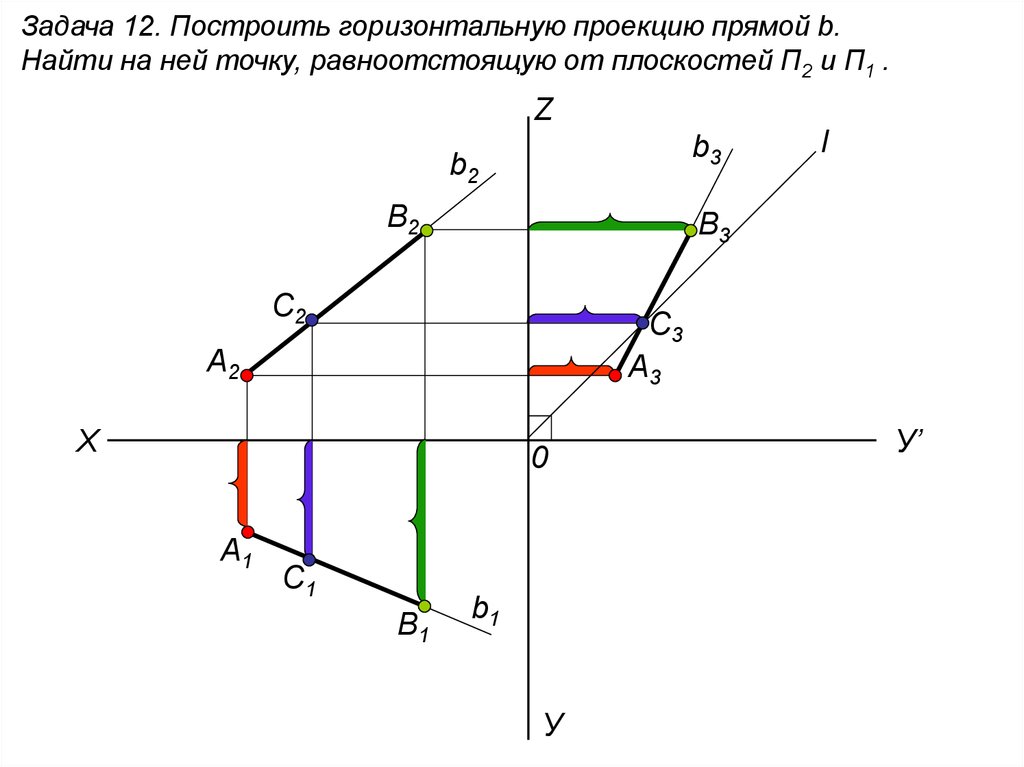 Она определена уравнением в общем виде. Если провести перпендикулярную прямую из P к заданной плоскости, то очевидно, что она пересечет последнюю в одной определенной точке Q (x 2 ; y 2 ; z 2). Q называется проекцией P на рассматриваемую плоскость. Длина отрезка PQ называется расстоянием от точки P до плоскости. Таким образом, сам PQ является перпендикулярным плоскости.
Она определена уравнением в общем виде. Если провести перпендикулярную прямую из P к заданной плоскости, то очевидно, что она пересечет последнюю в одной определенной точке Q (x 2 ; y 2 ; z 2). Q называется проекцией P на рассматриваемую плоскость. Длина отрезка PQ называется расстоянием от точки P до плоскости. Таким образом, сам PQ является перпендикулярным плоскости.
Как можно найти координаты проекции точки на плоскость? Сделать это не сложно. Для начала следует составить уравнение прямой, которая будет перпендикулярна плоскости. Ей будет принадлежать точка P. Поскольку вектор нормали n¯(A; B; C) этой прямой должен быть параллелен, то уравнение для нее в соответствующей форме запишется так:
(x; y; z) = (x 1 ; y 1 ; z 1) + λ*(A; B; C).
Где λ — действительное число, которое принято называть параметром уравнения. Изменяя его, можно получить любую точку прямой.
После того как записано векторное уравнение для перпендикулярной плоскости линии, необходимо найти общую точку пересечения для рассматриваемых геометрических объектов. Ее координаты и будут проекцией P. Поскольку они должны удовлетворять обоим равенствам (для прямой и для плоскости), то задача сводится к решению соответствующей системы линейных уравнений.
Ее координаты и будут проекцией P. Поскольку они должны удовлетворять обоим равенствам (для прямой и для плоскости), то задача сводится к решению соответствующей системы линейных уравнений.
Понятие проекции часто используется при изучении чертежей. На них изображаются боковые и горизонтальные проекции детали на плоскости zy, zx, и xy.
Вычисление расстояния от плоскости до точки
Как выше было отмечено, знание координат проекции на плоскость точки позволяет определить дистанцию между ними. Используя обозначения, введенные в предыдущем пункте, получаем, что искомое расстояние равно длине отрезка PQ. Для его вычисления достаточно найти координаты вектора PQ¯, а затем рассчитать его модуль по известной формуле. Конечное выражение для d расстояния между P точкой и плоскостью принимает вид:
d = |PQ¯| = √((x 2 — x 1) 2 + (y 2 — y 1) 2 + (z 2 — z 1) 2).
Полученное значение d представлено в единицах, в которых задается текущая декартова координатная система xyz.
Пример задачи
Допустим, имеется точка N(0; -2; 3) и плоскость, которая описывается следующим уравнением:
Следует найти точки проекцию на плоскость и вычислить между ними расстояние.
В первую очередь составим уравнение прямой, которая пересекает плоскость под углом 90 o . Имеем:
(x; y; z) = (0; -2; 3) + λ*(2; -1; 1).
Записывая это равенство в явном виде, приходим к следующей системе уравнений:
Подставляя значения координат из первых трех равенств в четвертое, получим значение λ, определяющее координаты общей точки прямой и плоскости:
2*(2*λ) — (-2 — λ) + λ + 3 + 4 = 0 =>
6*λ + 9 = 0 =>
λ = 9/6 = 3/2 = 1,5.
Подставим найденный параметр в и найдем координаты проекции исходной точки на плоскость:
(x; y; z) = (0; -2; 3) + 1,5*(2; -1; 1) = (3; -3,5; 4,5).
Для вычисления дистанции между заданными в условии задачи геометрическими объектами применим формулу для d:
d = √((3 — 0) 2 + (-3,5 + 2) 2 + (4,5 — 3) 2) = 3,674.
В данной задаче мы показали, как находить проекцию точки на произвольную плоскость и как вычислять между ними расстояние.
Будет построена, когда будет восстановлен перпендикуляр к данной плоскости, проходящий через точку и построена точка пересечения перпендикуляра с плоскостью:
Прямая и плоскость ;
Пересечение прямой с плоскостью
Будет построена, когда будет восстановлен перпендикуляр к данной плоскости, опущенный из точки на плоскость и построена точка пересечения перпендикуляра с плоскостью. Эти построения выполняются когда определяется расстояние от точки до плоскости способом прямоугольного треугольника.
Даны проекции: точки A (A`, A» ) и плоскости α (α H , α V ). Найти расстояние от точки A до плоскости α способом прямоугольного треугольника.
HTML код таблицы, примеры
Строится в графической работе №2 задача №4 для двух точек отрезка EF : Графическая работа 2
Построить эпюр точки B симметричной A относительно прямой m
Здесь показан один из многих путей решения данной задачи.
1. Используем косоугольное проецирование с направлением S параллельным заданной прямой m:
a) Через точку A проводим прямую n и находим следы nH, mH и nV, mV;
b) находим следы плоскости α по следам параллельных прямых ее образующих nH, mH и nV, mV;
c) находим следы kH и kV прямой k симметричной относительно прямой m на одноименных следах плоскости α.
2. Через точку A проводим плоскость β перпендикулярную параллельным прямым m, n и k плоскости α:
a) Через точку A проводим горизонталь и фронталь плоскости β;
b) Находим следы горизонтали и фронтали плоскости β;
c) Проводим следы плоскости β через следы ее горизонтали h и фронтали f.
3. Находим точку B встречи прямой k с плоскостью β:
a) Находим линию пересечения 1 — 2 плоскостей α и β;
b) Находим искомую точку B в пересечении линии 1-2 с прямой k.
Найти острый угол между диагоналями параллелограмма, построенного на векторах
5) Определить координаты вектора с, направленного по биссектрисе угла между векторами a и b, если вектор с= 3корней из 42.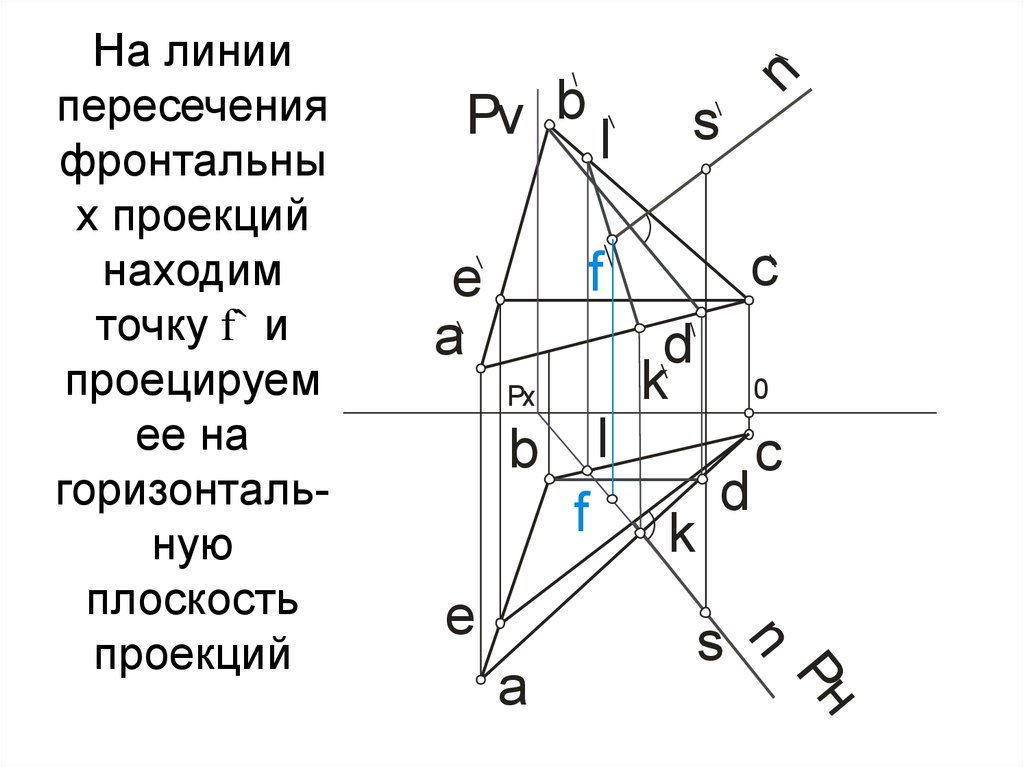 a={2;-3;6}, b={-1;2;-2}
a={2;-3;6}, b={-1;2;-2}
Найдем единичный вектор e_a сонаправленный с a:
аналогично e_b = b/|b|,
тогда искомый вектор будет направлен также как векторная сумма e_a+e_b, т.к. (e_a+e_b) это диагональ ромба, которая явл. биссектрисой его угла.
Обозначим (e_a+e_b)=d,
Найдем единичный вектор, который направлен по биссектрисе: e_c = d/|d|
Если |c| = 3*sqrt(42), тогда c = |c|*e_c. Вот и все.
Найти линейную зависимость между данными четырьмя некомпланарными векторами: p=a+b; q=b-c; r=a-b+c; s=b+(1/2)*c
Из первых трех равенств попробуйте выразить `a,b,c` через `p,q,r` (начните со сложения второго и третьего уравнений). Затем замените в последнем уравнении `b` и `c` найденными выражениями через `p,q,r`.
13) Найти уравнение плоскости, проходящей через точки А(2, -1, 4) и В(3, 2, -1) перпендикулярно плоскости х + у + 2z – 3 = 0. Искомое уравнение плоскости имеет вид: Ax + By + Cz + D = 0, вектор нормали к этой плоскости (A, B, C). Вектор (1, 3, -5) принадлежит плоскости. Заданная нам плоскость, перпендикулярная искомой имеет вектор нормали (1, 1, 2). Т.к. точки А и В принадлежат обеим плоскостям, а плоскости взаимно перпендикулярны, то Таким образом, вектор нормали (11, -7, -2). Т.к. точка А принадлежит искомой плоскости, то ее координаты должны удовлетворять уравнению этой плоскости, т.е. 11×2 + 7×1 — 2×4 + D = 0; D = -21. Итого, получаем уравнение плоскости: 11x — 7y – 2z – 21 = 0.
Вектор (1, 3, -5) принадлежит плоскости. Заданная нам плоскость, перпендикулярная искомой имеет вектор нормали (1, 1, 2). Т.к. точки А и В принадлежат обеим плоскостям, а плоскости взаимно перпендикулярны, то Таким образом, вектор нормали (11, -7, -2). Т.к. точка А принадлежит искомой плоскости, то ее координаты должны удовлетворять уравнению этой плоскости, т.е. 11×2 + 7×1 — 2×4 + D = 0; D = -21. Итого, получаем уравнение плоскости: 11x — 7y – 2z – 21 = 0.
14) Уравнение плоскости проходящее через прямую паралелльно вектору.
Пусть, искомая плоскость проходит через прямую (x-x1)/a1 = (y-y1)/b1 = (z-z1)/c1 параллельно прямой (x-x2)/a2 = (y-y2)/b2 = (z-z2)/c2 .
Тогда нормальный вектор плоскости есть векторное произведение направляющих векторов этих прямых:
Пусть, координаты векторного произведения (A;B;C). Искомая плоскость проходит через точку (x1;y1;z1). Нормальный вектор и точка, через которую проходит плоскость — однозначно определяют уравнение искомой плоскости:
A·(x-x1) + B·(y-y1) + C·(z-z1) = 0
17) Найти уравнение прямой, проходящей через точку A(5, -1) перпендикулярно к прямой 3x — 7y + 14 = 0.
18) Составить уравнение прямой, проходящей через точку М перпендикулярно к данной плоскости М(4,3,1) x+3y+5z-42=0
(x — x0) / n = (y — y0) / m = (z — z0) / p
M(x0,y0,z0) — твоя точка М(4,3,1)
{n, m, p} — направляющий вектор прямой, он же вектро нормали для заданной поверхности {1, 3, 5} (коэффициенты при переменных x,y,z в уравнении плоскости)
Найти проекцию точки на плоскость
Точка М(1,-3,2), плоскость 2x+5y-3z-19=0
Начертательная геометрия | Начертательная геометрия
Начертательная геометрия | Начертательная геометрия — nGeo.FXYZ.ruонлайн Начертательная геометрия предстала как наука в конце восемнадцатого века, когда гениальный французский геометр Гаспар Монж, читавший перед студентами парижской Политехнической школы курс лекций Начертательная геометрия впервые опубликовывает их.
+ |
Как найти проекции вектора на координатные оси.
 Проекция вектора на ось
Проекция вектора на осьПроектирование различных линий и поверхностей на плоскость позволяет построить наглядное изображение предметов в виде чертежа. Будем рассматривать прямоугольное проектирование, при котором проектирующие лучи перпендикулярны плоскости проекции. ПРОЕКЦИЕЙ ВЕКТОРА НА ПЛОСКОСТЬ считают вектор = (рис. 3.22), заключенный между перпендикулярами, опущенными из его начала и конца.
Рис. 3.22. Векторная проекция вектора на плоскость.
Рис. 3.23. Векторная проекция вектора на ось.
В векторной алгебре часто приходится проектировать вектор на ОСЬ, то есть на прямую, имеющую определенную ориентацию. Такое проектирование выполняется легко, если вектор и ось L лежат в одной плоскости (рис. 3.23). Однако задача усложняется, когда это условие не выполнено. Построим проекцию вектора на ось, когда вектор и ось не лежат в одной плоскости (рис. 3.24).
Построим проекцию вектора на ось, когда вектор и ось не лежат в одной плоскости (рис. 3.24).
Рис. 3.24. Проектирование вектора на ось
в общем случае.
Через концы вектора проводим плоскости, перпендикулярные прямой L. В пересечении с этой прямой данные плоскости определяют две точки А1 и B1 — вектор , который будем называть векторной проекцией данного вектора. Задача нахождения векторной проекции может быть решена проще, если вектор приведен в одну плоскость с осью, что возможно осуществить, так как в векторной алгебре рассматриваются свободные векторы.
Наряду с векторной проекцией, существует и СКАЛЯРНАЯ ПРОЕКЦИЯ, которая равна модулю векторной проекции, если векторная проекция совпадает с ориентацией оси L, и равна величине, ей противоположной, если векторная проекция и ось L имеют противоположную ориентацию. Скалярную проекцию будем обозначать:
Векторная и скалярная проекции не всегда терминологически разделяются строго на практике. Обычно пользуются термином «проекция вектора», подразумевая под этим скалярную проекцию вектора. При решении же необходимо четко эти понятия различать. Следуя установившейся традиции, будем использовать термины «проекция вектора», подразумевая скалярную проекцию, и «векторная проекция» — в соответствии с установленным смыслом.
При решении же необходимо четко эти понятия различать. Следуя установившейся традиции, будем использовать термины «проекция вектора», подразумевая скалярную проекцию, и «векторная проекция» — в соответствии с установленным смыслом.
Докажем теорему, позволяющую вычислять скалярную проекцию заданного вектора.
ТЕОРЕМА 5. Проекция вектора на ось L равна произведению его модуля на косинус угла между вектором и осью, то есть
(3.5)
Рис. 3.25. Нахождение векторной и скалярной
Проекций вектора на ось L
( и ось L одинаково ориентированы).
ДОКАЗАТЕЛЬСТВО . Выполним предварительно построения, позволяющие найти угол G Между вектором и осью L. Для этого построим прямую MN, параллельную оси L и проходящую через точку О — начало вектора (рис. 3.25). Угол и будет искомым углом. Проведем через точки А и О две плоскости, перпендикулярные оси L. Получим:
Так как ось L и прямая MN параллельны.
Выделим два случая взаимного расположения вектора и оси L.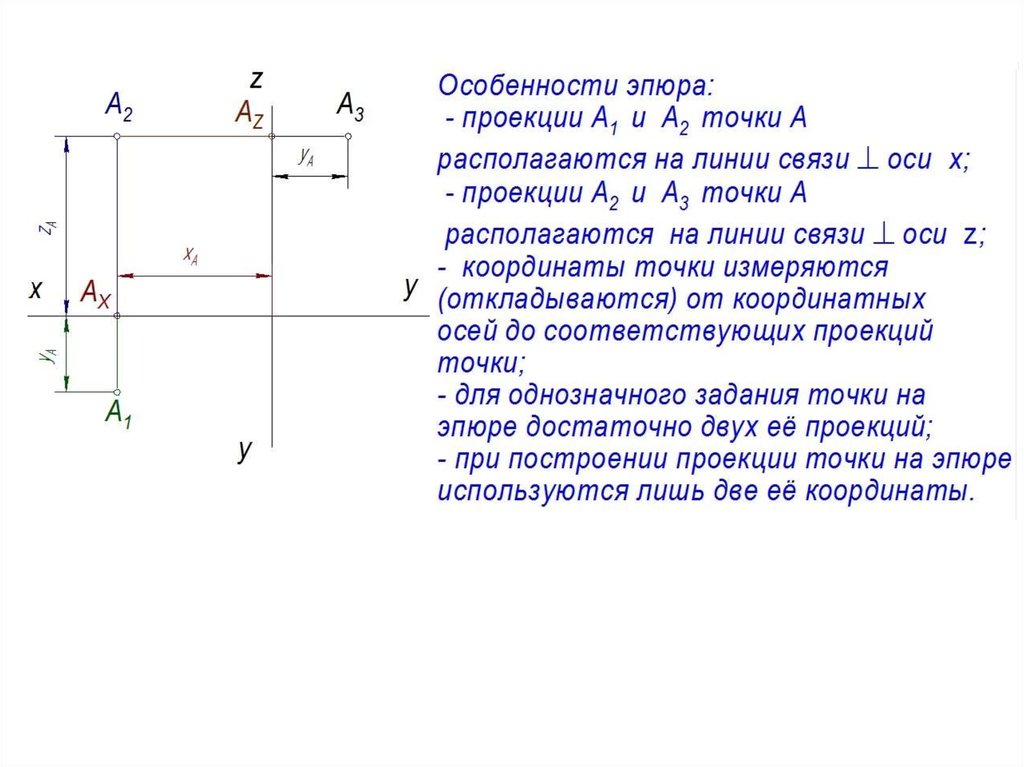
1. Пусть векторная проекция и ось L одинаково ориентированны (рис. 3.25). Тогда соответствующая скалярная проекция .
2. Пусть и L ориентированы в разные стороны (рис. 3.26).
Рис. 3.26. Нахождение векторной и скалярной проекций вектора на ось L ( и ось L ориентированы в противоположные стороны).
Таким образом, в обоих случаях справедливо утверждение теоремы.
ТЕОРЕМА 6. Если начало вектора приведено к некоторой точке оси L, и эта ось расположена в плоскости s, вектор образует с векторной проекцией на плоскость s угол , а с векторной проекцией на ось L — угол , кроме того сами векторные проекции образуют между собой угол , то
На чертежах изображения геометрических тел строятся при использовании метода проекции. Но для этого одного изображения недостаточно, необходимо минимум две проекции. С помощью них и определяются точки в пространстве. Следовательно, нужно знать, как найти проекцию точки.
Проекция точки
Для этого потребуется рассмотреть пространство двугранного угла, с расположенной внутри точкой (А).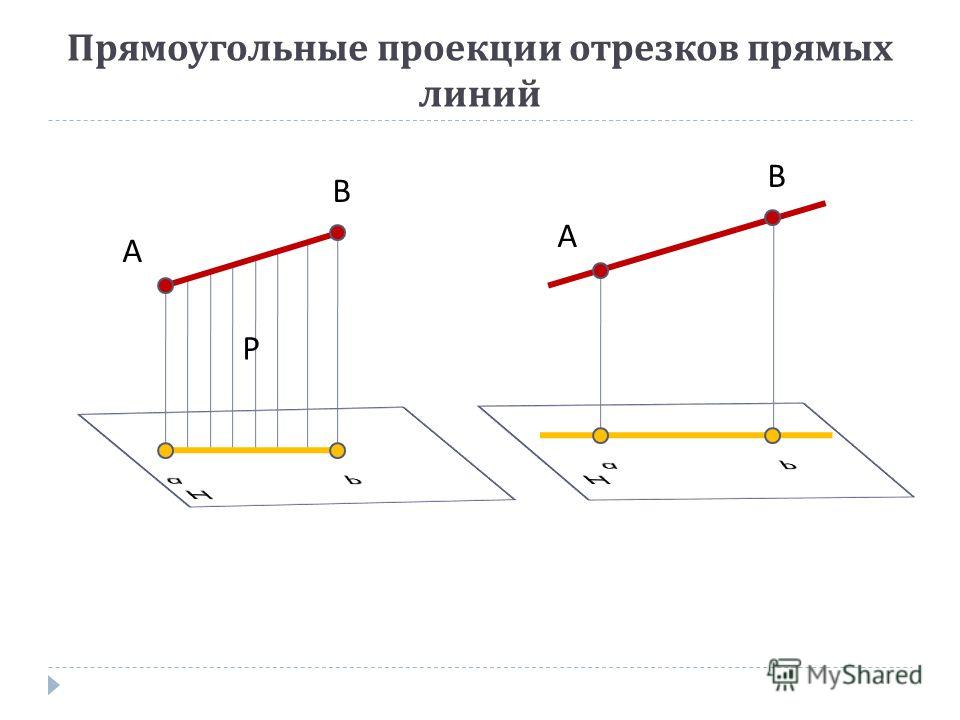 Здесь используются горизонтальная П1 и вертикальная П2 плоскости проекций. Точка (А) проецируется на проекционные плоскости ортогонально. Что касается перпендикулярных проецирующих лучей, то они объединяются в проецирующую плоскость, перпендикулярную плоскостям проекций. Таким образом, при совмещении горизонтальной П1 и фронтальной П2 плоскостей путем вращения по оси П2 / П1, получаем плоский чертеж.
Здесь используются горизонтальная П1 и вертикальная П2 плоскости проекций. Точка (А) проецируется на проекционные плоскости ортогонально. Что касается перпендикулярных проецирующих лучей, то они объединяются в проецирующую плоскость, перпендикулярную плоскостям проекций. Таким образом, при совмещении горизонтальной П1 и фронтальной П2 плоскостей путем вращения по оси П2 / П1, получаем плоский чертеж.
Затем перпендикулярно оси показывается линия с расположенными на ней точками проекции. Так получается комплексный чертеж. Благодаря построенным отрезкам на нем и вертикальной линии связи, легко можно определять положение точки относительно проекционных плоскостей.
Чтобы было проще понять, как найти проекцию, необходимо рассмотреть прямоугольный треугольник. Его короткая сторона является катетом, а длинная – гипотенузой. Если выполнить на гипотенузу проекцию катета, то она поделится на два отрезка. Для определения их величины, нужно выполнить расчет набора исходных данных. Рассмотрим на данном треугольнике, способы расчета основных проекций.
Как правило, в данной задаче указывают длину катета N и длину гипотенузы D, чью проекцию и требуется найти. Для этого узнаем, как найти проекцию катета.
Рассмотрим способ нахождения длины катета (А). Учитывая, что среднее геометрическое от проекции катета и длины гипотенузы равняется искомой нами величине катета: N = √(D*Nd).
Как найти длину проекции
Корень из произведения можно найти возведением в квадрат значения длины искомого катета (N), а затем поделенного на длину гипотенузы: Nd = (N / √ D)² = N² / D. При указании в исходных данных значений только катетов D и N, длину проекции следует находить при помощи теоремы Пифагора.
Найдем длину гипотенузы D. Для этого нужно воспользоваться значениями катетов √ (N² + T²), а затем подставить полученное значение в следующую формулу нахождения проекции: Nd = N² / √ (N² + T²).
Когда в исходных данных указаны данные о длине проекции катета RD, а также данные о величине гипотенузы D, следует вычислять длину проекции второго катета ND при помощи простой формулы вычитания: ND = D – RD.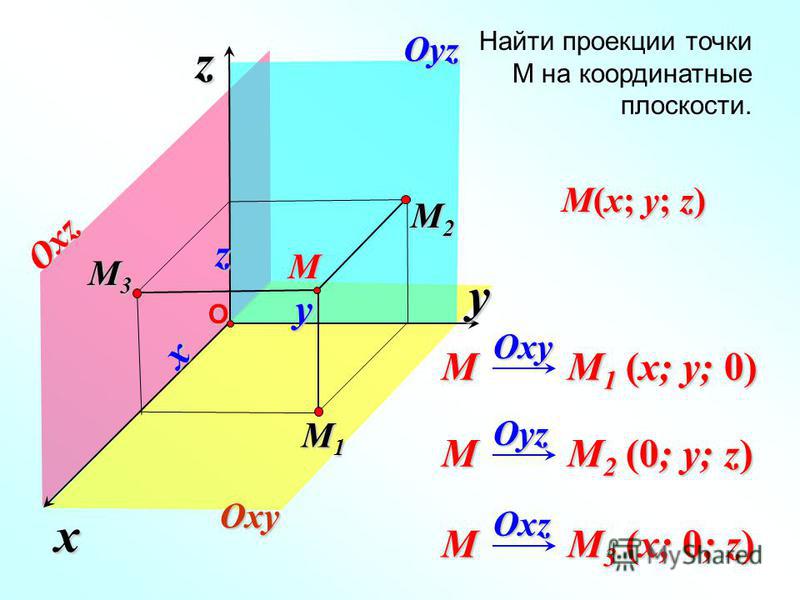
Проекция скорости
Рассмотрим, как найти проекцию скорости. Для того чтобы заданный вектор представлял описание движения, его следует разместить в проекции на координатные оси. Различают одну координатную ось (луч), две координатные оси (плоскость) и три координатные оси (пространство). При нахождении проекции необходимо из концов вектора опустить перпендикуляры на оси.
Для того чтобы уяснить значения проекции, необходимо узнать, как найти проекцию вектора.
Проекция вектора
При движении тела перпендикулярно относительно оси, проекция будет представлена в виде точки, и иметь значение равное нулю. Если же движение осуществляется параллельно координатной оси, то проекция будет совпадать с модулем вектора. В случае, когда тело движется таким образом, что вектор скорости направлен под углом φ относительно оси (х), проекция на данную ось будет являться отрезком: V(x) = V cos(φ), где V – это модель вектора скорости.Когда направления вектора скорости и координатной оси совпадают, то проекция является положительной, и наоборот. 2).
2).
Пусть в пространстве даны два вектора и . Отложим от произвольной точки O векторы и . Углом между векторами и называется наименьший из углов . Обозначается .
Рассмотрим ось l и отложим на ней единичный вектор (т.е. вектор, длина которого равна единице).
Под углом между вектором и осью l понимают угол между векторами и .
Итак, пусть l – некоторая ось и – вектор.
Обозначим через A 1 и B 1 проекции на ось l соответственно точек A и B . Предположим, что A 1 имеет координату x 1 , а B 1 – координату x 2 на оси l .
Тогда проекцией вектора на ось l называется разность x 1 – x 2 между координатами проекций конца и начала вектора на эту ось.
Проекцию вектора на ось l будем обозначать .
Ясно, что если угол между вектором и осью l острый, то x 2 > x 1 , и проекция x 2 – x 1 > 0; если этот угол тупой, то x 2 x 1
и проекция x 2 – x 1 l
, то x 2 = x 1 и x 2 – x 1 =0.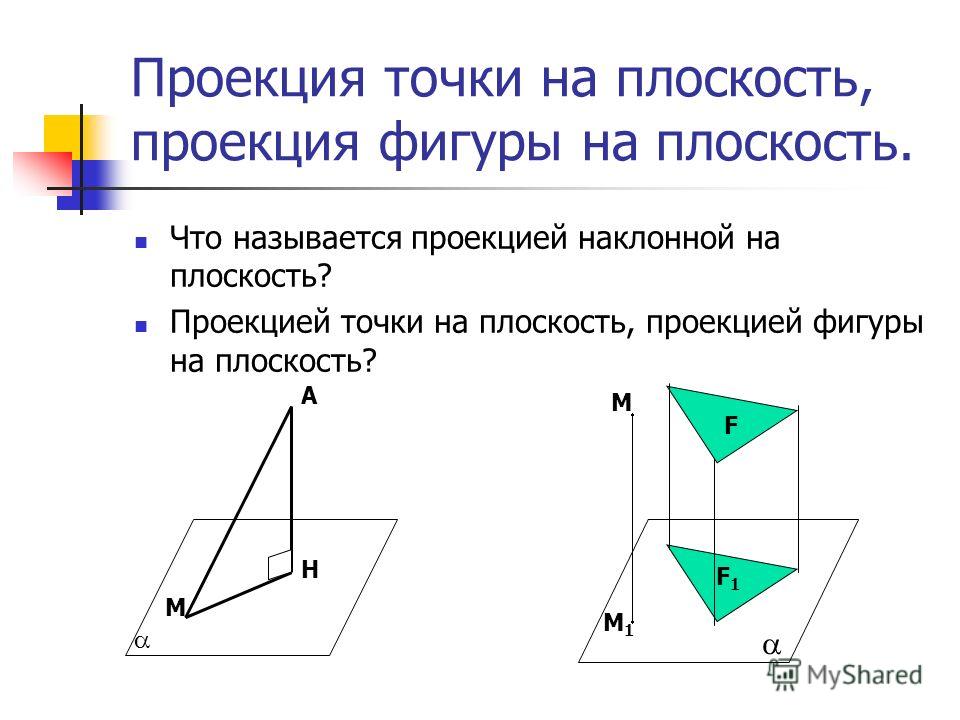
Таким образом, проекция вектора на ось l – это длина отрезка A 1 B 1 , взятая с определённым знаком. Следовательно, проекция вектора на ось это число или скаляр.
Аналогично определяется проекция одного вектора на другой. В этом случае находятся проекции концов даного вектора на ту прямую, на которой лежит 2-ой вектор.
Рассмотрим некоторые основные свойства проекций .
ЛИНЕЙНО ЗАВИСИМЫЕ И ЛИНЕЙНО НЕЗАВИСИМЫЕ СИСТЕМЫ ВЕКТОРОВ
Рассмотрим несколько векторов .
Линейной комбинацией данных векторов называется любой вектор вида , где — некоторые числа. Числа называются коэффициентами линейной комбинации. Говорят также, что в этом случае линейно выражается через данные векторы , т.е. получается из них с помощью линейных действий.
Например, если даны три вектора то в качестве их линейной комбинации можно рассматривать векторы:
Если вектор представлен как линейная комбинация каких-то векторов, то
говорят, что он разложен по этим
векторам.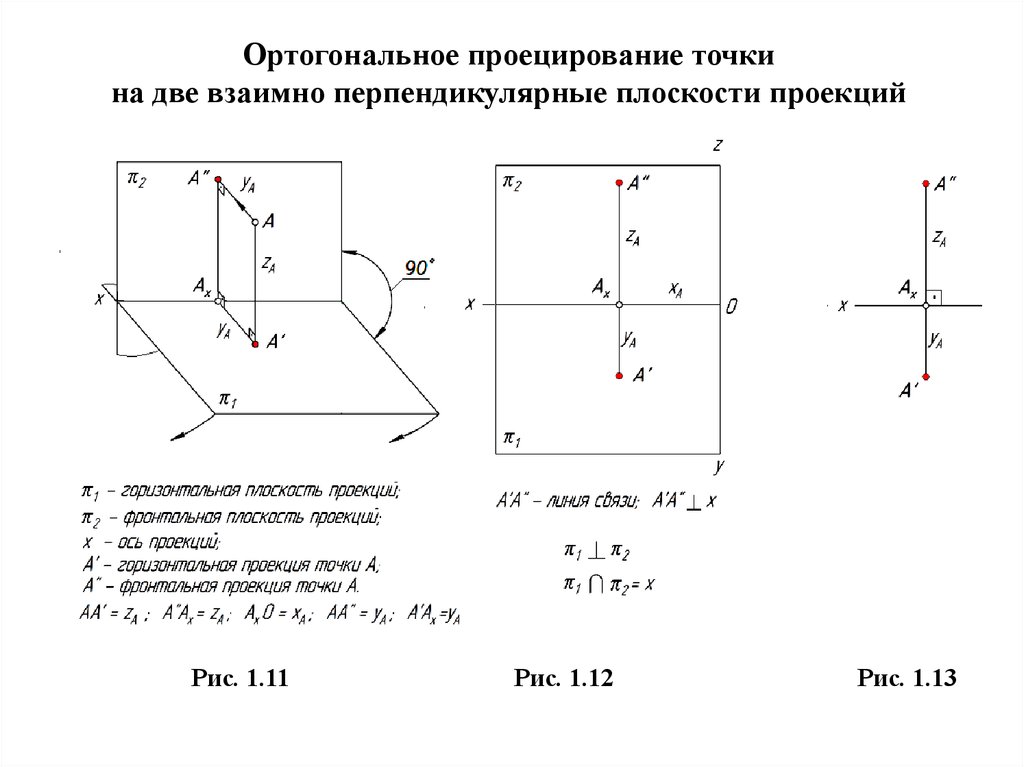
Векторы называются линейно зависимыми , если существуют такие числа, не все равные нулю, что . Ясно, что заданные векторы будут линейно зависимыми, если какой-либо из этих векторов линейно выражается через остальные.
В противном случае, т.е. когда соотношение выполняется только при , эти векторы называются линейно независимыми .
Теорема 1. Любые два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
Доказательство :
Аналогично можно доказать следующую теорему.
Теорема 2. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.
Доказательство .
БАЗИС
Базисом называется совокупность отличных от нулей линейно независимых векторов. Элементы базиса будем обозначать .
В предыдущем пункте мы видели, что два неколлинеарных вектора на
плоскости линейно независимы. Поэтому согласно теореме 1, из предыдущего
пункта, базисом на плоскости являются любые два неколлинеарных вектора на этой
плоскости.
Аналогично в пространстве линейно независимы любые три некомпланарных вектора. Следовательно, базисом в пространстве назовём три некомпланарных вектора.
Справедливо следующее утверждение.
Теорема. Пусть в пространстве задан базис . Тогда любой вектор можно представить в виде линейной комбинации , где x , y , z – некоторые числа. Такое разложение единственно.
Доказательство .
Таким образом, базис позволяет однозначно сопоставить каждому вектору тройку чисел – коэффициенты разложения этого вектора по векторам базиса: . Верно и обратное, каждой тройке чисел x, y, z при помощи базиса можно сопоставить вектор, если составить линейную комбинацию .
Если базис и , то числа x, y, z называются координатами вектора в данном базисе. Координаты вектора обозначают .
ДЕКАРТОВА СИСТЕМА КООРДИНАТ
Пусть в пространстве задана точка O и три некомпланарных вектора .
Декартовой системой координат в пространстве (на плоскости) называется совокупность точки и базиса, т.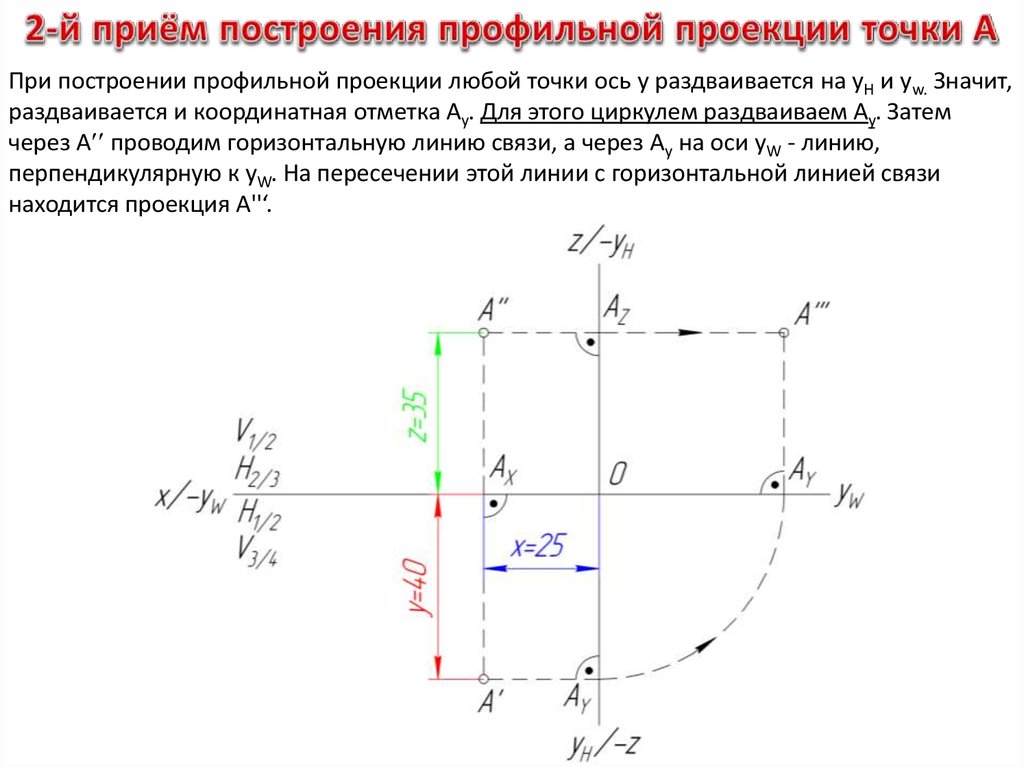 е.
совокупность точки и трёх некомпланарных векторов (2-х неколлинеарных векторов), выходящих из этой точки.
е.
совокупность точки и трёх некомпланарных векторов (2-х неколлинеарных векторов), выходящих из этой точки.
Точка O называется началом координат; прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат – осью абсцисс, ординат и аппликат. Плоскости, проходящие через оси координат, называют координатными плоскостями.
Рассмотрим в выбранной системе координат произвольную точку M . Введём понятие координаты точки M . Вектор , соединяющий начало координат с точкой M . называется радиус-вектором точки M .
Вектору в выбранном базисе можно сопоставить тройку чисел – его координаты: .
Координаты радиус-вектора точки M . называются координатами точки M . в рассматриваемой системе координат. M(x,y,z) . Первая координата называется абсциссой, вторая – ординатой, третья – аппликатой.
Аналогично определяются декартовы координаты на плоскости.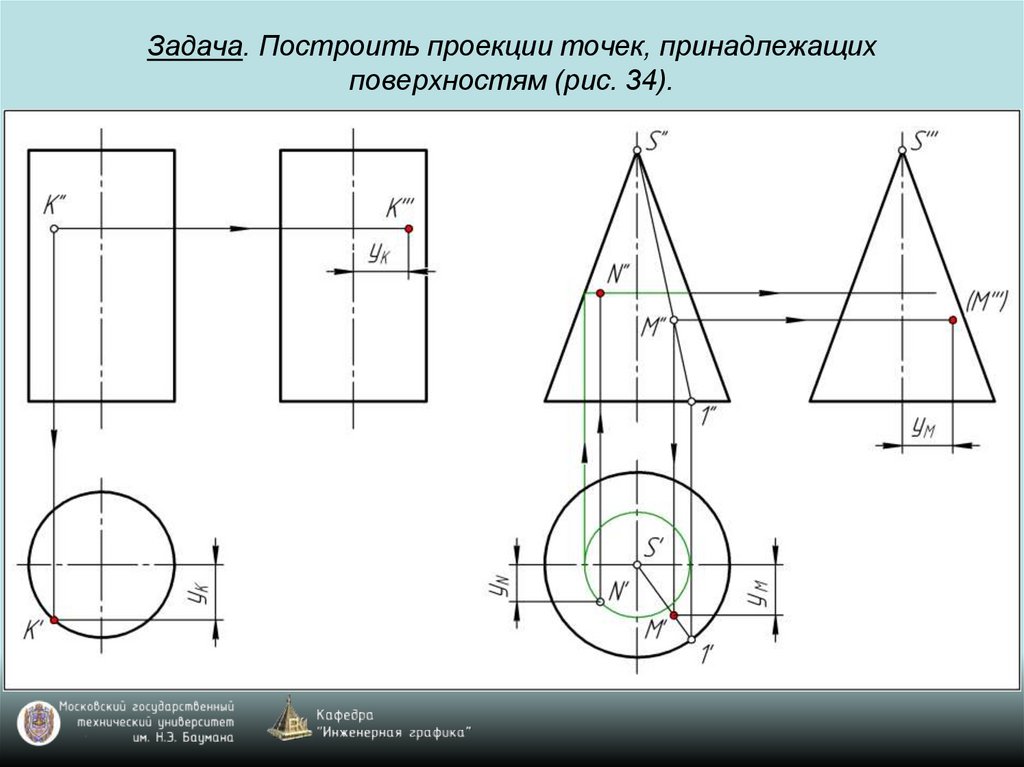 Здесь точка имеет только две координаты – абсциссу и ординату.
Здесь точка имеет только две координаты – абсциссу и ординату.
Легко видеть, что при заданной системе координат каждая точка имеет определённые координаты. С другой стороны, для каждой тройки чисел найдётся единственная точка, имеющая эти числа в качестве координат.
Если векторы, взятые в качестве базиса, в выбранной системе координат, имеют единичную длину и попарно перпендикулярны, то система координат называется декартовой прямоугольной.
Несложно показать, что .
Направляющие косинусы вектора полностью определяют его направление, но ничего не говорят о его длине.
Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:
Пр a b = |b|cos(a,b) или
Где a b — скалярное произведение векторов , |a| — модуль вектора a .
Инструкция
. Для нахождения проекции вектора Пp a b в онлайн режиме необходимо указать координаты векторов a и b . При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word
. Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор .
При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word
. Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор .
две координаты вектора
три координаты вектора
a: ; ;
b: ; ;
Классификация проекций вектора
Виды проекций по определению проекция вектора
Виды проекций по системе координат
Свойства проекции вектора
- Геометрическая проекция вектора есть вектор (имеет направление).
- Алгебраическая проекция вектора есть число.
Теоремы о проекциях вектора
Теорема 1 . Проекция суммы векторов на какую-либо ось равна проекции слагаемых векторов на ту же ось.
Теорема 2 . Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:
Пр a b = |b|cos(a,b)
Виды проекций вектора
- проекция на ось OX.

- проекция на ось OY.
- проекция на вектор.
| Проекция на ось OX | Проекция на ось OY | Проекция на вектор |
| Если направление вектора A’B’ совпадает с направлением оси OX, то проекция вектора A’B’ имеет положительный знак. | Если направление вектора A’B’ совпадает с направлением оси OY, то проекция вектора A’B’ имеет положительный знак. | Если направление вектора A’B’ совпадает с направлением вектора NM, то проекция вектора A’B’ имеет положительный знак. |
| Если направление вектора противоположно с направлением оси OX, то проекция вектора A’B’ имеет отрицательный знак. | Если направление вектора A’B’ противоположно с направлением оси OY, то проекция вектора A’B’ имеет отрицательный знак. | Если направление вектора A’B’ противоположно с направлением вектора NM, то проекция вектора A’B’ имеет отрицательный знак. |
Если вектор AB параллелен оси OX, то проекция вектора A’B’ равна модулю вектора AB. | Если вектор AB параллелен оси OY, то проекция вектора A’B’ равна модулю вектора AB. | Если вектор AB параллелен вектору NM, то проекция вектора A’B’ равна модулю вектора AB. |
| Если вектор AB перпендикулярен оси OX, то проекция A’B’ равна нулю (нуль-вектор). | Если вектор AB перпендикулярен оси OY, то проекция A’B’ равна нулю (нуль-вектор). | Если вектор AB перпендикулярен вектору NM, то проекция A’B’ равна нулю (нуль-вектор). |
1. Вопрос: Может ли проекция вектора иметь отрицательный знак. Ответ: Да, проекций вектора может быть отрицательной величиной. В этом случае, вектор имеет противоположное направление (см. как направлены ось OX и вектор AB)
2. Вопрос: Может ли проекция вектора совпадать с модулем вектора. Ответ: Да, может. В этом случае, векторы параллельны (или лежат на одной прямой).
3. Вопрос: Может ли проекция вектора быть равна нулю (нуль-вектор).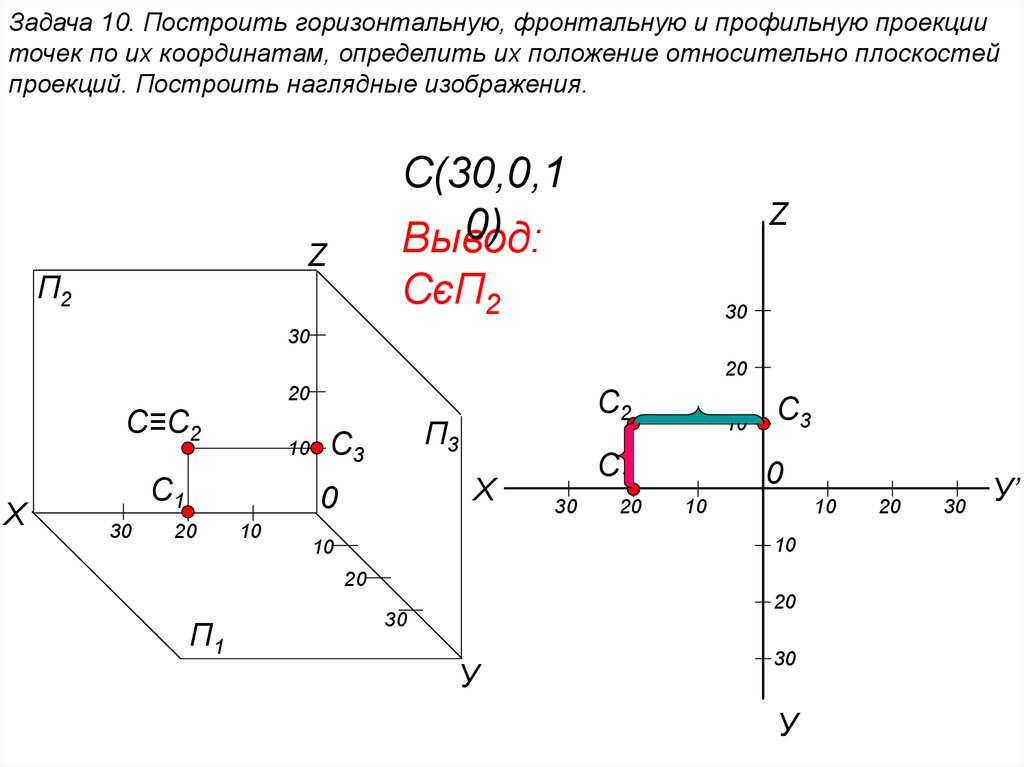 Ответ: Да, может. В этом случае вектор перпендикулярен соответствующей оси (вектору).
Ответ: Да, может. В этом случае вектор перпендикулярен соответствующей оси (вектору).
Пример 1
. Вектор (рис. 1) образует с осью OX (она задана вектором a) угол 60 о. Если OE есть единица масштаба, то |b|=4, так что .
Действительно, длина вектора (геометрической проекции b) равна 2, а направление совпадает с направлением оси OX.
Пример 2
. Вектор (рис. 2) образует с осью OX (с вектором a) угол (a,b) = 120 o . Длина |b| вектора b равна 4, поэтому пр a b=4·cos120 o = -2.
Действительно, длина вектора равна 2, а направление противоположно направлению оси.
а на ось или какой-либо другой вектор существуют понятия ее геометрической проекции и числовой (или алгебраической) проекции. Результатом геометрической проекции будет вектор, а результатом алгебраической – неотрицательное действительное число. Но перед тем, как перейти к этим понятиям вспомним необходимую информацию.
Предварительные сведения
Основное понятие – непосредственно понятие вектора.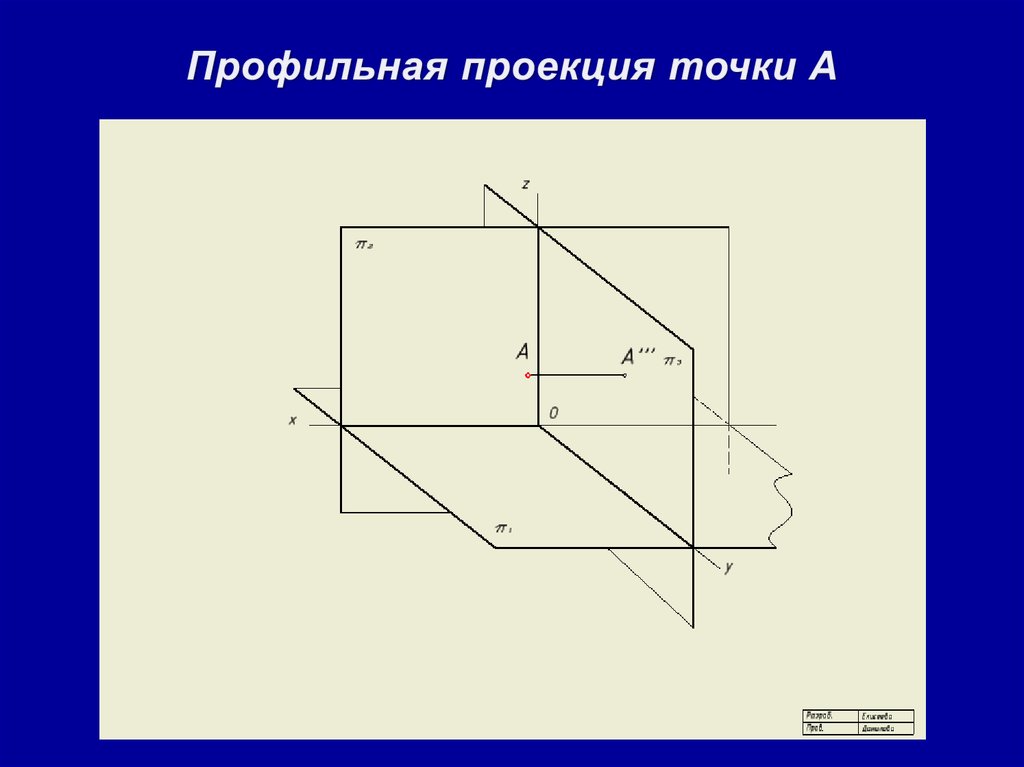 Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.
Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $\overline{a}$ (рис. 1).
Введем еще несколько понятий, связанных с понятием вектора.
Определение 3
Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой или на прямых, параллельных друг другу (рис.2).
Определение 4
Два ненулевых вектора будем называть сонаправленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.

- Если они будут направлены в одну сторону (рис. 3).
Обозначение: $\overline{a}\overline{b}$
Определение 5
Два ненулевых вектора будем называть противоположно направленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они направлены в разные стороны (рис. 4).
Обозначение: $\overline{a}↓\overline{d}$
Определение 6
Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|\overline{a}|$
Перейдем к определению равенства двух векторов
Определение 7
Два вектора будем называть равными, если они удовлетворяют двух условиям:
- Они сонаправлены;
- Их длины равны (рис. 5).
Геометрическая проекция
Как мы уже сказали ранее, результатом геометрической проекции будет вектор.
Определение 8
Геометрической проекцией вектора $\overline{AB}$ на ось будем называть такой вектор, который получается следующим образом: Точка начала вектора $A$ проецируется на данную ось.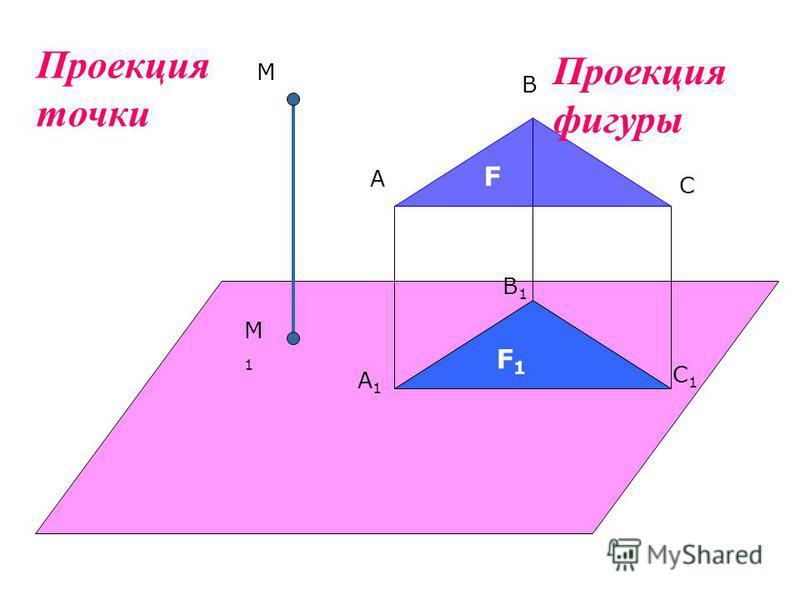 Получаем точку $A»$ — начало искомого вектора. Точка конца вектора $B$ проецируется на данную ось. Получаем точку $B»$ — конец искомого вектора. Вектор $\overline{A»B»}$ и будет искомым вектором.
Получаем точку $A»$ — начало искомого вектора. Точка конца вектора $B$ проецируется на данную ось. Получаем точку $B»$ — конец искомого вектора. Вектор $\overline{A»B»}$ и будет искомым вектором.
Рассмотрим задачу:
Пример 1
Постройте геометрическую проекцию $\overline{AB}$ на ось $l$, изображенные на рисунке 6.
Проведем из точки $A$ перпендикуляр к оси $l$, получим на ней точку $A»$. Далее проведем из точки $B$ перпендикуляр к оси $l$, получим на ней точку $B»$ (рис. 7).
Калькулятор векторной проекции
Создано Мирославом Йерковичем, доктором философии
Отредактировано Bogna Szyk и Jack Bowater
Последнее обновление: 31 августа 2022 г.
Содержание:- Что такое формула векторной проекции?
- Как вывести формулу векторной проекции?
- Как пользоваться калькулятором векторной проекции
- Векторная проекция в физике – игра с силами
- Каково применение векторных проекций в науке о данных?
- Часто задаваемые вопросы
Этот калькулятор векторной проекции находит ортогональную проекцию одного вектора на другой . Мы начинаем с двух векторов,
Мы начинаем с двух векторов, a и b , которые не лежат на одной прямой. Представьте себе источника света над векторами. Теперь подумайте о проекции вектора a на b как о тени , которую вектор a проецирует в направлении вектора b .
Вот почему этот тип вектора известен как ортогональная проекция вектор (отмечен как proj на изображении):
Представление векторной проекции в виде тени идет в том же направлении, что и вектор b ?Давайте теперь перейдем к деталям и обсудим формулу векторной проекции.
Что такое формула векторной проекции?
Вот формула ортогональной проекции вы можете использовать, чтобы найти проекцию вектора a на вектор b :
proj = (a·b / b·b) × b
В формуле используется скалярное произведение вектора, a ·b , также называемое скалярным произведением.
Но откуда взялась эта формула векторной проекции?
На изображении выше есть скрытый вектор. Это вектор , ортогональный вектору b, иногда также называемый вектором отклонения (обозначается цифрой 9).0045 или на изображении):
Векторная проекция и отклонениеКак вывести формулу векторной проекции?
Вот пошаговая процедура получения формулы векторной проекции:
Разложить вектор
aна сумму векторов проекции и отклонения:a = proj + ortЭкспресс проект как
проект = а-ортТакже с проект параллельно b, мы можем записать его как
proj = C × b, где C — некоторый неизвестный фактор, который мы хотим определитьТеперь у нас есть
C × b = a - ortВычислите скалярное произведение обеих частей этого уравнения с вектором b:
C × b·b = a·b - ort·bПоскольку вектор или ортогонален вектору b, их скалярное произведение равно нулю, и мы имеем
C × b·b = a·bНаконец, мы имеем
C = a·b / b·b.
Когда вы вставите это выражение для C в proj = C × b , вы получите формулу:
proj = (a·b / b·b) × b !
Поскольку в этой формуле используется скалярное произведение, которое может быть определено для векторов любой целочисленной размерности, эта формула охватывает векторы любой размерности . Его практическое применение для 2-D и 3-D векторов , поэтому наш калькулятор рассчитан на векторы с двумя или тремя компонентами.
Также имейте в виду, что эту формулу иногда называют формулой ортогональной проекции . Если бы мы следовали этой терминологии, нам пришлось бы называть наш калькулятор калькулятором ортогональной проекции . Нет большой разницы. В любом случае, это будет работать так же :)!
Как использовать калькулятор векторной проекции
Пусть a и b равны a = 2i -3j + 5k и б = 3i + 6j - 4k . С этого момента мы будем записывать эти трехмерные векторы в их компонентной форме
С этого момента мы будем записывать эти трехмерные векторы в их компонентной форме
a = [2, -3, 5] и b = [3, 6, -4] .
Используйте калькулятор проекции вектора, чтобы найти проекцию вектора a на вектор b . В результате мы получаем:
proj = [-1,5738, -3,1475, 2,0984]
Если вы хотите рассчитать проекцию вручную, используйте формулу векторной проекции p = (a·b / b·b) × b и выполните следующую пошаговую процедуру:
Вычислить скалярное произведение векторов a и b:
a·b = 2×3 + (-3)×6 + 5×(-4) = -32Вычислить скалярное произведение вектора b на самого себя:
b·b = 3×3 + 6×6 + (-4)×(-4) = 61Вставьте эти два скалярных произведения в формулу векторной проекции, чтобы получить
proj = (-32/61) × [3, 6, -4] = [-96/61, -192/61, 128/61].
Этот результат, выраженный в десятичном виде, равен результату, полученному этим калькулятором.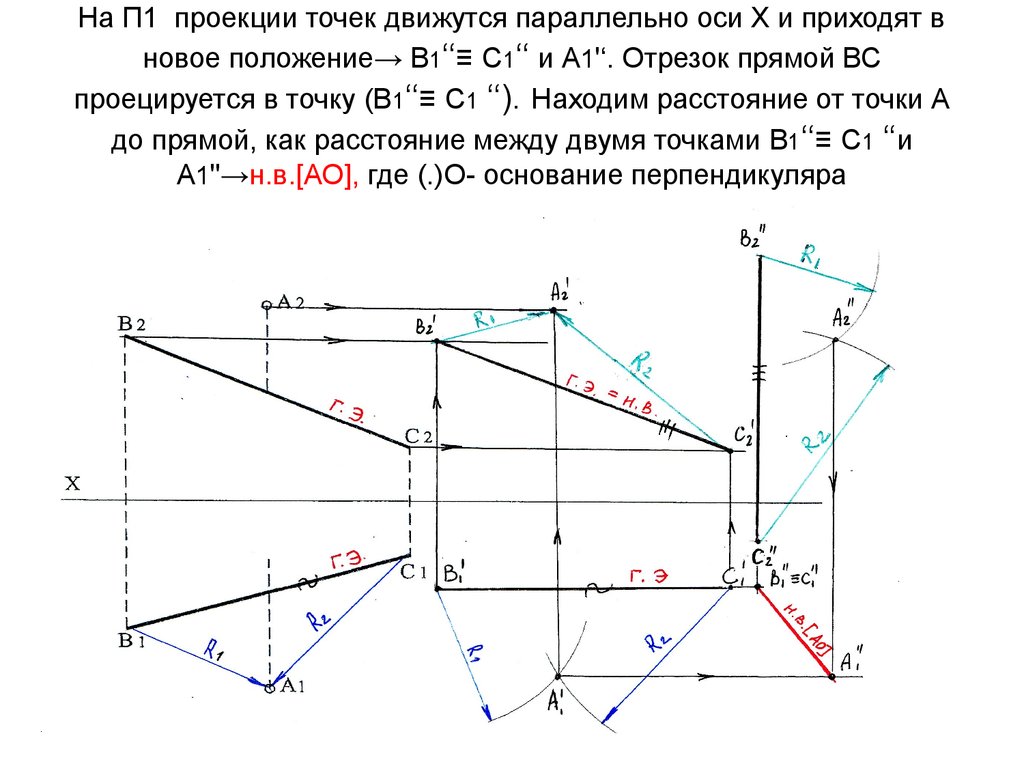
Возможно, вам интересно что происходит, когда a ортогонален b ; как выглядит проекция proj ? В этом случае тень вектора a, перпендикулярного b, должна отсутствовать, поэтому мы должны получить нулевой вектор.
Это отражено в формуле векторной проекции: если a и b ортогональны, их скалярное произведение равно нулю: a·b = 0 . Теперь у нас есть:
proj = (0 / b·b) × b = 0 × b = 0 .
Изучение этого особого случая показано в следующем примере:
a = [2, 6, -3] и b = [6, 4, 12] .
Не удивляйтесь, когда выскочит [0, 0, 0] , так как это правильный результат!
Векторная проекция в физике – игра с силами
Одно из самых простых и, возможно, самых интересных применений формулы векторной проекции связано с физикой сил и их разложением.
Представьте себе тележку , катящуюся по склону холма. Какую силу нужно приложить, чтобы уравновесить силу тележки? Конечно, эта противодействующая сила зависит от веса тележки: чем массивнее тележка, тем сложнее будет остановить . Также играет роль наклон самого холма — чем круче холм, тем больше силы вам понадобится чтобы остановить тележку. Вот изображение ситуации:
Также играет роль наклон самого холма — чем круче холм, тем больше силы вам понадобится чтобы остановить тележку. Вот изображение ситуации:
Здесь α — угол наклона холма относительно земли, а F — сила тяжести между телегой и Землей. Обратите внимание, что вектор F перпендикулярен земле, а не самому склону холма.
Чтобы найти силу, необходимую для уравновешивания действия силы тяжести на тележку, мы должны вычислить проекцию вектора силы F вдоль направления холма. Допустим, что F = 400 Н (что соответствует тележке массой около м = 40 кг ) и что наклон холма равен α = 45° .
Вопрос в том, как найти вектор вдоль направления склона холма , на который проецируется вектор силы F? Мы можем использовать любой вектор, который имеет то же направление, что и склон холма, поэтому наиболее удобным будет единичный вектор u = [cos 45°, sin 45°] , отмеченный синим вектором на изображении выше. Также для вектора силы F возьмем
Также для вектора силы F возьмем F = [0, -400] . Знак минус здесь означает, что сила F направлена вниз.
Воспользуйтесь калькулятором векторной проекции и выберите работу с векторами в двух измерениях, так как мы имеем дело с двумерной задачей . Итак, вектор а будет равен вектору силы F;
a = [0, -400] ,
, а вектор b получается из вектора u с помощью вычислителей синуса и косинуса, чтобы найти значения для sin 45° и cos 45° :
б = [0,70710678, 0,70710678] .
Работая с этими числами, получаем вектор проекции:
проект = [-200, -200] .
Поскольку мы хотим знать величину уравновешивающей силы , мы можем использовать калькулятор векторной величины, чтобы найти величину proj . Оно равно 282,84 N .
Если немного поиграть с наклоном холма, т. е. с углом α, то вы увидите, что чем менее узкий холм, тем меньшая сила вам потребуется, а в случае большего α – более крутого холма – вы потребуется большая требуемая реактивная сила.
Помимо физики и проблемы нахождения составляющей силы в заданном направлении, векторная проекция широко распространена в одном из самых модных реальных приложений науки, а именно в науке о данных.
Каковы применения векторных проекций в науке о данных?
Векторная проекция используется в важной статистической задаче линейной регрессии , а также в анализе главных компонентов , одном из наиболее часто используемых методов в наука о данных .
Здесь возникает задача представления множества, возможно, многомерных точек данных в пространстве меньшей размерности таким образом, чтобы потери информации были минимальными.
Часто задаваемые вопросы
Как вычислить проекцию вектора a на b?
Чтобы определить проекцию вектора a на вектор b :
- Вычислить скалярное произведение
a·b. - Вычислите скалярное произведение
b·b. Это то же самое, что квадрат нормы
Это то же самое, что квадрат нормы b. - Разделить результат шага 1 на результат шага 2. То есть
a·b / b·b. - Конечным результатом является коэффициент из шага 3, умноженный на вектор
b, на который мы проецируем:proj = (a·b / b·b) × b.
Какова длина проекции вектора?
Можно найти длину проекции вектора a на вектор b по формуле a·b / |b| , где a·b — скалярное произведение, а |b| — это длина вектора b (того, на который мы проецируем).
Какова проекция [3,4] на [1,1]?
Ответ: [3.5, 3.5] . Чтобы получить этот результат, мы применяем формулу proj = (a·b / b·b) b , где a = [3,4] и b = [1,1] . Действительно, имеем a·b = 7 и b·b = 2 , так что ответ легко следует.
Miroslav Jerkovic, PhD
Размеры
Вектор A
Вектор B
Проекция A на B
Проекционное коэффициент
Проверьте 38 аналогичные геометрические расчеты. подробнее
подробнее
Калькулятор векторной проекции — Найдите проекцию u на v
Получите мгновенный расчет проекции одного вектора на другой вектор с помощью этого бесплатного калькулятора векторной проекции. Да, определить тень одного вектора на другом теперь можно за пару кликов.
Так что оставайтесь с нами, чтобы понять, что это за физическая величина и как ее измерить с помощью этого бесплатного векторного калькулятора проекций.
Давайте углубимся немного дальше!
Что такое векторная проекция?
В физическом выражении:
«Длина тени, которую вектор создает поверх другого вектора, называется защитой вектора». используя следующую формулу: 92||} \vec{v} $$
Наш бесплатный калькулятор проекций также учитывает приведенное выше уравнение для расчета результирующего вектора, который будет отбрасывать контур своей величины над другим.
Скалярная проекция:
Скалярную резольвенту любого вектора можно легко вычислить с помощью следующего выражения:
$$ Скаляр \ Проекция \ | проект[\vec u]{\vec{v}}| = \frac{ \vec{v} \cdot \vec{u}}{|{\vec{u}}|}\ $$
Как найти векторную проекцию?
Несомненно, этот вектор калькулятора матричной проекции даст мгновенные результаты. Чтобы получить твердое представление о концепции, взгляните на следующие примеры:
Чтобы получить твердое представление о концепции, взгляните на следующие примеры:
Пример № 01:
Найдите проекцию вектора вектор B со значениями, указанными ниже:
$$ \vecA = 6\veci + 3\vecj + 8\veck $$
$$ \vecB = 3\veci + 7\vecj + 1\veck $$
Решение:
Здесь имеем:
92}.\Bigg(3,7,1\Bigg) $$$$ \ proj[\vec u]{\vec{v}}= \frac{47}{\Bigg(59\Bigg)}. \Bigg(3,7,1\Bigg) $$
$$ Вектор \ Projection \ proj[\vec
u]{\vec{v}}=\Bigg(\frac{141}{59},\frac {329}{59},\frac{47}{59}\Bigg) $$
Это требуемый ответ, который также можно определить с помощью этого калькулятора векторной проекции.
Как работает калькулятор векторной проекции?
Давайте посмотрим, как этот лучший калькулятор проекции u на v позволит вам вычислить проекцию одного вектора на другой вектор в мгновение ока:
Ввод:
- Прежде всего, выберите, хотите ли вы выполнять расчеты в системе 2D или системе 3D из первого списка
- После этого вам нужно выбрать, будете ли вы выбирать координаты или точки для первого вектора из второго раскрывающегося списка
- Теперь пришло время поместить значения первого вектора в назначенные им поля
- Повторите то же самое для второго вектора
- Когда вы закончите, нажмите кнопку расчета
Выход:
Лучший векторный калькулятор вычисляет:
- Векторная проекция
- Скалярная проекция
Часто задаваемые вопросы:
Что такое правило проецирования?
Закон о проекциях гласит:
«Если мы вычислим сумму двух сторон треугольника, образованного комбинацией векторов, она фактически будет равна третьей стороне»
Что такое ортогональная проекция?
Это средство отображения трехмерных объектов в пространстве в виде двухмерных объектов. Будучи особой формой параллельной проекции, она показывает линии, которые находятся точно под прямым углом к плоскости проекции. Этот бесплатный калькулятор ортогональной проекции также позволит вам мгновенно определить такую проекцию векторов.
Будучи особой формой параллельной проекции, она показывает линии, которые находятся точно под прямым углом к плоскости проекции. Этот бесплатный калькулятор ортогональной проекции также позволит вам мгновенно определить такую проекцию векторов.
В чем разница между 2D- и 3D-векторами проекций?
Двумерные векторы образуют плоское изображение, которое содержит только две координаты x и y. С другой стороны, 3D-вектор вводит другую координату Z, которая поможет вам глубже понять концепцию.
Почему мы используем орфографическую проекцию?
Орфографическая проекция позволяет анализировать каждую точку, нарисованную на векторном рисунке. Кроме того, это также поможет вам определить техническую информацию о векторных листах. И этот бесплатный калькулятор матрицы ортогональной проекции позволит вам оценить прямые углы, используемые в чертежах, чтобы уменьшить вероятность ошибки.
Вывод:
Векторная проекция — это метод в физике, помогающий вычислять недостающие компоненты вектора в прямоугольной системе координат. Это очень удобно для упрощения физических понятий, таких как сила и работа, чтобы лучше понять их. А что касается быстрых вычислений, этот лучший калькулятор векторной проекции всегда позволит вам сделать это без каких-либо препятствий.
Это очень удобно для упрощения физических понятий, таких как сила и работа, чтобы лучше понять их. А что касается быстрых вычислений, этот лучший калькулятор векторной проекции всегда позволит вам сделать это без каких-либо препятствий.
Ссылки:
Из источника Википедии: Векторная проекция, Нотация, Скалярная проекция, Векторная проекция, Скалярное отклонение, Векторное отклонение, Свойства
Из источника Академии Хана: проекция вектора на линию, скалярное произведение
Из источника Lumen Обучение: системы координат, полярные координаты, вектора в трех измерениях
Калькулятор векторной проекции — Решение с шагами
Вектор Projection Calculator — это пошаговый онлайн-калькулятор, который вычисляет проекцию одного вектора на другой. Он использует стандартную формулу векторной проекции, и независимо от ваших математических навыков, это довольно просто для всех. Важно отметить, что наш калькулятор векторной проекции можно использовать для поиска проекта как двумерных, так и трехмерных векторов. Помимо вычисления проекции одного вектора на другой, наш калькулятор также показывает коэффициент проекции.
Помимо вычисления проекции одного вектора на другой, наш калькулятор также показывает коэффициент проекции.
Кроме того, вы хотите узнать о перекрестном (векторном) произведении? Вы должны проверить всеобъемлющий Калькулятор перекрестного продукта.
Что такое вектор?
Вектор — это объект, состоящий из двух частей: величины и направления. Если мы посмотрим на вектор геометрически, мы будем считать его прямой линией, направление которой показано стрелкой. Величина вектора эквивалентна длине линии, тогда как направление выражается точкой, на которую указывает стрелка линии.
Как правило, два вектора остаются одинаковыми, если мы перемещаем их или меняем их положение, не влияя на их направление и величину. Наоборот, когда у нас есть два вектора и мы растягиваем его хвост или голову, мы уже не можем считать эти векторы одним и тем же. Однако независимо от того, насколько удалены векторы в системе координат, пока их направление (стрелка) и величина (длина линии) остаются неизменными, мы рассматриваем их как два равных вектора.
Тип векторов
Учитывая величину и направление векторов, мы разделяем их на шесть основных групп:
Нулевой или нулевой вектор
Нулевой или нулевой вектор — это вектор с величиной 0. Другими словами, нулевой вектор не имеет направления, а его начальная точка совпадает с конечной точкой.
Единичный вектор
Длина единичного вектора равна 1 единице. Например, вектор x с величиной x записывается как x̂.
Вектор положения
Вектор положения не указывает ничего, кроме конкретной точки на плоскости.
Соначальные векторы
Соначальный вектор говорит сам за себя. Два или более вектора с одной и той же начальной точкой считаются ко-начальными векторами.
Похожие и отличные векторы
Когда векторы указывают в одном направлении, мы называем их подобными векторами. В отличие от этого, когда два или более вектора имеют противоположное направление, мы считаем их неравноправными векторами.
Компланарные векторы
Если два вектора лежат в одной плоскости, мы считаем их компланарными векторами.
Коллинеарные или параллельные векторы
Если у нас есть два вектора, которые лежат в плоскости параллельно друг другу, мы называем их коллинеарными или параллельными векторами.
Равные векторы
Пока два вектора имеют одинаковую величину и направление, они равны независимо от их начальной и конечной точек.
Вектор смещения
Если точка смещена из точки A в точку B, вектор AB считается вектором смещения.
Отрицательный вектор
Предположим, мы представляем себе векторы a и b, предположительно. В этом случае они имеют одинаковую величину, но направлены в противоположные стороны — мы называем их отрицательными векторами. Другими словами, вектор b является отрицательным вектором a.
Угол между двумя векторами
Если мы рассмотрим два вектора и их положение в системе координат, они связаны друг с другом. Кроме того, мы можем вычислить или измерить угол между ними по следующей формуле:
Кроме того, мы можем вычислить или измерить угол между ними по следующей формуле:
cos \theta = \vec{a}.\vec{b} \div \left| а\право|.\лево| б\право|
Угол между двумя векторами равен косинусу угла между ними.
Скалярное произведение двух векторов
Скалярное произведение, или, проще говоря, (умножение двух векторов) — это математический расчет, который мы выполняем по следующей формуле:
\vec{a}.\vec{b} = a_ {1}b_{1} + a_{2}b_{2} + a_{3}b_{3}
Результатом этого вычисления является скалярная единица измерения или число, поэтому мы часто называем скалярным произведением скалярное произведение двух векторов. .
Проекция двух векторов
Проекция одного вектора на другой есть произведение их модулей и косеканса угла между ними. Например, предположим, что вектор a, спроецированный на вектор b, эквивалентен произведению вектора a и косеканса угла между векторами a и b. Значение, которое мы получаем из проекции, является скалярным.
Важно подчеркнуть, что величина вектора проекции является частью величины вектора a. Однако направление вектора проекции совпадает с направлением вектора b.
Формула векторной проекции
Уравнение векторной проекции = P = (a \cdot b \div b \cdot b) \times b!
Это стандартная формула векторной проекции, используемая для расчета проекции двумерных или трехмерных векторов. Поскольку в этой формуле используется ортогональный подход, теоретически было бы неправильным назвать ее и формулой ортогональной проекции.
Расчет векторной проекции с помощью нашего Калькулятора векторной проекции
Итак, мы увидели, как работает формула векторной проекции, но есть более простой способ расчета проекции двух векторов. Вместо того, чтобы вычислять его вручную, вы можете использовать наш бесплатный пошаговый онлайн-калькулятор векторной проекции, чтобы найти проекцию одного вектора на другой.
Перед вами наш калькулятор, но он кажется вам сложным или непонятным? Не волнуйтесь, потому что в этом разделе я объясню вам шаг за шагом процесс ввода значений координат двух векторов и вычисления проекции вектора a на вектор b. Итак, давайте запачкаем руки!
Итак, давайте запачкаем руки!
Шаги калькулятора проекции векторов:
1) Определить двумерные или трехмерные векторы
2) Предположим, у вас есть два двумерных вектора (вектор a [2, 8] и вектор b [1, 5]
3) Введите значения в соответствующие поля калькулятора
4) Вы можете выбрать ввод значений векторов в виде координат или точек (как вам больше нравится)
5) Посмотрите на скалярный результат
Проекция a на b = [ 1,6154, 8,077]
Коэффициент проекции = 1,6154
1,6154 – проекция на ось x
8,077 – проекция на ось y используем в своих расчетах. Скаляр — это значение (число), тогда как вектор — это не только число (величина), но и композиция величины и направления. Направление — это то, что отличает векторы от скаляров.
Имея это в виду, давайте установим формулы как для скалярной, так и для векторной проекций и прокомментируем различия в их подходах.
Скалярная проекция вектора b на a = (скалярное произведение a и b) \div (длина вектора b)
Для скалярных проекций мы сначала находим скалярное произведение векторов a и b, а затем делим это значение на длину вектора b.
Векторная проекция вектора b на a = Скалярная проекция вектора b \times (Единичный вектор a)
Для скалярных проекций мы сначала находим скалярное произведение векторов a и b, а затем делим это значение на длину вектора b.
Трехмерная проекция вектора
Трехмерная проекция одного вектора на другой использует тот же подход, что и двумерные векторы. Однако единственная разница заключается в количестве задействованных осей. Это связано с тем, что трехмерные векторы лежат в трехмерной системе координат и имеют свойства x, y, z. В приведенном выше примере мы показали, как рассчитывать векторные проекты, но для 2D-векторов. Поэтому давайте снова воспользуемся нашим пошаговым калькулятором векторной проекции и рассчитаем векторную проекцию двух 3D-векторов.
Вектор a [8, -2, 4]
Вектор b [2, 6, 1]
Проекция вектора [0,39024, 1,1707, 0,19512]
Коэффициент проекции = 0,19512
Реальные приложения векторной проекции
Одно из частых применений векторной проекции мы можем найти в физике для нахождения проекции силы в заданном направлении. Однако инженеры-строители сочли его полезным для измерения прочности материалов и конструкций. Кроме того, формула векторной проекции имеет решающее значение в навигационных системах космических кораблей и самолетов.
Однако инженеры-строители сочли его полезным для измерения прочности материалов и конструкций. Кроме того, формула векторной проекции имеет решающее значение в навигационных системах космических кораблей и самолетов.
По сути, все, что включает линейную алгебру, косвенно или напрямую использует формулу векторной проекции, например, машинное обучение и наука о данных. Кроме того, разработчики программного обеспечения используют векторные проекции при работе с матрицами и их умножениями.
Часто задаваемые вопросы
Что такое векторная проекция ?
Когда мы проецируем вектор на другой, мы разбиваем его на два составных вектора, один из которых параллелен второму вектору, а другой перпендикулярен второму вектору.
Как рассчитать векторную проекцию ?
Мы вычисляем проекцию одного вектора на другой, умножая их величины на косеканс угла между ними. Другими словами, векторная проекция векторов a и b эквивалентна произведению вектора a на косеканс угла между векторами a и b.
Другими словами, векторная проекция векторов a и b эквивалентна произведению вектора a на косеканс угла между векторами a и b.
Формула векторной проекции: P = (a \cdot b \div b \cdot b) \times b!
Как найти скалярную и векторную проекции
Скалярные проекции можно найти по следующей формуле:
Скалярная проекция вектора b на a = (точечный продукт a и b) \div (длина вектора b)
Векторные проекции можно найти по следующей формуле :
Векторная проекция вектора b на a = Скалярная проекция вектора b \times (Единичный вектор a)
Ортогональная проекция
Цели
- Понимать ортогональное разложение вектора относительно подпространства.
- Понимать взаимосвязь между ортогональной декомпозицией и ортогональной проекцией.
- Понять взаимосвязь между ортогональным разложением и ближайшим вектором на/расстоянии до подпространства.
- Изучите основные свойства ортогональных проекций как линейных преобразований и матричных преобразований.

- Рецепты: ортогональная проекция на прямую, ортогональная декомпозиция путем решения системы уравнений, ортогональная проекция через сложное матричное произведение.
- Картинки: ортогональное разложение, ортогональная проекция.
- Словарные слова: ортогональная декомпозиция , ортогональная проекция .
Пусть W — подпространство в Rn, и пусть x — вектор в Rn. В этом разделе мы научимся вычислять ближайший вектор xW к x в W. Вектор xW называется ортогональной проекцией x на W. Это именно то, что мы будем использовать для почти решения матричных уравнений, как обсуждалось во введении к главе 6.
Начнем с исправления некоторых обозначений.
Обозначение
Пусть W — подпространство в Rn, и пусть x — вектор в Rn. Обозначим ближайший к x вектор на W через xW.
Сказать, что xW является ближайшим вектором к x на W, означает, что разность x−xW ортогональна векторам в W:
WxWxx−xW Другими словами, если xW⊥=x−xW, то мы имеем x=xW+xW⊥, где xW принадлежит W, а xW⊥ принадлежит W⊥. Первым делом нужно доказать, что ближайший вектор всегда существует.
Первым делом нужно доказать, что ближайший вектор всегда существует.
Теорема (ортогональное разложение)
Пусть W — подпространство в Rn, и пусть x — вектор в Rn. Тогда мы можем однозначно записать x как
.х=хШ+хШ⊥
, где xW — ближайший к x вектор на W, а xW⊥ — в W⊥.
Доказательство
Пусть m=dim(W), поэтому n−m=dim(W⊥) по этому факту в разделе 6.2. Пусть v1,v2,…,vm — базис для W и пусть vm+1,vm+2,…,vn — базис для W⊥. При доказательстве этого факта в разделе 6.2 мы показали, что {v1,v2,…,vm,vm+1,vm+2,…,vn} линейно независима, поэтому образует базис для Rn. Следовательно, мы можем написать
x=(c1v1+···+cmvm)+(cm+1vm+1+···+cnvn)=xW+xW⊥,
, где xW=c1v1+···+cmvm и xW⊥=cm+1vm+1+···+cnvn. Поскольку xW⊥ ортогонален W, вектор xW является ближайшим вектором к x на W, что доказывает, что такое разложение существует.
Что касается уникальности, предположим, что
х=хW+xW⊥=yW+yW⊥
для xW,yW в W и xW⊥,yW⊥ в W⊥. Перестановка дает
Перестановка дает
хW-yW=yW⊥-xW⊥.
Поскольку W и W⊥ являются подпространствами, левая часть уравнения находится в W, а правая — в W⊥. Следовательно, xW−yW находится в W и в W⊥, поэтому он ортогонален самому себе, что влечет xW−yW=0. Следовательно, xW=yW и xW⊥=yW⊥, что доказывает единственность.
Определение
Пусть W — подпространство в Rn, и пусть x — вектор в Rn. Выражение
х=хШ+хШ⊥
для xW в W и xW⊥ в W⊥, называется ортогональным разложением x относительно W, а ближайший вектор xW является ортогональной проекцией x на W.
Поскольку xW является ближайшим вектором на W до x расстояние от x до подпространства W есть длина вектора от xW до x, т. е. длина xW⊥. Повторюсь:
Ближайший вектор и расстояние
Пусть W — подпространство в Rn, и пусть x — вектор в Rn.
- Ортогональная проекция xW является ближайшим вектором к x в W.
- Расстояние от x до W равно BxW⊥B.
Пример (ортогональное разложение относительно плоскости xy)
Пример (Ортогональное разложение вектора в W)
Пример (Ортогональное разложение вектора в W⊥)
Интерактив: Ортогональное разложение в R2
Интерактив: ортогональная декомпозиция в R3
Интерактив: ортогональная декомпозиция в R3
Теперь обратимся к задаче вычисления xW и xW⊥. Конечно, поскольку xW⊥=x−xW, на самом деле все, что нам нужно, это вычислить xW. Следующая теорема дает метод вычисления ортогональной проекции на столбцовое пространство. Чтобы вычислить ортогональную проекцию на общее подпространство, обычно лучше всего переписать подпространство как пространство-столбец матрицы, как в этом важном примечании в разделе 2.6.
Конечно, поскольку xW⊥=x−xW, на самом деле все, что нам нужно, это вычислить xW. Следующая теорема дает метод вычисления ортогональной проекции на столбцовое пространство. Чтобы вычислить ортогональную проекцию на общее подпространство, обычно лучше всего переписать подпространство как пространство-столбец матрицы, как в этом важном примечании в разделе 2.6.
Теорема
Пусть A — матрица размера m×n, пусть W=Col(A), и пусть x — вектор в Rm. Тогда матричное уравнение
ATAc=ATx
в неизвестном векторе c непротиворечиво, и xW равно Ac для любого решения c.
Доказательство
Пусть x=xW+xW⊥ — ортогональное разложение относительно W. По определению xW лежит в W=Col(A), поэтому в Rn существует вектор c, для которого Ac=xW. Выберите любой такой вектор c. Мы знаем, что x−xW=x−Ac лежит в W⊥, который равен Nul(AT) благодаря этому важному примечанию в разделе 6.2. Таким образом, мы имеем
0=AT(x-Ac)=ATx-ATAc
и так
ATAc=ATx.
Это точно означает, что ATAc=ATx непротиворечиво. Если c является любым решением ATAc=ATx, то, обращая приведенную выше логику, мы заключаем, что xW=Ac.
Пример (ортогональная проекция на прямую)
Пусть L=Span{u} — прямая в Rn, а x — вектор в Rn. По теореме, чтобы найти xL, мы должны решить матричное уравнение uTuc=uTx, где мы рассматриваем u как матрицу размера n × 1 (столбец этой матрицы равен L!). Но uTu=u·u и uTx=u·x, поэтому c=(u·x)/(u·u) является решением уравнения uTuc=uTx, и, следовательно, xL=uc=(u·x)/(u· у)у.
LuxxL=u·xu·uuxL⊥Повторить:
Рецепт: Ортогональная проекция на прямую
Если L=Span{u} является линией, то
xL=u·xu·uuandxL⊥=x−xLдля любого вектора x.
Пример (Проекция на строку в R2)
Пример (Проекция на строку в R3)
Когда A является матрицей с более чем одним столбцом, вычисление ортогональной проекции x на W=Col(A) означает решение матричного уравнения ATAc=ATx. Другими словами, мы можем вычислить ближайший вектор на решение системы линейных уравнений . Для ясности сформулируем теорему как рецепт:
Для ясности сформулируем теорему как рецепт:
Рецепт: вычисление ортогонального разложения
Пусть W — подпространство в Rm. Вот метод вычисления ортогонального разложения вектора x относительно W:
- Перепишите W как пространство столбцов матрицы A. Другими словами, найдите остовное множество для W и пусть A будет матрицей с этими столбцами.
- Вычислить матрицу ATA и вектор ATx.
- Сформируйте расширенную матрицу для матричного уравнения ATAc=ATx в неизвестном векторе c и уменьшите строку.
- Это уравнение всегда непротиворечиво; выбрать одно решение c. затем
хW=AcxW⊥=x−xW.
Пример (проекция на плоскость xy)
Пример (Проекция на плоскость в R3)
Пример (Проекция на другую плоскость в R3)
Пример (Проекция на 3-пространство в R4)
В контексте приведенного выше рецепта, если мы начнем с по основанию Вт, то получается, что квадратная матрица АТА автоматически обратима! (Всегда случается, что ATA является квадратным, и уравнение ATAc=ATx непротиворечиво, но в общем случае ATA не обязательно должно быть обратимым. )
)
Следствие
Пусть A — матрица размера m×n с линейно независимыми столбцами, и пусть W=Col(A). Тогда матрица ATA размера n×n обратима, и для всех векторов x в Rm имеем
xW=A(ATA)−1ATx.
Доказательство
Мы покажем, что Nul(ATA)={0}, что подразумевает обратимость по теореме об обратимой матрице в разделе 5.1. Предположим, что ATAc=0. Тогда ATAc=AT0, поэтому по теореме 0W=Ac. Но 0W=0 (ортогональное разложение нулевого вектора равно 0=0+0), поэтому Ac=0, и, следовательно, c находится в Nul(A). Поскольку столбцы A линейно независимы, мы имеем c = 0, поэтому Nul (ATA) = 0, что и требовалось.
Пусть x — вектор в Rn, а c — решение уравнения ATAc=ATx. Тогда c=(ATA)−1ATx, поэтому xW=Ac=A(ATA)−1ATx.
Следствие применимо, в частности, к случаю, когда у нас есть подпространство W в Rm и базис v1,v2,…,vn для W. Чтобы применить следствие, мы возьмем A как матрицу размера m × n со столбцами в1,в2,…,вн.
Пример (вычисление проекции)
В этом подразделе мы изменим перспективу и представим ортогональную проекцию xW как функцию от x. Эта функция оказывается линейным преобразованием со многими замечательными свойствами и является хорошим примером линейного преобразования, которое изначально не было определено как матричное преобразование.
Эта функция оказывается линейным преобразованием со многими замечательными свойствами и является хорошим примером линейного преобразования, которое изначально не было определено как матричное преобразование.
Свойства ортогональных проекций
Пусть W — подпространство Rn, и определим T:Rn→Rn равенством T(x)=xW. Тогда:
- T — линейное преобразование.
- T(x)=x тогда и только тогда, когда x находится в W.
- T(x)=0 тогда и только тогда, когда x принадлежит W⊥.
- Т◦Т=Т.
- Диапазон Т составляет Вт.
Мы вычисляем стандартную матрицу ортогональной проекции так же, как и для любого другого преобразования: оценивая стандартные координатные векторы. В данном случае это означает проецирование стандартных векторов координат на подпространство.
Пример (Матрица проекции)
Пример (Матрица проекции)
Пример (Матрица проекции)
В предыдущем примере мы могли бы использовать тот факт, что
ЭК10-1Д, К110ДФ
образует базис для W, так что
T(x)=xW=AA(ATA)−1ATBxforA=C1101−10D
по следствию. В этом случае мы уже выразили T как матричное преобразование с матрицей A(ATA)−1AT. См. этот пример.
В этом случае мы уже выразили T как матричное преобразование с матрицей A(ATA)−1AT. См. этот пример.
Пусть W — подпространство в Rn с базисом v1,v2,…,vm, и пусть A — матрица со столбцами v1,v2,…,vm. Тогда стандартная матрица для T(x)=xW равна
.А(АТА)-1АТ.
Мы можем преобразовать вышеуказанные свойства ортогональных проекций в свойства соответствующей стандартной матрицы.
Свойства проекционных матриц
Пусть W — подпространство в Rn, определим T:Rn→Rn как T(x)=xW, и пусть B — стандартная матрица для T. Тогда:
- Цвет(B)=W.
- Нуль(В)=W⊥.
- В2=В.
- Если WA={0}, то 1 является собственным значением B, а 1-собственное пространство для B равно W.
- Если WA=Rn, то 0 является собственным значением B, а 0-собственное пространство для B равно W⊥.
- B аналогична диагональной матрице с m единицами и n−m нулями на диагонали, где m=dim(W).
Подчеркнем, что свойства проекционных матриц было бы очень трудно доказать в терминах матриц. Переводя все утверждения в утверждения о линейных преобразованиях, они становятся намного более прозрачными. Например, рассмотрим матрицу проекции, которую мы нашли в этом примере. Просто взглянув на матрицу, совсем не очевидно, что, когда вы возводите матрицу в квадрат, вы получаете ту же самую матрицу.
Переводя все утверждения в утверждения о линейных преобразованиях, они становятся намного более прозрачными. Например, рассмотрим матрицу проекции, которую мы нашли в этом примере. Просто взглянув на матрицу, совсем не очевидно, что, когда вы возводите матрицу в квадрат, вы получаете ту же самую матрицу.
Пример
Комментарии, исправления или предложения? (Требуется бесплатная учетная запись GitHub)
Как найти проекцию точки на линию
Более общие понятия см. в разделах «Линейная алгебра проекций» и «Математика проекций». Проекция a на b a1 и отклонение a от b a2. При 90 < 180 a1 имеет противоположное направление по отношению к b. Векторная проекция вектора a на или на ненулевой вектор b, иногда обозначаемый как proj b, является ортогональной проекцией a на плоскость или вообще гиперплоскость.
В математике проективная геометрия — это изучение геометрических свойств, инвариантных относительно В двух измерениях она начинается с изучения конфигураций точек и линий. Понселе исследовал проективные свойства объектов, инвариантных относительно центральной проекции, и основывал свою теорию на конкретном полюсе.
Понселе исследовал проективные свойства объектов, инвариантных относительно центральной проекции, и основывал свою теорию на конкретном полюсе.
Как я уже говорил, PCA найдет лучшую линию в соответствии с двумя различными критериями того, что является Становится ясно, что дисперсия любой проекции будет определяться я обычно только на StackOverflow, и я был на StackExchange Нет независимо от того, как повернут эллипсоид, собственные векторы указывают на эти главные.
. пытается перечислить некоторые из общих вопросов, которые часто задают, например. о переполнении стека. Проекцию вашей карты можно задать через свойство view. импортировать карту из ‘ol/Map’; импортировать View из ‘ol/View’; // OpenLayers поставляется с Рекомендуемым значением является размер наибольшей ширины линии символа или метки.
В частности, это касается перспективных проекций на плоскости z оси a и o. Рецепты: ортогональная проекция на прямую ортогональное разложение путем решения Введите матрицу, и этот калькулятор покажет вам шаг за шагом, как вычислить значение, фиксированное однозначным определением, часто называемым символ е.
вид глаз’ с похожими чертами, то мы должны разместиться где-то в воздухе. Когда мы это делаем Аэрофотосъемка: фотография, сделанная с бортовой платформы с использованием точной оси, в то время как отвесная линия, проведенная от центра объектива к фотоплоскости, является известным примером центральной проекции. Проектирование.
необходимая основа для будущего изучения математики. Каждый раз, когда в длинном ряду пенни было больше монет, чем в более коротком ряду, согласно прогнозам занятости BLS до 2008 г. NAB Workforce Mullis I.V.S. М.О. Мартин Э.Дж. Гонсалес К.Д. Грего Рай Р.А. Гарден Рэндольф и А. Бейкер 440. Вашингтон.
Проекция Фишера состоит из горизонтальных и вертикальных линий. Первый пример превращает трехмерную структуру этана в двухмерную проекцию Фишера. Обратите внимание, что атомы красных шариков на рисунке А выше направлены в сторону от синих атомов, расположенных в плоскости экрана, поэтому они обозначены прямыми линиями.
Вы можете увидеть на Stack Overflow Trends то, чем был Python. У нас есть данные о представлениях вопросов Stack Overflow, начиная с конца 2011 года. Вы можете найти ответы на многие вопросы, скажем, в Java, поэтому новые пользователи не будут задавать новые вопросы. просто ужасное использование статистики, не связанной с этим.
У нас есть данные о представлениях вопросов Stack Overflow, начиная с конца 2011 года. Вы можете найти ответы на многие вопросы, скажем, в Java, поэтому новые пользователи не будут задавать новые вопросы. просто ужасное использование статистики, не связанной с этим.
Я новый директор отдела открытых вопросов и ответов в Stack Overflow. Дальше произошло то, что, с моей точки зрения, инженерная команда полностью растерялась. слова, которые написаны, но проецируют собственный эмоциональный отклик вместо В случае полных вопросов nohoper 90-строчная программа, которая должна.
точек с нуля coords cbindx y sp SpatialPointscoords # создание строк из одной или нескольких линий Ls1 LineslistL1 ID a Ls2 LineslistL2 L3 ncols valuesr3 runifnrows ncols # многоканальный стек s1 stacklistr1 r2 r3 SpatialLineslistLs1 proj4string CRSlatlong # Растровая CRS-проекция1.
Это форма параллельной проекции, при которой все линии проекции ортогональны плоскости сцены, появляющейся при аффинном преобразовании на поверхности просмотра. Инверсия матрицы проекции, которую можно использовать как непроекцию.
Инверсия матрицы проекции, которую можно использовать как непроекцию.
Этот онлайн-калькулятор поможет вам рассчитать произведение двух матриц. Чтобы найти изображение точки, мы умножаем матрицу преобразования на столбец из 176 сообществ вопросов и ответов, включая Stack Overflow — крупнейшее и наиболее надежное онлайн-сообщество.
Один из способов сделать это — найти точку на плоскости, а затем попытаться перевести все в исходную точку. Когда мы проецировали на линию, у A был только один столбец, поэтому это уравнение выглядело так: aTb xa 0. Нью-реддит коронавирус.
Проекции говорят нам, какая часть одного вектора лежит в направлении другого, и важны для использования скалярных произведений для вычисления угла между векторами. эту страницу и необходимо запросить альтернативный формат, свяжитесь с [email protected].
Затем мы описываем SVM линейных опорных векторов для разделяемых и не определяющих, на какой стороне линии точки должны быть назначены меткой 1. проекции Гессе или не более чем за l шагов с использованием сопряженного градиентного подъема.
проекции Гессе или не более чем за l шагов с использованием сопряженного градиентного подъема.
Проекции в линейной алгебре Начало темы Допустим, у меня есть линия, которая проходит через фразу ортогональная проекция даже для комплексных векторных пространств. Lineare Algebra Wikipedia Лекция 15: Проекции на подпространства Linear.
Каково определение проекции в строгом линейно-алгебраическом смысле этого слова. https://en.wikipedia.org/wiki/Projectionlinearалгебра Вторая строка представляет собой случайный единичный вектор из пространства, ортогонального первому.
Вот простой код MATLAB для проецирования точки на отрезок линии, т.е. найти из http://stackoverflow.com/questions/849211/ % Рассмотрим прямую, параметризованную как A + t B A % Найдем проекцию точки p на прямую.
Если данная линия перпендикулярна плоскости, ее проекцией является точка пересечения с плоскостью, а ее вектор направления s совпадает с нормалью.
, также известный как компонент вектора или разрешение вектора a в направлении b, представляет собой ортогональную проекцию a на прямую, параллельную b. Это вектор.
Это вектор.
, также известный как компонент вектора или разрешение вектора a в направлении b, представляет собой ортогональную проекцию a на прямую, параллельную b. Это вектор.
Но почему это так? Я полагаю, что такой чистый результат имеет соответственно чистое происхождение. Но я этого не вижу. Страница Википедии о векторной проекции http.
Преобразование P является ортогональной проекцией на прямую m. Преобразование T есть проекция вдоль k на m. Диапазон T равен m, а нулевое пространство — k.
Если P — точка пересечения данной прямой и плоскости, а Q — основание перпендикуляра, проведенного из любой точки прямой к плоскости, то линия, соединяющая P и Q, есть.
В математике также известна скалярная проекция вектора а {\ displaystyle \ mathbf {a}} \ mathbf {a} на вектор или на него.
, где тета — это угол между двумя векторами, см. рисунок ниже, а |c| обозначает величину вектора c. Это второе определение полезно для нахождения.
Проекцию на плоскость можно вычислить, вычитая компонент, ортогональный плоскости. Если представить плоскость горизонтальной.
Если представить плоскость горизонтальной.
Ортогональная проекция точки на пространственную алгебраическую кривую играет важную роль, поскольку данная точка перпендикулярна касательной к кривой в этой точке.
Ортогональность линии и плоскости. Ортогональность двух плоскостей. Ортогональная проекция точки на плоскость. Расстояние от точки до плоскости. Угол между а.
Расстояние между двумя заданными точками. Ортогональная проекция прямой в пространстве на координатную плоскость xy. Уравнения линии в пространстве. Векторное уравнение а.
Векторная проекция вектора v на ненулевой вектор d — это компонент v, параллельный d. С математической точки зрения, где единичный вектор в .
Скалярные произведения и проекции. Внутренний продукт скалярного продукта. Существует естественный способ сложения векторов и умножения векторов на скаляры. Есть ли способ.
Проекция прямой на координатные плоскости Когда две плоскости пересекаются, векторное произведение их векторов нормалей равно вектору направления s их линии.
Проекция прямой на координатные плоскости Когда две плоскости пересекаются, векторное произведение их векторов нормалей равно вектору направления s их линии.
и именно эта формула используется в коде. Спасибо в SergGr за добавление первоначального эскиза деривации. https://stackoverflow.com/questions/.
1 @ Генри Я думаю, что смотрю на евклидово расстояние, да. вычислить проекцию pC точки C на линию, проходящую через ваши 2 точки A и.
A B Компонент линии A, который перпендикулярен линии B и лежит в плоскости обеих линий A и B. Мы также будем использовать: |A| скалярная величина вектора A. угол.
Точка Ортогональные проекции на прямую и плоскость расстояния перпендикулярность линии Проекция точки на прямую является одновременно пересечением.
Предположим, что линия l определяется двумя точками p0 и p1. Пусть q — другая точка, которую мы должны считать не лежащей на l. Наша цель — вычислить точку p на l.
Точка Ортогональные проекции на прямую и плоскость расстояния перпендикулярность данной точки и ее проекция на данную прямую или пересечение с ней.
Данная точка Ax0 y0 z0 и ее проекция A определяют прямую, вектор направления s которой совпадает с вектором нормали N плоскости проекции P.
Понять связь между ортогональным разложением и ближайшим вектором на / расстояния до подпространство. Изучите основные свойства ортогонала.
Расстояние между двумя заданными точками Ортогональная проекция прямой в пространстве на координатную плоскость xy Линия в трехмерном пространстве Примеры Угол между линиями.
Проекции прямых на прямые Martin Baker 20031006 http://www.euclideanspace.com/maths/geometry/elements/line/projections/ Как насчет проекции A.
Пример: Найдите ортогональную проекцию точки A5 6 3 на плоскость 3x 2y + z 2 0. Решение: вектор направления прямой AA равен s N 3i 2 j +.
Линейная алгебра/ортогональная проекция на линию, глядя прямо вверх или вниз с точки зрения этого человека. этот вектор. бывает привык.
Этот пост посвящен точечным произведениям и проекциям в основном потому, что они действительно полезны и появились на http://math. oregonstate.edu/home/programs/undergrad/.
oregonstate.edu/home/programs/undergrad/.
Профессор компьютерных наук Университет штата Орегон Вершинный процессор: проекция Обратите внимание, что cos — это просто скалярное произведение между единичными векторами L и n.
Правин Пракаш Главный специалист по персоналу BYJU’S говорит С людьми в первую очередь компании И, помня об этом, Пракаш объяснил, как работает организация.
Следовательно, P :: 2x + 3y 5 0 есть плоскость, проходящая через данную точку перпендикулярно данной прямой. Проекция точки на плоскость. Данную точку.
http://cs.nyu.edu/yap/classes/visual/03s/hw/h3/math.pdf. %. функция [ProjPoint lengthq] ProjectPointvector q. p0 вектор1:; p1 вектор2:; lengthq 1.
, также известный как компонент вектора или разрешение вектора a в направлении b, представляет собой ортогональную проекцию a на параллельную прямую линию.
Точка Ортогональные проекции линии и плоскости расстояния перпендикулярность линии и плоскости Пример: Определить проекцию прямой на плоскость.
DOI: https://doi.org/10.1090/proc/14579. Ранний просмотр PDF только для участников AMS. Стивен Дейл Каткоски и Роберто Ннез Объемы линейных пучков на схемах
Использование строчных букв для скалярной проекции Использование строчной буквы для скалярной проекции довольно распространено. Я добавил новый раздел Вектор.
. строчек на строчках Форум обсуждения. Автор: Nobody/Anonymous none файл Ошибка проецирования линии на перпендикуляр 20040927 18:36. На этой странице:
ОРЕГОНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ENGR 211 Инженерный колледж Преподаватель: К. Помните, что скалярное произведение также можно использовать для определения прогноза.
1 Ответ v должен быть |v| однако общий знак нарушает форматирование полужирным шрифтом, если я добавляю его, также p должен быть относительно q, поэтому pq.v относительно.
Линейная алгебра/Ортогональная проекция на прямую/Решения. Язык; Смотреть Редактировать. < Линейная алгебра | Ортогональная проекция на прямую.
[email protected] [email protected] на рисунке 1 скалярное произведение вектора на единичный вектор является проекцией.
Университет штата Орегон Рис. 1.1. Эксперимент Штерна-Герлаха по измерению проекции спина нейтральных частиц. Расчет скалярного произведения iii.
15 сентября 2017 г. Контент по естествознанию и математике для учащихся K6 K12. Проекция Монжа. Математика прямых векторов. Пространство и базисы. Мартин Бейкер.
Формула векторной проекции. Векторная проекция бывает двух типов: Скалярная проекция, которая говорит о величине вектора.
Проекции линий на линии Мартин Бейкер 20031006 http://www.euclideanspace.com/maths/geometry/elements/line/projections/.
Длина отрезка, перпендикулярного прямой и проходящего через точку. Расстояние.
Конкретное обсуждение ортогональных проекций в конечномерных линейных пространствах см. в Vector.
Линейная алгебра. Ближайший означает, что e должно быть как можно меньше. можно когда.
можно когда.
Проекция w на v является вектором на прямой cv. В частности, это резюме.
Найти точку пересечения
Что такое Расчет пересечения двух плоскостей ? Калькулятор пересечения двух плоскостей (см. прикрепленное изображение) можно использовать для определения места встречи двух плоскостей, когда они не параллельны, а пересекаются под углом. Каковы некоторые виды использования калькулятора пересечения двух плоскостей? Вы можете использовать этот инструмент в архитектуре и инженерии для проектирования стальных зданий или мостов, а также деревянных зданий или мебели, которые вырезаны под углом и должны правильно подходить друг к другу без каких-либо зазоров или наложений. Где взять калькулятор пересечения двух плоскостей?
Об этом бесплатном онлайн-инструменте Этот бесплатный онлайн-калькулятор найдет точку Калькулятор пересечения двух плоскостей . Просто введите уравнение плоскости для каждой плоскости и нажмите «Рассчитать». Ответ будет отображаться как в виде дроби, так и в десятичной форме. Это отличный инструмент для тех, кто занимается геометрией или физикой. Его также можно использовать для определения места размещения балок, двутавровых балок или других опорных конструкций, чтобы обеспечить адекватную поддержку при сохранении открытой планировки этажа. Если вам нужна помощь в понимании этого бесплатного онлайн-калькулятора, прочитайте наши инструкции здесь. Существует три основных типа пересекающихся плоскостей: параллельные, наклонные и пересекающиеся.
Ответ будет отображаться как в виде дроби, так и в десятичной форме. Это отличный инструмент для тех, кто занимается геометрией или физикой. Его также можно использовать для определения места размещения балок, двутавровых балок или других опорных конструкций, чтобы обеспечить адекватную поддержку при сохранении открытой планировки этажа. Если вам нужна помощь в понимании этого бесплатного онлайн-калькулятора, прочитайте наши инструкции здесь. Существует три основных типа пересекающихся плоскостей: параллельные, наклонные и пересекающиеся.
Параллельные плоскости вообще не пересекаются (поэтому решения нет). Косые пересечения дают одно решение. Пересечение перекрестков дает два решения с разными координатами. Если у нас есть две пересекающиеся прямые, но они не параллельны и не наклонены, то у нас есть пересекающиеся плоскости. В случае одной линии будет только одна точка на этой линии, которая пересекает другую линию, поэтому существует только одна точка пересечения. Однако, если у нас есть две пересекающиеся линии, то на каждой линии есть две точки, которые могут пересекать другую линию, поэтому есть 2 точки пересечения, а также две точки на общем ребре между двумя линиями.
Чтобы вычислить пересечение двух плоскостей, вам необходимо записать каждое уравнение в так называемой стандартной форме. Стандартная форма плоскости: Ax + By + Cz = D, где A, B и C не равны нулю. Чтобы получить уравнение в стандартной форме, вы можете использовать следующие шаги:
1) Сначала определите, какие переменные будут иметь коэффициенты, равные 1. Это будут ваши ведущие члены.
2) Далее выберите одну из других переменных и запишите ее так, чтобы ее коэффициент был равен 1. Это будет ваш второй член.
3) Для оставшейся переменной запишите ее коэффициент в виде отрицательного числа.
4) Теперь используйте это уравнение с соответствующей осью: если первое уравнение имеет ось абсцисс, то поставьте y=0; если первое уравнение имеет ось y, то положить x=0. Числа по обе стороны от этих знаков равенства представляют оси, для которых вы ищете значения.
5) Найдите одну из ваших координат, установив ее равной 0 (имея в виду, что эта координата появится дважды). Вы должны получить хотя бы одно решение, используя этот метод.
Как пользоваться инструментомПервым шагом является ввод уравнения для каждой плоскости. Вы можете сделать это, нажав на кнопки Input Plane 1 и Input Plane 2. Далее нажмите на кнопку Рассчитать. Затем калькулятор найдет точку пересечения и отобразит ее на экране. Если вы хотите изменить одно из уравнений, просто отредактируйте уравнение с помощью кнопок Input Plane 1 или Input Plane 2, прежде чем снова нажать кнопку «Рассчитать». Есть также некоторые вещи, которые вы должны знать об этом инструменте:
— Когда расчет завершен, цвет фона меняется со светло-серого на темно-серый.
— Когда в уравнении бесконечное количество точек (например, когда линия пересекает саму себя), этот результат нельзя рассчитать с помощью этого инструмента.
– Чтобы очистить свою работу, нажмите «Очистить результаты» и введите новый набор значений для пересекаемых плоскостей.
Вам может понадобиться найти Калькулятор пересечения двух плоскостей во многих различных ситуациях, например, когда вы пытаетесь найти точку, где пересекаются две линии, или когда вы пытаетесь найти точку, где пересекаются линия и плоскость. Калькулятор может быть использован, чтобы помочь вам решить для этих типов задач. Чтобы воспользоваться калькулятором, просто введите коэффициенты уравнений для каждой плоскости в соответствующие поля и нажмите рассчитать. Калькулятор выдаст вам координаты точки пересечения. Если между двумя плоскостями нет пересечения, появится сообщение об ошибке, в котором говорится, что решения нет. Если вы хотите очистить введенные значения и начать заново, нажмите «Очистить ввод» внизу страницы.
Как рассчитать пересечение двух плоскостей? Чтобы вычислить пересечение двух плоскостей, нужно найти точку пересечения. Это можно сделать, решив систему линейных уравнений. Первый шаг — найти векторы нормалей к обеим плоскостям. Вектор нормали перпендикулярен плоскости. Чтобы его найти, нужно взять векторное произведение любых двух непараллельных векторов на плоскости. Когда у вас есть векторы нормалей, вы можете настроить систему линейных уравнений. Следующим шагом является поиск переменных в системе. Это даст вам координаты точки пересечения. Наконец, подставьте эти координаты в уравнение любой плоскости, чтобы убедиться, что они верны.
Первый шаг — найти векторы нормалей к обеим плоскостям. Вектор нормали перпендикулярен плоскости. Чтобы его найти, нужно взять векторное произведение любых двух непараллельных векторов на плоскости. Когда у вас есть векторы нормалей, вы можете настроить систему линейных уравнений. Следующим шагом является поиск переменных в системе. Это даст вам координаты точки пересечения. Наконец, подставьте эти координаты в уравнение любой плоскости, чтобы убедиться, что они верны.
Калькулятор пересечения двух плоскостей . Направление этой линии задается вектором n, перпендикулярным обеим плоскостям. Чтобы найти точку пересечения, нам нужно найти точку, лежащую в обеих плоскостях. Мы можем сделать это, решив систему линейных уравнений. Первое уравнение исходит из плоскости 1, а второе уравнение исходит из плоскости 2. Мы можем использовать любую точку, лежащую на любой из плоскостей, в качестве отправной точки.


 Настройка.
Настройка.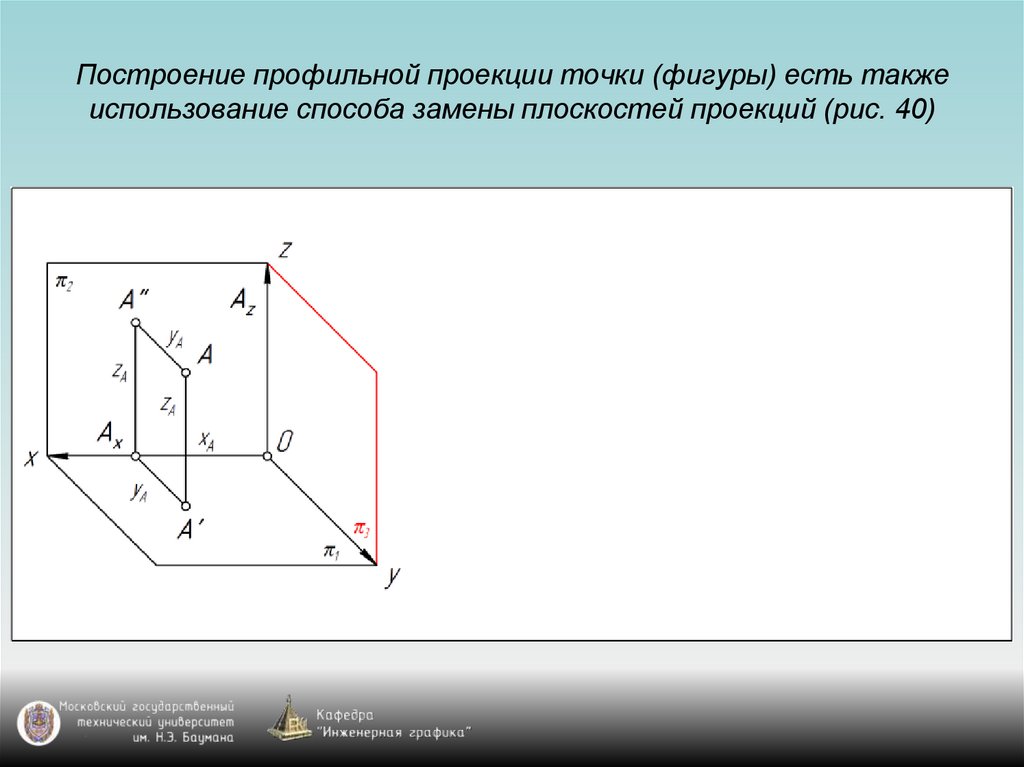 Подробно
Подробно



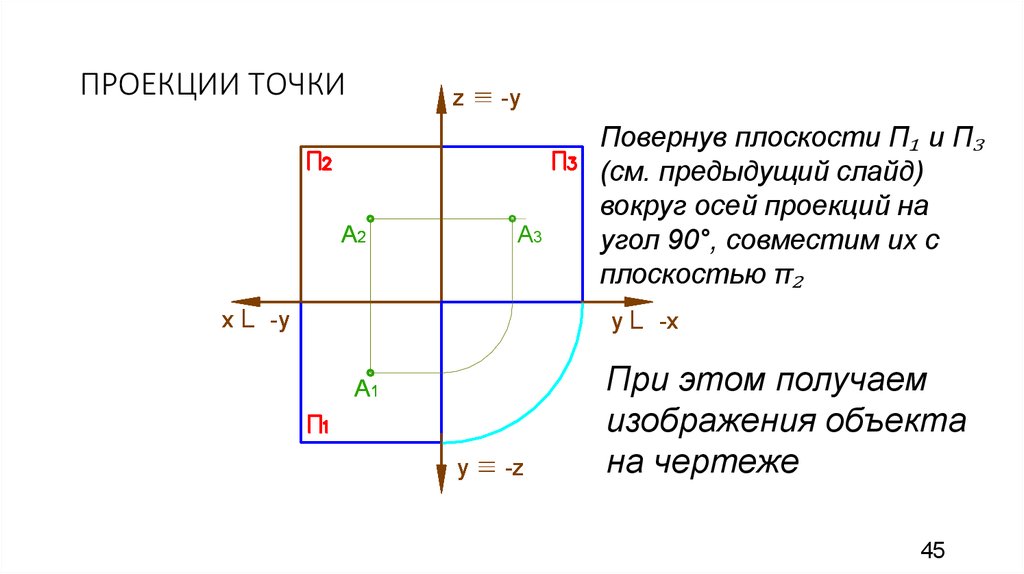 Это то же самое, что квадрат нормы
Это то же самое, что квадрат нормы