03. Определители. Определители второго и третьего порядков
Одним из источников появления определителей 2-го и 3-го порядков являются системы двух и трёх линейных уравнений с двумя и соответственно тремя переменными.
Пусть дана система (1)
Если обе части первого уравнения умножить на , а второго – на и уравнения почленно вычесть, то получим Аналогично, если первое уравнение умножить на И вычесть из него второе уравнение, умноженное на , то получим Если ¹ 0, то х = у = . Выражения, стоящие в числителях и знаменателях полученных формул, имеют одинаковую структуру. Для их составления используется четыре числа. Если числа, используемые для знаменателя, записать в виде матрицы , то знаменатели получаются по правилу: из произведения элементов одной диагонали таблицы вычитается произведение элементов второй диагонали. Используя отмеченное правило, введём понятие определителя.
Для матрицы диагональ, на которой стоят элементы , называется Главной диагональю, вторая диагональ называется Побочной диагональю.
Определение 2. Определителем 2-го порядка (определителем матрицы ) называется число, равное разности произведения элементов главной диагонали и произведения элементов побочной диагонали.
Определитель матрицы обозначается .
Обозначим D = , D1 = , D2 = . Используя определение 2, получим, что система (1) имеет единственное решение тогда и только тогда, когда D ¹ 0. Это решение можно найти по формулам х = , у = (2). Эти формулы называются формулами Крамера.
Пусть дана система трёх уравнений с тремя неизвестными:
(3)
Умножим первое уравнение на , второе уравнение – на , третье уравнение – на и почленно сложим. Получим Х× =
= . Легко заметить, что коэффициент при Х и правая часть составлены из девяти чисел по одному и тому же закону.
Пусть дана матрица А = .
Определение 3. Определителем матрицы А (определителем третьего порядка) называется число, равное D = (4).
Равенство (4) называется разложением определителя по элементам первого столбца. Итак, вычисление определителя третьего порядка сводится к вычислению определителей второго порядка. Если вычислить определители второго порядка, входящие в формулу (4), то получим, что (5).
Используя последнюю формулу, непосредственным вычислением можно получить:
1. Определитель не изменится, если в нём строки и столбцы поменять местами (эту операцию называют Транспонированием определителя). Следовательно в определителе строки и столбцы равноправны..
2. D = .
Итак, определитель можно разлагать по любому столбцу. Можно заметить, что знак перед множителем равен . Так как в определителе строки и столбцы равноправны, то аналогичные разложения имеют место и по любой строке определителя (запишите их самостоятельно).
3. Если в определителе одна из строк (или столбцов) целиком состоит из нулей, то определитель равен нулю.
4. Системы (3) имеет единственное решение тогда и только тогда, когда D ¹ 0. Это решение можно найти по формулам: х = , у = , (6),
Это решение можно найти по формулам: х = , у = , (6),
Где D1, D2, D3 получаются из определителя D заменой первого, второго, третьего столбца соответственно столбцом свободных членов. Формулы (6) тоже называются Формулами Крамера.
| < Предыдущая | Следующая > |
|---|
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Оснащения врачебно-сестринской бригады. Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов… Интересное: Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является.. Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья… Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
Стр 1 из 4Следующая ⇒ Тема 1. Понятие матрицы Определение 1. Матрицей размером называется прямоугольная таблица чисел или буквенных выражений , записанных в виде . Здесь, aij (i=1,2,…,m; j=1,2,…n) — элементы матрицы, i— номер строки, j — номер столбца. Матрицы обычно обозначаются большими буквами латинского алфавита A, B, Cи т.д., а также или . При m=n матрица называется квадратной матрицей порядка n. Квадратная матрица, у которой все элементы с неравными индексами i¹j равны нулю, называется диагональной: Если все отличные от нуля элементы диагональной матрицы равны единице, то матрица называется единичной. Единичную матрицу принято обозначать буквой E. Матрица, все элементы которой равны нулю, называется нулевой и обозначается θ. Существуют также матрицы, состоящие из одной строки или из одного столбца. — матрица строка Числовой характеристикой квадратной матрицы является определитель (или детерминант). Определители 2-го порядка и 3-го порядка, их свойства. Определители 2-го порядка Определение 2. Определителем второго порядка матрицы (или просто определителем второго порядка) называется число, обозначаемое символом и определяемое равенством , то есть . (3) Другие обозначения: , . Таким образом, понятие определителя предполагает одновременно и способ его вычисления. Числа называются элементами определителя. Диагональ, образованная элементами , называется главной, а элементами — побочной. Пример 1. Определитель матрицы равен . Определители 3-го порядка Определение 2. Определителем третьего порядка называется число, обозначаемое символом , и определяемое равенством = . Числа — элементы определителя. Элементы образуют главную диагональ, элементы — побочную. При вычислении определителя чтобы запомнить, какие слагаемые в правой части равенства (4) берутся со знаком «+», а какие со знаком «-», пользуются символическим правилом треугольников (правилом Саррюса): (+) (-) Со знаком «+» берутся произведения элементов главной диагонали и элементов, находящихся в вершинах треугольников с основаниями, параллельными главной диагонали; сл знаком «-» – произведения элементов побочной диагонали и элементов, расположенных в вершинах треугольников с основаниями, параллельными побочной диагонали. Вычисление определителя по правилу приписывания столбцов. 1. Приписываем справа от определителя последовательно первый и второй столбцы. 2. Вычисляем произведения трех элементов по диагонали слева — направо, сверху — вниз от  (-) (-) (-) (+) (+) (+) Пример 2. Вычислить определитель по правилу приписывания столбцов. 3. Определители n-ого порядка. Миноры и алгебраические дополнения. Вычисление определителей разложением по строке (столбцу). Рассмотрим понятие определителя n-ного порядка. Определителем n-ного порядка называется число, сопоставляемое матрице n-ного порядка и вычисляемое по определенному закону. , здесь — элементы определителя. Чтобы показать правило, по которому раскрывается определитель n-ного порядка, рассмотрим некоторые понятия. Определение 4. Минором элемента определителя n-го порядка называется определитель (n — 1) порядка, полученный вычеркиванием строки и столбца определителя, на пересечении которых расположен этот элемент. Определение 5. Алгебраическим дополнением некоторого элемента определителя n-го порядка называется минор этого элемента, умноженный на , то есть . В определителе третьего порядка можно рассмотреть, например, , . , . Определение 6.Определителем n-ного порядка называется число, равное сумме произведений элементов первой строки определителя, умноженных на их алгебраические дополнения. Это правило вычисления определителя называется разложением по первой строке. – сумма произведений элементов 1-го столбца на алгебраические дополнения 2-го столбца. Пример 3. Вычислить определитель четвертого порядка . Решение. Умножаем третью строку на (-1) и прибавляем ее к четвертой, затем раскладываем определитель по четвертой строке:
. Определитель третьего порядка разложили по первой строке. Метод Гаусса. Метод Гаусса заключается в том, что исходную систему путем исключения неизвестный преобразуют к ступенчатому виду. Метод Гаусса состоит из прямого хода и обратного хода. Прямым ходом метода Гаусса является приведение расширенной матрицы системы (1) к ступенчатому виду путем элементарных преобразований над строками. После чего происходит исследование системы на совместность и определенность. Затем по ступенчатой матрице восстанавливается система уравнений. Решение этой ступенчатой системы уравнений является обратным ходом метода Гаусса, в котором, начиная с последнего уравнения, последовательно вычисляются неизвестные с большим порядковым номером, и их значения подставляются в предыдущее уравнение системы. Исследование системы в конце прямого хода происходим по теореме Кронекера-Капелли сравнением рангов матрицы системы А и расширенной матрицы А´. При этом возможны следующие случаи. 1) Если , то система несовместна (по теореме Кронекера-Капелли). 2) Если , то система (1) является определенной, и наоборот (без доказательства). 3) Если , то система (1) является неопределенной, и наоборот (без доказательства). Неравенство не имеет места, так как матрица А является частью матрицы А´, неравенство не имеет места, так как число столбцов матрицы А равно п. Кроме того, для системы с квадратной матрицей, то есть если п = т, равенства равносильны тому, что . Если система является неопределенной, то есть выполняется , то некоторые ее неизвестные объявляются свободными, а остальные через них выражаются. Количество свободных неизвестных равно . При выполнении обратного хода метода Гаусса, если в очередном уравнении после подстановки найденных ранее переменных, неизвестных осталось более одного, то свободными неизвестными объявляются любые неизвестные, кроме одного. Рассмотрим реализацию метода Гаусса на примерах. Пример 4. Решить систему уравнений Решение. Решим систему методом Гаусса. ~ ~ ~ ~ ~ . , поэтому система совместна и имеет единственное решение, т.е. является определенной. Составим систему ступенчатого вида и решим ее (обратный ход). Проверку легко сделать подстановкой. Ответ: . Тема 2. Векторная алгебра. Проекция вектора на ось.
Под осью понимается прямая линия, на которой задано начало отсчета, масштаб и положительное направление. Определение 1. Проекцией точки М на ось l называется точка М1, которая является основанием перпендикуляра, проведенного из точки М на эту ось (см. рис.1).
Определение 2.Проекцией вектора на ось l называется число равное длине отрезка АВ этой оси, заключенного между проекциями начала и конца вектора , взятое со знаком «+», если отрезок АВ ориентирован (считая от А к В) в положительную сторону оси l и знаком «-» – в противном случае (см. Обозначение: . Теорема 1. Проекция вектора на ось равна произведению его модуля на косинус угла между вектором и положительным направлением оси (рис. 3): . (1)
Доказательство. Из (рис. 3) получаем . Направление отрезка совпадает с положительным направлением оси , поэтому справедливо равенство . В случае противоположной ориентации (рис.4) имеем . Теорема доказана. Рассмотрим свойства проекций. Свойство 1. Проекция суммы двух векторов и на ось равна сумме их проекций на ту же ось, то есть .
Доказательство в случае одного из возможных расположений векторов следует из рисунка 5. Действительно, по определению 2 . Свойство 1 справедливо для любого конечного числа слагаемых векторов. Свойство 2. При умножении вектора на число l его проекция умножается на это число . Докажем равенство (2). При векторы и образуют с осью один и тот же угол. По теореме 1 При векторы и образуют с осью соответственно углы и . Потеореме 1 . При , получаем очевидное равенство . Следствие из свойств 1 и 2. Проекция линейной комбинации векторов равна такой же линейной комбинации проекций этих векторов, т.е. . (3) Тема 1. Матрицы и системы Понятие матрицы Определение 1. Матрицей размером называется прямоугольная таблица чисел или буквенных выражений , записанных в виде . Здесь, aij (i=1,2,…,m; j=1,2,…n) — элементы матрицы, i— номер строки, j — номер столбца. Матрицы обычно обозначаются большими буквами латинского алфавита A, B, Cи т.д., а также или . При m=n матрица называется квадратной матрицей порядка n. Квадратная матрица, у которой все элементы с неравными индексами i¹j равны нулю, называется диагональной: Если все отличные от нуля элементы диагональной матрицы равны единице, то матрица называется единичной. Матрица, все элементы которой равны нулю, называется нулевой и обозначается θ. Существуют также матрицы, состоящие из одной строки или из одного столбца. — матрица строка; — матрица столбец. Числовой характеристикой квадратной матрицы является определитель (или детерминант). Определители 2-го порядка и 3-го порядка, их свойства. Определители 2-го порядка Определение 2. Определителем второго порядка матрицы (или просто определителем второго порядка) называется число, обозначаемое символом и определяемое равенством , то есть . (3) Другие обозначения: , . Таким образом, понятие определителя предполагает одновременно и способ его вычисления. Числа называются элементами определителя. Диагональ, образованная элементами , называется главной, а элементами — побочной. Пример 1. Определитель матрицы равен . Определители 3-го порядка Определение 2. Определителем третьего порядка называется число, обозначаемое символом , и определяемое равенством = . (4) Числа — элементы определителя. Элементы образуют главную диагональ, элементы — побочную. При вычислении определителя чтобы запомнить, какие слагаемые в правой части равенства (4) берутся со знаком «+», а какие со знаком «-», пользуются символическим правилом треугольников (правилом Саррюса): (+) (-) Со знаком «+» берутся произведения элементов главной диагонали и элементов, находящихся в вершинах треугольников с основаниями, параллельными главной диагонали; сл знаком «-» – произведения элементов побочной диагонали и элементов, расположенных в вершинах треугольников с основаниями, параллельными побочной диагонали. Вычисление определителя по правилу приписывания столбцов. 1. Приписываем справа от определителя последовательно первый и второй столбцы. 2. Вычисляем произведения трех элементов по диагонали слева — направо, сверху — вниз от а11 до а13 и берем их со знаком «+». Затем вычисляем произведения трех элементов по диагонали слева — направо, снизу вверх от а31 до а13 и берем их со знаком «-». (-) (-) (-) (+) (+) (+) Пример 2. Вычислить определитель по правилу приписывания столбцов. 3. Определители n-ого порядка. Миноры и алгебраические дополнения. Вычисление определителей разложением по строке (столбцу). Рассмотрим понятие определителя n-ного порядка. Определителем n-ного порядка называется число, сопоставляемое матрице n-ного порядка и вычисляемое по определенному закону. , здесь — элементы определителя. Чтобы показать правило, по которому раскрывается определитель n-ного порядка, рассмотрим некоторые понятия. Определение 4. Минором элемента определителя n-го порядка называется определитель (n — 1) порядка, полученный вычеркиванием строки и столбца определителя, на пересечении которых расположен этот элемент. Определение 5. Алгебраическим дополнением некоторого элемента определителя n-го порядка называется минор этого элемента, умноженный на , то есть . В определителе третьего порядка можно рассмотреть, например, , . , . Определение 6.Определителем n-ного порядка называется число, равное сумме произведений элементов первой строки определителя, умноженных на их алгебраические дополнения. Это правило вычисления определителя называется разложением по первой строке. Теорема ( о разложении определителя). Определитель можно вычислить разложением по любой строке или столбцу. – сумма произведений элементов 1-го столбца на алгебраические дополнения 2-го столбца. Пример 3. Вычислить определитель четвертого порядка . Решение. Умножаем третью строку на (-1) и прибавляем ее к четвертой, затем раскладываем определитель по четвертой строке:
. Определитель третьего порядка разложили по первой строке. 1234Следующая ⇒ Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… |
Видео с вопросами: Вычисление определителя третьего порядка заданной матрицы
Стенограмма видео
Найдите определитель матрицы один, два, три; три, два, два; ноль, девять, восемь.
Итак, в этой задаче нас просят найти определитель матрицы три на три. Теперь, чтобы найти определитель матрицы три на три, у нас есть общее правило. Итак, если мы посмотрим сюда, у нас есть матрица три на три 𝑎, 𝑏, 𝑐; 𝑑, 𝑒, 𝑓; 𝑔, ℎ, 𝑖. Таким образом, эти вертикальные линии говорят нам, что мы смотрим на определитель. Они означают определитель матрицы 𝑎, 𝑏, 𝑐; 𝑑, 𝑒, 𝑓; 𝑔, ℎ, 𝑖.
И чтобы найти определитель, он равен 𝑎 — потому что это первый член в первой строке — умноженный на определитель подматрицы, которая образуется, когда мы удаляем строку и столбец, в которых находится 𝑎. Таким образом, это будет подматрица 𝑒, 𝑓, ℎ, 𝑖, поэтому 𝑎 умножается на член в этой подматрице. Тогда минус 𝑏. И это потому, что у нас есть шаблон с нашими коэффициентами. Таким образом, мы выбираем каждый из первых терминов в первой строке. Но они следуют шаблону положительный, отрицательный, положительный.
Таким образом, как я уже сказал, это минус 𝑏, умноженный на подматрицу два на два, образованную, если вы удалите столбец и строку, в которой находится 𝑏. Плюс 𝑐, умноженный на подматрицу два на два, определитель этой , то есть 𝑑, 𝑒, 𝑔, ℎ. Итак, отлично, теперь мы знаем, как это решить. Давайте продолжим и найдем определитель нашей матрицы.
Плюс 𝑐, умноженный на подматрицу два на два, определитель этой , то есть 𝑑, 𝑒, 𝑔, ℎ. Итак, отлично, теперь мы знаем, как это решить. Давайте продолжим и найдем определитель нашей матрицы.
Таким образом, используя наше правило, мы можем сказать, что определитель матрицы один, два, три; три, два, два; ноль, девять, восемь можно вычислить как единицу, умноженную на определитель подматрицы два на два два, два, девять, восемь минус два, умноженную на определитель подматрицы два на два три, два, ноль, восемь плюс три умножается на определитель подматрицы три, два, ноль, девять. И я собираюсь просмотреть третий раздел, просто чтобы напомнить нам, как мы его нашли.
Итак, мы выбрали три, потому что это третий термин в верхней строке. И это положительно, потому что наш шаблон говорит, что первый столбец положительный, второй столбец отрицательный, третий столбец положительный и так далее. И мы нашли подматрицу три, два, ноль, девять, удалив строку и столбец, в которых была тройка. И тогда у нас осталось три, два, ноль, девять.
И тогда у нас осталось три, два, ноль, девять.
Хорошо, отлично. Итак, давайте теперь узнаем значение этого. Итак, чтобы вычислить значение нашего определителя матрицы три на три, нам нужно найти определители наших подматриц два на два. Мы делаем это, используя это общее правило. Если у нас есть определитель матрицы 𝑎, 𝑏, 𝑐, 𝑑, он равен 𝑎, умноженному на 𝑑 минус 𝑏, умноженному на 𝑐. Итак, мы собираемся использовать это, чтобы найти значение определителя нашей матрицы три на три.
Итак, прежде всего, умножим единицу на. Тогда у нас есть два, умноженные на восемь — потому что это наши 𝑎 и наши 𝑑 — минус два, умноженные на девять, наши 𝑏 и наши 𝑐. И тогда у нас будет минус два, умноженное на три, умноженное на восемь, минус два, умноженное на ноль, и, наконец, плюс три, умноженное на три, умноженное на девять, минус два, умноженное на ноль.
Хорошо, отлично. Итак, у нас теперь есть форма, в которой мы можем теперь просто продолжить и вычислить значение нашего определителя. Так что это даст нам отрицательную двойку. И это потому, что два, умноженные на восемь, равно 16, 16 минус 18, потому что два, умноженные на девять, равно 18, дают минус два. И это, умноженное на один, равно минус двум. Итак, это минус два минус 48 плюс 81, что равно 31. Следовательно, мы можем сказать, что определитель матрицы один, два, три; три, два, два; ноль, девять, восемь равно 31.
Так что это даст нам отрицательную двойку. И это потому, что два, умноженные на восемь, равно 16, 16 минус 18, потому что два, умноженные на девять, равно 18, дают минус два. И это, умноженное на один, равно минус двум. Итак, это минус два минус 48 плюс 81, что равно 31. Следовательно, мы можем сказать, что определитель матрицы один, два, три; три, два, два; ноль, девять, восемь равно 31.
матрицы — Как вычислить вторую производную определителя?
Задавать вопрос
спросил
Изменено 4 года, 1 месяц назад
Просмотрено 2к раз
$\begingroup$
Я работаю над следующим вопросом, и мне удалось сделать большую его часть, но, к сожалению, я застрял на последнем фрагменте.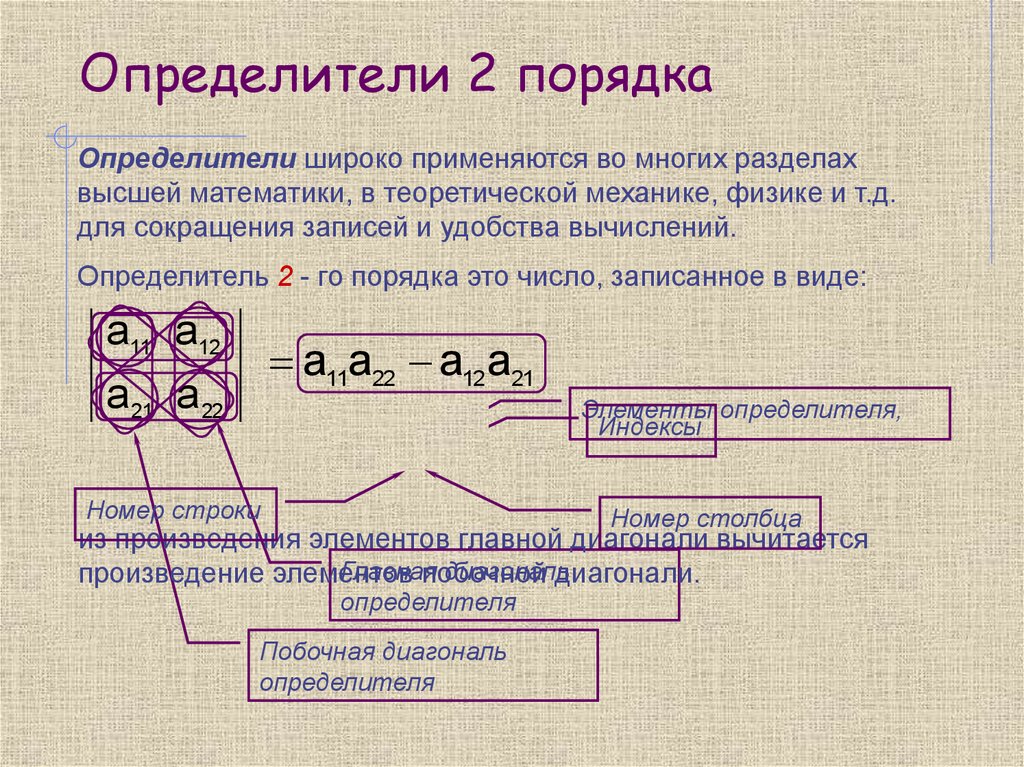

 .
.
 Матрицы и системы
Матрицы и системы
 (4)
(4)
 При этом преобразования выполняются над строками в расширенной матрице, так как преобразования, исключающие неизвестные эквивалентны элементарным преобразованиям строк матрицы.
При этом преобразования выполняются над строками в расширенной матрице, так как преобразования, исключающие неизвестные эквивалентны элементарным преобразованиям строк матрицы.
 Выпишем расширенную матрицу системы и приведем ее к ступенчатому виду элементарными преобразованиями строк (прямой ход).
Выпишем расширенную матрицу системы и приведем ее к ступенчатому виду элементарными преобразованиями строк (прямой ход). рис.2).
рис.2). (2)
(2) Единичную матрицу принято обозначать буквой E.
Единичную матрицу принято обозначать буквой E.


