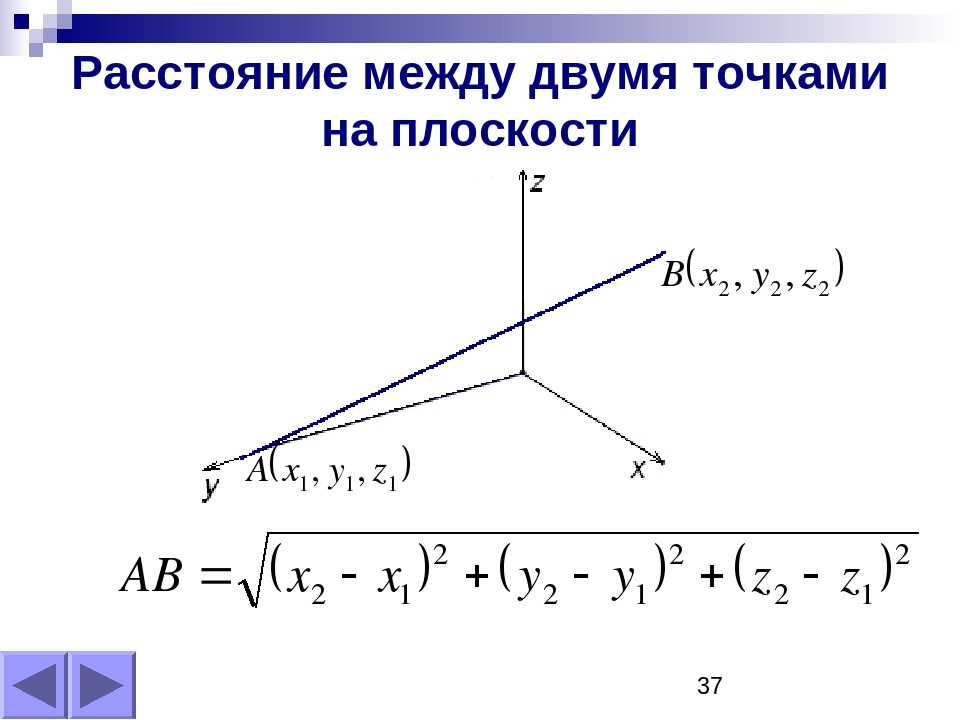
3.4.11. Расстояние между двумя точками в пространстве.
Пусть в пространстве заданы координаты точек: А(x1, y1, z1) и С(x2, y2, z2) , требуется найти расстояние между ними. Искомое расстояние равно модулю вектора АС, координаты которого равны разности координат его конца и начала:
.
Теперь находим модуль вектора, то есть расстояние между заданными токами: . (3)
3.4.12. Деление отрезка в заданном отношении.
Пусть
в пространстве задан отрезок, известны
координаты его начала и конца:
А(x1,
y1,
z1) и С(x2,
y2,
z2). Требуется найти координаты точки,
лежащей на этом отрезке и делящей его
в отношении
. Координаты этой точки определяются
формулами:
Координаты этой точки определяются
формулами:
, , . (4)
3.4.13. Векторы в экономике. В экономике вектором называется упорядоченный набор чисел, например, Р(1,5,3). Числа в векторе с учетом их расположения по номеру в наборе называются компонентами (составляющими) вектора. Число компонент вектора называется его размерностью. Так, Р(1,5,3)– трехмерный вектор. При этом на них распространяются все рассмотренные выше линейные операции над геометрическими векторами.
3.4.14. Пример. Завод производит электроутюги, электрочайники и электронагреватели. Годовой объем производства в 2002 году характеризуется вектором S2002( 1000, 1500, 800). В 2003 году произвели на 10% больше продукции, тогда S2003( 1100, 1650, 880). Найдем суммарный объем производства за 2 года S2002+ S2003=S(2100, 3150, 1680).
Действия
с векторами это распространение действий
над числами.
3.5. Скалярное произведение векторов.
3.5.1 Скалярным произведением двух векторов называется число, равное произведению длин (модулей) этих векторов на косинус угла между ними: .
3.5.2. Свойства скалярного произведения:
.
прa прb .
3.5.3. Необходимое и достаточное условие перпендикулярности двух не нулевых векторов: . Отсюда следует, что: . ; .
3.5.4.Скалярное произведение векторов может быть выражено через их координаты:
Пусть , , тогда
.
То есть, скалярное произведение векторов равно сумме парных произведений одноименных проекций.
3. 5.5. Пример. Годовой объем производства в
2002 году характеризуется вектором
5.5. Пример. Годовой объем производства в
2002 году характеризуется вектором
S2002( 1000, 1500, 800). Средняя цена за единицу продукции в условных единицах была С2002(15, 20, 50). Найти суммарную стоимость проданной продукции СПР.
Решение. Очевидно, что суммарная стоимость проданной продукции определится скалярным произведением:
СПР= S2002 С2002=100010+150020+80050=80000 у.е. Ответ. 80000 у.е.
Для геометрических векторов для определения длины вектора справедлива формула: . В тех случаях, когда компоненты вектора имеют разную размерность или наименование эта формула не применяется, например, на конкурсе красоты рассматривается вектор всем известная тройка чисел: (90,60,90) и всем понятно, что не имеет смысла ни модуль этого вектора, ни сложение его с другими векторами
3. 5.7. Из формулы скалярного произведения
векторов можно определить косинус угла
между векторами:
5.7. Из формулы скалярного произведения
векторов можно определить косинус угла
между векторами:
. (5)
Условие перпендикулярности двух векторов, выраженное через их координаты будет .
3.5.8.Пример. Найти вектор , если он перпендикулярен вектору и он составляет тупой угол с осью Оу.
Решение.. Так как , то . Так как , то . Получим систему и решаем ее:
Так как по условию составляет тупой угол с осью
3.5.9. Пример. Могут ли являться вершинами невырожденного треугольника координаты трех точек в пространстве: ?
Решение. Треугольник является невырожденным, если неколлинеарен .
Найдем координаты этих векторов:
Условие
коллинеарности не выполняется, так как .
Ответ: является невырожденным.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Brilliant Math & Science Wiki
Содержание
- Расстояние в одном измерении
- Расстояние в двух измерениях
- Идентификация фигур путем соединения точек графика
- Другие примеры
Предположим, что A=x1A=x_1A=x1 и B=x2B=x_2B=x2 — две точки, лежащие на прямой с действительными числами. Тогда расстояние между AAA и BBB равно
Тогда расстояние между AAA и BBB равно
d(A,B)=∣x1−x2∣. d(A,B) = \lvert x_1 — x_2 \rvert. d(A,B)=∣x1−x2∣.
На плоскости мы можем рассматривать ось ххх как одномерную числовую прямую, поэтому мы можем вычислить расстояние между любыми двумя точками, лежащими на оси ххх, как абсолютное значение разности их ххх-координат. Точно так же расстояние между любыми двумя точками, лежащими на оси yyy, является абсолютным значением разницы их координат yyy. 92}.d(P1,P2)=(x1-x2)2+(y1-y2)2.
Так как ∣x1−x2∣\lvert x_1 — x_2 \rvert∣x1−x2∣ есть расстояние между xxx-координатами двух точек и ∣y1−y2∣\lvert y_1 — y_2\rvert∣y1 −y2∣ — расстояние между координатами yyy двух точек, формулу расстояния в плоскости xyxyxy можно рассматривать как длину гипотенузы прямоугольного треугольника с вершинами P1=(x1,y1)P_1= (x_1,y_1)P1=(x1,y1), P2=(x2,y2),P_2 = (x_2,y_2),P2=(x2,y2) и P=(x2,y1 )P = (x_2,y_1) P=(x2,y1). Тогда формула расстояния — это просто формулировка теоремы Пифагора.
Как в 1D, так и в 2D функция расстояния удовлетворяет следующим свойствам:
- d(P,Q)≥0d(P,Q) \geq 0d(P,Q)≥0 для всех точек P,Q P,QP ,Q с равенством тогда и только тогда, когда P=QP = QP=Q
- d(P,Q)=d(Q,P)d(P, Q) = d(Q, P) d(P,Q)=d(Q,P) для всех точек P,QP,QP,Q
- d(P,Q)≤d(P,R)+d(R,Q) d(P,Q) \leq d(P, R) + d(R, Q) d(P,Q)≤d (P,R)+d(R,Q) для всех точек P,Q,RP P,Q,RP,Q,R.
Какое расстояние между точками (0,5)(0,5)(0,5) и (0,13)(0,13)(0,13)?
Обратите внимание, что обе эти точки лежат на оси yyy, и, следовательно, расстояние между точками является абсолютным значением разности координат yyy, которая составляет ∣5−13∣=∣−8∣=8. □ \lvert 5 — 13 \rvert = \lvert -8 \rvert =8 .\ _\square∣5−13∣=∣−8∣=8. □
Чтобы обобщить вышеприведенную задачу, если две точки P1=(x1,y1)P_1 = (x_1, y_1) P1=(x1,y1) и P2=(x2,y2)P_2 = ( x_2, y_2) P2=(x2,y2) имеют одинаковую xxx-координату, т.е. x1=x2x_1=x_2x1=x2, тогда расстояние между двумя точками равно d(P1,P2)=∣y1− y2∣ d(P_1, P_2) = |y_1-y_2|d(P1,P2)=∣y1−y2∣ и отрезок P1P2‾\overline{P_1P_2} P1P2 является вертикальной линией сегмент.
Аналогично, если P1P_1P1 и P2P_2P2 имеют одинаковую координату yyy (y1=y2y_1=y_2y1=y2), то d(P1,P2)=∣x1−x2∣d(P_1, P_2) = |x_1 -x_2|d(P1,P2)=∣x1−x2∣ и отрезок P1P2‾\overline{P_1P_2} P1P2 является горизонтальным отрезком.
Найти площадь прямоугольника в плоскости xyxyxy с вершинами
A=(6,−3),B=(6,7),C=(2,7) и D=(2,−3). A = (6, -3), B = (6, 7), C = (2, 7), \text{ и } D = (2, -3).A = (6, −3), B = (6,7),C=(2,7) и D=(2,−3).
Точки AAA и BBB имеют одинаковую xxx-координату, из чего следует, что d(A,B)=∣7−(−3)∣=10d(A,B) = \lvert 7 — (-3) \rvert = 10d( А,В)=∣7−(−3)∣=10. Точки BBB и CCC имеют одинаковые координаты yyy, что означает d(B,C)=∣6−2∣=4d(B,C) = \lvert 6 — 2 \rvert = 4d(B,C)=∣6− 2∣=4. Мы проверяем, что точки CCC и DDD имеют одинаковую координату xxx, а DDD и AAA имеют одинаковую координату yyy, подразумевая, что точки действительно являются вершинами прямоугольника. 92 &= 16\\ a-4 &= 4 ~\text{ или }~ a — 4 = -4\\ a &= 8 ~\text{ или }~ a = 0.
2}\\ & = \sqrt{92}\\ & = \sqrt{49 + 1}\\ & = \sqrt{50}\\ & = 5\квадрат{2}.\ _\квадрат \end{align}OP=x2+y2=72+12=49+1=50=52. □
Иногда нам дают четыре точки и просят прокомментировать природу четырехугольника, образованного их соединением. Для этого надо вспомнить следующее:
Четырехугольник
- прямоугольник, если его противоположные стороны равны и диагонали равны;
- квадратов, если все его стороны равны и диагонали равны;
- параллелограмм, если его противоположные стороны равны;
- ромб, если его стороны равны.
Покажите, что точки A=(−3,0),B=(1,−3),C=(4,1)A=(-3,0) , B=(1,-3) , C= (4,1)A=(−3,0),B=(1,−3),C=(4,1) — вершины равнобедренного прямоугольного треугольника. Также найдите площадь треугольника.
У нас есть
AB=(1−(−3))2+(−3−0)2=42+(−3)2=16+9=25=5BC=(4−1)2+(1−(−3) )/)2=32+42=9+16=25=5CA=(4−(−3))2+(1−0)2=72+12=492,AB2+BC2=52+52=50=CA2, он прямоугольный.
Теперь площадь треугольника равна (Площадь ABC)=12×AB×BC=12×5×5=12,5. □\begin{выровнено} \text{(Площадь ABC)} & = \dfrac{1}{2} × AB × BC\\ & = \dfrac{1}{2} × 5 × 5\\ & = 12,5.\ _\квадрат \end{align}(Площадь ABC)=21×AB×BC=21×5×5=12,5. □
Покажите, что точки A=(2,−2),B=(8,4),C=(5,7),D=(−1,1)A=(2,-2) , B=( 8,4) , C=(5,7) , D=(-1,1)A=(2,−2),B=(8,4),C=(5,7),D=(− 1,1) являются вершинами прямоугольника. Также найдите площадь прямоугольника. 92} & = \sqrt{90}\\& = 3\sqrt{10}, \end{align}AC=(5−2)2+(7+2)2BD=(−1−8)2+(1−4)2=90=310=90=310 , AC=BD, AC = BD, AC=BD, откуда следует, что ABCDABCDABCD — четырехугольник с равными диагоналями.
Следовательно, ABDABCDABCD — прямоугольник, а его площадь равна
(площадь ABCD)=AB×BC=62×32=36. □\begin{выровнено} \text{(Площадь ABCD)} & = AB × BC\\ & = 6\sqrt{2} × 3\sqrt{2}\\ & = 36.\ _\квадрат \end{выровнено}(Площадь ABCD)=AB×BC=62×32=36. □
92}& = \sqrt{81 + 81}\\& = 9\sqrt{2}, \end{выровнено}AC=(2−(−3))2+(−3−2)2BD=(4−(−5))2+(4−(−5))2=25 +25=52=81+81=92, AC≠BD,AC \neq BD,AC=BD, откуда следует, что ABCDABCDABCD — ромб, а не квадрат.Площадь ромба ABDABCDABCD равна (площадь ромба ABCD)=12×AC×BD=12×52×92=45. □\begin{выровнено} \text{(Площадь ромба ABCD)} & = \dfrac{1}{2} × AC × BD\\ & = \dfrac{1}{2} × 5\sqrt{2} × 9\sqrt{2}\\ & = 45.\ _\квадрат \end{выровнено}(Площадь ромба ABCD)=21×AC×BD=21×52×92} = \sqrt{81+144}& = 15, \end{выровнено}AB=(2−(−1))2+(3−(−1))2=9+16BC=(8−2)2+(11−3)2=36 +64AC=(8−(−1))2+(11−(−1))2=81+144=5=10=15, поэтому AB + BC = AC, AB + BC = AC, AB + BC = AC, что означает, что данные точки лежат на одной прямой. □_\квадрат□
Найдите точку на оси yyy, равноудаленную от точек A=(−3,4)A=(-3,4)A=(−3,4) и B=(7,6)B=(7 ,6)В=(7,6).
Поскольку точка лежит на оси yyy, координата xxx равна 000. Пусть P=(0,y)P=(0,y)P=(0,y) — искомая точка на оси yyy который равноудален от заданных точек. Затем 92 — 12 лет\\ 4г & = 60\\ у & = \dfrac{60}{4}\\ у & = 15. \end{выровнено}PAPA2(−3−0)2+(4−y)2(−3)2+(4−y)29+16+y2−8y4yyy=PB=PB2=(7−0)2 +(6−y)2=72+(6−y)2=49+36+y2−12y=60=460=15.
Следовательно, искомая точка равна (0,15).(0,15).(0,15). □_\квадрат□
Процитировать как: Формула расстояния. Brilliant.org . Извлекаются из https://brilliant.org/wiki/distance-formula/
| 9 | Оценить | квадратный корень из 12 | ||
| 10 | Оценить | квадратный корень из 20 | ||
| 11 | Оценить | квадратный корень из 50 | 94 | |
| 18 | Оценить | квадратный корень из 45 | ||
| 19 | Оценить | квадратный корень из 32 | ||
| 20 | Оценить | квадратный корень из 18 | 92 |
Урок по формуле расстояния — Бесплатная помощь по математике
Введение
Мы используем так называемую формулу расстояния , чтобы получить расстояние между любыми двумя точками в пространстве. Предположим, вам нужно определить расстояние между точками (2,0) и (5,0). Вот как они выглядят на графике:
Предположим, вам нужно определить расстояние между точками (2,0) и (5,0). Вот как они выглядят на графике:
С первого взгляда можно сказать, что они разделены на 3 единицы. Они оба на оси x, так что это просто измерение прямой линии. На самом деле, вам, возможно, даже не понадобился график, чтобы понять это. Но как измерить расстояние между двумя случайными точками на графике? Почему, используйте 92}$$
Разбивка
На первый взгляд, эта формула выглядит как настоящий беспорядок! Но просто подумайте о компонентах \(x_{2}-x_{1}\) и \(y_{2}-y_{1}\) как о длине в каждом направлении. Используя эти два значения, мы математически строим воображаемый треугольник с двумя катетами, длину которых мы можем вычислить. Позвольте мне показать вам, что я имею в виду визуально:
Мы просто измеряем расстояние вдоль каждой оси, а затем используем теорему Пифагора для вычисления длины гипотенузы, которая является воображаемой линией непосредственно между двумя нашими точками. Неважно, какая точка \((x_{1},y_{1})\), а какая \((x_{2},y_{2})\). Ключевая идея, которую следует вынести из этого сюжета, заключается в том, что вы заботитесь только о 92}$$
Неважно, какая точка \((x_{1},y_{1})\), а какая \((x_{2},y_{2})\). Ключевая идея, которую следует вынести из этого сюжета, заключается в том, что вы заботитесь только о 92}$$
Как мы пришли к этой формуле? Это просто теорема Пифагора, которая позволяет нам найти гипотенузу прямоугольного треугольника. В нашем случае гипотенуза — это расстояние между двумя точками!
Теперь рассмотрим простой пример:
Пример:
Найдите расстояние между двумя точками (5,5) и (1,2), используя формулу расстояния.
Решение:
Вместо того, чтобы слепо подставлять числа в формулу, нарисуйте график, чтобы вы знали, что происходит. 92} $$ $$ \text{расстояние}= \sqrt{16+9} $$ $$ \text{расстояние}= \sqrt{25} $$ $$ \text{расстояние}= 5 $$
Как только мы узнали, что \(x_{2}-x_{1}\) равно 4, а \(y_{2}-y_{1}\) равно 3, мы просто вставили эти числа в формулу расстояния до решать.
Вам может быть интересно, что произойдет, если вы поменяете местами точки? Помните, что мы имеем дело с расстояниями, которые по своей природе положительны. Расстояние одинаково в любом направлении, переходя из точки 1 в точку 2 или наоборот. Итак, просто используйте положительное расстояние между двумя точками. Если вы посмотрите на формулу, то заметите, что \(x_{2}-x_{1}\) и \(y_{2}-y_{1}\) возводятся в квадрат, что в любом случае автоматически делает их положительными. Так 92} $$
$$ \text{расстояние}= \sqrt{25+121} $$
$$ \text{расстояние}= \sqrt{146} $$
$$ \text{расстояние}= 12,08 $$
Расстояние одинаково в любом направлении, переходя из точки 1 в точку 2 или наоборот. Итак, просто используйте положительное расстояние между двумя точками. Если вы посмотрите на формулу, то заметите, что \(x_{2}-x_{1}\) и \(y_{2}-y_{1}\) возводятся в квадрат, что в любом случае автоматически делает их положительными. Так 92} $$
$$ \text{расстояние}= \sqrt{25+121} $$
$$ \text{расстояние}= \sqrt{146} $$
$$ \text{расстояние}= 12,08 $$
Формула расстояния несложная — вам просто нужно потренироваться с графиком, чтобы понять, что происходит. Вы просто строите треугольник и находите длину гипотенузы. Формула расстояния — это всего лишь теорема Пифагора!
Расширение до трех измерений
Как насчет трехмерного пространства? Как нам найти расстояние между точками (1,5,0) и (2,0,8)? Конечно, намного сложнее нарисовать график и измерить расстояние! Формула трехмерного расстояния на самом деле очень проста. Просто добавьте еще один член в формулу, потому что теперь мы должны учитывать ось Z.

 1 точки
1 точки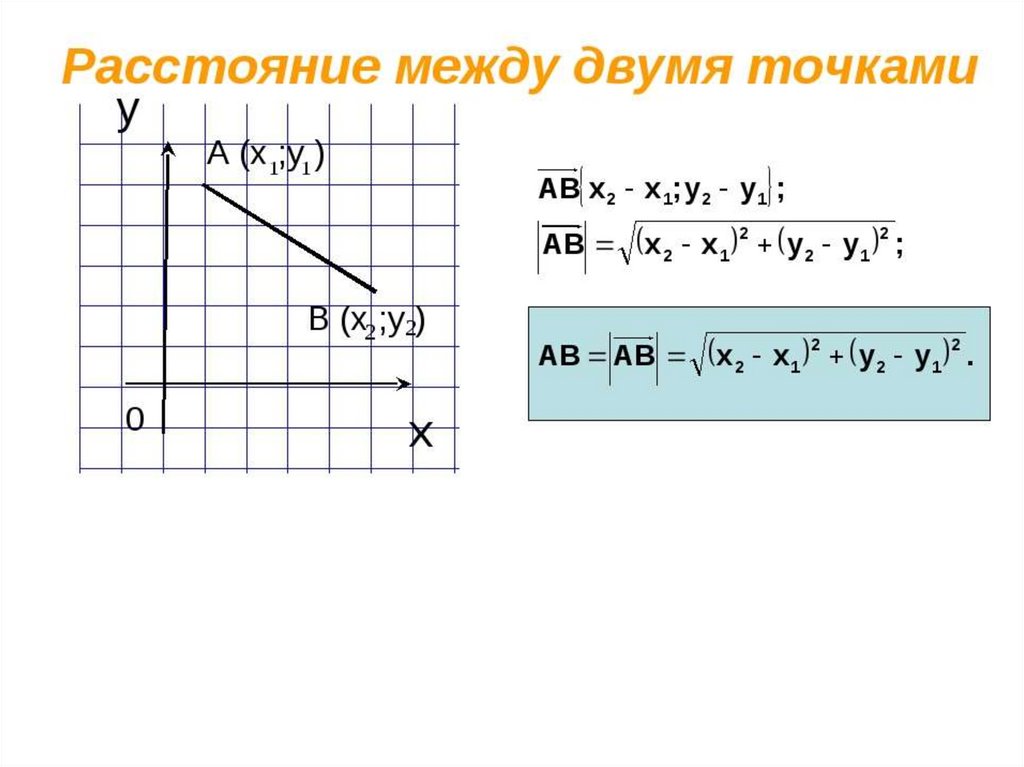 _1 точки 2-я_пр._1 _очки 1-я_пр._2_точки 2-я_пр._2_точки .
_1 точки 2-я_пр._1 _очки 1-я_пр._2_точки 2-я_пр._2_точки .
 5 , X2= -69 , Y2= -2.5 .
5 , X2= -69 , Y2= -2.5 . 5 , X2= -227 , Y2= 100.5 .
5 , X2= -227 , Y2= 100.5 .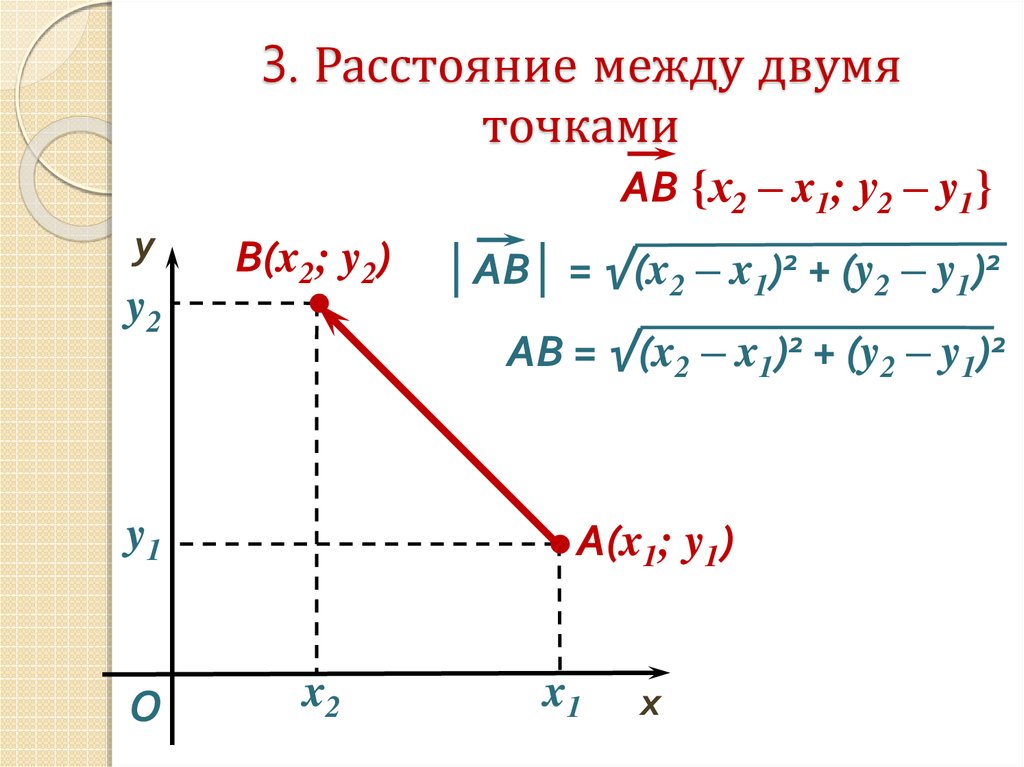

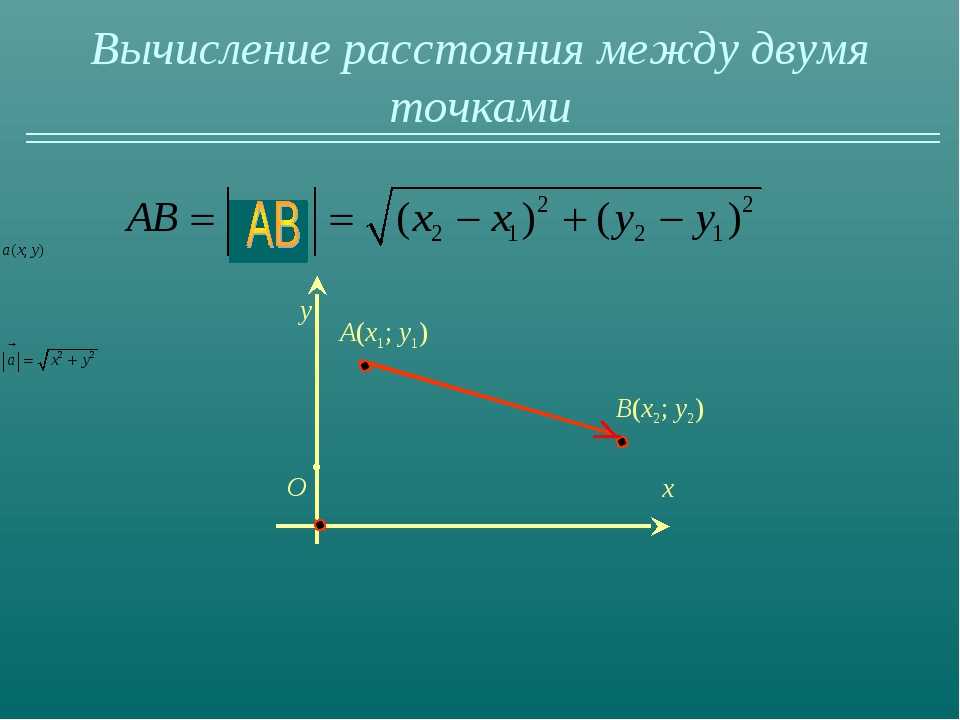
 2}\\
& = \sqrt{92}\\
& = \sqrt{49 + 1}\\
& = \sqrt{50}\\
& = 5\квадрат{2}.\ _\квадрат
\end{align}OP=x2+y2=72+12=49+1=50=52. □
2}\\
& = \sqrt{92}\\
& = \sqrt{49 + 1}\\
& = \sqrt{50}\\
& = 5\квадрат{2}.\ _\квадрат
\end{align}OP=x2+y2=72+12=49+1=50=52. □