Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Поиск по сайту:
| Справочник по математике | Геометрия (Планиметрия) | Четырехугольники |
| Основные определения и свойства трапеций |
| Свойства и признаки равнобедренных трапеций |
Основные определения и свойства трапеций
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Трапеция | Трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны. Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции | |
| Определение | Диагонали трапеции | Диагоналями трапеции называют отрезки, соединяющие противоположные вершины трапеции | |
| Определение | Высота трапеции | Высотой трапеции называют перпендикуляр, опущенный из любой точки одного оснований трапеции на другое основание или его продолжение | |
| Свойство | Точка пересечения диагоналей | Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой Более подробно об этом свойстве | |
| Определение | Средняя линия трапеции | Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции | |
| Свойство | Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме Посмотреть доказательство | ||
| Свойство | Биссектрисы углов при боковой стороне трапеции | Биссектрисы углов при боковой стороне трапеции перпендикулярны |
| Определение: трапеция | |
Трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны. Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции | |
| Определение: диагонали трапеции | |
| Диагоналями трапеции называют отрезки, соединяющие противоположные вершины трапеции | |
| Определение: высота трапеции | |
| Высотой трапеции называют перпендикуляр, опущенный из любой точки одного оснований трапеции на другое основание или его продолжение | |
| Свойство: точка пересечения диагоналей | |
Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой Более подробно об этом свойстве | |
| Определение: средняя линия трапеции | |
| Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции | |
| Свойство: средняя линия трапеции | |
Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме Посмотреть доказательство | |
| Свойство: биссектрисы углов при боковой стороне трапеции | |
| Биссектрисы углов при боковой стороне трапеции перпендикулярны | |
| Трапеция |
Определение: Трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны. Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции |
| Диагонали трапеции |
Определение: Диагоналями трапеции называют отрезки, соединяющие противоположные вершины трапеции |
| Высота трапеции |
Определение: Высотой трапеции называют перпендикуляр, опущенный из любой точки одного оснований трапеции на другое основание или его продолжение |
| Точка пересечения диагоналей |
Свойство: Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой Более подробно об этом свойстве |
| Средняя линия трапеции |
Определение: Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции Свойство: Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме Посмотреть доказательство |
| Биссектрисы углов при боковой стороне трапеции |
Свойство: Биссектрисы углов при боковой стороне трапеции перпендикулярны |
Подробнее со свойствами средней линии трапеции можно ознакомиться в разделе нашего справочника «Средняя линия трапеции».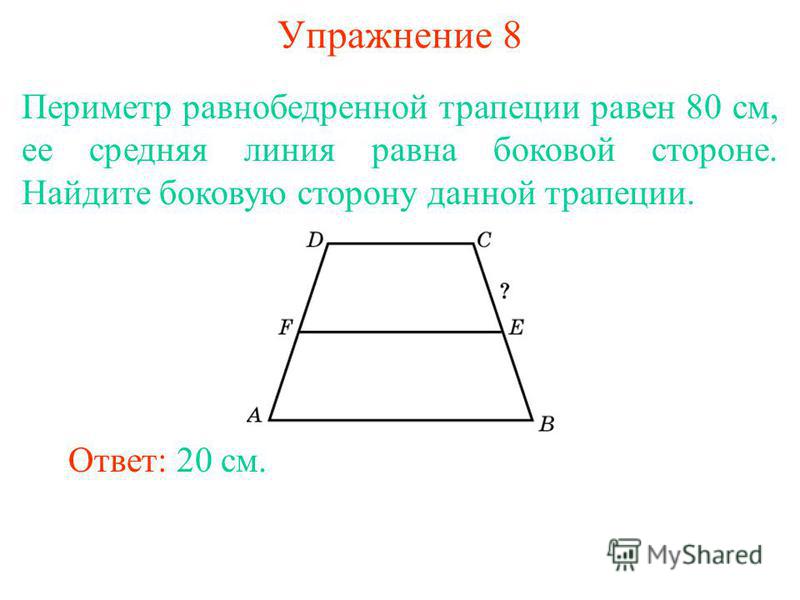
В разделе нашего справочника «Типы четырёхугольников» представлена схема классификации трапеций. В том же разделе представлена таблица, в которой описаны всевозможные типы трапеций.
Свойства и признаки равнобедренных трапеций
| Тип утверждения | Фигура | Рисунок | Формулировка |
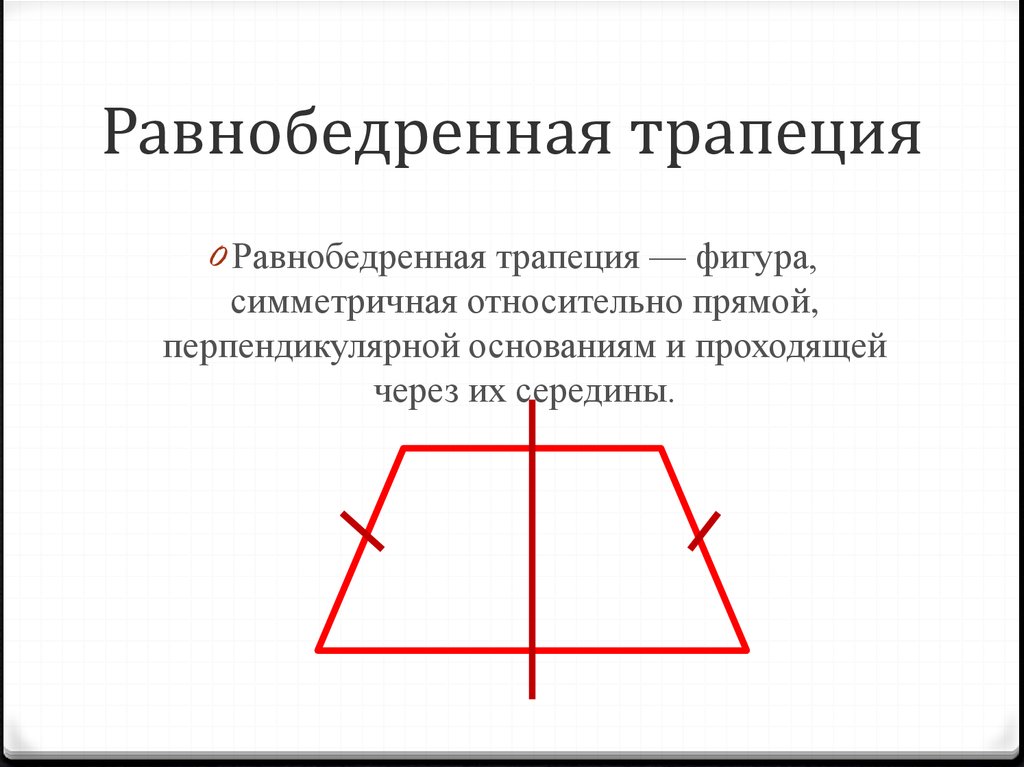
| Определение | Равнобедренная трапеция | Равнобедренной трапецией называют трапецию, у которой боковые стороны равны. | |
| Свойство | Равенство углов при основании | Если трапеция является равнобедренной, то углы при каждом из её оснований равны. | |
| Признак | Если у трапеции углы при одном из оснований равны, то углы равны и при другом основании, а трапеция является равнобедренной. | ||
| Свойство | Равенство диагоналей | Если трапеция является равнобедренной, то её диагонали равны. | |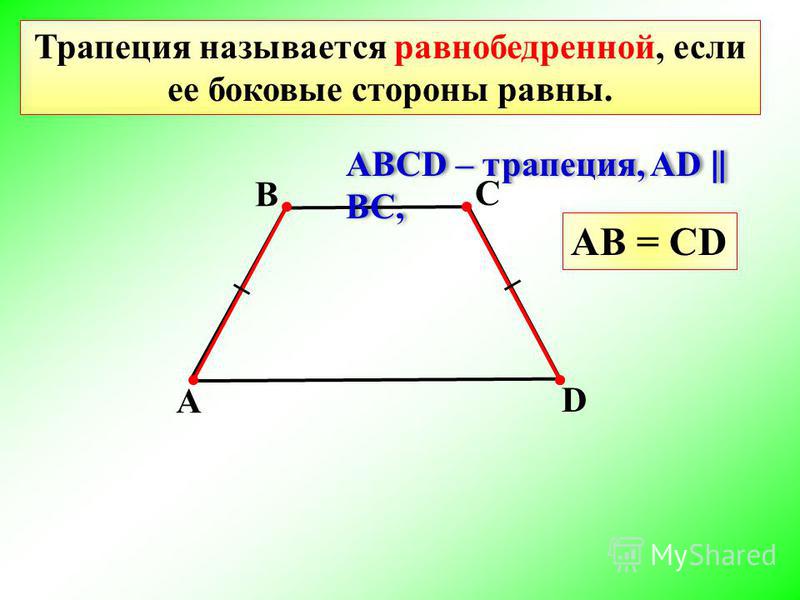
| Признак | Если у трапеции диагонали равны, то она является равнобедренной | ||
| Свойство | Углы, которые диагонали образуют с основаниями | Если трапеция является равнобедренной, то её диагонали образуют равные углы с каждым из её оснований. | |
| Признак | Если диагонали трапеции образуют равные углы с одним из оснований, то диагонали образуют равные углы и с другим основанием, а трапеция является равнобедренной. | ||
| Свойство | Описанная окружность | Если трапеция является равнобедренной, то около неё можно описать окружность. | |
| Признак | Если около трапеции можно описать окружность, то она является равнобедренной. | ||
| Свойство | Высоты трапеции | Основания высот равнобедренной трапеции, опущенных из вершин меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований |
| Определение: Равнобедренная трапеция | |
Равнобедренной трапецией называют трапецию, у которой боковые стороны равны. | |
| Свойство: равенство углов при основании | |
| Если трапеция является равнобедренной, то углы при каждом из её оснований равны. | |
| Признак: равенство углов при основании | |
| Если у трапеции углы при одном из оснований равны, то углы равны и при другом основании, а трапеция является равнобедренной. | |
| Свойство: равенство диагоналей | |
| Если трапеция является равнобедренной, то её диагонали равны. | |
| Признак: равенство диагоналей | |
| Если у трапеции диагонали равны, то она является равнобедренной | |
| Свойство: углы, которые диагонали образуют с основаниями | |
| Если трапеция является равнобедренной, то её диагонали образуют равные углы с каждым из её оснований. | |
| Признак: углы, которые диагонали образуют с основаниями | |
Если диагонали трапеции образуют равные углы с одним из оснований, то диагонали образуют равные углы и с другим основанием, а трапеция является равнобедренной. | |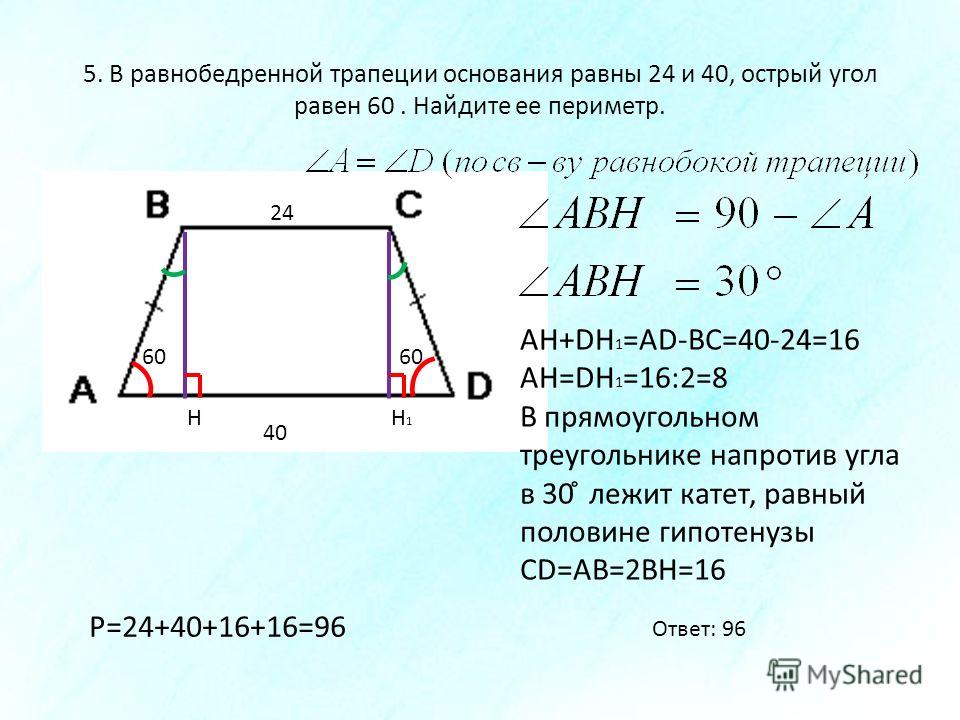
| Свойство: описанная окружность | |
| Если трапеция является равнобедренной, то около неё можно описать окружность. | |
| Признак: описанная окружность | |
| Если около трапеции можно описать окружность, то она является равнобедренной. | |
| Свойство: высоты трапеции | |
| Основания высот равнобедренной трапеции, опущенных из вершин меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований | |
| Равнобедренная трапеция |
Определение: Равнобедренной трапецией называют трапецию, у которой боковые стороны равны. |
| Равенство углов при основании |
Свойство: Если трапеция является равнобедренной, то углы при каждом из её оснований равны. Признак: Если у трапеции углы при одном из оснований равны, то углы равны и при другом основании, а трапеция является равнобедренной. |
| Равенство диагоналей |
Свойство: Если трапеция является равнобедренной, то её диагонали равны. Признак: Если у трапеции диагонали равны, то она является равнобедренной. |
| Углы, которые диагонали образуют с основаниями |
Свойство: Если трапеция является равнобедренной, то её диагонали образуют равные углы с каждым из её оснований. Признак: Если диагонали трапеции образуют равные углы с одним из оснований, то диагонали образуют равные углы и с другим основанием, а трапеция является равнобедренной. |
| Описанная окружность |
Свойство: Если трапеция является равнобедренной, то около неё можно описать окружность. Признак: Если около трапеции можно описать окружность, то она является равнобедренной. |
| Высоты трапеции |
Свойство: Основания высот равнобедренной трапеции, опущенных из вершин меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований |
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.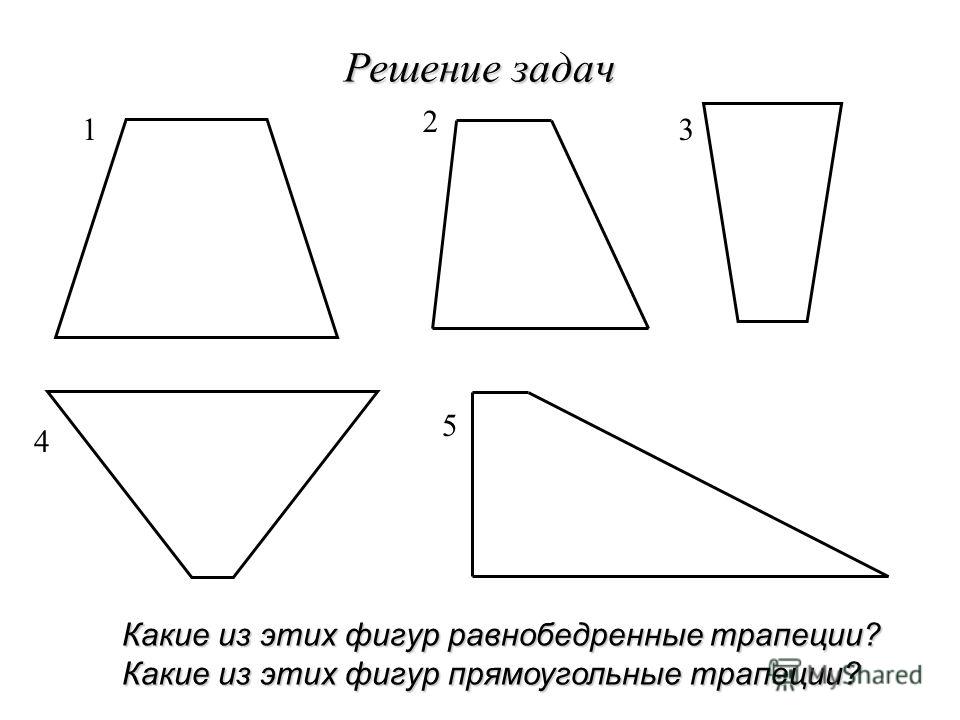
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
|
Равнобедренная трапеция — свойства, признаки и формулы
Равнобедренная трапеция, её ещё называют равнобокой, имеет равные боковые стороны. Кроме этого, у нее в арсенале есть еще множество интересных и полезных свойств, которые можно с легкостью применять на практике или при решении математических задач.
Содержание
- Определение, признаки и элементы трапеции
- Свойства равнобедренной трапеции
- Периметр равнобедренной трапеции
- Как найти стороны трапеции?
- Средняя линия
- Высота трапеции
- Диагональ трапеции
- Площадь равнобедренной трапеции
- Вписанная и описанные окружности
Определение, признаки и элементы трапеции
Трапецией в геометрии принято называть любой четырехугольник, у которого есть две параллельные друг другу стороны, при том что продолжения других двух сторон пересекаются.
Определение же равнобедренной трапеции идет от того, что у нее боковые стороны эквиваленты по длине.
Свойства равнобедренной трапеции
Существует всего несколько основных свойств, присущих именно данной фигуре. Сейчас мы рассмотрим каждое из них:
Первый отрезок АЕ будет равен сумме оснований, деленной на 2, а второй отрезок ЕВ — разности, разделенной на 2:
Периметр равнобедренной трапеции
Эту величину найти очень просто.
Простейшей формулой будет сложение всех ее сторон. Однако иногда составители задач не дают нам информацию обо всех из сторон.
В таком случае нам следует в первую очередь найти все стороны фигуры, а затем уже приступать к их сложению.
Как найти стороны трапеции?
Существует множество различных способов решения данной задачи, однако мы предложим только некоторые из них.
В первую очередь можно найти стороны с помощью средней линии:
Есть альтернатива, если вам известны высота и угол при большем основании:
Средняя линия
Средней линией в трапеции называется параллельный основаниям отрезок, который делит боковые стороны фигуры на равные части.
У нее есть множество интересных свойств и теорем с нетрудным доказательством, таких как, например, решение задач на подобие, однако мы на них останавливаться не будем.
Высота трапеции
Высотой трапеции называется самый короткий по длине отрезок, который продолжается ровно от одного основания до другого.
Он выполняет своеобразную вспомогательную роль в задачах вплоть до 10 класса с неизвестными сторонами и в тех задачах, где нужно дополнить фигуру до прямоугольника, например.
Для нахождения длины этого отрезка нам необходимо знать оба основания (a и b), а также боковую сторону c. Также полезно было бы знать угол при большем основании α. Формулы здесь довольно простые и не нуждаются в доказательстве.
Диагональ трапеции
Эта линия просто идет от одного угла трапеции к другому, причем эти углы противоположны. В равнобедренной трапеции довольно приятным фактом является то, что диагонали в ней равны друг другу.
А каким образом можно найти длину диагонали? Есть один очень простой способ. Мы можем сделать это, зная все три величины: боковую сторону и каждое из оснований:
Площадь равнобедренной трапеции
Самой простой формулой является полусумма оснований, умноженная на высоту.
Она подходит к любым трапециям.
Для второй формулы нужно знать все стороны трапеции. Это по сути усложненная версия первой, но подойдет она в том случае, если вы не знаете высоту.
Это самые базовые формулы, поэтому очень часто используются в различных задачах.
Вписанная и описанные окружности
Интересно, что вписать в трапецию окружность можно только при определенном условии. И это условие выполняется, если мы попарно сложим противоположные стороны нашего четырехугольника, и эти суммы окажутся равны.
Найти радиус этой окружности не составит труда. Нужно просто разделить высоту пополам.
А вот с описанной окружностью все не так гладко. Есть различные полезные формулы. Например, если диагональ составляет с основанием прямой угол, то диаметр описанной окружности будет равен противоположному основанию трапеции.
Теперь разберемся с формулой нахождения радиуса.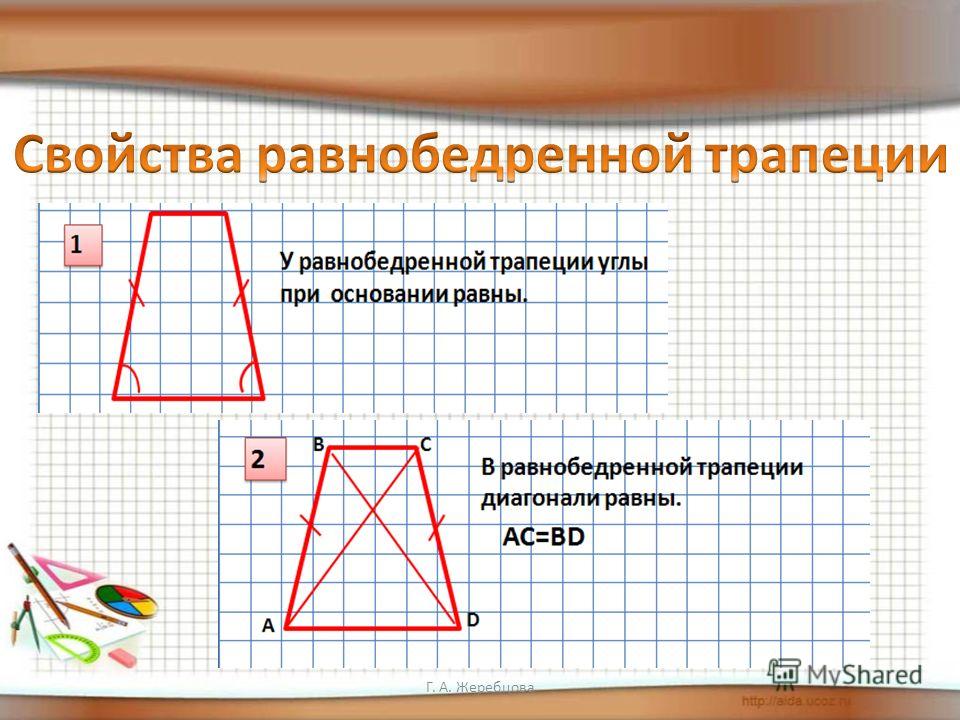
К слову, она здесь не очень простая. Сначала найдем p — полупериметр ∆DBC, а затем просто применим его в следующей формуле:
Математика бесспорно является матерью всех современных наук. Она по праву занимает свой престол и управляет абсолютно всеми мировыми законами.
Одной из наиболее интересных подразделений математики принято считать именно геометрию. Ее фигуры также подчиняются математическим правилам и формулам, поэтому она необходима при различных сложных расчетах.
Предыдущая
ГеометрияОкружность — определение, свойства и формулы вычисления площади
Следующая
ГеометрияГипотенуза — формула, правила и примеры вычислений
Углы равнобедренной трапеции
Получи беслпатные курсы подготовки к ЕГЭ и ОГЭ!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2015-10-14
Углы равнобедренной трапеции.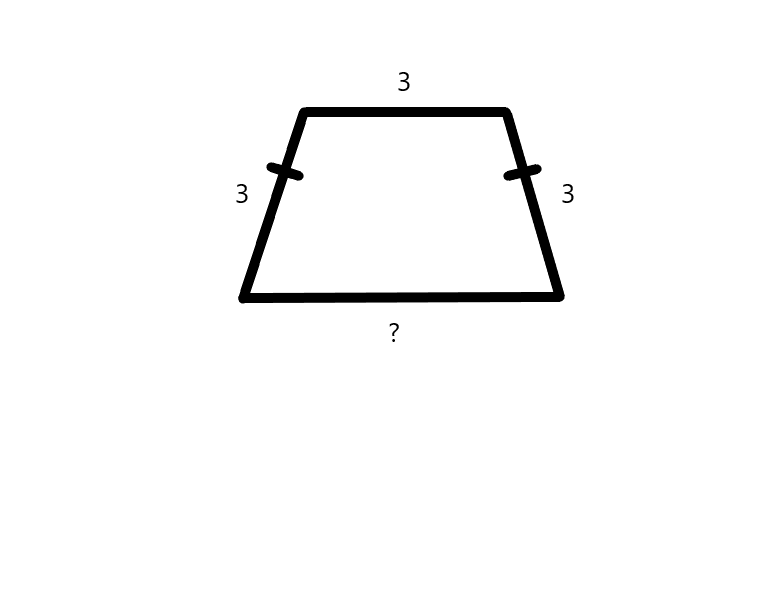
Здравствуйте! В этой статье речь пойдёт о решении задач с трапецией. Данная группа заданий входит в состав экзамена, задачки простые. Будем вычислять углы трапеции, основания и высоты. Решение ряда задач сводится к решению прямоугольного треугольника, как говориться: куда мы без теоремы Пифагора, синуса и косинуса?
Работать будем с равнобедренной трапецией. У неё равны боковые стороны и углы при основаниях. О трапеции есть статья на блоге, посмотрите.
Отметим небольшой и важный нюанс, который в процессе решения самих заданий подробно расписывать не будем. Посмотрите, если у нас дано два основания, то большее основание высотами, опущенными к нему, разбивается на три отрезка – один равен меньшему основанию (это противолежащие стороны прямоугольника), два других равны друг другу (это катеты равных прямоугольных треугольников):
Простой пример: дано два основания равнобедренной трапеции 25 и 65. Большее основание разбивается на отрезки следующим образом:
*И ещё! В задачах не введены буквенные обозначения.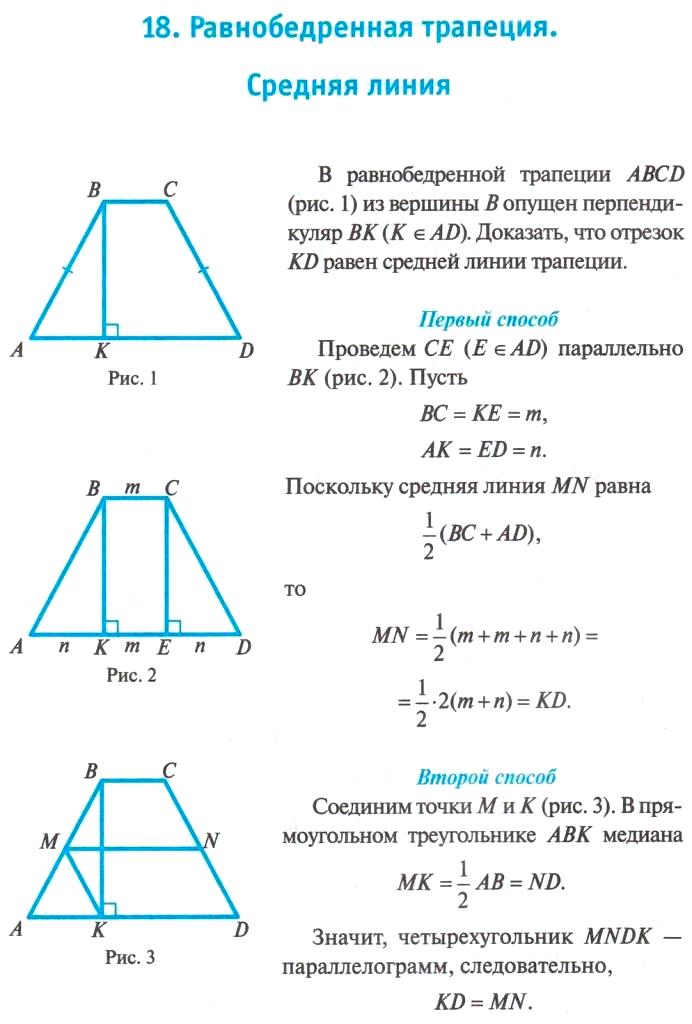
Это сделано умышленно, чтобы не перегружать решение алгебраическими изысками. Согласен, что это математически неграмотно, но цель донести суть. А обозначения вершин и прочих элементов вы всегда можете сделать сами и записать математически корректное решение.
Рассмотрим задачи:
27439. Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.
Для того чтобы найти угол необходимо построить высоты. На эскизе обозначим данные в условии величины. Нижнее основание равно 65, высотами оно разбивается на отрезки 7, 51 и 7:
В прямоугольном треугольнике нам известна гипотенуза и катет, можем найти второй катет (высоту трапеции) и далее уже вычислить синус угла.
По теореме Пифагора указанный катет равен:
Таким образом:
Ответ: 0,96
27440. Основания равнобедренной трапеции равны 43 и 73. Косинус острого угла трапеции равен 5/7. Найдите боковую сторону.
Построим высоты и отметим данные в условии величины, нижнее основание разбивается на отрезки 15, 43 и 15:
Ответ: 21
27441.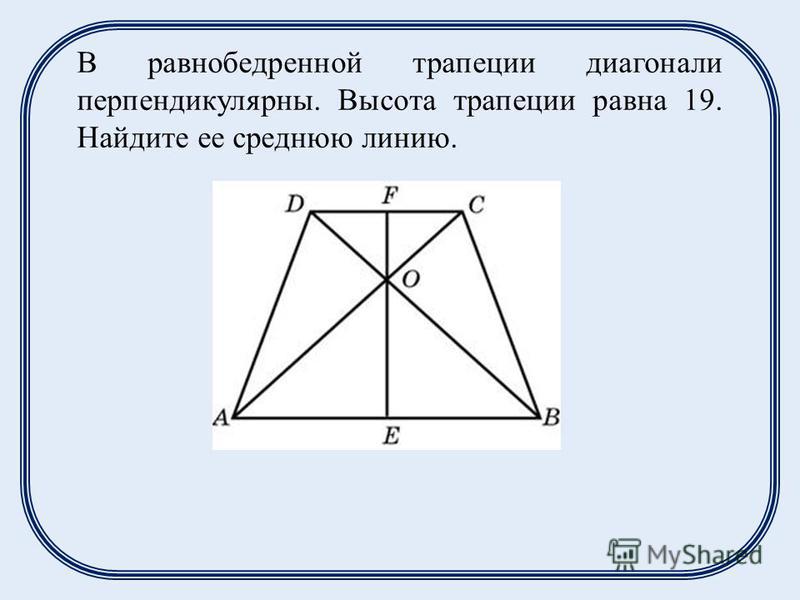
Большее основание равнобедренной трапеции равно 34. Боковая сторона равна 14. Синус острого угла равен (2√10)/7. Найдите меньшее основание.
Построим высоты. Для того чтобы найти меньшее основание нам необходимо найти чему равен отрезок являющийся катетом в прямоугольном треугольнике (обозначен синим):
Можем вычислить высоту трапеции, а затем найти катет:
По теореме Пифагора вычисляем катет:
Таким образом, меньшее основание равно:
Ответ: 22
27442. Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен 5/11. Найдите высоту трапеции.
Построим высоты и отметим данные в условии величины. Нижнее основание разбивается на отрезки:
Что делать? Выражаем тангенс известного нам угла при основании в прямоугольном треугольнике:
Ответ: 10
27443. Меньшее основание равнобедренной трапеции равно 23. Высота трапеции равна 39. Тангенс острого угла равен 13/8. Найдите большее основание.
Строим высоты и вычисляем чему равен катет:
Таким образом большее основание будет равно:
Ответ: 71
27444. Основания равнобедренной трапеции равны 17 и 87. Высота трапеции равна 14. Найдите тангенс острого угла.
Строим высоты и отмечаем известные величины на эскизе. Нижнее основание разбивается на отрезки 35, 17, 35:
По определению тангенса:
Ответ: 0,4
77152. Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону.
Построим эскиз, построим высоты и отметим известные величины, большее основание разбивается на отрезки 3, 6 и 3:
Выразим гипотенузу обозначенную как х через косинус:
Из основного тригонометрического тождества найдём cosα
Таким образом:
Ответ: 5
27818. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 500? Ответ дайте в градусах.
Из курса геометрии нам известно, что если имеем две параллельные прямые и секущую, что сумма внутренних односторонних углов равна 1800. В нашем случае это
C условии сказано, что разность противолежащих углов равна 500, то есть
Так как у равнобедренной трапеции углы при основании равны, то есть угол А равен углу В, то можем записать
Имеем два уравнения с двумя неизвестными, можем решить систему:
*Конечно, эту задачу можно было легко решить просто перебирая пары углов )
27833. В равнобедренной трапеции большее основание равно 25, боковая сторона равна 10, угол между ними 600. Найдите меньшее основание.
Построим высоты DE и CF:
Меньшее основание равно отрезку EF, так как DC и EF это противолежащие стороны прямоугольника. Отрезок EF мы можем найти если вычислим АЕ. Выразим этот катет прямоугольного треугольника ADE через функцию косинуса:
Так как AE=FB=5, то EF=25–5–5=15.
Следовательно и DC=15.
Ответ: 15
27837. Основания равнобедренной трапеции равны 15 и 9, один из углов равен 450. Найдите высоту трапеции.
Из точек D и C опустим две высоты:
Как уже сказано выше они разбивают большее основание на три отрезка: один равен меньшему основанию, два других равны друг другу.
В данном случае они равны 3, 9 и 3 (в сумме 15). Кроме того, отметим что высотами отсекаются прямоугольные треугольники, причём они являются равнобедренными, так как углы при основании равны по 450. Отсюда следует, что высота трапеции будет равна 3.
Ответ: 3
На этом всё! Успеха вам!
С уважением, Александр.
P.S: Расскажите о сайте в социальных сетях!
Категория: Четырёхугольники | ЕГЭ-№1ТрапецияУглы
Подготовка к ОГЭ по математике. Полный курс!
Полный Видеокурс по РУССКОМУ ЯЗЫКУ!
ПРЕМИУМ-КУРС по математике на 100 баллов!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.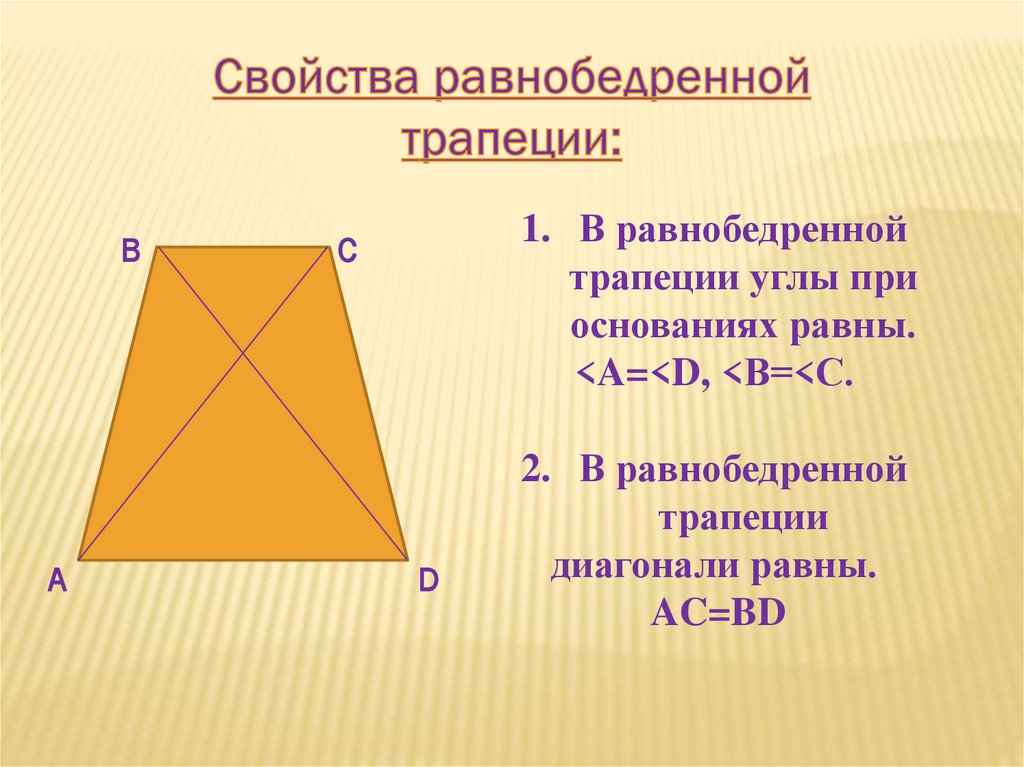
Предварительное исчисление по алгебре — Как разделить пополам равнобедренную трапецию на две части равной площади
Задавать вопрос
Спросил
Изменено 3 года, 7 месяцев назад
Просмотрено 5к раз
$\begingroup$
Дана равнобедренная трапеция:
Я хочу провести линию, параллельную основаниям (то есть параллельную AD и BC и находящуюся между ними), так, чтобы верхняя и нижняя половины имели одинаковую площадь.
В частности, если мы определим высоту трапеции как 1, я хочу знать, как далеко от более длинного основания упадет эта биссектриса. Назовем это значение м .
Для равнобедренной трапеции, у которой более короткое основание в k раз короче другого, я подозреваю, что m будет функцией только k .
Вот более подробная диаграмма:
Вот некоторые (возможно, неверные) уравнения, описывающие это:
- Площадь ABCD = ((a + ka) / 2) * 1
- Площадь EBCF = ((a + ja) / 2) * m
- Площадь AEFD = ((ja + ka) / 2) * (1 — m)
- Площадь EBCF = Площадь AEFD
- Площадь EBCF + Площадь AEFD = Площадь ABCD
Интуитивно я ожидаю, что j и a сократятся из этих уравнений и смогут получить m исключительно через k . Но мне трудно понять, как туда добраться.
- алгебра-предварительное исчисление
- геометрия
$\endgroup$
1
$\begingroup$
Важно отметить, что $(a-ka)=\frac {ja-ka}{1-m}$. Вы можете доказать это, опустив перпендикуляры из $A$ и $D$ на $BC$ и заметив, что треугольники на каждом конце подобны.
$\endgroup$
1
$\begingroup$
Подсказка: попробуйте разбить трапецию на прямоугольник и равнобедренный треугольник. Я думаю, вы обнаружите, что по мере увеличения высоты площадь прямоугольника будет увеличиваться линейно, а площадь треугольника будет увеличиваться квадратично.
$\endgroup$
$\begingroup$
Это основано на ответе Росса Милкмана и делает его более явным.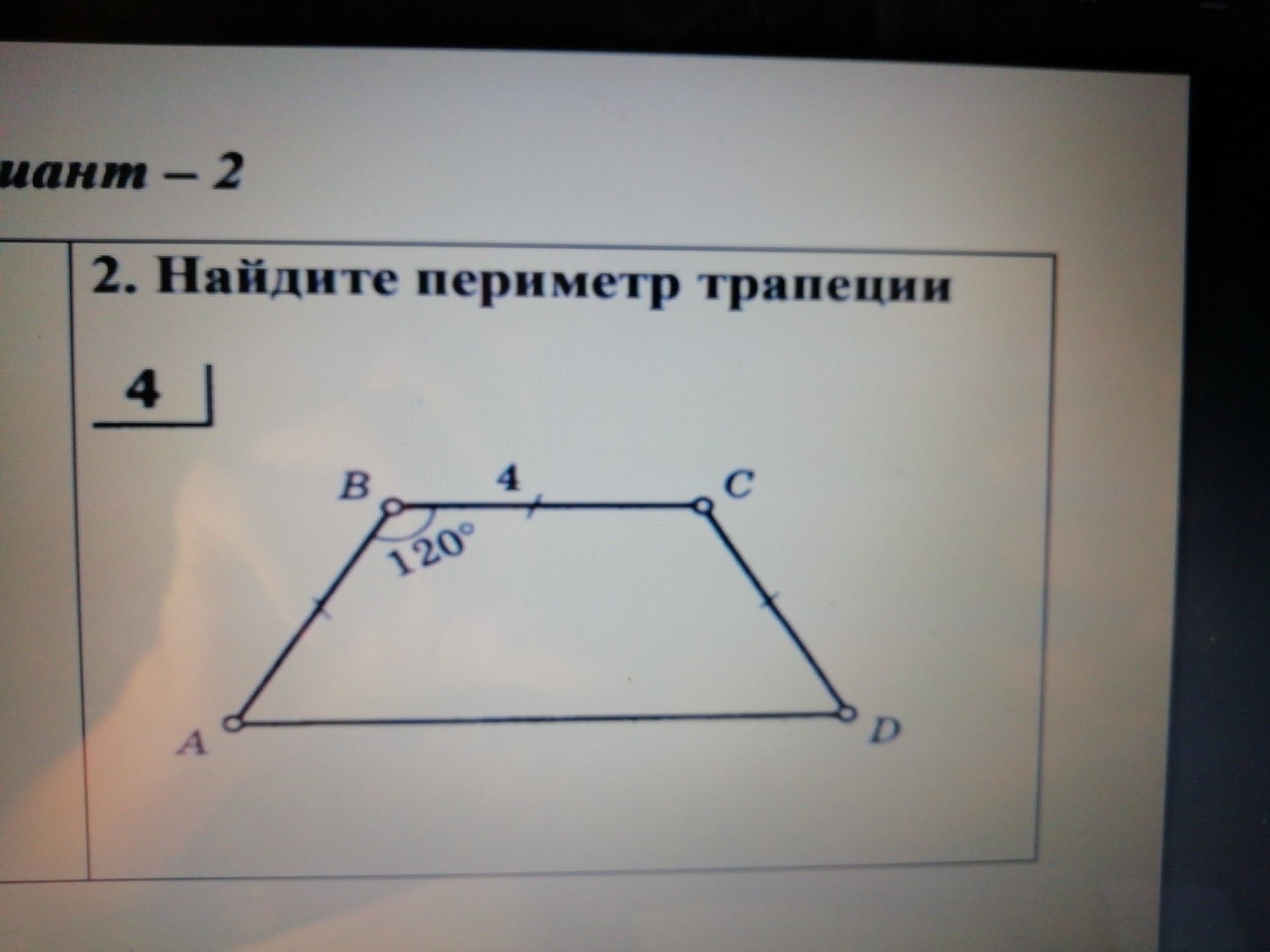
Я предложил это как редактирование его, но редактирование было отклонено.
Важно отметить, что $(a-ka)=\frac {ja-ka}{1-m}$. Вы можете доказать это, опустив перпендикуляры из $A$ и $D$ на $BC$ и заметив, что треугольники на каждом конце подобны. Вы можете взять $a$ из этого, чтобы получить $1-k=\frac {j-k}{1-m}$:
$$1-k=\frac{j-k}{1-m}\\ 1-m-k+km=j-k\\1-m+km=j$$
Соедините это с $(1+j)m=(j+k)(1-m)$ из равных площадей и у вас есть два уравнения с тремя неизвестными, которые дадут вам набор решений с одним параметром, который вы ищете. 92+4m-(1+k)=0$$
Затем используйте квадратное уравнение, чтобы получить $m$ через $k$:
$$\\m=\frac{-4±\sqrt {16-4(2k-2)(-1-k)}}{2(2k — 2)}$$
Тогда для $k=0,1$: $m=0,321518311$ или $m=1,
3911 $
Поскольку значение $m$ не может превышать высоту самой трапеции, в данном контексте имеет смысл только первый ответ.
$\endgroup$
$\begingroup$
Обобщение на произвольные трапеции не усложняет задачу, поэтому мы не будем предполагать, что трапеция равнобедренная или что ее высота равна $1$.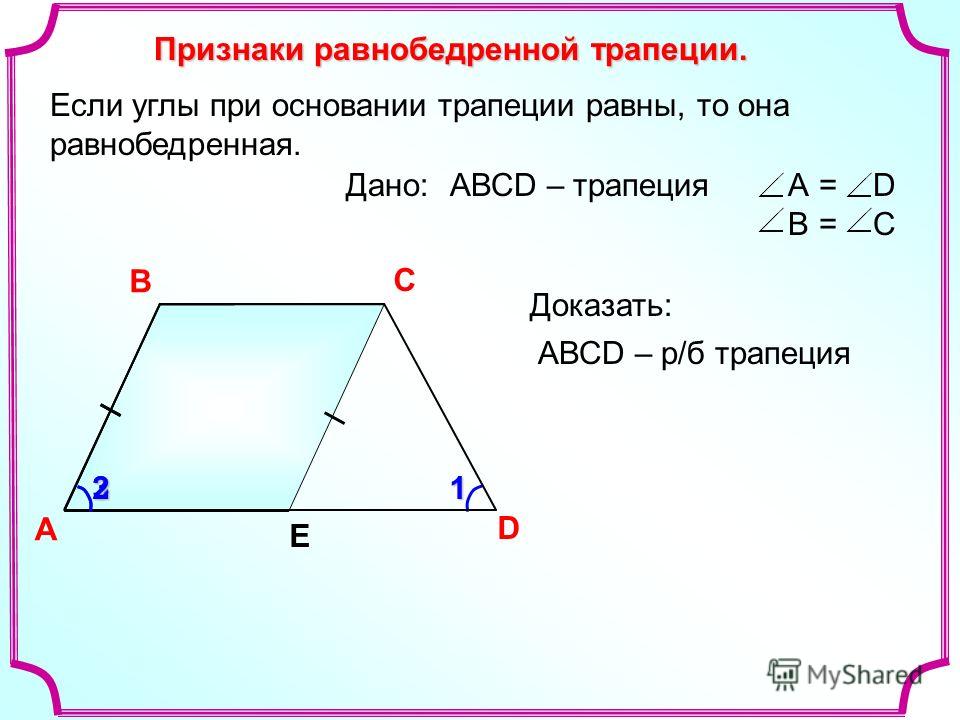
2} {2}}} {1-k} ч.
$$
Историческое отступление: Ключевой факт был известен в старовавилонские времена (~2000 г. до н.э. – ~1600 г. до н.э.). Например, он был использован в потрясающе элегантном решении задачи на клинописной табличке VAT 8512, которое объясняется в книге Йенса Хойрупа «Алгебра в клинописи: введение в древневавилонскую геометрическую технику»
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Свойства трапеций и воздушных змеев
Теперь, когда мы рассмотрели несколько типов
четырехугольников, являющихся
параллелограммами, давайте узнаем о фигурах, не обладающих свойствами
параллелограммов.
противоположных сторон параллельны. В этом разделе мы рассмотрим четырехугольники, у которых
противоположных сторон могут пересекаться в какой-то точке. Два типа четырехугольников, которые мы будем изучать
называются трапеции и воздушные змеи . Давайте начнем наше исследование с изучения некоторых свойств трапеций.
Трапеции
Определение: Трапеция — это четырехугольник с ровно одной парой параллельных
сторон.
Поскольку у трапеции должна быть ровно одна пара параллельных сторон, нам нужно будет
доказать, что одна пара противоположных сторон параллельна, а другая не лежит в нашей плоскости.0157
геометрические доказательства в два столбца. Если мы забудем доказать, что одна пара противоположных
сторон не параллельна, мы не исключаем возможность того, что четырехугольник
Поэтому этот шаг будет абсолютно необходим, когда мы будем работать над различными упражнениями с использованием трапеций. Прежде чем мы погрузимся непосредственно в изучение трапеций, необходимо будет выучить 90 157 названий различных частей этих четырехугольников, чтобы быть конкретным в отношении
его стороны и углы. Все трапеции состоят из двух основных частей: основания и ножки .
Противоположные стороны трапеции, параллельные друг другу, называются основаниями.
Остальные стороны трапеции, которые пересекаются в некоторой точке при продолжении
, называются катетами трапеции.
Верхняя и нижняя стороны трапеции идут параллельно друг другу, поэтому
они являются основаниями трапеции. Другие стороны трапеции пересекутся, если ее продолжить,
Отрезок, соединяющий середины катетов трапеции, называется
серединой .
Длина этого отрезка всегда равна половине суммы
оснований трапеции, или
Рассмотрим трапецию ABCD, показанную ниже.
Средний сегмент EF , показанный красным цветом, имеет длину
Измерение середины сегмента зависит только от длины 90 157 оснований трапеции. Однако есть важная характеристика, которой обладают некоторые трапеции:
опирается исключительно на свои ноги. Давайте теперь посмотрим на эти трапеции.
Равнобедренные трапеции
Определение: Равнобедренная трапеция — это трапеция, катеты которой конгруэнтны.
По определению, пока в четырехугольнике ровно одна пара параллельных прямых,
, то четырехугольник является трапецией. Определение равнобедренной трапеции
добавляет еще одно уточнение: стороны трапеции должны быть конгруэнтны.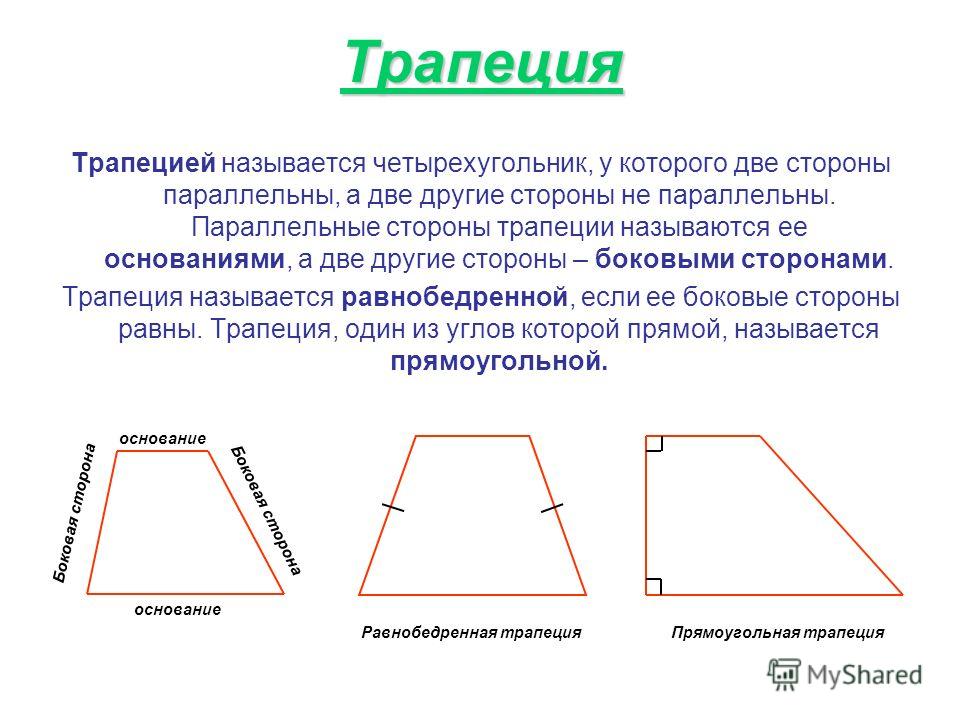
ABCD не является равнобедренной трапецией, потому что AD и BC не равны. Поскольку EH
и FG конгруэнтны, трапеция EFGH является равнобедренной трапецией.
Есть несколько теорем, которые мы можем использовать, чтобы доказать, что трапеция равнобедренная.
Эти свойства перечислены ниже.
(1) Трапеция равнобедренная тогда и только тогда, когда углы при основании равны.
(2) Трапеция равнобедренная тогда и только тогда, когда диагонали конгруэнтны.
(3) Если трапеция равнобедренная, то ее противоположные углы дополнительные.
Воздушные змеи
Определение: Воздушный змей — это четырехугольник с двумя различными парами смежных
сторон, которые конгруэнтны.
Напомним, что параллелограммы также имели пары конгруэнтных сторон.
Однако их равные
сторон всегда были противоположными сторонами. Воздушные змеи имеют две пары конгруэнтных сторон, которые встречаются с
в двух разных точках. Давайте посмотрим на иллюстрацию ниже, чтобы понять, как выглядит воздушный змей
.
Отрезок АВ примыкает к отрезку ВС и равен ему. Отрезки AD и CD также
смежных и конгруэнтных.
Воздушные змеи обладают парой свойств, которые помогут нам отличить их от других четырехугольников.
(1) Диагонали воздушного змея сходятся под прямым углом.
(2) Воздушные змеи имеют ровно одну пару противоположных углов, которые равны.
Эти два свойства показаны на диаграмме ниже.
Обратите внимание, что на пересечении диагоналей образуется прямой угол, который равен
в точке N. Также мы видим, что ?K??M.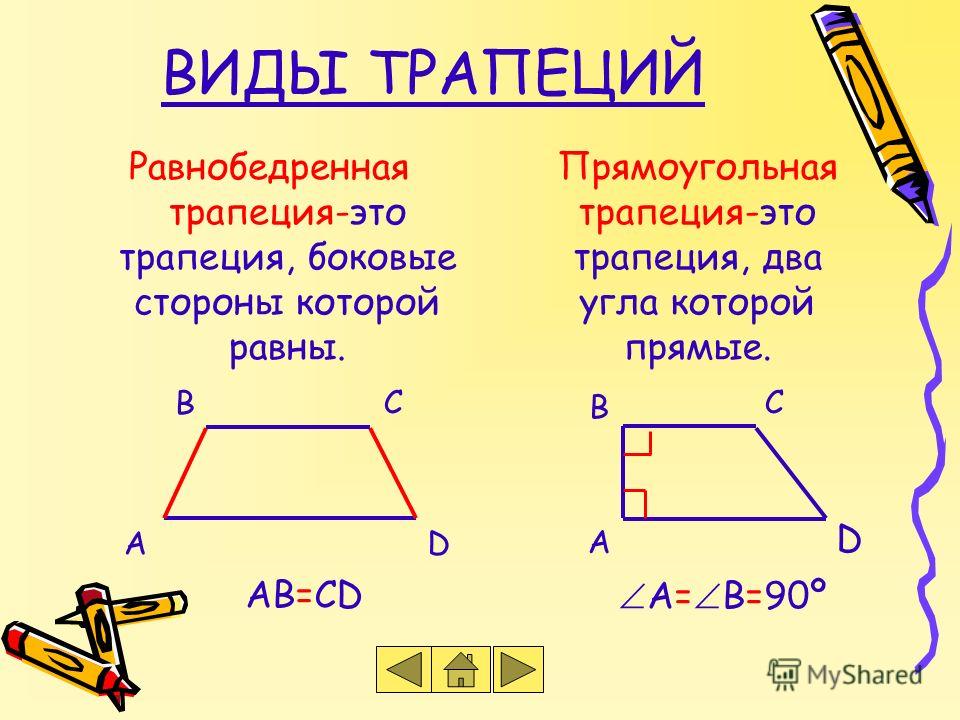
Это наша единственная пара равных углов, потому что
?J и ?L имеют разные меры.
Давайте попрактикуемся в решении некоторых задач, требующих использования свойств трапеций
и воздушных змеев, о которых мы только что узнали.
Упражнение 1
Найдите значение x в трапеции ниже.
Ответ:
Поскольку нам известны длины оснований трапеции, мы можем вычислить 9.0157, какой должна быть длина среднего сегмента. Давайте воспользуемся формулой, которую мы получили для среднего отрезка, чтобы вычислить это. (Помните, это половина суммы
оснований.)
Итак, теперь, когда мы знаем, что длина средней части равна 24 , мы можем перейти на
вперед и установить 24 равным 5x-1 .
Переменная разрешима
сейчас:
Упражнение 2
Найдите значение y в равнобедренной трапеции ниже.
Ответ:
На рисунке нам дана только мера одного угла, поэтому мы должны иметь возможность
вывести больше информации на основе этого одного элемента. Потому что четырехугольник равен
равнобедренная трапеция, мы знаем, что углы при основании равны. Это означает, что
?A также имеет меру 64° .
Теперь давайте разберемся, чему равна сумма ?A и ?P :
Вместе они составляют 128° . Напомним к Внутренний многоугольник
Сумма углов Теорема о том, что внутренние углы четырехугольника должны быть равны 360° .
Итак, давайте попробуем использовать это таким образом, чтобы определить меру
?R . Сначала просуммируем все углы и установим его равным 360° .
Теперь мы видим, что сумма ?T и ?R это 232° .
, потому что сегмент TR является другим основанием трапеции TRAP ,
Мы знаем, что углы в точках T и 9017 2 T и 9017 2 T и 9017 2 T . Таким образом, если мы определим меры ?T и ?R
переменной x , мы получим
Это значение означает, что мера ?T и ?R равна
116° .
Наконец, мы можем установить 116 равным выражению, показанному в ?R
, чтобы определить значение y . У нас есть
Итак, мы получаем х=9 .
В то время как описанный выше метод был углубленным способом решения упражнения, мы могли бы использовать
, просто используя свойство, заключающееся в том, что противоположные углы равнобедренных трапеций являются дополнительными.
Решение таким способом намного быстрее, так как нам нужно только найти дополнение
к углу 64° . Получаем
Как только мы дойдем до этой точки в нашей задаче, мы просто установим 116 равным
4(3y+2) и решим, как мы это делали раньше.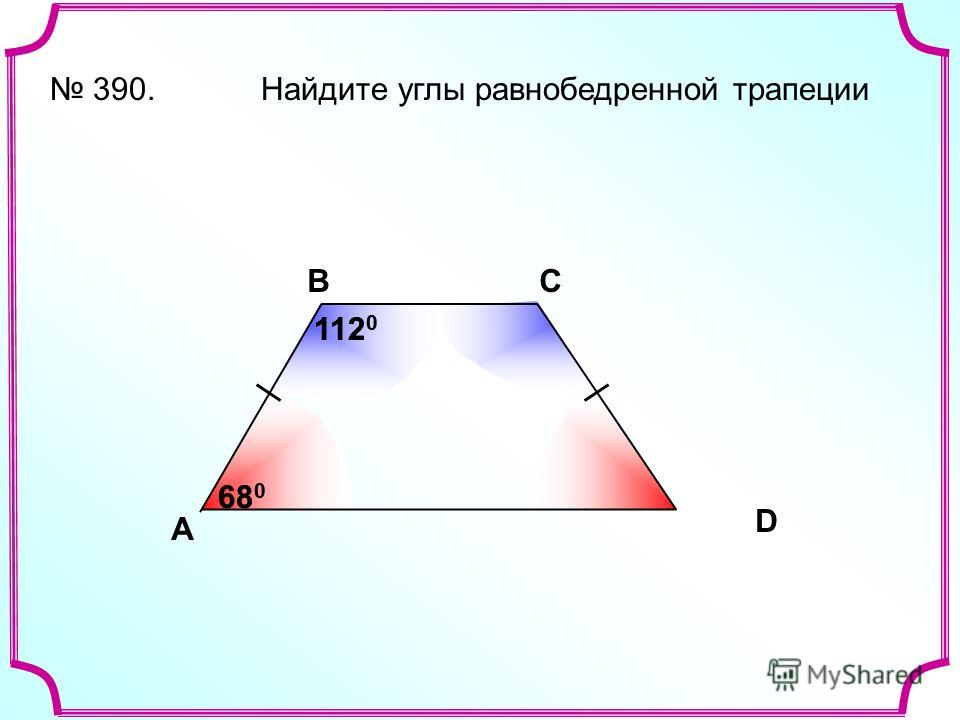
Упражнение 3
Ответ:
Прочитав задачу, мы видим, что нам дали ограниченное количество информации
и хотим сделать вывод, что четырехугольник DEFG — воздушный змей. Notice that
EF and GF are congruent, so if we can find a way to
prove that DE and DG are congruent, it would give us
two distinct pairs смежных сторон, которые конгруэнтны, что является определением
воздушного змея.
Нам также было дано, что ?EFD и ?GFD совпадают.
В прошлом мы узнали несколько теорем о конгруэнтности треугольников, которые могли бы быть применимы
в этой ситуации, если бы мы могли просто найти другую сторону или угол, которые конгруэнтны.
Поскольку отрезок DF составляет сторону ?DEF и ?DGF ,
, мы можем использовать рефлексивное свойство , чтобы сказать, что он конгруэнтен самому себе.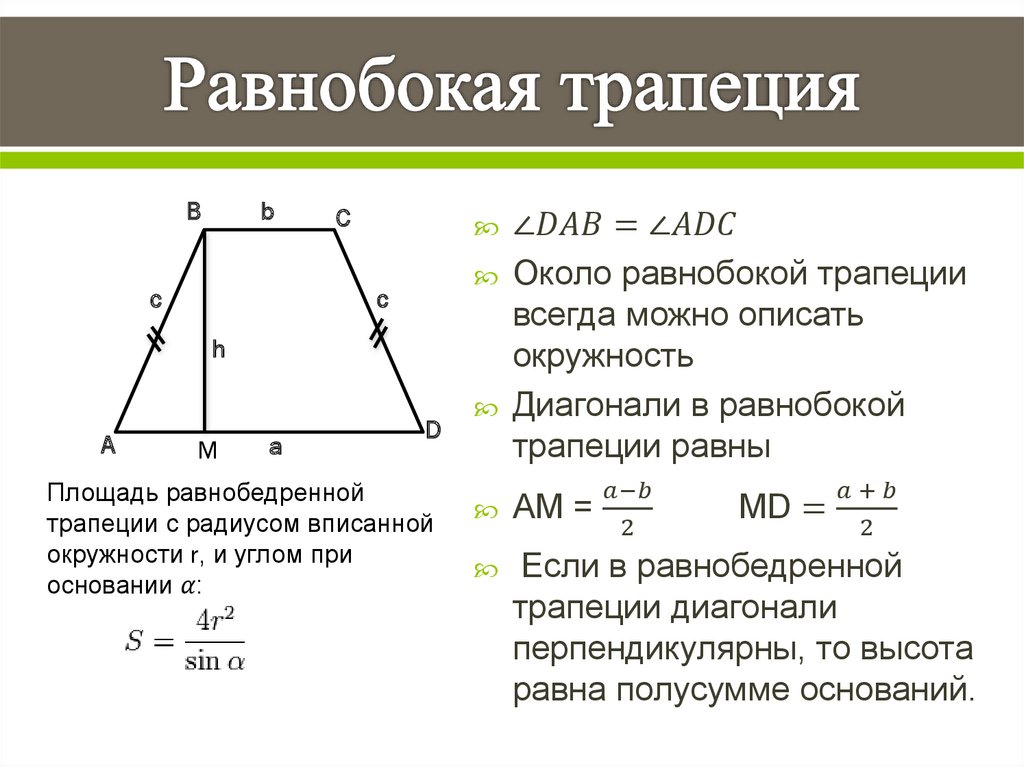
Таким образом, у нас есть два конгруэнтных треугольника по Постулат SAS .
Далее, мы можем сказать, что отрезки DE и DG конгруэнтны
, потому что соответствующие части конгруэнтных треугольников конгруэнтны. Наша новая иллюстрация
показана ниже.
Мы заключаем, что DEFG является воздушным змеем, потому что у него есть две различные пары
смежных сторон, которые конгруэнтны. Геометрическое доказательство в два столбца для этого упражнения
показан ниже.
Mathwords: Равнобедренная трапеция
Mathwords: Равнобедренная трапеция
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
