Решение неравенств и уравнений с модулем – Решение неравенств с модулем

Проект по алгебре на тему: Методика решения уравнений и неравенств с модулем

По теме: методические разработки, презентации и конспекты

Разработка урока по теме «Решение уравнений и неравенств с модулем»

Целью урока является совершенствование навыков решения уравнений и неравенств с модулем. В ходе урока рассматриваются рациональные приёмы и методы решения. Урок предназначен для классов с …

Программа элективного курса «Решение уравнений и неравенств с модулем.»

Элективный курс для 10 классов….

Элективный курс 8 -9 классы по теме:»Решение уравнений и неравенств с модулем»

Программа курса «Решение уравнений и неравенств с модулем» предполагает изучение таких вопросов, которые не входят в школьный курс математики основной школы, но необходимы при дальнейшем ее из…

Решение уравнений и неравенств с модулем. 7-8 класс

Решение уравнений и неравенств с модулем. 7-8 класс…

Элективный курс «Решение уравнений и неравенств с модулем»

Данный элективный курс является авторской разработкой. В данной работе даны рациональные способы решения уравнений и неравенств с модулем без раскрытия модуля. При решении уравнений и неравеств примен…

программа элективного курса «Решение уравнений и неравенств с модулями».

авторская программа элективного курса по математике…

Элективный курс «Решение уравнений и неравенств с модулем»

Элективный курс «Решение уравнений и неравенств с модулем» расчитан для 9 классов,12 часов…

nsportal.ru

Решение уравнений и неравенств с модулем ( из опыта работы).

Решение уравнений и неравенств с модулем

(Из опыта работы Кирьяновой Т.Ф. учителя математики

МБОУ СОШ № 9 г. Пушкино.).

В средней общеобразовательной школе (6 – 9 кл) тема «Решение уравнений и неравенств с модулем» не выделена отдельно. Поэтому на протяжении всех четырёх лет надо отводить уроки для последовательного рассмотрения основных способов решений таких уравнений и неравенств. Тогда в 10 – 11 классах освободиться время для нестандартных методов решений многих задач содержащих модуль.

Определение модуля даётся в 6 классе и поэтому уже в шестом классе можно вывести первые свойства.

1.

2.

3.

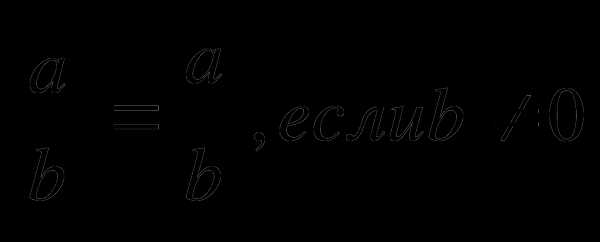
4.

И выделить время для решений простейших уравнений:

1. 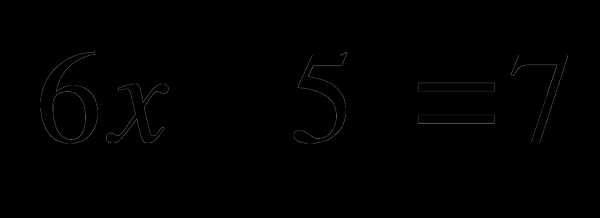3.

2. 4. при каких значениях p уравнение

В 8 классе, после прохождения тем: «квадратные и дробные рациональные уравнения», увеличивается разнообразие уравнений, решение которых основывается на правилах которые конечно же обосновываются)

1.

2.

3.

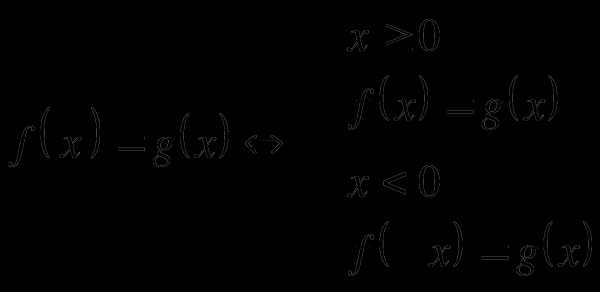
Например. а)

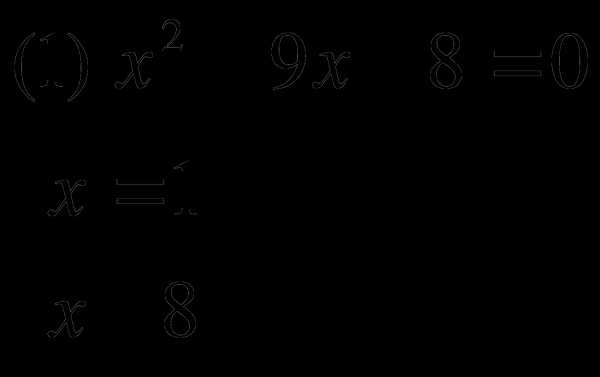Следовательно 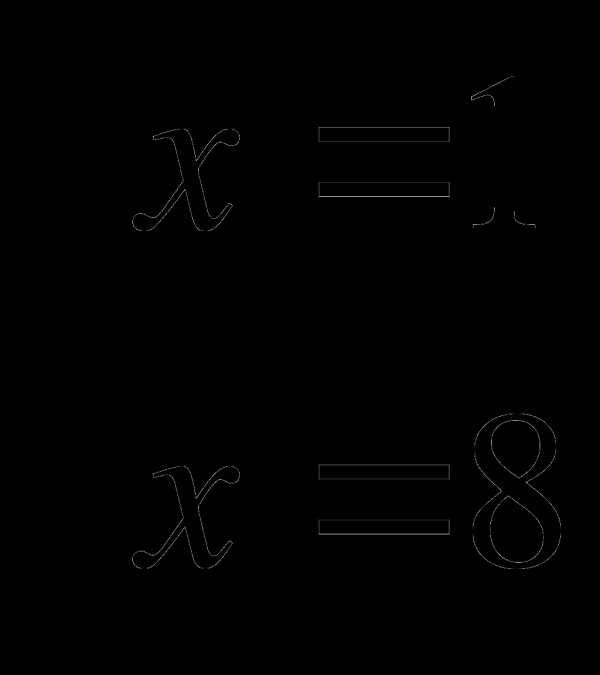Ответ:1;8.

б)

в)

После изучения темы: «Неравенство с одной переменной и их системы» следует вывести следующие соотношения:

1.

2.

3.

4.

5.

6.

7.

8.

9.

Доказательство этих соотношений очень хорошо приведены у В. П. Моденова «Математика»

Далее надо рассмотреть схемы решений следующих уравнений и неравенств:

1)

1 способ 2 способ

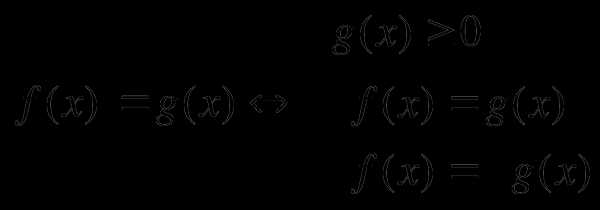
Второй способ хорош тем, что не надо сравнивать f(x) с нулём

Например,

(3)

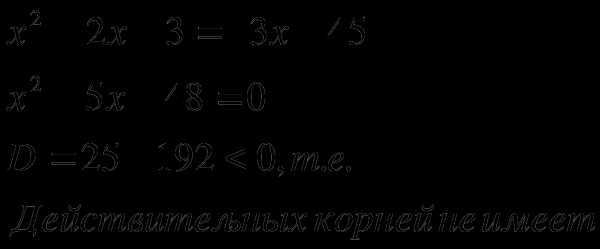
2)

3)

4)

5)

Все эти схемы надо отрабатывать на занятиях, которые не являются сложными. Так как, на первых уроках, самое главное это – теория.

а)

Ответ:

б)

в)

Ответ:

г)

Ответ: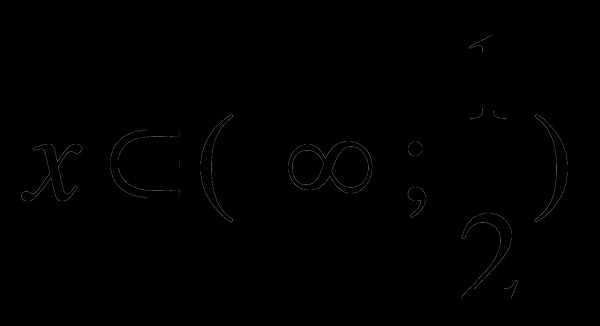

В девятом классе, после изучения квадратных неравенств, все предыдущие схемы просто надо разнообразить. А вот после «Метода интервалов» остаётся рассмотреть решение уравнений и неравенств содержащих более одного модуля

1. Находят О.Д.З. исходного уравнения

2. Определяют точки разрыва и нули функции

3. На каждом из промежутков, на которые найденные точки разбивают О.Д.З, исходное уравнение заменяется равносильным, не содержащим знаков абсолютной величины (это возможно в силу того, что функции на этих промежутках знакопостоянны).

1.

1) О.Д.З.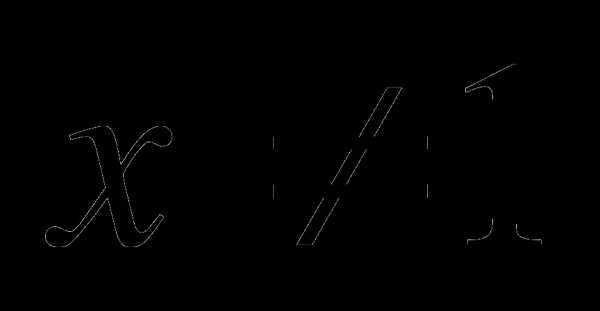

2) Нули модуля: x=0

3)

x

х + ⁰ — ¹ +

х-1

x — + +

x-1 — — +

Тогда исходное уравнение равносильно совокупности систем:

2.

1. О.Д.З.

2. Нули модуля:

3.

-1 4 x

x-4 — — +

x+1 — + +

Тогда данное неравенство равносильно совокупности систем неравенств:

Ответ:

В конце 9 класса следует оставить время для разбора некоторых способов решения уравнений и неравенств с параметром. Учащиеся уже знакомы с графиком функции 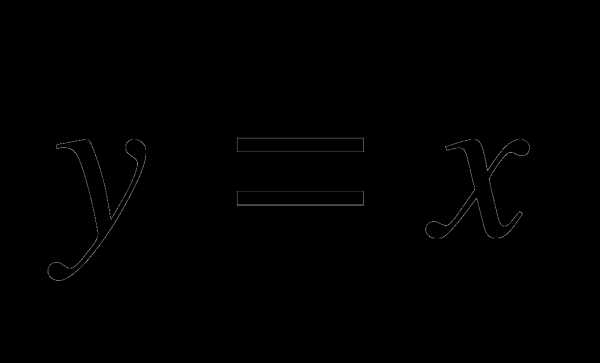и построением графиков с помощью преобразований. Полезно выполнить построение графиков с модулями, симметрией. Рассмотреть графики неравенств.

1.

Рассмотрим все случаи раскрытия модулей. Чтобы долго не выписывать, можно записывать формулы прямо в соответствующих координатных четвертях.

3.

Строим графики двух парабол и берём у каждой ту часть, где

(1) (2)

Ось симметрии задаётся уравнением Ось симметрии задаётся уравнением

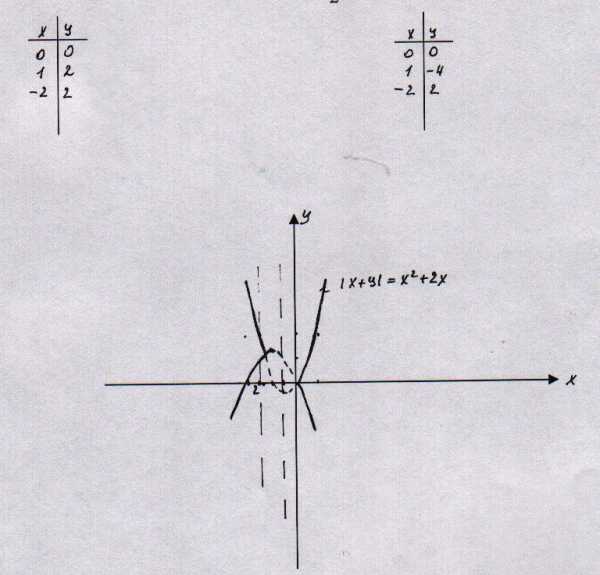
4.

1. строим границу

2. берём контрольную точку (0; 0) и подставляем в условие.

Если получим верное неравенство, то т.(0; 0) входит в заштрихованную область, если неравенство не будет верным, то точка (0; 0) не входит в заштрихованную область. Данный метод называется Методом областей. С помощью этого метода можно решать неравенства с параметром. В девятом классе такой метод надо рассматривать на простейшем примере.

Решить неравенство при всех значениях а

1. Построим график неравенства в системе ХОУ.

а)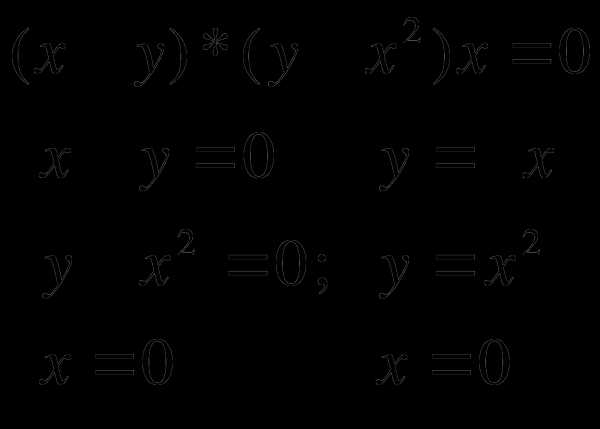

б) точка контрольная (100; 0) подходит. Далее следим за знаками скобок и заштриховываем области «через одну»

в) для решения неравенства описываем каждую кривую выразив х через у.

г) Мысленно перемещаем прямую у=а и прослеживаем, какая часть прямой попала в заштрихованную область

Ответ:

4. Найти число корней уравнения

в зависимости от параметра а

Построим графики функций

(можно было выделить полный квадрат.

Ось симметрии задаётся уравнением х=1

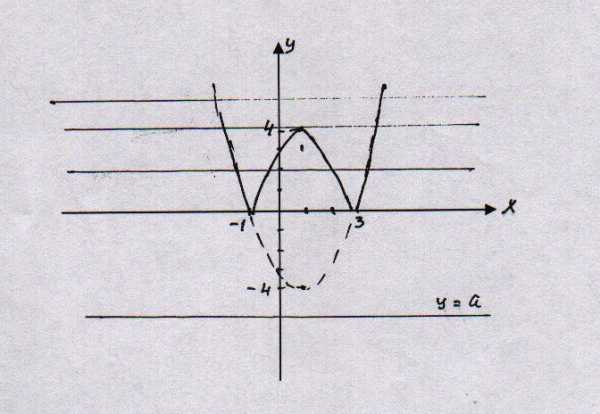
Ответ:

7. Уже в 9 классе можно познакомить с координатно – параметрическим методом.

Решить уравнение для каждого действительного а.

Решение: На плоскости аОУ с параметрической осью Оа и координатной плоскостью ОУ построим прямые х=а и х=-а-1

1. Прямые пересекаются в точке С ()

2. Образовались 4 области

в 1 области

во 2 области

в 3 области

в 4 области

3. в каждой области раскроем модуль

4. Значит на плоскости аОХ все точки границы дают

решение уравнения

Ответ:

5. Ответ при

Литература, которую очень полезно использовать для проведения уроков.

1. учебники: В.П. Моденов «Математика»

2. Родионов Е.М., Синакова С.А. «Математика»

3. Б.Г.Зив; В.А.Гольдиг «Дидактические материалы».

infourok.ru

«Решение уравнений и неравенств с модулем». Видеолекция 1

ВИДЕОЛЕКЦИИУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ

Содержание Видеолекции 1:
1. Определение понятия «модуль».

2. Геометрический смысл модуля.

3. Противоположные числа.

4. Уравнение |x|=a.

5. Полезные примеры: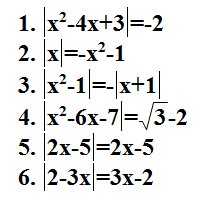

6. Неравенство |x|<a.

7. Полезные примеры:

8. Неравенство |x|>a.

9. Полезные примеры: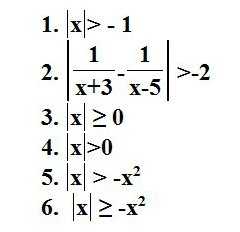

10. Решение уравнения ||=1.

11. Видеорешение уравнения .

12. Видеорешение неравенства  .

13. Видеорешение неравенства .

И.В. Фельдман, репетитор по математике.

Вернуться на страницу ВИДЕОЛЕКЦИИ

ege-ok.ru

Методическая разработка по алгебре (10 класс) по теме: Разработка урока по теме «Решение уравнений и неравенств с модулем»

Этапы урока и их содержание

Время (мин)

Деятельность

Организационный этап Постановка цели Сегодня на уроке мы продолжим отрабатывать навыки решения уравнений и неравенств с модулем, используя как традиционные методы, так и нестандартные  подходы Проверка домашнего задания На дом вам было предложено решить уравнения       и неравенства    различными способами. Посмотрим ваше решение Выполнение упражнений. Многообразие приёмов решения задач с модулем подталкивает нас  к выбору более рационального из них при решении конкретных уравнений или неравенств. № 1. (устно) Решить уравнение   Решение (на основе аналитического определения модуля). Т.к. , то х2 -6х-7-1.  № 2  Решить уравнение Решение (применение геометрической интерпретации модуля). На геометрическом языке: требуется  найти точки с координатами х такие, что сумма расстояний от этих точек до точек с координатами -1 и 1 равна 2. Очевидно, что эти точки располагаются на отрезке Ответ: . № 3  Решите неравенство cos x1+. Решение (функционально графический метод). Обе части неравенства определены на R. Левая часть неравенства принимает значения из отрезка , а значения правой части составляют луч . Следовательно, исходное неравенство может иметь решение только, если выполняется система х=0. Ответ: 0 № 4 Найти все значения параметра b при которых уравнениеимеет ровно три различных корня. Решение (графический способ). Рассмотрим функцию у = и  построим её  график используя  преобразования, содержащие модуль, а также параллельный перенос. Графиком функции у =b  является прямая параллельная  оси х. Очевидно, что исходное уравнение имеет ровно три различных корня при b=-1. Ответ: b=-1. № 5  Решить неравенство . Решение (метод интервалов). Пусть  f(x)= , тогда   Df  = (-∞;-1)(-1;2) (2;+∞). Решим уравнение f(x)=0. Получим: 2=х2-х-2 Осталось установить знак f(x) на промежутках:       (-∞;-4),  (-4;-1),     (-1;2),  (2;5),  (5;+∞). Ответ:  (-4;-1)(2;5).     Домашнее задание  (заранее приготовлен слайд на интерактивной доске)       1) Решить неравенство   2) Найти все значения параметра b при которых уравнение   имеет ровно два различных корня. 3) Решить уравнение (приложение №5) Подведение итогов урока. Решение уравнений и неравенств с модулем требует от учащихся глубоких теоретических знаний, умений применять их на практике, требует внимания трудолюбия, сообразительности.  Наверное, поэтому  такие задания и включены в материалы ЕГЭ. Сегодня на уроке  все очень хорошо поработали, 15  человек получили оценки. Молодцы ребята!

1 3 10 2 6 5 5 8 3 2

Организационная сообщает тему урока, дату проведения, цель урока Если учащиеся не готовы показать все способы, то решение показывается на экране интерактивной доски,(приложение 1). Вызывает по желанию 7-х человек к доске, параллельно проводит фронтальную беседу по теоретическим вопросам (приложение  2) Выставляет оценку за д/з. Направляет на выбор рационального метода решения Совместно с учащимися выбирает метод решения уравнения. Следит за грамотным решением предложенного уравнения и одновременно проверяет индивидуальные решения уравнений у  учащихся работающих на боковой доске по карточке, выставляет оценки за работу. Направляет на выбор рационального метода решения Следит за верностью рассуждений учащихся и одновременно проверяет решение заданий по карточкам, выставляет оценки за работу. Обсуждает совместно с учащимися метод решения неравенства, следит за грамотностью рассуждений учащихся и верной записью решения неравенства. Выставляет оценку за работу. Поясняет домашнее задание, обращая внимание учащихся на то, что аналогичные задания были разобраны на уроке. Первое неравенство можно решить методом интервалов, второе уравнение –графически, а третье-с помощью аналитического определения модуля, рассматривая три случая (подмодульное выражение больше нуля, равно нулю и меньше нуля ) отдельно.

Сообщают об отсутствующих записывают в тетради 7 учащихся работают у доски, остальные принимают активное участие в устном теоретическом опросе Предлагают методы решения, один учащийся устно объясняет решение уравнения №1. 2 человека работают на боковой доске индивидуально (приложение №3), остальные записывают в тетрадь решение уравнения №2. Один ученик решает неравенство № 3. Остальные участвуют в выборе рационального метода решения неравенства. Записывают решение в тетрадь. Один ученик решает задание № 4 у доски. Три ученика работают по карточкам (приложение №4), остальные записывают в тетрадь решение задания  № 4. Один ученик решает  у доски, остальные записывают решение неравенства №5 в тетради. Внимательно прослушав пояснение учителя, записывают домашнее задание.

nsportal.ru

Внеклассный урок — Уравнения и неравенства с модулем

Уравнения и неравенства с модулем

Модулем числа называется само это число, если оно неотрицательное, или это же число с противоположным знаком, если оно отрицательное.

Например, модулем числа 6 является 6, модулем числа –6 тоже является 6.

То есть под модулем числа понимается абсолютная величина, абсолютное значение этого числа без учета его знака.

Обозначается так: |6|, |х|, |а| и т.д.

(Подробнее – в разделе «Модуль числа»).

 

Уравнения с модулем.

Пример 1. Решить уравнение

|10х – 5| = 15.

Решение.

В соответствии с правилом, уравнение равносильно совокупности двух уравнений:

│10х – 5 = 15
│10х – 5 = –15

Решаем:

│10х = 15 + 5 = 20
│10х = –15 + 5 = –10

↕

│х = 20 : 10
│х = –10 : 10

↕

│х = 2
│х = –1

Ответ: х₁ = 2, х₂ = –1.

Пример 2. Решить уравнение

|2х + 1| = х + 2.

Решение.

Поскольку модуль – число неотрицательное, то х + 2 ≥ 0. Соответственно:

х ≥ –2.

Составляем два уравнения:

│2х + 1 = х + 2
│2х + 1 = –(х + 2)

Решаем:

│2х + 1 =  х + 2
│2х + 1 = –х – 2

↕

│2х – х =  2 – 1
│2х + х = –2 – 1

↕

│х = 1
│х = –1

Оба числа больше –2. Значит, оба являются корнями уравнения.

Ответ: х₁ = –1, х₂ = 1.

 

Пример 3. Решить уравнение

  |х + 3| – 1
————— = 4
     х – 1

Решение.

Уравнение имеет смысл, если знаменатель не равен нулю – значит, если х ≠ 1. Учтем это условие. Наше первое действие простое – не просто освобождаемся от дроби, а преобразуем ее так, чтобы получить подмодульное выражение в чистом виде:

|х + 3| – 1 = 4 · (х – 1),

|х + 3| – 1 = 4х – 4,

|х + 3| = 4х – 4 + 1,

|х + 3| = 4х – 3.

Теперь у нас в левой части уравнения только выражение под модулем. Идем дальше.

Модуль числа есть неотрицательное число – то есть он должен быть больше нуля или равен нулю. Соответственно, решаем неравенство:

4х – 3 ≥ 0

4х ≥ 3

х ≥ 3/4

Таким образом, у нас появилось второе условие: корень или корни уравнения должны быть не меньше 3/4.

В соответствии с правилом модуля составляем совокупность двух уравнений и решаем их:

│х + 3 = 4х – 3
│х + 3 = –(4х – 3)

↕

│ х + 3 = 4х – 3
│ х + 3 = –4х + 3

↕

│х – 4х = –3 – 3
│х + 4х = 3 – 3

↕

│х = 2
│х = 0

Мы получили два ответа. Проверим, являются ли они корнями исходного уравнения.

У нас было два условия: корень уравнения должен быть не меньше 3/4, но не может быть равен 1. То есть х ≠ 1, х ≥ 3/4. Обоим этим условиям соответствует только один из двух полученных ответов – число 2. Значит, только оно и является корнем исходного уравнения.

Ответ: х = 2.

 

Неравенства с модулем.

Пример 1. Решить неравенство:

|х — 3| < 4

Решение.

Правило модуля гласит:

|а| = а, если а ≥ 0.
|а| = –а, если а < 0.

Модуль может иметь и неотрицательное, и отрицательное число. Значит, мы должны рассмотреть оба случая:
х – 3 ≥ 0 и х – 3 < 0.

1) При х – 3 ≥ 0 наше исходное неравенство остается как есть, только без знака модуля:

х – 3 < 4.

2) При х – 3 < 0 в исходном неравенстве надо поставить знак минус перед всем подмодульным выражением:

–(х – 3) < 4. Раскрыв скобки, получаем:

–х + 3 < 4.

Таким образом, от этих двух условий мы пришли к объединению двух систем неравенств:

│ х – 3 ≥ 0
│ х – 3 < 4

и

│ х – 3 < 0
│–х + 3 < 4

Решим их:

│х ≥ 3
│ х < 7

и

│х < 3
│х > –1

Итак, у нас в ответе объединение двух множеств:

3 ≤ х < 7  U  –1 < х < 3.

Определяем наименьшее и наибольшее значения. Это –1 и 7. При этом х больше –1, но меньше 7. Кроме того, х ≥ 3. Значит, решением неравенства является все множество чисел от –1 до 7, исключая эти крайние числа.

Ответ: –1 < х < 7.

Или: х ∈ (–1; 7).

 

Дополнения.

1) Есть более простой и короткий способ решения нашего неравенства — графический. Для этого надо нарисовать горизонтальную ось (рис.1).

  

Выражение |х — 3| < 4 означает, что расстояние от точки х до точки 3 меньше четырех единиц. Отмечаем на оси число 3 и отсчитываем влево и вправо от от него 4 деления. Слева мы придем к точке -1, справа – к точке 7. Таким образом, точки х мы просто увидели, не вычисляя их.

При этом, согласно условию неравенства, сами -1 и 7 не включены во множество решений. Таким образом, получаем ответ:

–1 < х < 7.

 

2) Но есть еще одно решение, которое проще даже графического способа. Для этого наше неравенство надо представить в следующем виде:

–4 < х – 3 < 4.

Ведь так оно и есть по правилу модуля. Неотрицательное число 4 и аналогичное отрицательное число –4 являются границами решения неравенства.

Далее мы просто переносим влево и вправо число –3 с обратным знаком, оставляя х в одиночестве:

–4 + 3 < х < 4 + 3

–1 < х < 7.

 

Пример 2. Решить неравенство

|х – 2| ≥ 5

Решение.

Этот пример существенно отличается от предыдущего. Левая часть больше 5 либо равна 5. С геометрической точки зрения, решением неравенства являются все числа, которые от точки 2 отстоят на расстоянии 5 единиц и больше (рис.2). По графику видно, что это все числа, которые меньше или равны –3 и больше или равны 7. А значит, мы уже получили ответ.

Ответ: –3 ≥ х ≥ 7.

Попутно решим это же неравенство способом перестановки свободного члена влево и вправо с противоположным знаком:

–5 ≥ х – 2 ≥ 5

–5 + 2 ≥ х ≥ 5 + 2

Ответ тот же: –3 ≥ х ≥ 7.

Или: х ∈ [–3; 7]

Пример решен.

 

Пример 3. Решить неравенство:

6х² – |х| – 2 ≤ 0

Решение.

Число х может быть и положительным числом, и отрицательным, и нулем. Поэтому нам надо учесть все три обстоятельства. Как вы знаете, они учитываются в двух неравенствах: х ≥ 0 и х < 0. При х ≥ 0 мы просто переписываем наше исходное неравенство как есть, только без знака модуля:

6х² – х – 2 ≤ 0.

Теперь о втором случае: если х < 0. Модулем отрицательного числа является это же число с противоположным знаком. То есть пишем число под модулем с обратным знаком и опять же освобождаемся от знака модуля:

6х² – (–х) – 2 ≤ 0.

Раскрываем скобки:

6х² + х – 2 ≤ 0.

Таким образом, мы получили две системы уравнений:

│6х² – х – 2 ≤ 0
│ х ≥ 0

и

│6х² + х – 2 ≤ 0
│ х < 0

Надо решить неравенства в системах – а это значит, надо найти корни двух квадратных уравнений. Для этого приравняем левые части неравенств к нулю.

Начнем с первого:

6х² – х – 2 = 0.

Как решается квадратное уравнение – см. раздел «Квадратное уравнение». Мы же сразу назовем ответ:

х₁ = –1/2, х₂ = 2/3.

Из первой системы неравенств мы получаем, что решением исходного неравенства является все множество чисел от  –1/2 до 2/3. Пишем объединение решений при х ≥ 0:
[–1/2; 2/3].

Теперь решим второе квадратное уравнение:

6х² + х – 2 = 0.

Его корни:

х₁ = –2/3, х₂ = 1/2.

Вывод: при х < 0 корнями исходного неравенства являются также все числа от –2/3 до 1/2.

Объединим два ответа и получим итоговый ответ: решением является все множество чисел от –2/3 до 2/3, включая и эти крайние числа.

Ответ: –2/3 ≤ х ≤ 2/3.

Или: х ∈ [–2/3; 2/3].

raal100.narod.ru

Решение уравнений и неравенств с модулем Исследовательская работа Холодных Сергей

Муниципальное бюджетное нетиповое общеобразовательное учреждение

«Лицей № 4»

НОУ «Прорыв»

Решение уравнений и неравенств с модулем

Исследовательская работа

Выполнил:

Холодных Сергей

Александрович,11 класс,

Научный руководитель :

Атапина Елена Никаноровна,

учитель математики

Ленинск-Кузнецкий,

2012
Оглавление

1. 
   Введение…………………………………………………………………3
   
2. 
   Простейшие уравнения и неравенства с модулем……………………5
   
3. 
   Графическое решение уравнений и неравенств с модулем………….8
   
4. 
   Иные способы решения уравнений и неравенств с модулем…………10
   
5. 
   Заключение ……………………………………………………………..16
   
6. 
   Список литературы………………………………………………………18
   

1. Введение

Понятие абсолютной величины (модуля) является одной из важнейших характеристик числа как в области действительных, так и в области комплексных чисел.

Это понятие широко применяется не только в различных разделах школьного курса математики, но и в курсах высшей математики, физики и технических наук, изучаемых в вузах. Например, в теории приближенных вычислений используются понятия абсолютной и относительной погрешностей приближенного числа. В механике и геометрии изучаются понятия вектора и его длины (модуля вектора). В математическом анализе понятие абсолютной величины числа содержится в определениях таких основных понятий, как предел, ограниченная функция и др. Задачи, связанные с абсолютными величинами, часто встречаются на математических олимпиадах, вступительных экзаменах в вузы и на ЕГЭ. И поэтому для нас стало важно изучить некоторые аспекты этой темы.

Главной целью в нашей работе является изучение различных методов решения уравнений и неравенств с модулями.

Данная цель должна быть достигнута при решении следующих задач:

• 
  Изучить определение и некоторые свойства модуля.
  
• 
  Освоить решение простейших уравнений и неравенств с модулем через равносильные переходы
  
• 
  Рассмотреть различные методы решения уравнений и неравенств с модулем.
  

Объектом исследования являются некоторые типы уравнений и неравенств с модулем.

Предмет исследования – различные методы решения уравнений и неравенств с модулем, а именно: графический способ, метод геометрической интерпретации, использование тождества , применение теоремы о знаках, метод перехода к следствию, метод интервалов, метод домножения на положительный множитель ,метод раскрытия модулей.

В ходе исследования применялись такие методы, как изучение литературы по данному вопросу и практический метод.

В ходе работы мы исследовал такие источники, как:

1. «Большая математическая энциклопедия» для школьников и студентов;

2. 
   Математика. ЕГЭ – 2011-2012. Типовые экзаменационные варианты. / Под редакцией А.Л. Семенова, И.В. Ященко.
   
3. 
   М.Я. Выгодский. Справочник по элементарной математике
   
4. 
   «Новейший справочник школьника»;
   
5. 
   Энциклопедия «Я познаю мир» Математика;
   
6. 
   http://ru.wikipedia.org/wiki/Заглавная_страница;
   

2. Простейшие уравнения и неравенства с модулем

К простейшим уравнениям мы будем относить уравнения, решаемые одним из нижеприведенных равносильных переходов:

Примеры решения простейших уравнений.

Пример 1 Решим уравнение .

Решение.

Ответ. .

Пример 2 Решим уравнение .

Решение.

Ответ. .

Пример 3 Решим уравнение .

Решение.

Ответ. .

Ряд уравнений решается с использованием следующей теоремы.

Теорема.4 Сумма модулей равна алгебраической сумме подмодульнх величин тогда и только тогда, когда каждая величина имеет тот знак, с которым она входит в алгебраическую сумму.

Пример 5 Решить уравнение

Решение. Так как , то мы имеем равенство вида , где , . Поэтому исходное уравнение равносильно системе:

Ответ. .

Примеры решения простейших неравенств.

Пример 6 Решим неравенство .

Решение.

.

Ответ. .
Пример 7 Решим неравенство .

Решение.

Ответ. .

Как ни странно, но достаточно, чтобы избавиться от знака модуля в любых неравенствах.

Пример 8 Решить неравенство

Решение.

Ответ. .

3. Графическое решение уравнений и неравенств с модулем

Решение уравнений, содержащих знак абсолютной величины часто гораздо удобнее решать не аналитически, а графически (особенно уравнения содержащие параметры).

Пример 9 (С5, ЕГЭ — 2010)

C5. Для каждого значения a укажите число решений уравнения

Решение. Построим график функции . Для этого выделим полный квадрат :

Число точек пересечения графика функции у = с горизонтальными прямыми у = а равно числу решений уравнения.

Ответ: если 0 4, то два решения.

Иные способы решения уравнений и неравенств с модулем

• Метод раскрытия модулей

Метод раскрытия модулей рассмотрим на примере:

Пример 10 Решить уравнение

Решение. Это уравнение содержит более одного модуля.

Метод решения уравнений, содержащих переменные под знаком двух и более модулей, состоит в следующем.

1. Найти значения переменной, при которых каждый из модулей обращается в нуль: , ; , ; , .

2. Отметить эти точки на числовой прямой.

3. Рассматриваем уравнение на каждом из промежутков и устанавливаем знак выражений, которые находятся под модулями.

1) При или . Чтобы определить знак каждого из выражений под модулем на этом промежутке, достаточно взять любое значение из этого промежутка и подставить в выражение. Если полученное значение отрицательно, значит, при всех из этого промежутка выражение будет отрицательным; если полученное числовое значение положительно, значит, при всех значениях из этого промежутка выражение будет положительным.

Возьмем значение из промежутка и подставим его значение в выражение , получаем , значит на этом промежутке отрицательно, а следовательно «выйдет» из под модуля со знаком «минус», получим: .

При этом значении , выражение получит значение , значит, оно на промежутке также принимает отрицательные значения и «выйдет» из модуля со знаком «минус», получим: .

Выражение получит значение и «выйдет» из под модуля со знаком «минус»: .

Уравнение на этом промежутке получится таким: , решая его, находим: .

Выясняем, входит ли это значение в промежуток . Оказывается входит, значит является корнем уравнения.

2) При . Выбираем любое значение из этого промежутка. Пусть . Определяем знак каждого из выражений под модулем при этом значении . Оказывается, что выражение положительно, а два других отрицательны.

Уравнение на этом промежутке примет вид: . Решая его, находим . Это значение не входит в промежуток , а значит, не является корнем уравнения.

3) При . Выбираем произвольное значение из этого промежутка, скажем, и подставляем в каждое из выражений. Находим, что выражения и положительны, а — отрицательно. Получим следующее уравнение: .

После преобразования, получим: , а значит, уравнение не имеет корней на этом промежутке.

4) При . Нетрудно установить, что все выражения на этом промежутке положительны, а значит получим уравнение: , , которое входит в промежуток и является корнем уравнения.

Ответ. , .

• Решение уравнений содержащих модули неотрицательных выражений

Пример 11 Чему равна сумма корней уравнения (корень, если он один) уравнения

Решение. Рассмотрим выражение

и преобразуем его к виду

Очевидно, что числитель дроби при любых значениях переменной является положительным числом. Значит дробное выражение положительно, если (т.к. ). Преобразуем полученное выражение, при условии . Получим уравнение, равносильное исходному:

Ответ. .

Пример 12 Решить уравнение

Решение. Поскольку левая часть уравнения неотрицательна, при всех допустимых значениях переменной, на множестве корней уравнения правая его часть тоже должна быть неотрицательной, отсюда условие , на этом промежутке знаменатели обеих дробей равны, и остается решить уравнение . Решая его и учитывая ограничение , получаем

Ответ. .

• Решение уравнений с использованием геометрической интерпретации

Геометрический смысл выражения — длина отрезка координатной оси, соединяющего точки с абсциссами и . Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких выкладок.

Пример 13 Решим уравнение .

Решение. Будем рассуждать следующим образом: исходя из геометрической интерпретации модуля, левая часть уравнения представляет собой сумму расстояний от некоторой точки с абсциссой до двух фиксированных точек с абсциссами 1 и 2. Тогда все точки с абсциссами из отрезка обладают требуемым свойством, а точки, расположенные вне этого отрезка, — нет.

Ответ. .

Пример 14 Решить неравенство .

Решение. Изобразим на координатной прямой точки, сумма расстояний от которых до точек и в точности равна . Это все точки отрезка . Для всех чисел вне данного отрезка сумма расстояний будет больше двух.

Ответ. .

• 
  Решение уравнений с использованием тождества
  

Пример (С3, ЕГЭ — 2010)15 Решить уравнение

Решение. Дважды применяя тождество , получим уравнение

решением которого является интервал .

Ответ. .

Пример (С3, ЕГЭ — 2011)16 17 Решить уравнение

Решение. .

Ответ. .

• Применение теоремы о знаках при решении уравнений

Сформулируем теорему, удобную при решении неравенств, относительно произведений или частных разности модулей:

Теорема 18 Знак разности модулей двух выражений совпадает со знаком разности квадратов этих выражений.

Пример 19 Решить неравенство

Решение. Воспользуемся теоремой:

Используя формулу разности квадратов, разложим числитель и знаменатель на множители и решим полученное рациональное неравенство.

Ответ.

• Решение уравнений переходом к следствию

Все уравнения с модулями могут быть решены следующим образом: рассмотрим весь набор уравнений, который может получится при раскрытии модулей, но не будем выписывать соответствующие промежутки. Решая каждое из полученных уравнений, получим следствия исходного уравнения. Остается только проверить не приобрели ли мы посторонних корней прямой их подстановкой в исходное уравнение.

Пример 20 Решим уравнение

Решение. Последовательно переходя к следствиям, получаем:

Нетрудно убедиться, что найденные числа не являются корнями исходного уравнения.

Ответ. нет решения.

• Решение неравенств методом интервалов

Применение метода интервалов основано на следующей теореме.

Теорема 21 Функция, непрерывная на промежутке и необращающаяся на нем в нуль, сохраняет на этом промежутке свой знак.

Это означает, что нули функции и границы промежутков ее непрерывности разделяют область определения функции на участки, где она сохраняет постоянный знак. Применение метода поясним на примере.

Пример 22 Решим неравенство

Пусть . Областью определения данной функции есть . Решая уравнение получим, что функция не обращается в нуль ни при каком значении переменной. Это означает, что на всей области определения функция является знакопостоянной. Вычисляя, например, , получаем, что функция принимает только положительные значения.

Ответ. .

Метод интервалов позволяет решать более сложные уравнения и неравенства с модулями, но в этом случае он имеет несколько иное назначение. Суть состоит в слудующем. Находим корни всех подмодульных выражений и разбиваем числовую ось на промежутки знакопостоянства этих выражений. Это позволяет, последовательно перебирая эти промежутки, одновременно избавляться от всех модулей и решать обычное уравнение или неравенство (проверяя при этом, что найденный ответ входит в данный промежуток).

• Решение уравнений домножением на положительный множитель

Пример 23 Решить неравенство

Решение. «Ловушка» заключается в том, что в задаче имеется несколько модулей, раскрывать которые — значит получить, громоздкое решение. Умножим дробь на некоторое выражение, принимающее лишь положительные значения и такое, чтобы упростить исходное неравенство:

Ответ. .

Заключение.

Подводя итог нашей работы, можно сказать следующее.

Целью работы было изучение различных методов решения уравнений и неравенств с модулями.

Мы рассмотрели некоторые разновидности простейших уравнений и неравенств с модулем, решаемых с помощью равносильных переходов,а также теоремы о сумме модулей; графический способ решения уравнений. Нужно сказать, что в школьном курсе математики именно эти методы решения наиболее часто используются. Графический метод особо актуален при решении задач C5 из контрольно-измерительных материалов ЕГЭ.

Далее мы изучили на нескольких примерах иные способы решения уравнений и неравенств с модулями, а именно: метод раскрытия модулей; решение уравнений, содержащих модули неотрицательных выражений; решение уравнений с использованием геометрической интерпретации; с использованием тождества ; применение теоремы о знаках; решение уравнений переходом к следствию, домножением на положительный множитель,а также решение неравенств методом интервалов.

Таким образом, в ходе исследования мы пришли к следующим выводам.

Наиболее универсальными и применимыми к наибольшему количеству задач мы считаем метод раскрытия модулей, графический метод и метод интервалов. Это убеждение возникло в результате решения большого числа задач из контрольно-измерительных материалов ЕГЭ, предметных чемпионатов, олимпиадных задач, а также изучение литературы по данному вопросу. Также очень важным мы считаем знание и применение тождества , так как оно используется не только при решении уравнений и неравенств, но и для преобразования многих выражений с радикалами. Остальные методы решения, которые мы рассмотрели, безусловно, представляют большой интерес в плане расширения математического кругозора и общего математического развития. Поэтому мы планируем использовать их для подготовки к государственной итоговой аттестации в форме ЕГЭ и подготовке к обучению в высшем учебном заведении.

Список используемой литературы.

1. 
   «Большая математическая энциклопедия» для школьников и студентов;
   
2. 
   Математика. ЕГЭ – 2011, 2012. Типовые экзаменационные варианты. / Под редакцией А.Л. Семенова, И.В. Ященко.
   
3. 
   М.Я. Выгодский. Справочник по элементарной математике
   
4. 
   «Новейший справочник школьника»;
   
5. 
   Энциклопедия «Я познаю мир. Математика»;
   
6. 
   http://ru.wikipedia.org/wiki/Заглавная_страница;
   

docs.likenul.com

Видеолекция 2. «Решение уравнений и неравенств с модулем.»

ВИДЕОЛЕКЦИИОНЛАЙН КУРСЫУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ

Содержание Видеолекции 2:

1. Повторение основных эквивалентностей для решения уравнения , неравенств ;  ;  ;   .

2. Алгоритм решения уравнения 

3. Видеорешение уравнения 

4. Видеорешение уравнения 

5. Алгоритм решение уравнения 

6. Решение неравенств вида ;  ;   ;   ; 

7. Видеорешение неравенства 

8. Видеорешение неравенства 

9. Видеорешение неравенства 

10. Как правильно раскрывать модуль, примеры.

11. Решение уравнений и неравенств, содержащих несколько модулей

12. Видеорешение уравнения 

13. Видеорешение неравенства

14. Видеорешение уравнения 

Фрагмент видеолекции:

 

 

Получить ссылку на просмотр видеолекции.

 

Вернуться на страницу ВИДЕОЛЕКЦИИ

 

 

 

И.В. Фельдман, репетитор по математике.

 

ege-ok.ru