Калькулятор алгебры с шагами — онлайн и бесплатно!
Калькулятор алгебры с шагами — онлайн и бесплатно!Алгебраические задачи Рассчитать медиану Рассчитать интеграл Рассчитать предел
Поделиться калькулятором алгебры
Добавить в закладки
Добавьте калькулятор алгебры в закладки вашего браузера
1. Для Windows или Linux — нажмите Ctrl + D .
2. Для MacOS — нажмите Cmd + D .
3. Для iPhone (Safari) — нажмите и удерживайте , затем нажмите Добавить закладку
4. Для Google Chrome : нажмите 3 точки в правом верхнем углу, затем нажмите знак звездочки
Как пользоваться?
Как пользоваться калькулятором алгебры
1
Шаг 1
Введите задачу по алгебре в поле ввода.
2
Шаг 2
Нажмите Enter на клавиатуре или на стрелку справа от поля ввода.
3
Шаг 3
Во всплывающем окне выберите нужную операцию. Вы также можете воспользоваться поиском.
Что такое алгебра
Алгебра — это часть математики, которая изучает общие свойства действий над разными значениями и решение уравнений, связанных с этими действиями. Это раздел математики, который можно описать как обобщение и расширение арифметики; в этом разделе числа и другие математические объекты отмечены буквами и другими символами, что позволяет им записывать и исследовать их свойства самым общим способом.
Слово алгебра также используется в общей алгебре в названиях различных алгебраических систем. В более широком смысле алгебра понимается как раздел математики, посвященный изучению операций над элементами произвольной природы, суммируя обычные операции сложения и умножения чисел.
Классификация
Алгебра как раздел математики традиционно включает следующие категории.
- Элементарная алгебра , изучающая свойства операций с действительными числами. В нем константы и переменные обозначаются буквенными символами. Элементарная алгебра содержит правила преобразования математических выражений и уравнений с использованием этих символов. Обычно преподают в школе под названием алгебра.
- Общая алгебра , иногда называемая современной алгеброй или абстрактной алгеброй, где аксиоматизируются и изучаются максимально общие алгебраические структуры, такие как группы, кольца и поля.
- Универсальная алгебра , изучающая свойства, общие для всех алгебраических структур (считается подразделом общей алгебры).
- Линейная алгебра , в которой изучаются свойства векторных пространств (включая матрицы).
- Алгебраическая комбинаторика , в которой методы абстрактной алгебры используются для изучения вопросов комбинаторики.
История алгебры
Термин алгебра взят из сочинения среднеазиатского ученого Аль-Хорезми Краткая книга по исчислению аль-джабра и аль-мукабаль (825 лет). Слово аль-джабр означает операцию переноса франшизы из одной части уравнения в другую и его буквальное значение составить.В XII веке алгебра достигла Европы. С этого времени начинается его бурное развитие. Были открыты способы решения уравнений 3 и 4 степени. Распространены отрицательные и комплексные числа. Доказано, что любое уравнение выше 4-й степени не может быть решено алгебраическим способом.
Тест по алгебре Решение уравнений (7 класс) онлайн
Последний раз тест пройден 49 минут назад.
Для учителя
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Вопрос 1 из 10
Решите уравнение: -5х — 3 = -13
2
3,2
-2
-3,2
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 2 из 10
Соберите в левой части уравнения 2х + 6 = -3х — 10 все слагаемые, содержащие неизвестное, а в правой — не содержащие неизвестное
2х + 3х = 6 — 10
2х — 3х = 6 — 10
2х + 3х = -6 — 10
2х — 3х = -6 — 10
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 3 из 10
Чему равен корень уравнения -х — 3 = -8 + 7х?
0,8
0,625
1,1
-0,625
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 4 из 10
Решите уравнение: 5,3х + 7,8 = -4,7х — 7,8
0
-1,56
1,52
-26
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 5 из 10
Какое из чисел является корнем уравнения -8х = х
2 +16? ПодсказкаПравильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 6 из 10
Решите уравнение -9х + 1 = х — 6
0,7
-0,7
7/8
-7/8
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 7 из 10
Чему равен корень уравнения 1,6(5х — 1) = 1,8х — 4,7?
0,5
2
-0,5
-2
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 8 из 10
При каком значении а выражение 5а + 1 на 6 больше выражения 4 — 7а
0.
5-0,5
0,75
-0,75
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 9 из 10
Корнем уравнения 12 — 0,8у = 26 + 0,6у является:
1
-2
-10
-1
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 10 из 10
Найдите корень уравнения: 5х — 11 = 2х + 7
11
4
-6
6
Правильный ответ
Неправильный ответ
В вопросе ошибка?
5Доска почёта
Чтобы попасть сюда — пройдите тест.
Рейтинг теста
3.
6
Средняя оценка: 3.6
Всего получено оценок: 874.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
Не найдено | Пошаговое решение математических задач
- Решение уравнений и
неравенств - Упростить выражения
- Факторные полиномы
- Графические уравнения и неравенства
- Расширенные решатели
- Все решатели
- Учебники
Назад
Расширенные решатели
Дифференцировать
- Базовый
- Расширенный
Интегрировать
- Базовый
- Расширенный
Частичные дроби
- Базовый
- Расширенный
Матрицы
- Арифметика
- Обратный
- Определитель
Упростить
- Базовый
- Расширенный
Решить
- Базовый
- Расширенный
Фактор
- Базовый
- Расширенный
Расширить
- Базовый
- Расширенный
График
- Базовый
- Расширенный
Назад
Все решатели
Арифметика
- Проценты
- Научное обозначение
Выражения
- Упростить
- Расширить
- Фактор
Уравнения
- Квадратика
- Решить
- График
Неравенства
- Решить
- График
Дроби
- Уменьшить
- Добавить
График
- Уравнения
- Неравенства
Добро пожаловать в Quickmath Solvers!
Пожалуйста, введите вашу проблему ниже:
- Решить
- Упростить
- Фактор
- Расширить
- График
- ГКФ
- ЛКМ
Новый Пример
Справка Tutorial
Решите уравнение, неравенство или систему.
Пример: 2x-1=y,2y+3=x
Алгебра — решения и наборы решений
Онлайн-заметки Пола
Главная
/
Алгебра
/
Решение уравнений и неравенств
/ Решения и наборы решений
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 2-1: Растворы и наборы растворов
Мы начнем эту главу с довольно короткого раздела с некоторой базовой терминологией, которую мы довольно регулярно используем при решении уравнений и неравенств.
Во-первых, решением уравнения или неравенства является любое число, которое при подстановке в уравнение/неравенство будет удовлетворять уравнению/неравенству. Итак, что мы подразумеваем под удовлетворением? Давайте рассмотрим пример или два, чтобы проиллюстрировать это.
Пример 1. Покажите, что каждое из следующих чисел является решением данного уравнения или неравенства. 9? 0\\ 9 — 9 & = 0\\ 0 & = 0 \,\,\,\,{\mbox{OK}}\end{align*}\]
Итак, мы спрашиваем здесь, равна ли правая сторона левой стороне после того, как мы подставим предложенное решение. В этом смысл «?» над знаком равенства в первой строке.
Поскольку правая и левая стороны одинаковы, мы говорим, что \(x = 3\) удовлетворяет уравнению.
b \(y = 8\) in \(3\left( {y + 1} \right) = 4y — 5\) Показать решение 9? 4\влево(8\вправо) — 5\\ 27 & = 27\,\,\,\,{\mbox{OK}}\end{align*}\]
Итак, \(y = 8\) удовлетворяет уравнению и, следовательно, является решением.
c \(z = 1\) in \(2\left( {z — 5} \right) \le 4z\) Показать решение
В этом случае у нас есть неравенство, и в этом случае «удовлетворить» означает немного другое. В этом случае мы будем говорить, что число будет удовлетворять неравенству, если после его подстановки мы получим в результате истинное неравенство. 9? 4\left( 1 \right)\\ — 8 & \le 4 \,\,\,\,{\mbox{OK}}\end{align*}\]
Итак, -8 меньше или равно 4 (на самом деле меньше), и поэтому мы имеем истинное неравенство. Поэтому \(z = 1\) будет удовлетворять неравенству и, следовательно, является решением
d \(z = — 5\) in \(2\left( {z — 5} \right) \le 4z\) Показать решение
Это то же самое неравенство с другим значением, так что давайте проверим это.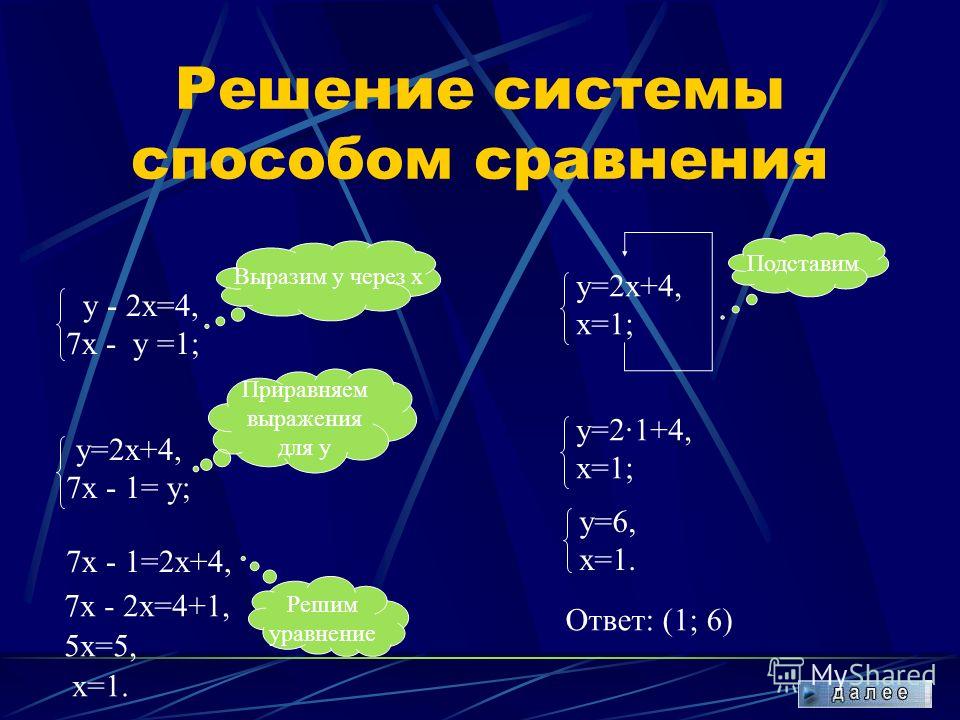
? 4\left( { — 5} \right)\\ — 20 & \le — 20\,\,\,\,{\mbox{OK}}\end{align*}\]
В этом случае -20 меньше или равно -20 (в данном случае оно равно) и, таким образом, снова мы получаем истинное неравенство и, следовательно, \(z = — 5\) удовлетворяет неравенству и, следовательно, будет решением.
Мы также должны сделать быстрый пример чисел, которые не являются решениями, чтобы мы могли увидеть, как они будут работать.
Пример 2. Покажите, что следующие числа не являются решениями данного уравнения или неравенства.
- \(y = — 2\) в \(3\left( {y + 1} \right) = 4y — 5\)
- \(z = — 12\) в \(2\влево( {z — 5} \вправо) \le 4z\)
Показать все решения Скрыть все решения
a \(y = — 2\) in \(3\left( {y + 1} \right) = 4y — 5\) Показать решение
В этом случае мы делаем то же самое, что и в предыдущем примере.
Подставьте число и покажите, что на этот раз оно не удовлетворяет уравнению. Для уравнений это будет означать, что правая часть уравнения не будет равна левой части уравнения. 9? 4\влево( { — 2} \вправо) — 5\\ — 3 & \ne — 13\,\,\,\,{\mbox{НЕ ОК}}\end{выравнивание*}\]
Таким образом, -3 не равно -13, поэтому уравнение не выполняется. Поэтому \(y = — 2\) не является решением уравнения.
b \(z = — 12\) in \(2\left( {z — 5} \right) \le 4z\) Показать решение
На этот раз у нас есть неравенство. Число не будет удовлетворять неравенству, если мы получим неверное неравенство после подстановки числа. 9? 4\left( { — 12} \right)\\ — 34\require{cancel} & \bcancel{\le} — 48\,\,\,\,{\mbox{NOT OK}}\end{align* }\]
В этом случае -34 НЕ меньше или равно -48, поэтому неравенство не выполняется. Поэтому \(z = — 12\) не является решением неравенства.
Теперь нет причин думать, что данное уравнение или неравенство будет иметь только одно решение.
2} — 9= 0\). В этом случае \(x = — 3\) также является решением.
Мы называем полный набор всех решений набором решений для уравнения или неравенства. Существует также некоторая формальная нотация для наборов решений, хотя мы не будем часто использовать ее в этом курсе. Независимо от этого факта, мы все равно должны признать это.
Для уравнений мы обозначаем множество решений, заключая все решения в фигурные скобки, \(\left\{ {} \right\}\). Для двух уравнений, которые мы рассмотрели выше, здесь представлены наборы решений. 92} — 9 & = 0 & \hspace{0.25in} & {\mbox{Набор решений}} :\,\,\,\left\{ { — 3,3} \right\}\end{align*} \]
Для неравенств используются аналогичные обозначения. В зависимости от сложности неравенства набор решений может быть одним числом или диапазоном чисел. Если это одно число, то мы используем те же обозначения, что и для уравнений. Если набор решений представляет собой диапазон чисел, как тот, который мы рассмотрели выше, мы будем использовать нечто, называемое 9.
0239 установить обозначение построителя . Вот набор решений для неравенства, которое мы рассмотрели выше.
\[\left\{ {z|z \ge — 5} \right\}\]
Это читается как: «Набор всех \(z\) таких, что \(z\) больше или равен -5».
Большинство неравенств, которые мы будем рассматривать, будут иметь достаточно простые наборы решений, которые мы часто просто обозначаем как
. \[г \гэ — 5\] 92} & < 0\конец{выравнивание*}\]
Если мы ограничимся только реальными решениями (что мы не всегда будем делать), то у уравнения нет решения. Возведение в квадрат \(x\) делает \(x\) больше, чем равным нулю, затем добавление 1 к этому означает, что левая часть гарантированно будет не менее 1. Другими словами, у этого уравнения нет реального решения. По той же основной причине неравенство не имеет решения. Возведение в квадрат любого действительного числа \(x\) делает его положительным или нулевым и, следовательно, никогда не будет отрицательным.