Решение задач № 20 ЕГЭ (базовый уровень)
Математика Базовый уровень. Решение задания 20.
Обмен фишек
- Петя меняет маленькие фишки на большие, зайдя на обмен он получает 6 больших фишек отдав 9 маленьких. Сначала у Пети было 100 фишек (больших и маленьких), Осталось 79 сколько обменов он совершил?
Решение:
- 9-6=3. этим действием мы узнаем сколько Петя теряет (назовём это так) фишек за 1 обмен.
- 100-79=21 фишку он потерял
- 21:3 и получаем 7 Ответ: 7
Обмен наклеек
- Петя обменивался наклейками. Одну наклейку он меняет на 5 других Вначале у него была 1 наклейка. Сколько наклеек у него будет после 50 обменов?
- Решение:
1)50*5=250 – всего получит наклеек
2)но при обмене он отдавал по 1 наклейке получается 250-49=201. Ответ. 201
Оценка за четверть
- В конце четверти Петя выписал подряд все свои отметки по одному из предметов, их оказалось 5, и поставил между некоторыми из них знаки умножения.

- Решение:
Число 3530 разложим на множители таким образом, чтобы остаток от разложения состоял из чисел 2, 3, 4 и 5 (т.к. только такие оценки ставит учитель). 3530=2⋅5⋅353, при этом оценки 353 не бывает, но оно записано в виде ряда оценок 3, 5 и 3.
Таким образом, получается ряд оценок 2, 5, 353 (как и по условию у нас оценок получилось 5 штук). Найдем среднее арифметическое данных оценок 2+5+3+5+3=3,6, округлив до целого получим оценку 4.
Ответ: 4.
- В конце четверти Петя выписал подряд все свои отметки по одному из предметов, их оказалось 5, и поставил между некоторыми из них знаки умножения. Произведение получившихся чисел оказалось равным 3495.
 Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2″, «3″, «4″ или «5″ и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округленным по правилам округления? ()
Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2″, «3″, «4″ или «5″ и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округленным по правилам округления? () - Ответ: 3
Среднее арифметическое
- Среднее арифметическое 6 различных натуральных чисел равно 8. На сколько нужно увеличить наибольшее из этих чисел, чтобы их среднее арифметическое стало на 1 больше?
- Решение:
Ответ: 6
Партия в теннис
- Миша, Коля и Леша играют в настольный теннис: игрок, проигравший партию, уступает место игроку, не участвовавшему в ней. В итоге оказалось, что Миша сыграл 12 партий, а Коля — 25. Сколько партий сыграл Леша?
- Решение:
Ответ: 13
Чёрно-белое поле
- Клетки таблицы 6 х 5 раскрашены в черный и белый цвета. Пар соседних клеток разного цвета 26, пар соседних клеток черного цвета всего 6.
 Сколько пар соседних клеток белого цвета?
Сколько пар соседних клеток белого цвета? - Решение:
Ответ: 17
Договор о дружбе
- Из десяти стран семь подписали договор о дружбе ровно с тремя другими странами, а каждая из оставшихся трех — ровно с семью. Сколько всего было подписано договоров?
- Решение:
Ответ: 21
Плоскость
- Три луча, выходящие из точки, разбивают плоскость на 3 разных угла, измеряемых целым числом градусов. Наибольший угол в 3 раза больше наименьшего. Сколько значений может принимать величина среднего угла?
- Решение:
Ответ: 20
Задача о столбах
- Семь столбов соединены между собой проводами так, что от каждого столба отходит ровно 4 провода. Сколько всего проводов протянуто между этими семью столбами?
- Решение:
Ответ: 14
- Десять столбов соединены между собой проводами так, что от каждого столба отходит ровно 8 проводов.
 Сколько всего проводов протянуто между этими десятью столбами?
Сколько всего проводов протянуто между этими десятью столбами?
Ответ: 40
Вазы с розами
- На прилавке цветочного магазина стоят 3 вазы с розами: черная, зеленая и оранжевая. Слева от черной вазы 32 розы, справа от оранжевой вазы 9 роз. Всего в вазах 37 роз. Сколько роз в зеленой вазе?
- Решение:
- На прилавке цветочного магазина стоят 3 вазы с розами: белая, синяя и красная. Слева от красной вазы 15 роз, справа от синей вазы 12 роз. Всего в вазах 22 розы. Сколько роз в белой вазе?
Ответ: 5
Маша и медведь
- Маша и Медведь съели 160 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь — печенье, но в какой-то момент они поменялись. Медведь и то, и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенье они съели поровну?
- Решение:
Ответ: 144
Маша и Медведь съели 51 печенье и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь-печенье, но в какой-то момент они поменялись. Медведь и то, и другое ест в четыре раза быстрее. Сколько печений съел Медведь, если варенья они съели поровну?
Сначала Маша ела варенье, а Медведь-печенье, но в какой-то момент они поменялись. Медведь и то, и другое ест в четыре раза быстрее. Сколько печений съел Медведь, если варенья они съели поровну?
- Ответ : 48
Маша и Медведь съели 100 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь – печенья, но в какой-то момент они поменялись. Медведь и то, и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну?
- Ответ: 90
Порванная книга
- Из книги выпало несколько идущих подряд листков. Номер последней страницы перед выпавшими листами — 352, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало?
- Решение:
Ответ: 85
- Про натуральные числа A, B и C известно, что каждое из них больше 4, но меньше 8.
 Загадали натуральное число, затем его умножили на А, потом прибавили к полученному произведению B и вычли C. Получилось 165. Какое число было загадано?
Загадали натуральное число, затем его умножили на А, потом прибавили к полученному произведению B и вычли C. Получилось 165. Какое число было загадано? - Решение:
Цветные линии
- На палке отмечены поперечные линии красного, желтого и зеленого цвета. Если распилить палку по красным линиям, получится 8 кусков, если по желтым – 12 кусков, а если по зеленым — 6 кусков. Сколько кусков получится, если распилить палку по линиям всех трех цветов?
- Решение:
Ответ: 24
ЕГЭ — 2017
- На ленте с разных сторон от середины отмечены две поперечные полоски: синяя и красная. Если разрезать ленту по синей полоске, то одна часть будет длиннее другой на A см. Если разрезать по красной, то одна часть будет длиннее другой на B см. Найдите расстояние от красной до синей полоски.
- Решение:
Ответ: 30
Деление амёб. Способ 1
- Биологи открыли разновидность амёб, каждая из которых ровно через минуту делится на две.
 Биолог кладёт амёбу в пробирку, и ровно через час пробирка оказывается полностью заполненной амёбами. Сколько минут потребуется, чтобы вся пробирка заполнилась амёбами, если в неё положить не одну, а четыре амёбы?
Биолог кладёт амёбу в пробирку, и ровно через час пробирка оказывается полностью заполненной амёбами. Сколько минут потребуется, чтобы вся пробирка заполнилась амёбами, если в неё положить не одну, а четыре амёбы? - Решение:
Переведем часы в минуты, так как ответ должен быть в минутах:
1 час = 60 минут
Через 60 минут одна амеба произведет полную пробирку амеб. Если амеб будет 4, то за тот же час будет заполнено 4 пробирки. Однако пробирка лишь одна, поэтому каждой амебе нужно заполнить лишь 1/4 от пробирки.
Если 1 амеба заполняет всю пробирку за 60 минут, то 1/2 пробирки (половина) будет заполнена 1 амебой за 59 минут, а 1/4 пробирки (половина от половины) будет заполнена ею за 58 минут. Поскольку все 4 амебы будут делиться одновременно, за 58 минут они полностью заполнят пробирку.
Способ 2
- Переведем часы в минуты, так как ответ должен быть в минутах:
- 1 час = 60 минут
- Пусть количество минут, которое будет происходить деление, равно x.
 Тогда за это время 1 амеба поделится на 2x амеб, а 4 амебы – на 4 ⋅ 2x. При этом они полностью заполнят пробирку. Кроме этого известно, что 1 амеба за 60 минут полностью заполнит пробирку, то есть при этом получится 260 амеб. Составляем уравнение и решаем его:
Тогда за это время 1 амеба поделится на 2x амеб, а 4 амебы – на 4 ⋅ 2x. При этом они полностью заполнят пробирку. Кроме этого известно, что 1 амеба за 60 минут полностью заполнит пробирку, то есть при этом получится 260 амеб. Составляем уравнение и решаем его:
- 260 = 4 ⋅ 2x
- 260 = 2log24 ⋅ 2x
- 260 = 2x + log24
- 60 = x + log24
- x = 60 – log24 = 60 – 2 = 58 минут
- Заметим, что при вычислениях нам понадобилось привести число 4 к степени с основанием 2. Для этого было использовано основное логарифмическое тождество:
- 4 = 2log24
Ответ: 58
Манекенщицы
- При демонстрации летней одежды наряды каждой манекенщицы отличаются хотя бы одним из трёх элементов: блузкой, юбкой и туфлями. Всего модельер приготовил для демонстрации 5 видов блузок, 3 вида юбок и 4 вида туфель. Сколько различных нарядов будет показано на этой демонстрации?
- Решение:
Поскольку существует 5 видов блузок, 3 вида юбок и 4 вида туфель, число различных нарядов равно произведению этих чисел:
5 ⋅ 3 ⋅ 4 = 60
Ответ: 60
Кубики
- Сколькими способами можно поставить в ряд два одинаковых красных кубика, три одинаковых зелёных кубика и один синий кубик?
- Решение:
Нам важен порядок кубиков, поэтому нам нужно посчитать количество перестановок всех кубиков: Р = (2 + 3 + 1)! = 6! Однако у нас есть одинаковые кубики, от перемены мест которых результат не изменится: 3 зеленых (это 3! перестановок) и 2 красных (это 2! перестановок).
6! / (2! ⋅ 3!) = 1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 ⋅ 6 / (1 ⋅ 2 ⋅ 1 ⋅ 2 ⋅ 3) = 2 ⋅ 5 ⋅ 6 = 60
ОТВЕТ: 60
Горный перевал
- Группа туристов преодолела горный перевал. Первый километр подъёма они преодолели за 50 минут, а каждый следующий километр проходили на 15 минут дольше предыдущего. Последний километр перед вершиной был пройден за 95 минут. После десятиминутного отдыха на вершине туристы начали спуск, который был более пологим. Первый километр после вершины был пройден за час, а каждый следующий на 10 минут быстрее предыдущего. Сколько часов группа затратила на весь маршрут, если последний километр спуска был пройден за 10 минут.
- Решение:
Ответ: 8,5
Произведение чисел
- Произведение десяти идущих подряд чисел разделили на 7. Чему может быть равен остаток?
- Решение:
Так как количество чисел, произведение которых берется, больше заданного делителя, остаток от деления будет равен 0. Поскольку среди чисел из произведения обязательно найдется число, которое делится нацело на заданный делитель.
Поскольку среди чисел из произведения обязательно найдется число, которое делится нацело на заданный делитель.
Приведем несколько примеров:
1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 ⋅ 6 ⋅ 7 ⋅ 8 ⋅ 9 ⋅ 10 / 7 = 1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 ⋅ 6 ⋅ 8 ⋅ 9 ⋅ 10
16 ⋅ 17 ⋅ 18 ⋅ 19 ⋅ 20 ⋅ 21 ⋅ 22 ⋅ 23 ⋅ 24 ⋅ 25 / 7 = 3 ⋅ 16 ⋅ 17 ⋅ 18 ⋅ 19 ⋅ 20 ⋅ 22 ⋅ 23 ⋅ 24 ⋅ 25
Ответ: 0
Места в кинозале
- В первом ряду кинозала 24 места, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в восьмом ряду?
- Решение:
Вычислим количество мест в каждом ряду кинозала последовательно:
Ряд 1: 24
Ряд 2: 24 + 2 = 26
Ряд 3: 26 + 2 = 28
Ряд 4: 28 + 2 = 30
Ряд 5: 30 + 2 = 32
Ряд 6: 32 + 2 = 34
Ряд 7: 34 + 2 = 36
Ряд 8: 36 + 2 = 38
Ответ: 38
Закон Мура
- По эмпирическому закону Мура среднее число транзисторов на микросхемах каждый год удваивается.
 Известно, что в 2005 году среднее число транзисторов на микросхеме равнялось 520 млн. Определите, сколько в среднем миллионов транзисторов было на микросхеме в 2003 году.
Известно, что в 2005 году среднее число транзисторов на микросхеме равнялось 520 млн. Определите, сколько в среднем миллионов транзисторов было на микросхеме в 2003 году. - Решение:
Пусть в 2003 году было x миллионов транзисторов, тогда в 2005 году их стало:
x ⋅ 2 ⋅ 2 = 4x = 520
Осталось найти значение x:
x = 520 / 4 = 130
Ответ: 130
Продажа холодильников
По условию задачи в апреле было продано 10 холодильников. С мая по август (4 месяца) продажи увеличивались на 15 холодильников каждый месяц. Получили арифметическую прогрессию a1 = 10 d = 15 n = 5 Число n равно 5, так как в расчеты мы включили месяц апрель. Необходимо найти сумму 5 членов арифметической прогрессии. Воспользуемся формулами: Sn = (a1 + an) ⋅ n / 2 an = a1 + d(n — 1) Вычислим n-ый член арифметической прогрессии и сумму n членов: a5 = a1 + d(n — 1) = 10 + 15 ⋅ (5 – 1) = 10 + 60 = 70 S5 = (10 + 70) ⋅ 5 / 2 = 80 ⋅ 5 / 2 = 400 / 2 = 200 С сентября объем продаж начал уменьшаться на 15 холодильников каждый месяц (4 месяца). Значит в сентябре было продано: 70 – 15 = 55 холодильников Получили убывающую арифметическую прогрессию: a1 = 55 d = –15 n = 4 Вычислим n-ый член арифметической прогрессии и сумму n членов: a4 = a1 + d(n — 1) = 55 – 15 ⋅ (4 – 1) = 55 – 45 = 10 S4 = (55 + 10) ⋅ 4 / 2 = 65 ⋅ 4 / 2 = 260 / 2 = 130 холодильников Таким образом, в январе, феврале и марте было продано по 10 холодильников, с апреля по август включительно было продано 200 холодильников, а с сентября по декабрь включительно было продано 130 холодильников. Общее количество проданных за год холодильников равно: 10 + 10 + 10 + 200 + 130 = 360 холодильников
Значит в сентябре было продано: 70 – 15 = 55 холодильников Получили убывающую арифметическую прогрессию: a1 = 55 d = –15 n = 4 Вычислим n-ый член арифметической прогрессии и сумму n членов: a4 = a1 + d(n — 1) = 55 – 15 ⋅ (4 – 1) = 55 – 45 = 10 S4 = (55 + 10) ⋅ 4 / 2 = 65 ⋅ 4 / 2 = 260 / 2 = 130 холодильников Таким образом, в январе, феврале и марте было продано по 10 холодильников, с апреля по август включительно было продано 200 холодильников, а с сентября по декабрь включительно было продано 130 холодильников. Общее количество проданных за год холодильников равно: 10 + 10 + 10 + 200 + 130 = 360 холодильников
- В магазине бытовой техники объём продаж холодильников носит сезонный характер. В январе было продано 10 холодильников, и в три последующих месяца продавали по 10 холодильников. С мая продажи увеличивались на 15 единиц по сравнению с предыдущим месяцем. С сентября объём продаж начал уменьшаться на 15 холодильников каждый месяц относительно предыдущего месяца. Сколько холодильников продал магазин за год?
- Решение:
Ответ: 360
Таблица чисел
- В таблице три столбца и несколько строк.
 В каждую клетку таблицы вписали по натуральному числу так, что сумма всех чисел в первом столбце равна 103, во втором — 97, в третьем — 93, а сумма чисел в каждой строке больше 21, но меньше 24. Сколько всего строк в таблице?
В каждую клетку таблицы вписали по натуральному числу так, что сумма всех чисел в первом столбце равна 103, во втором — 97, в третьем — 93, а сумма чисел в каждой строке больше 21, но меньше 24. Сколько всего строк в таблице? - Решение:
Вычислим сумму натуральных чисел во всей таблице, для этого нужно сложить суммы чисел во всех столбцах:
103 + 97 + 93 = 293
Теперь найдем диапазон, в котором лежит число строк таблицы. Для этого разделим сумму чисел в таблице на сумму чисел в строке.
Поскольку сумма чисел в строке больше 21, но меньше 24, она может быть равна 22 или 23. Если сумма в строке равна 22, то:
293 / 22 ≈ 13,3
Если сумма чисел в строке равна 23, то:
293 / 23 ≈ 12,7
Получается, что число строк в таблице лежит в диапазоне от 12,7 и 13,3. Единственное целое число, лежащее в данном диапазоне, равно 13.
Использованные источники:
- http://www.ege-math.ru
- http://worksbase.
 ru/matematika/kak-reshat/egeb-20
ru/matematika/kak-reshat/egeb-20
Линейное программирование — тест с ответами
Математика дается не всем. Но сдавать её нужно чтобы получить за нее зачет или какую либо оценку. Сейчас чаще всего проводится проверка знаний в виде тестирования. Мы собрали частые вопросы встречающиеся в тестах на этой странице. Обратите внимание что правильные варианты ответов выделены символом [+].
Каждую секунду бактерия делится на две новые бактерии. Известно, что весь объём одного стакана бактерии заполняют за 1 час. За сколько секунд бактерии заполняют половину стакана?
[+] Ответ: 3599
На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 15 кусков, если по жёлтым — 5 кусков, а если по зелёным — 7 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
[+] Ответ: 25
Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за один прыжок. Кузнечик начинает прыгать из начала координат. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 11 прыжков?
Кузнечик начинает прыгать из начала координат. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 11 прыжков?
[+] Ответ: 12
Саша пригласил Петю в гости, сказав, что живёт в седьмом подъезде в квартире № 462, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом семиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)
[+] Ответ: 5
Саша пригласил Петю в гости, сказав, что живёт в восьмом подъезде в квартире № 468, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом двенадцатиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)
[+] Ответ: 10
Саша пригласил Петю в гости, сказав, что живёт в двенадцатом подъезде в квартире № 465, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом пятиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)
На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)
[+] Ответ: 4
Саша пригласил Петю в гости, сказав, что живёт в десятом подъезде в квартире № 333, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом девятиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.)
[+] Ответ: 3
Тренер посоветовал Андрею в первый день занятий провести на беговой дорожке 15 минут, а на каждом следующем занятии увеличивать время, проведённое на беговой дорожке, на 7 минут. За сколько занятий Андрей проведёт на беговой дорожке в общей сложности 2 часа 25 минут, если будет следовать советам тренера?
[+] Ответ: 5
Врач прописал пациенту принимать лекарство по такой схеме: в первый день он должен принять 3 капли, а в каждый следующий день — на 3 капли больше, чем в предыдущий. Приняв 30 капель, он ещё 3 дня пьёт по 30 капель лекарства, а потом ежедневно уменьшает приём на 3 капли. Сколько пузырьков лекарства нужно купить пациенту на весь курс приёма, если в каждом содержится 20 мл лекарства (что составляет 250 капель)?
Сколько пузырьков лекарства нужно купить пациенту на весь курс приёма, если в каждом содержится 20 мл лекарства (что составляет 250 капель)?
[+] Ответ: 2
Врач прописал пациенту принимать лекарство по такой схеме: в первый день он должен принять 20 капель, а в каждый следующий день — на 3 капли больше, чем в предыдущий. После 15 дней приёма пациент делает перерыв в 3 дня и продолжает принимать лекарство по обратной схеме: в 19-й день он принимает столько же капель, сколько и в 15-й день, а затем ежедневно уменьшает дозу на 3 капли, пока дозировка не станет меньше 3 капель в день. Сколько пузырьков лекарства нужно купить пациенту на весь курс приёма, если в каждом содержится 200 капель?
[+] Ответ: 7
Произведение десяти идущих подряд чисел разделили на 7. Чему может быть равен остаток?
[+] Ответ: 0
Сколькими способами можно поставить в ряд два одинаковых красных кубика, три одинаковых зелёных кубика и один синий кубик?
[+] Ответ: 60
В бак объёмом 38 литров каждый час, начиная с 12 часов, наливают полное ведро воды объёмом 8 литров. Но в днище бака есть небольшая щель, и из неё за час вытекает 3 литра. В какой момент времени (в часах) бак будет заполнен полностью.
Но в днище бака есть небольшая щель, и из неё за час вытекает 3 литра. В какой момент времени (в часах) бак будет заполнен полностью.
[+] Ответ: 18
Какое наименьшее число идущих подряд чисел нужно взять, чтобы их произведение делилось на 7?
[+] Ответ: 2
В результате паводка котлован заполнился водой до уровня 2 метра. Строительная помпа непрерывно откачивает воду, понижая её уровень на 20 см в час. Подпочвенные воды, наоборот, повышают уровень воды в котловане на 5 см в час. За сколько часов работы помпы уровень воды в котловане опустится до 80 см?
[+] Ответ: 8
В меню ресторана имеется 6 видов салатов, 3 вида первых блюд, 5 видов вторых блюд и 4 вида десерта. Сколько вариантов обеда из салата, первого, второго и десерта могут выбрать посетители этого ресторана?
[+] Ответ: 360
Нефтяная компания бурит скважину для добычи нефти, которая залегает, по данным геологоразведки, на глубине 3 км. В течение рабочего дня бурильщики проходят 300 метров в глубину, но за ночь скважина вновь «заиливается», то есть заполняется грунтом на 30 метров. За сколько рабочих дней нефтяники пробурят скважину до глубины залегания нефти?
В течение рабочего дня бурильщики проходят 300 метров в глубину, но за ночь скважина вновь «заиливается», то есть заполняется грунтом на 30 метров. За сколько рабочих дней нефтяники пробурят скважину до глубины залегания нефти?
[+] Ответ: 11
Какое наименьшее число идущих подряд чисел нужно взять, чтобы их произведение делилось на 9?
[+] Ответ: 2
В обменном пункте можно совершить одну из двух операций: • за 2 золотых монеты получить 3 серебряных и одну медную; • за 5 серебряных монет получить 3 золотых и одну медную. У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 50 медных. На сколько уменьшилось количество серебряных монет у Николая?
[+] Ответ: 10
На поверхности глобуса фломастером проведены 12 параллелей и 22 меридиана. На сколько частей проведённые линии разделили поверхность глобуса? Меридиан — это дуга окружности, соединяющая Северный и Южный полюсы. Параллель — это окружность, лежащая в плоскости, параллельной плоскости экватора.
Параллель — это окружность, лежащая в плоскости, параллельной плоскости экватора.
[+] Ответ: 286
В корзине лежит 50 грибов: рыжики и грузди. Известно, что среди любых 28 грибов имеется хотя бы один рыжик, а среди любых 24 грибов хотя бы один груздь. Сколько груздей в корзине?
[+] Ответ: 27
Группа туристов преодолела горный перевал. Первый километр подъёма они преодолели за 50 минут, а каждый следующий километр проходили на 15 минут дольше предыдущего. Последний километр перед вершиной был пройден за 95 минут. После десятиминутного отдыха на вершине туристы начали спуск, который был более пологим. Первый километр после вершины был пройден за час, а каждый следующий на 10 минут быстрее предыдущего. Сколько часов группа затратила на весь маршрут, если последний километр спуска был пройден за 10 минут.
[+] Ответ: 8,5
На кольцевой дороге расположены четыре бензоколонки: A, B, C и D. Расстояние между A и B — 35 км, между A и C — 20 км, между C и D — 20 км, между D и A — 30 км (все расстояния измеряются вдоль кольцевой дороги в кратчайшую сторону). Найдите расстояние между B и C. Ответ дайте в километрах.
Найдите расстояние между B и C. Ответ дайте в километрах.
[+] Ответ: 15
На кольцевой дороге расположены четыре бензоколонки: A, B, C и D. Расстояние между A и B — 50 км, между A и C — 40 км, между C и D — 25 км, между D и A — 35 км (все расстояния измеряются вдоль кольцевой дороги в кратчайшую сторону). Найдите расстояние между B и C.
[+] Ответ: 10
В классе учится 25 учащихся. Несколько из них ходили в кино, 18 человек ходили в театр, причём и в кино, и в театр ходили 12 человек. Известно, что трое не ходили ни в кино, ни в театр. Сколько человек из класса ходили в кино?
[+] Ответ: 16
По эмпирическому закону Мура среднее число транзисторов на микросхемах каждый год удваивается. Известно, что в 2005 году среднее число транзисторов на микросхеме равнялось 520 млн. Определите, сколько в среднем миллионов транзисторов было на микросхеме в 2003 году.
[+] Ответ: 130
В первом ряду кинозала 24 места, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в восьмом ряду?
Сколько мест в восьмом ряду?
[+] Ответ: 38
На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 5 кусков, если по жёлтым — 7 кусков, а если по зелёным — 11 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
[+] Ответ: 21
В магазине бытовой техники объём продаж холодильников носит сезонный характер. В январе было продано 10 холодильников, и в три последующих месяца продавали по 10 холодильников. С мая продажи увеличивались на 15 единиц по сравнению с предыдущим месяцем. С сентября объём продаж начал уменьшаться на 15 холодильников каждый месяц относительно предыдущего месяца. Сколько холодильников продал магазин за год?
[+] Ответ: 360
В обменном пункте можно совершить одну из двух операций: 1) за 3 золотых монеты получить 4 серебряных и одну медную; 2) за 6 серебряных монет получить 4 золотых и одну медную. У Николы были только серебряные монеты. После посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 35 медных. На сколько уменьшилось количество серебряных монет у Николы?
У Николы были только серебряные монеты. После посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 35 медных. На сколько уменьшилось количество серебряных монет у Николы?
[+] Ответ: 10
Саша пригласил Петю в гости, сказав, что живёт в седьмом подъезде в квартире № 462, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом семиэтажный. На каком этаже живёт Саша? (На каждом этаже число квартир одинаково, номера квартир в доме начинаются с единицы.)
[+] Ответ: 5
Во всех подъездах дома одинаковое число этажей, а на каждом этаже одинаковое число квартир. При этом число этажей в доме больше числа квартир на этаже, число квартир на этаже больше числа подъездов, а число подъездов больше одного. Сколько этажей в доме, если всего в нём 110 квартир?
[+] Ответ: 11
комбинаторика — Способы расставить 3 красных, 4 синих и 5 зеленых вагонов так, чтобы 2 синих вагона не стояли рядом друг с другом
Вот другой подход.
Сначала мы выстраиваем три красных и пять зеленых вагонов (оставляя достаточно места между каждой парой вагонов, чтобы между ними можно было поставить еще один вагон). Это можно сделать, выбрав, какие три из восьми позиций будут зарезервированы для красных вагонов, что можно сделать $\binom{8}{3}$ способами. Теперь мы выбираем четыре из девяти доступных мест (семь между последовательными парами восьми вагонов, которые уже были припаркованы, и два в конце), чтобы разместить синие вагоны, что можно сделать в $\binom{9{4}$ способов. Следовательно, количество способов, которыми мы можем расположить три красных, четыре синих и пять зеленых вагонов так, чтобы никакие два синих вагона не стояли подряд, равно $$\binom{8}{3} \cdot \binom{9}{4} = 7056$$
Чтобы ваш подход работал, мы должны использовать принцип включения-исключения, причем случаи должны быть как минимум двумя последовательными. синих вагонов, по крайней мере три синих вагона подряд, и все четыре синих вагона идут подряд. Случай двух последовательных синих вагонов сложен, поскольку подсчет случаев, в которых есть по крайней мере два последовательных синих вагона, учитывает случаи, в которых есть две непересекающиеся пары синих вагонов, дважды.
Случай двух последовательных синих вагонов сложен, поскольку подсчет случаев, в которых есть по крайней мере два последовательных синих вагона, учитывает случаи, в которых есть две непересекающиеся пары синих вагонов, дважды.
Как вы поняли, количество компоновок трех красных, четырех синих и пяти красных вагонов равно $$\binom{12}{3}\binom{9}{4}\binom{5}{5} = \frac{12!}{3!4!5!}$$ Мы должны вычесть из них количество расстановок, в которых по крайней мере два синих вагона стоят подряд.
Количество способов, при которых по крайней мере два синих вагона идут подряд, можно определить, представив двенадцать вагонов как пару синих вагонов, два дополнительных синих вагона, три красных вагона и пять зеленых вагонов. Это дает нам в общей сложности одиннадцать объектов. Мы можем разместить пару синих вагонов $\binom{11}{1}$ способами, два других синих вагона — $\binom{10}{2}$ способами, так как после размещения пары остается десять мест, а три красные вагоны в оставшихся восьми местах $\binom{8}{3}$ способами, а пять зеленых вагонов — $\binom{5}{5}$ способами. Это дает
$$\binom{11}{1}\binom{10}{2}\binom{8}{3}\binom{5}{5} = \frac{11!}{1!2!3!5! }$$
договоренности, в которых два синих вагона идут подряд. Однако мы дважды посчитали каждый случай, когда есть две непересекающиеся пары синих вагонов. Поскольку пара может начинаться с любого из первых одиннадцати мест, есть $\binom{11}{2}$ мест для начала пары. Однако $\binom{10}{1}$ из них идут подряд, поэтому пара не будет непересекающейся. Таким образом, существуют $\binom{11}{2} — \binom{10}{1} = \binom{10}{2}$ (по тождеству Паскаля) способов разместить две непересекающиеся пары синих вагонов. После того, как они будут размещены, останется восемь мест. Мы можем разместить три красных вагончика на этих восьми ячейках $\binom{8}{3}$ способами, а пять зеленых вагончиков на пяти оставшихся ячейках $\binom{5}{5}$ способами. Таким образом, есть
$$\binom{10}{2}\binom{8}{3}\binom{5}{5} = \frac{10!}{2!3!5!}$$
схемы, в которых есть две непересекающиеся пары синих вагонов. Таким образом, количество расстановок, в которых по крайней мере два синих вагона идут подряд, равно
$$\frac{11!}{1!2!3!5!} — \frac{10!}{2!3!5!}$$
Это дает
$$\binom{11}{1}\binom{10}{2}\binom{8}{3}\binom{5}{5} = \frac{11!}{1!2!3!5! }$$
договоренности, в которых два синих вагона идут подряд. Однако мы дважды посчитали каждый случай, когда есть две непересекающиеся пары синих вагонов. Поскольку пара может начинаться с любого из первых одиннадцати мест, есть $\binom{11}{2}$ мест для начала пары. Однако $\binom{10}{1}$ из них идут подряд, поэтому пара не будет непересекающейся. Таким образом, существуют $\binom{11}{2} — \binom{10}{1} = \binom{10}{2}$ (по тождеству Паскаля) способов разместить две непересекающиеся пары синих вагонов. После того, как они будут размещены, останется восемь мест. Мы можем разместить три красных вагончика на этих восьми ячейках $\binom{8}{3}$ способами, а пять зеленых вагончиков на пяти оставшихся ячейках $\binom{5}{5}$ способами. Таким образом, есть
$$\binom{10}{2}\binom{8}{3}\binom{5}{5} = \frac{10!}{2!3!5!}$$
схемы, в которых есть две непересекающиеся пары синих вагонов. Таким образом, количество расстановок, в которых по крайней мере два синих вагона идут подряд, равно
$$\frac{11!}{1!2!3!5!} — \frac{10!}{2!3!5!}$$
Количество способов, которыми по крайней мере три синих вагона идут подряд, можно определить, представив двенадцать вагонов как десять объектов, а именно три последовательных синих вагона, другой синий вагон, три красных вагона и пять зеленых вагонов. . Мы можем разместить три последовательных синих вагона $\binom{10}{1}$ способами, другой синий вагон в одном из девяти оставшихся мест $\binom{9}{1}$ способами, три красных вагона в восьми оставшихся клетках $\binom{8}{3}$ способами, а пять зеленых вагонов в последних пяти клетках $\binom{5}{5}$ способами. Следовательно, есть
$$\бином{10}{1}\бином{9}{1}\binom{8}{3}\binom{5}{5} = \frac{10!}{1!1!3!5!}$$
способы расположения вагонов так, чтобы по крайней мере три синих вагона шли подряд.
. Мы можем разместить три последовательных синих вагона $\binom{10}{1}$ способами, другой синий вагон в одном из девяти оставшихся мест $\binom{9}{1}$ способами, три красных вагона в восьми оставшихся клетках $\binom{8}{3}$ способами, а пять зеленых вагонов в последних пяти клетках $\binom{5}{5}$ способами. Следовательно, есть
$$\бином{10}{1}\бином{9}{1}\binom{8}{3}\binom{5}{5} = \frac{10!}{1!1!3!5!}$$
способы расположения вагонов так, чтобы по крайней мере три синих вагона шли подряд.
Количество способов, которыми мы можем расположить повозки, в которых все четыре синих повозки идут подряд, можно определить, представив четыре синих повозки как один объект. Затем у нас есть девять объектов для размещения: блок из четырех последовательных синих фургонов, трех красных фургонов и пяти зеленых фургонов. Мы можем разместить четыре последовательных синих вагона $\binom{9}{1}$ способами, три красных вагона — $\binom{8}{3}$ способами, а пять зеленых вагонов — $\binom{5}. {5}$ способов. Таким образом, есть
$$\бином{9}{1}\binom{8}{3}\binom{5}{5} = \frac{9!}{1!3!5!}$$
договоренности, в которых все четыре синих вагона идут подряд.
Таким образом, есть
$$\бином{9}{1}\binom{8}{3}\binom{5}{5} = \frac{9!}{1!3!5!}$$
договоренности, в которых все четыре синих вагона идут подряд.
В соответствии с принципом включения-исключения число расстановок из трех красных вагонов, четырех синих вагонов и пяти зеленых вагонов, в которых нет двух последовательных синих вагонов, равно $$\frac{12!}{3!4!5!} — \left[\frac{11!}{1!2!3!5!} — \frac{10!}{2!3!5! }\right] + \frac{10!}{1!1!3!5!} — \frac{9!}{1!3!5!} = 7056$$ что согласуется с полученным выше результатом.
Перестановки и комбинации – Перестановки идентичных объектов (Часть 2)
До сих пор у нас были идентичные объекты только одного типа. То есть одинаковыми были только красные шарики, а остальные все разные.
В этом уроке будет рассмотрено еще несколько случаев, связанных с идентичными объектами более чем одного типа. Например, 3 красных шара и 2 зеленых шара. Или 2 красных, 3 зеленых и 4 других разноцветных шара.
Предположим, нам нужно выстроить в ряд 5 шаров, из которых 3 красных и 2 зеленых. Сколько различных аранжировок возможно?
Сколько различных аранжировок возможно?
Как и прежде, обозначим 5 мест, каждое из которых должно быть заполнено одним шаром.
Сначала мы разместим красные шары на любых 3 из 5 ячеек. Это можно сделать 5 C 3 способами. Вот один из них.
Далее в оставшиеся 2 коробки мы поместим оставшиеся 2 мяча. Это можно сделать только 1 способом (поскольку они оба идентичны)
И все. Общее количество аранжировок будет 5 C 3 x 1 или \( \frac{5!}{3!2!} \)
Мы также можем сначала разместить зеленые шары 5 C 2 способами (выберите 2 из 5 ячеек и поместите по одному шарику в каждую), а затем поместите красные шары в оставшиеся ячейки. Количество расстановок осталось прежним: 5 C 2 или \( \frac{5!}{2!3!} \)
Теперь возьмем другой случай: 7 шаров, из которых 3 красных, 2 зеленый, а остальные разного цвета.
Начнем с размещения красных шаров в 7 C 3 пути.
Затем разместите зеленые в 4 C 2 направлениях. (Поскольку у нас осталось 4 ящика, из которых нужно выбрать 2)
Наконец, мы разместим оставшиеся отдельные шары. На этот раз нас 2! способами, потому что расположение этих двух шаров имеет значение.
Или
Всего аранжировок 7 C 3 x 4 C 2 x 2! = \( \frac{7!}{3!4!} \times \frac{4!}{2!2!} \times 2! = \frac{7!}{3!2!} \)
Вы видите закономерность? В первом случае у нас было 5 шаров, из них 3 красных и 2 зеленых. Количество размещений оказалось равным \( \frac{5!}{3!2!} \)
Если бы все 5 шаров были различными, наш ответ был бы 5!. Теперь, если 3 из них заменить одинаковыми красными шарами, ответ изменится на 5!/3!, а если оставшиеся 2 заменить также одинаковыми зелеными шарами, количество аранжировок изменится на \( \frac{5!}{ 3!2!} \)
Во втором случае у нас было 7 шаров, из которых 3 красных, 2 зеленых и остальные разные.


 Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2″, «3″, «4″ или «5″ и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округленным по правилам округления? ()
Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки «2″, «3″, «4″ или «5″ и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округленным по правилам округления? () Сколько пар соседних клеток белого цвета?
Сколько пар соседних клеток белого цвета?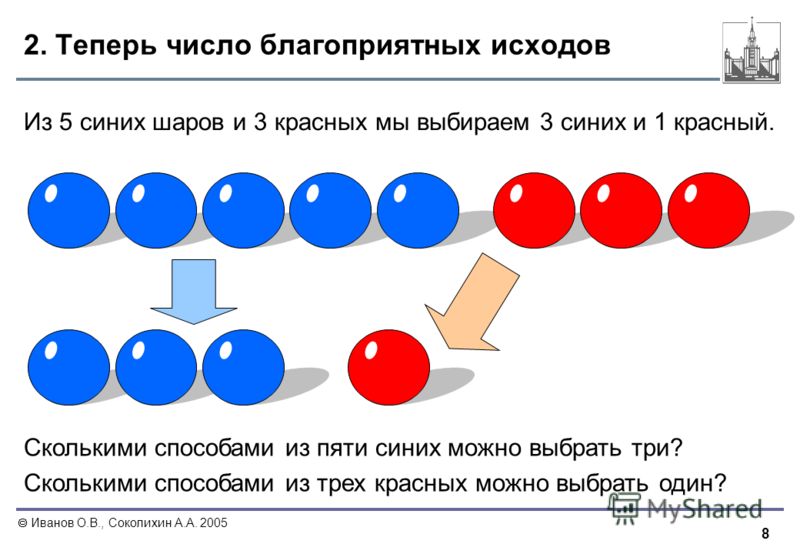 Сколько всего проводов протянуто между этими десятью столбами?
Сколько всего проводов протянуто между этими десятью столбами?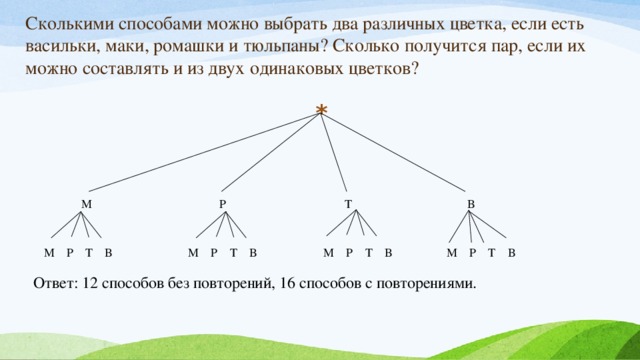 Загадали натуральное число, затем его умножили на А, потом прибавили к полученному произведению B и вычли C. Получилось 165. Какое число было загадано?
Загадали натуральное число, затем его умножили на А, потом прибавили к полученному произведению B и вычли C. Получилось 165. Какое число было загадано? Биолог кладёт амёбу в пробирку, и ровно через час пробирка оказывается полностью заполненной амёбами. Сколько минут потребуется, чтобы вся пробирка заполнилась амёбами, если в неё положить не одну, а четыре амёбы?
Биолог кладёт амёбу в пробирку, и ровно через час пробирка оказывается полностью заполненной амёбами. Сколько минут потребуется, чтобы вся пробирка заполнилась амёбами, если в неё положить не одну, а четыре амёбы? Тогда за это время 1 амеба поделится на 2x амеб, а 4 амебы – на 4 ⋅ 2x. При этом они полностью заполнят пробирку. Кроме этого известно, что 1 амеба за 60 минут полностью заполнит пробирку, то есть при этом получится 260 амеб. Составляем уравнение и решаем его:
Тогда за это время 1 амеба поделится на 2x амеб, а 4 амебы – на 4 ⋅ 2x. При этом они полностью заполнят пробирку. Кроме этого известно, что 1 амеба за 60 минут полностью заполнит пробирку, то есть при этом получится 260 амеб. Составляем уравнение и решаем его: Известно, что в 2005 году среднее число транзисторов на микросхеме равнялось 520 млн. Определите, сколько в среднем миллионов транзисторов было на микросхеме в 2003 году.
Известно, что в 2005 году среднее число транзисторов на микросхеме равнялось 520 млн. Определите, сколько в среднем миллионов транзисторов было на микросхеме в 2003 году. В каждую клетку таблицы вписали по натуральному числу так, что сумма всех чисел в первом столбце равна 103, во втором — 97, в третьем — 93, а сумма чисел в каждой строке больше 21, но меньше 24. Сколько всего строк в таблице?
В каждую клетку таблицы вписали по натуральному числу так, что сумма всех чисел в первом столбце равна 103, во втором — 97, в третьем — 93, а сумма чисел в каждой строке больше 21, но меньше 24. Сколько всего строк в таблице? ru/matematika/kak-reshat/egeb-20
ru/matematika/kak-reshat/egeb-20