Сложение и умножение вероятностей: Сложение вероятностей — урок. Алгебра, 11 класс.

Сложение и умножение вероятностей — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

2. Основные понятия

Познание действительности в естественных науках происходит в результате испытаний
(эксперимента, наблюдений, опыта).
Испытанием или опытом называется осуществление какого-нибудь определенного комплекса условий,
который может быть воспроизведено сколь угодно большое число раз.
Случайным (СС)называется событие, которое может произойти или не произойти в результате
некоторого испытания (опыта).
Таким образом, событие
рассматривается как результат
испытания.
Пример.
Бросание монеты – это испытание.
Появление орла при бросании –
событие.

3. Основные понятия

Наблюдаемые нами события различаются по
степени возможности их появления и по характеру
их взаимосвязи.
Событие называется достоверным, если оно
обязательно произойдет в результате данного
испытания.
Пример. Получение студентом положительной
или отрицательной оценки на экзамене есть
событие достоверное, если экзамен протекает
согласно обычным правилам.
Событие называется невозможным, если оно не
может произойти в результате данного испытания.
Пример. Извлечение из урны белого шара, в
которой находятся лишь цветные (небелые) шары,
есть событие невозможное.
Два или несколько событий
называются равновозможными в данном испытании, если
имеются основания считать, что ни одно из этих событий не
является более возможным или менее возможным, чем
другие.
Пример. При одном бросании одной и той же игральной
кости появление 1, 2, 3, 4, 5 и 6 очков — все это события
равновозможные.
Два события называются несовместными в данном
испытании, если появление одного из них исключает
появление другого, и совместными в противном случае.
Пример. В ящике имеются стандартные и нестандартные
детали. Берем на удачу одну деталь. Появление стандартной
детали исключает появление нестандартной детали. Эти
события несовместные.
События А и В называются противоположными, если
всякое наступление события А означает ненаступление
события В.
Обозначение:
А -событие А
_
А — событие противоположное событию А
(читается «не A»).
Пример. Попадание и промах при одном выстреле по
цели — события противоположные.

4. ИТАК…

Случайное событие -это событие, которое либо
произойдёт, либо нет.
Каждое случайное событие иметь свою вероятность
произойти (сбыться, реализоваться).
Испытание – любое действие, которое может привести к
одному или нескольким результатам.
Исход — конечный результат испытания. Значит испытание
может иметь один или несколько исходов.
Благоприятный исход — желаемый исход.

5. Классическое определение вероятности

Р(А) –вероятность события А
Вероятность
события
Число благоприятных исходов
=
Число всех исходов
m– число благоприятных
исходов
n – число всех исходов
Р(А) = m/n
ПРАВИЛО:
Вероятность всегда равна
от 0 до 1.
НИ БОЛЬШЕ,НИ МЕНЬШЕ!

6. Классная работа (дистанционно)

Двадцать шестое марта
КЛАССНАЯ РАБОТА
(ДИСТАНЦИОННО)

7. Сложение и умножение вероятностей

Событие называют противоположным событию А, если оно происходит только тогда,
когда не происходит событие А. Обозначается А
Сумма вероятностей противоположных событий равна 1
Р( А) Р( А) 1
Два события называются несовместными, если в одном и том же испытании
Они не могут произойти одновременно, т. е. наступление одного из них
исключает наступление другого.
Теорема о сумме вероятностей
Если событие С означает, что наступает одно из двух
несовместных событий А или В, то вероятность события С
равна сумме вероятностей событий А и В.
Р(C ) Р( А) Р( В)
Два события называются независимыми, если наступление одного из них
не влияет на вероятность наступления другого события.
Теорема о произведении вероятностей
Если событие С означает совместное наступление двух
независимых событий А и В, то вероятность события С
равна произведению вероятностей событий А и В.
Р(C ) Р( А) Р( В)
Пример 1. В коробке находятся 19 шаров:10 белых, 4 красных и 5 зелёных.
Из коробки наугад вынимают шар. Какова вероятность, что он окажется не белым?
Решение: Пусть событие А – шар оказался красным;
событие В – шар оказался зелёным.
Тогда событие С – вынутый шар не белый (красный или зелёный).
Р(C ) Р( А) Р( В)
Значит
Р( А)
.
4
5
9
; Р( В) Р(С ) .
19
19
19
Ответ:
Р (С )
9
.
19
Пример 2: В одном ящике 15 деталей, из которых 2 детали – нестандартные,
а в другом ящике – 20 деталей, из которых 3 нестандартные. Из каждого ящика
вынимают наугад по одной детали. Какова вероятность, что обе детали
окажутся нестандартными?
Решение: Пусть событие А – из первого ящика вынули нестандартную деталь;
событие В- из второго ящика вынули нестандартную деталь.
Для события А — 15 исходов, 2 из которых благоприятные, а для события В – 20
исходов, 3 из которых благоприятные, значит
Р( А)
2
3
, Р( В) ;
15
20
Р(C ) Р( А) Р( В)
Р(С)=0,02
Ответ: 0,02

10. Задача №3

Бросают две
игральные кости.
Какова
вероятность
появления на его
первой кости
четного числа
очков, а на второй
трех очков?

11. Решение задачи 3:

А- появление на
первой кости
четного числа
очков
В -появление на
второй кости трех
очков
С- появление на
первой кости
четного числа
очков, а на второй
кости нечетного.
С состоит в
совместном
появлении
независимых
событий А и В.

12. Ответьте на вопросы:

1.
2.
3.
4.
5.
Какие события называют
несовместными?
Правило сложения вероятностей.
Свойство вероятностей
противоположных событий.
Какие события называются
независимыми?
Правило умножения вероятностей.

13. Классная работа

П.36 стр. 214
№821; 822; 823;828

14. Домашнее задание:

П.36, №820; 824; 827;
задание из ОГЭ 2020:
Стрелок 4 раза стреляет по мишеням.
Вероятность попадания в мишень при
одном выстреле равна 0,5. Найдите
вероятность того, что стрелок первые
3 раза попал в мишени, а последний
раз промахнулся.

English     Русский Правила

Теоремы сложения и умножения вероятностей. Примеры решения задач



Образовательные онлайн сервисы: теория и практика

• Главная
• Примеры
  • Математический анализ
  • Векторная алгебра и аналитическая геометрия
  • Линейная алгебра
  • Теория вероятностей и математическая статистика
  • Математическое программирование
    Методы оптимизации
  • Математика в экономике
    Экономическая статистика
• Видео-уроки
  • Математический анализ
  • Векторная алгебра и Аналитическая геометрия
  • Линейная алгебра
  • Теория вероятностей и математическая статистика
  • Математическое программирование. Методы оптимизации
• Готовые работы
  • Математический анализ
  • Векторная алгебра и аналитическая геометрия
  • Линейная алгебра
  • Теория вероятностей и математическая статистика
  • Математическое программирование
    Методы оптимизации
  • Математика в экономике
    Экономическая статистика
  • Другое
• Контакты

Полезные материалы:

• Учебники
• Справочники
• Онлайн калькуляторы

• Помощь в решении
• Онлайн занятия в Zoom

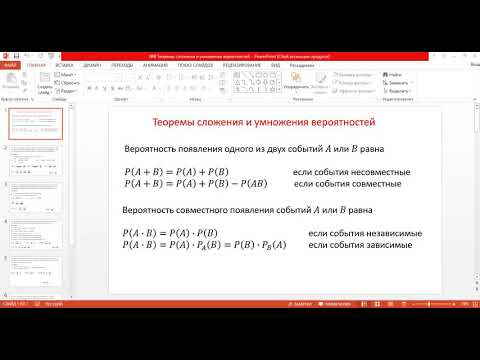
Теоремы сложения и умножения вероятностей

Основные понятия
События называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании. В противном случае они называются совместными.
Полной группой называют совокупность событий, объединение которых есть событие достоверное.

Противоположными называют два единственно возможных события, образующих полную группу.
События называются зависимыми, если вероятность появления одного из них зависит от наступления или ненаступления других событий.
События называются независимыми, если вероятность одного из них не зависит от наступления или ненаступления других.
Теорема сложения вероятностей несовместных событий
Р(A+B)=Р(A)+Р(B),
где А, В — несовместные события.

Теорема сложения вероятностей совместных событий
Р(A+B)=Р(A)+Р(B)-P(AB), где А и В — совместные события.

Теорема умножения вероятностей независимых событий
,
где А и В независимые события.
Теорема умножения вероятностей зависимых событий
Р(АВ)=Р(А)Р_A(B),
где Р_A(B) — вероятность наступления события В при условии, что произошло событие А; А и В- зависимые события.

Задача 1.
Стрелок производит два выстрела по мишени. Вероятность попадания при каждом выстреле 0,8. Составить полную группу событий и найти их вероятности. Решение.
Испытание — Производится два выстрела по мишени.
Событие А — оба раза промахнулся.
Событие В — попал один раз.
Событие С — оба раза попал.
.

Контроль: P(A) + P(B) + P(C) = 1.
Задача 2.
Согласно прогнозу метеорологов Р(дождь)=0,4; Р(ветер)=0,7; Р(дождь и ветер)=0,2. Какова вероятность того, что будет дождь или ветер? Решение. По теореме сложения вероятностей и в силу совместности предложенных событий имеем:
Р(дождь или ветер или то и другое)=Р(дождь) +Р(ветер) –Р(дождь и ветер)=0,4+0,7-0,2=0,9.

Задача 3.
На станции отправления имеется 8 заказов на отправку товара: пять – внутри страны, а три – на экспорт. Какова вероятность того, что два выбранных наугад заказа окажутся предназначенными для потребления внутри страны? Решение. Событие А – первый взятый наугад заказ – внутри страны. Событие В – второй тоже предназначен для внутреннего потребления. Нам необходимо найти вероятность  Тогда по теореме об умножении вероятностей зависимых событий имеем

Задача 4.
Из партии изделий товаровед наудачу отбирает изделия высшего сорта. Вероятность того, что выбранная вещь окажется высшего сорта равна, 0,8; первого сорта – 0,7; второго сорта – 0,5. Найти вероятность того, что из трех наудачу отобранных изделий будут:
а) только два высшего сорта;

б) все разные. Решение. Пусть событие  — изделие высшего сорта; событие — изделие первого сорта; событие — изделие второго сорта.
По условию задачи ; ;  События — независимы.
а) Событие А – только два изделия высшего сорта будет выглядеть так тогда

б) Событие В – все три изделия различны — выразим так:, тогда .
Задача 5.
Вероятности  попадания в цель при стрельбе из трех орудий таковы: p1=0,8;  p2=0,7;  p3=0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий. Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события  (попадание первого орудия),  (попадание второго орудия) и  (попадание третьего орудия) независимы в совокупности.
Вероятности событий, противоположных событиям  (т.е. вероятности промахов), соответственно равны:

Искомая вероятность
Задача 6.
В типографии имеется 4 печатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина (событие А). Решение. События «машина работает» и «машина не работает» (в данный момент) – противоположные, поэтому сумма их вероятностей равна единице:
Отсюда вероятность того, что машина в данный момент не работает, равна
Искомая вероятность . Задача 7. В читальном зале имеется 6 учебников по теории вероятностей , из которых три в переплете . Библиотекарь наудачу взял два учебника. Найти вероятность того, что оба учебника окажутся в переплете.

Решение. Рассмотрим следующие события:
А1- первый взятый учебник в переплете;
A2- второй взятый учебник в переплете.
Событие, состоящее в том, что оба взятых учебника в переплете . События А1 и А2 являются зависимыми, так как вероятность наступления события А2 зависит от наступления события А1. Для решения указанной задачи воспользуемся теоремой умножения вероятностей зависимых событий: .
Вероятность наступления события А1  p(A1) в соответствии с классическим определением вероятности:
P(A1)=m/n=3/6=0,5.
Вероятность наступления события А2 определяется условной вероятностью наступления события А2 при условии наступления события А1 , т.е. (A2)==0,4.
Тогда искомая вероятность наступления события:
P(A)=0,5*0,4=0,2.



Задать вопрос

Заказать помощь

Отзывы

+7-911-7987704

vk.com/id286009794

Написать в Whatsapp

Написать в Viber

@matem96

Skype: matem96.ru



Расчет вероятностей с использованием правил сложения и умножения

Правило сложения

Правило сложения вероятностей — это правило определения, используемое для нахождения вероятности того, что произойдет событие A или событие B. Это связано с использованием союза «или». Например,

• Мы можем захотеть найти вероятность того, что на правом кубике выпадет 3 или 6
• Страховая компания может захотеть определить вероятность того, что претензия исходит от надежного страхователя или претензия превышает 5000 долларов.

Существует две версии правила добавления в зависимости от того, являются ли задействованные события взаимоисключающими (не имеют общих элементов) или невзаимоисключающими (совместно используемые элементы).

Давайте посмотрим, как выглядит каждая версия.

1.1 Правило добавления для невзаимоисключающих событий

Не взаимоисключающие события — это события, которые могут произойти одновременно с . На языке вероятностей говорят, что такие события имеют некоторые общие элементы. Примеры включают проигрыш и выигрыш в игре в футбол, вождение автомобиля и прослушивание музыки или роды днем ​​и рождение девочки. Более практические примеры в области финансов и страхования включают владение домом и наличие действующего страхового полиса, наличие кредитной карты при одновременном обслуживании автокредита или неуплату страхового взноса и попадание в аварию.

Когда два события, A и B, не являются взаимоисключающими, правило сложения говорит нам, что вероятность того, что A или B произойдут, равна сумме вероятностей

того, что либо событие произойдет минус вероятность того, что произойдет и то, и другое:

$$ P(A \чашка B) = P(A) + P(B) − P(A \cap B) $$

Последний член, \(P(A \cap B)\), входит в уравнение дважды, т. е. один раз в P(A) и один раз в P(B). Таким образом, мы должны вычесть это один раз, чтобы оно не было двойной счет .

Диаграмма Венна прекрасно иллюстрирует идею двойного счета. Пересечение между A и B необходимо вычесть при рассмотрении вероятности A или B.

$$ \begin{align*} \textbf{Рисунок 1.1.1 – }& \textbf{Правило сложения для невзаимоисключающих событий} \\ & \textbf{События} \end{align*} $$

Пример 1.1.1

Допустим, вы вынули одну карту из обычной колоды карт. Какова вероятность того, что карта туз или сердце?

Пусть событие A — выпадение туза, а событие B — выпадение червы.

\(P(A) = \frac {4}{52}\) и \(P(B) = \frac {13}{52}\)

\(P(A \text{ и } B) = \frac {1}{52}\)

Эти два события не исключают друг друга, потому что всегда есть шанс, что карта окажется и тузом, и червой.

Таким образом,

$$ \begin{align*} P(A \cup B) & = P(A) + P(B) − P(A \cap B) \\ & = \frac {4}{52} + \frac {13}{52} – \frac {1}{52} \\ & = \frac {16}{52} = \frac {4}{13} \end{align*} $$

Примечание. В стандартной колоде карт четыре масти: черви, трефы, пики и бубны. В каждой масти по тринадцать карт: туз, 2, 3, 4, 5, 6, 8, 9, 10, валет, дама и король. Таким образом, во всей колоде всего 52 карты.

Пример 1.1.2

Гендерная разбивка в математическом классе из 40 учеников: 25 мальчиков и 15 девочек. На экзамене в конце года 12 мальчиков и 5 девочек получили пятерку. Если бы мы выбрали случайного ученика из класса, какова была бы вероятность выбрать мальчика или отличника?

Пусть G — событие выбора девушки, а A — событие выбора отличника.

\(P(G) =\frac {15}{40}\) и \(P(A) = \frac {17}{40}\)

Вероятность выбора девушки, получившей оценку А, равна \(\frac {5}{40}\), т. е.

\(P(G \text{ и } A) = \frac {5}{40} \)

Эти два события не исключают друг друга, потому что всегда есть шанс, что выбранная ученица будет и девушкой, и отличницей.

Таким образом,

$$ \begin{align*} P(G \cup A) & = P(G) + P(A) − P(G \cap A) \\ & = \frac {15}{40} + \frac {17}{40} – \frac {5}{40} \\ & = \frac {27}{40} \end{align*} $$

Пример 1. 1.3

В консалтинговой фирме работает 100 человек. 51 из них имеют степень в области финансов, 63 — в области экономики и 28 — в обеих сферах. Какова вероятность того, что случайно выбранный работник имеет высшее финансовое или экономическое образование?

Пусть F и E — события, свидетельствующие о том, что сотрудник имеет высшее финансовое и экономическое образование соответственно.

Наш интерес равен \(P(F \cup E)\)

$$ \begin{align*} P(F \cup E) & = P(F) + P(E) − P(F \cap E) \\ & = 0,51 + 0,63 – 0,28 \\ & = 0,86 = 86\% \end{align*} $$

Примечание. Для трех невзаимоисключающих событий A, B и C правило сложения выглядит следующим образом:

$$ \begin{align*} P(A \чашка B \чашка C) & = {P(A) + P(B) + P(C) – P(A \cap B) – P(B \cap C)} \\ & {- P(A \cap C) + P(A \cap B \cap C)} \end{align*} $$

Вопрос 1.1.1

Компания по страхованию жизни подвергает потенциальных страхователей медицинскому осмотру разного уровня в зависимости от определенных факторов, таких как возраст и статус курения человека. Вероятность того, что посещение Life Office не приведет ни к анализу, ни к специалисту, составляет 50%. Из тех, кто обращается в Life Office, 25% направляют к специалистам, а 35% требуют лабораторных исследований. 9В)\)

$$ P(L \cap S) = 0,35 + 0,25 – 1 + 0,50 = 0,10 $$

1.2 Правило добавления для взаимоисключающих событий

Взаимоисключающие — это термин, описывающий два или более события, которые не могут произойти одновременно . В большинстве случаев это означает ситуацию, когда один исход заменяет другой. Бросание игральных костей является основным примером. Невозможно одновременно выбросить и четверку, и шестерку. Точно так же получение четырех на начальном броске не влияет на то, выпадет ли последующий бросок на шестерку. Все броски игральной кости независимы.

Когда два события, A и B, являются взаимоисключающими, правило сложения говорит нам, что вероятность того, что произойдет A или B , равна сумме вероятностей того, что либо событие произойдет.

$$ P(A \чашка B) = P(A) + P(B) $$

Пример 1.2.1

Спиннер состоит из четырех равных частей, каждая из которых окрашена в желтый, синий, оранжевый и черный цвета. Насколько вероятно, что счетчик остановится на желтом или синем после одного вращения?

Пусть:

Y = событие, когда счетчик приземляется на желтый

B = событие, когда спиннер приземляется на красное

\(P(Y) =\frac {1}{4}\)

\(P(B) = \frac {1}{4} \)

Все четыре раздела не могут происходить одновременно, поэтому

$$ P(A \cup B) = P(A) + P(B) = \frac {1}{4} + \frac {1}{4} = \frac {1}{2} $$

Пример 1.2.2

Какова вероятность того, что из колоды из 52 игральных карт выпадет валет или дама?

Пусть J представляет событие выпадения валета, а B представляет событие выпадения дамы.

$$ P(J \cup B) = P(J) + P(B) = \frac {4}{52} + \frac {4}{52} = \frac {8}{52} $$

Вероятность того, что два события произойдут вместе

Вероятность того, что два события произойдут вместе: обзор или добавить вероятности.

Выяснение того, есть ли у вас зависимые события (одно событие влияет на другое) или независимые (они не влияют друг на друга)

Посмотрите видео с обзором и примерами:

Вероятность одновременного возникновения двух событий

Посмотрите это видео на YouTube.

Видео не видно? Кликните сюда.

Должен ли я умножать или складывать вероятности?

Вы бы добавили вероятности, если хотите узнать, будет ли одно событие или может произойти другое. Например, если вы бросаете игральную кость и хотите узнать вероятность того, что выпадет 1 или и 6, то вы должны сложить вероятности:

• Вероятность выпадения 1: 1/6
• Вероятность выпадения 6:1/6

Таким образом, вероятность выпадения 1 или 6 равна 1/6 + 1/6 = 2/6 = 1/3.

Вероятность того, что оба события одновременно произойдут на одном кубике, равна нулю, по крайней мере, при одном броске. Но если вы хотите узнать вероятность того, что выпадет 1, а затем , выбрасывая 6, вот тогда вы должны умножить (вероятность будет 1/6 * 1/6 = 1/36).

Изучение того, когда складывать или умножать, может привести к путанице! Лучший способ узнать, когда складывать, а когда умножать, — решить как можно больше вероятностных задач. А вообще:

• Если у вас в формулировке есть «или», добавьте вероятности.
• Если в формулировке есть «и», умножьте вероятности.

Это просто общее правило: бывают исключения!

Зависимое и независимое

Зависимые события связаны друг с другом. Например:

• Чтобы выиграть в Монополию, вам нужно сыграть в игру
• Чтобы найти парковочное место, вам нужно проехать
• Выбор двух карт из стандартной колоды без замены (первый выбор имеет шанс 1/52, второй 1/51).

Независимые события не связаны; вероятность одного события не влияет на другое. Например:

• Игра в «Монополию» не связана с выигрышем в «Эрудит».
• Выигрыш в лотерею не связан с выигрышем в Монополии.
• Выбор карты и последующий бросок кубика не связаны.

Если вы не уверены в разнице между независимыми и зависимыми событиями, вы можете сначала прочитать эту статью:
Зависимое или независимое событие? как рассказать.

Совет: Найдите в вопросе ключевые фразы, которые говорят вам, является ли событие зависимым или нет. Например, когда вы пытаетесь вычислить вероятность того, что два события произойдут вместе, а фраза «Вне этой группы» или «Из этой группы—» включена, это говорит о том, что событий, вероятно, 9.0002 зависимый .

Вероятность того, что два события произойдут вместе: независимые

Используйте специальную формулу правила умножения. Просто умножьте вероятность первого события на второе. Например, если вероятность события А равна 2/9, а вероятность события В равна 3/9, то вероятность того, что оба события произойдут одновременно, равна (2/9)*(3/9) = 6/81. = 2/27.

Пример задачи: Вероятность получить работу, на которую вы претендуете, составляет 45%, а вероятность того, что вы получите квартиру, на которую вы претендуете, составляет 75%. Какова вероятность получить оба новых места работы и новая машина?

Шаг 1: Преобразуйте проценты двух событий в десятичные дроби. В приведенном выше примере:

• 45% = .45.
• 75% = .75.

Шаг 2: Умножьте десятичные дроби из шага 1 вместе:

0,45 x 0,75 = 0,3375 или 33,75 процента.

Вероятность получить работу и машину 33,75%

Вот и все!

Вероятность того, что два события произойдут вместе: Зависимая

Уравнение, которое вы используете, немного отличается.

P(A и B) = P(A) · P(B|A)

, где P(B|A) просто означает «вероятность B при условии, что A уже произошло».

Пример задачи: Восемьдесят пять процентов сотрудников имеют медицинскую страховку. Из этих 85% 45% имели франшизы выше 1000 долларов. У какого процента людей франшизы превышают 1000 долларов?»

Шаг 1: Преобразуйте проценты двух событий в десятичные дроби. В приведенном выше примере:

• 85% = 0,85.
• 45% = .45.

Шаг 2: Умножьте десятичные дроби из шага 1 вместе:

0,85 x 0,45 = 0,3825 или 38,35 процента.

Вероятность того, что кто-то имеет франшизу более 1000 долларов, составляет 38,35%

Вот как найти вероятность того, что два события произойдут вместе!

Совет: Иногда полезно сделать набросок или рисунок проблемы, чтобы визуализировать то, что вы пытаетесь сделать. На следующей диаграмме показаны группа людей (85 % населения) и подгруппа (45 % населения), что делает более очевидным, что вы должны умножать (потому что, когда вы переводите 45 % из 85 % (имеют страховку с высокие франшизы) к математике вы получаете 0,45 * 0,85).