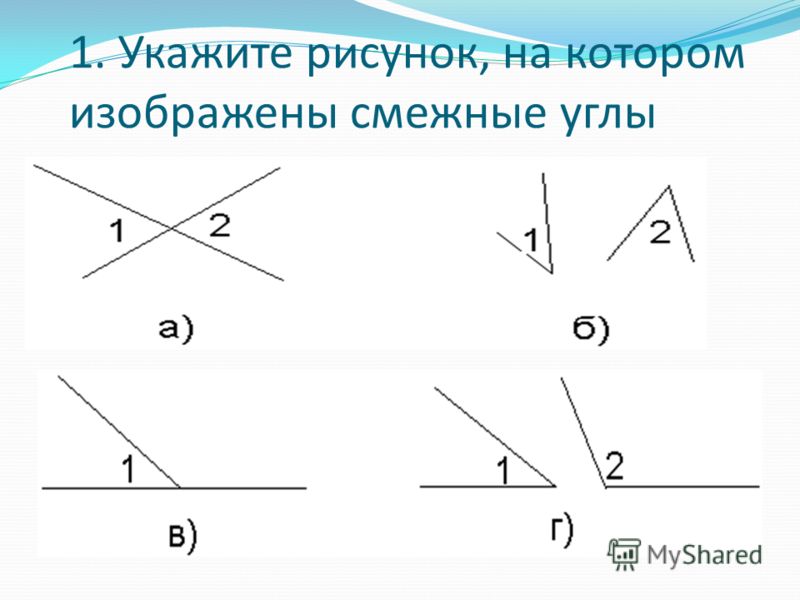
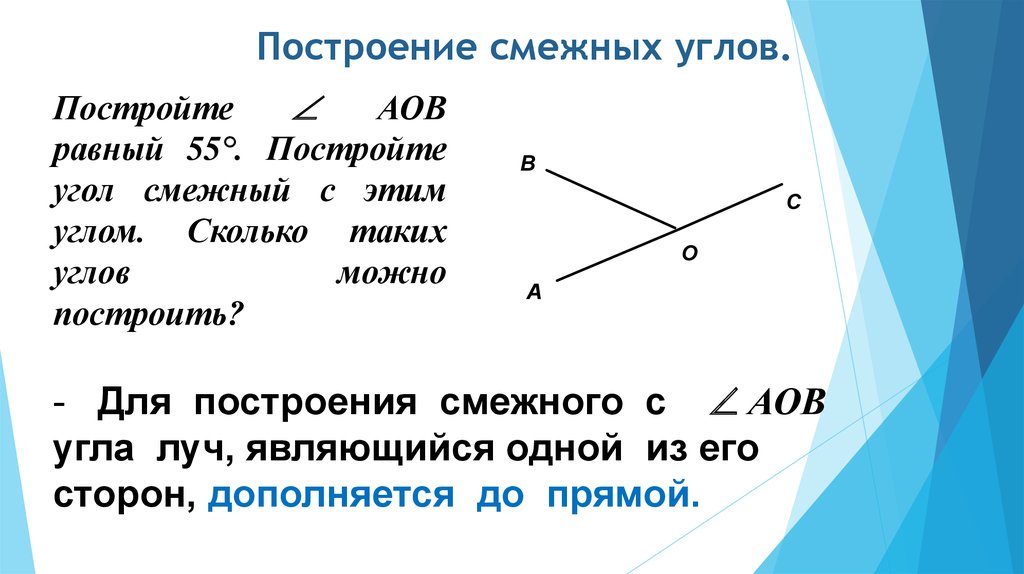
Смежные и вертикальные углы. Перпендикулярные прямые. Какие углы называются смежными чему равна сумма смежных углов
Г Л А В А I.
ОСНОВНЫЕ ПОНЯТИЯ.
§11. СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ.
1. Смежные углы.
Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (черт. 72): / А ВС и / СВD, у которых одна сторона ВС общая, а две другие АВи ВD составляют прямую линию.
Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами.
Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы.
Например, / АDF и / FDВ — углы смежные (черт. 73).
Смежные углы могут иметь самые разнообразные положения (черт. 74).
Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 2d.
Отсюда прямой угол можно определить как угол, равный своему смежному углу.
Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла.
Например, если один из смежных углов равен 3 / 5 d , то второй угол будет равен:
2d — 3 / 5 d = l 2 / 5 d .
2. Вертикальные углы.
Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На чертеже 75 углы EOF и АОС- вертикальные; углы АОЕ и СОF — также вертикальные.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.
Пусть / 1 = 7 / 8 d (черт. 76). Смежный с ним / 2 будет равен 2d — 7 / 8 d , т. е. 1 1 / 8 d .
Таким же образом можно вычислить, чему равны / 3 и / 4.
/ 3 = 2d — 1 1 / 8 d = 7 / 8 d ; / 4 = 2d — 7 / 8 d = 1 1 / 8 d (черт.
Мы видим, что / 1 = / 3 и / 2 = / 4.
Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой.
Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными.
Убедиться в справедливости свойства вертикальных углов необходимо путём рассуждения, путём доказательства.
Доказательство можно провести следующим образом (черт. 78):
/ a + / c = 2d ;
/ b + / c = 2d ;
(так как сумма смежных углов равна 2d ).
/ a + / c = / b + / c
(так как и левая часть этого равенства равна 2d , и правая его часть тоже равна 2d ).
В это равенство входит один и тот же угол с .
Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: / a = / b , т. е. вертикальные углы равны между собой.
При рассмотрении вопроса о вертикальных углах мы сначала объяснили, какие углы называются вертикальными, т. е. дали определение вертикальных углов.
Затем мы высказали суждение (утверждение) о равенстве вертикальных углов и в справедливости этого суждения убедились путём доказательства. Такие суждения, справедливость которых надо доказывать, называются теоремами . Таким образом, в данном параграфе мы дали определение вертикальных углов, а также высказали и доказали теорему об их свойстве.
В дальнейшем при изучении геометрии нам постоянно придётся встречаться с определениями и доказательствами теорем.
3. Сумма углов, имеющих общую вершину.
На чертеже 79 / 1, / 2, / 3 и / 4 расположены по одну сторону прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют развёрнутый угол, т. е.
В сумме эти углы составляют развёрнутый угол, т. е.
/ 1+ / 2+/ 3+ / 4 = 2d .
На чертеже 80 / 1, / 2, / 3, / 4 и / 5 имеют общую вершину. В сумме эти углы составляют полный угол, т. е. / 1 + / 2 + / 3 + / 4 + / 5 = 4d .
Упражнения.
1. Один из смежных углов равен 0,72 d. Вычислить угол, составленный биссектрисами этих смежных углов.
2. Доказать, что биссектрисы двух смежных углов образуют прямой угол.
3. Доказать, что если два угла равны, то равны и их смежные углы.
4. Сколько пар смежных углов на чертеже 81?
5. Может ли пара смежных углов состоять из двух острых углов? из двух тупых углов? из прямого и тупого угла? из прямого и острого угла?
6. Если один из смежных углов прямой, то что можно сказать о величине смежного с ним угла?
7. Если при пересечении двух прямых линий один угол прямой, то что можно сказать о величине остальных трёх углов?
Два угла размещнные на одной прямой и имеющие одну вершину называются смежными.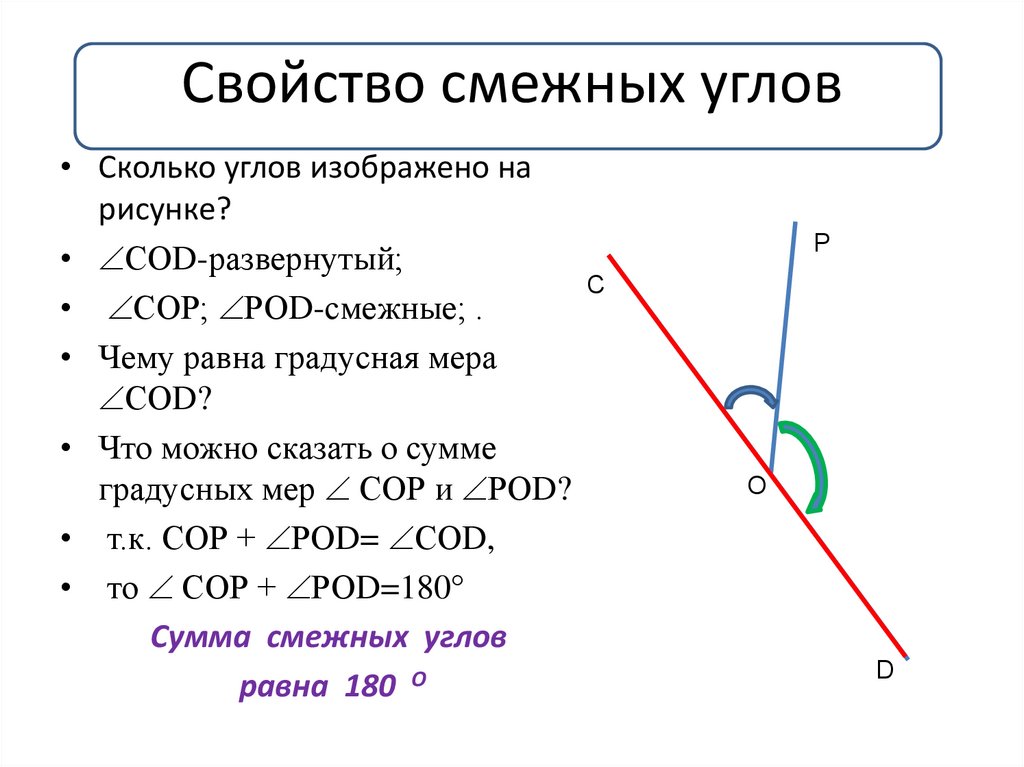
Иначе — если сумма двух углов на одной прямой равна 180 градусам и одна сторона у них общая, то это смежные углы.
1 смежный угол + 1 смежный угол = 180 градусов.
Смежные углы -это два угла, у которых одна сторона общая, а две другие стороны в целом образуют прямую линию.
Сумма двух смежных углов всегда равна 180 градусам. К примеру, если один угол 60 градусов, то второй обязательно будет равен 120 градусам (180-60).
Углы АОС и ВОС являются смежными углами, потому что соблюдается все условия характеристики смежных углов:
1.ОС -общая сторона двух углов
2.АО -сторона угла АОС, ОВ -сторона угла ВОС. Вместе эти стороны образуют прямую линию АОВ.
3.Угла два и сумма их равна 180 градусов.
Вспоминая школьный курс геометрии, про смежные углы мы можем сказать следующее:
у смежных углов — одна сторона общая, а другие две стороны принадлежат одной прямой, то есть находятся на одной прямой. Если по рисунку, то углы СОВ и ВОА — это смежные углы, сумма которых всегда равна 180 , так как они разделяют развернутый угол, а развернутый угол всегда равен 180 .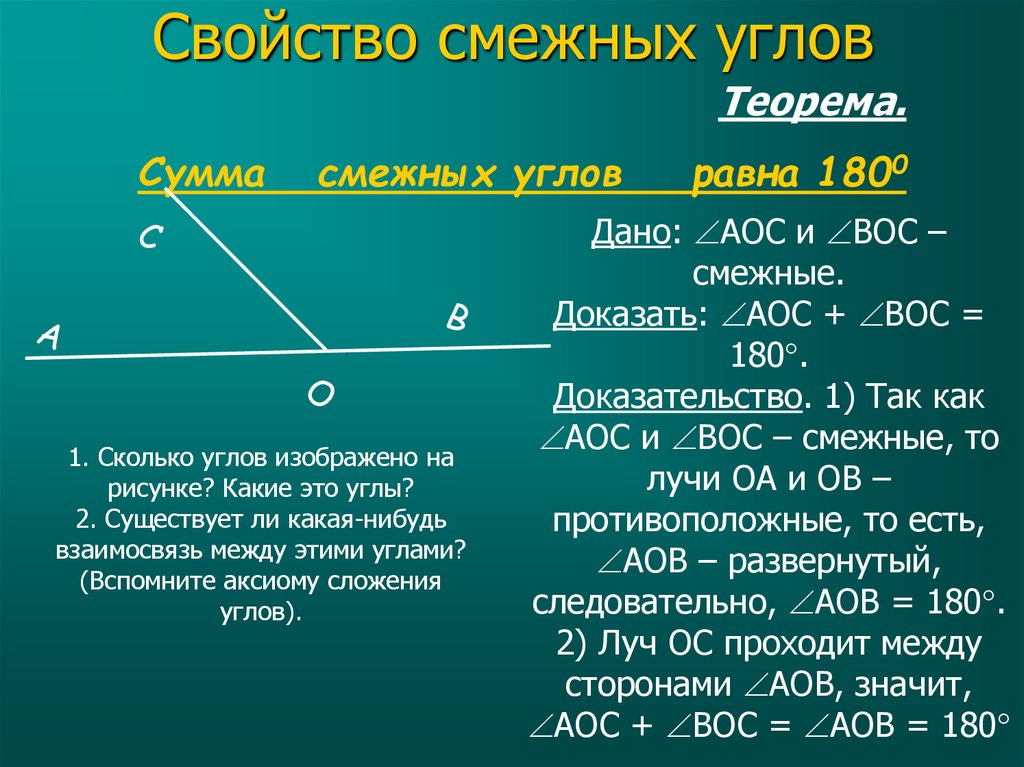
Смежные углы понятие легкое в геометрии. Смежные углы, угол плюс угол дают 180 градусов в общей сумме.
Два смежных угла — это будет один развернутый угол.
Есть еще несколько свойств. Со смежными углами задачи решать и теоремы доказывать легко.
Смежные углы образуются при проведении луча из произвольной точки прямой. Тогда эта произвольная точка оказывается вершиной угла, луч — общей стороной смежных углов, а прямая от которой проведен луч — двумя оставшимися сторонами смежных углов. Смежные углы могут быть как одинаковыми в случае перпендикуляра, так и отличатся при наклонном луче. Легко понять, что сумма смежных углов равна 180 градусов или попросту прямой линии. По другому этот угол можно объяснить простым примером — вы сперва шли в одном направлении по прямой, потом передумали, решили вернуться назад и развернувшись на 180 градусов отправились по той же прямой в обратном направлении.
Итак, что же такое смежный угол? Определение:
Смежными называются два угла с общей вершиной и одной общей стороной, причем две другие стороны этих углов лежат на одной прямой.
И небольшой видео урок, где толково показано про смежные углы, вертикальные углы, плюс про перпендикулярные прямые, которые являются частным случаем смежных и вертикальных углов
Смежные углы — это углы, у которых одна сторона общая, а вторая является одной линией.
Смежные углы — это углы, зависящие друг от друга. То есть если общую строну слегка повернуть, то один угол уменьшится на сколько-то градусов и автоматически второй угол увеличится на столько же градусов. Это свойство смежных углов позволяет в Геометрии решать различные задачи и осуществлять доказательства различных теорем.
Общая же сумма смежных углов всегда равна 180 градусов.
Смежные углы это два угла с общей вершиной, одна из сторон которых общая, а оставшиеся стороны лежат на одной прямой (не совпадая).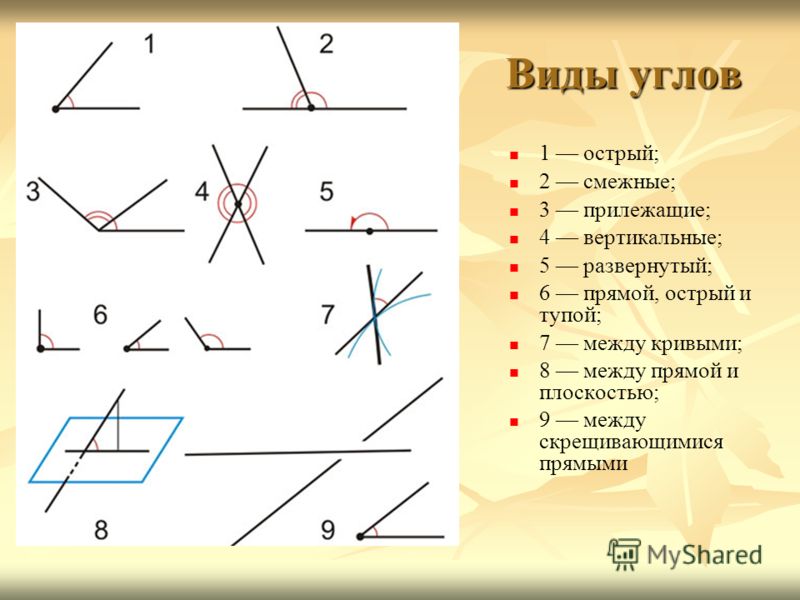 Сумма смежных углов равна ста восьмидесяти градусам. А вообще все это очень легко находится в гугле или учебнике геометрии.
Сумма смежных углов равна ста восьмидесяти градусам. А вообще все это очень легко находится в гугле или учебнике геометрии.
Два угла называются смежными, если у них есть общие вершина и одна сторона, а две другие стороны составляют прямую линию. Сумма смежных углов равна 180 градусам.
На рисунке углы АОВ и ВОС являются смежными.
Смежными называются углы имеющие общую вершину, одну общую сторону, а другие стороны являются продолжением друг друга и образуют развернутый угол. Замечательным свойством смежных углов является — сумма этих углов всегда равна 180 градусам.
Углы с общей вершиной и одной общей стороной в геометрии называются смежными
Сумма смежных углов равна 180 градусов
Нужно отметить тот факт, что у смежных углов синусы равны
Что бы узнать больше про смежные углы — читайте вот здесь
2)Сколько общих точек могут иметь 2 прямые?
3)Объясните что такое отрезок?
4)Объясните что такое луч.Как обозначаются лучи?
5)Какая фигура называется углом?Объясните что такое вершина и стороны угла?
6)Какой угол называется развернутым?
7)Какие фигуры называют равными?
8)Объясните как сравнить 2 отрезка
9)Какая точка называется серединой отрезка?
10)Объясните как сравнить 2 угла.
11)Какой луч называется биссектрисой угла?
12)Точка С делит отрезок АВ на 2 отрезка.Как найти длину отрезка АВ если известны длины отрезков АС и СВ?
14)Что такое градусная мера угла?
15)Луч ОС делит угол АОВ на 2 угла. Как найти градусную меру угла АОВ если известны градусные меры углов АОС и СОВ?
16)Какой угол называется острым?прямым?тупым?
17)Какие углы называют смежными?Чему равна сумма смежных углов?
18)Какие углы называются вертикальными?Каким свойством обладают вертикальные углы?
19)Какие прямы называются перпендикулярными?
20)Объясните почему 2 прямые перпендикулярные к 3-ей не пересекаются?
21)Какие приборы применяют для построения прямых углов на местности? 1сколько прямых можно провести через две точки?
2сколько общих точек могут иметь две прямые?
3обьясните что такое отрезок
4обьясните что такое луч.Как обозначаются лучи?
5какая фигура называется углом? обьясните что такое вершина и стороны угла
6какой угол называется развёрнутым
7какие фигуры называются равными
8обьясните как сравнить два отрезка
9какая точка называется серединой отрезка
10обьясните как сравнить два угла
11какой луч называется биссектрисой угла
12точка с делит отрезок аб на два отрезка.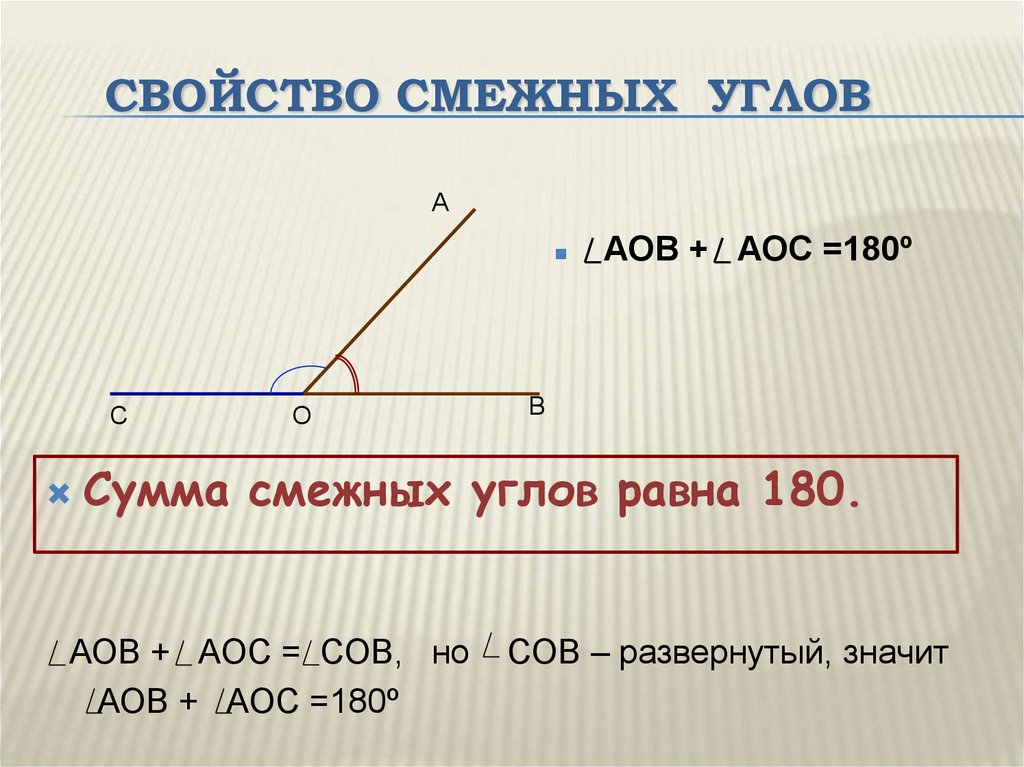 Как найти длину отрезка аб если известны длины отрезков ас и сб
Как найти длину отрезка аб если известны длины отрезков ас и сб
13какими инструментами пользуются для измерения расстояний
14что такое градусная мера угла
15луч ос делит угол аоб на два угла.Как найти градусную меру угла аоб,если известны меры углов аос в соб
16какой угол называется острым?,прямым?,тупым?.
17какие углы называются смежными?чему равна сумма смежных углов?
18какие углы называются вертикальными?каким свойством обладают вертикальные углы
19какие прямые называются перпендикулярными
20обьясните почему две прямые перпендикулярные к третьей не пересикаются
21какие приборы применяют для построения прямых углов на местности?
вертикальными каким свойством обладают вертикальные углы 5)
Помогите плиз, !! плизз=**7. Докажите, что если две параллельные прямые пересекаются третьей прямой, то внутренние накрест лежащие углы равны, а сумма внутренних односторонних углов равна 180 градусов.
8. Докажите, что две прямые, перпендикулярные третьей, параллельны. Если прямая перепендикулярна одной из двух параллелных прямых, то она перепендикулярна и другой.
9. Докажите, что сумма углов треугольника равна 180 градусов.
10. Докажите, что у любого треугольника по крайней мере два угла острые.
11. Что такое внешний угол треугольника?
12. Докажите, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
13. Докажите, что внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
14. Какой треугольник называется прямоугольным?
15. Чему равна сумма острых углов прямоугольного треугольника?
16. Какая сторона прямоугольного треугольника называется гипотенузой? Какие стороны называются катетами?
17. Сформулируйте признак равенства прямоугольных треугольников по гипотенузе и катету.
18. Докажите, что из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один.
19. Что называется расстоянием от точки до прямой?
20. Объясните, что такое расстояние между параллельными прямыми.
Вопрос 1. Какие углы называются смежными?
Ответ. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
На рисунке 31 углы (a 1 b) и (a 2 b) смежные. У них сторона b общая, а стороны a 1 и a 2 являются дополнительными полупрямыми.
Вопрос 2. Докажите, что сумма смежных углов равна 180°.
Ответ. Теорема 2.1. Сумма смежных углов равна 180°.
Доказательство. Пусть угол (a 1 b) и угол (a 2 b) — данные смежные углы (см. рис.31). Луч b проходит между сторонами a 1 и a 2 развёрнутого угла. Поэтому сумма углов (a 1 b) и (a 2 b) равна развёрнутому углу, т. е. 180°. Что и требовалось доказать.
Вопрос 3. Докажите, что если два угла равны, то смежные с ними углы также равны.
Ответ.
Из теоремы 2. 1 следует, что если два угла равны, то смежные с ними углы равны.
1 следует, что если два угла равны, то смежные с ними углы равны.
Допустим, углы (a 1 b) и (c 1 d) равны. Нам нужно доказать, что углы (a 2 b) и (c 2 d) тоже равны.
Сумма смежных углов равна 180°. Из этого следует, что a 1 b + a 2 b = 180° и c 1 d + c 2 d = 180°. Отсюда, a 2 b = 180° — a 1 b и c 2 d = 180° — c 1 d. Так как углы (a 1 b) и (c 1 d) равны, то мы получаем, что a 2 b = 180° — a 1 b = c 2 d. По свойству транзитивности знака равенства следует, что a 2 b = c 2 d. Что и требовалось доказать.
Вопрос 4. Какой угол называется прямым (острым, тупым)?
Ответ. Угол, равный 90°, называется прямым углом.
Угол, меньший 90°, называется острым углом.
Угол, больший 90° и меньший 180°, называется тупым.
Вопрос 5. Докажите, что угол, смежный с прямым, есть прямой угол.
Ответ. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом, есть прямой угол: x + 90° = 180°, x= 180° — 90°, x = 90°.
Вопрос 6. Какие углы называются вертикальными?
Какие углы называются вертикальными?
Ответ. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.
Вопрос 7. Докажите, что вертикальные углы равны.
Ответ. Теорема 2.2. Вертикальные углы равны.
Доказательство. Пусть (a 1 b 1) и (a 2 b 2)- данные вертикальные углы (рис. 34). Угол (a 1 b 2) является смежным с углом (a 1 b 1) и с углом (a 2 b 2). Отсюда по теореме о сумме смежных углов заключаем, что каждый из углов (a 1 b 1) и (a 2 b 2) дополняет угол (a 1 b 2) до 180°, т.е. углы (a 1 b 1) и (a 2 b 2) равны. Что и требовалось доказать.
Вопрос 8. Докажите, что если при пересечении двух прямых один из углов прямой, то остальные три угла тоже прямые.
Ответ. Предположим, что прямые AB и CD пересекают друг друга в точке O. Предположим, что угол AOD равен 90°. Так как сумма смежных углов равна 180°, то получаем, что AOC = 180°-AOD = 180°- 90°=90°. Угол COB вертикален углу AOD, поэтому они равны. То есть угол COB = 90°. Угол COA вертикален углу BOD, поэтому они равны. То есть угол BOD = 90°. Таким образом, все углы равны 90°, то есть они все – прямые. Что и требовалось доказать.
То есть угол COB = 90°. Угол COA вертикален углу BOD, поэтому они равны. То есть угол BOD = 90°. Таким образом, все углы равны 90°, то есть они все – прямые. Что и требовалось доказать.
Вопрос 9. Какие прямые называются перпендикулярными? Какой знак используется для обозначения перпендикулярности прямых?
Ответ. Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Перпендикулярность прямых обозначается знаком \(\perp\). Запись \(a\perp b\) читается: «Прямая a перпендикулярна прямой b».
Вопрос 10. Докажите, что через любую точку прямой можно провести перпендикулярную ей прямую, и только одну.
Ответ. Теорема 2.3. Через каждую прямую можно провести перпендикулярную ей прямую, и только одну.
Доказательство. Пусть a — данная прямая и A — данная точка на ней. Обозначим через a 1 одну из полупрямых прямой a с начальной точкой A (рис. 38). Отложим от полупрямой a 1 угол (a 1 b 1), равный 90°. Тогда прямая, содержащая луч b 1 , будет перпендикулярна прямой a.
Тогда прямая, содержащая луч b 1 , будет перпендикулярна прямой a.
Допустим, что существует другая прямая, тоже проходящая через точку A и перпендикулярная прямой a. Обозначим через c 1 полупрямую этой прямой, лежащую в одной полуплоскости с лучом b 1 .
Углы (a 1 b 1) и (a 1 c 1), равные каждый 90°, отложены в одну полуплоскость от полупрямой a 1 . Но от полупрямой a 1 в данную полуплоскость можно отложить только один угол, равный 90°. Поэтому не быть другой прямой, проходящей через точку A и перпендикулярной прямой a. Теорема доказана.
Вопрос 11. Что такое перпендикуляр к прямой?
Ответ. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называется основанием перпендикуляра.
Вопрос 12. Объясните, в чём состоит доказательство от противного.
Ответ. Способ доказательства, который мы применили в теореме 2. 3, называется доказательством от противного. Этот способ доказательства состоит в том, что мы cначала делаем предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждений, опираясь на аксиомы и доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.
3, называется доказательством от противного. Этот способ доказательства состоит в том, что мы cначала делаем предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждений, опираясь на аксиомы и доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.
Вопрос 13. Что называется биссектрисой угла?
Ответ. Биссектрисой угла называется луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам.
Что такое смежный угол
Угол – это геометрическая фигура (рис.1), образованная двумя лучами OA и OB (стороны угла), исходящими из одной точки O (вершина угла).
СМЕЖНЫЕ УГЛЫ — два угла, сумма которых равна 180°. Каждый из этих углов дополняет другой до развернутого угла.
Смежные углы — (Agles adjacets) такие, которые имеют общую вершину и общую сторону. Преимущественно под этим именем подразумеваются такие углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через.
Преимущественно под этим именем подразумеваются такие углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через.
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
рис. 2
На рисунке 2 углы a1b и a2b смежные. У них общая сторона b, а стороны a1, a2 — дополнительные полупрямые.
рис. 3
На рисунке 3 изображена прямая AB, точка C расположена между точками A и B. Точка D — точка не лежащая на прямой AB. Получается, что углы BCD и ACD смежные. У них общая сторона CD, а стороны CA и CB дополнительные полупрямые прямой AB, так как точки A, B разделены начальной точкой C.
Теорема о смежных углах
Теорема: сумма смежных углов равна 180°
Доказательство:
Углы a1b и a2b смежные (см. рис. 2) Луч b проходит между сторонами a1, и a2 развернутого угла. Следовательно, сумма углов a1b и a2b равна развернутому углу, то есть 180°.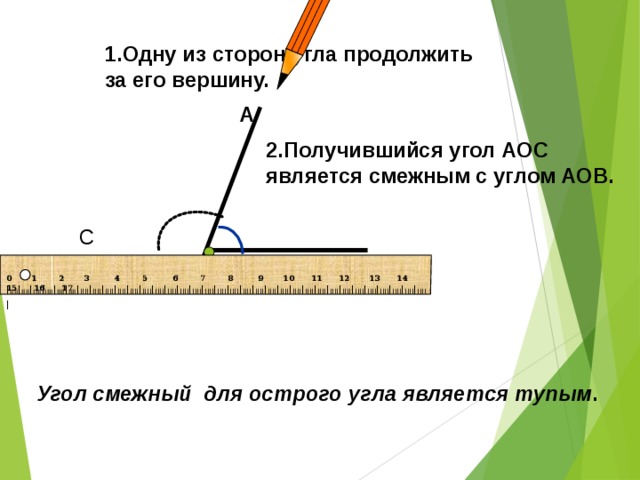 Теорема доказана.
Теорема доказана.
Угол, равный 90° называется прямым. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом также прямой угол. Угол, меньший 90° называется острым, а угол больше 90° — тупым. Так как сумма смежных углов равна 180°, значит угол, смежный с острым углом — тупой угол. А угол смежный с тупым углом — острый угол.
Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.
Определение 1. Углом называется часть плоскости, ограниченная двумя лучами с общим началом.
Определение 1.1. Углом называют фигуру, состоящую из точки — вершины угла — и двух различных полупрямых, исходящих из этой точки, — сторон угла.
Например, угол ВОС на рис1 Рассмотрим сначала две пересекающиеся прямые. При пересечении прямые образуют углы. Есть частные случаи:
Определение 2. Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым.
Определение 3. Прямой угол — это угол величиной в 90 градусов.
Определение 4. Угол, меньший 90 градусов, называется острым углом.
Определение 5. Угол, больший 90 градусов и меньший 180 градусов, называется тупым углом.
пересекающиеся прямые.
Определение 6. Два угла, одна сторона которых общая, а другие стороны лежат на одной прямой, называются смежными.
Определение 7. Углы, стороны которых продолжают друг друга, называются вертикальными углами.
На рисунке 1:
смежные: 1 и 2; 2 и 3; 3 и 4; 4 и 1
вертикальные: 1 и 3; 2 и 4
Теорема 1. Сумма смежных углов равна 180 градусов.
Для доказательства рассмотрим на рис. 4 смежные углы АОВ и ВОС. Их суммой является развернутый угол АОС. Поэтому сумма данных смежных углов равна 180 градусов.
рис. 4
Связь математики с музыкой
«Раздумывая об искусстве и науке, об их взаимных связях и противоречиях, я пришел к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая духовная деятельность человека и, что между ними размещается все, что человечество создало в области науки и искусства. «
«
Г. Нейгауз
Казалось бы, искусство — весьма отвлеченная от математики область. Однако связь математики и музыки обусловлена как исторически, так и внутренне, несмотря на то, что математика — самая абстрактная из наук, а музыка — наиболее отвлеченный вид искусства.
Консонанс определяет приятное для слуха звучание струны
В основе этой музыкальной системы были два закона, которые носят имена двух великих ученых — Пифагора и Архита. Вот эти законы:
1. Две звучащие струны определяют консонанс, если их длины относятся как целые числа, образующие треугольное число 10=1+2+3+4, т.е. как 1:2, 2:3, 3:4. Причем, чем меньше число n в отношении n:(n+1) (n=1,2,3), тем созвучнее получающийся интервал.
2. Частота колебания w звучащей струны обратно пропорциональна ее длине l .
w = a: l ,
где а — коэффициент, характеризующий физические свойства струны.
Так же предложу вашему внимаю забавную пародию про спор двух математиков =)
Геометрия вокруг нас
Геометрия в нашей жизни имеет немаловажное значение. Ввиду того, что когда оглядеться вокруг, то не сложно будет заметить, что нас окружают различные геометрические фигуры. Мы с ними сталкиваемся повсюду: на улице, в классе, дома, в парке, в спортивном зале, в школьной столовой, в принципе везде, где бы мы с вами не находились.
Но темой сегодняшнего урока являются смежные угли. Поэтому давайте оглянемся вокруг и попытаемся в этом окружении найти углы. Если вы внимательно посмотрите в окно, то можете увидеть, что некоторые ветки дерева образуют смежные углы, а в перегородках на воротах можно заметить множество вертикальных углов.
Приведите свои примеры смежных углов, которые вы наблюдаете в окружающей обстановке.
Ввиду того, что когда оглядеться вокруг, то не сложно будет заметить, что нас окружают различные геометрические фигуры. Мы с ними сталкиваемся повсюду: на улице, в классе, дома, в парке, в спортивном зале, в школьной столовой, в принципе везде, где бы мы с вами не находились.
Но темой сегодняшнего урока являются смежные угли. Поэтому давайте оглянемся вокруг и попытаемся в этом окружении найти углы. Если вы внимательно посмотрите в окно, то можете увидеть, что некоторые ветки дерева образуют смежные углы, а в перегородках на воротах можно заметить множество вертикальных углов.
Приведите свои примеры смежных углов, которые вы наблюдаете в окружающей обстановке.
Задание 1.
1. Вот на столе на книжной подставке стоит книга. Какой угол она образует?
2. А вот ученик работает за ноутбуком. Какой угол вы видите здесь?
3. Какой угол образует фото рамка на подставке?
4. Как вы думаете, возможно ли, чтобы два смежных угла были равными?
Задание 2.
Перед вами изображена геометрическая фигура.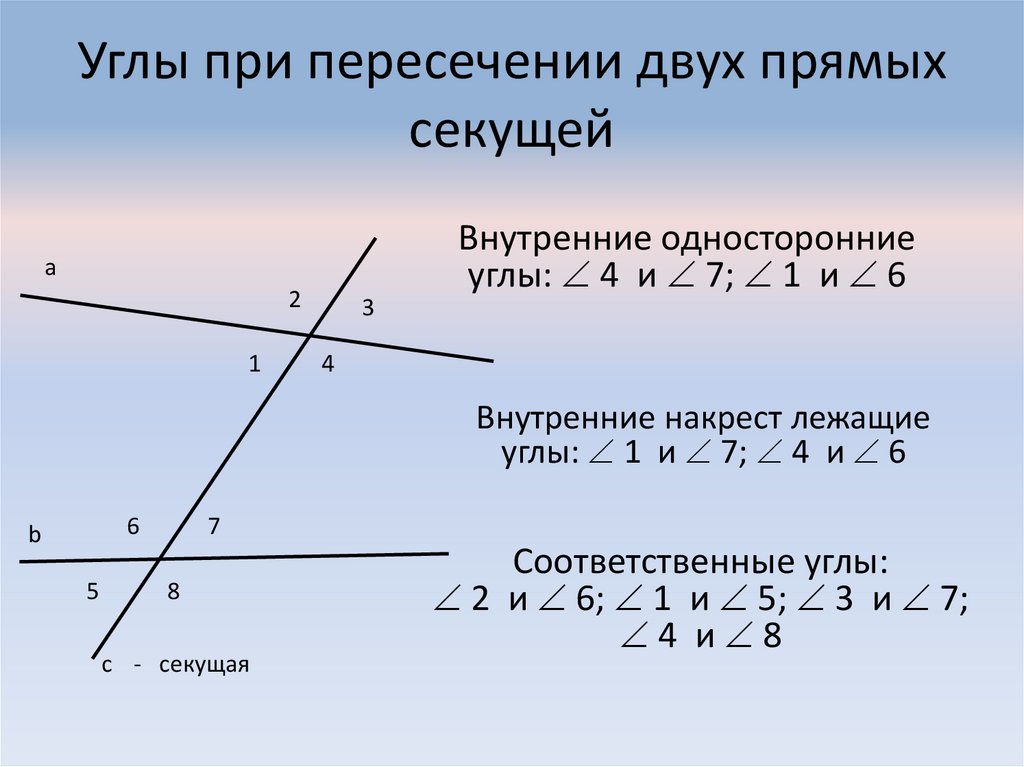 Что это за фигура, назовите ее? А теперь назовите все смежные углы, которые вы можете увидеть на этой геометрической фигуре.
Что это за фигура, назовите ее? А теперь назовите все смежные углы, которые вы можете увидеть на этой геометрической фигуре.
Задание 3.
Перед вами изображение рисунка и картины. Рассмотрите их внимательно и скажите, какие виды улов вы видите на картине, а какие углы на рисунке.
Решение задач
1) Даны два угла, относящиеся друг к другу как 1: 2, а смежные с ними — как 7: 5. Нужно найти эти углы.2) Известно, что один из смежных углов больше другого в 4 раза. Чему равны смежные углы?
3) Необходимо найти смежные углы, при условии, что один из них на 10 градусов больше от второго.
Математический диктант на повторение ранее выученного материала
1) Выполните рисунок: прямые a I b пересекаются в точке А. Отметьте меньший из образованных углов цифрой 1, а остальные углы – последовательно цифрами 2,3,4; дополняющие лучи прямой а — через а1 и а2, а прямой b — через b1 i b2.2) Пользуясь выполненным рисунком, впишите нужные значения и объяснения в места пропусков в тексте:
а) угол 1 и угол ….
 смежные, поскольку…
смежные, поскольку…б) угол 1 и угол …. вертикальные, поскольку…
в) если угол 1 = 60°, то угол 2 = …, потому что…
г) если угол 1 = 60°, то угол 3 = …, потому что…
Решите задачи:
1. Может ли сумма 3-х углов, образованных при пересечении 2-х прямых, равняться 100°? 370°?
2. На рисунке найдите все пары смежных углов. А теперь вертикальных углов. Назовите эти углы.
3. Нужно найти угол, когда он втрое больше, чем смежный с ним.
4. Две прямые пересеклись между собой. В результате этого пересечения образовались четыре угла. Определите величину любого из них, при условии что:
а) сумма 2-х углов из четырех 84°;
б) разность 2-х углов из них равна 45°;
в) один угол в 4 раза меньше чем второй;
г) сумма трех из данных углов равна 290°.
Итог урока
1. назовите углы, которые образуются при пересечении 2-х прямых?
2. Назовите все возможные пары углов, находящихся на рисунке, и определите их вид.
Домашнее задание:
1. Найдите отношение градусных мер смежных углов, когда один из них на 54° больше второго.
2. Найдите углы, которые образуются при пересечении 2-х прямых, при условии, что один из углов равняется сумме 2-х других углов, смежных с ним.
3. Необходимо найти смежные углы, когда биссектриса одного из них образует со стороной второго угол, который больше чем второй угол на 60°.
4. Разница 2-х смежных углов равна трети от суммы этих двух углов. Определите величины 2-х смежных углов.
5. Разница и сумма 2-х смежных углов относятся как 1: 5 соответственно. Найдите смежные углы.
6. Разница двух смежных составляет 25% от их суммы. Как относятся величины 2-х смежных углов? Определите величины 2-х смежных углов.
Вопросы:
- Что такое угол?
- Какие бывают типы углов?
- Какая особенность смежных углов?
Чему равно сумма смежных углов.
 Вертикальные и смежные углы. Сумма углов, имеющих общую вершину
Вертикальные и смежные углы. Сумма углов, имеющих общую вершинуДва угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.
Сумма смежных углов равна 180°
Теорема 1. Сумма смежных углов равна 180°.
Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .
Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.
Вертикальные углы равны
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).
Теорема 2. Вертикальные углы равны.
Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1
∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.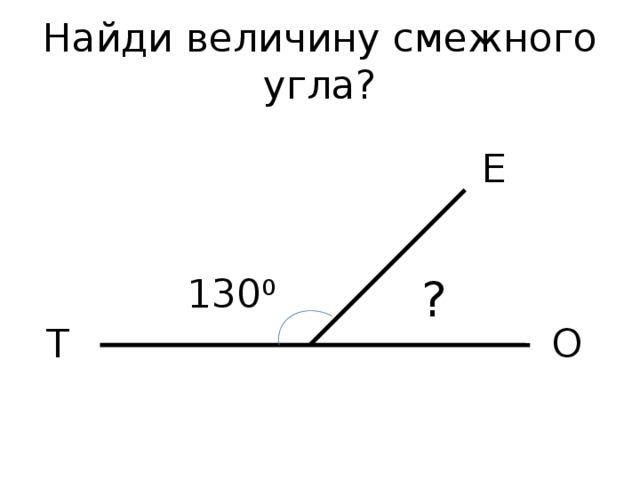
Отсюда заключаем, что ∠ АОВ = ∠ COD.
Следствие 1. Угол, смежный с прямым углом, есть прямой угол.
Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.
АН — перпендикуляр к прямой
Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.
Чертежный угольник
Справедлива следующая теорема.
Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).
Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.
Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».
Пример 1. Один из смежных углов равен 44°. Чему равен другой?
Решение. Обозначим градусную меру другого угла через x , тогда согласно теореме 1.
44° + х = 180°.
Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.
Следовательно, другой угол равен 136°.
Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?
Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1.2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.
∠ АОС = 180° — ∠ COD = 180° — 45° = 135°.
Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.
Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.
Значит, смежные углы равны 45° и 135°.
Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.
Решение. Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол
АОС) смежный с углом COD, и, значит, по теореме 1
Угол BOD (также и угол
АОС) смежный с углом COD, и, значит, по теореме 1
∠ BOD = ∠ АОС = 180° — 50° = 130°.
Как найти смежный угол?
Математика — древнейшая точная наука, которую в обязательном порядке изучают в школах, колледжах, институтах и университетах. Однако, базовые знания всегда закладываются еще в школе. Порой, ребенку задают достаточно сложные задания, а родители не в силах помочь, потому что просто забыли некоторые вещи из математики. Например, как найти смежный угол по величине основного угла и т.п. Задача проста, но может вызвать затруднения при решении из-за незнания того, какие углы называются смежными и как их найти.
Рассмотрим подробнее определение и свойства смежных углов, а также как их вычислить по данным в задаче.
Определение и свойства смежных углов
Два луча, исходящие из одной точки образуют фигуру под названием «плоский угол». При этом эта точка именуется вершиной угла, а лучи являются его сторонами. Если продолжить один из лучей дальше начальной точки по прямой, то образуется еще один угол, который и называется смежным. У каждого угла в этом случае есть два смежных угла, так как стороны угла равнозначны. То есть всегда присутствует еще смежный угол в 180 градусов.
У каждого угла в этом случае есть два смежных угла, так как стороны угла равнозначны. То есть всегда присутствует еще смежный угол в 180 градусов.
К основным свойствам смежных углов относят
- Смежные углы имеют общую вершину и одну сторону;
- Сумма смежных углов равна всегда 180 градусам или числу Пи, если вычисление ведется в радианах;
- Синусы смежных углов всегда равны;
- Косинусы и тангенсы смежных углов равны, но имеют противоположные знаки.
Как найти смежные углы
Обычно даются три вариации задач на нахождение величины смежных углов
- Дана величина основного угла;
- Дано соотношение основного и смежного угла;
- Дана величина вертикального угла.
Каждый вариант задачи имеет свое решение. Рассмотрим их.
Дана величина основного угла
Если в задаче указана величина основного угла, то найти смежный угол очень просто. Для этого достаточно из 180 градусов вычесть величину основного угла, и вы получите величину смежного угла. Данное решение исходит из свойства смежного угла — сумма смежных углов равна всегда 180 градусам.
Данное решение исходит из свойства смежного угла — сумма смежных углов равна всегда 180 градусам.
Если же величина основного угла дана в радианах и в задаче требуется найти смежный угол в радианах, то необходимо вычесть из числа Пи величину основного угла, так как величина полного развернутого угла в 180 градусов равна числу Пи.
Дано соотношение основного и смежного угла
В задаче может быть дано соотношение основного и смежного угла вместо градусов и радиан величины основного угла. В этом случае решение будет выглядеть, как уравнение пропорции:
- Обозначаем долю пропорции основного угла, как переменную «Y».
- Долю относящуюся к смежному углу обозначаем, как переменную «Х».
- Количество градусов, которые приходятся на каждую пропорцию, обозначим, например, «a».
- Общая формула будет выглядеть так — a*X+a*Y=180 или a*(X+Y)=180.
- Находим общий множитель уравнения «a» по формуле a=180/(X+Y).
- Затем полученное значение общего множителя «а» умножаем на долю угла, который необходимо определить.

Таким образом мы можем найти величину смежного угла в градусах. Однако, если необходимо найти величину в радианах, то нужно просто перевести градусы в радианы. Для этого умножаем угол в градусах на число Пи и делим все на 180 градусов. Полученное значение будет в радианах.
Дана величина вертикального угла
Если в задаче не дана величина основного угла, но дана величина вертикального угла, то вычислить смежный угол можно по такой же формуле, что и в первом пункте, где дана величина основного угла.
Вертикальный угол — это угол, который исходит из той же точки, что и основной, но при этом он направлен в строго противоположном направлении. Тем самым получается зеркальное отражение. Это значит, что вертикальный угол по величине равен основному. В свою очередь, смежный угол вертикального угла равен смежному углу основного угла. Благодаря этому можно вычислить смежный угол основного угла. Для этого просто вычитаем из 180 градусов величину вертикального и получаем значение смежного угла основного угла в градусах.
Если же величина дана в радианах, то необходимо вычесть из числа Пи величину вертикального угла, так как величина полного развернутого угла в 180 градусов равна числу Пи.
Также вы можете прочесть наши полезные статьи и .
1. Смежные углы.
Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (рис. 72): ∠АВС и ∠СВD, у которых одна сторона ВС общая, а две другие, АВ и ВD, составляют прямую линию.
Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами.
Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы.
Например, ∠АDF и ∠FDВ — углы смежные (рис. 73).
Смежные углы могут иметь самые разнообразные положения (рис. 74).
Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 180°
Отсюда прямой угол можно определить как угол, равный своему смежному углу.
Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла.
Например, если один из смежных углов равен 54°, то второй угол будет равен:
180° — 54° = l26°.
2. Вертикальные углы.
Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На рисунке 75 углы EOF и АОС- вертикальные; углы АОЕ и СОF — также вертикальные.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.
Пусть ∠1 = \(\frac{7}{8}\) ⋅ 90°(рис. 76). Смежный с ним ∠2 будет равен 180° — \(\frac{7}{8}\) ⋅ 90°, т. е. 1\(\frac{1}{8}\) ⋅ 90°.
Таким же образом можно вычислить, чему равны ∠3 и ∠4.
∠3 = 180° — 1\(\frac{1}{8}\) ⋅ 90° = \(\frac{7}{8}\) ⋅ 90°;
∠4 = 180° — \(\frac{7}{8}\) ⋅ 90° = 1\(\frac{1}{8}\) ⋅ 90° (рис. 77).
Мы видим, что ∠1 = ∠3 и ∠2 = ∠4.
Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой.
Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными.
Убедиться в справедливости свойства вертикальных углов необходимо путём доказательства.
Доказательство можно провести следующим образом (рис. 78):
∠a + ∠c = 180°;
∠b + ∠c = 180°;
(так как сумма смежных углов равна 180°).
∠a + ∠c = ∠b + ∠c
(так как и левая часть этого равенства равна 180°, и правая его часть тоже равна 180°).
В это равенство входит один и тот же угол с .
Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: ∠a = ∠b , т. е. вертикальные углы равны между собой.
3. Сумма углов, имеющих общую вершину.
На чертеже 79 ∠1, ∠2, ∠3 и ∠4 расположены по одну сторону прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют развёрнутый угол, т. е.
В сумме эти углы составляют развёрнутый угол, т. е.
∠1 + ∠2 + ∠3 + ∠4 = 180°.
На чертеже 80 ∠1, ∠2, ∠3, ∠4 и ∠5 имеют общую вершину. В сумме эти углы составляют полный угол, т. е. ∠1 + ∠2 + ∠3 + ∠4 + ∠5 = 360°.
Другие материалы
Геометрия — это весьма многогранная наука. Она развивает логику, воображение и интеллект. Конечно, из-за своей сложности и огромного количества теорем и аксиом, она не всегда нравится школьникам. Кроме этого, существует необходимость постоянно доказывать свои выводы, используя общепринятые стандарты и правила.
Смежные и вертикальные углы — это неотъемлемая составляющая геометрии. Наверняка многие школьники просто обожают их по той причине, что их свойства понятны и просты в доказательстве.
Образование углов
Любой угол образуется путем пересечения двух прямых или проведения двух лучей из одной точки. Они могут называться либо одной буквой, либо тремя, которые последовательно обозначают точки построения угла.
Углы измеряются в градусах и могут (в зависимости от их значения) по-разному называться. Так, существует прямой угол, острый, тупой и развернутый. Каждому из названий соответствует определенная градусная мера или ее промежуток.
Острым называется угол, мера которого не превышает 90 градусов.
Тупым является угол, превышающий 90 градусов.
Угол называется прямым в том случае, когда его градусная мера равна 90.
В том случае, когда он образован одной сплошной прямой, и его градусная мера равна 180, его называют развернутым.
Углы, имеющие общую сторону, вторая сторона которых продолжает друг друга, называются смежными. Они могут быть как острыми, так и тупыми. Пересечение линией образует смежные углы. Свойства их следующие:
- Сумма таких углов будет равна 180 градусам (существует теорема, доказывающая это). Поэтому можно легко вычислить один из них, если известен другой.
- Из первого пункта следует, что смежные углы не могут быть образованы двумя тупыми или двумя острыми углами.

Благодаря этим свойствам, можно всегда вычислить градусную меру угла, имея значение другого угла или, по крайней мере, отношение между ними.
Вертикальные углы
Углы, стороны которых являются продолжением друг друга, называются вертикальными. В качестве такой пары могут выступать любые их разновидности. Вертикальные углы всегда равны между собой.
Они образуются при пересечении прямых. Совместно с ними всегда присутствуют и смежные углы. Угол может быть одновременно смежным для одного и вертикальным для другого.
При пересечении произвольной линией также рассматривают еще несколько видов углов. Такая линия называется секущей, она и образует соответственные, односторонние и накрест лежащие углы. Они равны между собой. Их можно рассматривать в свете свойств, которые имеют вертикальные и смежные углы.
Таким образом, тема углов представляется довольно простой и понятной. Все их свойства легко запомнить и доказать. Решение задач не представляется сложным до тех пор, пока углам соответствует числовое значение. Уже дальше, когда начнется изучение sin и cos, придется запоминать множество сложных формул, их выводов и следствий. А до того времени можно просто наслаждаться легкими задачками, в которых необходимо найти смежные углы.
Уже дальше, когда начнется изучение sin и cos, придется запоминать множество сложных формул, их выводов и следствий. А до того времени можно просто наслаждаться легкими задачками, в которых необходимо найти смежные углы.
Г Л А В А I.
ОСНОВНЫЕ ПОНЯТИЯ.
§11. СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ.
1. Смежные углы.
Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (черт. 72): / А ВС и / СВD, у которых одна сторона ВС общая, а две другие АВи ВD составляют прямую линию.
Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами.
Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы.
Например, / АDF и / FDВ — углы смежные (черт. 73).
Смежные углы могут иметь самые разнообразные положения (черт. 74).
Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 2d.
Отсюда прямой угол можно определить как угол, равный своему смежному углу.
Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла.
Например, если один из смежных углов равен 3 / 5 d , то второй угол будет равен:
2d — 3 / 5 d = l 2 / 5 d .
2. Вертикальные углы.
Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На чертеже 75 углы EOF и АОС- вертикальные; углы АОЕ и СОF — также вертикальные.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.
Пусть / 1 = 7 / 8 d (черт. 76). Смежный с ним / 2 будет равен 2d — 7 / 8 d , т. е. 1 1 / 8 d .
Таким же образом можно вычислить, чему равны / 3 и / 4.
/ 3 = 2d — 1 1 / 8 d = 7 / 8 d ; / 4 = 2d — 7 / 8 d = 1 1 / 8 d (черт. 77).
77).
Мы видим, что / 1 = / 3 и / 2 = / 4.
Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой.
Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными.
Убедиться в справедливости свойства вертикальных углов необходимо путём рассуждения, путём доказательства.
Доказательство можно провести следующим образом (черт. 78):
/ a + / c = 2d ;
/ b + / c = 2d ;
(так как сумма смежных углов равна 2d ).
/ a + / c = / b + / c
(так как и левая часть этого равенства равна 2d , и правая его часть тоже равна 2d ).
В это равенство входит один и тот же угол с .
Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: / a = / b , т. е. вертикальные углы равны между собой.
При рассмотрении вопроса о вертикальных углах мы сначала объяснили, какие углы называются вертикальными, т. е. дали определение вертикальных углов.
Затем мы высказали суждение (утверждение) о равенстве вертикальных углов и в справедливости этого суждения убедились путём доказательства. Такие суждения, справедливость которых надо доказывать, называются теоремами . Таким образом, в данном параграфе мы дали определение вертикальных углов, а также высказали и доказали теорему об их свойстве.
В дальнейшем при изучении геометрии нам постоянно придётся встречаться с определениями и доказательствами теорем.
3. Сумма углов, имеющих общую вершину.
На чертеже 79 / 1, / 2, / 3 и / 4 расположены по одну сторону прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют развёрнутый угол, т. е.
В сумме эти углы составляют развёрнутый угол, т. е.
/ 1+ / 2+/ 3+ / 4 = 2d .
На чертеже 80 / 1, / 2, / 3, / 4 и / 5 имеют общую вершину. В сумме эти углы составляют полный угол, т. е. / 1 + / 2 + / 3 + / 4 + / 5 = 4d .
Упражнения.
1. Один из смежных углов равен 0,72 d. Вычислить угол, составленный биссектрисами этих смежных углов.
2. Доказать, что биссектрисы двух смежных углов образуют прямой угол.
3. Доказать, что если два угла равны, то равны и их смежные углы.
4. Сколько пар смежных углов на чертеже 81?
5. Может ли пара смежных углов состоять из двух острых углов? из двух тупых углов? из прямого и тупого угла? из прямого и острого угла?
6. Если один из смежных углов прямой, то что можно сказать о величине смежного с ним угла?
7. Если при пересечении двух прямых линий один угол прямой, то что можно сказать о величине остальных трёх углов?
Смежные и вертикальные углы.
 Их свойства
Их свойства1. Смежные углы.
Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (рис. 72): ∠АВС и ∠СВD, у которых одна сторона ВС общая, а две другие, АВ и ВD, составляют прямую линию.
Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами.
Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы.
Например, ∠АDF и ∠FDВ — углы смежные (рис. 73).
Смежные углы могут иметь самые разнообразные положения (рис. 74).
Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 180°
Отсюда прямой угол можно определить как угол, равный своему смежному углу.
Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла.
Например, если один из смежных углов равен 54°, то второй угол будет равен:
180° — 54° = l26°.
2. Вертикальные углы.
Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На рисунке 75 углы EOF и АОС- вертикальные; углы АОЕ и СОF — также вертикальные.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.
Пусть ∠1 = \(\frac{7}{8}\) ⋅ 90°(рис. 76). Смежный с ним ∠2 будет равен 180° — \(\frac{7}{8}\) ⋅ 90°, т. е. 1\(\frac{1}{8}\) ⋅ 90°.
Таким же образом можно вычислить, чему равны ∠3 и ∠4.
∠3 = 180° — 1\(\frac{1}{8}\) ⋅ 90° = \(\frac{7}{8}\) ⋅ 90°;
∠4 = 180° — \(\frac{7}{8}\) ⋅ 90° = 1\(\frac{1}{8}\) ⋅ 90° (рис. 77).
Мы видим, что ∠1 = ∠3 и ∠2 = ∠4.
Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой.
Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными.
Убедиться в справедливости свойства вертикальных углов необходимо путём доказательства.
Доказательство можно провести следующим образом (рис. 78):
∠a + ∠c = 180°;
∠b + ∠c = 180°;
(так как сумма смежных углов равна 180°).
∠a + ∠c = ∠b + ∠c
(так как и левая часть этого равенства равна 180°, и правая его часть тоже равна 180°).
В это равенство входит один и тот же угол с .
Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: ∠a = ∠b , т. е. вертикальные углы равны между собой.
3. Сумма углов, имеющих общую вершину.
На чертеже 79 ∠1, ∠2, ∠3 и ∠4 расположены по одну сторону прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют развёрнутый угол, т. е.
∠1 + ∠2 + ∠3 + ∠4 = 180°.
На чертеже 80 ∠1, ∠2, ∠3, ∠4 и ∠5 имеют общую вершину. В сумме эти углы составляют полный угол, т. е. ∠1 + ∠2 + ∠3 + ∠4 + ∠5 = 360°.
е. ∠1 + ∠2 + ∠3 + ∠4 + ∠5 = 360°.
Другие материалы
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.
Сумма смежных углов равна 180°
Теорема 1. Сумма смежных углов равна 180°.
Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .
Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.
Вертикальные углы равны
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).
Теорема 2. Вертикальные углы равны.
Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1
∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.
Отсюда заключаем, что ∠ АОВ = ∠ COD.
Следствие 1. Угол, смежный с прямым углом, есть прямой угол.
Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.
АН — перпендикуляр к прямой
Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.
Чертежный угольник
Справедлива следующая теорема.
Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).
Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.
Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».
Пример 1. Один из смежных углов равен 44°. Чему равен другой?
Решение. Обозначим градусную меру другого угла через x , тогда согласно теореме 1.
44° + х = 180°.
Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.
Следовательно, другой угол равен 136°.
Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?
Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1.2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.
∠ АОС = 180° — ∠ COD = 180° — 45° = 135°.
Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.
Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.
Значит, смежные углы равны 45° и 135°.
Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.
Решение. Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол
АОС) смежный с углом COD, и, значит, по теореме 1
Угол BOD (также и угол
АОС) смежный с углом COD, и, значит, по теореме 1
∠ BOD = ∠ АОС = 180° — 50° = 130°.
Геометрия — это весьма многогранная наука. Она развивает логику, воображение и интеллект. Конечно, из-за своей сложности и огромного количества теорем и аксиом, она не всегда нравится школьникам. Кроме этого, существует необходимость постоянно доказывать свои выводы, используя общепринятые стандарты и правила.
Смежные и вертикальные углы — это неотъемлемая составляющая геометрии. Наверняка многие школьники просто обожают их по той причине, что их свойства понятны и просты в доказательстве.
Образование углов
Любой угол образуется путем пересечения двух прямых или проведения двух лучей из одной точки. Они могут называться либо одной буквой, либо тремя, которые последовательно обозначают точки построения угла.
Углы измеряются в градусах и могут (в зависимости от их значения) по-разному называться. Так, существует прямой угол, острый, тупой и развернутый.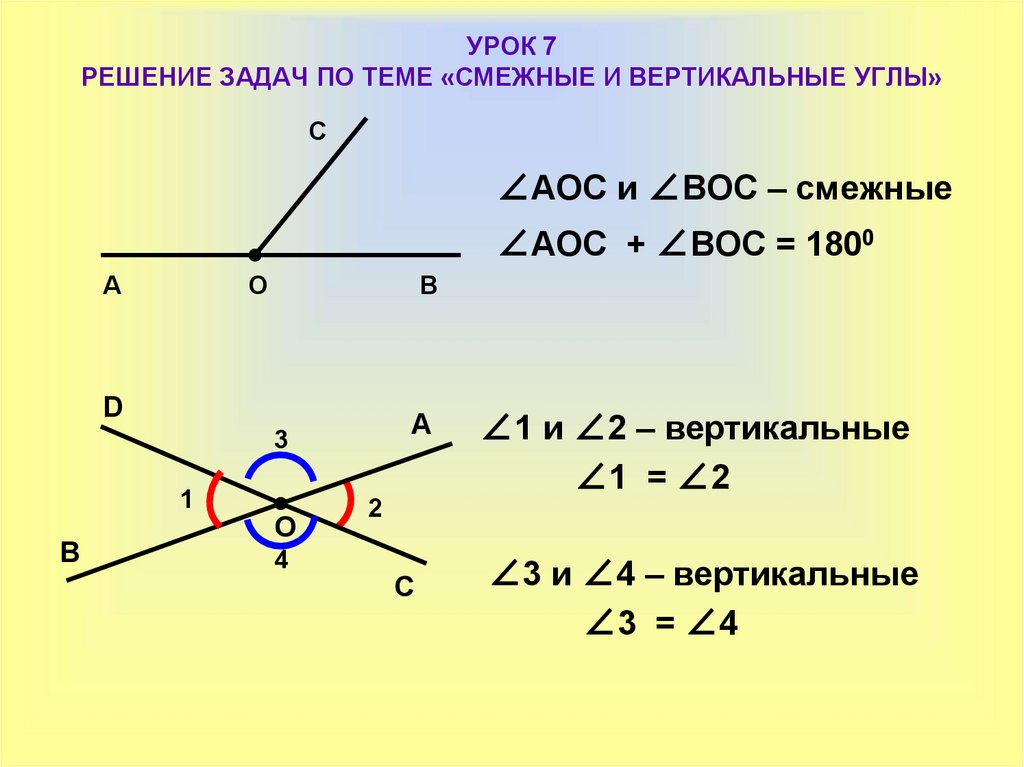 Каждому из названий соответствует определенная градусная мера или ее промежуток.
Каждому из названий соответствует определенная градусная мера или ее промежуток.
Острым называется угол, мера которого не превышает 90 градусов.
Тупым является угол, превышающий 90 градусов.
Угол называется прямым в том случае, когда его градусная мера равна 90.
В том случае, когда он образован одной сплошной прямой, и его градусная мера равна 180, его называют развернутым.
Углы, имеющие общую сторону, вторая сторона которых продолжает друг друга, называются смежными. Они могут быть как острыми, так и тупыми. Пересечение линией образует смежные углы. Свойства их следующие:
- Сумма таких углов будет равна 180 градусам (существует теорема, доказывающая это). Поэтому можно легко вычислить один из них, если известен другой.
- Из первого пункта следует, что смежные углы не могут быть образованы двумя тупыми или двумя острыми углами.
Благодаря этим свойствам, можно всегда вычислить градусную меру угла, имея значение другого угла или, по крайней мере, отношение между ними.
Вертикальные углы
Углы, стороны которых являются продолжением друг друга, называются вертикальными. В качестве такой пары могут выступать любые их разновидности. Вертикальные углы всегда равны между собой.
Они образуются при пересечении прямых. Совместно с ними всегда присутствуют и смежные углы. Угол может быть одновременно смежным для одного и вертикальным для другого.
При пересечении произвольной линией также рассматривают еще несколько видов углов. Такая линия называется секущей, она и образует соответственные, односторонние и накрест лежащие углы. Они равны между собой. Их можно рассматривать в свете свойств, которые имеют вертикальные и смежные углы.
Таким образом, тема углов представляется довольно простой и понятной. Все их свойства легко запомнить и доказать. Решение задач не представляется сложным до тех пор, пока углам соответствует числовое значение. Уже дальше, когда начнется изучение sin и cos, придется запоминать множество сложных формул, их выводов и следствий.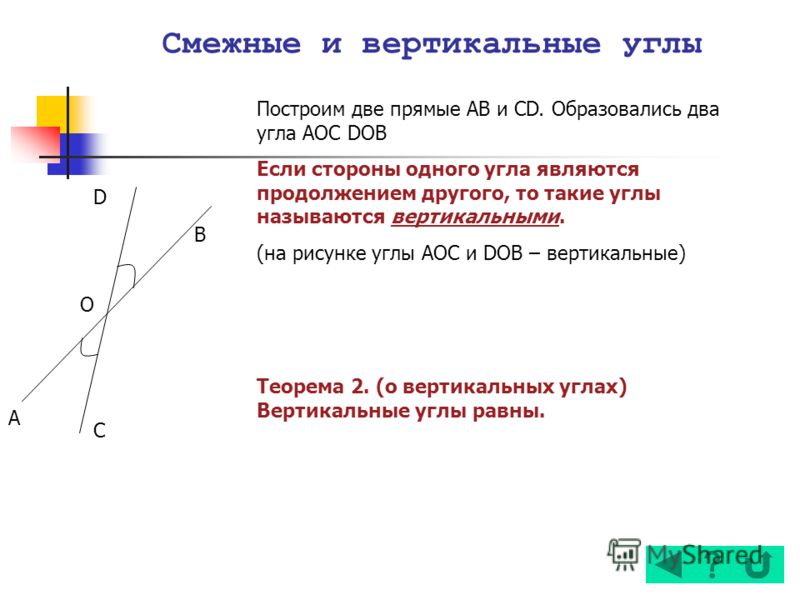 А до того времени можно просто наслаждаться легкими задачками, в которых необходимо найти смежные углы.
А до того времени можно просто наслаждаться легкими задачками, в которых необходимо найти смежные углы.
Смежные углы – два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой.
Сумма смежных углов равна 180°
Вертикальные углы — это два угла, у которых стороны одного угла являются продолжение сторон другого.
Вертикальные углы равны.
2. Признаки равенства треугольников:
I признак : Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
II признак : Если стороны и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
III признак : Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны
3. Признаки параллельности двух прямых: односторонние углы, накрест лежащие и соответственные:
Две прямые на плоскости называются параллельными , если они не пересекаются.
Накрест лежащие углы: 3 и 5, 4 и 6;
Односторонние углы: 4 и 5, 3 и 6; рис. Стр55
Соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7;
Теорема : Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Теорема : Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Теорема : Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
Теорема : если две параллельные прямые пересечены секущей, то накрест лежащие углы равны
Теорема : если две параллельные прямые пересечены секущей, то соответственные углы равны
Теорема : если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°
4. Сумма углов треугольника:
Сумма углов треугольника равна 180°
5. Свойства равнобедренного треугольника:
Теорема: В равнобедренном треугольнике углы при основании равны.
Теорема: В равнобедренном треугольнике биссектриса, проведенная к основанию, являетсямедианой и высотой (медиана наоборот), (биссектриса делит угол пополам, медиана делит сторону пополам, высота образует угол 90°)
Признак: Если два угла треугольника равны, то треугольник равнобедренный.
6. Прямоугольный треугольник:
Прямоугольный треугольник — это треугольник, в котором один угол прямой (то есть составляет 90 градусов)
В прямоугольном треугольнике гипотенуза больше катета
1. Сумма двух острых углов прямоугольного треугольника равна 90°
2. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы
3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°
7. Равносторонний треугольник:
РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК, плоская фигура, имеющая три стороны равной длины; три внутренних угла, образуемых сторонами, также равны и составляют 60 °С.
Сумма углов четырёхугольника равна 2 π = 360°.
Четырёхугольник можно вписать в окружность тогда и только тогда, сумма противоположных углов равна 180°
10. Признаки подобия треугольников:
I признак : если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны
II признак : если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
III признак : если три стороны одного треугольника порциональны трем сторонам другого, то такие треугольники подобны
11. Формулы:
· Теорема Пифагора: a 2 +b 2 =c 2
· Теорема sin:
· Теорема cos:
· 3 формулы площади треугольника:
· Площадь прямоугольного треугольника: S= S=
· Площадь равностороннего треугольника:
· Площадь параллелограмма: S = ah
· Площадь квадрата: S = a2
· Площадь трапеции:
· Площадь ромба:
· Площадь прямоугольника: S=ab
· Равносторонний треугольник. Высота: h=
Высота: h=
· Тригонометрическая единица: sin 2 a+cos 2 a=1
· Средняя линия треугольника: S=
· Средняя линия трапеции : МК=
©2015-2019 сайт
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2017-12-12
по теме: Смежные и вертикальные углы, их свойства.
(3 занятия)
В результате изучения темы нужно:
УМЕТЬ:
Понятия: смежных и вертикальных углов, перпендикулярных прямых
Различать понятия смежные и вертикальные углы
Теоремы смежных и вертикальных углов
Решать задачи с использованием свойств смежных и вертикальных углов
Свойства смежных и вертикальных углов
Строить смежные и вертикальные углы, перпендикулярные прямые
ЛИТЕРАТУРА:
1. Геометрия. 7 класс. Ж. Кайдасов, Г. Досмагамбетова, В. Абдиев. Алматы «Мектеп». 2012
Алматы «Мектеп». 2012
2. Геометрия. 7 класс. К.О.Букубаева, А.Т. Миразова. Алматы « Атамұра ». 2012
3. Геометрия. 7 класс. Методическое руководство. К.О.Букубаева. Алматы « Атамұра ». 2012
4. Геометрия. 7 класс. Дидактический материал. А.Н.Шыныбеков. Алматы « Атамұра ». 2012
5. Геометрия. 7 класс. Сборник задач и упражнений. К.О.Букубаева, А.Т.Миразова. Алматы « Атамұра ». 2012
Помни, что работать нужно по алгоритму!
Не забывай проходить проверку, делать пометки на полях,
Пожалуйста, не оставляй без ответа, возникшие у тебя вопросы.
Будь объективен во время взаимопроверки, это поможет и тебе, и тому,
кого ты проверяешь.
ЖЕЛАЮ УСПЕХА!
ЗАДАНИЕ №1.
Прочитай определение и выучи (2б):
Определение. Углы, у которых одна сторона общая, а две другие стороны являются дополнительными лучами, называются смежными.
2) Выучи и запиши в тетрадь теорему: (2б)
Сумма смежных углов равна 180.
Дано:
∠ АОД и ∠ ДОВ –данные смежные углы
ОД — общая сторона
Доказать:
∠ АОД + ∠ ДОВ = 180
Доказательство:
На основе аксиомы III 4:
∠ АОД + ∠ ДОВ = ∠ АОВ.
∠ АОВ — развернутый. Следовательно,
∠ АОД + ∠ ДОВ = 180
Теорема доказана.
3) Из теоремы следует: (2б)
1) Если два угла равны, то смежные с ними углы равны;
2) если смежные углы равны, то градусная мера каждого из них равна 90°.
Запомни!
Угол, равный 90°, называется прямым углом.
Угол, меньше 90°, называется острым углом.
Угол, больше 90° и меньше 180°, называется тупым углом.
Прямой угол Острый угол Тупой угол
Так как сумма смежных углов равна 180°, то
1) угол, смежный с прямым углом, прямой;
2) угол, смежный с острым углом, тупой;
3) угол, смежный с тупым углом, острый.
4) Рассмотри образец решения з адачи:
а) Дано:
∠
h
k
и
∠
kl
— смежные;
∠
h
k
больше
∠
kl
на 50° .
Найти: ∠ h k и ∠ kl .
Решение: Пусть ∠ kl = х, тогда ∠ h k = х + 50°. По свойству о сумме смежных углов ∠ kl + ∠ h k = 180°.
х + х + 50° = 180°;
2х = 180° — 50°;
2х = 130°;
х = 65°.
∠ kl = 65°; ∠ h k = 65°+ 50° = 115°.
Ответ: 115° и 65°.
б) Пусть ∠ kl = х, тогда ∠ h k = 3х
х + 3х = 180°; 4х = 180°; х = 45°; ∠ kl = 45°; ∠ hk = 135°.
Ответ: 135° и 45°.
5) Работа с определением смежных углов: (2 б)
6) Найди ошибки в определениях: (2б)
Пройди проверку №1
Задание №2
1)Построй 2 смежных угла так, чтобы их общая сторона проходила через точку C и сторона одного из углов совпадала с лучом AB.(2б)
2). Практическая работа на открытие свойства смежных углов: (5б)
Ход работы
1. Построй угол смежный углу а , если а : острый, прямой, тупой.
2. Измерь величины углов.
3. Данные измерений занеси в таблицу.
Данные измерений занеси в таблицу.
4. Найди соотношение между величинами углов а и .
5. Сделай вывод о свойстве смежных углов.
Пройди проверку №2
Задание №3
Начертите неразвернутый ∠ АОВ и назовите лучи, являющиеся сторонами этого угла.
Проведите луч О, являющийся продолжение луча ОА, и луч ОД, являющийся продолжение луча ОВ.
Запишите в тетради: углы ∠ АОВ и ∠ СОД называются вертикальными. (3б)
Выучи и запиши в тетрадь: (4б)
Определение: Углы, у которых стороны одного из них являются дополнительными лучами другого, называются вертикальными углами.
1 и
Лучи OF и OA , OC и OE являются попарно дополнительными лучами.
Теорема: Вертикальные углы равны.
Доказательство.
Вертикальные углы образуются при пересечении двух прямых. Пусть прямые а и b пересекаются в точке О. ∠ 1 и ∠ 2 –вертикальные углы.
∠
АОС-развернутый, значит
∠
АОС= 180°.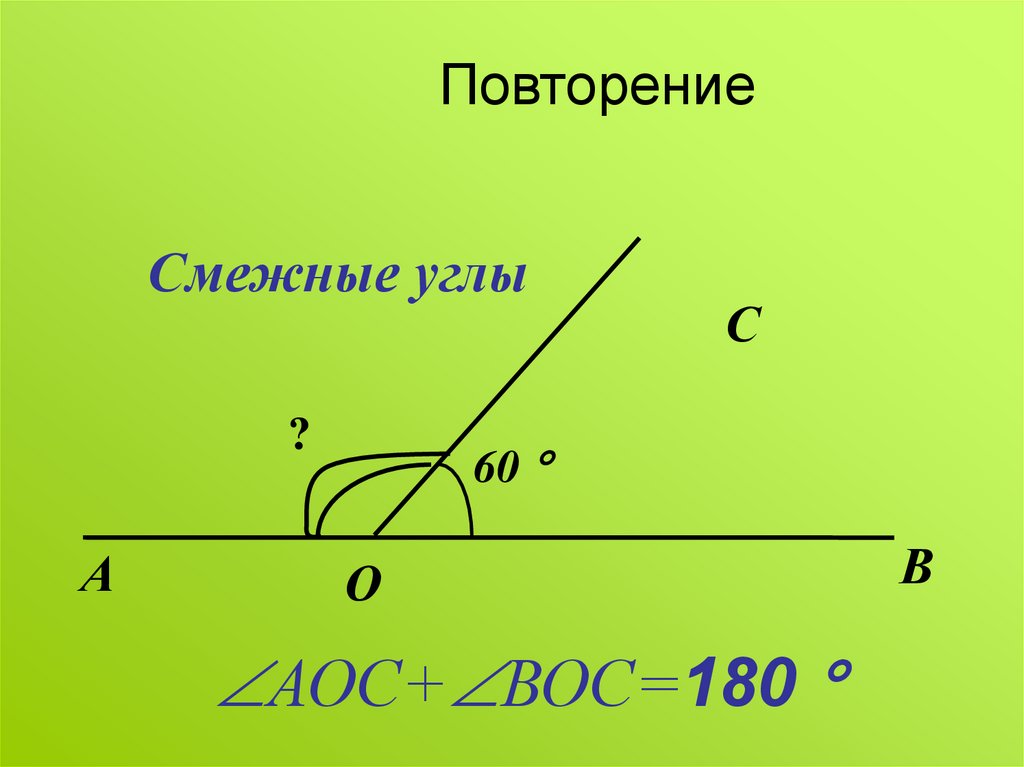 Однако
∠
1+
∠
2=
∠
АОС, т.е.
Однако
∠
1+
∠
2=
∠
АОС, т.е.
∠ 3+ ∠ 1= 180°, отсюда имеем:
∠ 1= 180 — ∠ 3. (1)
Также имеем, что ∠ ДОВ= 180°, отсюда ∠ 2+ ∠ 3= 180°, или ∠ 2= 180°- ∠ 3. (2)
Так как в равенствах (1) и (2) прямые части равны, то ∠ 1= ∠ 2.
Теорема доказана.
5). Работа с определением вертикальных углов:(2б)
6) Найди ошибку в определении:(2б).
Пройди проверку №3
Задание №4
1)Практическая работа на открытие свойства вертикальных углов:(5б)
Ход работы:
1.Построй угол β вертикальный углу α , если α :
острый, прямой, тупой.
2.Измерь величины углов.
3.Данные измерений занеси в таблицу
4.Найди соотношение между величинами углов α и β.
5.Сделай вывод о свойстве вертикальных углов.
2)Доказательство свойств смежных и вертикальных углов. (3б)
2) Рассмотри образец решения з
адачи.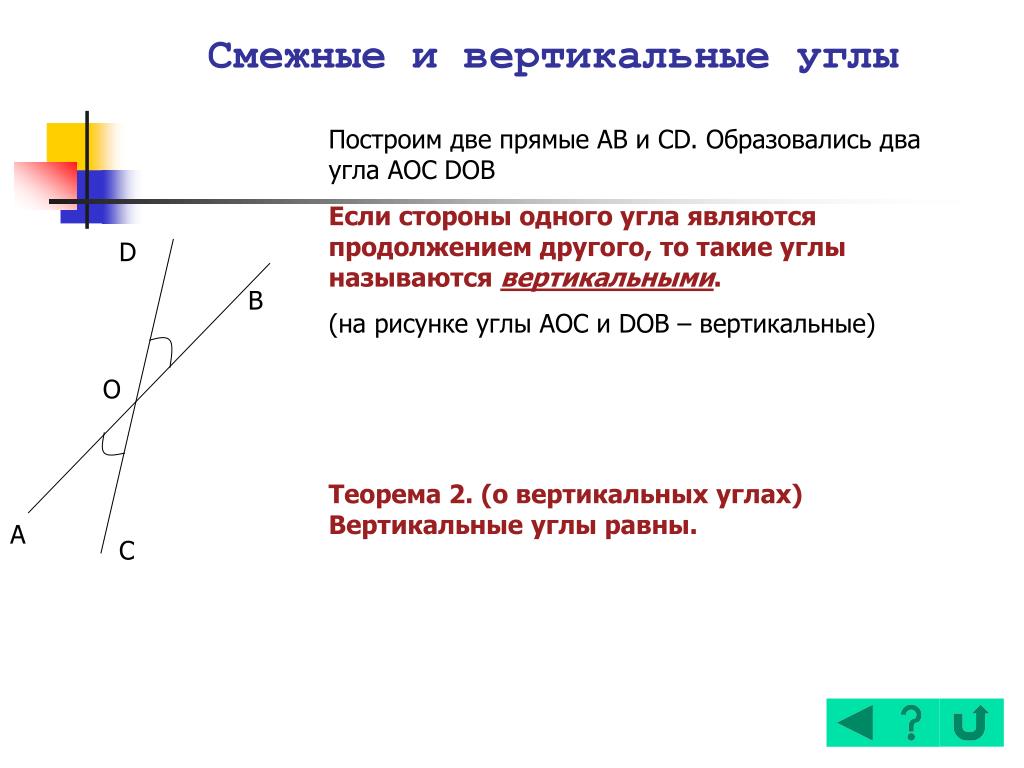
Задача. Прямые АВ и СД пересекаются в точке О так, что ∠ AOД = 35°. Найдите углы АОС и ВОС.
Решение:
1) Углы АОД и АОС смежные, поэтому ∠ BOC = 180° — 35° = 145°.
2) Углы АОС и ВОС также смежные, поэтому ∠ BOC = 180° — 145° = 35°.
Значит, ∠ BOC = ∠ АОД = 35°, причем эти углы являются вертикальными. Вопрос: верно ли утверждение, что любые вертикальные углы равны?
3) Решение задач на готовых чертежах: (3б)
1. Найти углы АОВ, АОD, COD.
3) Найти углы BOC, FOA.: (3б)
3. Найди на рисунке смежные и вертикальные углы. Пусть известны величины двух углов, отмеченных на чертеже, 28? и 90?. Можно ли найти величины остальных углов, не выполняя измерений (2б)
Пройди проверку №4
Задание №5
Проверь свои знания, выполнив проверочную работу №1
Задание №6
1) Самостоятельно докажи свойства вертикальных углов и запиши эти доказательства в тетрадь. (3б)
Учащиеся самостоятельно, используя свойства вертикальных и смежных углов, должны обосновать тот факт, что если при пересечении двух прямых один из образовавшихся углов прямой, то остальные углы также прямые.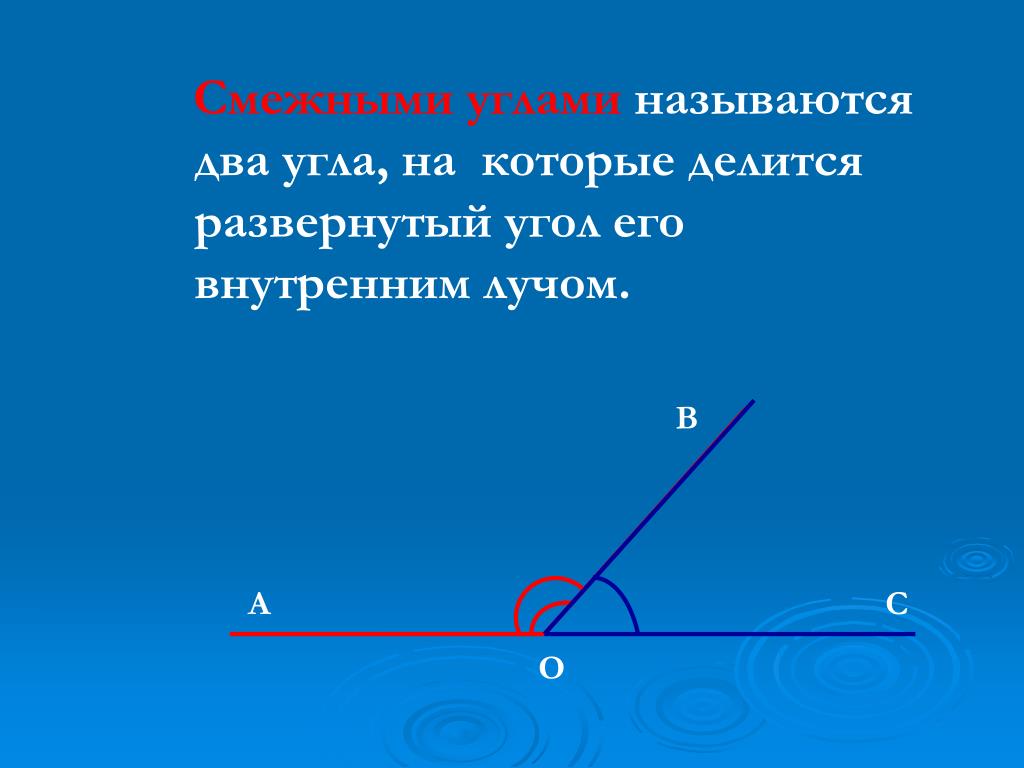
2) Реши на выбор две задачи:
1.Градусные меры смежных углов относятся как 7:2. Найдите эти углы.(2б)
2.Один из углов, образовавшихся при пересечении двух прямых, в 11 раз меньше другого.Найдите каждый из углов.(3б)
3.Найдите смежные углы,если их разность и их сумма относятся как 2:9.(3б)
Задание №7
Молодец! Можешь приступать к проверочной работе №2.
Проверочная работа №1.
Реши на выбор любой из вариантов (10б)
Вариант 1
г)
Смежные
д) Начертите (на глаз) угол в 30° и
е) Какие углы называются вертикальными?
Два угла называются вертикальными, если орни равны.
ж) Из точки А провести две прямые, перпендикулярные прямой а
Можно провести только одну прямую.
Вариант 2
1.Ученик, отвечая на вопросы учителя, дал соответствующие ответы. Проверьте, верны ли они, пометив в третьем столбике словом «ДА», «НЕТ», «НЕ ЗНАЮ». В случает «НЕТ» запишите там же верный ответ или добавьте недостающее.
Д)
Нет. Они вертикальные
Е) Какие прямые называются перпендикулярными?
Две прямые называются перпендикулярными, если они пересекаются под прямым углом
Ж) Начертите вертикальные углы так, чтобы их стороны были перпендикулярными прямыми.
2. Назовите вертикальные углы на данном рисунке.
Итого:10 баллов
«5»-10баллов;
«4»-8-9 баллов;
«3»-5-7 баллов.
Проверочная работа №2.
Реши на выбор любой вариант
Вариант I
Найдите смежные углы, если их разность и их сумма относятся как 2:9. (4б)
Найдите все неразвернутые углы, образованные при пересечении двух прямых, если один из них на 240°, меньше суммы двух других.(6б)
Вариант II
1) Найдите смежные углы, если их разность и их сумма относятся как 5:8(4б)
2) Найдите все неразвернутые углы, образованные при пересечении двух прямых, если один из них на 60°, больше суммы двух других. (6б)
(6б)
Итого:10 баллов
«5»-10баллов;
«4»-8-9 баллов;
«3»-5-7 баллов.
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град.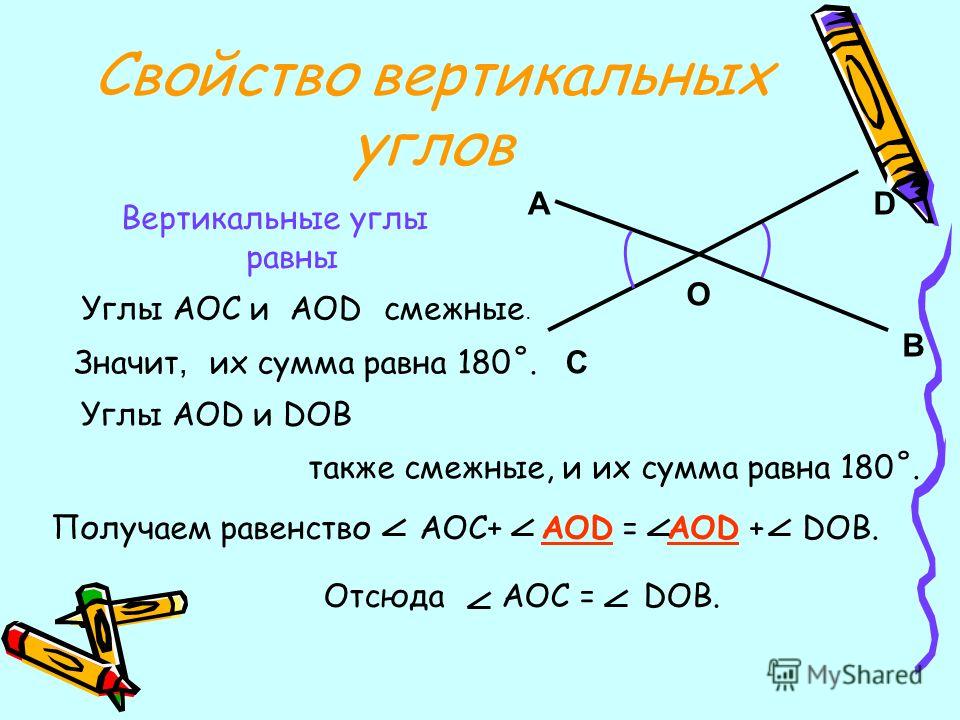 ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град.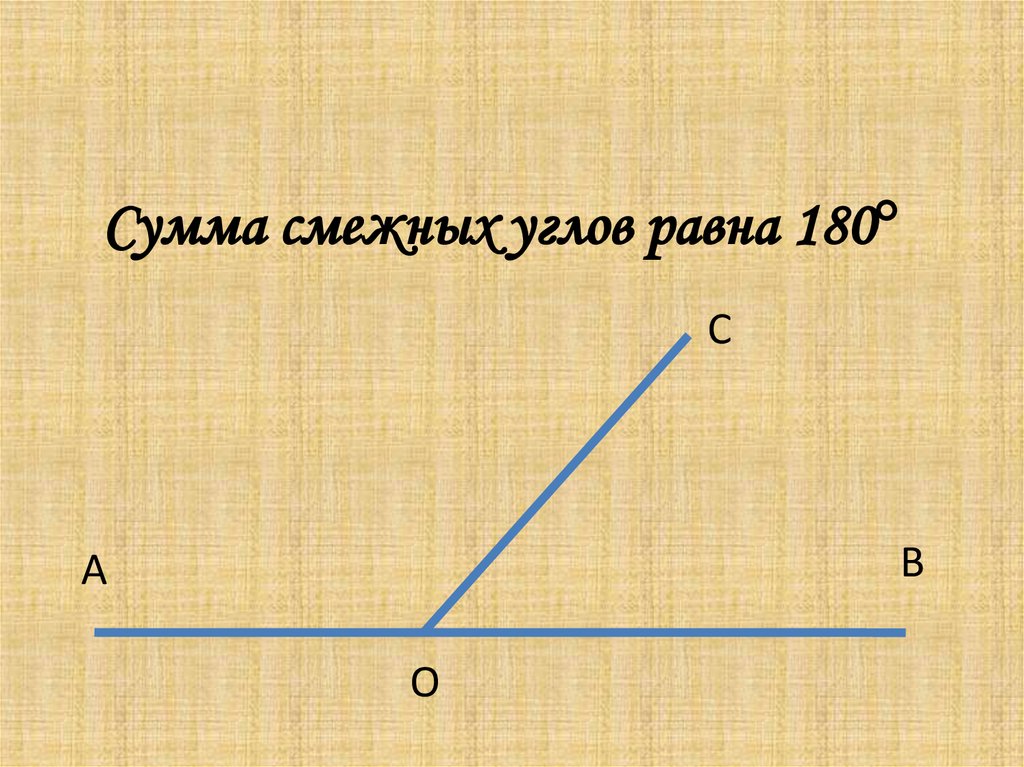 ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.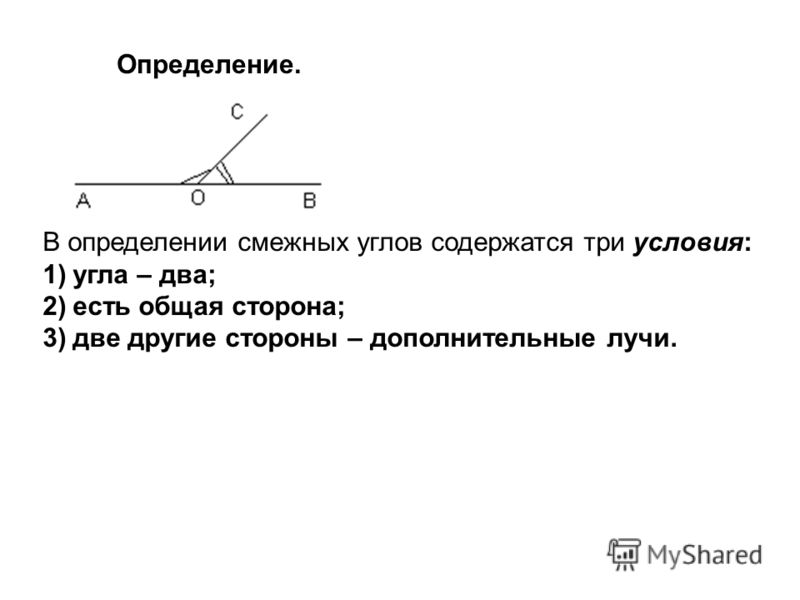 ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.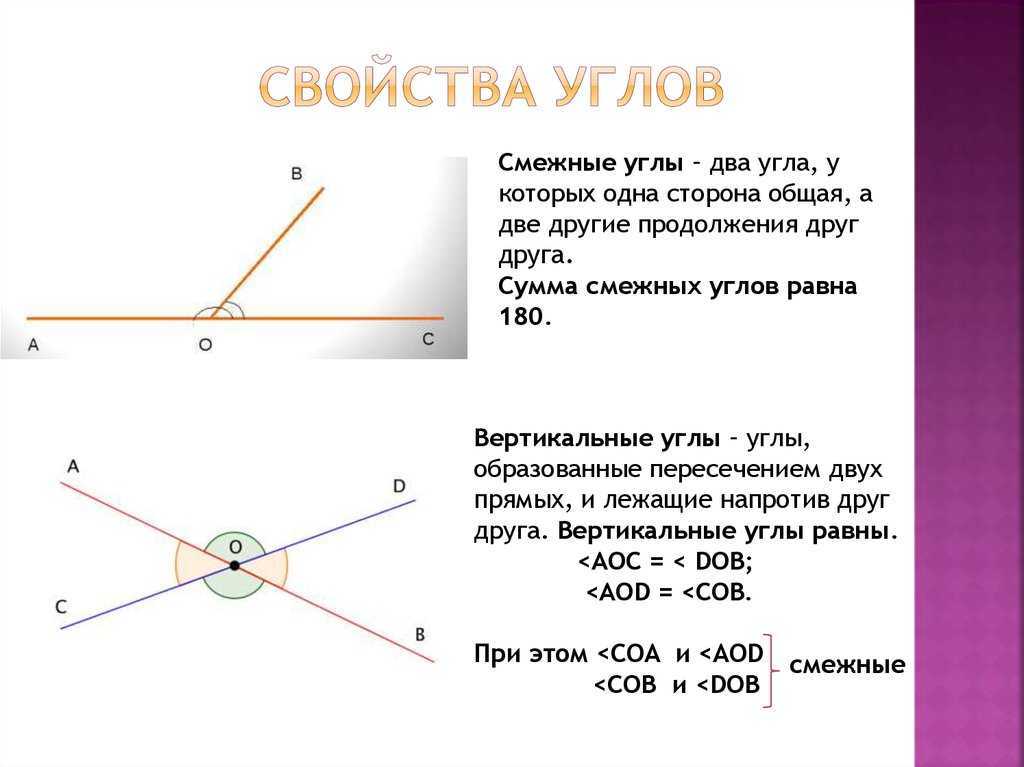 ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Как найти смежный угол треугольника. Смежные и вертикальные углы
Геометрия — это весьма многогранная наука. Она развивает логику, воображение и интеллект. Конечно, из-за своей сложности и огромного количества теорем и аксиом, она не всегда нравится школьникам.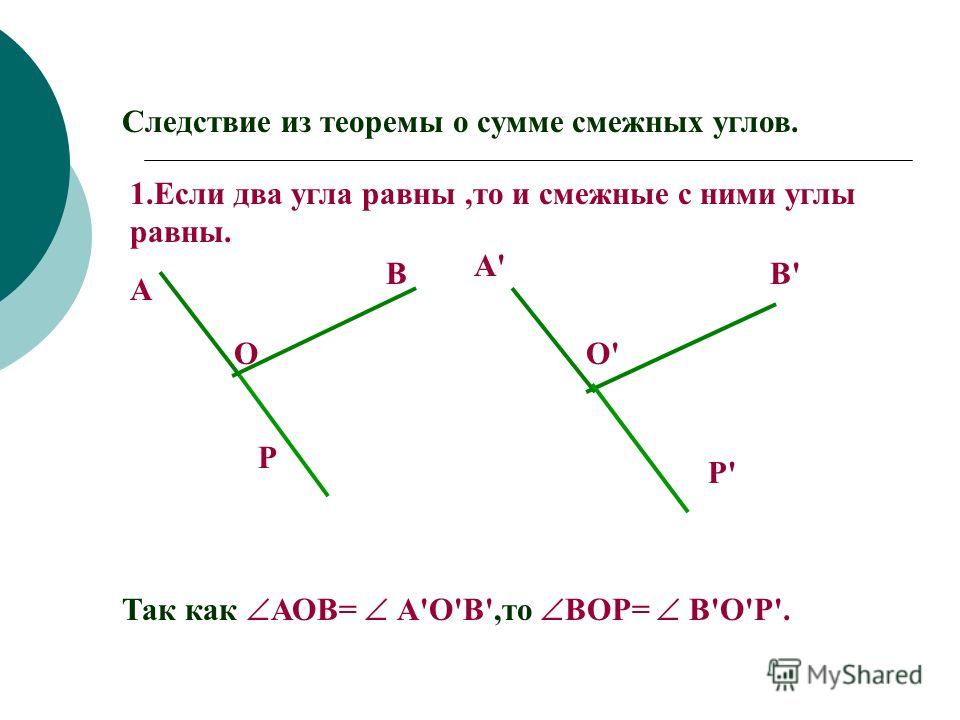 Кроме этого, существует необходимость постоянно доказывать свои выводы, используя общепринятые стандарты и правила.
Кроме этого, существует необходимость постоянно доказывать свои выводы, используя общепринятые стандарты и правила.
Смежные и вертикальные углы — это неотъемлемая составляющая геометрии. Наверняка многие школьники просто обожают их по той причине, что их свойства понятны и просты в доказательстве.
Образование углов
Любой угол образуется путем пересечения двух прямых или проведения двух лучей из одной точки. Они могут называться либо одной буквой, либо тремя, которые последовательно обозначают точки построения угла.
Углы измеряются в градусах и могут (в зависимости от их значения) по-разному называться. Так, существует прямой угол, острый, тупой и развернутый. Каждому из названий соответствует определенная градусная мера или ее промежуток.
Острым называется угол, мера которого не превышает 90 градусов.
Тупым является угол, превышающий 90 градусов.
Угол называется прямым в том случае, когда его градусная мера равна 90.
В том случае, когда он образован одной сплошной прямой, и его градусная мера равна 180, его называют развернутым.
Углы, имеющие общую сторону, вторая сторона которых продолжает друг друга, называются смежными. Они могут быть как острыми, так и тупыми. Пересечение линией образует смежные углы. Свойства их следующие:
- Сумма таких углов будет равна 180 градусам (существует теорема, доказывающая это). Поэтому можно легко вычислить один из них, если известен другой.
- Из первого пункта следует, что смежные углы не могут быть образованы двумя тупыми или двумя острыми углами.
Благодаря этим свойствам, можно всегда вычислить градусную меру угла, имея значение другого угла или, по крайней мере, отношение между ними.
Вертикальные углы
Углы, стороны которых являются продолжением друг друга, называются вертикальными. В качестве такой пары могут выступать любые их разновидности. Вертикальные углы всегда равны между собой.
Они образуются при пересечении прямых. Совместно с ними всегда присутствуют и смежные углы. Угол может быть одновременно смежным для одного и вертикальным для другого.
При пересечении произвольной линией также рассматривают еще несколько видов углов. Такая линия называется секущей, она и образует соответственные, односторонние и накрест лежащие углы. Они равны между собой. Их можно рассматривать в свете свойств, которые имеют вертикальные и смежные углы.
Таким образом, тема углов представляется довольно простой и понятной. Все их свойства легко запомнить и доказать. Решение задач не представляется сложным до тех пор, пока углам соответствует числовое значение. Уже дальше, когда начнется изучение sin и cos, придется запоминать множество сложных формул, их выводов и следствий. А до того времени можно просто наслаждаться легкими задачками, в которых необходимо найти смежные углы.
2)Сколько общих точек могут иметь 2 прямые?
3)Объясните что такое отрезок?
4)Объясните что такое луч.Как обозначаются лучи?
5)Какая фигура называется углом?Объясните что такое вершина и стороны угла?
6)Какой угол называется развернутым?
7)Какие фигуры называют равными?
8)Объясните как сравнить 2 отрезка
9)Какая точка называется серединой отрезка?
10)Объясните как сравнить 2 угла.
11)Какой луч называется биссектрисой угла?
12)Точка С делит отрезок АВ на 2 отрезка.Как найти длину отрезка АВ если известны длины отрезков АС и СВ?
13)Какими инструментами пользуются для измерения расстояний?
14)Что такое градусная мера угла?
15)Луч ОС делит угол АОВ на 2 угла. Как найти градусную меру угла АОВ если известны градусные меры углов АОС и СОВ?
16)Какой угол называется острым?прямым?тупым?
17)Какие углы называют смежными?Чему равна сумма смежных углов?
18)Какие углы называются вертикальными?Каким свойством обладают вертикальные углы?
19)Какие прямы называются перпендикулярными?
20)Объясните почему 2 прямые перпендикулярные к 3-ей не пересекаются?
21)Какие приборы применяют для построения прямых углов на местности?
1сколько прямых можно провести через две точки?
2сколько общих точек могут иметь две прямые?
3обьясните что такое отрезок
4обьясните что такое луч.Как обозначаются лучи?
5какая фигура называется углом? обьясните что такое вершина и стороны угла
6какой угол называется развёрнутым
7какие фигуры называются равными
8обьясните как сравнить два отрезка
9какая точка называется серединой отрезка
10обьясните как сравнить два угла
11какой луч называется биссектрисой угла
12точка с делит отрезок аб на два отрезка. Как найти длину отрезка аб если известны длины отрезков ас и сб
Как найти длину отрезка аб если известны длины отрезков ас и сб
13какими инструментами пользуются для измерения расстояний
14что такое градусная мера угла
15луч ос делит угол аоб на два угла.Как найти градусную меру угла аоб,если известны меры углов аос в соб
16какой угол называется острым?,прямым?,тупым?.
17какие углы называются смежными?чему равна сумма смежных углов?
18какие углы называются вертикальными?каким свойством обладают вертикальные углы
19какие прямые называются перпендикулярными
20обьясните почему две прямые перпендикулярные к третьей не пересикаются
21какие приборы применяют для построения прямых углов на местности?
1)что такое градусная мера угла? 2)какие фигуры называются равными 3)какие углы называются смежными,чему равна сумма смежныхуглов 4)какие углы называются
вертикальными каким свойством обладают вертикальные углы 5)
Помогите плиз, !! плизз=**
7.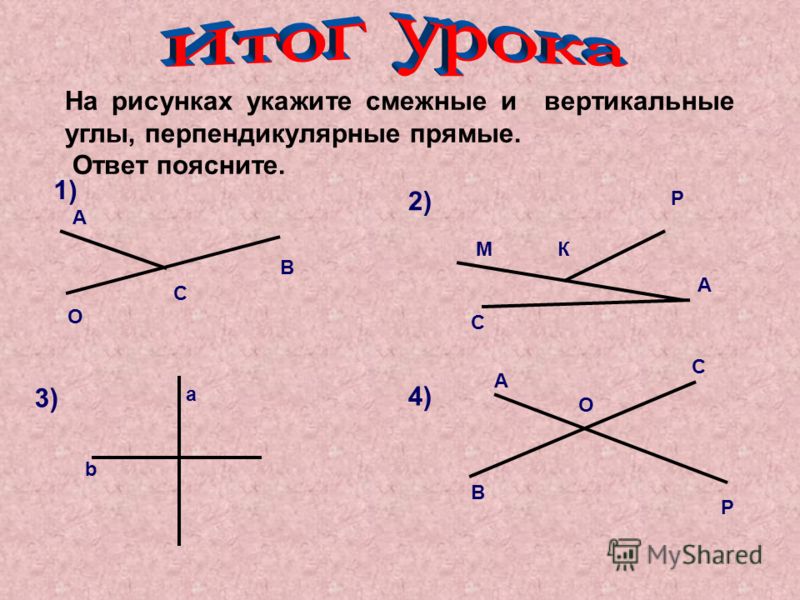 Докажите, что если две параллельные прямые пересекаются третьей прямой, то внутренние накрест лежащие углы равны, а сумма внутренних односторонних углов равна 180 градусов.
Докажите, что если две параллельные прямые пересекаются третьей прямой, то внутренние накрест лежащие углы равны, а сумма внутренних односторонних углов равна 180 градусов.
8. Докажите, что две прямые, перпендикулярные третьей, параллельны. Если прямая перепендикулярна одной из двух параллелных прямых, то она перепендикулярна и другой.
9. Докажите, что сумма углов треугольника равна 180 градусов.
10. Докажите, что у любого треугольника по крайней мере два угла острые.
11. Что такое внешний угол треугольника?
12. Докажите, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
13. Докажите, что внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
14. Какой треугольник называется прямоугольным?
15. Чему равна сумма острых углов прямоугольного треугольника?
16. Какая сторона прямоугольного треугольника называется гипотенузой? Какие стороны называются катетами?
17. Сформулируйте признак равенства прямоугольных треугольников по гипотенузе и катету.
18. Докажите, что из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один.
19. Что называется расстоянием от точки до прямой?
20. Объясните, что такое расстояние между параллельными прямыми.
Г Л А В А I.
ОСНОВНЫЕ ПОНЯТИЯ.
§11. СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ.
1. Смежные углы.
Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (черт. 72): / А ВС и / СВD, у которых одна сторона ВС общая, а две другие АВи ВD составляют прямую линию.
Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами.
Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы.
Например, / АDF и / FDВ — углы смежные (черт. 73).
Смежные углы могут иметь самые разнообразные положения (черт. 74).
Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 2d.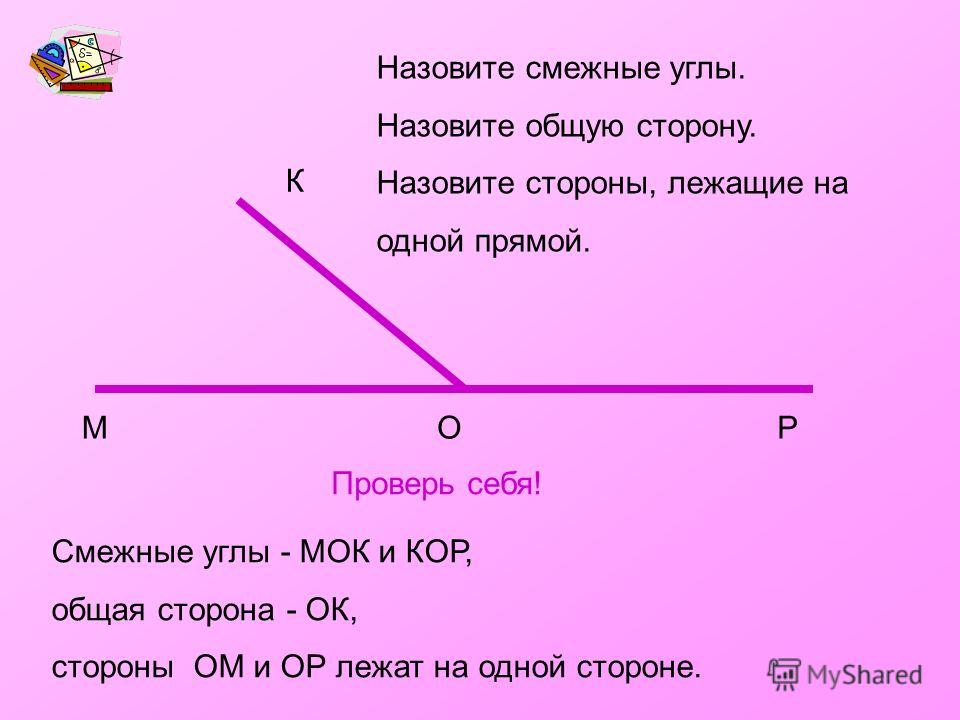
Отсюда прямой угол можно определить как угол, равный своему смежному углу.
Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла.
Например, если один из смежных углов равен 3 / 5 d , то второй угол будет равен:
2d — 3 / 5 d = l 2 / 5 d .
2. Вертикальные углы.
Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На чертеже 75 углы EOF и АОС- вертикальные; углы АОЕ и СОF — также вертикальные.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.
Пусть / 1 = 7 / 8 d (черт. 76). Смежный с ним / 2 будет равен 2d — 7 / 8 d , т. е. 1 1 / 8 d .
Таким же образом можно вычислить, чему равны / 3 и / 4.
/ 3 = 2d — 1 1 / 8 d = 7 / 8 d ; / 4 = 2d — 7 / 8 d = 1 1 / 8 d (черт. 77).
77).
Мы видим, что / 1 = / 3 и / 2 = / 4.
Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой.
Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными.
Убедиться в справедливости свойства вертикальных углов необходимо путём рассуждения, путём доказательства.
Доказательство можно провести следующим образом (черт. 78):
/ a + / c = 2d ;
/ b + / c = 2d ;
(так как сумма смежных углов равна 2d ).
/ a + / c = / b + / c
(так как и левая часть этого равенства равна 2d , и правая его часть тоже равна 2d ).
В это равенство входит один и тот же угол с .
Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: / a = / b , т. е. вертикальные углы равны между собой.
При рассмотрении вопроса о вертикальных углах мы сначала объяснили, какие углы называются вертикальными, т. е. дали определение вертикальных углов.
Затем мы высказали суждение (утверждение) о равенстве вертикальных углов и в справедливости этого суждения убедились путём доказательства. Такие суждения, справедливость которых надо доказывать, называются теоремами . Таким образом, в данном параграфе мы дали определение вертикальных углов, а также высказали и доказали теорему об их свойстве.
В дальнейшем при изучении геометрии нам постоянно придётся встречаться с определениями и доказательствами теорем.
3. Сумма углов, имеющих общую вершину.
На чертеже 79 / 1, / 2, / 3 и / 4 расположены по одну сторону прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют развёрнутый угол, т. е.
В сумме эти углы составляют развёрнутый угол, т. е.
/ 1+ / 2+/ 3+ / 4 = 2d .
На чертеже 80 / 1, / 2, / 3, / 4 и / 5 имеют общую вершину. В сумме эти углы составляют полный угол, т. е. / 1 + / 2 + / 3 + / 4 + / 5 = 4d .
Упражнения.
1. Один из смежных углов равен 0,72 d. Вычислить угол, составленный биссектрисами этих смежных углов.
2. Доказать, что биссектрисы двух смежных углов образуют прямой угол.
3. Доказать, что если два угла равны, то равны и их смежные углы.
4. Сколько пар смежных углов на чертеже 81?
5. Может ли пара смежных углов состоять из двух острых углов? из двух тупых углов? из прямого и тупого угла? из прямого и острого угла?
6. Если один из смежных углов прямой, то что можно сказать о величине смежного с ним угла?
7. Если при пересечении двух прямых линий один угол прямой, то что можно сказать о величине остальных трёх углов?
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами.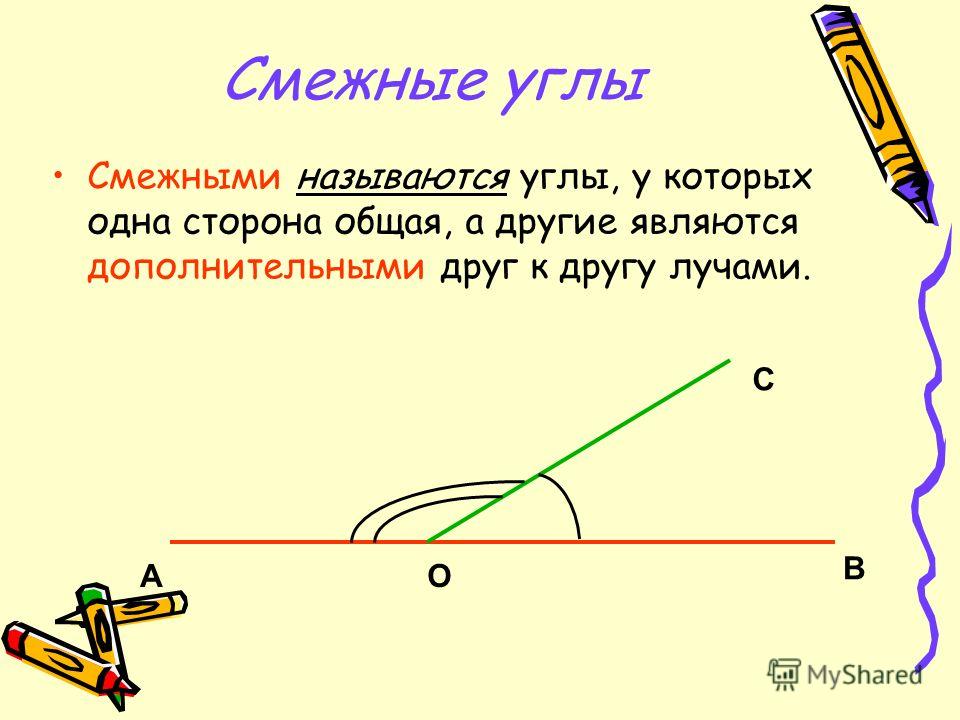 На рисунке 20 углы АОВ и ВОС смежные.
На рисунке 20 углы АОВ и ВОС смежные.
Сумма смежных углов равна 180°
Теорема 1. Сумма смежных углов равна 180°.
Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .
Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.
Вертикальные углы равны
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).
Теорема 2. Вертикальные углы равны.
Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1 ∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.
Отсюда заключаем, что ∠ АОВ = ∠ COD.
Следствие 1. Угол, смежный с прямым углом, есть прямой угол.
Рассмотрим две пересекающиеся прямые АС и BD (рис.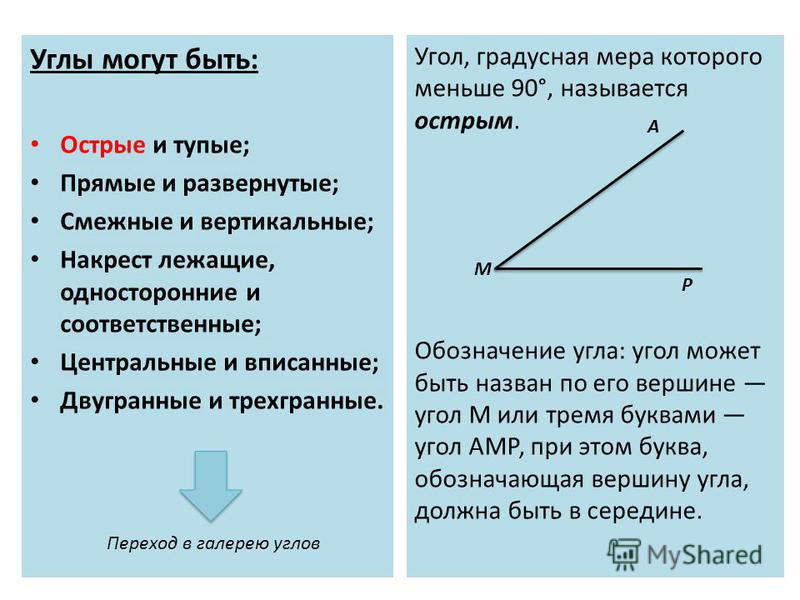 3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.
3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.
АН — перпендикуляр к прямой
Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.
Чертежный угольник
Справедлива следующая теорема.
Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис. 5).
5).
Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.
Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».
Пример 1. Один из смежных углов равен 44°. Чему равен другой?
Решение. Обозначим градусную меру другого угла через x , тогда согласно теореме 1.
44° + х = 180°.
Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.
Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?
Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1. 2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.
2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.
∠ АОС = 180° — ∠ COD = 180° — 45° = 135°.
Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.
Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.
Значит, смежные углы равны 45° и 135°.
Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.
Решение. Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол
АОС) смежный с углом COD, и, значит, по теореме 1
∠ BOD = ∠ АОС = 180° — 50° = 130°.
Что такое смежный угол
Угол – это геометрическая фигура (рис.1), образованная двумя лучами OA и OB (стороны угла), исходящими из одной точки O (вершина угла).
СМЕЖНЫЕ УГЛЫ — два угла, сумма которых равна 180°. Каждый из этих углов дополняет другой до развернутого угла.
Смежные углы — (Agles adjacets) такие, которые имеют общую вершину и общую сторону. Преимущественно под этим именем подразумеваются такие углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через.
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
рис. 2
На рисунке 2 углы a1b и a2b смежные. У них общая сторона b, а стороны a1, a2 — дополнительные полупрямые.
рис. 3
На рисунке 3 изображена прямая AB, точка C расположена между точками A и B. Точка D — точка не лежащая на прямой AB. Получается, что углы BCD и ACD смежные. У них общая сторона CD, а стороны CA и CB дополнительные полупрямые прямой AB, так как точки A, B разделены начальной точкой C.
Теорема о смежных углах
Теорема: сумма смежных углов равна 180°
Доказательство:
Углы a1b и a2b смежные (см.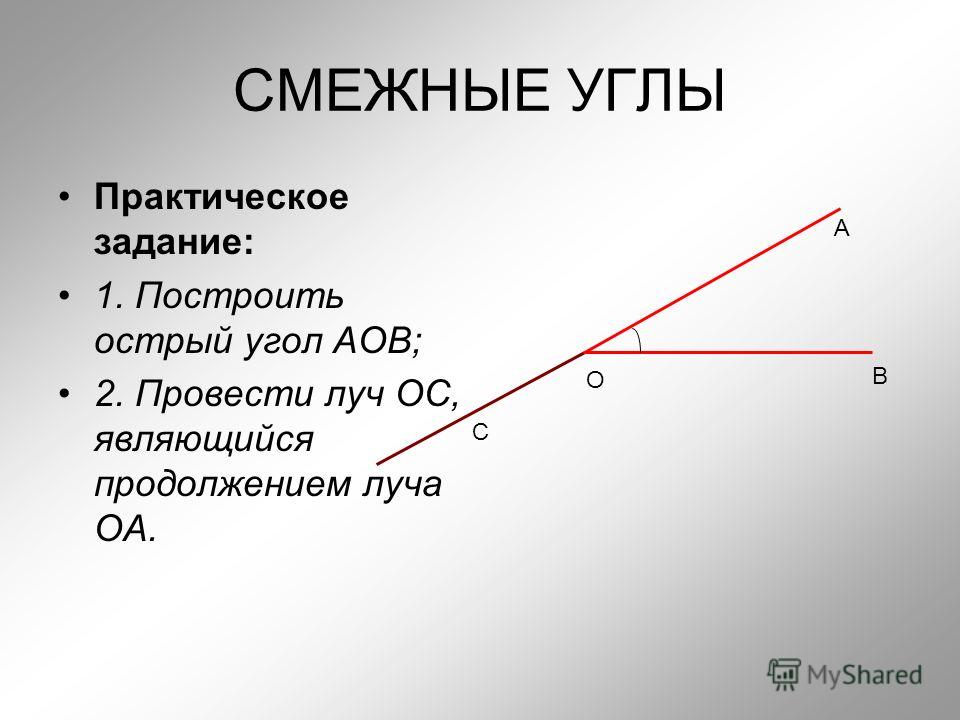 рис. 2) Луч b проходит между сторонами a1, и a2 развернутого угла. Следовательно, сумма углов a1b и a2b равна развернутому углу, то есть 180°. Теорема доказана.
рис. 2) Луч b проходит между сторонами a1, и a2 развернутого угла. Следовательно, сумма углов a1b и a2b равна развернутому углу, то есть 180°. Теорема доказана.
Угол, равный 90° называется прямым. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом также прямой угол. Угол, меньший 90° называется острым, а угол больше 90° — тупым. Так как сумма смежных углов равна 180°, значит угол, смежный с острым углом — тупой угол. А угол смежный с тупым углом — острый угол.
Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.
Определение 1. Углом называется часть плоскости, ограниченная двумя лучами с общим началом.
Определение 1.1. Углом называют фигуру, состоящую из точки — вершины угла — и двух различных полупрямых, исходящих из этой точки, — сторон угла.
Например, угол ВОС на рис1 Рассмотрим сначала две пересекающиеся прямые. При пересечении прямые образуют углы. Есть частные случаи:
При пересечении прямые образуют углы. Есть частные случаи:
Определение 2. Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым.
Определение 3. Прямой угол — это угол величиной в 90 градусов.
Определение 4. Угол, меньший 90 градусов, называется острым углом.
Определение 5. Угол, больший 90 градусов и меньший 180 градусов, называется тупым углом.
пересекающиеся прямые.
Определение 6. Два угла, одна сторона которых общая, а другие стороны лежат на одной прямой, называются смежными.
Определение 7. Углы, стороны которых продолжают друг друга, называются вертикальными углами.
На рисунке 1:
смежные: 1 и 2; 2 и 3; 3 и 4; 4 и 1
вертикальные: 1 и 3; 2 и 4
Теорема 1. Сумма смежных углов равна 180 градусов.
Для доказательства рассмотрим на рис. 4 смежные углы АОВ и ВОС. Их суммой является развернутый угол АОС. Поэтому сумма данных смежных углов равна 180 градусов.
рис. 4
Связь математики с музыкой
«Раздумывая об искусстве и науке, об их взаимных связях и противоречиях, я пришел к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая духовная деятельность человека и, что между ними размещается все, что человечество создало в области науки и искусства.»
Г. Нейгауз
Казалось бы, искусство — весьма отвлеченная от математики область. Однако связь математики и музыки обусловлена как исторически, так и внутренне, несмотря на то, что математика — самая абстрактная из наук, а музыка — наиболее отвлеченный вид искусства.
Консонанс определяет приятное для слуха звучание струны
В основе этой музыкальной системы были два закона, которые носят имена двух великих ученых — Пифагора и Архита. Вот эти законы:
1. Две звучащие струны определяют консонанс, если их длины относятся как целые числа, образующие треугольное число 10=1+2+3+4, т. е. как 1:2, 2:3, 3:4. Причем, чем меньше число n в отношении n:(n+1) (n=1,2,3), тем созвучнее получающийся интервал.
е. как 1:2, 2:3, 3:4. Причем, чем меньше число n в отношении n:(n+1) (n=1,2,3), тем созвучнее получающийся интервал.
2. Частота колебания w звучащей струны обратно пропорциональна ее длине l .
w = a: l ,
где а — коэффициент, характеризующий физические свойства струны.
Так же предложу вашему внимаю забавную пародию про спор двух математиков =)
Геометрия вокруг нас
Геометрия в нашей жизни имеет немаловажное значение. Ввиду того, что когда оглядеться вокруг, то не сложно будет заметить, что нас окружают различные геометрические фигуры. Мы с ними сталкиваемся повсюду: на улице, в классе, дома, в парке, в спортивном зале, в школьной столовой, в принципе везде, где бы мы с вами не находились.
Но темой сегодняшнего урока являются смежные угли. Поэтому давайте оглянемся вокруг и попытаемся в этом окружении найти углы. Если вы внимательно посмотрите в окно, то можете увидеть, что некоторые ветки дерева образуют смежные углы, а в перегородках на воротах можно заметить множество вертикальных углов. Приведите свои примеры смежных углов, которые вы наблюдаете в окружающей обстановке.
Приведите свои примеры смежных углов, которые вы наблюдаете в окружающей обстановке.
Задание 1.
1. Вот на столе на книжной подставке стоит книга. Какой угол она образует?
2. А вот ученик работает за ноутбуком. Какой угол вы видите здесь?
3. Какой угол образует фото рамка на подставке?
4. Как вы думаете, возможно ли, чтобы два смежных угла были равными?
Задание 2.
Перед вами изображена геометрическая фигура. Что это за фигура, назовите ее? А теперь назовите все смежные углы, которые вы можете увидеть на этой геометрической фигуре.
Задание 3.
Перед вами изображение рисунка и картины. Рассмотрите их внимательно и скажите, какие виды улов вы видите на картине, а какие углы на рисунке.
Решение задач
1) Даны два угла, относящиеся друг к другу как 1: 2, а смежные с ними — как 7: 5. Нужно найти эти углы.
2) Известно, что один из смежных углов больше другого в 4 раза. Чему равны смежные углы?
Чему равны смежные углы?
3) Необходимо найти смежные углы, при условии, что один из них на 10 градусов больше от второго.
Математический диктант на повторение ранее выученного материала
1) Выполните рисунок: прямые a I b пересекаются в точке А. Отметьте меньший из образованных углов цифрой 1, а остальные углы – последовательно цифрами 2,3,4; дополняющие лучи прямой а — через а1 и а2, а прямой b — через b1 i b2.
2) Пользуясь выполненным рисунком, впишите нужные значения и объяснения в места пропусков в тексте:
а) угол 1 и угол …. смежные, поскольку…
б) угол 1 и угол …. вертикальные, поскольку…
в) если угол 1 = 60°, то угол 2 = …, потому что…
г) если угол 1 = 60°, то угол 3 = …, потому что…
Решите задачи:
1. Может ли сумма 3-х углов, образованных при пересечении 2-х прямых, равняться 100°? 370°?
2. На рисунке найдите все пары смежных углов. А теперь вертикальных углов. Назовите эти углы.
3. Нужно найти угол, когда он втрое больше, чем смежный с ним.
4. Две прямые пересеклись между собой. В результате этого пересечения образовались четыре угла. Определите величину любого из них, при условии что:
а) сумма 2-х углов из четырех 84°;
б) разность 2-х углов из них равна 45°;
в) один угол в 4 раза меньше чем второй;
г) сумма трех из данных углов равна 290°.
Итог урока
1. назовите углы, которые образуются при пересечении 2-х прямых?
2. Назовите все возможные пары углов, находящихся на рисунке, и определите их вид.
Домашнее задание:
1. Найдите отношение градусных мер смежных углов, когда один из них на 54° больше второго.
2. Найдите углы, которые образуются при пересечении 2-х прямых, при условии, что один из углов равняется сумме 2-х других углов, смежных с ним.
3. Необходимо найти смежные углы, когда биссектриса одного из них образует со стороной второго угол, который больше чем второй угол на 60°.
4. Разница 2-х смежных углов равна трети от суммы этих двух углов. Определите величины 2-х смежных углов.
5. Разница и сумма 2-х смежных углов относятся как 1: 5 соответственно. Найдите смежные углы.
6. Разница двух смежных составляет 25% от их суммы. Как относятся величины 2-х смежных углов? Определите величины 2-х смежных углов.
Вопросы:
- Что такое угол?
- Какие бывают типы углов?
- Какая особенность смежных углов?
Предмети > Математика > Математика 7 класс
геометрия Flashcards | Chegg.com
Смежные углы, определение и свойства
Смежные углы — углы, у которых одна сторона общая, а другие стороны лежат на одной прямой. Свойство: сумма смежных углов 180º.
Вертикальные углы, определение и свойства
Вертикальные углы — пары углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого. Свойство: вертикальные углы равны.
Свойство: вертикальные углы равны.
Признаки равенства треугольников
(1) по двум сторонам и углу между ними, (2) по стороне и двум прилежащим углам, (3) по трем сторонам
Равнобедренный треугольник, свойства, признаки.
Свойства: 1) углы при основании равны. 2) медиана, проведенная к основанию, является биссектрисой и высотой
Признаки: 1) если в треугольнике два угла равны, то он равнобедренный. 2) если в треугольнике биссектриса является медианой или высотой, то он равнобедренный
Соответственные углы, определение
Соответственные углы — углы, образованные при пересечении двух прямых секущей.
Прямые параллельные, аксиома, свойства, признаки.
Аксиома: через данную точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Свойства: если две параллельные прямые пересечены третьей секущей, то 1) накрест лежащие и соответственные углы равны. 2) сумма односторонних углов равна 180°.
Признаки: Если две прямые пересечены третьей и 1) 2 накрест лежащих угла или 2 соответственных угла равны. 2) сумма двух односторонних углов 180°, то прямые параллельны.
2) сумма двух односторонних углов 180°, то прямые параллельны.
Теорема о сумме углов треугольника и выпуклого многоугольника
Сумма углов треугольника 180º.
Сумма внутренних углов выпуклого многоугольника (n — 2) •180°
Внешний угол треугольника, определение, теорема
Внешний угол — угол, смежный с внутренним углом треугольника.
Теорема: Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Соотношения между сторонами и углами треугольника
1) против большей стороны лежит больший угол.
2) против большего угла лежит большая сторона.
3) каждая сторона треугольника меньше суммы двух других сторон.
Неравенство треугольника
Неравенство треугольника: длина любой стороны треугольника меньше суммы длин двух других сторон.
признаки равенства прямоугольных треугольников
Признаки равенства прямоугольных треугольников: по 2 катетам, по катету и гипотенузе, по гипотенузе и острому углу, по катету и острому углу
Свойство медиан прямоугольного треугольника
Свойства медиан в прямоуг. △:
△:
1) Все медианы прямоугольного △ пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.
2) Медиана, проведенная к гипотенузе, равна половине гипотенузы.
3)Медиана, проведенная к гипотенузе, равна радиусу описанной окружности.
1) Свойство серединного перпендикуляра к отрезку. 2) Свойство серединных перпендикуляров к сторонам треугольника.
3) Существование окружности, описанной около треугольника.
4) Свойство высот треугольника.
Серединный перпендикуляр к отрезку — это прямая, ⊥ данному отрезку и проходящая через его середину.
1) Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
2) Серединные перпендикуляры к сторонам △ пересекаются в одной точке. Эта точка является центром описанной окружности.
3) Если около многоугольника можно описать окружность, то центр этой описанной окружности является точкой пересечения серединных перпендикуляров к сторонам многоугольника.
4) В прямоугольном △ высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.
Свойство биссектрис треугольника. Существование окружности, вписанной в треугольник.
1) Биссектриса △ делит сторону на отрезки, пропорциональные двум другим сторонам.
2) Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.
Параллелограмм, определение, свойства
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны.
Свойства параллелограмма:
1) Противоположные стороны и углы параллельны и равны.
2) Сумма углов параллелограмма, прилежащих к одной стороне, равна 180.
3) Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
4) Угол между высотами параллелограмма, проведенными из вершины тупого угла, равен острому углу параллелограмма.
5) Угол между высотами параллелограмма, проведенными из вершины острого угла, равен тупому углу параллелограмма.
Свойство диагоналей параллелограмма
Диагонали параллелограмма в точке пересечения делятся пополам.
Признаки параллелограмма
Признаки параллелограмма:
1) Если диагонали четырехугольника пересекаются и в точке пересечения делятся пополам, то этот четырехугольник параллелограмм.
2) Если в четырехугольнике две противоположные стороны параллельны и равны, то этот четырехугольник параллелограмм.
3) Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник параллелограмм.
4) Если в четырехугольнике противоположные углы попарно равны, то этот четырехугольник параллелограмм.
Прямоугольник, определение, свойства, признаки
Прямоугольник — это параллелограмм, у которого все углы прямые.
Свойства:
1) все свойства параллелограмма
2) диагонали прямоугольника в точке пересечения делятся пополам, равны.
Признаки:
1) Если в четырехугольнике все углы равны, то это прямоугольник.
2) Если в параллелограмме хотя бы один угол прямой, то это прямоугольник.
3) Если диагонали параллелограмма равны, то это прямоугольник.
4) Если около параллелограмма можно описать окружность, то это прямоугольник.
5) Если в параллелограмме квадрат диагонали равен сумме квадратов смежных сторон, то это прямоугольник.
Ромб, определение, свойства, признаки
Ромб — это параллелограмм, у которого все стороны равны.
Свойства:
1) все свойства параллелограмма
2) диагонали ромба взаимно ⊥, являются биссектрисами его углов.
Признаки:
1) Если у параллелограмма диагонали взаимно ⊥, то это ромб.
2) Если диагональ параллелограмма является биссектрисой его углов, то это ромб.
3) Если у четырехугольника все стороны равны, то это ромб.
4) Если смежные стороны параллелограмма равны, то это ромб.
Квадрат, определение, свойства
Квадрат — это прямоугольник, у которого все стороны равны.
Свойства:
1) Все свойства ромба и прямоугольника
2) Диагонали квадрата равны, точкой пересечения делятся пополам, взаимно ⊥, являются биссектрисами его углов.
Трапеция. Равнобедренная трапеция. Определение, свойства.
Трапеция — это четырехугольник, у которого две стороны параллельны, и две не параллельны.
Равнобедренная трапеция — это трапеция, у которой боковые стороны равны.
Свойства равнобедренной трапеции:
1) Углы при основании равнобедренной трапеции равны.
2) Сумма противолежащих углов равнобедренной трапеции равна 180°.
3) Диагонали равнобедренной трапеции равны.
4) Около любой равнобедренной трапеции можно описать окружность.
5) Высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, а другой — полуразности оснований.
Теорема Фалеса
Если параллельные прямые отсекают на одной стороне угла равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Средняя линия треугольника и трапеции, определения, свойства.
Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон.
Свойства: Средняя линия △, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине.
Средняя линия трапеции — это отрезок, соединяющий середины боковых сторон трапеции.
Свойства: Средняя линия трапеции параллельна основаниям и равна их полусумме.
Теорема Пифагора
В прямоугольном △ квадрат гипотенузы равен сумме квадратов катетов.
Перпендикуляр и наклонная к прямой. Расстояние от точки до прямой.
Наклонная — отличный от перпендикуляра отрезок, соединяющий точку с некоторой точкой на прямой.
Расстояние от точки до прямой — длина перпендикуляра, опущенного из данной точки на прямую.
Свойства перпендикуляра и наклонной:
1) Любая наклонная больше перпендикуляра.
2) Равные наклонные имеют равные проекции.
3) Из двух наклонных больше та, у которой проекция больше
Соотношения между углами и сторонами в прямоугольном △. sin/cos/tg/ctg
Соотношения между углами и сторонами в прямоугольном △ задаются тригонометрическими функциями : синусом, косинусом, тангенсом, котангенсом.
Синус — отношение противолежащего катета к гипотенузе.
Косинус — отношение прилежащего катета к гипотенузе.
Тангенс — отношение противолежащего катета к прилежащему.
Котангенс — отношение прилежащего катета к противолежащему.
sin/cos/tg 30, 45, 60
sin30= 1/2
sin45= (корень из 2)/2
sin60= (корень из 3)/2
cos30= (корень из 3)/2
cos45= (корень из 2)/2
cos60= 1/2
tg30= (корень из 3)/3
tg45= 1
tg60= корень из 3
Основное тригонометрическое тождество
sin² + cos² = 1
tg = sin / cos
ctg = cos / sin
sin (180 — a) = sin(a)
cos (180 — a) = -cos(a)
Окружность и круг. Диаметр и радиус. Концентрические окружности.
Окружность — геометрическое место точек плоскости, расстояние от которых до центра окружности равно.
Круг — это часть плоскости, ограниченная окружностью.
Диаметр — хорда, проходящая через центр.
Радиус — отрезок, соединяющий центр окружности с любой ее точкой.
Концентрические окружности — окружности, имеющие общий центр.
Касание двух окружностей. Внутреннее и внешнее касание.
Внешнее касание окружностей — касание, при котором центры окружностей лежат по разные стороны от общей касательной.
Внутреннее касание окружностей — касание, при котором центры окружностей лежат по одну сторону от общей касательной.
Взаимное расположение прямой и окружности. Касательная к окружности. Свойство.
Взаимное расположение прямой к окружности:
(d — расстояние от прямой до центра окружности)
1) если d > r, то прямая и окружность не имеют общих точек
2) если d = r, то прямая и окружность имеют 1 общую точку (касательная)
3) если d < r, то прямая и окружность имеют 2 общих точки (секущая)
Касательная — прямая, имеющая с окружностью 1 общую точку.
Свойство:
1) Касательная к окружности ⊥ к радиусу, проведенному в точку касания.
2) Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности
Хорда окружности. Свойство диаметра окружности, перпендикулярного хорде.
Свойство диаметра окружности, перпендикулярного хорде.
Хорда — отрезок, соединяющий любые две точки окружности.
Свойство: если хорда ⊥ диаметру, то диаметр проходит через её середину.
Свойство отрезков пересекающихся хорд.
Если две хорды окружности пересекаются в точке, то произведение отрезков одной хорды равно произведению отрезков другой хорды
Углы в окружности : центральный, вписанный. градусная мера дуги окружности. Теорема о вписанном угле.
Центральный угол — это угол, вершина которого находится в центре окружности.
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают ее. Равен половине соответствующего ему центрального угла.
Градусная мера дуги = градусная мера соответствующего центрального угла. Для дуги, большей полуокружности, градусной мерой будет разность (360 — центральный угол)
Свойство угла, опирающегося на диаметр, с вершиной, лежащей на окружности
Вписанный угол (угол с лежащей на окружности вершиной), опирающийся на диаметр, прямой.
Подобные треугольники, определение, признаки. Коэффициент подобия.
Подобные △ — △, у которых углы равны, а стороны пропорциональны.
Признаки:
1) Если два угла одного △ равны двум углам другого △, то такие △ подобны (по 2 углам)
2) Если две стороны одного △ пропорциональны двум сторонам другого △ и углы, образованные этими сторонами, равны, то такие △ подобны (по 2 сторонам и углу между ними)
3) Если стороны одного △ пропорциональны сторонам другого треугольника, то такие △ подобны (по 3 сторонам)
Коэффициент подобия — это число, равное отношению сходственных сторон в подобных фигурах.
Отношение площадей подобных треугольников
Отношение площадей подобных △ равно квадрату коэффициента подобия
Координаты точки. Координаты середины отрезка. Вычисление расстояния между двумя точками через их координаты.
Координаты точки — это пара чисел, в которой на первом месте стоит абсцисса, а на втором — ордината точки.
Координаты середины отрезка АВ с концами A (xa) и B(xb) имеет вид (xa+xb)/2
Расстояние между двумя точками A(xa, ya) и B(xb, yb):
AB = √(xb — xa)2 + (yb — ya)2 (все под корнем)
Уравнение окружности
Уравнение окружности: x² + y² = r²
Теорема синусов
Теорема синусов:
Стороны △ пропорциональны синусам противолежащих углов.
a/sin(a) = b/sin(b) = c/sin(c)
Теорема косинусов
Теорема косинусов:
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a² = b² + c² — 2bc * cos(a)
Площадь треугольников ( формул)
1) половина произведения его стороны на высоту, проведённую к этой стороне.
1/2 a*ha
2) половина произведения двух его сторон на синус угла между ними.
1/2 a*b*sin
3) квадратный корень из произведения полупериметра этого треугольника и разностей полупериметра и всех его сторон.
√p*(p-a)(p-b)(p-c)
4) отношение произведения всех его сторон к четырём радиусам описанной окружности.
abc/4R
5) произведение полупериметра и радиуса вписанной окружности
(a+b+c)/2 * r
=
pr
Площадь прямоугольного △
половина произведения катетов
1/2 a*b
Площадь равностороннего △
четверть произведения квадрата стороны этого треугольника и квадратного корня из трёх
(a² √3)/4
Площадь прямоугольника
произведение 2 соседних сторон
a*b
Площадь квадрата
1) квадрат стороны
a²
2) половина квадрата его диагонали
1/2d²
Площадь параллелограмма
1) произведение стороны на высоту, проведённую к этой стороне.
a*ha
2) произведение двух соседних сторон на синус угла между ними.
a*b*sin (a)
Площадь ромба
1) произведение квадрата его стороны на синус одного из его углов.
a²*sin a
2) половина произведения диагоналей
1/2*d1*d2
Площадь трапеции
1) произведение полусуммы её оснований на высоту
(a+b)/2 * h
2) произведение средней линии на высоту.
m*h
Площадь вписанного четырёхугольника
квадратный корень из произведения разностей полупериметра этого четырёхугольника и всех его сторон
√(p-a)(p-b)(p-c)(p-d)
Площадь круга
1) произведение числа «пи» на квадрат радиуса.
пи*r²
2) четверть произведения числа «пи» на квадрат диаметра
(пи*d²)/4
Площадь кругового сектора
1) (пи*R²*n)/360, где n = угол дуги в градусах
2) 1/2 * n * R
Формула длины дуги окружности, ее длины, площади круга
1) Формула длины дуги окружности:
l = (пи*R*n)/180, где n = угол дуги в градусах
2) Формула длины окружности:
C = 2*пи*R = пи*D
1) Понятие вектора
2) Модуль вектора
1) Вектор — отрезок, для которого указано, какая из его граничных точек считается началом, а какая концом
Коллинеарные вектора — ненулевые вектора, которые лежат либо на одной прямой, либо на параллельных прямых.
Равные вектора — сонаправленные вектора, у которых длины равны.
2) Модуль вектора — длина направленного вектора
|a| = √x2 + y2
Сумма векторов
1) правило треугольника:
от конца 1 вектора откладываем 2 вектор, при соединении начала 1 вектора с концом 2 вектора образуется 3 вектор, который будет являться суммой первых двух векторов.
2) правило параллелограмма:
из любого начала О строим векторы ОА и ОВ;
на отрезках ОА, ОВ строим параллелограмм ОАСВ. Вектор диагонали ОС = сумма векторов OA и OB.
Разность векторов
Объединим концы векторов a и b. Вектор, у которого конец совпадает с началом вектора a, начало с началом вектора b, и будет разностью векторов.
a — b = a + (-b)
Произведение вектора на число
Произведение вектора на число а называется такой вектор b, длина которого равна l k l * l a l, тоесть |b| = |k| * |a|
причем a↑↑b, если k > 0
a↑↓b, если k < 0
k * a = {k * ax; k * ay}
1) Координаты вектора.
2) Вычисление модуля вектора по его координатам.
1) Чтобы найти координаты вектора AB, необходимо из координат конца вычесть координаты начала.
AB = {Bx — Ax ; By — Ay}
2) Вычисление модуля вектора по его координатам: |a| = √x2 + y2
1) Нахождение координат суммы и разности векторов.
2) Нахождение координат произведения вектора на число по кординатам векторов
1) Каждая координата суммы 2 векторов равна сумме соотв. координат этих векторов
a + b {x1+x2; y1+y2}
— Каждая координата разности 2 векторов равна разности соотв. координат этих векторов
a — b {x1-x2; y1-y2}
2) Каждая координата произведения вектора на число равна произведению соотв. координаты вектора на это число.
ka {kx1; ky1}
Скалярное произведение двух векторов и его свойства
Скалярное произведение двух векторов — произведение модулей этих векторов умноженного на косинус угла между ними: a * b = |a| * |b| * cos(a)
Свойства:
1) Скалярное произведение вектора самого на себя равно квадрату его модуля:
a * a = |a|²
2) Если скалярное произведение двух не нулевых векторов равно нулю, то угол между векторами равен 90°
a * b = 0 a^b = 90°; (a ┴ b)
3) Если скалярное произведение двух не нулевых векторов больше нуля, то угол между векторами больше или равен 0°, но меньше 90°
a * b > 0 0° ≤ a^b < 90°
4) Если скалярное произведение двух не нулевых векторов меньше нуля, то угол между векторами больше 90°, но меньше или равен 180°
a * b < 0 90° < a^b ≤ 180°
5) Если вектора a и b сонаправлены, то их скалярное произведение равно произведению l a l * l b l
если a↑↑b, то l a l * l b l
Примеры фигур, имеющих центр или ось симметрии
Центральная симметрия — это симметрия относительно точки.
Примеры фигур:
1) параллелограмм (ц. сим. — точка пересечения диагоналей)
2) окружность (ц.с. — её центр)
3) прямая (любая точка прямой)
Осевая симметрия — это симметрия относительно прямой.
Примеры фигур: прямоугольник, ромб, квадрат, окружность, равнобедренная трапеция, равнобедренный треугольник
Правильный многоугольник. Сумма углов. Угол. Формула стороны a(n).
Правильный многоугольник — это многоугольник, у которого все стороны и углы равны.
Сумма углов: 180(n-2)
Сумма угла:
180(n-2) / n
Формула стороны правильного n-угольника через радиус описанной окружности:
a(n) = 2*R*sin* (180/n)
Формула радиуса вписанной окружности :
r = R * cos (180/n)
Пропорциональные отрезки в прямоугольном треугольнике
1) Высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу.
2) Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу
Нахождение стороны в прямоугольном треугольнике
Нахождение стороны, зная другую сторону и угол
Мы можем найти неизвестную сторону в прямоугольном треугольнике, зная:
- одну длину и
- один угол (кроме прямого угла, т.
 е.).
е.).
Пример: Глубина до морского дна
Корабль стоит на якоре на морском дне.
Мы знаем:
- длину кабеля (30 м) и
- угол, который кабель образует с морским дном
Итак, мы должны найти глубину!
Но как?
Ответ: использовать синус, косинус или тангенс!
Но какой?
Какой из синус, косинус или тангенс использовать?
Чтобы узнать какой, сначала присваиваем наименования сторонам:
- Смежный примыкает (рядом) к углу,
- Противоположный напротив угла,
- и самая длинная сторона Гипотенуза .
Теперь, для стороны, которую мы уже знаем , и стороны , которую мы пытаемся найти , мы используем первые буквы их имен и фразу «SOHCAHTOA», чтобы решить, какая функция:
SOH . | S ine: sin(θ) = O pposite / H ypotenuse | |
…КАХ… | C осин: cos(θ) = A djacent / H ypotenuse | |
…ТОА | T угол: tan(θ) = O pposite / A djacent |
Так:
Пример: глубина до морского дна (продолжение)
Найдите названий двух сторон, над которыми мы работаем:
- сторона, которую мы знаем, это 0 гипотенуза 8030
- сторона, которую мы хотим найти, равна . Противолежащая угол (проверьте сами, что «d» находится напротив угла 39°)
Теперь используйте первые буквы этих двух сторон ( O pposite и H ypotenuse) и фразу «SOHCAHTOA», которая дает нам « SOH cahtoa», что говорит нам о том, что нам нужно использовать Sine :
S ine: sin(θ) = O pposite / H ypotenuse
90 Теперь мы поместим 90 значений
sin(39°) = d / 30
И решить это уравнение
Но как вычислить sin(39°) . .. ?
.. ?
Воспользуйтесь калькулятором.
Введите 39 и нажмите клавишу «sin».
Это просто!
sin(39°) = 0,6293…
Итак, теперь у нас есть:
0,6293… = d / 30
Теперь немного переставляем: 50 0090, и решаем немного: где: 0,6293… = d / 30
Поменять стороны местами: d / 30 = 0,6293…
Умножить обе стороны на 30:d = 0,6293… x 30
Вычислить:d = 18,88 к 2 десятичные знаки
Глубина анкерного кольца под отверстием составляет 18,88 м
Шаг за шагом
Вот четыре шага, которые нужно выполнить:
- Шаг 1 Найдите названия двух сторон, которые мы используем, одну, которую мы пытаемся найти, и другую, которую мы уже знаем, из противоположного, прилежащего и гипотенузы.
- Шаг 2 Используйте SOHCATOA, чтобы решить, какой из синус, косинус или тангенс использовать в этом вопросе.

- Шаг 3 Для синуса запишите Противоположность/Гипотенуза, для Косинуса запишите Смежность/Гипотенуза или для Тангенса запишите Противоположный/Смежный. Одним из значений является неизвестная длина.
- Шаг 4 Решите, используя свой калькулятор и свои навыки в алгебре.
Примеры
Давайте рассмотрим еще несколько примеров:
Пример: найти высоту самолета.
Мы знаем, что расстояние до самолета равно 1000
А угол равен 60°
Какова высота самолета?
Осторожно! Угол 60° находится вверху, поэтому сторона «h» равна Смежному углу!
- Шаг 1 Мы используем две стороны: A djacent (h) и H ypotenuse (1000).
- Шаг 2 SOH CAH TOA говорит нам использовать C озин.
- Шаг 4 Решить:
Начните с: cos 60° = h/1000
Swap: h/1000 = cos 60°
Calculate cos 60°: h/1000 = 0. 5
5
Multiply both sides by 1000: h = 0.5 x 1000
ч = 500
Высота плоскости = 500 метров
Пример: найдите длину боковой
Y :- Шаг 1 . ппозит (у)
и A djacent (7).
- Шаг 2 SOHCAH TOA говорит нам использовать агент T .
- Шаг 4 Решить:
Начните с:tan 53° = y/7
Перестановка:y/7 = tan 53°
Умножьте обе стороны на 7:y = 7 tan 53°
Вычислите:y = 7 x 1,32704…
y = 9,29 (до 2 знаков после запятой)
Сторона y = 9,29
Пример: Радиомачта
Имеется мачта высотой 70 метров.
Трос идет к вершине мачты под углом 68°.
Какой длины провод?
- Шаг 1 Мы используем две стороны: O pposite (70) и H ypotenuse (w).
- Шаг 2 SOH CAHTOA говорит нам использовать S ine.

- Шаг 3 Запишите:
sin 68° = 70/ш
- Шаг 4 Решить:
Неизвестная длина стоит внизу (в знаменателе) дроби!
Таким образом, мы должны использовать несколько иной подход при решении:
Начните с:sin 68° = 70/w
Умножьте обе части на w:w × (sin 68°) = 70
Разделите обе части на » sin 68°»:w = 70 / (sin 68°)
Рассчитать:w = 70 / 0,9271…
w = 75,5 м (на 1 место)
Длина провода = 75,5 м
Тригонометрия прямоугольного треугольника | Алгебра и тригонометрия
Эверест, расположенный на границе между Китаем и Непалом, является самой высокой горой в мире. Измерение его высоты — непростая задача, и на самом деле фактическое измерение было источником споров на протяжении сотен лет. Процесс измерения включает использование треугольников и раздел математики, известный как тригонометрия. В этом разделе мы определим новую группу функций, известных как тригонометрические функции, и выясним, как их можно использовать для измерения высоты, например высоты самых высоких гор.
Использование прямоугольных треугольников для вычисления тригонометрических функций
(Рисунок) показывает прямоугольный треугольник с вертикальной стороной, длина которой [латекс]\,у\,[/латекс], а горизонтальная сторона имеет длину[латекс]\,х.\ ,[/latex]Обратите внимание, что треугольник вписан в окружность радиусом 1. Такая окружность с центром в начале координат и радиусом 1 называется единичной окружностью.
Рис. 1.
Тригонометрические функции можно определить через угол t и длины сторон треугольника. Прилегающая сторона — это сторона, ближайшая к углу, х . (Смежный означает «рядом с».) Противоположная сторона — это сторона напротив угла, y . Гипотенуза — это сторона треугольника, противоположная прямому углу 1. Эти стороны обозначены на (рис.).
Рис. 2. Стороны прямоугольного треугольника по отношению к углу[латекс]\,t[/латекс]
Дан прямоугольный треугольник с острым углом[латекс]\,t,[/латекс] перечислены первые три тригонометрические функции.
[латекс]\begin{array}{ccc}\phantom{\rule{2.5em}{0ex}}\text{Sine}\hfill & \phantom{\rule{1em}{0ex}}\text{sin }t\hfill & =\frac{\text{напротив}}{\text{гипотенуза}}\hfill \end{массив}[/latex]
[латекс]\begin{array}{ccc}\phantom{\rule{1.5em}{0ex}}\text{Косинус}\hfill & \phantom{\rule{1em}{0ex}}\text{cos }t\hfill & =\frac{\text{смежный}}{\text{гипотенуза}}\hfill\end{массив}[/latex]
[латекс]\begin{array}{ccc}\hfill \text {Tangent} & \phantom{\rule{1em}{0ex}}\text{tan} t\hfill & =\frac{\text{напротив}}{\text{смежный}}\hfill \end{массив}[ /latex]
Обычная мнемоника для запоминания этих отношений — SohCahToa, образованная из первых букв « S ine is o pposite over h ypotenuse, C osine is a djacent over h ypotenuse, T angent is или рядом с и рядом».
Для треугольника, показанного на (Рисунок), имеем следующее.
[латекс]\begin{array}{ccc}\hfill \text{sin }t& =& \frac{y}{1}\hfill \\ \hfill \text{cos }t& =& \frac{x} {1}\hfill \\ \hfill \text{tan }t& =& \frac{y}{x}\hfill \end{массив}[/latex]
Как сделать
Зная длины сторон прямоугольного треугольника и одного из острых углов, найдите синус, косинус и тангенс этого угла.
- Найдите синус как отношение противолежащего катета к гипотенузе.
- Найдите косинус как отношение прилежащего катета к гипотенузе.
- Найдите тангенс как отношение противолежащего катета к прилежащему.
Вычисление тригонометрической функции прямоугольного треугольника
Учитывая треугольник, показанный на рисунке, найдите значение [latex]\,\mathrm{cos}\,\alpha .[/latex]
Рисунок 3.
Показать решение
Попробуйте
Учитывая треугольник, показанный на (Рисунок), найдите значение [латекс]\,\текст{sin}\,t. [/латекс]
[/латекс]
Рис. 4.
Показать решение
Взаимные функции
Помимо синуса, косинуса и тангенса есть еще три функции. Они также определяются в терминах сторон треугольника.
[латекс]\begin{array}{ccc}\phantom{\rule{2em}{0ex}}\text{Secant}\hfill & \phantom{\rule{1em}{0ex}}\text{sec} t\hfill & =\frac{\text{гипотенуза}}{\text{adjacent}}\hfill \end{array}[/latex]
[latex]\begin{array}{ccc}\hfill \phantom{ \rule{1.3em}{0ex}}\text{Косеканс}& \hfill \phantom{\rule{1em}{0ex}}\text{csc }t& =\frac{\text{гипотенуза}}{\text{ напротив}}\hfill \end{массив}[/latex]
[латекс]\begin{array}{ccc}\hfill \text{Котангенс}& \phantom{\rule{1em}{0ex}}\text{ кроватка }t& =\frac{\text{смежный}}{\text{напротив}}\hfill \end{массив}[/latex]
Взгляните еще раз на эти определения. Эти функции обратны первым трем функциям.
[латекс]\begin{array}{cccccc}\hfill \text{sin}t& =& \frac{1}{\text{csc}t}\hfill & \hfill\phantom{\rule{2em}{ 0ex}}\text{csc }t& =& \frac{1}{\text{sin }t}\hfill \\ \hfill \text{cos }t& =& \frac{1}{\text{sec }t }\hfill & \hfill \phantom{\rule{2em}{0ex}}\text{sec}t& =& \frac{1}{\text{cos}t}\hfill \\ \hfill\text{tan} t& =& \frac{1}{\text{cot }t}\hfill & \hfill \phantom{\rule{2em}{0ex}}\text{cot }t& =& \frac{1}{\text{ загар }t}\hfill \end{массив}[/latex]
При работе с прямоугольными треугольниками помните, что одни и те же правила применяются независимо от ориентации треугольника. Фактически, мы можем вычислить шесть тригонометрических функций любого из двух острых углов треугольника на (рис.). Сторона, противолежащая одному острому углу, является стороной, примыкающей к другому острому углу, и наоборот.
Фактически, мы можем вычислить шесть тригонометрических функций любого из двух острых углов треугольника на (рис.). Сторона, противолежащая одному острому углу, является стороной, примыкающей к другому острому углу, и наоборот.
Рис. 5. Сторона, примыкающая к одному углу, противоположна другому углу.
Многие задачи требуют всех шести тригонометрических функций для данного угла в треугольнике. Возможная стратегия заключается в том, чтобы сначала найти синус, косинус и тангенс углов. Затем легко найдите другие тригонометрические функции, используя обратные величины.
How To
Зная длины сторон прямоугольного треугольника, вычислите шесть тригонометрических функций одного из острых углов.
- При необходимости нарисуйте прямоугольный треугольник и обозначьте полученный угол.
- Определите угол, прилежащую сторону, сторону, противоположную углу, и гипотенузу прямоугольного треугольника.

- Найдите нужную функцию:
- синус как отношение противолежащего катета к гипотенузе
- косинус как отношение прилежащего катета к гипотенузе
- тангенс как отношение противоположной стороны к прилежащей стороне
- секанс как отношение гипотенузы к прилежащему катету
- косеканс как отношение гипотенузы к противолежащему катету
- котангенс как отношение прилежащей стороны к противолежащей стороне
Вычисление тригонометрических функций углов, не находящихся в стандартном положении
Используя треугольник, показанный на (рис.), вычислите[latex]\,\mathrm{sin}\,\alpha ,\mathrm{cos}\,\alpha ,\mathrm {tan}\,\alpha ,\mathrm{sec}\,\alpha ,\mathrm{csc}\,\alpha ,\text{and}\,\mathrm{cot}\,\alpha .[/latex]
Рис. 6.
Показать решение
Анализ
Другой подход состоял бы в том, чтобы сначала найти синус, косинус и тангенс. Затем найдите их обратные значения, чтобы определить другие функции.
Затем найдите их обратные значения, чтобы определить другие функции.
[латекс]\text{sec}\alpha =\frac{1}{\text{cos}\alpha}=\frac{1}{\frac{3}{5}}=\frac{5}{ 3}[/латекс]
[латекс]\текст{csc}\alpha =\frac{1}{\text{csc}\alpha}=\frac{1}{\frac{4}{5}}= \frac{5}{4}[/latex]
[латекс]\text{cot}\alpha =\frac{1}{\text{tan}\alpha}=\frac{1}{\frac{4 }{3}}=\frac{3}{4}[/latex]
Попробуйте
Используя треугольник, показанный на (Рисунок), оцените [латекс]\,\text{sin}\,t,\text{cos}\,t,\text{tan}\,t,\text {sec}\,t,\text{csc}\,t,\text{and}\,\text{cot}\,t.[/latex]
Рис. 7.
Показать решение
Нахождение тригонометрических функций специальных углов с использованием длин сторон
Полезно оценивать тригонометрические функции, поскольку они связаны со специальными углами — кратными [латекс]\, 30°, 60°, [/латекс] и [латекс] \,45°.\,[/latex]Помните, однако, что при работе с прямоугольными треугольниками мы ограничены углами между[latex]\,0°\text{ и 90°}\text{. }[/latex]
}[/latex]
Предположим, у нас есть [латекс]\,30°,60°,90°\,[/латекс]треугольник, который также можно описать как[латекс]\ ,\frac{\pi }{6},\frac{\pi }{3},\frac{\pi }{2}\,[/latex]треугольник. Стороны имеют длины в соотношении [латекс]\,s,\sqrt{3}s,2s.\,[/latex]Стороны a[латекс]\,45°,45°,90°\,[/ латекс]треугольник, который также может быть описан как [латекс]\,\frac{\pi }{4},\frac{\pi }{4},\frac{\pi }{2}\,[/latex ]треугольник, имеют длины в отношении[латекс]\,s,s,\sqrt{2}s.\,[/latex]Эти отношения показаны на (Рисунок).
Рисунок 8. Длины сторон особых треугольников
Затем мы можем использовать отношения длин сторон для вычисления тригонометрических функций особых углов.
How To
Учитывая тригонометрические функции специального угла, оцените их, используя длины сторон.
- Используйте длины сторон, показанные на (Рисунок), для специального угла, который вы хотите оценить.
- Используйте соотношение длин сторон, соответствующее функции, которую вы хотите оценить.

Вычисление тригонометрических функций специальных углов с использованием длин сторон
Найдите точное значение тригонометрических функций [латекс]\,\frac{\pi }{3},[/латекс]с использованием длин сторон.
Показать решение
Попробуйте
Найдите точное значение тригонометрических функций [латекс]\,\frac{\pi }{4},[/латекс], используя длины сторон.
Показать решение
Использование равных кофункций дополнений
Если мы более внимательно посмотрим на соотношение между синусом и косинусом специальных углов, мы заметим закономерность. В прямоугольном треугольнике с углами [латекс]\,\frac{\pi }{6}\,[/latex]и [латекс]\,\frac{\pi }{3},[/latex] мы видим, что синус [латекс]\,\frac{\pi }{3},[/latex], а именно [латекс]\,\frac{\sqrt{3}}{2},[/latex] также является косинусом [латекс]\,\frac{\pi }{6},[/latex], а синус [латекс]\,\frac{\pi }{6},[/latex], а именно [латекс]\,\frac {1}{2},[/latex] также является косинусом [latex]\,\frac{\pi }{3}. [/latex]
[/latex]
[латекс]\begin{array}{cccc}\hfill \mathrm{sin}\frac{\pi }{3}& =\mathrm{cos}\frac{\pi }{6}\hfill & =\ frac{\ sqrt {3} s} {2s} \ hfill & = \ frac {\ sqrt {3}} {2} \ hfill \\ \ hfill \ mathrm {sin} \ frac {\ pi} {6} & = \mathrm{cos}\frac{\pi}}{3}\hfill & =\frac{s}{2s}\hfill & =\frac{1}{2}\hfill \end{array}[/latex]
См. (рисунок).
Рисунок 9. Синус [латекс]\,\frac{\pi }{3}\,[/latex] равен косинусу [латекс]\,\frac{\pi }{6}\, [/латекс] и наоборот.
Этот результат не должен вызывать удивления, поскольку, как видно из (рис.), сторона, противоположная углу [латекс]\,\frac{\pi }{3}\,[/латекс], также является стороной, примыкающей к [латекс]\,\frac{\pi} {6},[/latex]так[латекс]\,\mathrm{sin}\left(\frac{\pi}}{3}\right)\,[/latex ] и [латекс]\,\mathrm{cos}\left(\frac{\pi }{6}\right)\,[/latex]являются точно таким же отношением одних и тех же двух сторон,[латекс]\,\ sqrt{3}s\,[/latex]и[латекс]\,2s.\,[/latex]Аналогично,[латекс]\,\mathrm{cos}\left(\frac{\pi}{3}\ right)\,[/latex] и [latex]\,\mathrm{sin}\left(\frac{\pi }{6}\right)\,[/latex] также являются одним и тем же отношением с использованием тех же двух сторон ,[латекс]\,с\,[/латекс]и[латекс]\,2с. [/латекс]
[/латекс]
Взаимосвязь между синусом и косинусом [латекса]\,\frac{\pi }{6}\,[/latex]и [латекс]\,\frac{\pi }{3}\,[/latex ] также верно для двух острых углов в любом прямоугольном треугольнике, так как в любом случае отношение тех же двух сторон будет составлять синус одного угла и косинус другого. Поскольку сумма трех углов треугольника составляет [латекс]\,\pi ,[/latex], а прямой угол равен [латекс]\,\frac{\pi }{2},[/latex] оставшиеся два угла должны также дают в сумме [латекс]\,\frac{\pi }{2}.\,[/latex]Это означает, что можно составить прямоугольный треугольник с любыми двумя углами, складывающимися с [латекс]\,\frac{\ pi }{2}\,[/latex] — другими словами, любые два дополнительных угла. Таким образом, мы можем констатировать тождество кофункции : Если любые два угла дополняют друг друга, то синус одного равен косинусу другого, и наоборот. Это тождество показано на (рис.).
Рис. 10. Кофункциональное тождество синуса и косинуса дополнительных углов
Используя это тождество, мы можем, не вычисляя, например, утверждать, что синус [латекс]\,\frac{\pi }{12}\ ,[/latex]равно косинусу [latex]\,\frac{5\pi }{12},[/latex]и синусу [latex]\,\frac{5\pi }{12}\ ,[/latex]равно косинусу[latex]\,\frac{\pi }{12}. \,[/latex]Мы также можем утверждать, что если для заданного угла[latex]\,t,\mathrm {cos}\text{}t=\frac{5}{13},[/latex],затем[latex]\,\mathrm{sin}\left(\frac{\pi}{2}-t\right) =\frac{5}{13}\,[/latex]тоже.
\,[/latex]Мы также можем утверждать, что если для заданного угла[latex]\,t,\mathrm {cos}\text{}t=\frac{5}{13},[/latex],затем[latex]\,\mathrm{sin}\left(\frac{\pi}{2}-t\right) =\frac{5}{13}\,[/latex]тоже.
Идентичности кофункций
Идентичности кофункций в радианах перечислены на (Рисунок).
| [латекс]\mathrm{cos}\,t=\mathrm{sin}\left(\frac{\pi}{2}-t\right)[/latex] | [латекс]\mathrm{sin}\,t=\mathrm{cos}\left(\frac{\pi}{2}-t\right)[/latex] |
| [латекс]\mathrm{tan}\,t=\mathrm{cot}\left(\frac{\pi}{2}-t\right)[/latex] | [латекс]\mathrm{кроватка}\,t=\mathrm{tan}\left(\frac{\pi} {2}-t\right)[/latex] |
| [латекс]\mathrm{sec}\,t=\mathrm{csc}\left(\frac{\pi}{2}-t\right)[/latex] | [латекс]\mathrm{csc}\,t=\mathrm{sec}\left(\frac{\pi}{2}-t\right)[/latex] |
Как
Зная синус и косинус угла, найдите синус или косинус его дополнения.
- Чтобы найти синус дополнительного угла, найдите косинус исходного угла.
- Чтобы найти косинус дополнительного угла, найдите синус исходного угла.
Использование тождеств кофункций
If[latex]\,\mathrm{sin}\,t=\frac{5}{12},[/latex]find[latex]\,\mathrm{cos}\left(\ frac{\pi }{2}-t\right).[/latex]
Показать решение
Попробуйте
sec}\,\left(\frac{\pi }{3}\right).[/latex]
Показать решение
Использование тригонометрических функций
В предыдущих примерах мы вычисляли синус и косинус в треугольниках, для которых были известны все три стороны. Но настоящая сила тригонометрии прямоугольного треугольника проявляется, когда мы смотрим на треугольники, в которых мы знаем угол, но не знаем всех сторон.
Как сделать
Зная прямоугольный треугольник, длину одной стороны и величину одного острого угла, найдите остальные стороны.
- Для каждой стороны выберите тригонометрическую функцию с неизвестной стороной либо в числителе, либо в знаменателе. Известная сторона, в свою очередь, будет знаменателем или числителем.
- Напишите уравнение, в котором значение функции известного угла равно отношению соответствующих сторон.
- Используя значение тригонометрической функции и известную длину стороны, найдите недостающую длину стороны.
Нахождение недостающих длин сторон с помощью тригонометрических соотношений
Найдите неизвестные стороны треугольника на (рис.).
Рис. 11.
Показать решение
Попробуйте
Прямоугольный треугольник имеет один угол [латекс]\,\frac{\pi }{3}\,[/латекс] и гипотенузу 20. Найдите неизвестные стороны и угол треугольника.
Показать решение
Использование тригонометрии прямоугольного треугольника для решения прикладных задач
Тригонометрия прямоугольного треугольника имеет множество практических применений. Например, способность вычислять длины сторон треугольника позволяет найти высоту высокого предмета, не взбираясь на его вершину и не протягивая рулетку по его высоте. Мы делаем это, измеряя расстояние от основания объекта до точки на земле на некотором расстоянии, откуда мы можем смотреть на вершину высокого объекта под углом. Угол возвышения объекта над наблюдателем относительно наблюдателя — это угол между горизонталью и линией, проведенной от объекта к глазу наблюдателя. Прямоугольный треугольник, создаваемый этим положением, имеет стороны, которые представляют собой неизвестную высоту, измеренное расстояние от основания и наклонную линию обзора от земли до вершины объекта. Зная измеренное расстояние до основания объекта и угол луча зрения, мы можем использовать тригонометрические функции для вычисления неизвестной высоты.
Например, способность вычислять длины сторон треугольника позволяет найти высоту высокого предмета, не взбираясь на его вершину и не протягивая рулетку по его высоте. Мы делаем это, измеряя расстояние от основания объекта до точки на земле на некотором расстоянии, откуда мы можем смотреть на вершину высокого объекта под углом. Угол возвышения объекта над наблюдателем относительно наблюдателя — это угол между горизонталью и линией, проведенной от объекта к глазу наблюдателя. Прямоугольный треугольник, создаваемый этим положением, имеет стороны, которые представляют собой неизвестную высоту, измеренное расстояние от основания и наклонную линию обзора от земли до вершины объекта. Зная измеренное расстояние до основания объекта и угол луча зрения, мы можем использовать тригонометрические функции для вычисления неизвестной высоты.
Точно так же мы можем составить треугольник из вершины высокого объекта, глядя вниз. Угол наклона предмета ниже наблюдателя относительно наблюдателя — это угол между горизонталью и линией, проведенной от предмета к глазу наблюдателя. См. (Рисунок).
См. (Рисунок).
Рисунок 12.
Как сделать
Имея высокий объект, косвенно измерьте его высоту.
- Сделайте набросок проблемной ситуации, чтобы отслеживать известную и неизвестную информацию.
- Отметьте измеренное расстояние от основания объекта до точки, где хорошо виден верх объекта.
- На другом конце измеренного расстояния посмотрите на верхнюю часть объекта. Измерьте угол, который линия взгляда образует с горизонтом.
- Напишите уравнение, связывающее неизвестную высоту, измеренное расстояние и тангенс угла луча зрения.
- Решите уравнение для неизвестной высоты.
Косвенное измерение расстояния
Чтобы найти высоту дерева, человек идет к точке в 30 футах от основания дерева. Она измеряет угол [латекс]\,57°\,[/латекс] между линией обзора верхушки дерева и землей, как показано на (Рисунок). Найдите высоту дерева.
Рис. 13.
13.
Показать решение
Попробуйте
Какой длины требуется лестница, чтобы добраться до подоконника на высоте 50 футов над землей, если лестница упирается в здание под углом [латекс]\,\frac{5\pi }{12}\,[ /латекс] с землей? Округлить до ближайшего фута.
Показать решение
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики по тригонометрии прямоугольного треугольника.
- Поиск триггерных функций на калькуляторе
- Нахождение триггерных функций с помощью прямоугольного треугольника
- Связь триггерных функций со сторонами прямоугольного треугольника
- Определение шести триггерных функций из треугольника
- Определить длину стороны прямоугольного треугольника
Ключевые уравнения
| Тригонометрические функции | [латекс]\begin{array}{cc}\text{Sine}\hfill & \phantom{\rule{1em}{0ex}}\text{sin}t=\frac{\text{напротив}}{\ text{гипотенуза}}\hfill \\ \text{Косинус}\hfill & \phantom{\rule{1em}{0ex}}\text{cos} t=\frac{\text{adjacent}}{\text{гипотенуза }}\hfill \\ \text{Tangent}\hfill & \phantom{\rule{1em}{0ex}}\text{tan }t=\frac{\text{напротив}}{\text{смежный}}\ hfill \\ \text{Secant}\hfill & \phantom{\rule{1em}{0ex}}\text{sec}t=\frac{\text{гипотенуза}}{\text{adjacent}}\hfill \\ \text{Косеканс}\hfill & \phantom{\rule{1em}{0ex}}\text{csc }t=\frac{\text{гипотенуза}}{\text{напротив}}\hfill \\ \text{ Котангенс}\hfill & \phantom{\rule{1em}{0ex}}\text{cot}t=\frac{\text{смежный}}{\text{напротив}}\hfill\end{массив}[/latex ] |
| Обратные тригонометрические функции | [латекс]\begin{array}{cc}\text{sin}t=\frac{1}{\text{csc}t}\hfill & \phantom{\rule{1em}{0ex}}\text{ csc }t=\frac{1}{\text{sin}t}\hfill \\ \text{cos}t=\frac{1}{\text{sec}t}\hfill & \phantom{\rule{ 1em}{0ex}}\text{sec}t=\frac{1}{\text{cos}t}\hfill \\ \text{tan}t=\frac{1}{\text{cot}t} \hfill & \phantom{\rule{1em}{0ex}}\text{cot}t=\frac{1}{\text{tan}t}\hfill\end{array}[/latex] |
| Идентичности кофункций | [латекс]\begin{array}{c}\text{cos}t=\mathrm{sin}\left(\frac{\pi}{2}-t\right)\hfill\\\text{sin} t = \ mathrm {cos} \ left (\ frac {\ pi} {2} -t \ right) \ hfill \\ \ text {tan} t = \ mathrm {cot} \ left (\ frac {\ pi }{ 2}-t\right)\hfill \\ \text{cot}t=\mathrm{tan}\left(\frac{\pi}{2}-t\right)\hfill \\ \text{sec}t =\ mathrm{csc}\left(\frac{\pi }{2}-t\right)\hfill \end{массив}[/latex] |
Ключевые понятия
- Мы можем определить тригонометрические функции как отношение длин сторон прямоугольного треугольника.
 См. (Рисунок).
См. (Рисунок). - Одинаковую длину сторон можно использовать для вычисления тригонометрических функций любого острого угла в прямоугольном треугольнике. См. (Рисунок).
- Мы можем вычислить тригонометрические функции специальных углов, зная длины сторон треугольников, в которых они встречаются. См. (Рисунок).
- Любые два дополнительных угла могут быть двумя острыми углами прямоугольного треугольника.
- Если два угла дополняют друг друга, тождества кофункций утверждают, что синус одного равен косинусу другого и наоборот. См. (Рисунок).
- Мы можем использовать тригонометрические функции угла, чтобы найти неизвестные длины сторон.
- Выберите тригонометрическую функцию, представляющую отношение неизвестной стороны к известной стороне. См. (Рисунок).
- Тригонометрия прямоугольного треугольника облегчает измерение недоступных высот и расстояний.
- Неизвестную высоту или расстояние можно найти, составив прямоугольный треугольник, в котором неизвестная высота или расстояние является одной из сторон, а другая сторона и угол известны.
 См. (Рисунок).
См. (Рисунок).
Упражнения на секции
Вербальные
Для данного прямоугольного треугольника обозначьте прилежащую сторону, противоположную сторону и гипотенузу для указанного угла.
Показать решение
Когда прямоугольный треугольник с гипотенузой 1 помещается в окружность радиуса 1, какие стороны треугольника соответствуют координатам x и y ?
Тангенс угла сравнивает какие стороны прямоугольного треугольника?
Показать решение
Каково соотношение между двумя острыми углами в прямоугольном треугольнике?
Объясните тождество кофункции.
Показать решение
Алгебраический
В следующих упражнениях используйте кофункции дополнительных углов.
[латекс]\mathrm{cos}\left(34°\right)=\mathrm{sin}\left(\_\_\_°\right)[/latex]
[латекс]\mathrm{cos }\left(\frac{\pi }{3}\right)=\mathrm{sin}\left(\_\_\_\right)[/latex]
Показать решение
[латекс]\mathrm{csc}\left(21°\right)=\mathrm{sec}\left(\_\_\_°\right)[/latex]
[латекс]\mathrm{tan }\left(\frac{\pi }{4}\right)=\mathrm{cot}\left(\_\_\_\right)[/latex]
Показать решение
В следующих упражнениях найдите длины недостающих сторон, если сторона[латекс]\,а\,[/латекс]противолежащий угол[латекс]\,А,[/латекс]сторона[латекс]\,b\ ,[/latex]противоположный угол[latex]\,B,[/latex], а сторона[latex]\,c\,[/latex]является гипотенузой.
[латекс]\mathrm{cos}\,B=\frac{4}{5},a=10[/латекс]
[латекс]\mathrm{sin}\,B=\frac{1}{2},a=20[/latex]
Показать решение
[латекс]\mathrm{tan}\,A=\frac{5}{12},b=6[/latex]
[латекс]\mathrm{tan}\,A=100,b=100[ /латекс]
Показать решение
[латекс]\mathrm{sin}\,B=\frac{1}{\sqrt{3}},a=2[/latex]
[латекс]a=5,\measuredangle \,A=60 °[/latex]
Показать решение
[латекс]c=12,\измеренный угол \,A=45°[/латекс]
Графический
В следующих упражнениях используйте (Рисунок) для вычисления каждой тригонометрической функции угла[латекс]\,A.[ /латекс]
Рисунок 14.
[латекс]\mathrm{sin}\,A[/латекс]
Показать решение
[латекс]\mathrm{cos}\,A[/латекс]
[латекс]\mathrm{tan}\,A[/латекс]
Показать решение
[латекс]\mathrm{csc}\,A[/латекс]
[латекс]\mathrm{sec}\,A[/латекс]
Показать решение
[латекс]\mathrm{cot}\,A[/латекс]
В следующих упражнениях используйте (Рисунок) для вычисления каждой тригонометрической функции угла[латекс]\,А[/латекс]
Рисунок 15.
[латекс]\mathrm{sin}\,A[/латекс]
Показать решение
[латекс]\mathrm{cos}\,A[/латекс]
[латекс]\mathrm{tan}\,A[/латекс]
Показать решение
[латекс]\mathrm{csc}\,A[/латекс]
[латекс]\mathrm{sec}\,A[/латекс]
Показать решение
[латекс]\mathrm{cot}\,A[/латекс]
В следующих упражнениях найдите неизвестные стороны данного треугольника.
Показать решение
Показать решение
Технология
В следующих упражнениях используйте калькулятор, чтобы найти длину каждой стороны с точностью до четырех знаков после запятой.
Показать решение
Показать решение
[латекс]b=15,\измеренный угол \,B=15°[/латекс]
Показать решение
[латекс]c=200,\измеренный угол \,B=5°[/латекс]
[латекс]c=50,\измеренный угол \,B=21°[/латекс]
Показать решение
[латекс]a=30,\измеренный угол \,A=27°[/латекс]
[латекс]b=3,5,\измеренный угол \,A=78°[/латекс]
Показать решение
Расширения
Найти[латекс]\,x. [/латекс]
[/латекс]
Найти[латекс]\,х.[/латекс]
Показать решение
Найти[латекс]\,x.[/латекс]
Найти[латекс]\,x.[/латекс]
Показать решение
Радиомачта расположена в 400 футах от здания. Из окна в здании человек определяет, что угол подъема на вершину башни составляет[латекс]\,36°,[/латекс]и что угол падения на низ башни составляет[латекс] \,23°.\,[/latex]Какой высоты башня?
Радиомачта расположена в 325 футах от здания. Из окна в здании человек определяет, что угол подъема на вершину башни составляет[латекс]\,43°,[/латекс]и что угол падения на низ башни составляет[латекс] \,31°.\,[/latex]Какой высоты башня?
Показать решение
Вдалеке находится памятник высотой 200 футов. Из окна в здании человек определяет, что угол подъема к вершине памятника составляет[латекс]\,15°,[/латекс]и что угол падения к основанию памятника составляет[латекс] \,2°. \,[/latex]Как далеко человек от памятника?
\,[/latex]Как далеко человек от памятника?
Вдалеке находится монумент высотой 400 футов. Из окна в здании человек определяет, что угол подъема к вершине памятника составляет[латекс]\,18°,[/латекс]и что угол падения к низу памятника составляет[латекс] \,3°.\,[/latex]Как далеко человек от памятника?
Показать решение
На крыше здания есть антенна. Из места в 300 футах от основания здания угол возвышения до вершины здания измеряется как[латекс]\,40°.\,[/латекс]Из того же места угол возвышения до верхняя часть антенны измерена как [латекс]\,43°.\,[/латекс]Найдите высоту антенны.
Громоотвод на крыше здания. Из места в 500 футах от основания здания угол подъема к вершине здания измеряется как[латекс]\,36°.\,[/латекс]Из того же места угол возвышения к верхняя часть громоотвода измерена как[латекс]\,38°.\,[/латекс]Найдите высоту громоотвода.
Показать решение
Реальные приложения
33-футовая лестница прислонена к зданию так, что угол между землей и лестницей составляет [латекс]\,80°. \,[/латекс]Насколько высоко лестница достигает сторона здания?
\,[/латекс]Насколько высоко лестница достигает сторона здания?
23-футовая лестница прислонена к зданию так, что угол между землей и лестницей составляет [латекс]\,80°.\,[/латекс]На какую высоту лестница достигает стены здания?
Показать решение
Установлено, что угол подъема на вершину здания в Нью-Йорке составляет 9 градусов от земли на расстоянии 1 мили от основания здания. Используя эту информацию, найдите высоту здания.
Установлено, что угол подъема на вершину здания в Сиэтле составляет 2 градуса от земли на расстоянии 2 миль от основания здания. Используя эту информацию, найдите высоту здания.
Показать решение
Предполагая, что гигантское красное дерево высотой 370 футов растет вертикально, если я пройду определенное расстояние от дерева и измерю угол подъема к вершине дерева, который будет [латекс]\,60°,[/латекс]как далеко ли я от основания дерева?
Глоссарий
- смежная сторона
- в прямоугольном треугольнике, сторона между данным углом и прямым углом
- угол наклона
- угол между горизонталью и линией от объекта до глаза наблюдателя, при условии, что объект расположен ниже, чем наблюдатель
- угол возвышения
- угол между горизонталью и линией от объекта до глаза наблюдателя, при условии, что объект расположен выше, чем наблюдатель
- противоположная сторона
- в прямоугольном треугольнике, сторона которого наиболее удалена от заданного угла
- гипотенуза
- сторона прямоугольного треугольника, противоположная прямому углу
- единичный круг
- круг с центром в [латекс]\,\влево(0,0\вправо)\,[/латекс] и радиусом 1
Объяснение урока: Тригонометрия прямоугольного треугольника: Нахождение угла
В этом объяснении мы узнаем, как найти недостающий угол в прямоугольном треугольнике, используя соответствующую тригонометрическую функцию, зная длины двух сторон.
При работе с тригонометрией прямоугольного треугольника полезно помнить аббревиатуру «СОХ КАХ ТОА». Это помогает нам помнить о определения тригонометрических отношений синуса, косинуса и тангенса в терминах сторон относительно угла, который мы называем противоположным, смежная и гипотенуза. Перечислим здесь соотношения.
Тригонометрические соотношения
Гипотенуза всегда является наибольшей стороной прямоугольного треугольника, противолежащая сторона — это сторона, прямо противоположная рассматриваемый угол, а прилежащая сторона — это сторона, следующая за углом (которая не является гипотенузой). Примером этого является показано здесь.
Чтобы найти меры неизвестных углов в прямоугольных треугольниках (с помощью тригонометрии), мы должны быть уверены
в нашей способности правильно обозначить треугольник с точки зрения противолежащего, прилежащего и гипотенузы и правильно запомнить
тригонометрические соотношения. Как только мы удовлетворимся этими двумя вещами, мы сможем приступить к решению тригонометрии. задачи на нахождение меры неизвестного угла. Мы всегда можем найти недостающую меру прямого угла.
треугольник из двух длин его сторон, используя следующий процесс.
задачи на нахождение меры неизвестного угла. Мы всегда можем найти недостающую меру прямого угла.
треугольник из двух длин его сторон, используя следующий процесс.
Как найти недостающий угол в прямоугольном треугольнике по двум длинам его сторон
- Если у нас нет диаграммы прямоугольного треугольника, мы должны начать с наброска имеющейся информации.
- Обозначьте стороны прямоугольного треугольника в зависимости от их положения относительно угла, который мы хотим определить.
- Используйте аббревиатуру SOH CAH TOA, чтобы определить, какое тригонометрическое соотношение включает известные длины сторон.
- Мы используем кнопку Shift, а затем соответствующее тригонометрическое отношение на калькуляторе, а затем отношение известных длин, чтобы определить меру угла.
Например, если мы знаем, что cos𝜃=12, то нажимаем следующее shiftcos12=»’∘
Начнем с примера.
Пример 1. Нахождение меры неизвестного угла в прямоугольном треугольнике
Для заданной фигуры найдите величину угла 𝜃,
с точностью до секунды.
Ответ
Наш первый шаг в ответе на этот вопрос — обозначить треугольник относительно угла 𝜃.
Обратите внимание, что здесь мы обвели A и H, так как это две стороны, длину которых мы знаем. Если мы затем вспомним аббревиатуру «SOH CAH TOA», мы увидим, что «CAH» — единственный, который содержит буквы A и H, что означает, что нам нужно использовать отношение косинуса. Напомним, что cosAH𝜃=.
Теперь подставим значения A и H, чтобы найти, что cos𝜃=38.
Используя наши калькуляторы, мы можем найти 𝜃, вычислив cos138, пример последовательности кнопок, которую нам может понадобиться нажать, — shiftcos38=»’∘. Однако конкретные кнопки будут различаться от калькулятора к калькулятору.
Если мы посчитаем это, то получим 6758′32′′.∘ до ближайшей секунды
В некоторых вопросах нас могут попросить вычислить меры всех неизвестных углов в прямоугольном треугольнике. В этом
случае мы должны использовать тригонометрию, чтобы найти один из неизвестных углов, а затем мы можем использовать тот факт, что меры
сумма углов треугольника равна 180∘. Давайте рассмотрим пример, где это так.
Давайте рассмотрим пример, где это так.
Пример 2. Нахождение мер всех неизвестных углов прямоугольного треугольника
Для данной фигуры найдите меры ∠𝐴𝐶𝐵 и ∠𝐵𝐴𝐶, с точностью до секунды.
Ответ
Наш первый шаг — выбрать один из двух неизвестных углов для вычисления в первую очередь. Здесь мы собираемся начать с поиска ∠𝐴𝐶𝐵, которую мы будем называть 𝑥. Затем мы можем обозначить стороны треугольника по отношению к углу 𝑥, как показано на рисунке.
Мы обвели O и A, так как это известные нам длины. Если мы затем вспомним о аббревиатура «SOH CAH TOA», мы видим, что нам нужно использовать касательную отношение, так как «ТОА» содержит буквы О и А. Напомним, что танОА𝑥=.
Подставляя длины О и А, получаем загар𝑥=45.
Используя наши калькуляторы, мы можем найти 𝑥, вычислив tan45,
пример последовательности кнопок, которые нам может понадобиться нажать, это
shifttan45=»’∘. Однако конкретные кнопки будут различаться от калькулятора к калькулятору.
Однако конкретные кнопки будут различаться от калькулятора к калькулятору.
Если мы вычислим это, мы обнаружим, что 𝑥=3839′35′′.∘
Чтобы найти величину второго неизвестного угла в треугольнике, нужно воспользоваться фактом что сумма мер углов треугольника равна 180∘. Если мы назовем ∠𝐵𝐴𝐶 𝑦, у нас есть это 𝑦+38,66+90=180.
Это упрощает до 𝑦+128,66=180, и вычитая 128,66 с обеих сторон, находим, что 𝑦=5120′25′′.∘
В некоторых вопросах по тригонометрии нам не дается диаграмма, и часть навыка вопроса заключается в том, чтобы нарисовать соответствующую схему. В следующем примере мы продемонстрируем этот навык.
Пример 3. Решение треугольников с помощью тригонометрии
𝐴𝐵𝐶 — прямоугольный треугольник с вершиной 𝐵, где 𝐵𝐶=10 см
и 𝐴𝐶=18см. Найдите длину 𝐴𝐵 с точностью до
сантиметр и меры углов 𝐴 и 𝐶
до ближайшей степени.
Ответ
Начнем с построения диаграммы. Обычно полезно попытаться нарисовать примерно в масштабе. Совершенно не обязательно, но это помогает нам проверить правильность наших ответов при сравнении их с диаграммой. Поэтому мы рисуем треугольник 𝐴𝐵𝐶 и обозначаем известные нам длины ребер.
Первое, что нам нужно найти, это длину 𝐴𝐵. Для этого можно воспользоваться теоремой Пифагора, которая утверждает, что 𝑐=𝑎+𝑏, где 𝑐 — длина гипотенузы. В треугольнике, который нам дан, 𝐴𝐶 — гипотенуза. Следовательно, мы можем записать теорему Пифагора для треугольника как 𝐴𝐶=𝐴𝐵+𝐵𝐶.
Следовательно, 𝐴𝐵=𝐴𝐶−𝐵𝐶.
Подставляя 𝐵𝐶=10 и 𝐴𝐶=18, получаем 𝐴𝐵=18−10=324−100=224.
Извлекая квадратный корень, имеем 𝐴𝐵=√224=14,966…=15см с точностью до сантиметра.
Теперь нам нужно найти величины углов при
𝐴 и 𝐶. Для этого мы можем найти один из углов, а затем использовать тот факт, что сумма углов в треугольнике равна
180∘. Мы найдем меру
∠𝐴, который мы будем обозначать 𝜃. Чтобы узнать, какое тригонометрическое отношение мы должны использовать, нам сначала нужно обозначить стороны треугольника. Мы знаем это
𝐴𝐶 — гипотенуза. Поскольку мы рассматриваем ∠𝐴, 𝐵𝐶
является противоположным, а 𝐴𝐵 является смежным.
Мы найдем меру
∠𝐴, который мы будем обозначать 𝜃. Чтобы узнать, какое тригонометрическое отношение мы должны использовать, нам сначала нужно обозначить стороны треугольника. Мы знаем это
𝐴𝐶 — гипотенуза. Поскольку мы рассматриваем ∠𝐴, 𝐵𝐶
является противоположным, а 𝐴𝐵 является смежным.
Поскольку мы знаем длины всех сторон, мы можем использовать любое тригонометрическое соотношение. Однако лучше всего использовать две длины, которые нам дали в вопросе. Есть две веские причины
для этого. Во-первых, это означает, что если мы ошиблись в вычислении третьей стороны, это не повлияет на наш ответ на вопрос.
эта часть вопроса. Во-вторых, мы можем легко сделать ошибки округления, если будем использовать длину третьей стороны, поскольку
его точная форма не является целым числом. Поэтому мы хотели бы вычислить ∠𝐴, используя противоположное и гипотенузу. Это означает, что мы будем использовать отношение синусов:
грехОН𝜃=.
Подставляя длины противоположной (𝐵𝐶=10) и гипотенузы (𝐴𝐶=18), имеем грех𝜃=1018=59.
Мы можем найти 𝜃, используя наши калькуляторы для вычисления sin59, пример последовательности кнопок, которую нам может понадобиться нажать, — shiftsin59=»’∘. Однако конкретные кнопки будут различаться от калькулятора к калькулятору.
Если мы вычислим это, мы обнаружим, что 𝜃=33,748…=34∘ до ближайшей степени. Следовательно, 𝑚∠𝐴=34∘ с точностью до градуса.
Теперь мы можем использовать тот факт, что сумма углов треугольника равна 180∘, чтобы найти 𝑚∠𝐶. С 𝑚∠𝐴+𝑚∠𝐵+𝑚∠𝐶=180, у нас есть 𝑚∠𝐶=180−𝑚∠𝐵−𝑚∠𝐴.
Подставляя значения 𝑚∠𝐵 и 𝑚∠𝐴, имеем 𝑚∠𝐶=180−90−33,748…=56,251…=56∘ до ближайшей степени.
Тригонометрические вопросы также могут быть представлены в виде задач по истории. В этом случае, если связанная диаграмма
не дано, всегда стоит рисовать один. Примером такого типа вопроса может быть следующий.
Примером такого типа вопроса может быть следующий.
Пример 4. Использование тригонометрии для нахождения меры углов в трапециях
𝐴𝐵𝐶𝐷 — это участок земли в форме трапеции, где 𝐴𝐷 параллелен 𝐵𝐶 и 𝐴𝐵⟂𝐵𝐶. Находить 𝑚∠𝐶 учитывая, что 𝐴𝐷=20м, 𝐵𝐶=35м, и 𝐷𝐶=25м. Дайте ответ с точностью до секунды.
Ответ
Мы можем начать с выделения ∠𝐶 на диаграмме:
Мы можем провести перпендикулярную линию из 𝐷 на 𝐵𝐶 в точке 𝐸.
Мы видим, что треугольник 𝐷𝐸𝐶 прямоугольный в точке 𝐸. Находим длину 𝐸𝐶 заметив, что 𝐴𝐷=𝐵𝐸=20м. Мы можем использовать это вместе с тем фактом, что 𝐵𝐶=𝐵𝐸+𝐸𝐶=35m, чтобы найти 𝐸𝐶. Замена 𝐵𝐸=20м в уравнение дает нам 20+𝐸𝐶=35.
Затем мы вычитаем 20 из обеих частей уравнения, чтобы получить 𝐸𝐶=15.m
Мы можем добавить это на нашу диаграмму.
Мы можем определить 𝑚∠𝐶
заметив, что это угол в прямоугольном треугольнике с двумя известными длинами сторон, поэтому мы можем найти меру этого угла с помощью тригонометрии.
Для этого начнем с обозначения сторон прямоугольного треугольника 𝐷𝐸𝐶 на основе их позиции относительно ∠𝐶. Мы видим, что 𝐸𝐶 сторона, прилегающая к ∠𝐶 в прямоугольном треугольнике 𝐷𝐸𝐶 и 𝐷𝐶 является гипотенузой прямоугольного треугольника, так как он противоположен прямому углу.
Теперь мы можем определить соответствующее тригонометрическое соотношение. Для этого мы будем использовать аббревиатуру SOH CAH TOA, чтобы помочь нам вспомнить, какие отношения дает каждая тригонометрическая функция.
Нам известны длины стороны, прилегающей к углу и гипотенузе, поэтому воспользуемся функцией косинуса cosAHcos𝐶==1525𝐶=35.
Мы можем использовать наш калькулятор, чтобы вычислить это выражение. Мы используем следующие inputsshiftcos35=»’∘
Однако на других калькуляторах нужные кнопки могут отличаться.
Это дает нам 𝑚∠𝐶=537′48,37∘
Следовательно, с точностью до секунды 𝑚∠𝐶=537′48∘.
Пример 5.
 Решение задач по рассказу с помощью тригонометрии
Решение задач по рассказу с помощью тригонометрииА 5 м Лестница прислонена к перпендикулярной стене так, что ее основание равно 2 м. от стены. Определите угол между лестницей и полом, давая ответ с точностью до секунды.
Ответ
Наш первый шаг в решении подобного вопроса — нарисовать схему ситуации.
На этой диаграмме относительно угла 𝑥, мы пометили стороны, длины которых нам известны. Здесь мы знаем длину прилежащего и гипотенузу, поэтому нам нужно использовать отношение косинуса, чтобы найти величину неизвестного угла. Мы знаем это cosAH𝑥=.
Если мы подставим длины A и H, мы получим cos𝑥=25.
Мы можем найти 𝑥, используя наши калькуляторы для вычисления cos25, пример последовательности кнопок, которую нам может понадобиться нажать, — shiftcos25=»’∘. Однако конкретные кнопки будут различаться от калькулятора к калькулятору.
Вычисляя это, мы находим, что
𝑥=6625′19′′. ∘
∘
Мы закончим рассмотрением одной последней сюжетной задачи.
Пример 6. Решение задач с помощью тригонометрии
Высота лыжной трассы 16 метров, длина 20 метров. Найдите меру ∠𝜃 давая ответ с точностью до секунды.
Ответ
В этом вопросе нам повезло, что нам дали связанную диаграмму, а это значит, что нам не нужно рисовать эту себя. Наш первый шаг — обозначить стороны относительно угла тета.
Здесь мы знаем длину противоположной стороны и гипотенузы и, следовательно, должны использовать отношение синуса к найти величину неизвестного угла. Напомним, что грехОН𝜃=. Если подставить длины O и H, то получим грех𝜃=1620.
Мы можем найти 𝜃, используя наши калькуляторы для вычисления sin1620, пример последовательности кнопок, которую нам может понадобиться нажать, — shiftsin1620=»’∘. Однако конкретные кнопки будут различаться от калькулятора к калькулятору.
Вычисляя это, мы находим, что
𝜃=537′48′′. ∘
∘
Ключевые точки
- При работе с прямоугольными треугольниками мы используем термины напротив , рядом с , и гипотенуза для обозначения сторон треугольника. Гипотенуза всегда лежит против прямого угла и является самой длинной стороной. Противоположные и смежные помечаются относительно данного угла, часто обозначаемого 𝜃. Прилегающая сторона – это сторона рядом с угол 𝜃, который не является гипотенузой. Что касается обратного, то это последняя сторона треугольника. Он называется противоположным, потому что он противоположен данному углу.
- Вспомните аббревиатуру «SOH CAH TOA», где O означает противоположное, A — соседнее, H — гипотенузу, а 𝜃 — угол. Тригонометрические отношения sinOHcosAHandtanOA𝜃=,𝜃=,𝜃=.
- Мы можем найти меру угла по длинам сторон, используя кнопку Shift, а затем соответствующее тригонометрическое отношение
на калькуляторе с последующим отношением известных длин.

Смежные и противоположные углы в прямоугольных треугольниках (тригонометрия)
Задавать вопрос
Спросил
Изменено 1 год, 1 месяц назад
Просмотрено 2к раз
$\begingroup$
Итак, я первокурсник средней школы и хочу знать, как синус, косинус и тангенс помогают найти длины сторон. (Это не вопрос для домашнего задания)
Я знаю, что в прямоугольном треугольнике 30-60-90 градусов отношение равно 1, корень квадратный из 3, а гипотенуза равна 2.
Я также понимаю следующее:
- Синус противоположен гипотенузе
- Косинус примыкает к гипотенузе
- Касательная противоположна соседней
Главное, с чем у меня проблема, это определить, какие стороны какие; какой из них напротив, а какой рядом.
Например, какой угол вы бы использовали для sin30 (где угол c — прямой угол, a — верхний угол, а b — угол вправо) и какой угол вы бы использовали для sin60?
- тригонометрия
$\endgroup$
3
$\begingroup$
Допустим, у вас есть треугольник, как показано ниже. $A, B, C$ — его вершины, $a, b, c$ — его стороны, $\alpha, \beta, \gamma$ — углы (я не отметил $\beta$ и $\gamma$ , поэтому опишем все, что нам нужно для $\alpha$).
$\alpha$ — острый угол прямоугольного треугольника $ABC$. Сторона $BC$ (или $a$, как ей присвоено другое обозначение) является противоположным ему катетом, а $AC$ (или $b$) — примыкающим к нему катетом. $AB$ (или $c$) — гипотенуза.
Учитывая это, например, $\sin \alpha = \frac{\text{напротив}}{\text{гипотенуза}} = \frac{BC}{AB} = \frac ac$. Это очень похоже на другие функции, надеюсь, вы сможете с ними справиться.
Как правильно заметил @abel, тригонометрические функции определены не для треугольника, а для угла, поэтому вам нужно проверить, что треугольник прямоугольный, найти в нем заданный острый угол, и тогда у вас будут две стороны, прилегающие к этому углу ( гипотенуза и прилежащий катет) и одна сторона, противоположная ей. 9\circ.$
давайте сосредоточимся на $\угол A.$ противоположная сторона $BC$ и смежная сторона $AC.$
если вы переключитесь на $\угол B,$ то противоположное сторона равна $AC$, а соседняя сторона равна $BC.$
имеет ли это смысл?
$\endgroup$
8
$\begingroup$
Гипотенуза — самая длинная сторона, обычно обозначаемая H. Он находится напротив прямого угла.
Другие стороны зависят от интересующего вас ракурса.
Может помочь то, что смежный — это причудливое слово, означающее «рядом с». Таким образом, угол, по отношению к которому вы отмечаете стороны, будет между гипотенузой и соседним. Он находится рядом с углом. Обычно называется A
Таким образом, угол, по отношению к которому вы отмечаете стороны, будет между гипотенузой и соседним. Он находится рядом с углом. Обычно называется A
Последний угол — это угол, противоположный углу, который вы выбрали для обозначения сторон. Обычно он называется О.
Интересующий вас ракурс будет варьироваться от задачи к задаче.
$\endgroup$
$\begingroup$
Google сказал мне это.
Гипотенуза – это сторона прямоугольного треугольника, противолежащая угол 90 градусов. Это термин, относящийся к математике, особенно к геометрии. Гипотенуза происходит от греческого слова гипотенуза, что означает «растягивание под». Гипотенуза «вытягивается» под прямым углом треугольника, угол которого равен 90 градусов.
Вы сами решаете, какой угол вы хотите исследовать.
После того, как вы выбрали его, , вы также выбрали , какие стороны противоположны, смежны и гипотенуза.
Затем вы решаете использовать синус, косинус или тангенс в зависимости от того, что вы знаете и что пытаетесь сделать.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Противолежащая смежная гипотенуза – объяснение и примеры
Термины противоположная, смежная и гипотенуза называются длинами сторон прямоугольного треугольника. Прямоугольный треугольник считается одной из самых мощных фигур в математике. Мы можем легко решать сложные задачи с реальными словами, если знаем, как вычислить глубокую связь сторон прямоугольного треугольника.
Прямоугольный треугольник считается одной из самых мощных фигур в математике. Мы можем легко решать сложные задачи с реальными словами, если знаем, как вычислить глубокую связь сторон прямоугольного треугольника.
Термины гипотенуза, смежная, противоположная используются для обозначения сторон прямоугольного треугольника. Опыт строительных блоков в тригонометрии позволяет обсуждать и решать различные стороны прямоугольного треугольника, тесно связанные друг с другом, для решения реальных проблем.
Можете ли вы представить себе определение высоты самой высокой башни в мире — Бурдж-Халифа — стоя на земле на определенном расстоянии от нее? Одна идея состоит в том, чтобы сделать приблизительное предположение, но лучший подход к нахождению высоты состоит в том, чтобы использовать знание прямоугольного треугольника . Если вы просто знаете приблизительный угол, который башня образует с землей, вы можете определить высоту Бурдж-Халифа, стоя на земле.
Только представьте, всего две части информации — расстояние на земле и примерный угол, который башня образует с землей — вы можете добиться невозможного иначе. Но как? Это именно то, что мы попытаемся изучить в тригонометрии , используя прямоугольные треугольники. Вот почему прямоугольных треугольников являются одним из самых влиятельных понятий в математике.
Ожидается, что после изучения этого урока мы изучим концепции, основанные на следующих вопросах, и будем готовы давать точные, конкретные и последовательные ответы на эти вопросы.
- Как найти прилежащую, гипотенузу и противолежащие стороны прямоугольного треугольника?
- Чему равна противоположная сторона прямоугольного треугольника?
- Чему равна прилежащая сторона прямоугольного треугольника?
- Как разные стороны (гипотенуза, прилежащая, противолежащая) треугольника глубоко связаны друг с другом?
- Как мы можем решить реальные проблемы, используя прямоугольный треугольник?
Этот урок призван прояснить любую путаницу, которая может у вас возникнуть в отношении понятий, связанных с прямоугольными треугольниками. 9{\ circ} $. На следующем рисунке 1-1 показан типичный прямоугольный треугольник. Длины трех катетов (сторон) прямоугольного треугольника называются $a$, $b$ и $c$. Углы, лежащие напротив катетов длин $a$, $b$ и $c$, называются $\alpha$, $\beta$ и $\gamma$. Крошечный квадрат, обозначенный углом $\gamma$, показывает, что это прямой угол.
9{\ circ} $. На следующем рисунке 1-1 показан типичный прямоугольный треугольник. Длины трех катетов (сторон) прямоугольного треугольника называются $a$, $b$ и $c$. Углы, лежащие напротив катетов длин $a$, $b$ и $c$, называются $\alpha$, $\beta$ и $\gamma$. Крошечный квадрат, обозначенный углом $\gamma$, показывает, что это прямой угол.
Общепринятая практика состоит в том, что треугольник обозначается с точки зрения обозначения сторон строчными буквами и углов (вершин), противоположных сторонам, соответствующими строчными буквами.
Следующая диаграмма 1-2 представляет гипотенузу — самую длинную сторону — прямоугольного треугольника. Из диаграммы видно, что гипотенуза прямоугольного треугольника противоположна прямому углу $\gamma$. Эта сторона всегда будет оставаться гипотенузой независимо от того, под каким углом мы смотрим, потому что это уникальная сторона.
Две другие стороны — смежная и противолежащая — называются в соответствии с расположением опорного угла. Пожалуйста, убедитесь, что вы четко понимаете, как обозначены стороны треугольников.
Пожалуйста, убедитесь, что вы четко понимаете, как обозначены стороны треугольников.
На следующей диаграмме 1-3 представлена смежная сторона . Из диаграммы видно, что смежная сторона прямоугольного треугольника равна рядом с к опорному углу $\alpha$ .
На следующей диаграмме 1-4 показана сторона , противоположная , полностью поперек другой стороны от опорного угла $\alpha$ . Из диаграммы видно, что противоположная сторона прямоугольного треугольника лежит точно напротив к опорному углу $\alpha$ .
Объединяя все относящиеся к опорному углу $\alpha$ , получаем иллюстрацию, показанную на рис. 1-5.
Например, с помощью прямоугольного треугольника, показанного на рисунке ниже, чтобы определить противоположный, смежный и гипотенузу прямоугольного треугольника относительно угла $\alpha %%EDITORCONTENT%%nbsp;как показано ниже.
Противоположная сторона прямоугольного треугольника
Глядя на приведенную выше диаграмму, сторона $a%%EDITORCONTENT%%nbsp;пролегает точно против к опорному углу $\alpha$ . Таким образом, $a$ — это противоположная сторона прямоугольного треугольника относительно исходного угла $\alpha$, как показано ниже.
Прилежащая сторона прямоугольного треугольника
Из той же диаграммы видно, что сторона $b%%EDITORCONTENT%%nbsp;равна рядом с до опорного угла α . Таким образом, $b$ — это смежная сторона прямоугольного треугольника относительно базового угла $\alpha$, как показано ниже.
Гипотенуза прямоугольного треугольника
На диаграмме также ясно видно, что сторона $c$ равна , противоположная прямому углу $\gamma$ . Таким образом, $c$ — это гипотенуза прямоугольного треугольника, как показано ниже.
Таким образом, $c$ — это гипотенуза прямоугольного треугольника, как показано ниже.
Связь между прямоугольным треугольником и теоремой Пифагора
Теорема Пифагора — одно из самых мощных понятий в математике. Нам нужно нарисовать прямоугольный треугольник, чтобы понять эту концепцию. На рис. 1-6 изображен простой прямоугольный треугольник со сторонами $a$, $b$ и $c$.
Что такого уникального в этом треугольнике или в этой теореме?
Теорема Пифагора утверждает, что гипотенуза имеет особые отношения с двумя другими катетами. Там написано, что 9{2}$
Используя теорему Пифагора, мы можем решать многочисленные задачи с реальными словами.
Например:
Предположим, мистер Тони проходит 12$ километров на восток, а затем 5$ километров на север. Определите, на каком расстоянии он от исходной позиции?
Шаг $1$: Начертите диаграмму
Шаг $2$: Составьте уравнение и решите его
На диаграмме ясно видно, что оно представляет собой прямоугольный треугольник. Здесь:
Здесь:
Пройденное расстояние в восточном направлении $= b = 12$ км 9{2}=169$
$c = 13$ км
Таким образом, мистер Тони находится в $13$ километрах от своего начального положения
Пример $1$
Дан прямоугольный треугольник $XYZ$, который сторона смежна по отношению к опорному углу $X$?
Решение n:
Из диаграммы видно, что сторона $XZ%%EDITORCONTENT%%nbsp;равна рядом с относительно опорного угла $X$. Таким образом, $XZ$ — это смежных сторон прямоугольного треугольника $XYZ$ относительно исходного угла $X$.
Пример $2$
Какая сторона прямоугольного треугольника $PQR$ противоположна относительно угла $P$?
На диаграмме сторона $QR$ лежит ровно против к опорному углу $P$ . Таким образом, $QR$ является противоположной стороной прямоугольного треугольника $PQR$ относительно исходного угла $P$.
Пример $3$
Какая сторона прямоугольного треугольника $LMN$ является гипотенузой?
Решение n:
Глядя на диаграмму выше, $∠N$ — прямой угол.
Кроме того, сторона $LM$ равна против прямого угла $N$ . Таким образом, $LM$ является гипотенузой прямоугольного треугольника $LMN$ .
Пример $4$
Учитывая прямоугольный треугольник, определите
$1$. наоборот
$2$ . соседний
$3$ . гипотенуза
прямоугольного треугольника относительно угла $\alpha$.
Решение n:
$1$ . Противоположный угол
Глядя на диаграмму выше, угол $\gamma$ прямой.
Понятно, что сторона $5%%EDITORCONTENT%%nbsp;лежит ровно против к опорному углу $\alpha$.
Таким образом,
Противоположная сторона = 5$ единиц
$2 $ . Смежный
Ясно, что сторона $12%%EDITORCONTENT%%nbsp;является правой рядом с опорным углом $\alpha$ .
Таким образом,
Прилежащая сторона = 12$ единиц
3$ . Гипотенуза
На диаграмме ясно видно, что сторона $13$ противоположна прямому углу $\gamma$ .
Таким образом,
Гипотенуза = $13$ единиц
Сводка тригонометрических формул
Сводка тригонометрических формулЭти формулы связывают длины и площади определенных кругов или треугольников. На следующей странице вы найдете личности. Тождества не относятся к конкретным геометрическим фигурам, но справедливы для всех углов.
Формулы для дуг и секторов окружностей
Вы можете легко найти длину дуги и площадь сектора для угла θ в окружности радиусом r .
| Длина дуги. Длина дуги равна радиусу r , умноженному на угол θ , где угол измеряется в радианах. Чтобы перевести градусы в радианы, умножьте количество градусов на π /180. | |
| Площадь сектора. Площадь сектора равна половине квадрата радиуса, умноженного на угол, где, опять же, угол измеряется в радианах. |
Формулы для прямоугольных треугольников
Наиболее важными формулами тригонометрии являются формулы прямоугольного треугольника. Если θ — один из острых углов в треугольнике, то синус теты — это отношение противолежащего катета к гипотенузе, косинус — отношение прилежащего катета к гипотенузе, а тангенс — это отношение противоположная сторона соседней стороне.
Эти три формулы вместе известны мнемоникой SohCahToa. Кроме того, есть очень важная формула Пифагора, которая гласит, что квадрат гипотенузы равен сумме квадратов двух других сторон.
Зная, что два острых угла дополняют друг друга, то есть дают в сумме 90°, можно решить любой прямоугольный треугольник:
- Зная две из трех сторон, можно найти третью сторону и оба острых угла.
- Если вы знаете один острый угол и одну из трех сторон, вы можете найти другой острый угол и две другие стороны.
Формулы для косоугольных треугольников
Эти формулы работают для любого треугольника, острого, тупоугольного или прямоугольного. Мы будем использовать стандартные обозначения, в которых три вершины треугольника обозначаются прописными буквами A , B и C , а три противоположные им стороны соответственно обозначаются строчными буквами a , b и c .
Есть две важные формулы для косоугольных треугольников. Они называются законом косинусов и законом синусов.
Закон косинусов обобщает формулу Пифагора на все треугольники. Он говорит, что c 2 , квадрат одной стороны треугольника, равен a 2 + b 2 , сумма квадратов двух других сторон минус 2. ab cos  C , удвоенное произведение их на косинус противоположного угла. Когда угол C правильный, он становится формулой Пифагора.
Он говорит, что c 2 , квадрат одной стороны треугольника, равен a 2 + b 2 , сумма квадратов двух других сторон минус 2. ab cos  C , удвоенное произведение их на косинус противоположного угла. Когда угол C правильный, он становится формулой Пифагора.
Закон синусов гласит, что отношение синуса одного угла к противоположной стороне одинаково для всех трех углов.
С помощью этих двух формул вы можете решить любой треугольник:
- Зная два угла и сторону, можно найти третий угол и две другие стороны.
- Если известны две стороны и угол между ними, то можно найти третью сторону и оба других угла.
- Если известны две стороны и угол, противолежащий одной из них, то для угла, противолежащего другой, есть два варианта (один острый и один тупой), и для обоих вариантов можно определить оставшийся угол и оставшуюся сторону.