Текстовые задачи с решениями 9 класс: Решение текстовых задач. 9-й класс

Текстовые задачи — задачи с решениями

Задача 1 передается от Ксения

Сумма трех последовательных четных чисел ровна 78. Найди эти три числа.

25, 26, 27

24, 26, 27

22, 26, 30

24, 26, 28

Задача 2

Коля забирается на 60 ступенек за 40 секунд. Если он будет забираться с той же скоростью, то сколько ступенек он преодолеет за 150 секунд?

Задача 3

С января по июнь 46200 иммигрантов подали на гражданство. А в прошлом году за этот же период заявки подали 120000 иммигрантов. На сколько процентов уменьшилось количество заявок?
Ответ: %

Задача 4

В магазине после обеда продавали в два раза больше вишней, чем с утра. Всего за день было продано 360 кг. Сколько килограммов было продано после обеда?

Задача 5

Два велосипедиста выехали из одного и того же места и поехали по кругу. Первый проезжает круг за 3 минуты, а второй за 4 минуты. Через какое время (в минутах) они опять встретятся в начальной точке?

Задача 6

У нас есть следующая информация об изгороди на гонках.
Всего есть 10 направляющих в изгороди. Расстояние между последующими двумя направляющими (которые показывают направление) равно 9,14 м. Расстояние между первой направляющей и линией старта 13,72 м, а между последней направляющей и финишной чертой равно 14,02 м. Длина каждой направляющей равна 106 см.

Какова обшая длина трека в см?
Ответ: см.

Задача 7

Если некое число разделить на 3, а затем разделить на половину, то получится 13. С какого числа мы начинали?

Задача 8

Машина проехала 375 км за 3 часа. Какова скорость машины в км/ч?

Задача 9

Поезд уходит из города A в 9:15, а приезжает в город Б в 10:35. Если скорость поезда равна 180 км/ч, то какое расстояние между двумя городами?

Задача 10

Тим едет на велосипеде в школу и приезжает через 15 минут. Если его скорость составляет 8 м/с, каково расстояние между школой и его домом?

Ответ: км.

Задача 11

Велосипедист едет в гору длиной 400 м со скоростью 7,2 км/ч. Когда он спускается с горы, то едет в два раза быстрее. Сколько секунд займёт забраться и съехать с холма?
Ответ: секунд.

Задача 12

Расстояние между двумя станциями метро равно 4,5 км. Если поезд отходит от одной станции в 9:10 со скоростью 90км/ч, то в какое время он прибывает на другую станцию?
Ответ в формате: чч:мм

Задача 13

Машина проезжает расстояние между городами А и Б за 3 часа и 30 минут со скоростью 180 км/ч. Мотоциклист проезжает это же расстояние за 5 часов. Какая у мотоциклиста скорость в км/ч?

Задача 14

Расстояние между двумя городами равно 1200 км. Машина четверть пути едет со скоростью 80 км/ч, а оставшуюся часть пути со скоростью 120 км/ч. Сколько времени понадобится, чтобы пройти весь путь? Ответ в формате ЧЧ:ММ (часы ЧЧ и минуты ММ)

Прислать задачу

Правильный:

Неверный:

Неразрешенные задачи:

Текстовые задачи — Математика — Факультативы

Текстовые задачи

Пояснительная записка

Анализ результатов проведения ЕГЭ с момента его существования говорит о том, что решаемость задания, содержащего текстовую задачу, составляет в среднем около 30% . Такая ситуация позволяет сделать вывод, что большинство учащихся не в полной мере владеют техникой решения текстовых задач и не умеют за их часто нетрадиционной формулировкой увидеть типо­вые задания, которые были достаточно хорошо отра­ботаны на уроках в рамках школьной программы. По этой причине возникла необходимость более глубоко­го изучения этого традиционного раздела элементар­ной математики.

Данный элективный курс рассчитан в первую оче­редь на учащихся, желающих расширить и углубить свои знания по математике, сделать прав ильный вы­бор профиля обучения в старших классах и качест­венно подготовиться к ЕГЭ и конкурсным экзаменам в вузы. Он поможет школьникам систематизировать полученные на уроках знания по решению текстовых задач и открыть для себя новые методы их решения, которые не рассматриваются в рамках школьной про­граммы.

Полный минимум знаний, необходимых для ре­шения всех типов текстовых задач, формируется в те­чение первых девяти лет обучения в школе, поэтому представленный элективный курс «Текстовые зада­чи» рекомендуется вводить с 9-го класса.

Представленный элективный курс содержит 8 тем.

Первая тема «Текстовые задачи и техника их реше­ния» является обзорной. При ее раскрытии акцент должен быть сделан на выделение основных этапов решения текстовых задач и их назначение. Следу­ет также обратить внимание учащихся на важность умелого письменного оформления. Следующие четы­ре темы – «Задачи на движение», «Задачи на смеси, сплавы, paствоpы», «Задачи на работу», «Задачи на прогрессии» — закрепляют и дополняют знания уча­щихся, полученные на уроках. Последние три темы ­«Задачи с экономическим содержанием», «Задачи на числа», «Разные задачи» — выходят за рамки школь­ной программы и значительно совершенствуют навы­ки учащихся в решении текстовых задач.

Всего на проведение занятий отводится 24 часа. На изучение методов решения типовых задач выделено 11 часов.

Провести занятия можно в форме обзорных лек­ций с разбором ключевых задач или в форме семина­ров, нацелив учащихся на предварительную подго­товку и самостоятельный поиск материалов с их пос- ледующим обсуждением. На практические занятия и отработку умений и навыков отведено 10 часов, из них 2 часа на самостоятельную итоговую работу и ре­шение задач повышенной сложности, предлагаемых на вступительных экзаменах в вузы и на ЕГЭ. В про­грамме предусмотрено проведение трех тематических зачетов (по одному часу каждый).

Цели и задачи курса:

• определить уровень способностей учащихся и уровень их готовности к профильному обучению в школе и вузе;

• систематизировать ранее полученные знания по решению текстовых задач;

• познакомить учащихся с разными типами задач, особенностями методики и различными способами их решения;

• реализовать межпредметные связи.

Ожидаемые результаты

После изучения курса учащиеся должны:

• уметь определять тип текстовой задачи, знать особенности методики ее решения, использовать при решении различные способы;

• уметь применять полученные математические знания при решении задач;

• уметь использовать дополнительную математи­ческую литературу.

Содержание курса

Текстовые задачи и техника их решения (1 ч) Текстовая задача. Виды текстовых задач и их при­меры. Решение текстовой задачи. Этапы решения текстовой задачи. Решение текстовых задач ариф­метическими приемами (по действиям). Решение текстовых задач методом составления уравнения, неравенства или их систем. Значение правильного письменного оформления решения текстовой задачи. Решение текстовой задачи с помощью графика. Чер­теж к текстовой задаче и его значение для построения математической модели.

Задачи на движение (6 ч)

Движение тел по течению и против течения. Рав­номерное и равноускоренное движение тел по прямой линии в одном направлении и навстречу друг другу. Движение тел по окружности в одном направлении и навстречу друг другу. Формулы зависимости расстоя­ния, пройденного телом, от скорости, ускорения и времени в различных видах движения. Графики дви­жения в прямоугольной системе координат. Чтение графиков движения и применение их для решения текстовых задач. Решение текстовых задач с исполь­зованием элементов геометрии. Особенности выбора переменных и методика решения задач на движение. Составление таблицы данных задачи и ее значение для составления математической модели.

Зачет по теме «Задачи на движение».

Задачи на сплавы, смеси, растворы (4 ч)

Формула зависимости массы или объема вещес­тва от концентрации и массы или объема. Особенно­сти выбора переменных и методика решения задач на сплавы, смеси, растворы. Составление таблицы дан­ных задачи и ее значение для составления математи­ческой модели.

Зачет по теме «Задачи на сплавы, cмecи, pacтвopы».

Задачи на работу (3 ч)

Формула зависимости объема выполненной рабо­ты от производительности и времени ее выполнения. Особенности выбора переменных и методика решения задач на работу. Составление таблицы данных задачи и ее значение для составления математической моде­ли.

Задачи на прогрессии (3 ч)

Формула общего члена и суммы первых п членов арифметической и геометрической прогрессиЙ. Осо­бенности выбора переменных и методика решения за­дач на прогрессии.

Задачи с экономическим содержанием (3 ч)

Формулы процентов и сложных процентов. Осо­бенности выбора переменных и методики решения за­дач с экономическим содержанием.

Зачет по темам «Задачи на работу», «Задачи на прогрессии», «Задачи с экономическим содержанием».

Задачи на числа (1 ч)

Представление многозначного числа в виде сумму разрядных слагаемых. Особенности выбора перемен­ных и методика решения задач на числа.

Разные задачи (1 ч)

Задачи и оптимальный выбор. Задачи с выборкой целочисленных решений.

Повторение (2 ч)

Практикум по решению задач. Самостоятельная работа

Раздаточные материалы — MPM1D1 — Академическая математика 9 класса

	Ċ	1 — Word Problems with 1 Unknown. pdf Посмотреть Скачать		347к	т. 1	8 августа 2017 г., 9:29	Ванесса Пик [Посох]
	Ċ	2 — Percent.pdf Посмотреть Скачать		121к	т. 1	8 августа 2017 г., 9:29	Ванесса Пик [Посох]
	Ċ	2 — Word Problems with 2 Unknowns.pdf Посмотреть Скачать		123к	т. 1	8 августа 2017 г., 9:29	Ванесса Пик [Посох]
	Ċ	3 — Проценты от числа.pdf Посмотреть Скачать		116к	т. 1	8 августа 2017 г., 9:29	Ванесса Пик [Посох]
	Ċ	3 — Word Problems with Totals.pdf Посмотреть Скачать		117к	т. 1	8 августа 2017 г., 9:29	Ванесса Пик [Посох]
	Ċ	4 — Проблемы с деньгами.pdf Посмотреть Скачать		77к	т. 1	8 августа 2017 г., 9:29	Ванесса Пик [Посох]
	Ċ	4 — Percent Discount & Tax.pdf Посмотреть Скачать		185к	т. 1	8 августа 2017 г., 9:29	Ванесса Пик [Посох]
	Ċ	5 — Денежные проблемы с итоговыми суммами. pdf Просмотреть Скачать		35к	т. 1	8 августа 2017 г., 9:29	Ванесса Пик [Посох]
	Ċ	5 — Percent Applications.pdf Посмотреть Скачать		95к	т. 1	8 августа 2017 г., 9:29	Ванесса Пик [Посох]
	Ċ	6 — Начальное значение в процентах.pdf Посмотреть Скачать		112к	т. 1	8 августа 2017 г., 9:29	Ванесса Пик [Посох]
	Ċ	6 — Word Problem Practice.pdf Посмотреть Скачать		145к	т. 1	8 августа 2017 г., 9:29	Ванесса Пик [Посох]
	Ċ	MPM1D1 U2 EQAO Practice.pdf Посмотреть Скачать		477к	т. 1	8 августа 2017 г., 9:29	Ванесса Пик [Посох]
	Ċ	MPM1D U2 Progress Check.pdf Посмотреть Скачать		252к	т. 1	8 августа 2017 г., 9:29	Ванесса Пик [Посох]
	Ċ	MPM1D U2 Progress Check Solutions.pdf Посмотреть Скачать		1871к	т. 1	6 марта 2019 г., 6:10	Эллисон Миллер Зонненбург [Персонал]
	Ċ	MPM1D Тест на отработку задач Word с решениями. pdf Посмотреть Скачать		261к	т. 1	28 февраля 2019 г., 5:09	Эллисон Миллер Зонненбург [Персонал]
	Э	U2 5 — Word Problems (Money) (1).doc Посмотреть Скачать		73к	т. 1	1 марта 2017 г., 17:04	Неизвестный пользователь

100 задач со сложными словами по алгебре

Ниже вы найдете множество сложных задач по алгебре. Здесь рассматриваются самые сложные и трудные задачи по алгебре. Если вы можете решить их, вы, вероятно, сможете решить любые задачи по алгебре.

Учителя! Не стесняйтесь выбирать из этого списка и давать их своим ученикам, чтобы проверить, освоили ли они, как решать сложные задачи по алгебре.

Узнайте ниже, как распечатать эти задачи. При необходимости вы также можете приобрести раствор.

1.   бензин подорожал на 2 цента за литр. на прошлой неделе мужчина купил 20 литров по старой цене. На этой неделе он купил 10 литров в новом цена. В целом бензин стоит 9,20 доллара. Какая была старая цена 1 литр?

2. Учителя разделил студентов на группы по 3 человека. Каждая группа из 3 человек написала отчет в котором было 9 картинок. Всего студенты использовали 585 изображений. Сколько всего было учеников?

3. Вера и Викки сестры. Вере 4 года, а Викки 13 лет. Сколько лет будет каждой из сестер, когда Викки будет вдвое старше Веры?

4.  А может выполнить работу за 14 дней, и, работая вместе, А и В могут сделать то же самое работа через 10 дней. За какое время В один может выполнить эту работу?

5. 7 рабочие могут изготовить 210 пар чашек за 6 дней. Сколько рабочих требуется сделать 450 пар чашек за 10 дней?

6. Десять лет назад соотношение между возрастами Мохана и Сумана было 3:5. 11 лет, следовательно, это будет 11:16. Каков нынешний возраст Мохана?

7. соотношение девочек и мальчиков в классе 9 к 7, а в классе 80 учеников класс. Сколько девочек в классе?

8.   Один унция раствора X содержит только ингредиенты a и b в соотношении 2:3. Одна унция раствора Y содержит только ингредиенты a и b в соотношении  1:2. Если раствор Z создается путем смешивания растворов X и Y в соотношении  3:11, затем 25:20 унций раствора Z содержит сколько унций a?

9.   Это неделю Боб заправляет свой грузовик бензином когда бак был примерно наполовину пуст. Пять дней спустя Боб снова заправляет газом, когда в баке было около трех четверти заполнены. Если Боб купил 24 галлона бензина, сколько галлонов бак держит?

10. А коммерческий самолет, летящий со скоростью 700 миль/ч, обнаружен на расстоянии 1000 миль прочь с радаром. Через полчаса самолет-перехватчик, летевший с скорость 800 миль / ч отправляется. Сколько времени потребуется перехватчику самолет, чтобы встретиться с другим самолетом?

11. Есть 40 свиней и кур на ферме. Джозеф насчитал 100 ног за все. Сколько свиней и сколько кур?

12. Верх коробки представляет собой прямоугольник с периметром 72 дюйма. Если поле высота 8 дюймов, какие размеры дадут максимальный объем?

13. Вы собирают деньги на благотворительность. Кто-то сделал фиксированное пожертвование в размере 500. Затем вы требуете, чтобы каждый участник внес залог в размере 25 долларов. Какова минимальная сумма сбора, если участников 224 .

14. сумма двух положительных чисел равна 4, а сумма их квадратов 28. Какие два числа?

15. Полет против реактивного течения реактивный самолет проходит 1880 миль за 4 часа. Полет с реактивный поток, тот же реактивный самолет проходит 5820 миль за 6 часов. Что это скорость струи в неподвижном воздухе и какова скорость струйного течения?

16.   Дженна и ее друг Халил соревнуются, кто сможет спасти больше всего денег. Дженна уже накопила 110 долларов и каждую неделю откладывает дополнительные 20 долларов. Халил уже накопил 80 долларов и каждую неделю откладывает дополнительные 25 долларов. Пусть x представляет количество недель, а y представляет  общая сумма сэкономленных денег. Определите, через сколько недель Дженна и Халил будет столько же денег.

17. сумма трех последовательных членов геометрической прогрессии равна 104, а их  продукт 13824.узнать условия.

18. сумма первого и последнего из четырех последовательных нечетных целых чисел равна 52. Что четыре целых числа?

19. А оздоровительный клуб взимает единовременный вступительный взнос и ежемесячная плата. Джон заплатил 100 долларов за 2 месяца членства. Однако Питер заплатил 200 за 6 месяцев членства. Сколько Сильвия заплатит за 1 год членство?

20. сумма двух положительных чисел равна 4, а сумма их кубов равна 28. Что произведение двух чисел?

21. А человек, продающий компьютерные комплектующие, понимает, что когда он продает 16 компьютерных комплектующих, его заработок составляет 1700 долларов. Когда он продает 56 компьютерных комплектующих, его доход составляет 4300 долларов. Каков будет доход, если мужчина продаст 30 деталей для компьютеров?

22. А у человека в карманах 15 монет. Эти монеты десятицентовики и четверти которые добавляют до 2,4 долларов. Сколько четвертаков и сколько десятицентовиков у человека?

23. длины сторон треугольника относятся как 4:3:5. Находить длины сторон, если периметр равен 18 дм.

24. отношение основания к высоте равностороннего треугольник 3:4. Если площадь треугольник равен 6, чему равен периметр треугольника?

25. процентная доходность фонда роста, фонда дохода и денежного рынка 10%, 7% и 5% соответственно. Предположим, у вас есть 3200 долларов США для инвестирования, и вы хотите вложить в фонд роста вдвое больше, чем на денежный рынок, чтобы максимизировать ваше возвращение.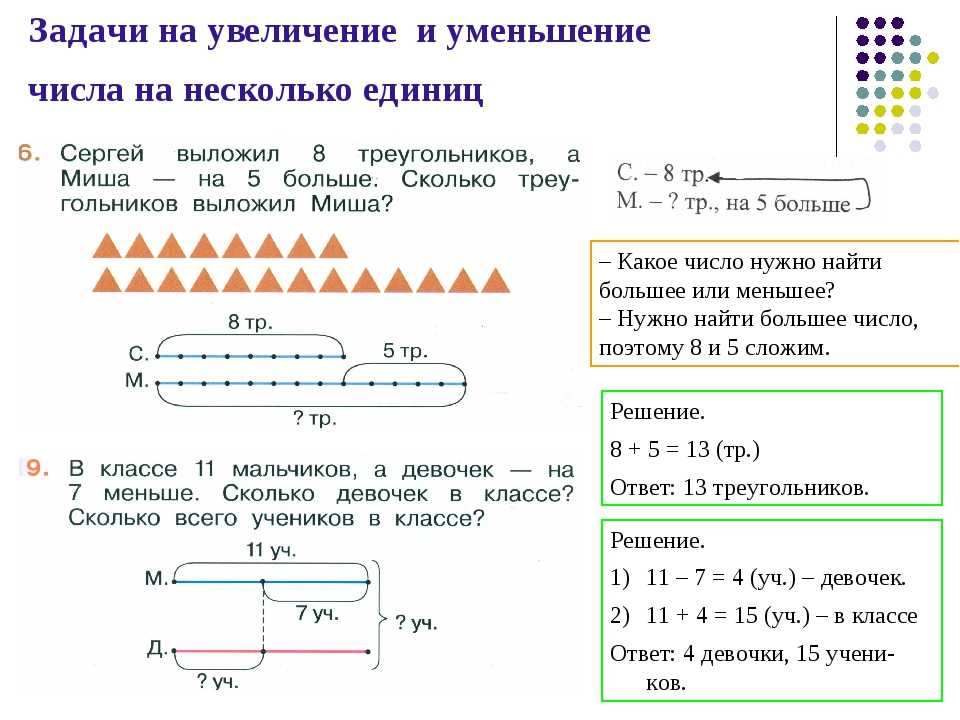 Как вы должны инвестировать, чтобы получить доход в 250 долларов за 1 год?

26. А была поймана акула, хвост которой весил 200 фунтов. Глава акула взвешенная столько, сколько его хвост плюс половина его тела. Его тело весило столько как его голова и хвост. Каков вес акулы?

27. квадратный корень из число плюс два равно количество. какая это количество?

28. Допустим у вас есть купон на 6 долларов на любой товар в торговом центре. Вы идете на магазин в торговом центре со скидкой 20%. Что вам нужно делать сэкономить больше всего денег?

29. Допустим ваши оценки на трех экзаменах по математике: 80, 93 и 91. Какую оценку вы нужно на следующем экзамене иметь средний балл не ниже 90 по четырем экзаменам?

30. Питер имеет фотографию шириной 5 дюймов и длиной 6 дюймов. Она увеличила с каждой стороны на одинаковую сумму. Насколько увеличена фотография если новая площадь составляет 182 квадратных дюйма?

31. стоимость создания книги составляет 1200 для начала плюс 9 долларов за книгу. книга продается по 15 долларов каждая. Сколько книг нужно продать, чтобы получить прибыль?

32. Магазин А продает компакт-диски по 2 доллара за штуку при единовременной оплате комиссия 104 долларов. Магазин B предлагает 12 бесплатных компакт-дисков и взимает 10 долларов за каждый дополнительный CD. Сколько компакт-дисков вы должны купить, чтобы они стоили одинаково в обоих случаях? планы?

33. Когда К двум числам добавляется 4, соотношение 5:6. Когда 4 вычитается из двух чисел соотношение 1:2. Найдите два числа.

34. А владелец магазина хочет продать 200 фунтов смеси фисташек и грецких орехов вместе. Грецкие орехи стоят 4 доллара за фунт, а фисташки — 6. долларов за фунты. Сколько фунтов каждого вида орехов нужно смешать, если владелец магазина будет брать 5 долларов за смесь?

35. А производитель коробок с хлопьями изготавливает коробки с хлопьями на 32 унции. В идеальном мира, коробка будет весить 32 унции каждый раз. Однако, поскольку мир не идеален, они допускают разницу в 0,06 унции. Найди диапазон допустимых размеров коробки с хлопьями.

36. А мужчина весом 600 кг каждый месяц теряет 3,12% своего веса с некоторыми тяжелые упражнения и правильное питание. Сколько будет весить человек после 20 месяцев?

37. Ан предмет подброшен в воздух на высоту 60 футов. Через 1 секунду и 2 секунды объект находится в воздухе на высоте 88 футов и 84 фута соответственно. какая начальная скорость тела?

38. А транзит находится в 200 футах от основания здания. есть человек стоит на крыше здания. Углы подъема сверху и низ мужчины 45 градусов и 44 градуса. Что это рост человека?

39. А лимонад состоит из 6% лимонного сока и клубничного сока состоит из 15% чистого фруктового сока. Сколько каждого вида должно быть смешать вместе, чтобы получить 4 литра 10% концентрации фруктов сок?

40. Эллен может помыть машину за 60 минут. Ее старшая сестра Сара может сделать та же работа за 45 минут. Сколько времени это займет, если они помоют машину вместе?

41. А самолет летит со скоростью 500 миль в час. Самолет может пролететь 1100 миль с ветром за то же время, за которое он проходит 900 миль против ветра. Какова скорость ветра?

42. А Компания производит коробки длиной 5 футов, шириной 4 фута и 3 фута. высокая. Компания хочет увеличить каждое измерение на одинаковую величину. чтобы новый объем был в два раза больше. На сколько увеличивается измерение?

43. Джеймс вложил половину своих денег в землю, десятую часть в акции и двадцатую в сберегательных облигациях. Затем он вложил оставшиеся 21000 в компакт-диск. Сколько деньги Джеймс сэкономил или вложил?

44. материнские платы для настольного компьютера могут быть изготовлены за 50 долларов каждый. Стоимость разработки 250000. Первые 20 материнских плат являются образцами и продаваться не будет. Сколько продаваемых материнских плат будет иметь среднюю стоимость 6325 долларов?

45. Как большая часть 70-процентного апельсинового сока должна быть смешана с 44 галлонами 20% апельсинового сока выпить, чтобы получить смесь, состоящую из 50% апельсинового сока?

46. А Компания реализует орехи оптом. При покупке оптом арахис продавать по 1,20 доллара США за фунт, миндаль по 2,20 доллара США за фунт и кешью по 3,20 доллара за фунт. Предположим, специализированному магазину нужна смесь из 280 фунтов, что будет стоить 2,59 доллара за фунт. Найдите количество фунтов каждого вида ореха, если сумма количества фунтов миндаля и орехов кешью в три раза больше, чем арахиса. Вокруг вашего ответы с точностью до фунта.

47. А Баскетболист успешно выполнил 36 из своих последних 48 штрафных бросает. Находить количество штрафных бросков подряд, необходимое игроку, чтобы увеличить вероятность успеха до 80%.

48. Джон может мыть машины в 3 раза быстрее, чем его сын Эрик. Работать вместе, им нужно помыть 30 машин за 6 часов. Сколько часов это займет каждый из них работает в одиночку?

49. В колледже, около 36% студентов моложе 20 лет и 15% старше 40 лет. Какова вероятность того, что студент, выбранный в random моложе 20 лет или старше 40 лет? 92 . Какова сила света на расстоянии 2 метров от лампочки?

52. длины двух сторон треугольника равны 2 и 6. найдите радиус значения возможных длин третьей стороны.

53. Найти три последовательных целых числа, половина их суммы находится между 15 и 21.

54. После вы открываете книгу, вы замечаете, что продукт два номера страниц на лицевых страниц 650. Каковы два номера страниц?

55. Допустим вы начинаете с числа. Вы умножаете число на 3, прибавляете 7, делите на ½, вычесть 5, а затем разделить на 12. В результате получится 5. Что число, с которого вы начали?

56. Вы иметь 156 футов ограждения, чтобы окружить прямоугольный сад. Ты хочешь длина сада в 5 раз больше его ширины. Найдите размеры сада.

57. количество воды, которую сбрасывает капающий кран, зависит от количество времени, в течение которого кран капает. Если из крана капает 2 стакана воды каждые 6 минут, узнайте, сколько времени потребуется крану, чтобы капнуть 10,6465 литров воды.

58. А стиральная машина стоит на 25% дороже сушилки. Если продавец магазина дал скидку 10 % на сушилку и скидка 20% на стиральную машину, сколько стоит стиральная машина перед скидкой, если вы заплатили 1900 долларов.

59. Выпечка на поднос кексов с черникой уходит 4 стакана молока и 3 стакана пшеницы мука. На поднос тыквенных кексов уходит 2 стакана молока и 3 стакана пшеничная мука. У пекаря есть 16 чашек молока и 15 чашек пшеничной муки. Вы зарабатываете 3 доллара прибыли за поднос черничных кексов и 2 доллара прибыль с лотка тыквенных кексов. Сколько лотков каждого типа кексы вы должны сделать, чтобы максимизировать прибыль?

60. А компания установила, что -2p + 1000 моделей количество телевизоров, продаваемых в месяц где p может быть установлено от 200 до 300. Как может компания максимизирует доход?

Другие сложные задачи по алгебре

61. Ваш друзья говорят, что у него есть 2 доллара 40 центов равным количеством четвертаков, десятицентовиков, и никель. Сколько у него каждой монеты?

62. я двузначное число, цифра в десятом разряде которого на 1 меньше удвоенная цифра в разряде единиц. Когда цифра на десятом месте делится на цифру, стоящую в разряде единиц, частное равно 1, а остаток равен 4. Какой у меня номер?

63. А двузначное число формируется путем случайного выбора из цифр 2, 4, 5, и 7 без замены. Какова вероятность того, что двузначное число содержит 2 или 7?

64. Допустим вы берете интервью у 30 девушек и 20 юношей в вашей школе, чтобы выяснить, кто среди них используют электрическую зубную щетку. Ваш опрос показал что только 2 мужчины используют электрическую зубную щетку, а 6 женщин. Какова вероятность того, что респондент не пользовался электричеством? зубная щетка, учитывая, что респондент — женщина?

65. Ан работодатель платит 15 долларов в час плюс дополнительные 5 долларов в час за каждый час, отработанный сверх 8 часов, до максимальной дневной заработной платы 220 долларов. Находить кусочная функция, моделирующая эту ситуацию.

66. Разделить меня на 7, остаток равен 5. Раздели меня на 3, остаток равен 1 и мое частное в 2 раза меньше, чем мое предыдущее частное. Какой номер я?

67. А компании, производящей багаж, должны соблюдать эти требования. Длина на 15 дюймов больше глубины и суммы длины, ширины и глубина не должна превышать 50 дюймов. Какое максимальное значение для глубина, если производитель будет использовать только целые числа?

68. Кому сделать открытую коробку, человек отрезает равные квадраты от каждого угла лист металла шириной 12 дюймов и длиной 16 дюймов. Найдите выражение объема через х.

69. Десять кандидаты баллотируются на пост президента, вице-президента и секретаря в студенческом самоуправлении. Вы можете проголосовать не более чем за 3 кандидатов. Сколькими способами можно проголосовать за 3 или менее кандидатов?

70. период полувыведения лекарства, назначенного врачом, составляет 6 часов. Как много мг этого лекарства остается через 78 часов, если врач прописал 100 мг?

71. Допустим вы бросаете красный кубик с числами и желтый кубик с числами. Находить P(красный 2, желтый 2) и вероятность получить любые совпадающие пары числа.

72. А кинотеатр в маленьком городе обычно открывает свои двери 3 дня подряд а затем закрывается на следующий день на техническое обслуживание. Другой кинотеатр 3 миль открыто 4 дня подряд, а затем закрывается на следующий день для та же самая причина. Предположим, оба кинотеатра закрыты сегодня и сегодня среда, когда в следующий раз они оба снова будут закрыты тот же день?

73. Ан инвестор вкладывает 5000 долларов под 10%, остальное под 5%. Сколько было инвестируется под 5%, если доход составляет одну пятую от суммы, инвестированной в 10%?

74. 20000 учащиеся сдали стандартизированный тест по математике. Баллы по тесту такие нормально распределены, со средним баллом 85 и стандартным отклонение 5. Сколько студентов набрали от 90 до 95 баллов?

75. А спутник, расположенный на высоте 2400 км над поверхностью Земли, находится в круговом орбиту вокруг земли. Если для завершения спутника требуется 3 часа 1 орбита, на каком расстоянии находится спутник через 1 час?

76. В группе из 10 человек, какова вероятность того, что хотя бы двое люди в у группы один день рождения?

77. Во время сбор средств для борьбы с раком на гала-концерте, все пожимают друг другу руки все остальные в комнате до события и после события законченный. Если n человек посетили торжество, сколько различных рукопожатий произошло?

78. Два кубы имеют длины сторон, равные 2x и 4x. Во сколько раз больше чем поверхность маленького куба, равна площади поверхности большого куб?

79. Допустим у вас есть работа в ресторане, где вам платят 8 долларов в час. У вас также есть работа в Walmart с оплатой 10 долларов в час. Вы хотите зарабатывать как минимум 200 в неделю. Однако вы хотите работать не более 25 часов в сутки. неделя . Покажите 3 различных способа, которыми вы могли бы работать на каждой работе.

80. Два Компания предлагает услуги репетитора. Компания А понимает, что когда они репетитора на 3 часа, они делают 45 долларов. Когда репетитор по 7 часов они составляют 105 часов. Компания B понимает, что, когда они занимаются репетиторством за 2 часов, они составляют 34 доллара. Когда они занимаются репетиторством по 6 часов, они делают 102 часа. Предполагая, что количество часов, которое студенты подписали за репетиторство одинаково для обеих компаний, какая компания будет генерировать больше дохода?

81. Вы хочу огородить прямоугольную детскую площадку во дворе. Чтобы сэкономить на заборы, вы будете использовать заднюю часть вашего дома в качестве одной из четырех сторон. Найдите возможные размеры, если дом имеет ширину 60 футов и вы хотите использовать по крайней мере 160 футов ограждения.

82. Когда число увеличивается на 20%, результат тот же, когда оно уменьшилось на 10% плюс 12. Какое число?

83. среднее из трех чисел равно 47. Самое большое число на пять больше, чем в два раза меньше. Диапазон 35. Какие три числа?

84. процент увеличения числа от его исходного количества до 36 составляет 80%. какая исходная сумма числа?

85. Когда Питер едет на работу со средней скоростью 45 миль в час из-за движение. На обратном пути домой он набирает в среднем 60 миль в час, потому что трафик не такой плохой. Общее время в пути 2 часа. Как далеко Дом Питера с работы?

86. Ан рекламная компания берет 20% со всей выручки, которую она генерирует для его филиалы. Если бы аффилиатам в этом месяце заплатили 15200 долларов, какой доход рекламная компания сгенерировала в этом месяце?

87. А Выручка компании может быть смоделирована с помощью квадратного уравнения. Компания заметила, что когда они продают 2 или 12 товаров, доход равен 0. Каков доход, когда они продают 20 предметов?

88. А мяч отскочил 4 раза, достигнув трех четвертей своей предыдущей высоты с каждым отскоком. После четвертого отскока мяч достиг высоты 25 см. На какой высоте находился мяч в момент падения?

89. А Компания по прокату взимает 40 долларов в день плюс 0,30 доллара за милю. Ты арендовать автомобиль и вернуть его через 4 дня. Сколько миль вы проехали автомобиль, если вы заплатили 325,5 долларов, включая 5% налога с продаж?

90. Два ученики покидают школу в одно и то же время и едут в противоположном направлении направления по той же дороге. Одна прогулка со скоростью 3 км/ч. другие велосипеды со скоростью 8,5 миль в час. Через сколько им будет 23 часть миль?

91. Коричневый имеет столько же братьев, сколько и сестер. Его сестра Сильвия как вдвое больше братьев, чем сестер. Сколько детей в семья?

92. Итан имеет такое же количество одноклассников мужского пола, как и одноклассников женского пола. Его у одноклассницы Оливии на три четверти больше одноклассниц, чем мужчин одноклассники. Сколько учеников в классе?

93. Ной хочет разделить определенную сумму денег с 10 человек. Однако на в последнюю минуту он думает о том, чтобы уменьшить сумму на 20, поэтому он может оставить себе 20 и разделить деньги только с 5 людьми. Сколько денег Ной пытается разделить, если каждый человек по-прежнему получает то же количество?

94. квадратный корень из меня плюс квадратный корень из меня — это я. Кто я?

95. А Денежный ящик содержит 160 купюр, все 10 и 50. Если общая стоимость из 10-х и 50-х годов составляет 1760 долларов. Сколько купюр каждого типа находится в чертежник?

96. Вы хотите приготовить 28 грамм протеиновой смеси для закусок с арахисом и мюсли. Арахис содержит 7 граммов белка на унцию и мюсли содержат 3 грамма белка на унцию. Сколько унций мюсли вы должны использовать на 1 унцию арахиса?

97. длина прямоугольной призмы вчетверо, ширина в два раза, а высота урезана пополам. Если V — объем прямоугольного призмы перед модификацией, выразить объем после модификация с точки зрения V.

98. А Прокат автомобилей имеет проигрыватели компакт-дисков в 85% своих автомобилей. Проигрыватели компакт-дисков случайным образом распределены по автопарку. Если человек арендует 4 машины, какова вероятность того, что хотя бы 3 из них будут с КД игроки?

99. Джейкобс почасовая оплата в 4 раза больше, чем у Ноя. Когда Джейкоб получил рейз на 2 долларов, Ной согласился на новую должность, на которой ему платят на 2 доллара меньше. в час. Джейкоб теперь зарабатывает в 5 раз больше денег, чем Ной. Сколько сколько денег они зарабатывают в час после того, как Джейкоб получил прибавку?

100.

Ты собственный ресторанный бизнес, который делает фирменные торты. Ваша компания имеет решили создать три вида тортов. Для создания таких тортов принимает команду, состоящую из декоратора, пекаря и дизайнера консультант. Торт А занимает у декоратора 9 часов, у пекаря 6 часов, и консультант по дизайну 1 час. Торт B берет декоратор 10 часов, пекарь 4 часа и консультант по дизайну 2 часы. Торт C занимает у декоратора 12 часов, у пекаря 4 часа, а у пекаря консультант по дизайну 1 час. Без найма дополнительных сотрудников 39Доступно 8 часов декоратора, 164 часа пекаря и 58 часов. доступны часы работы консультанта по дизайну. Сколько тортов каждого вида можно быть создан?

Хотите решить эти сложные задачи по алгебре? Добавьте в корзину и купите Подробное РЕШЕНИЕ НА 150+ СТРАНИЦАХ и ПРЕВОСХОДНЫЕ ОБЪЯСНЕНИЯ с помощью PayPal.

1. Двоичная система счисления

   17, 22 ноября 10:53

   Этот урок познакомит вас с двоичной системой счисления.

   No related posts.