Тест на сложение и вычитание: Сложение и вычитание натуральных чисел — Пройти онлайн тест

Онлайн тест по Математике по теме Сложение и вычитание

Математика – наука настолько древняя, насколько интересная, увлекательная и занимательная. Привить к ней интерес нужно, начиная с начальной школы. Именно этот период обучения закладывает главные математические знания, без понимания которых нельзя представить дальнейшее успешное развитие способностей математика. Сложение и вычитание школьникам знакомо с первого класса. Во втором классе закрепляют изученный теоретический материал, вычислительные навыки, приобретают новые знания – от умения складывать и вычитать в пределах чисел первого десятка переходят к новым счетным единицам. Чтобы почувствовать достаточную уверенность при решении примеров и задач, моно обратиться к тестам.

Тестовые задания предназначены для развития логического мышления, внимания, наблюдательности. Они повторяют и закрепляют компоненты сложения и вычитания. При решении примеров понадобится знание как можно найти уменьшаемое, неизвестное слагаемое.

С терпением и упорством прорабатывая тестовые вопросы, закрепляется умение определять, на сколько одно число больше или меньше другого. Самостоятельно сравнивая разные варианты вычислений, школьник приобретает способность выбирать более удобный.

Индивидуальная работа с тестом обучает к такому математическому, при котором задача становиться объектом тщательного изучения, ее решение – запланированное конструирование и изобретение. Выполнение тестовых упражнений вырабатывает творческое отношение к алгоритмам арифметических действий. Задания теста вырабатывают прочные умения составлять уравнения, решать несложные задачи, формируют устойчивый познавательный интерес к новым математическим приемам и способам.

---

---

Пройти тест онлайн

1. Найди уменьшаемое, если вычитаемое равно 7, а разность равна 9:

2


15


16

2. Найди второе слагаемое, если первое равно 4, а сумма равна 13:

9


17


8

3. На сколько 30 больше, чем 29?

на 10


на 1


другой ответ

4. Уменьши 27 на 20:

7


47


другой ответ

5. Найди верную запись выражения: сумму чисел 70 и 9 увеличь на 1.

(70 – 9) + 1


(70 + 9 ) – 1


(70 +9) + 1

6.

Выбери удобный способ вычисления для выражения: (40 + 4) + 20

40 + (4 + 20)


(40 + 20) + 4


(40 + 4) + 20

7. Найди примеры без ошибок:

16+20 = 36


16 + 2 = 36


68 – 3 = 64

8. Сравни: 30 – 3 и 21 + 9

меньше


больше


равно

9. Реши задачу: В одном мешке 60 кг пшена, а в другом 40 кг.

Продали 25 кг пшена. Сколько кг пшена осталось?

5 кг


65 кг


75 кг

10. Составь уравнение: Первое слагаемое 6, второе неизвестно, сумма равна 30.

x + 6 = 30


6 + x = 30


x – 6 = 30

---

---

Ещё никто не оставил комментария, вы будете первым.

Написать комментарий

Другие тесты

Тест: Сложение и вычитание многозначных чисел

Тест: Сложение и вычитание многозначных чисел — Математика 4 класс

Английский язык

Астрономия

Белорусский язык

Биология

География

ИЗО

Информатика

История

Итальянский язык

Краеведение

Литература

Математика

Музыка

Немецкий язык

ОБЖ

Обществознание

Окружающий мир

ОРКСЭ

Русский язык

Технология

Физика

Физкультура

Химия

Черчение

Для учителей

Дошкольникам

VIP — доступ

• Предметы
»
• Математика
»
• 4 класс
»
• Сложение и вычитание многозначных чисел

Сложение и вычитание многозначных чисел

Проверка владения устными вычислениями, сложение и вычитание многозначных чисел, названия компонентов действий сложения и вычитания

Математика 4 класс | Автор: Полетаева | ID: 10351 | Дата: 10. 10.2018

+26 -18

Помещать страницу в закладки могут только зарегистрированные пользователи
Зарегистрироваться

Вопрос № 1

Уменьшите на 200 число 56900

5670
56100
57100
56700

Вопрос № 2

На сколько 689 больше 400?

на 289
на 1089
на 989
на 389

Вопрос № 3

Какое число увеличили на 300, чтобы получить 625?

425
874
925
325

Вопрос № 4

Одно число 450, а другое на 30 меньше. Чему равна сумма этих чисел?

930
870
420
480

Вопрос № 5

Укажите разность двух сумм: 560 и 40, 380 и 120.

380
240
680
100

Вопрос № 6

Если первое слагаемое 670, второе слагаемое — разность чисел 653 153, то их сумма:

1270
1170
170
1070

Вопрос № 7

К какому задуманному числу прибавили 580 и получили 1200?

720
480
620
520

Вопрос № 8

Сумма чисел 610 и 120 равна разности чисел 1000 и …

260
270
280
370

Вопрос № 9

Чему равна разность чисел 3890 и 2890?

5090 — 4000
сумме чисел 360 и 640
573 + 327
разности чисел 2630 и 1600

Вопрос № 10

Чему могут равняться слагаемые, если сумма равна 2730?

1630 и 1200
670 и 2050
1312 и 1418
590 и 2014

Вопрос № 11

Укажите правильно записанное выражение и его значение: «Из числа 6530 вычесть сумму чисел 640 и 360».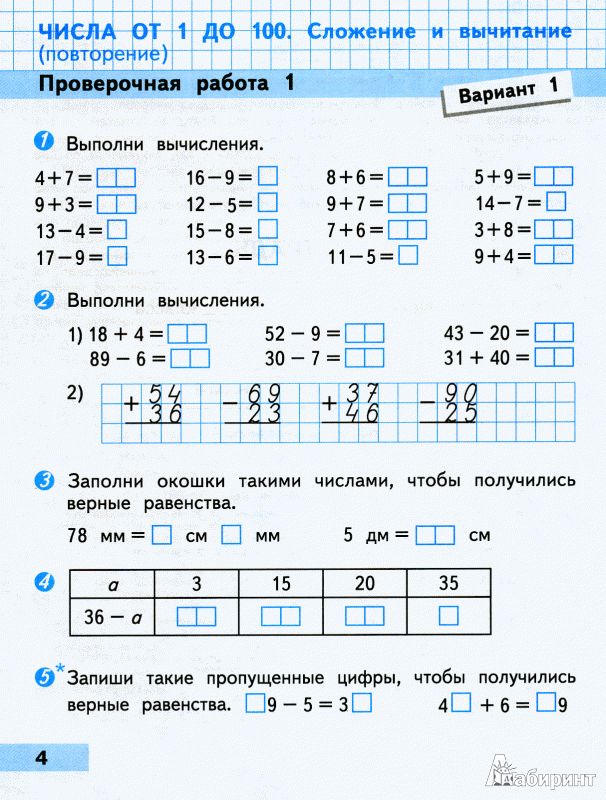

6530 + 640 — 360 = 6810
6530 + (640 — 360) = 6810
6530 — (640 + 360) = 5530
6530 — (640 + 360) = 5430

Вопрос № 12

Значение какого выражения равно 0?

730 + 620 — 280 — 1120
85030 + 70 — 500 — 84500
900 — 500 — 400 + 1
26400 — 20000 + 200 — 6600

Вопрос № 13

Значение какого выражения равно 450 — 290?

740 — 570
780 — 620
490 — 160
820 — 650

Вопрос № 14

В какой строке все ответы одинаковые?

600 — 400, 840 — 640, 120 + 80, 490 — 390
700 + 100, 600 + 200, 1000 — 200, 900 — 20 — 70
50 + 0, 150 — 100, 370 — 320, 630 — 580
800 — 400, 200 + 200, 560 — 160, 500 — 200

Вопрос № 15

Разность чисел 30056 и 156 больше:

суммы чисел 28900 и 10000
суммы 29000 и 900
разности 50000 и 20200
суммы 29000 и 1000

Показать ответы

Получение сертификата
о прохождении теста

Доступно только зарегистрированным пользователям

© TestEdu. ru 2013-2022

E-mail администратора: [email protected]

Справка по алгебре

Студенты, нуждающиеся в помощи по алгебре, получат большую пользу от нашей интерактивной программы. Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по предварительной алгебре. Имея под рукой обязательные концепции обучения и соответствующие практические вопросы, вы мгновенно получите много помощи по предварительной алгебре. Получите помощь сегодня с нашей обширной коллекцией необходимой информации по предварительной алгебре.

Если алгебра — это дом мечты, который вы надеетесь когда-нибудь построить, то предварительная алгебра — это фундамент дома. После завершения строительства дома его не будет видно снаружи, и большинство людей не упоминают об этом в разговоре. Тем не менее, он обеспечивает структурную поддержку дома; без него дом рухнул бы на землю. Предварительную алгебру обычно преподают ученикам седьмого класса в Соединенных Штатах, и это тот этап, когда учащиеся переходят от базовой арифметики к таким понятиям, как целые числа, отрицательные числа, десятичные числа, дроби и абсолютное значение. Эти новые понятия заложили математический фундамент не только алгебры, но и всей высшей математики. Нужны ли вам репетиторство по алгебре в Буффало, репетиторство по алгебре в Кливленде или репетиторство по алгебре в Хьюстоне, работа один на один с экспертом может быть именно тем, что вам нужно для учебы.

Справочник по предварительному изучению алгебры, доступный с помощью средств обучения Varsity Tutors Learn by Concept, поможет вам создать эту основу. Всеобъемлющий материал размещен на веб-сайте в виде интерактивной программы с несколькими основными категориями и рядом более мелких тем. Нажав на эти темы, вы получите ряд примеров вопросов, которые проверят вас по рассматриваемой теме. Каждый пример вопроса включает в себя набор ответов с несколькими вариантами ответов. Просмотрев возможные ответы, вы можете поработать над проблемой, а затем выбрать правильный ответ, когда закончите. Затем вы сверяете свой ответ с правильным. Varsity Tutors предлагает такие ресурсы, как бесплатные пробные тесты по алгебре , которые помогут вам в самостоятельном обучении, или вы можете подумать о преподавателе по алгебре .

Что еще более важно, Learn by Concept не останавливается на достигнутом. Его наиболее полезной особенностью являются пошаговые объяснения, прилагаемые к каждому примерному вопросу, которые показывают вам, как прийти к правильному ответу. Независимо от того, определяете ли вы объем конуса или учитесь рисовать линии, вы можете увидеть, как прийти к правильному ответу на многошаговые задачи. Независимо от того, дали ли вы ответ правильно или нет, вы можете проверить свою работу — либо подтвердить, что вы выполнили работу правильно, либо найти, где вы сбились с пути и как вернуться на правильный курс. В дополнение к справочному разделу по предварительной алгебре и урокам по алгебре вы также можете рассмотреть некоторые из наших карточек по предварительной алгебре.

Вы можете использовать инструмент «Обучение по концепции» в качестве учебного пособия для подготовки к предстоящему тесту, получения форы или повторения темы, по которой вам нужна помощь. Инструмент проведет вас через основные доалгебраические категории алгебраических уравнений, геометрии, построения графиков, теории чисел, операций и свойств и многочленов, а также углубится в конкретные темы, которые вам нужно будет охватить в каждой категории. Тысячи типовых вопросов означают, что учебный материал Pre-Algebra доступен для каждой возможной темы, которая может возникнуть.

Инструмент «Обучение по концепции» предназначен для использования вместе с другими доступными бесплатными инструментами обучения университетских преподавателей. Хорошим местом для начала является один из бесплатных полных практических тестов, которые охватывают различные темы предварительной алгебры, чтобы определить, в каких областях вам может понадобиться помощь. Существуют также сотни более коротких практических тестов предварительной алгебры, которые позволяют вам чтобы сосредоточиться на конкретных темах. После того, как вы ответили на примеры вопросов «Учитесь по концепции» в своих основных областях, вы можете получить дополнительную помощь в учебе с помощью карточек «Инструменты обучения» от преподавателей университетов. Вы можете настроить карточки для своих конкретных потребностей или следовать тем же категориям, что и в вопросах «Узнай по концепции». Во время занятий по предварительной алгебре вы можете использовать инструмент «Вопрос дня», чтобы ежедневно получать вопрос по случайной теме, что поможет вам понять ваше общее понимание предмета. Использование инструментов обучения Varsity Tutors может помочь вам сосредоточиться, пока вы закладываете основы высшей математики с Pre-Algebra.

• Предварительная алгебра

• Алгебраические уравнения

• Одношаговые уравнения

• Одношаговые уравнения с десятичными знаками

• Одношаговые уравнения с дробями

• Одношаговые уравнения с целыми числами

• Двухшаговые уравнения

• Двухшаговые уравнения с десятичными знаками

• Двухшаговые уравнения с дробями

• Двухшаговые уравнения с целыми числами

• Проблемы со словами

• Word Проблемы с одним неизвестным

• Задачи на слова с двумя неизвестными

• Геометрия

• Район

• Площадь круга

• Площадь параллелограмма

• Площадь прямоугольника или квадрата

• Площадь треугольника

• Периметр

• Длина окружности

• Периметр прямоугольника или квадрата

• Периметр треугольника

• Том

• Объем конуса

• Объем цилиндра

• Объем пирамиды

• Объем прямоугольного твердого тела

• Объем сферы

• Графики

• Анализ графиков и рисунков

• Графические линии

• Графические точки

• Теория чисел

• Целые числа и типы чисел

• Иррациональные числа

• Номер строки

• Реальные числа

• Операции и свойства

• Идентичности и свойства

• Свойство аддитивной идентификации

• Аддитивное обратное свойство

• Ассоциативное свойство дополнения

• Ассоциативное свойство умножения

• Коммутативное свойство сложения

• Коммутативное свойство умножения

• Распределительная собственность

• Свойство мультипликативной идентичности

• Мультипликативное обратное свойство

• Другие предалгебраические свойства

• Операции

• Абсолютное значение

• Сложение и вычитание

• Умножение и деление

• Отрицательные числа

• Порядок действий

• Полиномы

• Сложение и вычитание многочленов

• Умножение и деление многочленов

• Силовое правило экспонентов

• Продукт Правило экспонентов

• Решение многочленов

Протокол оценки сложения и вычитания

Ресурс печати

  Ресурс печати или сохранение в формате PDF

Функция печати в настоящее время несовместима с Firefox.

ДРЕМЕ ТЕ

Ресурс печати

  Ресурс печати или сохранение в формате PDF

Функция печати в настоящее время несовместима с Firefox.

• PreviousFormative Assessment: It Add Up
• NextВидео оценивания сложения и вычитания

Пересмотрено 30 марта 2019 г. Раньше этот ресурс назывался «Протокол клинического интервью сложения и вычитания».

Задания в этом протоколе могут помочь вам изучить эти идеи о понимании ребенком сложения и вычитания. Вот три идеи, которые можно исследовать.

• Наборы объектов можно изменять, складывая их вместе.
• Набор объектов можно изменить, разделив их на вычитание.
• Язык и символы могут использоваться для отображения операций и взаимосвязей.

Ресурс Math Thinking Conversations содержит рекомендации по использованию подобных заданий для изучения математических знаний ребенка .

Следующие задания были организованы в соответствии с вопросами, перечисленными выше. Отдельные видео примеры элементов оценки доступны в   Оценочные видеоролики сложения и вычитания  и  Дополнительные видеоролики об операциях .

Сложение и вычитание объектов

• Обнаружить и объяснить изменение числа  Показать ребенку ряд предметов, например 4 медведя и скажите, что собираетесь сделать что-то особенное. Затем спрячьте медведей бумагой или тканью и тайком добавьте или уберите одного или двух медведей. Можно сказать: «Закрой глаза. Я собираюсь что-нибудь сделать». Затем раскройте мишек, чтобы ребенок увидел результат сложения или вычитания. Ваша цель должна заключаться в том, чтобы выяснить, понимает ли ребенок, как то, что вы сделали, повлияло на предметы. «Как вы думаете, что случилось? Сейчас медведей больше, или меньше, или столько же? Как вы думаете, почему сейчас их больше (или меньше)? Сколько медведей добавили (или убрали)? Сколько сейчас всего медведей?»
• Сложение или вычитание (с видимыми объектами)   Покажите ребенку двух медведей (или другие мелкие предметы) и покажите еще одного медведя сбоку. Спросите: «Сколько у меня будет медведей, если я добавлю еще одного? Как ты узнал? Как ты это понял? Подготовьте манипуляторы на случай, если ребенок захочет использовать их для решения задачи и покажите вам результат.
• Цифровые истории (со многими видимыми и доступными объектами)  Поставьте на стол около десяти медведей (или других мелких предметов), а также фишки, маркер и бумагу. Скажите: «Я хочу, чтобы вы нашли ответ на мои вопросы любым удобным для вас способом. Вы можете использовать свои пальцы, эти чипы, эту бумагу и карандаш, считать или думать в уме. У моего друга Томми был один кекс, а потом его мама дала ему еще два». Если ребенок реагирует быстро, попробуйте увеличить число, чтобы вы могли исследовать стратегии ребенка. «Сколько у него сейчас? Откуда вы знаете?» Это можно сделать и с помощью вычитания.
• Истории с числами (без видимых объектов) Скажите ребенку, что вы расскажете историю с числами. Скажите: «Представьте, что есть 3 морковки. Затем вы получаете еще 4 моркови. Сколько всего морковок?» Посмотрите, сможет ли ребенок мысленно найти сумму. Сделайте то же самое с задачей на вычитание. Скажите: «Теперь есть 7 морковок. Что будет, если я съем 2 из них? Сколько осталось?» Смотреть Magic Math Thinking Minute: дополнение здесь.
• Количество историй (проверь свою работу) Попросите ребенка, решившего в уме числовую историю, проверить свой ответ, используя манипуляции. Обратите внимание, как ребенок формулирует проблему. Например, если задача была 3 + 4, создает ли ребенок один набор из 3 манипуляторов, а затем добавляет к нему набор из 4, по одному, чтобы получить общее количество? Создает ли ребенок набор из 3 и набор из 4, а затем складывает их все вместе и считает новый объединенный набор? Смотрите Мередит: История чисел здесь.

Символы операций

• Формальный математический язык (плюс и минус)    Спросите: «Сколько будет четыре плюс два? Точно так же вы можете спросить: «Сколько будет пять минус три?» Если кажется, что ребенок к этому готов, предложите задачи на суммы больше 10. Например, спросите: «Сколько будет 8 плюс 3?» Попросите ребенка объяснить, откуда он это знает, чтобы вы могли выяснить, какие стратегии он использовал. Например, ребенок может сказать, что считал на пальцах. Ребенок может решить, что 8 + 2 — это 10, значит, 8 + 3 — это на 1 больше. В задаче на вычитание, такой как 12 — 4, ребенок может начать с 4 и считать до тех пор, пока не достигнет 12, показывая 8 пальцев. Ребенок также может посчитать на пальцах в обратном порядке или нарисовать картинку. Смотреть Лулу: 8 плюс 3 здесь 11 .
• Математические символы (плюс и минус)    Определите, может ли ребенок использовать стандартную письменную символику для задач, представляя такие задачи, как 2 + 3 и 5 – 2. Посмотрите, распознает ли ребенок символы плюс и минус и понимает их значение . Часы Таша: 3 + 1 равно 2 здесь и Чандра: 5 – 3 = 2 здесь .
• Математические символы (знак равенства)    Определите, понимает ли ребенок, что знак равенства показывает эквивалентность. Например, если ребенок правильно пишет, что 1 + 2 = 3, посмотрите, как ребенок реагирует на числовые предложения, такие как 3 = 1 + 2, 1 + 2 = 2 + 1 или 3 = 3. Некоторые дети могут сказать, что 3 должен быть справа от знака равенства, потому что он относится к результату сложения или вычитания. Другими словами, они могут увидеть знак равенства как указание на то, что «вы должны поставить ответ после него». Раннее математическое образование должно помочь ребенку выйти за рамки этого узкого взгляда на знак равенства. Часы Чандра: Знак равенства здесь и Чандра: 3 = 1 + 2 неверно здесь.
• Анализ неправильных ответов (ошибок)   Иногда дети используют ошибочные стратегии или ошибки для решения проблем. В этих случаях то, что делает ребенок, имеет некоторый смысл, хотя и не дает правильного ответа. Детям нравится играть в учителя, поэтому представьте задачу, которую ребенок правильно решил, например, 12–8, но скажите: «Предположим, вы были учителем, и ребенок написал это: 12–8 = 16. Почему они могут это сделать? ” Напишите задачу 12 – 8 = 16 вертикально. Посмотрите, сможет ли ребенок понять, как ребенок мог получить такой неправильный ответ. Другой способ приблизиться к этому — представить проблему и спросить, какую ошибку может совершить другой ребенок. Например, предъявите 8 + 3 и спросите, какую ошибку может сделать ребенок. Изучите, как ребенок узнает, что тот или иной ответ неверен. Например, если вы представляете 8 + 3 = 83, посмотрите, как ребенок узнает, что сумма неверна. Они говорят, что это неправильно, потому что знают, что правильный ответ — 11, или потому что они просто знают, что 83 слишком много, чтобы быть правильной суммой? (Дополнительную информацию об анализе ошибок см.

  No related posts.