Tg | это… Что такое Tg?
Рис. 1
Графики тригонометрических функций: синуса, косинуса, тангенса, секанса, косеканса, котангенса
Тригонометрические функции — вид элементарных функций. Обычно к ним относят синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x), секанс (sec x) и косеканс (cosec x), последняя пара функций в настоящее время сравнительно малоупотребительна (про ещё менее употребляемые функции см. здесь). В англоязычной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x. Обычно тригонометрические функции определяются геометрически, но можно определить их аналитически через суммы рядов или как решения некоторых дифференциальных уравнений, что позволяет расширить область определения этих функций на комплексные числа.
Содержание
|
Способы определения
Геометрическое определение
Рис. 2
Определение тригонометрических функций
Обычно тригонометрические функции определяются геометрически. Пусть дана декартова система координат на плоскости и построена окружность радиуса R с центром в начале координат O. Будем измерять углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим xB, ординату обозначим yB (см. рисунок.)
Будем измерять углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим xB, ординату обозначим yB (см. рисунок.)
- Синусом называется отношение
- Косинусом называется отношение
- Тангенс определяется как
- Котангенс определяется как
- Секанс определяется как
- Косеканс определяется как
Рис. 3.
Тригонометрические функции угла α в тригонометрической окружности с радиусом, равным единице.
Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате

Если α — действительное число, то синусом α в математическом анализе называется синус угла, радианная мера которого равна α, аналогично для прочих тригонометрических функций.
Определение тригонометрических функций для острых углов
Рис. 4.
Тригонометрические функции острого угла
Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α. Тогда:
- Синусом α называется отношение AB/OB (противолежащего катета к гипотенузе)
- Косинусом α называется отношение ОА/OB (прилежащего катета к гипотенузе)
- Тангенсом α называется отношение AB/OA (отношение противолежащего катета к прилежащему)
- Котангенсом α называется отношение ОА/AB (отношение прилежащего катета к противолежащему)
- Секансом α называется отношение ОB/OA (гипотенузы к прилежащему катету)
- Косекансом α называется отношение ОB/AB (гипотенузы к противолежащему катету)
Построив систему координат с началом в точке O, направлением оси абсцисс вдоль OA и в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее.
Определение тригонометрических функций как решений дифференциальных уравнений
Функции косинус и синус можно определить как чётное (косинус) и нечётное (синус) решение дифференциального уравнения
с начальными условиями cos(0) = sin'(0) = 1, то есть как функций одной переменной, вторая производная которых равна самой функции, взятой со знаком минус:
Определение тригонометрических функций как решений функциональных уравнений
Функции косинус и синус можно определить как непрерывные решения (f и g соответственно) системы функциональных уравнений:
Определение тригонометрических функций через ряды
Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу.
Пользуясь этими формулами, а также уравнениями и можно найти разложения в ряд Тейлора и других тригонометрических функций:
- где Bn — числа Бернулли.
- где En — числа Эйлера.
Значения тригонометрических функций для некоторых углов
Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице.
Значения косинуса и синуса на окружности.
| 0°(0 рад) | 30° (π/6) | 45° (π/4) | 60° (π/3) | 90° (π/2) | 180° (π) | 270° (3π/2) | 360° (2π) | |
|---|---|---|---|---|---|---|---|---|
Значения тригонометрических функций нестандартных углов
Свойства тригонометрических функций
Простейшие тождества
Так как синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α то, согласно уравнению единичной окружности или теореме Пифагора, имеем:
Деля это уравнение на квадрат косинуса и синуса соответственно имеем далее:
Чётность
Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:
Остальные четыре функции — нечётные, то есть:
Периодичность
Функции y = sin α, y = cos α, y = sec α, y = cosec α — периодические с периодом 2π. Функции: y = tg α, y = ctg α — c периодом π
Формулы приведения
Здесь f — любая тригонометрическая функция, g — соответствующая ей другая функция из пары (то есть косинус для синуса, синус для косинуса и аналогично для остальных функций). Нужный знак в правой части равенства определяется следующим образом: предположим что угол α находится в первой четверти, тогда определяем знаки значений функций в левой и правой части равенства и в случае их несовпадения перед правой частью пишем знак -, например:
Формулы сложения
Другие тригонометрические тождества.
Однопараметрическое представление
Все тригонометрические функции можно выразить через тангенс половинного угла.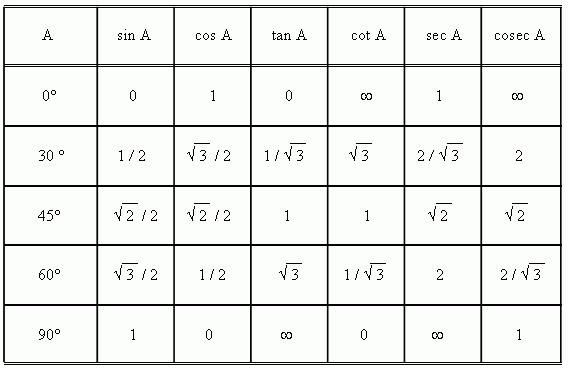
Производные и интегралы
Все тригонометрические функции непрерывно дифференцируемы на всей области определения:
Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:
- См. также Список интегралов от тригонометрических функций
История
Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива»), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха».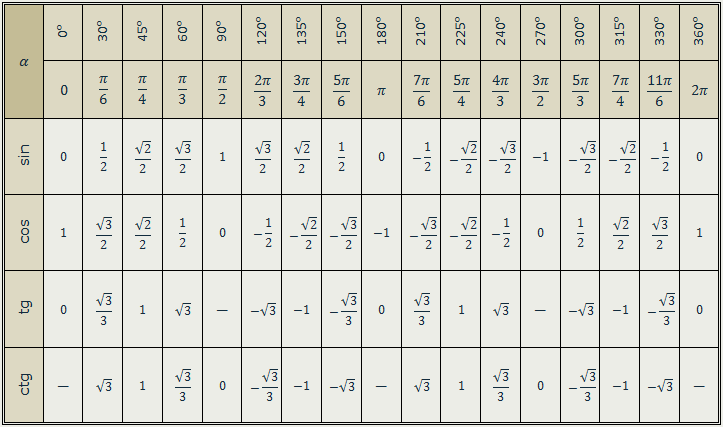 При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
Современное обозначение синуса sin и косинуса cos введено Леонардом Эйлером в XVIII веке.
Термины «тангенс» (от лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583)
Сам термин
См. также
- Гиперболические функции
- Обратные тригонометрические функции
- Редко используемые тригонометрические функции
- Эллиптические функции
- Теорема косинусов
- Теорема синусов
- Тригонометрические формулы
- Четырёхзначные математические таблицы (Таблицы Брадиса)
- Функция Гудермана связывает тригонометрические функции и гиперболические функции без привлечения комплексных чисел.

Ссылки
- GonioLab: Проясненная Единичная Окружность, Тригонометрические и Гиперболические функции (Java Web Start)
- Weisstein, Eric W. Тригонометрические функции на сайте Wolfram MathWorld.(англ.)
- Онлайн калькулятор: вычисление значений тригонометрических функций
Tg | это… Что такое Tg?
Рис. 1
Графики тригонометрических функций: синуса, косинуса, тангенса, секанса, косеканса, котангенса
Тригонометрические функции — вид элементарных функций. Обычно к ним относят синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x), секанс (sec x) и косеканс (cosec x), последняя пара функций в настоящее время сравнительно малоупотребительна (про ещё менее употребляемые функции см. здесь). В англоязычной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x. Обычно тригонометрические функции определяются геометрически, но можно определить их аналитически через суммы рядов или как решения некоторых дифференциальных уравнений, что позволяет расширить область определения этих функций на комплексные числа.
Содержание
|
Способы определения
Геометрическое определение
Рис.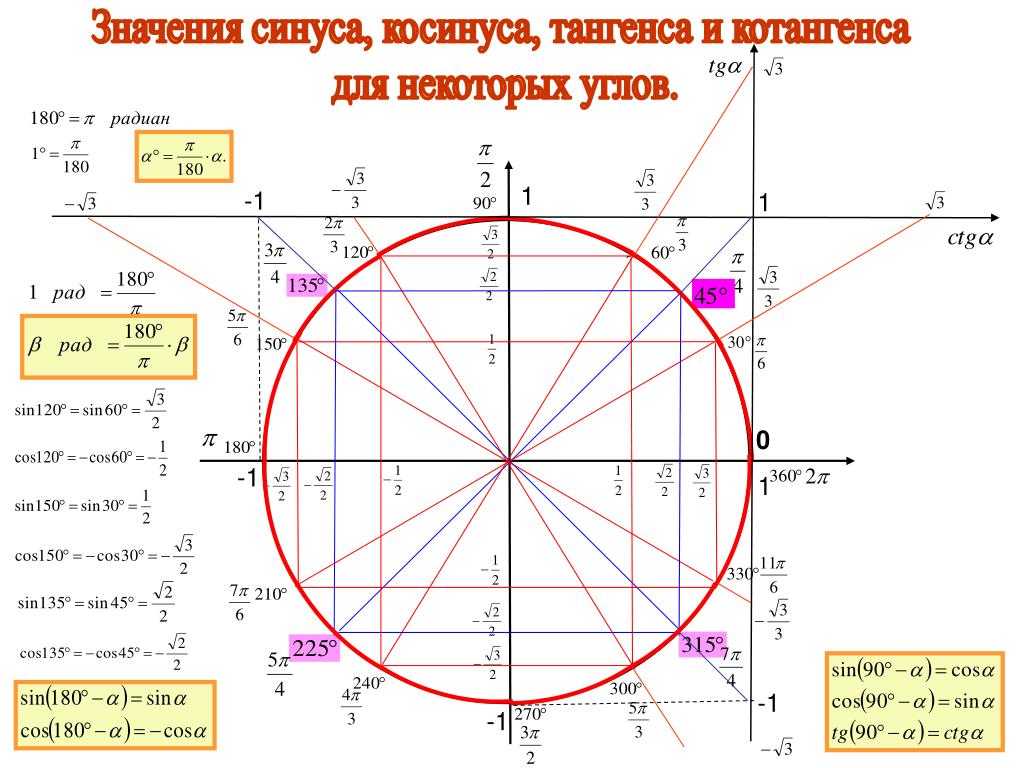 2
2
Определение тригонометрических функций
Обычно тригонометрические функции определяются геометрически. Пусть дана декартова система координат на плоскости и построена окружность радиуса R с центром в начале координат O. Будем измерять углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначим xB, ординату обозначим yB (см. рисунок.)
- Синусом называется отношение
- Косинусом называется отношение
- Тангенс определяется как
- Котангенс определяется как
- Секанс определяется как
- Косеканс определяется как
Рис. 3.
Тригонометрические функции угла α в тригонометрической окружности с радиусом, равным единице.
Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате yB, а косинус — абсциссе xB. На рисунке 3 показаны величины тригонометрических функций для единичной окружности.
Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате yB, а косинус — абсциссе xB. На рисунке 3 показаны величины тригонометрических функций для единичной окружности.
Если α — действительное число, то синусом α в математическом анализе называется синус угла, радианная мера которого равна α, аналогично для прочих тригонометрических функций.
Определение тригонометрических функций для острых углов
Рис. 4.
Тригонометрические функции острого угла
Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α. Тогда:
- Синусом α называется отношение AB/OB (противолежащего катета к гипотенузе)
- Косинусом α называется отношение ОА/OB (прилежащего катета к гипотенузе)
- Тангенсом α называется отношение AB/OA (отношение противолежащего катета к прилежащему)
- Котангенсом α называется отношение ОА/AB (отношение прилежащего катета к противолежащему)
- Секансом α называется отношение ОB/OA (гипотенузы к прилежащему катету)
- Косекансом α называется отношение ОB/AB (гипотенузы к противолежащему катету)
Построив систему координат с началом в точке O, направлением оси абсцисс вдоль OA и в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее. Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см. Теорема синусов, Теорема косинусов).
Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см. Теорема синусов, Теорема косинусов).
Определение тригонометрических функций как решений дифференциальных уравнений
Функции косинус и синус можно определить как чётное (косинус) и нечётное (синус) решение дифференциального уравнения
с начальными условиями cos(0) = sin'(0) = 1, то есть как функций одной переменной, вторая производная которых равна самой функции, взятой со знаком минус:
Определение тригонометрических функций как решений функциональных уравнений
Функции косинус и синус можно определить как непрерывные решения (f и g соответственно) системы функциональных уравнений:
Определение тригонометрических функций через ряды
Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу.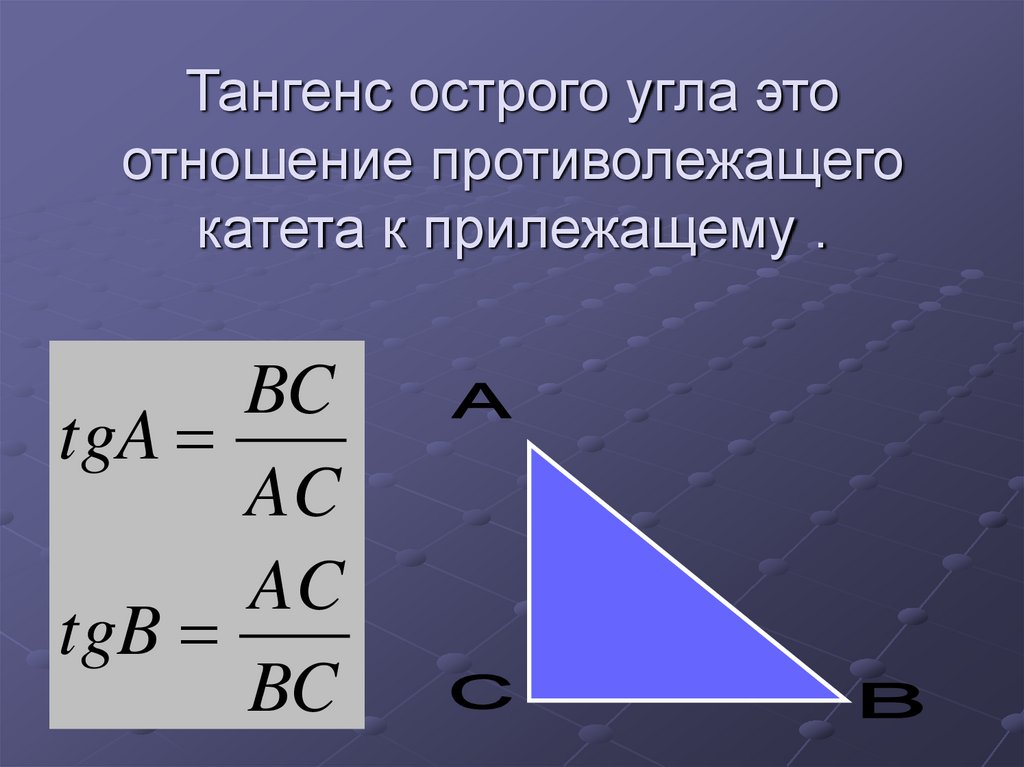 Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде суммы степенны́х рядов:
Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде суммы степенны́х рядов:
Пользуясь этими формулами, а также уравнениями и можно найти разложения в ряд Тейлора и других тригонометрических функций:
- где Bn — числа Бернулли.
- где En — числа Эйлера.
Значения тригонометрических функций для некоторых углов
Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице.
Значения косинуса и синуса на окружности.
| 0°(0 рад) | 30° (π/6) | 45° (π/4) | 60° (π/3) | 90° (π/2) | 180° (π) | 270° (3π/2) | 360° (2π) | |
|---|---|---|---|---|---|---|---|---|
Значения тригонометрических функций нестандартных углов
Свойства тригонометрических функций
Простейшие тождества
Так как синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α то, согласно уравнению единичной окружности или теореме Пифагора, имеем:
Деля это уравнение на квадрат косинуса и синуса соответственно имеем далее:
Чётность
Косинус и секанс — чётные.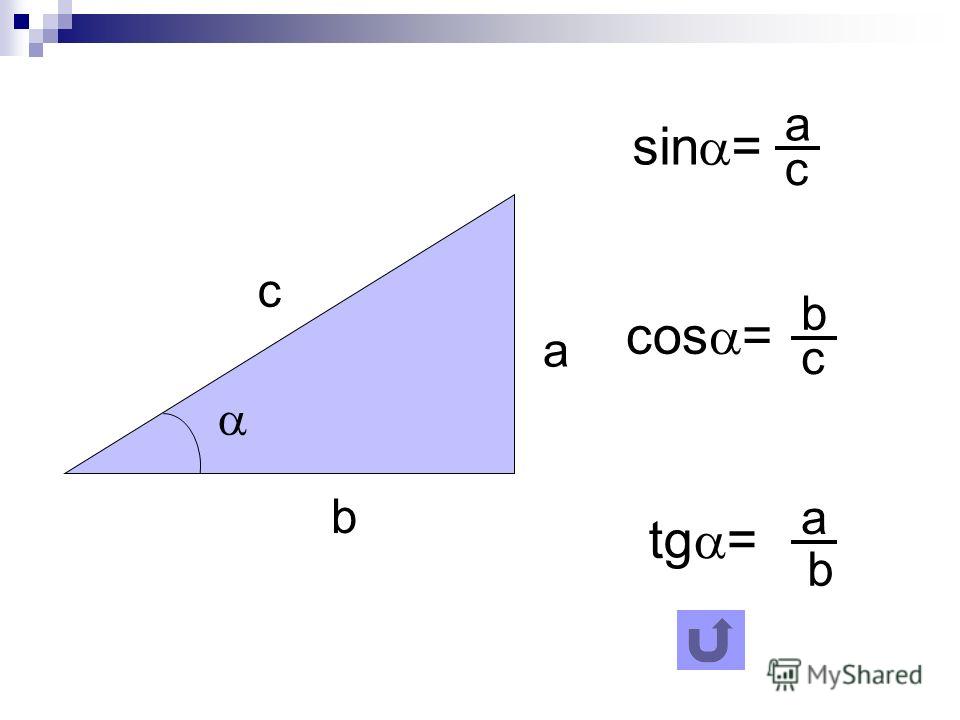 Остальные четыре функции — нечётные, то есть:
Остальные четыре функции — нечётные, то есть:
Периодичность
Функции y = sin α, y = cos α, y = sec α, y = cosec α — периодические с периодом 2π. Функции: y = tg α, y = ctg α — c периодом π
Формулы приведения
Здесь f — любая тригонометрическая функция, g — соответствующая ей другая функция из пары (то есть косинус для синуса, синус для косинуса и аналогично для остальных функций). Нужный знак в правой части равенства определяется следующим образом: предположим что угол α находится в первой четверти, тогда определяем знаки значений функций в левой и правой части равенства и в случае их несовпадения перед правой частью пишем знак -, например:
Формулы сложения
Другие тригонометрические тождества.
Однопараметрическое представление
Все тригонометрические функции можно выразить через тангенс половинного угла.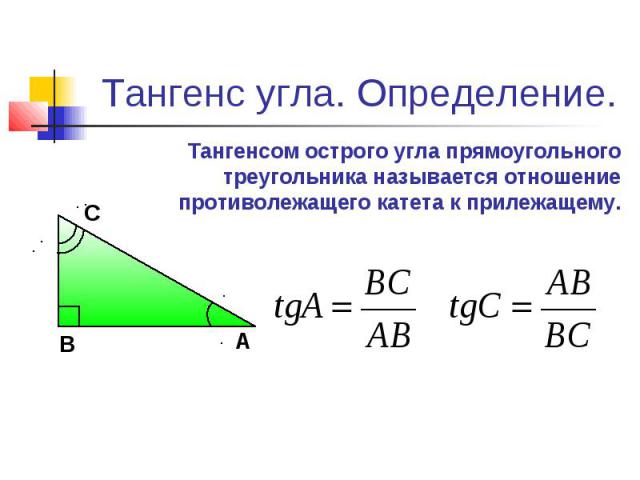
Производные и интегралы
Все тригонометрические функции непрерывно дифференцируемы на всей области определения:
Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:
- См. также Список интегралов от тригонометрических функций
История
Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива»), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
Современное обозначение синуса sin и косинуса cos введено Леонардом Эйлером в XVIII веке.
Термины «тангенс» (от лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583)
Сам термин тригонометрические функции введён Клюгелем в 1770.
См. также
- Гиперболические функции
- Обратные тригонометрические функции
- Редко используемые тригонометрические функции
- Эллиптические функции
- Теорема косинусов
- Теорема синусов
- Тригонометрические формулы
- Четырёхзначные математические таблицы (Таблицы Брадиса)
- Функция Гудермана связывает тригонометрические функции и гиперболические функции без привлечения комплексных чисел.

Ссылки
- GonioLab: Проясненная Единичная Окружность, Тригонометрические и Гиперболические функции (Java Web Start)
- Weisstein, Eric W. Тригонометрические функции на сайте Wolfram MathWorld.(англ.)
- Онлайн калькулятор: вычисление значений тригонометрических функций
Что такое Tg, температура стеклования? | Пластыри
Время потренировать старое серое вещество! Заказчики часто запрашивают у технических консультантов Permabond и химиков-разработчиков данные об измерениях Tg (температуры стеклования) наших инженерных клеевых материалов.
Что такое Tg, как его измеряют?
Температура стеклования (Tg) — это точка, при которой материал изменяет свое состояние, переходя от стеклообразного жесткого твердого вещества к более гибкому резиноподобному соединению. Tg обычно измеряют на дифференциальном сканирующем калориметре (DSC) на оборудовании wizzy. DSC автоматически строит график, по которому можно рассчитать приблизительную Tg. Стеклование происходит в определенном диапазоне на графике, поэтому точная цифра не получается автоматически, но опытный глаз может интерпретировать хороший график и может сделать квалифицированную оценку, если требуется конкретная цифра.
Стеклование происходит в определенном диапазоне на графике, поэтому точная цифра не получается автоматически, но опытный глаз может интерпретировать хороший график и может сделать квалифицированную оценку, если требуется конкретная цифра.
Зачем беспокоиться?!
Хороший вопрос, но это важное измерение, если добросовестный инженер-конструктор хочет оценить, как его клеевое соединение будет работать в диапазоне рабочих температур и как это может повлиять на другие материалы, которые он или она склеивает. Например, при склеивании разнородных материалов в автомобилестроении — скажем, металла какого-либо типа с композитом, температура в зимних условиях, скорее всего, будет ниже точки замерзания, а затем в летнее время температура в герметичной кабине может достигать более 60°C, не забыв упомянуть гораздо более высокие температуры в моторном отсеке. Важно, чтобы автомобильный клей выдерживал эти экстремальные условия, сохраняя при этом высокую прочность, ударопрочность и устойчивость к вибрации.
Будет ли клей работать при температуре выше Tg? Температура стеклования эпоксидного клея выглядит достаточно низкой?
Клеи, такие как эпоксидные смолы и другие конструкционные клеи, продолжают работать значительно выше температуры Tg. Они становятся немного более гибкими, что на самом деле улучшает некоторые характеристики, такие как ударопрочность и вибростойкость, а также немного более высокую прочность на отрыв. Эпоксидные смолы на самом деле не плавятся, это термореактивные смолы (в отличие от термопластов, которые плавятся при высоких температурах). Низкие температуры и условия замерзания делают клеи более хрупкими. Это важно помнить, если вы склеиваете разнородные материалы с разными коэффициентами теплового расширения — в этом случае рекомендуется использовать более прочный и эластичный клей. Интересно, что коэффициент теплового расширения (КТР) клея больше выше Tg и ниже ниже Tg. Еще один интересный момент, о котором следует упомянуть (если вы в этом заинтересованы), заключается в том, что вы можете увеличить Tg двухкомпонентного эпоксидного клея, отверждающегося при комнатной температуре, вместо этого осуществляя термическое отверждение продукта (хотя это может не подходить для быстрого отверждения).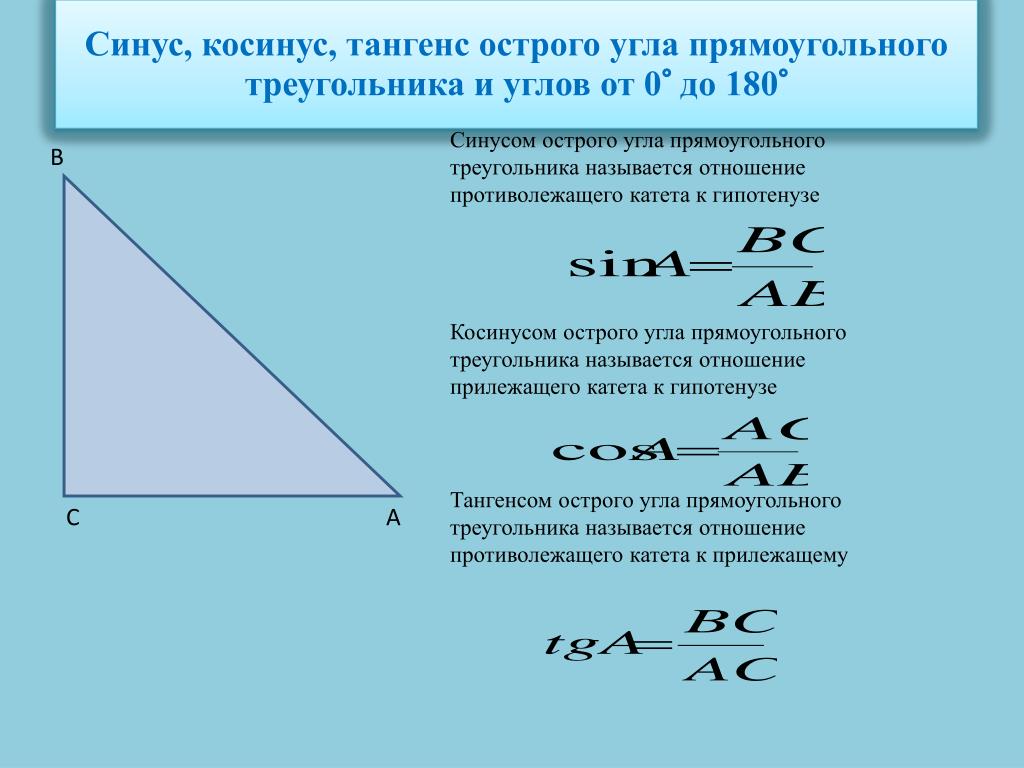 при отверждении эпоксидных смол или при массовом отверждении за счет экзотермической реакции – в этом случае вторичное отверждение при нагревании может обеспечить более высокую Tg).
при отверждении эпоксидных смол или при массовом отверждении за счет экзотермической реакции – в этом случае вторичное отверждение при нагревании может обеспечить более высокую Tg).
Почему цифры не во всех даташитах?
Большинству инженеров необходимо провести собственные тесты, соответствующие их индивидуальным требованиям и конкретным материалам подложки, чтобы убедиться, что клей достаточно прочен и сможет ли он выдержать испытания на ускоренное старение, испытания на термический удар и термоциклирование. Однако некоторые инженеры запрашивают у нас эти данные, и в этом случае у нас есть оборудование для проведения испытаний в случае необходимости.
Для получения дополнительной помощи, пожалуйста, обращайтесь к технической команде Permabond.
Что означает TG? Бесплатный словарь
Также найдено в: Словарь, Тезаурус, Медицинский, Финансовый, Энциклопедия, Википедия.
Фильтр категорий: Показать все (98)Наиболее распространенные (0)Технологии (12)Правительство и военные (8)Наука и медицина (20)Бизнес (17)Организации (19)Сленг / жаргон (30)
| Акроним | Определение | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ТГ | Великий (группа) | |||||||||||||||||||||||
| ТГ | The Game (online game) | |||||||||||||||||||||||
| TG | Top Gear (British car show) | |||||||||||||||||||||||
| TG | Glass Transition Temperature | |||||||||||||||||||||||
| TG | Togo (top level domain) | |||||||||||||||||||||||
| TG | Transgender | |||||||||||||||||||||||
| TG | Task Group | |||||||||||||||||||||||
| TG | The Gathering | |||||||||||||||||||||||
| TG | The Garden (Guns N’ Roses song) | |||||||||||||||||||||||
| TG | Top Gun (movie) | |||||||||||||||||||||||
| TG | Transgendered | |||||||||||||||||||||||
| TG | Thank God | |||||||||||||||||||||||
| TG | That’s Good | |||||||||||||||||||||||
| TG | That Guy | |||||||||||||||||||||||
| TG | Thanksgiving | |||||||||||||||||||||||
| TG | Thai Airways International | |||||||||||||||||||||||
| TG | Thurgau (Thurgovie; Swiss Canton) | |||||||||||||||||||||||
| TG | The Gap | |||||||||||||||||||||||
| TG | Transgenic | |||||||||||||||||||||||
| TG | ThinkGeek (website) | |||||||||||||||||||||||
| TG | Triglyceride | |||||||||||||||||||||||
| TG | Top Girls (игра Кэрил Черчилль) | |||||||||||||||||||||||
| TG | Texas Guaranteed (образование) | |||||||||||||||||||||||
| Техническое руководство | TG | 0037 | ||||||||||||||||||||||
| TG | 6-Thioguanine (chemotherapy drug) | |||||||||||||||||||||||
| TG | Too Good | |||||||||||||||||||||||
| TG | Thyroglobulin | |||||||||||||||||||||||
| TG | That’s Great | |||||||||||||||||||||||
| TG | Thai Airways International (код аэропорта IATA) | |||||||||||||||||||||||
| TG | TurboGrafx | |||||||||||||||||||||||
| TG | Tagesgeld (немецкий) 7 | |||||||||||||||||||||||
| TG | The Gamers | |||||||||||||||||||||||
| TG | Third Grade | |||||||||||||||||||||||
| TG | Toyoda Gosei Co.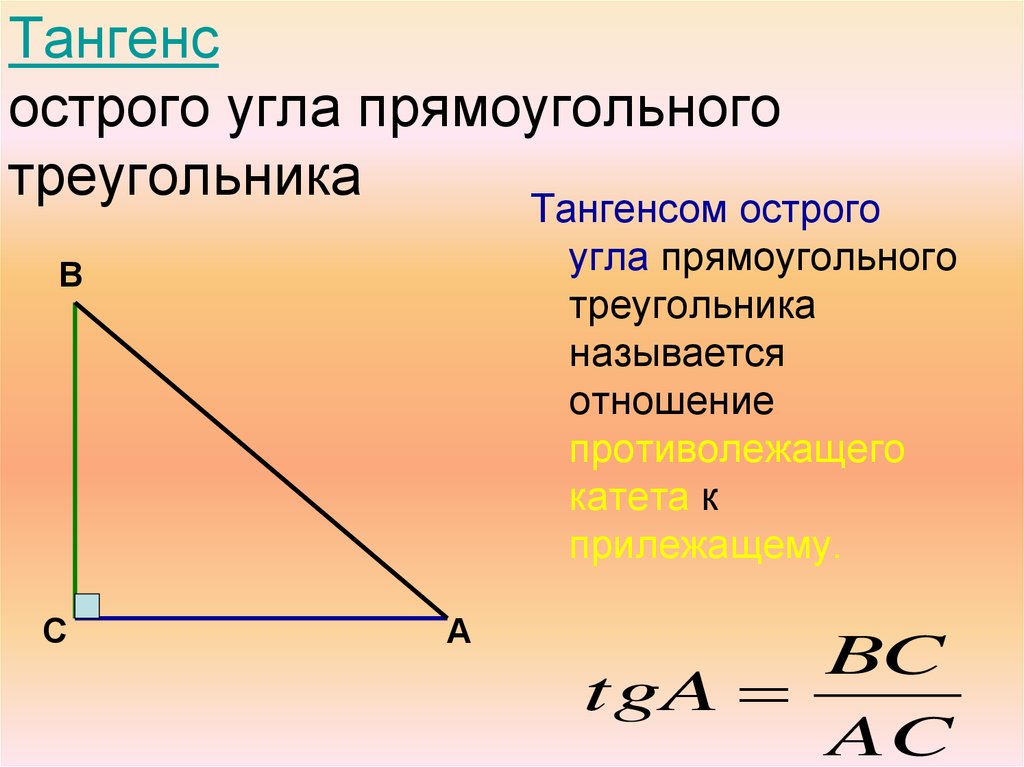 , Ltd. (Japan) , Ltd. (Japan) | |||||||||||||||||||||||
| TG | Total Girl (magazine) | |||||||||||||||||||||||
| TG | Throbbing Gristle (полоса 1970S) | |||||||||||||||||||||||
| TG | Target Group | |||||||||||||||||||||||
| TG | TRIGUN (ТВС ШОСС.0036 TG | Tokyo Gas Co., Ltd. (Tokyo, Japan) | ||||||||||||||||||||||
| TG | Thermogravimetry (mass change study) | |||||||||||||||||||||||
| TG | Terry Gilliam (director) | |||||||||||||||||||||||
| TG | Twynstra Gudde (consulting firm; Netherlands) | |||||||||||||||||||||||
| TG | Tiefgarage (German: underground parking) | |||||||||||||||||||||||
| TG | Touch-and-Go | |||||||||||||||||||||||
| TG | Traditional Grammar | |||||||||||||||||||||||
| TG | Temperature Gradient | |||||||||||||||||||||||
| TG | Topical Guide | |||||||||||||||||||||||
| TG | Turbine Generator | |||||||||||||||||||||||
| TG | Talkgroup | |||||||||||||||||||||||
| TG | Техническая группа | |||||||||||||||||||||||
| ТГ | Хвостовой стрелок | |||||||||||||||||||||||
| ТГ | Тераграмм (метрическая единица массы) | |||||||||||||||||||||||
| TG | Total Guitar (magazine) | |||||||||||||||||||||||
| TG | Trunk Group | |||||||||||||||||||||||
| TG | Tactical Gamer (online community) | |||||||||||||||||||||||
| TG | Ta Gueule (French: Заткнись) | |||||||||||||||||||||||
| TG | TONENGENERAL (Oil Company; Япония) | |||||||||||||||||||||||
| TG | True Good (Gaming) | |||||||||||||||||||||||
| (Gaming) | ||||||||||||||||||||||||
| 9 | Titan’s Grip (World of Warcraft) | |||||||||||||||||||||||
| TG | Trésorerie Générale (French: General Treasury) | |||||||||||||||||||||||
| TG | Transmission Group | |||||||||||||||||||||||
| TG | Transformational Grammar | |||||||||||||||||||||||
| TG | Генератор синхронизации | |||||||||||||||||||||||
| TG | Руководство по переводу (округ Марикопа, система муниципальных колледжей Аризоны) | |||||||||||||||||||||||
| TG | Трансформационная генератива (грамматика) | |||||||||||||||||||||||
| TG | Trinidad Guardian (газета) | |||||||||||||||||||||||
Demless-Games. com. com. | Togdheer (почтовый регион, Сомали) | |||||||||||||||||||||||
| TG | Taux de Gravité (французский: Severity Rate) | |||||||||||||||||||||||
| 0037 | ||||||||||||||||||||||||
| TG | Trunking Gateway | |||||||||||||||||||||||
| TG | Thompson Gun | |||||||||||||||||||||||
| TG | Troop Guide (Boy Scouts of America) | |||||||||||||||||||||||
| TG | Totino-Grace (Minnesota High School ) | |||||||||||||||||||||||
| TG | Toy Guy | |||||||||||||||||||||||
| TG | Task Graph | |||||||||||||||||||||||
| TG | Twin Groves (Illinois, USA) | |||||||||||||||||||||||
| TG | Transactions on Graphics | |||||||||||||||||||||||
| TG | True Gravity | |||||||||||||||||||||||
| TG | Tail Grab (skiing and snowboarding) | |||||||||||||||||||||||
| TG | Triple Glazing (windows) | |||||||||||||||||||||||
| TG | Transmitter Group | |||||||||||||||||||||||
| TG | Trinity Grammar (школа) | |||||||||||||||||||||||
| TG | Transaction Group | Transaction Group | 0035 | TG | Tote Gote (mini bike) | |||||||||||||||||||
| TG | Tanner Graph | |||||||||||||||||||||||
| TG | Tigre Géant (Canadian retailer) | |||||||||||||||||||||||
| TG | Tangent Galvanometer (physics) | |||||||||||||||||||||||
| TG | Общий градиент (гравитация и магнитная) | |||||||||||||||||||||||
| TG | . |

 2 Определение тригонометрических функций как решений дифференциальных уравнений
2 Определение тригонометрических функций как решений дифференциальных уравнений
