The binary system uses powers of: binary system | Infoplease

Двоичная система счисления | Encyclopedia.com

Двоичная система счисления, также называемая системой счисления с основанием 2 , представляет собой метод представления чисел, который считается путем использования комбинаций только двух цифр: нуля (0) и единицы (1). Компьютеры используют двоичную систему счисления для обработки и хранения всех своих данных, включая числа, слова, видео, графику и музыку.

Термин «бит», наименьшая единица цифровой технологии, расшифровывается как «двоичная цифра». Байт — это группа из восьми битов. Килобайт — это 1024 байта или 8,19.2 бита.

Используя двоичные числа, 1 + 1 = 10, потому что «2» не существует в этой системе. Другая система счисления, обычно используемая десятичная система счисления или система счисления с основанием 10 , считает с использованием 10 цифр (0,1,2,3,4,5,6,7,8,9), поэтому 1 + 1 = 2 и 7 + 7 = 14. Другой системой счисления, используемой программистами, является шестнадцатеричная система с основанием 16 , в которой используется 16 символов (0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F), поэтому 1 + 1 = 2 и 7 + 7 = E. Системы счисления с основанием 10 и 16 более компактны, чем двоичная система. Программисты используют шестнадцатеричную систему счисления как удобный и более компактный способ представления двоичных чисел, потому что ее очень легко преобразовать из двоичной в шестнадцатеричную и наоборот. Сложнее преобразовать из двоичного в десятичное и из десятичного в двоичное.

Преимуществом двоичной системы является ее простота. Вычислительное устройство может быть создано из всего, что имеет ряд переключателей, каждый из которых может переключаться между положением «включено» и положением «выключено». Эти переключатели могут быть электронными, биологическими или механическими, если их можно перемещать по команде из одного положения в другое. Большинство компьютеров имеют электронные переключатели.

Когда переключатель находится в положении «включено», он представляет собой единицу, а когда переключатель находится в положении «выключено», он представляет собой нулевое значение. Цифровые устройства выполняют математические операции, включая и выключая двоичные переключатели.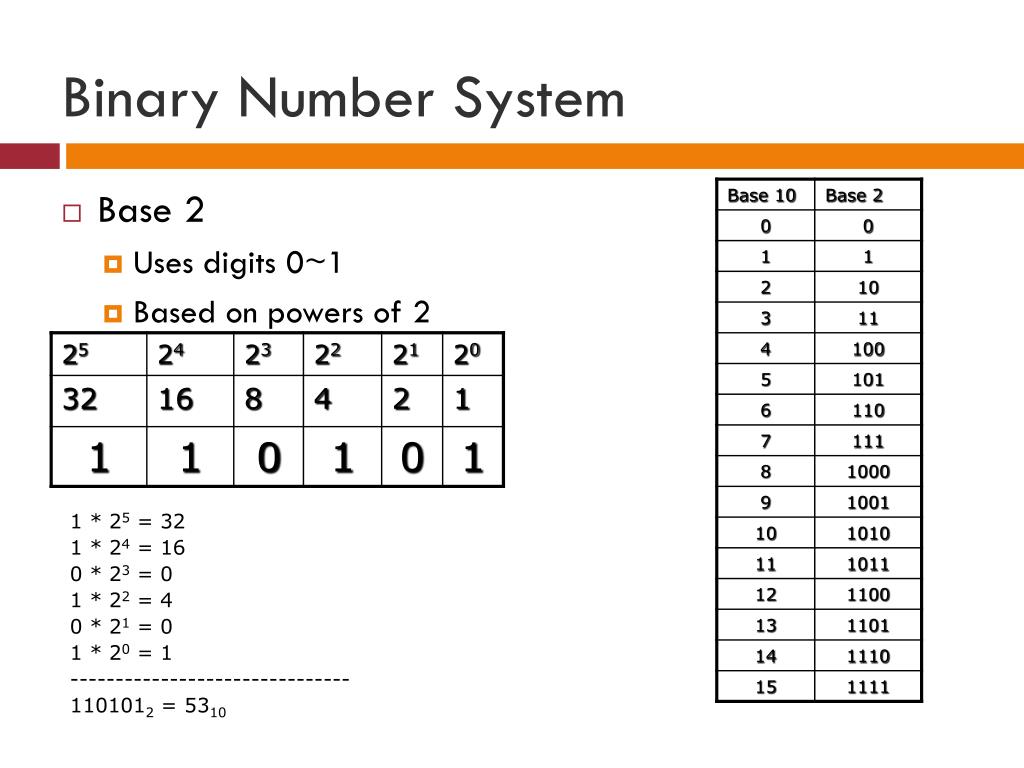 Чем быстрее компьютер может включать и выключать переключатели, тем быстрее он может выполнять свои вычисления.

1

Binary	Decimal	Hexadecimal
Number	Number	Number
System	System	Система
0	0	0
1	1
	0020	10	2	2
11	3	3
100	4	4
101	5	5
110	6	6
111	7	7
1000	8	8
1001	9	9
1010	10	A
1011	11	B
1100	12	C
1101	13	D
1110	14	E
1111	15	F
10000	16	10

позиционированная номера по номеру.

Это называется позиционной записью. Это понятие также применимо к десятичным числам.

Например, десятичное число 123 представляет десятичное значение 100 + 20 + 3. Число один представляет сотни, число два представляет десятки, а число три представляет единицы. Математическая формула для получения числа 123 может быть создана путем умножения числа в столбце сотен (1) на 100, или 10 ² ; умножение числа в столбец десятков (2) на 10 или 10 ¹ ; умножение числа в столбце единиц (3) на 1 или 10 ⁰ ; а затем добавить продукты вместе. Формула: 1 × 10 ² + 2 × 10 ¹ + 3 × 10 ⁰ = 123.

Это показывает, что каждое значение умножается на основание (10), возведенное в возрастающую степень. Значение степени начинается с нуля и увеличивается на единицу в каждой новой позиции формулы.

Эта концепция позиционной записи также применима к двоичным числам с той разницей, что основание равно 2. Например, чтобы найти десятичное значение двоичного числа 1101, формула имеет вид 1 × 2

3 + 1 × 2 ² + 0 × 2 ¹ + 1 × 2 ⁰ = 13.

Двоичные операции

Двоичные числа можно обрабатывать с помощью тех же операций, что и для вычисления десятичных чисел, но используя только нули и единицы. Чтобы сложить два числа, нужно запомнить только четыре правила:

Поэтому, чтобы решить следующую задачу на сложение, начните с крайнего правого столбца и прибавьте 1 + 1 = 10; запишите 0 и перенесите 1. Работая с каждым столбцом слева, продолжайте добавлять, пока проблема не будет решена.

Чтобы преобразовать двоичное число в десятичное, каждая цифра умножается на степень двойки. Затем продукты складываются. Например, чтобы преобразовать двоичное число 11010 в десятичное, формула будет следующей:

Чтобы преобразовать двоичное число в шестнадцатеричное, разделите двоичное число на группы по четыре, начиная справа, а затем переведите каждую группу в свою шестнадцатеричный эквивалент. Нули могут быть добавлены слева от двоичного числа, чтобы завершить группу из четырех. Например, чтобы перевести число 11010 в шестнадцатеричное, формула будет выглядеть так:

Цифровые данные

Биты являются фундаментальным элементом цифровых вычислений. Термин «оцифровка» означает преобразование аналогового сигнала — диапазона напряжений — в цифровой сигнал, или ряд чисел, представляющих напряжения. Музыкальное произведение можно оцифровать, взяв очень частые его сэмплы, называемые сэмплированием, и переведя их в дискретных числа, которые затем переводятся в нули и единицы. Если сэмплы берутся очень часто, музыка при воспроизведении звучит как непрерывный тон.

Черно-белую фотографию можно оцифровать, наложив на изображение мелкую сетку и вычислив количество серого на каждом пересечении сетки, называемое

пикселем . Например, используя 8-битный код, чисто белая часть изображения может быть оцифрована как 11111111. Точно так же чисто черная часть может быть оцифрована как 00000000. Каждое из 254 чисел, попадающих между этими двумя крайними значениями (числа от 00000001 до 11111110) представляет собой оттенок серого. Когда пришло время реконструировать фотографию, используя ее набор двоичных цифр, компьютер декодирует изображение, присваивает правильный оттенок серого каждому пикселю, и изображение появляется. Чтобы улучшить разрешение, можно использовать более мелкую сетку, чтобы изображение можно было увеличить до больших размеров без потери деталей.

Цветная фотография оцифровывается аналогичным образом, но требует гораздо больше битов для хранения цвета пикселя. Например, 8-битная система использует восемь битов, чтобы определить, какой из 256 цветов представлен каждым пикселем (2

8 равно 256). Аналогично, 16-битная система использует шестнадцать бит для определения каждого из 65 536 цветов (2 ¹⁶ равно 65 536). Поэтому цветные изображения требуют гораздо больше места для хранения, чем черно-белые.

см. также Первые компьютеры; Объем памяти.

Энн МакИвер Макхоус

Библиография

Блиссмер, Роберт Х. Знакомство с компьютерными концепциями, системами и приложениями. Нью-Йорк: John Wiley & Sons, Inc., 1989.

Диллиган, Роберт Дж. Вычисления в эпоху Интернета: интерактивное веб-введение. Нью-Йорк: Plenum Press, 1998.

Уайт, Рон. Как работают компьютеры: выпуск тысячелетия. Indianapolis: Que Corporation, 1999.

Что такое двоичный код? Понимание того, как компьютеры используют Base 2

Двоичные числа необходимы для вычислений, поскольку все данные, которые проходят через ваш телефон или компьютер, представлены в двоичном виде. Но поскольку люди естественным образом не используют двоичную систему счисления, ее может быть трудно понять.

Давайте рассмотрим, что такое двоичный файл. К концу вы узнаете, чем двоичная система отличается от нашей обычной системы счета, как работают двоичные числа, что означают «32-битные» и «64-битные» и почему все это имеет значение.

Понимание основания 10: десятичное число

Прежде чем мы приступим к изучению двоичной системы, полезно рассмотреть систему счисления, используемую в современном мире. Десятичная система, или основание 10, — это система, в которой каждое возможное место в числе может быть одной из 10 цифр.

Чтобы выразить однозначное число в десятичном виде, мы используем цифры от 0 до 9. Чтобы подняться выше, мы добавляем еще один разряд, дойдя до 10, 100, 1000 и выше. Например, запись числа 1972 в разбивке представляет собой следующее:

.

1,000	100	10	1
1	9	7	2

Таким образом, число 1972 состоит из 1х1000, 9х100, 7х10 и 2х1. Поскольку вы использовали эту систему с детства, это то, как вы думаете о числах.

Binary — это другой подход к числам: меняется не значение, а то, как мы его представляем.

Счет по основанию 2 с двоичным кодом

Двоичная система счисления использует только два числа для каждого разряда: 0 и 1. Двоичная система также известна как «основание 2». В двоичном формате для представления большего числа, чем 1, вам нужно второе место.

В то время как каждый дополнительный разряд в десятичной системе умножается на 10, каждый дополнительный разряд в двоичной системе умножается на 2. Таким образом, когда вы добавляете единицы в двоичной системе, они представляются следующим образом, считая справа налево от первых 10 разрядов:

512, 256, 128, 64, 32, 16, 8, 4, 2, 1

Другими словами, самое правое значение в двоичном числе показывает, сколько в нем единиц. Цифра слева от нее представляет, сколько двоек, следующая сколько четверок и так далее. Эти значения могут показаться знакомыми, поскольку варианты хранения доступны на телефонах и других носителях — вот откуда они берутся.

Запись чисел в двоичном формате очень помогает их пониманию, так как это не естественный способ счета для нас. См. приведенную ниже диаграмму, иллюстрирующую двоичный счет:

00243 9450359

8

9 25

9

9 0

9 03024

5

19

9. 0319

1

3

031993 3

Взгляните на таблицу и убедитесь, что вы поняли идею. Например, если вы посмотрите на десятичное число 25, вы сможете разбить его двоичный аналог (11001) на 9.0349 16 + 8 + 1 .

Преобразование из двоичного в десятичное и обратно

Чтобы выяснить, что представляет собой двоичное число в десятичном виде, вы можете нарисовать диаграмму, подобную приведенной выше. Это медленно, но поможет вам надежно это проверить.

Поработав некоторое время с двоичным кодом, вы сможете вычислять небольшие значения в уме. Например, если вы видите число 1101001, вы можете изменить его, добавив 1, 8, 32 и 64, чтобы в сумме получить 105.

Переход от десятичного числа к двоичному отличается. Для этого нужно сначала вычислить наибольшую двоичную единицу, которая вписывается в ваше число. Например, если вы хотите узнать, что такое 73 в двоичном формате, самое большое двоичное значение под этим числом — 64, поэтому место 64 — это 1,9.0005

Разница между 73 и 64 равна 9, а это означает, что нам нужна 1 на месте 8 и 1 на месте 1, чтобы получить 9. Собрав все это вместе, двоичное значение для 73 равно 1001001.

Когда вы привыкнете к местам, вы сможете выполнять эти вычисления быстрее. Однако со значениями больше 512 или 1024 становится трудно работать вручную.

При работе с большими числами помогут такие инструменты, как калькулятор Programmer в Windows и macOS. Они позволяют вводить число в десятичном виде и видеть его эквивалент в двоичном формате (или наоборот). Существует также удобный режим переключения битов, который позволяет включать и выключать отдельные двоичные цифры, чтобы увидеть обновление значения в режиме реального времени.

Биты, байты и более крупные единицы

Мы используем определенные термины для обозначения размера двоичных чисел. Одна цифра — это бит ; как мы видели выше, один бит сам по себе может представлять только 1 или 0. Этого достаточно для хранения булевой переменной, где 0 — ложь, а 1 — истина.

Восемь бит вместе известны как байт , что является наименьшим объемом памяти, с которым может работать большинство компьютеров. С помощью одного байта вы можете представить десятичные числа от 0 до 255, что составляет 256 возможных значений.

Для подсчета более высоких двоичных чисел в области современных объемов памяти мы используем стандартные префиксы СИ, такие как кило-, мега- и гига-. Килобайт — это тысяча байтов, мегабайт — миллион байтов, а гигабайт — миллиард байтов. Это продолжается с терабайтами и далее.

Как ни странно, поскольку мы измеряем эти размеры в десятичном виде, а компьютеры — в двоичном, иногда вы обнаружите, что устройство имеет меньше памяти, чем заявлено. Наше объяснение различий в размерах жестких дисков подробно объясняет, почему это происходит.

Как двоичный код используется на практике

байта являются важной точкой отсчета. В первых компьютерах один байт использовался для хранения одного текстового символа.

Многие ранние видеоигры ограничивали количество счетчиков до 255 по той же причине. Например, такие аркадные игры, как Pac-Man, вылетают после 255-го уровня, потому что игре не хватает памяти. В оригинальной Zelda для NES максимальное количество рупий (игровой валюты) равно 255, потому что для хранения этого числа игра использует один байт. Из-за ограниченной памяти программисты не хотели выделять больше места для этих значений, поскольку необходимо учитывать множество других факторов. 98 или примерно 18 квинтиллионов возможных адресов. Это число находится за пределами человеческого понимания, а это означает, что предел оперативной памяти намного превышает все, что мы используем сейчас.

Точно так же адреса IPv4 состоят из четырех байтов (каждая цифра в адресе, например 192.168.100.47, может принимать значения от 0 до 255). Сегодня в сети насчитывается более четырех миллиардов устройств, подключенных к Интернету, поэтому у нас закончились адреса IPv4. Мир медленно движется к IPv6, у которого такой же гораздо более высокий лимит.

Теперь, когда вы понимаете двоичную систему, вы можете понять, почему при ее обсуждении появляются одни и те же числа (степени двойки).

Decimal Value	128	64	32	16	8	4	2	1
1								1
2							1
3							1	1
4						1
5
1		1
6						1	1
7						1	1	9
				1
9					1			1
10					1	4	40024	1
11					1		1	1
12					1	1
			1	1		1
14					1	1	1
15				1	1	1
16				1
17				1				1	10 52924 80
			1			1
19				1			1	1
20				2 1	1
21				1		1		1
22				1		1	1 4
23				1		1	1	1
24				1	1
25						1			1
26				1	1		1
27				1	1		1	1
28				1	1	1
29				1	1	1		1 30020	30				1	1	1	1
31				1	1	1	1	1
. ..
…
…
…
254	1	1	1	1	1	1		1
255	1	1	1	1	1	1	1
256	1	1	1	1	1	1	1	1