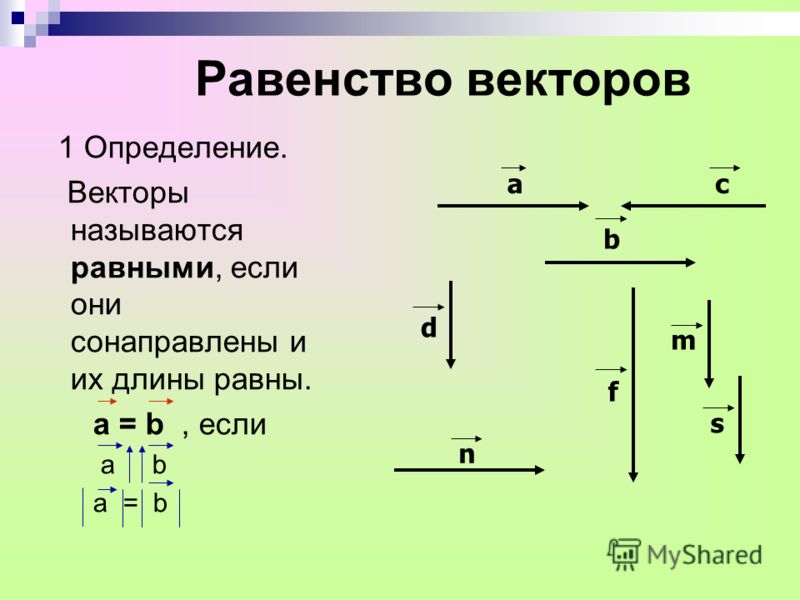
1.Векторы Основные сведения
1. Вектор обозначается графически отрезком прямой, на котором ставится стрелка, указывающая направление вектора .
Вектор можно обозначать , где т. A — начало и т. B — конец вектора.
Можно обозначать вектор одной буквой с черточкой над ней, например, , а модуль этого вектора обозначается .
2. Вектор считается заданным, если известна его длина и направление.
Вектор можно задать координатами начала и конца А(х1 ; у1) и В(х2 ; у2 ). На рис. 1 приведен вектор , начальная точка которого имеет координаты А(2; 5) , а конечная точка В(6; 7).
Рис. 1
Вектор
можно задать координатами. Для
задания координат вектора
нужно из координат конечной точки
вычесть координаты начальной точки:
(х
Для , начальная точка которого имеет координаты А(2; 5) , а конечная точка В(6; 7), (6 — 2; 7- 5), т. е. (4; 2)
На рис. 1 приведен вектор (4; 2) равный вектору , так как он без изменения длины и направления получен параллельным переносом начала вектора в начало координат.
3. Для задания вектора в трехмерном пространстве должны быть определены три его координаты (x; y; z)
На рис. 2 показан вектор в трехмерном пространстве с координатами (2; 3; 4).
Рис. 2
4. Вектор равен нулю, если его модуль (длина) равен нулю. Такой вектор называется нулевым.
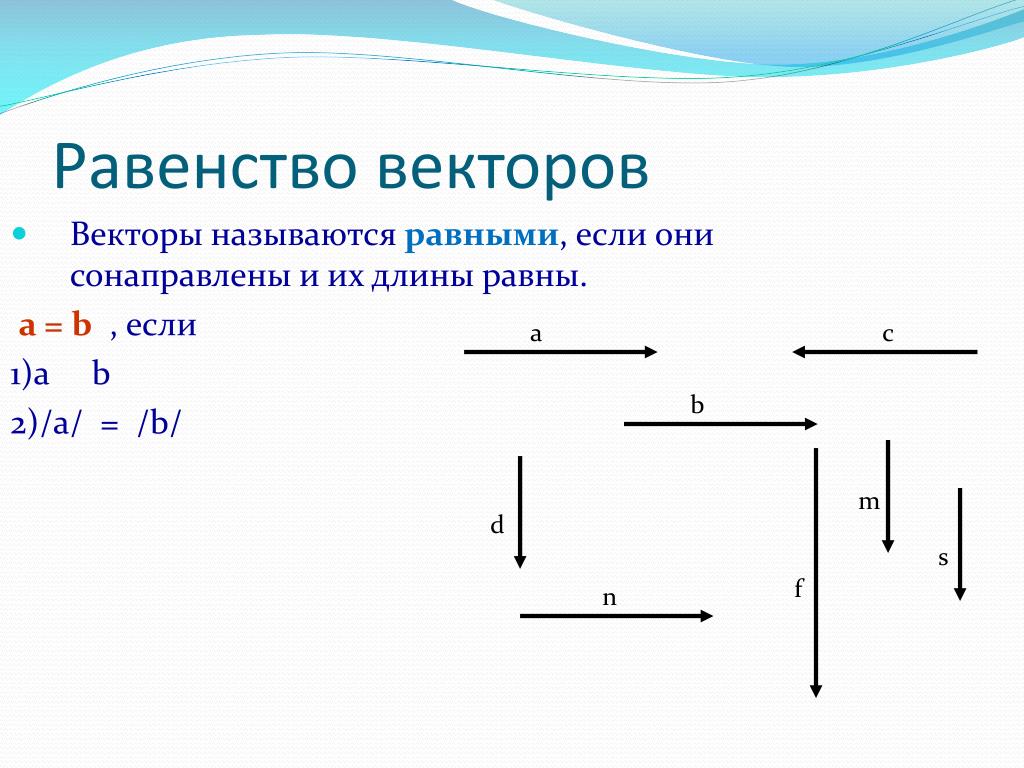
5. Два вектора и называются равными, если равны их модули, они лежат на параллельных прямых (коллинеарные) и направлены в одну и ту же сторону.
Два
вектора с равными модулями, лежащие на
параллельных прямых, но противоположно
направленные, называются противоположными.
Вектор, противоположный вектору , обозначается через .
6. Сложение векторных величин, заданных графически, производится по одному из двух правил.
Правило параллелограмма: сумма двух векторов и , приведенных к общему началу, есть третий вектор , длина которого равна длине диагонали параллелограмма, построенного на векторах и , а направлен он от точки A( начала векторов , и ) к точке B.
Правило треугольников.
Сумму нескольких векторов, например , , и , строят так: берут произвольную точку O плоскости и из нее строят вектор , равный вектору ; из точки
Вектор , замыкающий полученную ломаную линию OABCD, и будет суммой векторов , , и (см. рисунок):
По
такому же правилу строится и сумма
любого числа векторов.
7. Разностью двух векторов и называется такой третий вектор , который равен сумме векторов и (см. рисунок). Вектор параллелен вектору , равен ему по модулю, но противоположно направлен:
8. При умножении вектора на скаляр k получается вектор , модуль которого равен модулю вектора , умноженному на k, т. е.
= k .
Направления векторов и совпадают, если k > 0, и они противоположны, если k < 0.
9. Два вектора, лежащие на параллельных прямых, независимо от того, направлены они одинаково или противоположно, называются коллинеарными.
Если два вектора в пространствеколлинеарны, то координаты их пропорциональны, т.е.
Если
два вектора
на
плоскости (х1 ; у1)
и (х2 ; у2 ),
коллинеарны, то
координаты их пропорциональны, т. е.
е.
.
Зачёт №1 по геометрии, 11 класс
Зачет по геометрии №1 по теме «Векторы в пространстве»
1. Определение вектора. Определение нулевого вектора. Длина вектора. Сложение векторов правилом треугольника.
2. Определение вектора. Определение коллинеарных векторов. Сонаправленные и противоположно направленные векторы. Вычитание векторов.
3. Определение вектора. Определение равных векторов. Сложение векторов правилом параллелограмма.
4. Определение произведения ненулевого вектора на число. Основные свойства умножения вектора на число.
5. Определение компланарных векторов. Признак компланарности трех векторов.
6. Доказательство теоремы о разложении вектора по трем некомпланарным векторам.
7. В
правильной треугольной пирамиде DABC точки P, M, K, T –
середины соответственно рёбер DA, BC, BA, DC. Запишите
векторы с началами и концами в вершинах пирамиды или точках P, M, K, и T, которые:
а) сонаправлены вектору ; б) противоположно направлены вектору; в) равны вектору
Запишите
векторы с началами и концами в вершинах пирамиды или точках P, M, K, и T, которые:
а) сонаправлены вектору ; б) противоположно направлены вектору; в) равны вектору
8. В правильной четырехугольной пирамиде PABCD точки K, M, T, E – середины соответственно рёбер AB, PA, PC, BC. а) Перечислите пары сонаправленных векторов с концами в точках K, M, T, E. б) Перечислите пары равных векторов с концами в точках K, M, T, E. в) Перечислите векторы, имеющие равные длины, с концами в точках K, M, T, Е.
9. Изобразите тетраэдр ABCD и вектор, равный .
10. ABCDA1B1C1D1— параллелепипед. Упростите выражение .
11. Изобразите тетраэдр ABCD и вектор, равный
12. Точка А лежит на отрезке ВС и делит его в отношении 4:3, считая от вершины В. Выразите: а) вектор через вектор ; б) вектор через вектор ; в) вектор через вектор .
13. ВМ – медиана
треугольника АВС, О – произвольная точка пространства. Разложите вектор по векторам
Разложите вектор по векторам
14. Дан параллелепипед
АВСDA
15. Докажите, что если М – точка пересечения медиан треугольника АВС, а О — произвольная точка пространства, то
16. При каких значениях k в равенстве , где – ненулевой вектор, векторы и : а) коллинеарны; б) сонаправлены; в) противоположно направлены; г) являются противоположными?
17. Векторы и коллинеарны. Докажите, что векторы и коллинеарны.
18. Упростите выражение: а) ;
б)
№1
1. Определение вектора. Определение нулевого вектора. Длина вектора. Сложение векторов правилом треугольника.
2. В правильной треугольной пирамиде DABC точки P, M, K, T – середины соответственно рёбер DA, BC, BA, DC. Запишите векторы с началами и концами в вершинах пирамиды или точках P, M, K, и T, которые: а) сонаправлены вектору ; б) противоположно направлены вектору; в) равны вектору
3. ВМ – медиана
треугольника АВС, О – произвольная точка пространства. Разложите вектор по векторам
ВМ – медиана
треугольника АВС, О – произвольная точка пространства. Разложите вектор по векторам
№2
1. Определение вектора. Определение коллинеарных векторов. Сонаправленные и противоположно направленные векторы. Вычитание векторов.
2. Дан параллелепипед АВСDA1B1C1D1. Медианы треугольника BB1C пересекаются в точке М. Разложите вектор по векторам
3. В правильной четырехугольной пирамиде PABCD точки K, M, T, E – середины соответственно рёбер AB, PA, PC, BC. а) Перечислите пары сонаправленных векторов с концами в точках K, M, T, E. б) Перечислите пары равных векторов с концами в точках K, M, T, E. в) Перечислите векторы, имеющие равные длины, с концами в точках K, M, T, Е.
№3
1. Определение вектора. Определение равных векторов. Сложение векторов правилом параллелограмма.
2. Изобразите тетраэдр ABCD и вектор, равный ..
3. Докажите,
что если М – точка пересечения медиан треугольника АВС, а О — произвольная
точка пространства, то .
№4
1. Определение произведения ненулевого вектора на число. Основные свойства умножения вектора на число.
2. ABCDA1B1C1D1— параллелепипед. Упростите выражение .
3. При каких значениях k в равенстве , где – ненулевой вектор, векторы и : а) коллинеарны; б) сонаправлены; в) противоположно направлены; г) являются противоположными?
№5
1. Определение компланарных векторов. Признак компланарности трех векторов.
2. Изобразите тетраэдр ABCD и вектор, равный
3. Векторы и коллинеарны. Докажите, что векторы и коллинеарны.
№6
1. Доказательство теоремы о разложении вектора по трем некомпланарным векторам.
2. Точка А лежит на отрезке ВС и делит его в отношении 4:3, считая от вершины В. Выразите: а) вектор через вектор ; б) вектор через вектор ; в) вектор через вектор .
3. Упростите выражение: а) ;
б)
№7
1. Определение
вектора. Определение нулевого вектора. Длина вектора. Сложение векторов
правилом треугольника.
Определение
вектора. Определение нулевого вектора. Длина вектора. Сложение векторов
правилом треугольника.
2. В правильной четырехугольной пирамиде PABCD точки K, M, T, E – середины соответственно рёбер AB, PA, PC, BC. а) Перечислите пары сонаправленных векторов с концами в точках K, M, T, E. б) Перечислите пары равных векторов с концами в точках K, M, T, E. в) Перечислите векторы, имеющие равные длины, с концами в точках K, M, T, Е.
3. Докажите, что если М – точка пересечения медиан треугольника АВС, а О — произвольная точка пространства, то
№8
1. Определение вектора. Определение коллинеарных векторов. Сонаправленные и противоположно направленные векторы. Вычитание векторов.
2. Изобразите тетраэдр ABCD и вектор, равный ..
3. При каких значениях k в равенстве , где – ненулевой вектор, векторы и : а) коллинеарны; б) сонаправлены; в) противоположно направлены; г) являются противоположными?
№9
1. Определение
вектора. Определение равных векторов. Сложение векторов правилом
параллелограмма.
Определение равных векторов. Сложение векторов правилом
параллелограмма.
2. ABCDA1B1C1D1— параллелепипед. Упростите выражение .
3. Векторы и коллинеарны. Докажите, что векторы и коллинеарны.
№10
1. Определение произведения ненулевого вектора на число. Основные свойства умножения вектора на число.
2. Изобразите тетраэдр ABCD и вектор, равный
3. Упростите выражение: а) ;
б)
№11
1. Определение компланарных векторов. Признак компланарности трех векторов.
2. Точка А лежит на отрезке ВС и делит его в отношении 4:3, считая от вершины В. Выразите: а) вектор через вектор ; б) вектор через вектор ; в) вектор через вектор .
3. ВМ – медиана треугольника АВС, О – произвольная точка пространства. Разложите вектор по векторам
№12
1. Доказательство
теоремы о разложении вектора по трем некомпланарным векторам.
2. В правильной треугольной пирамиде DABC точки P, M, K, T – середины соответственно рёбер DA, BC, BA, DC. Запишите векторы с началами и концами в вершинах пирамиды или точках P, M, K, и T, которые: а) сонаправлены вектору ; б) противоположно направлены вектору; в) равны вектору
3. Дан параллелепипед АВСDA1B1C1D1. Медианы треугольника BB1C пересекаются в точке М. Разложите вектор по векторам
№13
1. Определение вектора. Определение нулевого вектора. Длина вектора. Сложение векторов правилом треугольника.
2. Изобразите тетраэдр ABCD и вектор, равный ..
3. Векторы и коллинеарны. Докажите, что векторы и коллинеарны.
№14
1. Определение вектора. Определение коллинеарных векторов. Сонаправленные и противоположно направленные векторы. Вычитание векторов
2. ABCDA1B1C1D1—
параллелепипед. Упростите выражение .
3. Упростите выражение: а) ;
б)
№15
1. Определение вектора. Определение равных векторов. Сложение векторов правилом параллелограмма.
2. Изобразите тетраэдр ABCD и вектор, равный
3. ВМ – медиана треугольника АВС, О – произвольная точка пространства. Разложите вектор по векторам
№16
1. Определение произведения ненулевого вектора на число. Основные свойства умножения вектора на число.
2. Точка А лежит на отрезке ВС и делит его в отношении 4:3, считая от вершины В. Выразите: а) вектор через вектор ; б) вектор через вектор ; в) вектор через вектор ..
3. Дан параллелепипед АВСDA1B1C1D1. Медианы треугольника BB1C пересекаются в точке М. Разложите вектор по векторам
№17
1. Определение компланарных векторов. Признак компланарности трех векторов.
2. В
правильной треугольной пирамиде DABC точки P, M, K, T –
середины соответственно рёбер DA, BC, BA, DC.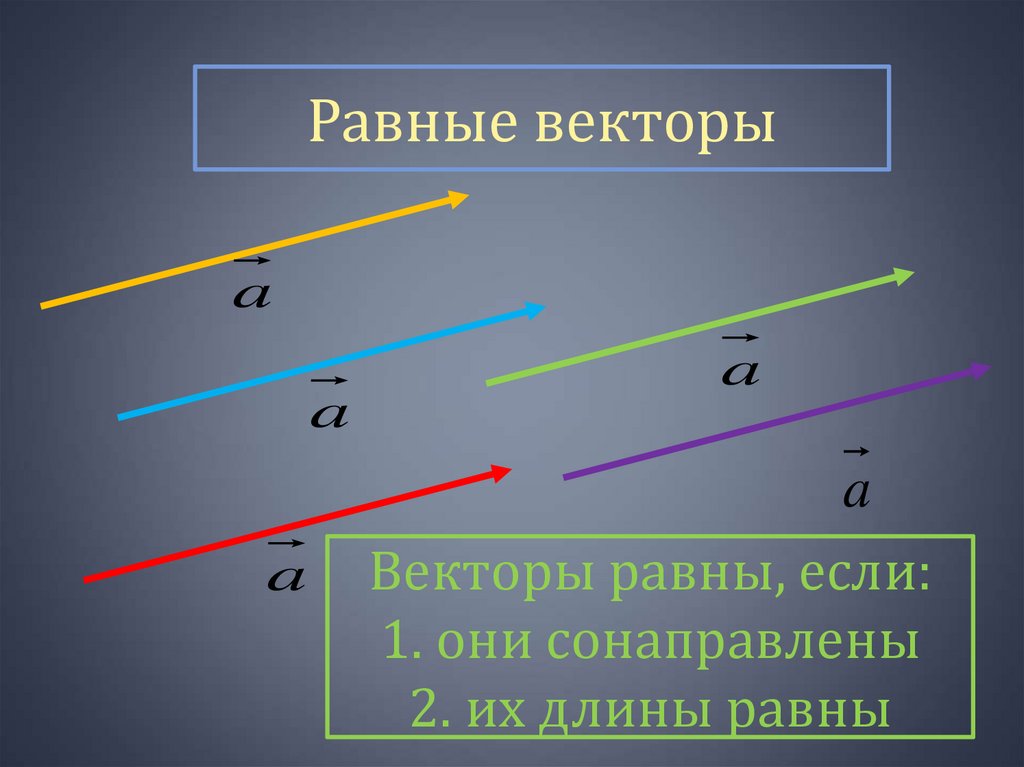 Запишите
векторы с началами и концами в вершинах пирамиды или точках P, M, K, и T, которые:
а) сонаправлены вектору ; б) противоположно направлены вектору; в) равны вектору
Запишите
векторы с началами и концами в вершинах пирамиды или точках P, M, K, и T, которые:
а) сонаправлены вектору ; б) противоположно направлены вектору; в) равны вектору
3. Докажите, что если М – точка пересечения медиан треугольника АВС, а О — произвольная точка пространства, то
№18
1. Доказательство теоремы о разложении вектора по трем некомпланарным векторам.
2. В правильной четырехугольной пирамиде PABCD точки K, M, T, E – середины соответственно рёбер AB, PA, PC, BC. а) Перечислите пары сонаправленных векторов с концами в точках K, M, T, E. б) Перечислите пары равных векторов с концами в точках K, M, T, E. в) Перечислите векторы, имеющие равные длины, с концами в точках K, M, T, Е.
3. При каких значениях k в равенстве , где – ненулевой вектор, векторы и : а) коллинеарны; б) сонаправлены; в) противоположно направлены; г) являются противоположными?
№19
1. Определение
вектора. Определение нулевого вектора. Длина вектора. Сложение векторов
правилом треугольника.
Длина вектора. Сложение векторов
правилом треугольника.
2. ABCDA1B1C1D1— параллелепипед. Упростите выражение .
Дан параллелепипед АВСDA1B1C1D1. Медианы треугольника BB1C пересекаются в точке М. Разложите вектор по векторам
3. Векторы и коллинеарны. Докажите, что векторы и коллинеарны.
№20
1. Определение вектора. Определение коллинеарных векторов. Сонаправленные и противоположно направленные векторы. Вычитание векторов.
2. Изобразите тетраэдр ABCD и вектор, равный
3. Докажите, что если М – точка пересечения медиан треугольника АВС, а О — произвольная точка пространства, то
№21
1. Определение вектора. Определение равных векторов. Сложение векторов правилом параллелограмма.
2. Точка А
лежит на отрезке ВС и делит его в отношении 4:3, считая от вершины В. Выразите:
а) вектор через вектор ; б) вектор через вектор ; в) вектор через вектор . .
.
3. При каких значениях k в равенстве , где – ненулевой вектор, векторы и : а) коллинеарны; б) сонаправлены; в) противоположно направлены; г) являются противоположными?
№22
1. Определение произведения ненулевого вектора на число. Основные свойства умножения вектора на число.
2. ВМ – медиана треугольника АВС, О – произвольная точка пространства. Разложите вектор по векторам
3. Векторы и коллинеарны. Докажите, что векторы и коллинеарны.
№23
1. Определение компланарных векторов. Признак компланарности трех векторов.
2. Дан параллелепипед АВСDA1B1C1D1. Медианы треугольника ВВ1С пересекаются в точке М. Разложите вектор АМ по векторам АА1=а, АВ=в, АD=c.
3. Упростите выражение: а) ;
б)
№24
1. Доказательство теоремы о разложении вектора по трем некомпланарным векторам.
2. Докажите, что если М – точка пересечения медиан треугольника АВС, а О — произвольная точка пространства, то
3. ВМ – медиана
треугольника АВС, О – произвольная точка пространства. Разложите вектор по векторам
ВМ – медиана
треугольника АВС, О – произвольная точка пространства. Разложите вектор по векторам
Линейная алгебра: как нулевой вектор может быть равен 1?
спросил
Изменено 4 года назад
Просмотрено 2к раз
$\begingroup$
Этот пример приведен в моем учебнике по линейной алгебре.
Пример 4.1.6. Пусть $V =\{x\in\mathbb R: x > 0\}$ — множество всех положительных действительных чисел. Мы определим странное «сложение» и «скалярное умножение» на $V$, и, чтобы избежать путаницы, мы используем $\oplus$ для нашего определения сложения и $\odot$ для нашего определения скалярного умножения. 9c > 0$, поскольку $a > 0$).
Наконец, пусть $\vec0 = 1$.
x$ требует добавления к умножению, и на самом деле она будет служить 90=1$, который является нейтральным элементом для операции $\oplus$ (умножения). Выписка, личность $$\tilde0\oplus х=х$$ переводится как $$1\cdot x=x$$
(Обратите внимание, что любое положительное действительное число работает как основание для экспоненты вместо $e$.)
$\endgroup$
$\begingroup$
Вашему векторному пространству нужен вектор $0$.
Для странного дополнения, определяемого как продукт, единственным кандидатом является $1$.
Меня больше беспокоит утверждение «Дано a ∈ V и c ∈ R, пусть c a = a c (обратите внимание, что a c > 0, поскольку a > 0)».
Если $c$ — произвольный скаляр в $R$, тогда почему $ac>0$, потому что $c>0 ?$
$\endgroup$
$\begingroup$
Примечание Я проверяю все векторное пространство для тех, кто не понимает, что еще связано с этим конкретным векторным пространством, но ваш конкретный вопрос касается свойств 5 и 6, поэтому вы можете просто перейти к ним, если хотите.
Если у нас есть набор с именем $V$ и определены две произвольные операции, которые мы называем «сложением» ($+$) и «скалярным умножением» ($*$) на $V$, тогда $V$ будет векторным пространством на $\Bbb C$ оно должно удовлетворять следующим свойствам:
- Аддитивное замыкание: для $\mathbf a, \mathbf b \in V$ тогда $\mathbf a + \mathbf b\in V$
- (Скалярное) мультипликативное замыкание: если у нас есть некоторый скаляр $c \in \Bbb C$ и $\mathbf a \in V$, то $c* \mathbf a$ также должен быть в $V$
- Коммутативность: $\mathbf a, \mathbf b \in V$, тогда $\mathbf a + \mathbf b = \mathbf b + \mathbf a$
- Ассоциативность дополнительно: $\mathbf a, \mathbf b, \mathbf c \in V$, тогда $(\mathbf a + \mathbf b) + \mathbf c= \mathbf a + (\mathbf b +\mathbf c) $
- Аддитивный элемент идентичности (нулевой вектор): должен существовать некоторый $\mathbf 0$ такой, что для всех $\mathbf a \in V$ тогда $\mathbf a + \mathbf 0 = \mathbf a$
- Аддитивное обращение: должен существовать некоторый $- \mathbf a$ для всех $\mathbf a$ такой, что $\mathbf a + (-\mathbf a) = \mathbf 0$
- (Скалярная) мультипликативная ассоциативность: если $c, k \in \Bbb C$ и $\mathbf a \in V$, то $(ck)\mathbf a = c(k \mathbf a)$
- Дистрибутивное сложение векторов: $c \in \Bbb C$ и $\mathbf a, \mathbf b \in V$, тогда $c(\mathbf a + \mathbf b) = c \mathbf a + c\mathbf b$
- Распределительное над скалярным сложением: $c, k \in \Bbb C$ и $\mathbf a \in V$, тогда $(c+k) \mathbf a = c \mathbf a + k \mathbf a$
С заданным вами набором и операциями все эти свойства выполняются:
- При определении $+$ как обычной операции умножения для любых двух векторов вы «добавляете», потому что все векторы являются положительными действительными числами, а умножение между двумя действительными числами числа всегда дают другое положительное действительное число, сложение всегда дает вам другой вектор в $V$
- Поскольку все ваши векторы являются положительными действительными числами, а «умножение» возводит в степень, все векторы, возвращаемые вашей операцией, также будут положительными действительными числами и, следовательно, находятся в $V$ (даже если скалярная степень была отрицательной, вы просто получить дробь)
- Обычная операция умножения коммутативна, поэтому «сложение» в этом векторном пространстве также коммутативно
- Так как обычная операция умножения ассоциативна, то и ваша операция «сложения»
- Одним из свойств нулевого вектора является то, что он является элементом идентичности при сложении в векторном пространстве, что просто означает, что если вы делаете $что-нибудь + \mathbf 0 = что-нибудь$.
Вот почему в вашем векторном пространстве, поскольку мы используем умножение как «сложение», действительное число 1 является нулевым вектором, поскольку оно возвращает все, что получает ввод, то есть потому, что $1*что-нибудь=что-нибудь$ ваши операции дают $что-нибудь + \mathbf = что-нибудь$
- Аддитивным обратным значением будет величина, обратная любому вектору, находящемуся в этом векторном пространстве. Обратное должно производить нулевой вектор, и с помощью этих операций вы можете получить нулевой вектор. $a*1/a= \mathbf 0$, так как нулевой вектор равен числу 1.
- Поскольку умножение ассоциативно, то и операция «сложение»
- Умножение является дистрибутивным со скалярами и векторами, удовлетворяющими свойствам 8 и 9.
Будем надеяться, что этот действительно интересный (и странный) пример векторного пространства проясняет любую путаницу. Основная причина, по которой его учат, состоит в том, чтобы просто абстрагироваться от идеи нулевого вектора и действительно показать, что он имеет меньше общего с конкретным числом ноль и больше со свойствами, которыми обладает ноль (что это аддитивная идентичность, и что аддитивная инверсия производит его).
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.

 x$ требует добавления к умножению, и на самом деле она будет служить 90=1$, который является нейтральным элементом для операции $\oplus$ (умножения). Выписка, личность
$$\tilde0\oplus х=х$$
переводится как
$$1\cdot x=x$$
x$ требует добавления к умножению, и на самом деле она будет служить 90=1$, который является нейтральным элементом для операции $\oplus$ (умножения). Выписка, личность
$$\tilde0\oplus х=х$$
переводится как
$$1\cdot x=x$$
 Вот почему в вашем векторном пространстве, поскольку мы используем умножение как «сложение», действительное число 1 является нулевым вектором, поскольку оно возвращает все, что получает ввод, то есть потому, что $1*что-нибудь=что-нибудь$ ваши операции дают $что-нибудь + \mathbf = что-нибудь$
Вот почему в вашем векторном пространстве, поскольку мы используем умножение как «сложение», действительное число 1 является нулевым вектором, поскольку оно возвращает все, что получает ввод, то есть потому, что $1*что-нибудь=что-нибудь$ ваши операции дают $что-нибудь + \mathbf = что-нибудь$