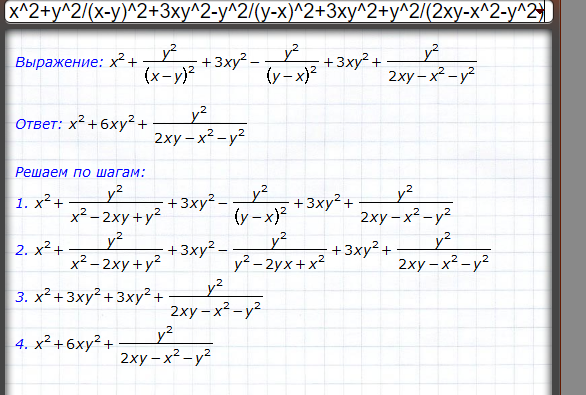Y 2xy xy 2: Решите дифференциальное уравнение y’=2xy+xy^2 (у штрих первого (1-го) порядка равно 2 х у плюс х у в квадрате)

Филиппов § 10. Уравнения, допускающие понижение порядка

 

Бесплатные решения из сборника задач по дифференциальным уравнениям А.Ф. Филиппова. Решения дифференциальных уравнений в данном разделе доступны в режиме онлайн без регистрации.

§ 10. Уравнения, допускающие понижение порядка

421. Решить уравнение: x2y» = y’2.

422. Решить уравнение: 2xy’y» = y’2 — 1.

423. Решить уравнение: y3y» = 1.

424. Решить уравнение: y’2 + 2yy» = 0.

425. Решить уравнение: y» = 2yy’.

426. Решить уравнение: yy» + 1 = y’2.

427. Решить уравнение: y»(ex + 1) + y’ = 0.

428. Решить уравнение: y»’ = y»2.

429. Решить уравнение: yy» = y’2 — y’3.

430. Решить уравнение: y»’ = 2(y» — 1) ctg x.

432. Решить уравнение: y»3 + xy» = 2y’.

433.

 Решить уравнение: y»2 + y’ = xy».

434. Решить уравнение: y» + y’2 = 2e-y.

435. Решить уравнение: xy»’ = y» — xy».

436. Решить уравнение: y»2 = y’2 + 1.

438. Решить уравнение: y» — xy»’ + y»’3 = 0.

439. Решить уравнение: 2y'(y» + 2) = xy»2.

441. Решить уравнение: y’2 = (3y — 2y’)y».

442. Решить уравнение: y»(2y’ + x) = 1.

443. Решить уравнение: y»2 — 2y’y»’ + 1 = 0.

444. Решить уравнение: (1 -x2)y» + xy’ = 2.

445. Решить уравнение: yy» — 2yy’ ln y = y’2.

446. Решить уравнение: (y’ + 2y)y» = y’2.

447. Решить уравнение: xy» = y’ + x sin(y’/x).

448. Решить уравнение: y»’y’2 = y»3.

449. Решить уравнение: yy» + y = y’2.

450. Решить уравнение: xy» = y’ + x(y’2 + x2).

452. Решить дифференциальное уравнение, воспользовавшись формулой, сводящей многократное интегрирование к однократному. 
xy» = sin x.

455. Решить уравнение, преобразовав его к такому виду, чтобы обе части уравнения являлись полными производными. 
yy»’ + 3y’y» = 0.

456. Решить уравнение, преобразовав его к такому виду, чтобы обе части уравнения являлись полными производными. 
y’y»’ = 2y»2.

457. Решить уравнение, преобразовав его к такому виду, чтобы обе части уравнения являлись полными производными. 
yy» = y'(y’ + 1).

458. Решить уравнение, преобразовав его к такому виду, чтобы обе части уравнения являлись полными производными. 
5y»’2 — 3y»yIV = 0.

459. Решить уравнение, преобразовав его к такому виду, чтобы обе части уравнения являлись полными производными. 

yy» + y’2 = 1.

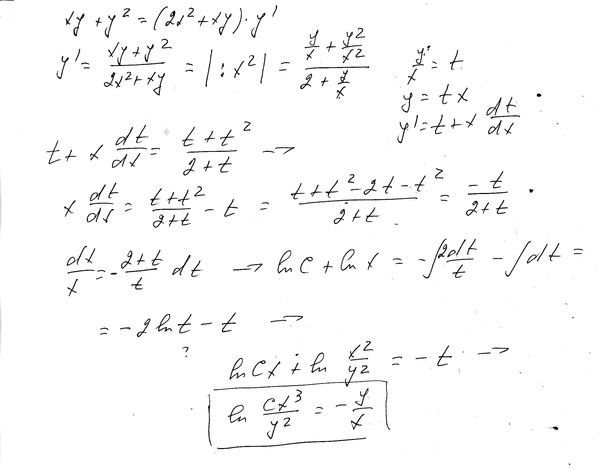
460. Решить уравнение, преобразовав его к такому виду, чтобы обе части уравнения являлись полными производными. 
y» = xy’ + y + 1.

461. Решить уравнение, преобразовав его к такому виду, чтобы обе части уравнения являлись полными производными. 
xy» = 2yy’ — y’.

462. Решить уравнение, преобразовав его к такому виду, чтобы обе части уравнения являлись полными производными. 
xy» — y’ = x2yy’.

463. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
xyy» — xy’2 = yy’.

464. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 

yy» = y’2 + 15y2 sqrt(x).

465. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
(x2 + 1)(y’2 — yy») = xyy’.

466. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение.  
xyy» + xy’2 = 2yy’.

467. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
x2yy» = (y — xy’)2.

468. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
y» + y’/x + y/x2 = y’2/y.

469. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
y(xy» + y’) = xy’2(1 — x).

470. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 

x2yy» + y’2 = 0.

471. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
x2(y’2 — 2yy») = y2.

472. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
xyy» = y'(y + y’).

473. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение.  
4x2y3y» = x2 — y4.

474. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
x3y» = (y — xy’)(y — xy’ — x).

475. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
y2/x2 + y’2 = 3xy» + 2yy’/x.

476.

 Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
y» = (2xy — 5/x)y’ + 4y2 — 4y/x2.

477. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
x2(2yy» — y’2) = 1 — 2xyy’.

478. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
x2(yy» — y’2) + xyy’ = (2xy’ — 3y)x3/2.

479. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
x4(y’2 — 2yy») = 4x3yy’ + 1.

480. Понизить порядок данного уравнения, пользуясь его однородностью, и решить это уравнение. 
yy’ + xyy» — xy’2 = x3.

482. Понизив порядок данного дифференциального уравнения, свести его к уравнению первого порядка. 

y»2 — y’y»’ = (y’/x)2.

487. Понизив порядок данного дифференциального уравнения, свести его к уравнению первого порядка. 
y2(y’y»’ — 2y»2) = y’4.

500. Понизив порядок данного дифференциального уравнения, свести его к уравнению первого порядка. 
x2(y2y»’ — y’3) = 2y2y’ — 3xyy’2…

501. Найти решение, удовлетворяющие заданным начальным условиям. 
yy» = 2xy’2; y(2) = 2, y'(2) = 0,5.

502. Найти решение, удовлетворяющие заданным начальным условиям. 
2y»’ — 3y’2 = 0; y(0) = -3, y'(0) = 1, y»(0) = -1.

503. Найти решение, удовлетворяющие заданным начальным условиям. {2C}$, но я не знаю, как избавиться от абсолютного значения, а затем найти y. Я слышал, что в дифференциальных уравнениях абсолютным значением можно пренебречь. Это правда? 9{2C}$ и найти $y$. (Поскольку $C$ — произвольная константа, $D$ будет произвольной

ненулевой константой .)

$\endgroup$

$\begingroup$

дифференциальное уравнение $$\frac{dy}{dx} = xy(y+2) $$ имеет два постоянных решения $y = 0$ и $y = -2.$ правая часть всюду непрерывна и удовлетворяет условию условие Липшица всюду, так что оно удовлетворяет критериям единственности. что это означает для решений этого дифференциального уравнения, так это то, что решения захвачены в трех областях $y <-2, -2

Шаг 1 :

 y
 Упростить —
            Икс
 

Уравнение в конце шага 1 :

 x y
  (2xy-—)•((x•(y  2  ))+(2•—))
       у х
 

Шаг 2 :

Преобразование целого в виде эквивалентной дроби:

 2.

1   Прибавление дроби к целому

Преобразование целого в виде дроби, используя x в качестве знаменателя:

 xy  2  ху  2  • х
     ху  2  = ——— = ———————
             1 х
 

Эквивалентная дробь : Полученная таким образом дробь выглядит иначе, но имеет то же значение, что и целое

Общий знаменатель : Эквивалентная дробь и другая дробь, участвующая в вычислении, имеют один и тот же знаменатель

Сложение дробей, имеющих общий знаменатель:

 2.2       Сложение двух эквивалентных дробей
Сложение двух эквивалентных дробей, которые теперь имеют общий знаменатель

Объедините числители, подведите сумму или разность к общему знаменателю, затем приведите к наименьшему числу, если возможно:

 xy  2  • x + 2y x  2  y  2  + 2y
 "="
      х х
 

Уравнение в конце шага 2 :

 x (x  2  y  2  + 2y)
  (2xy - —) • ———————————
          у х
 

Шаг 3 :

  x
 Упростить —
            у
 

Уравнение в конце шага 3 :

 x (x  2  y  2  + 2y)
  (2xy - —) • ———————————
          у х
 

Шаг 4 :

Преобразование целого в виде эквивалентной дроби:

 4. 1   Вычитание дроби из целого

Преобразование целого в виде дроби с использованием y в качестве знаменателя:

 2xy 2xy •
     2ху = ——— = ———————
             1 год
 

Сложение дробей, имеющих общий знаменатель:

 4.2       Сложение двух эквивалентных дробей

 2xy • y - (x) 2xy  2  - x
 "="
       у у
 

Уравнение в конце шага 4 :

 (2xy  2  - x) (x  2  y  2  + 2y)
  —————————— • ———————————
      у х
 

Шаг 5 :

Шаг 6 :

Вытягивание одинаковых членов:

 6.1     Вытягивание одинаковых факторов :

   2xy ² — x  =   x • (2y ² — 1) 

Шаг 7 :

   (x

² y ² + 2y)  =   y • (x ² y + 2) 

Попытка разложить на множители как разность квадратов :

 7.2      Разложение на множители:  2y ² — 1 два квадрата: совершенная разность

3 А ²  — B ²   можно разложить на  (A+B) • (A-B)

Доказательство:  (A+B)• (A-B) =
         A ²

— AB + BA — B ²  =
         A 2 6 6 0 6 0 AB 9 0 + 0 AB
         А ² — B ²

Примечание: AB = BA — это коммутативное свойство умножения.

No related posts.