«Первый признак равенства треугольников» (7 класс)
Дата______________
Класс: 7
Тема: Первый признак равенства треугольников.
Цели:
1. Познакомиться с формулировкой и доказательством 1 признака равенства треугольников.
2. Тренировать способность решать задачи, используя признаки равенства треугольников.
3. Развивать умение решать задачи по готовым чертежам, развивать логическое
мышление. Расширять пространственные представления учащихся.
4. Воспитывать аккуратность и прилежание.
Планируемые образовательные результаты:
Личностные: формирования способности к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
Метапредметные: способности адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения.
Предметные: умения работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический), развития способности обосновывать суждения, проводить классификацию.
Тип урока: изучение нового материала.
Оборудование: учебник, тетрадь, интерактивная доска, презентация, компьютер, раздаточный материал
Ход урока:
Организационный момент.
Проверка готовности учащихся к уроку. Сообщение темы урока (слайд 1), целей и задачей урока (слайд 2)
Актуализация опорных знаний.
Вопросы: (слайд 3)
1. Объясните, какая фигура является треугольником?
2. Назовите вершины, стороны и углы треугольника.
3. Назовите сторону, лежащую против угла D, против угла E, против угла F.
4. Укажите углы, лежащие против сторон DE, EF, FD.
5. Укажите углы, прилежащие к сторонам DE, EF, FD.
Объяснение новой темы.
Мы докажем теорему, которая устанавливает равенство двух треугольников по двум сторонам и углу между ними. (слайд 4)
Вопрос 1: Что такое теорема? (утверждение, справедливость которого устанавливается путем рассуждений, называется теоремой).
Вопрос 2: А как называются сами рассуждения? (доказательством теоремы)
Формулировка теоремы. (слайд 4)
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Рисунок теоремы (слайд 5)
Доказательство теоремы (слайд 6-9)
Т.к A=А1, то АВС можно наложить на А1В1С1 так, что вершина А совместится с вершиной А1, астороны АВ и АС наложатся на стороны А1В1 и А1С1.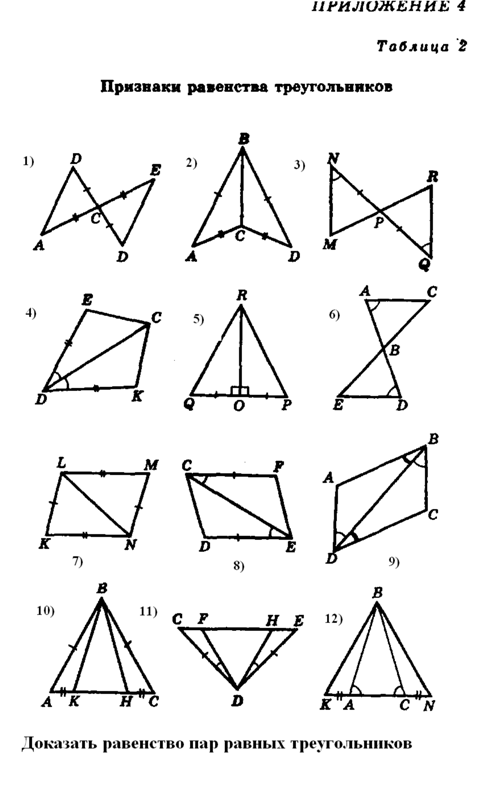
Поскольку АВ = А1В1, то сторона АВ совместится со стороной А1В1, в частности, совместятся точки В и В1.
Поскольку АС = А1С1, то сторона АС совместится со стороной А1С1, в частности, совместятся точки С и С1.
Следовательно, совместятся стороны ВС и В1С1, т.к. через совпадающие точки (С и С1, В и В1) можно провести только одну прямую.
Итак, треугольники АВС и А1В1С1 полностью совместились, значит, они равны.
Доказанная теорема выражает I признак равенства треугольников по двум сторонам и углу между ними.
Что такое признак?
Признак (от слова знак) – это показатель, по которому можно узнать, определить что-либо. (Слайд 10)
Первичная проверка понимания материала.
Используются слайды презентации.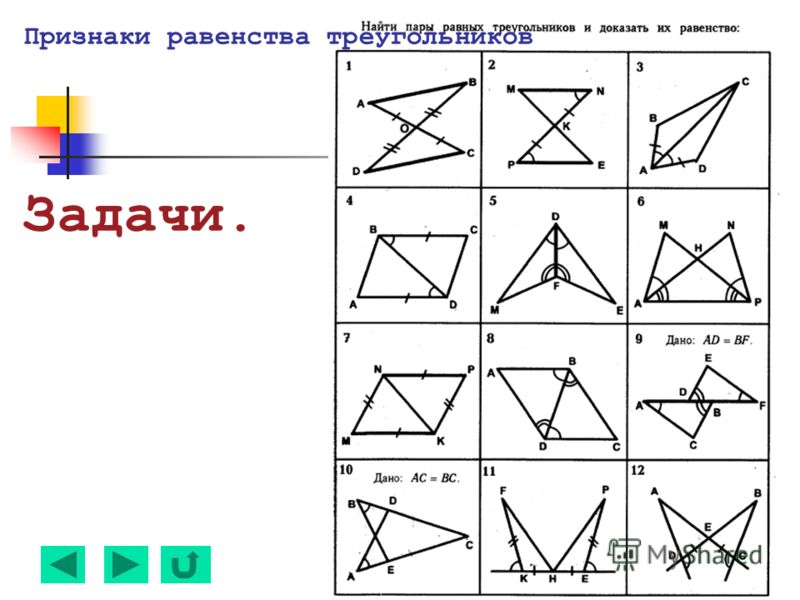 Закрепляется навык учащихся доказывать равенство треугольников, используя 1 признак, ведется работа по формированию правильной математической речи учащихся.
Закрепляется навык учащихся доказывать равенство треугольников, используя 1 признак, ведется работа по формированию правильной математической речи учащихся.
Решение задачи № 93 с подробной записью в тетради. (Слайд 11 )
По готовому чертежу докажите равенство треугольников. (слайд 12)
Доказать, заполняя пропуски (слайд 13)
Закрепление материала
Итог урока
Познакомились с формулировкой и доказательством первого признака равенства треугольников. Давайте повторим…
2. Научились решать задачи, используя 1 признак равенства треугольников.
3. Развивали логическое мышление, пространственное представление и умение решать задачи по готовым чертежам.
Домашнее задание
Рефлексия
И так ребята, что вы узнали на сегодняшнем уроке? Все ли вам было понятно? Со всем ли мы справились? Не возникали ли у вас затруднения в ходе нашего урока, если да то почему?
4
Первый признак равенства треугольников
Цели урока:
- Повторить понятие смежных и вертикальных углов.

- Закрепить навык решения задач на вычисление вертикальных и смежных углов.
- Отработать навык решения задач на применение 1 признака равенства треугольников
ц е л и и з а д а ч и
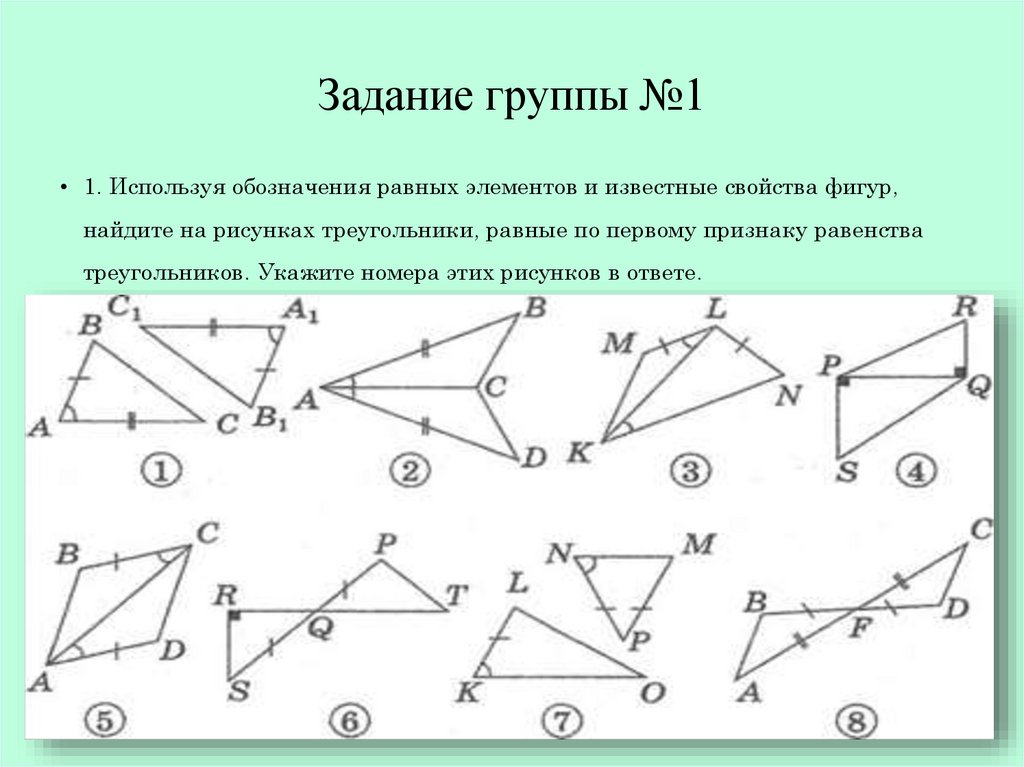
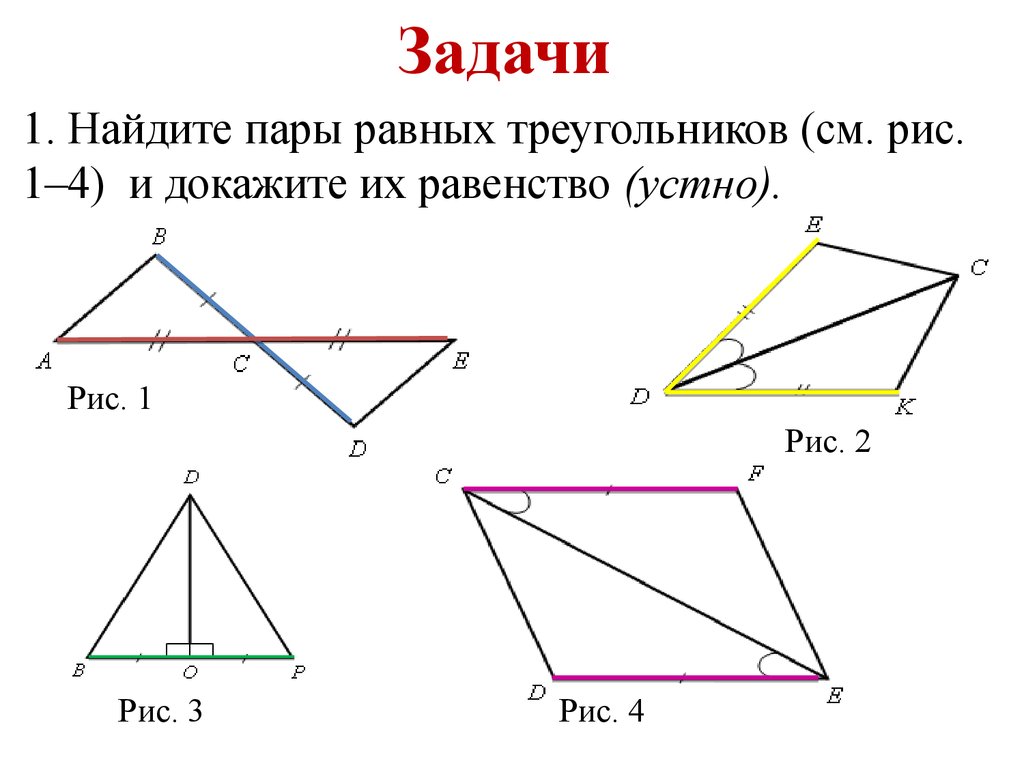
- Распознавать на чертежах равные треугольники по указанным равным элементам, применяя признаки равенства треугольников;
- Непосредственно применять признаки равенства треугольников;
- Делать выводы из равенства треугольников;
- Читать чертежи, сопровождающие текст задачи, сопоставлять текст задачи с данным чертежом, выделять на чертеже необходимую для решения задачи конфигурацию;
- Формировать и развивать логическое мышление и культуру речи.
Работа по готовым чертежам.
B
C
- Назовите пары смежных углов.
O
А
D
O
R
P
S
O
- Назовите вертикальные углы;
- — сформулируйте свойство вертикальных углов.

М
D
О
К
C
Свойство вертикальных углов : вертикальные углы равны.
1
75 О
2
3
Найдите углы при пересечении двух прямых, если один из углов равен 75 О .
Дан Δ CDM.
а) Назовите углы, прилежащие
стороне CD.
б) Назовите угол, лежащий
против стороны СМ.
в) Назовите углы, заключённые
между сторонами СМ и MD,
CD и DM.
А
∆ QRP = ∆ ABC
Это означает, что
В
А =
В =
С =
АВ =
ВС =
АС =
Р
С
R
Q
P
На рисунке изображены равные треугольники.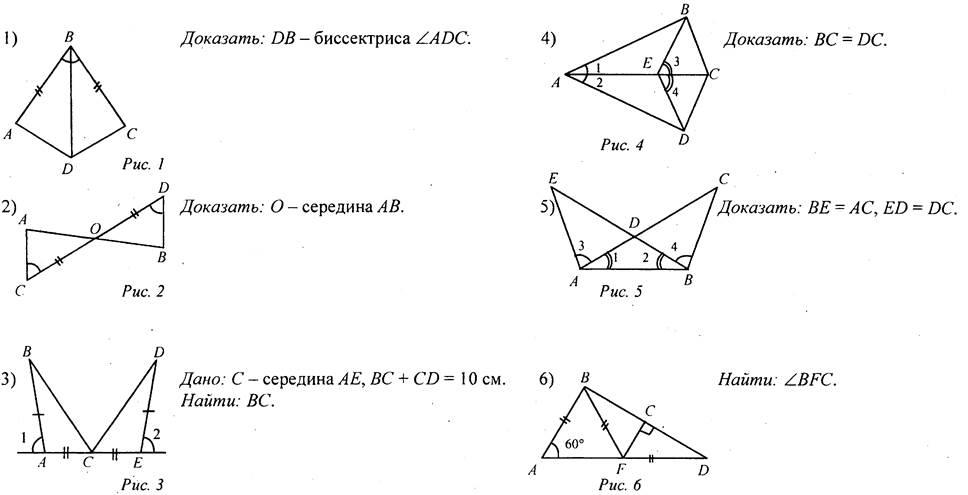
А
P
В
30°
5см
Q
R
С
- Установите, какая из следующих записей верна:
а) ∆ABC = ∆PQR; б) ∆ABC = ∆RQP ; в) ∆ABC = ∆PRQ .
- Известно ,что АС = 5см, ے В = 30°.
а) Длину какой стороны ∆RQP вы можете указать?
б) Какой угол ∆RQP известен ?
RQ = 5см
ے Q = 30°
Используя чертеж, найдите равные треугольники,
Если AB=PQ=MK, A = P = K, AC=PR=MN
P
Q
C
N
Ответ:
∆ ABC=∆PQR
R
B
A
M
K
- В древнем искусстве были широко распространены изображения равностороннего треугольника .
- Вожди племен североамериканских
индейцев носили на груди символ власти:
равносторонний треугольник с точкой в центре.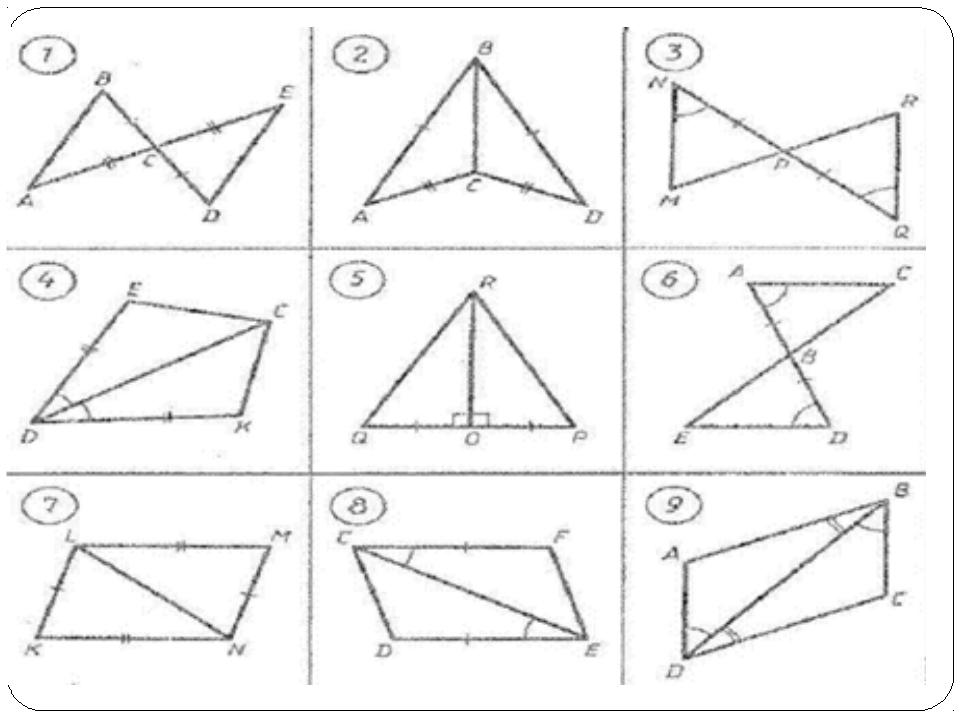
- В Африке женщины украшали себя большими пластинами из равносторонних треугольников.
4
В 7 классе у нас появился новый предмет — «Геометрия».
Первая геометрическая фигура, свойства которой мы начали изучать — треугольник.
На уроках, мы не задумывались над тем, где с треугольником встречаемся в жизни.
Изучив литературу и статьи электронной энциклопедии, можно узнать, что в жизни можно встретить:
- Созвездие треугольник.
- Музыкальный треугольник.
- Бермудский треугольник.
- Солдатский треугольник.
- Треугольник Пенроуза.
- Бильярдный треугольник.
Музыкальный треугольник.
- ТРЕУГОЛЬНИК, самозвучащий музыкальный инструмент — стальной прут, согнутый в виде треугольника, по которому ударяют палочкой. Применяется в оркестрах и инструментальных ансамблях.
Бермудский треугольник — район в Атлантическом океане, в котором происходят якобы таинственные исчезновения морских и воздушных судов. Район ограничен линиями от Флориды к Бермудским островам, далее к Пуэрто-Рико и назад к Флориде через Багамы.
Район ограничен линиями от Флориды к Бермудским островам, далее к Пуэрто-Рико и назад к Флориде через Багамы.
Бермудские
острова
Флорида
http://ru.wikipedia.org/wiki/%D0%91%D0%B5%D1%80%D0%BC%D1%83%D0%B4%D1%81%D0%BA%D0%B8%D0%B9_%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA
Пуэрто-Рико
Солдатский треугольник .
Солдатское письмо без конверта, свёрнутое уголком, которое отправлялось солдатами во время войны .
Созвездие треугольник.
- ТРЕУГОЛЬНИК — созвездие Северного полушария; с территории России лучше всего видно в конце лета, осенью и зимой.
- Созвездие Треуго́льник содержит 25 звезд, видимых невооружённым глазом.
Треугольник Пенроуза.
- Треугольник Пенроуза -невозможный объект. Плоский рисунок может обманывать, изображая невозможное.
 Закройте одну из вершин этого треугольника, и станет ясно, что одна из его сторон направлена к нам, а другая от нас, т.е. они не могут соединиться в пространстве.
Закройте одну из вершин этого треугольника, и станет ясно, что одна из его сторон направлена к нам, а другая от нас, т.е. они не могут соединиться в пространстве.
Начиная игру в бильярд, необходимо расположить шары в виде треугольника. Для этого используют специальную треугольную рамку.
http://www.bogato.info/index/?node_id=2822
http://www.labirint-shop.ru/screenshot/189362/1/
Расстановка кеглей в игре Боулинг в виде равностороннего треугольника.
http://www.akatuy.ru/bouling.asp?page=./6939/6952/7040/7062
http://rnd.onegintime.ru/game.html?game=3&count=90&limit=10&page_num=8
Для составления красивых паркетов часто использовали треугольники.
Треугольники в конструкции мостов.
http://mirrorsoul.narod.ru/pictures/P1010096_2.htm
Высоковольтные линии электропередачи.
Треугольники делают конструкции надежными.
http://orsk.ru/index.php?option=com_content&task=view&id=4359&Itemid=110
Треугольник играет в
геометрии особую роль.
Без преувеличения
можно сказать, что вся
(или почти вся) геометрия
со времён «Начал» Евклида
покоится на «трёх китах» –
признаках равенства
треугольников.
Первый признак равенства треугольников
К
С
В
Р
М
(По двум сторонам и углу между ними )
А
Какое условие должно еще выполняться, что бы треугольники были равны?
2)
1)
3)
4
Задача №1
В
С
О
А
D
Доказать: Δ ВОС=Δ АОD
Задача 2
В
С
А
D
Δ АВС=Δ АDС
Обухова Н.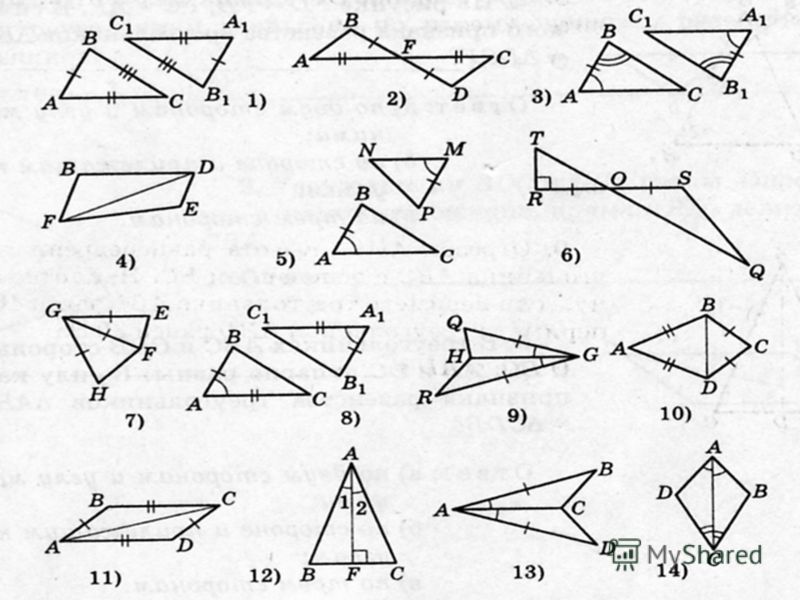 С, МОУ СОШ № 17 г.Заволжья Нижегородской области
С, МОУ СОШ № 17 г.Заволжья Нижегородской области
Задача №3
В
С
1
2
А
D
Доказать: Δ АВD=Δ ВСD
AD – биссектриса угла А; АВ = АС.
Докажите: BD = CD.
Достигнуты ли были цели урока?
Сегодня на уроке :
1.У меня все получилось,
я готов идти дальше!
2. У меня были затруднения, но я с ними справился.
3.У меня были трудности, мне нужна тренировка.
Q7 Нарисуйте пять треугольников и измерьте их стороны. В каждом случае проверьте, равна ли сумма длин любых двух…
Перейти к
- Упражнение 5.1
- Упражнение 5.
 2
2 - Упражнение 5.3
- Упражнение 5.4
- Упражнение 5.5
- Упражнение 5.6
- Упражнение 5.7
- Упражнение 5.8
- Упражнение 5.

- Зная наши цифры
- Целые числа
- Игра с числами
- Основные геометрические идеи
- Понимание элементарных форм
- Целые числа
- Фракции
- Десятичные
- Обработка данных
- Измерение
- Алгебра
- Соотношение и пропорция
- Симметрия
- Практическая геометрия
Главная >
Решения НЦЭРТ
Класс 6
Математика
>
Глава 5.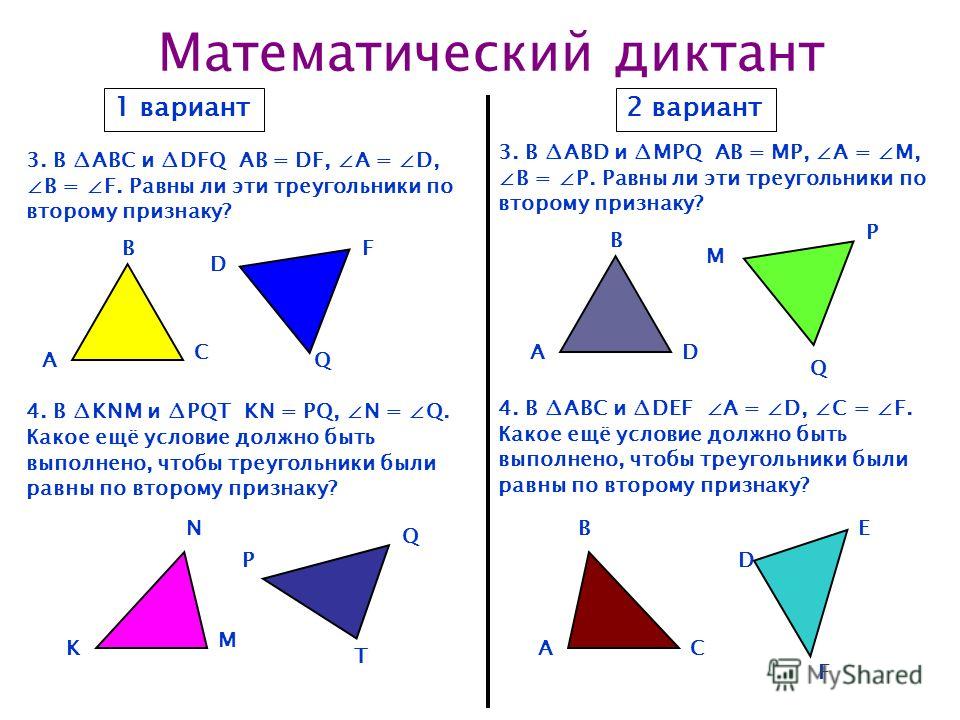 Понимание элементарных форм
>
Упражнение 5.1
>
Вопрос 5
Понимание элементарных форм
>
Упражнение 5.1
>
Вопрос 5
Вопрос 5 Упражнение 5.1
В7) Нарисуйте пять треугольников и измерьте их стороны. Проверяем в каждом случае, если сумма
длин любых двух сторон всегда меньше третьей стороны.
Ответ:
РЕШЕНИЕ:
Стенограмма видео
Добро пожаловать, дорогая домашняя работа по Лидо. Сегодня. Мы решаем вопрос номер 7, который состоит в том, чтобы нарисовать 5 треугольников и измерить их размер, проверить в каждом случае. Если сумма длин любых двух сторон всегда меньше третьей стороны. Хорошо. Итак, давайте поймем, как это сделать. Итак, прежде всего, я уже сделал треугольники. Я надеюсь, что вы можете сделать это самостоятельно. Вы можете сделать любую линзу, а затем проверить длину размера с помощью линейки. Хорошо, главное, что вы должны понять, это вторая часть. Хорошо. Итак, вы уже нашли площадь длин сторон? Следующая часть состоит в том, чтобы просто понять вторую часть, потому что первая часть довольно проста.
Хорошо, давайте разберемся, что вторая для второй части говорит, что это сумма линзы любых двух сторон. Итак, что мы сделаем, так это добавим две стороны. Так что в этом случае пять баллов два плюс пять баллов дадут вам десять целых четыре балла — это сумма кубов, и их нужно проверить. Если это число, каким бы ни было сложение двух сторон, всегда больше, чем какое бы ни было значение третьей стороны. Так что в этом случае третья сторона тоже равна пяти целых двум десятым, что явно меньше, чем здесь. Поэтому. Это действительно в первой части. Давайте выясним это во второй и каких двух сторон это не имеет значения. Итак, в этом мы добавляем 17 и 8, поэтому наш ответ будет 25. Опять же, 25 больше, чем 15. Это верно во втором. Найдем в третьем.
Третьему 15 плюс мы можем сделать это на 19-9 равно 19, а 19 больше 15.
Хорошо, главное, что вы должны понять, это вторая часть. Хорошо. Итак, вы уже нашли площадь длин сторон? Следующая часть состоит в том, чтобы просто понять вторую часть, потому что первая часть довольно проста.
Хорошо, давайте разберемся, что вторая для второй части говорит, что это сумма линзы любых двух сторон. Итак, что мы сделаем, так это добавим две стороны. Так что в этом случае пять баллов два плюс пять баллов дадут вам десять целых четыре балла — это сумма кубов, и их нужно проверить. Если это число, каким бы ни было сложение двух сторон, всегда больше, чем какое бы ни было значение третьей стороны. Так что в этом случае третья сторона тоже равна пяти целых двум десятым, что явно меньше, чем здесь. Поэтому. Это действительно в первой части. Давайте выясним это во второй и каких двух сторон это не имеет значения. Итак, в этом мы добавляем 17 и 8, поэтому наш ответ будет 25. Опять же, 25 больше, чем 15. Это верно во втором. Найдем в третьем.
Третьему 15 плюс мы можем сделать это на 19-9 равно 19, а 19 больше 15. Итак, опять же, это справедливо и в третьем случае. Найдем его в четвертом случае 5 плюс 5 равно 10 10 больше его. Итак, опять же, это действительно в последнем. Я думаю, что они не дали нам этот сайт. Так что да, эта сторона будет всего лишь секундой. Таким образом, длина этой стороны будет корнем, я думаю.
Это root 3. Спасибо.
Итак, опять же, это справедливо и в третьем случае. Найдем его в четвертом случае 5 плюс 5 равно 10 10 больше его. Итак, опять же, это действительно в последнем. Я думаю, что они не дали нам этот сайт. Так что да, эта сторона будет всего лишь секундой. Таким образом, длина этой стороны будет корнем, я думаю.
Это root 3. Спасибо.
Связанные вопросы
Q2) Почему при измерении длины отрезка лучше использовать делитель, а не линейку?
В4) Если А, В, С — три точки на прямой, такие что АВ = 5 см, ВС = 3 см и АС = 8 см, какая из них…
Q5) Проверьте, является ли D средней точкой AG.
Q6) Если B — середина AC, а C — середина BD, где A, B, C, D лежат на прямой…
Q1) В чем недостаток сравнения отрезков путем простого наблюдения?
Q3) Нарисуйте любой отрезок, скажем, AB. Возьмем любую точку C, лежащую между точками A и B. Измерьте длины…
Возьмем любую точку C, лежащую между точками A и B. Измерьте длины…
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Упражнение 5.1
Упражнение 5.2
Упражнение 5.3
Упражнение 5.4
Упражнение 5.5
Упражнение 5.6
Упражнение 5.7
Упражнения 5.8
Упражнение 5.9
ГЛАВЫ
ЗНАЧЕНИЯ
.
Игра с числами
Основные геометрические идеи
Понимание элементарных фигур
Целые числа
Дроби
Десятичные числа
Обработка данных
Измерение
Алгебра
Отношение и пропорция
Симметрия
Практическая геометрия
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены
Линии симметрии плоских форм
Линия симметрии
Вот морда моей собаки «Пламя»
сделано идеально симметрично с немного
фото магии.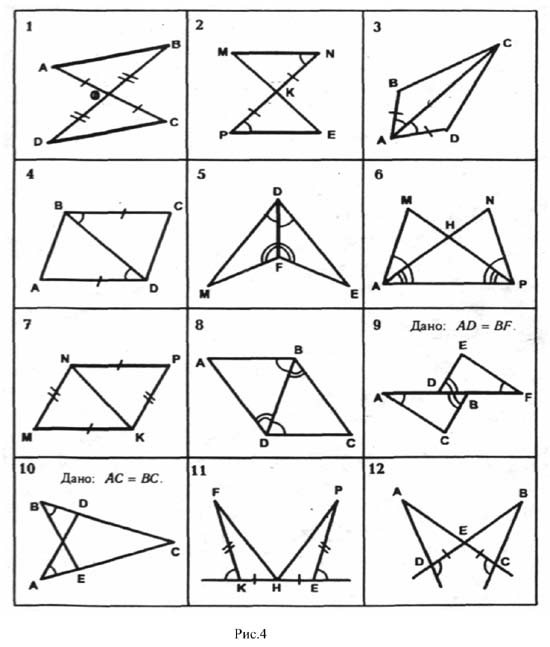
Белая линия по центру — это Линия симметрии
Подробнее читайте в разделе «Симметрия отражения».
Тест на складывание
Вы можете определить, имеет ли фигура линию симметрии, сложив ее .
Когда сложенная деталь идеально располагается сверху (все края совпадают), линия сгиба является линией симметрии.
Здесь я сложил прямоугольник в одну сторону, и не получилось .
Итак, это вместо Линия симметрии
Но когда я пытаюсь сделать так, работает (согнутая часть идеально сидит сверху, все края совпадают):
Итак, это есть линия симметрии
Треугольники
Треугольник может иметь 3 или 1 или без линий симметрии:
| Равносторонний треугольник (все стороны равны, все углы равны) | Равнобедренный треугольник (две стороны равны, два угла равны) | Разносторонний треугольник (нет равных сторон, нет равных углов) | ||
| 3 Линии симметрии | 1 Линия симметрии | № Линии симметрии |
Четырехугольники
Различные типы четырехугольников (четырехсторонняя плоская форма):
| Квадрат (все стороны равны, все углы 90°) | Прямоугольник (противоположные стороны равны, все углы 90°) | Неправильный Четырехугольник | ||
| 4 Линии симметрии | 2 Линии симметрии | № Линии симметрии |
| Воздушный змей | Ромб (все стороны одинаковой длины) | |
| 1 Линия симметрии | 2 Линии симметрии |
Правильные многоугольники
У правильного многоугольника все стороны равны и все углы равны:
Равносторонний треугольник (3 стороны)
имеет 3 линии симметрии
A Квадрат (4 стороны)
имеет 4 линии симметрии
Правильный пятиугольник (5 сторон)
имеет 5 линий симметрии
A Правильный шестиугольник (6 сторон)
имеет 6 линий симметрии
A Правильный семиугольник (7 сторон)
имеет 7 линий симметрии
A Обычный восьмиугольник (8 сторон)
имеет 8 линий симметрии
И шаблон продолжается:
- Правильный многоугольник из 9 сторон имеет 9 линий симметрии
- Правильный многоугольник из 10 сторон имеет 10 линий симметрии
- .



 Закройте одну из вершин этого треугольника, и станет ясно, что одна из его сторон направлена к нам, а другая от нас, т.е. они не могут соединиться в пространстве.
Закройте одну из вершин этого треугольника, и станет ясно, что одна из его сторон направлена к нам, а другая от нас, т.е. они не могут соединиться в пространстве. 2
2