Что значит функция в математике? Обясните своими словами, а то решаю всякие функции, не понимая что такое функция.
Понятие не простое. И даже в книжках существует не одно определение функции. Я в учебниках встречал по крайней мере два определения. Функция представляет собой некую зависимость, когда одна величина полностью определяет значение другой величины. Я не говорю «представляет собой формулу» потому, что не всякую зависимость можно выразить формулой. «Закон», «правило», «соответствие» — это подходящие понятия, чтоб с их применением значение одной переменной однозначно определяло значение другой переменной. Тут ключевое слово «однозначно». Это слово иногда опускают из определения, и тогда появляются непонятки, уводящие от исконного понятия функции. Например, нарисуй окружность как график — по формуле, на координатной плоскости. Одному значению Х соответствует два значения Y и наоборот. Именно поэтому уравнение окружности нельзя назвать функцией — неоднозначное соответствие. Нарисуй параболу простейшую у=х^2. Одному значению Х соответствует строго одно значение У — зависимость однозначная. Поэтому уравнение параболы можно рассматривать как функцию у от х (или наоборот). Вот это и есть главная фишка — если по какому-либо правилу из одной величины можно о д н о з н а ч н о прийти к конкретному значению другой величины — это правило и есть функция.
<a href=»/» rel=»nofollow» title=»15907216:##:2cBgadA»>[ссылка заблокирована по решению администрации проекта]</a>
это правило, по которому нужно что-либо сделать с поступающим числом. например функция f(x)=x*2 или у=х*2 Значит нужно умножить число на 2. f(3) В этом случае у=2*3=6 На входе число 3, на выходе число 6. В жизни мы постоянно составляем и решаем такие функции
Функция — это правило, которое позволяет, зная значение х, найти соответствующее значение у
Своими словами: функция это закон по которому из входных данных получается результат. Простой пример из жизни. У вас есть рука и горячий предмет, это входные данные, если коснутся, то обожжешься — это результат. Возьмем и наденем на руку перчатку изменив входные данные — результат будет иной, но закон останется таким же — нагрев одного предмета другим.
touch.otvet.mail.ru
02. Функции. Предельное значение функции
2. Понятие функции. Предельное значение функции
1 из 26
Рассматривается понятие функции, её предельного значения в точке и на бесконечности.
2 из 26
Функция – одно из фундаментальных понятий математики. Она описывает зависимость между несколькими переменными.
Определение 2.1. Если каждому значению переменной из множества{ } ставят в соответствие по определённому правилу некоторое число , то говорят, что на множестве{ } задана функция= ( ) или= ( ).
Примеры функций
= 2. Функция задана на всей числовой оси( 2) = , множество значений( 2) = + — полупрямая неотрицательных чисел.
= !. Функция определена на множестве натуральных чисел(!) = . Множество значений – множество натуральных чисел вида!.
3 из 26
0,= ( ) = {1, — функция Дирихле. Область определе-
ния — ,область значений два числа 0 и 1.
−1, < 0;= ( ) = { 0, = 0; — функция знака. Область опреде-
1, > 0
ления — ,область значений три числа-1,0и 1.
= – целая часть числа. Область определения- ,область значений – целые числа.
4 из 26
2.1. Понятие предельного значения функции
Определение 2.2 (Гейне). Число называют предельным значением функции= ( ) в точке= (или пределом функции при→ ), если для любой сходящейся к последователь-
ности { |
| } значений аргумента , элементы которой отличны | ||
|
|
|
| |
от ( | ≠ ), соответствующая последовательность значе- | |||
|
|
|
|
|
ний функции { ( | )} сходится к |
| ||
|
|
|
|
|
|
|
| lim ( ) = . | (2.1) |
|
|
| → |
|
5 из 26
Определение 2.3. Число называют правым (левым) предельным значением функции= ( ) в точке= (или односторонним пределом функции при→ ), если для любой сходящейся к последовательности{ } значений аргумента , элементы которой больше (меньше) , соответствующая последовательность значений функции{ ( )} сходится к .
Правый предел
lim ( ) = ( + 0) = . | (2.2) |
→ +0 |
|
Левый предел
lim ( ) = ( − 0) = . | (2.3) |
→ −0 |
|
6 из 26
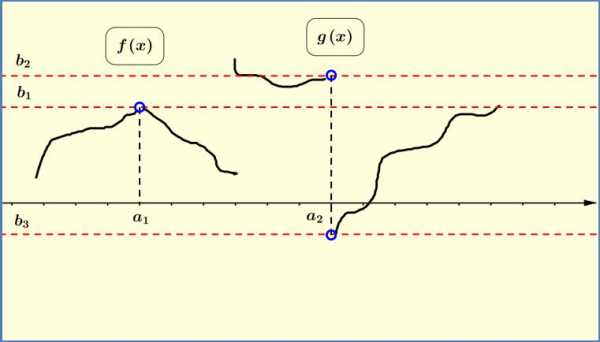
Рис. 2.1. Предел и односторонние пределы функции в точке
Определение 2.4. Число называют предельным значением функции= ( ) при→ ∞ (или пределом функции при→ ∞), если для любой бесконечно большой последовательности
7 из 26
значений аргумента соответствующая | последовательность |
значений функции { ( )} сходится к . |
|
|
|
lim ( ) = . | (2.4) |
→∞ |
|
Определение 2.5. Число называют предельным значением функции= ( ) при стремлении аргумента к положительной (отрицательной) бесконечности, если для любой бесконечно большой последовательности значений аргумента, элементы которой, начиная с некоторого номера положительны (отрицательны) соответствующая последовательность зна-
чений функции { ( | )} сходится к . |
| |
|
|
|
|
| lim | ( ) = . | (2.5) |
| →+∞ |
|
|
| lim | ( ) = . | (2.6) |
| →−∞ |
|
|
|
|
| 8 из 26 |
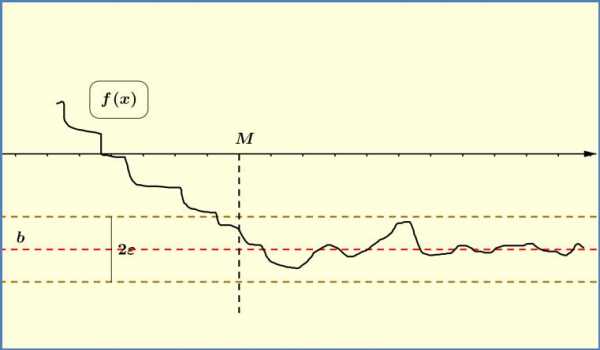
Рис. 2.2. Предел функции на бесконечности
9 из 26
2.2. Свойства функций, имеющих предельное
значение
Свойства сформулированы для случая стремления переменной к конечному числу: → . Однако, они остаются справедливыми и для односторонних пределов в точке, а так же и для предела на бесконечности.
Теорема 2.1. Пусть функции( ) и( ) имеют в точке=предельные значения и . Тогда функции( ) + ( ),( ) −
( ),( ) ( ) и( ) имеют в точке= предельные значе-
( )
ния (частное при условии ≠ 0), равные соответственно+ ,
− , и .
Доказательство. Пусть{ } — произвольная сходящаяся к последовательность значений аргумента функций( ) и( ).
10 из 26
studfiles.net
Что называется областью значения функции?
Все значения, которые может принимать игрек в функции y = f(x)
Все значения, которые принимает зависимая переменная, образуют область значений функции.ягуарчика выпей и просветлеешь…
Область определения и область значений функции. В элементарной математике изучаются функции только на множестве действительных чисел R. Это значит, что аргумент функции может принимать только те действительные значения, при которых функция определена, т. e. она также принимает только действительные значения. Множество X всех допустимых действительных значений аргумента x, при которых функция y = f ( x ) определена, называется областью определения функции. Множество Y всех действительных значений y, которые принимает функция, называется областью значений функции.
touch.otvet.mail.ru
что значит «найти нули функции»?
Где икс и игрик принимают нулевые значения, по русский сказать где они равны нулю)
Найти точки пересечения с осями координат, если мне не изменяет память)
Подставь вместо у или f(x) ноль, реши уравнение, найди х. Это и будет ноль функции.
Найти точки, где график пересекает ось икс
нули функции: 1) f(0) 2) f(x)=0
Теоретическая справка Определение нуля ~ Нуль порядка n ~ Простой нуль ~ Необходимое и достаточное условия нуля порядка n ~ Порядок нуля произведения анал. функций Пусть функция f (z) является аналитической в точке z0. Точка z0 называется нулем функции f (z), если ее значение в этой точке равно нулю, т. е. f (z0) = 0. В разложении функции в ряд Тейлора в окрестности нуля этой функции (т. z0) отсутствует свободный член: С0 = f(z0) = 0. Если при этом в разложении отсутствуют и слагаемые, содержащие степени разности (z-z0) до n-ой степени, т. е. разложение имеет вид: или то точка z0 называется нулем порядка n функции f(z). Нуль первого порядка (n = 1) называется простым нулем. Следующие условия являются необходимым и достаточным условиями нуля порядка n функции f (z) в точке z0: a). b). представление функции в виде произведения: Порядок нуля в точке z0 функции, полученной в результате перемножения аналитических функций f (z) = f1(z) f2(z) равен сумме порядков нуля (n1 + n2) в этой точке функций сомножителей ( n1 — порядок нуля в точке z0 функции f1(z), n2 — порядок нуля в точке z0 функции f2(z) ). ПРИМЕР 1. Определить порядок нуля в точке для функции f(z). ПРИМЕР 2. Найти нули функции f(z) и определить их порядок. ПРИМЕР 3. Найти нули функции f(z) и определить их порядок. ПРИМЕР 4. Определить порядок нуля в точке для функции f(z).
Найти нули функции — значит найти значения х при которых у обращается в нуль. Ну или найти координаты точек пересечения графика с осью ох.
Нули функции-это значения аргумента при которых функция равна нулю. Для нахождения их надо функцию приравнять к нулю и решить это уравнение. Значения «х» и будут нулями функции. Это точки которые лежат на оси Ох. Точнее точки пересечения графика функции с осью Ох.
нули функции — это значения переменной х при которых значеня фунции равно нулю, если проще, у=0, а х некоторому числу при этом значении
touch.otvet.mail.ru
