Как решать через теорему виета – О применении теоремы Виета при решении квадратных уравнений

Теорема Виета

Теорема Виета звучит так:

Теорема Виета широко используется при решении задач, в которых

• не требуется найти корни квадратного уравнения, а лишь некоторое их соотношение;
• нужно найти значение параметра, при котором значение корней удовлетворяет заданному соотношению.

С помощью теоремы Виета можно устно находить корни квадратного уравнения, а также проверять, являются ли заданные числа корнями уравнения.

Чтобы грамотно использовать теорему Виета, ее нужно хорошо понимать.

Остановимся подробнее на каждом слове этой теоремы. Сначала о коэффициентах квадратного уравнения:

Квадратное уравнение называется приведенным, если старший коэффициент равен 1, то есть если

В общем случае не каждое квадратное уравнение является приведенным, например, уравнение не является приведенным. В этом уравнении .

Но каждое квадратное уравнение можно сделать приведенным, для этого достаточно обе части уравнения вида разделить на :

В полученном уравнении старший коэффициент равен 1, второй коэффициент равен  , свободный член равен .

То есть корни  произвольного квадратного уравнения, согласно теоремы Виета,  удовлетворяют системе:

Например корни уравнения

удовлетворяют системе

Обратная теорема Виета позволяет составить квадратное уравнение по значениям его корней:

Например, числа -7 и -2 являются корнями уравнения ,   или 

Решим несколько задач с использованием теоремы Виета.

Задача 1. Составьте квадратное уравнение с рациональными коэффициентами, если известно, что один из корней равен

Так как произведение корней должно быть числом рациональным, второй корень может представлять выражение, сопряженное выражению , то есть дополняющее его до формулы разности квадратов. Это выражение :

Тогда ;

Отсюда получаем уравнение:

   

Задача 2. Найдите значения выражения , где и — корни уравнения .

Если в задаче не требуется найти значения корней квадратного уравнения, а только их соотношение, следовательно, нужно воспользоваться теоремой Виета.

Запишем теорему Виета для этого уравнения:

Теперь мы знаем, чему равны сумма и произведение корней. Представим выражение  в виде комбинации суммы и произведения. Приведем дроби к общему знаменателю.

   

Ответ: -8

Задача 3. Найдите значение выражения , где и — корни уравнения .

Эта задача аналогична предыдущей, только в ней чуть сложнее преобразование выражения  в комбинацию выражений  и .

Вспомним формулу квадрата суммы: . Перенесем  влево и получим соотношение (1)

Запишем теорему Виета для уравнения :

(по формуле 1)

Ответ: 20,5

Задача 4. Решите устно уравнение:

Теорем Виета позволяет в некоторых случаях легко находить корни квадратного уравнения.

Для этого удобно придерживаться такой последовательности шагов:

1. Выписываем теорему Виета для данного уравнения.
2. Определяем знаки корней.
3. Раскладываем на два множителя свободный член, и определяем,  какая пара множителей в сумме дает второй коэффициент, взятый с противоположным знаком.

Для данного уравнения 

1  

2  Определим знаки корней.

Для определения знаков удобно пользоваться такой таблицей:

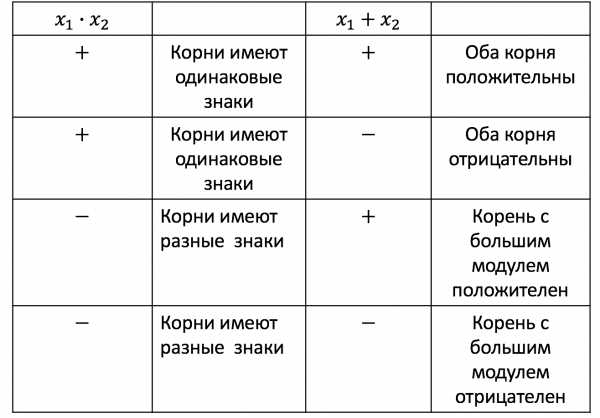
Так как в уравнении  произведение корней отрицательно, корни имеют разные знаки. Сумма корней также отрицательна, следовательно, корень с большим модулем отрицателен.

3. Будем раскладывать на множители число 24, имея в виду, что множитель с большим модулем отрицателен, и выбираем пару чисел, сумма которых равна -2.

Очевидно, что это числа -6 и 4.

Ответ: -6; 4

 

Задача 5. Решите устно уравнение:

1  

2 Определим знаки корней.

Так как в уравнении

произведение корней отрицательно, корни имеют разные знаки. Сумма корней отрицательна, следовательно, корень с большим модулем отрицателен.

В данном случае корни проще подобрать, зная их сумму: . Можно предположить, что . Проверим, чему равно произведение этих выражений:

Предположение верное.

Ответ: 

 

Следствием из теоремы Виета являются такие полезные факты:

Задача 6. Найти корни уравнения:

Заметим, что  , следовательно, .

Задача 7.

Найти корни уравнения:

Заметим, что  , следовательно,

 

Как решать задачи с параметром с помощью теоремы Виета читайте здесь.

И.В. Фельдман, репетитор по математике.

 

 

 

 

ege-ok.ru

формула, алгоритм использования, приведенный вид

 

Для начала сформулируем саму теорему: 

Пусть у нас есть приведённое квадратное уравнение вида x^2+b*x + c = 0. Допустим, это уравнение содержит корни x1 и x2. Тогда по теореме следующие утверждения допустимы:

1) Сумма корней x1 и x2 будет равняться отрицательному значению коэффициента b. 

X1+X2 = — b ;

2) Произведение этих самых корней будет давать нам коэффициент c . 

X1*X2 = c ;

Но что же такое приведённое уравнение

Приведённым квадратным уравнением называется квадратное уравнение, коэффициент старшей степени, которой равен единицы, т.е. это уравнение вида x^2 + b*x + c = 0. (а уравнение a*x^2 + b*x + c = 0 неприведенное). Другими словами, чтобы привести уравнение к приведённому виду, мы должны разделить это уравнение на коэффициент при старшей степени (a). Задача привести данное уравнение к приведённому виду:

3*x^2 12*x + 18 = 0;

−4*x^2 + 32*x + 16 = 0;

1,5*x^2 + 7,5*x + 3 = 0; 2*x^2 + 7*x − 11 = 0.

Поделим каждое уравнение на коэффициент старшей степени, получим : 

X^2 4*x + 6 = 0; X^2 8*x − 4 = 0; X^2 + 5*x + 2 = 0;

X^2 + 3,5*x − 5,5 = 0.

Как можно увидеть из примеров, даже уравнения содержащие дроби, можно привести к приведённому виду.

Использование теоремы Виета

Дальше мы должны воспользоваться теоремой Виета на практике, для этого нужно решить несколько квадратных уравнений без применения основной формулы:

X^2 5*x + 6 = 0 ⇒ x1 + x2 = − (−5) = 5; x1*x2 = 6;

получаем корни: x1 = 2; x2 = 3;

X^2 + 6*x + 8 = 0 ⇒ x1 + x2 = −6; x1*x2 = 8;

в результате получаем корни: x1 = -2 ; x2 = -4;

X^2 + 5*x + 4 = 0 ⇒ x1 + x2 = −5; x1*x2 = 4;

получаем корни : x1 = −1; x2 = −4.

Значение теоремы Виета

Теорема Виета позволяет нам решить любое квадратное приведённое уравнение практически за секунды. На первый взгляд это кажется достаточно сложной задачей, но после 5 10 уравнений, можно научиться видеть корни сразу.

Из приведённых примеров, и пользуясь теоремой, видно как можно значительно упростить решение квадратных уравнений, ведь используя эту теорему, можно решить квадратное уравнение практически без сложных расчётов и вычисления дискриминанта, а как известно чем меньше расчётов, тем сложнее допустить ошибку, что немаловажно.

Во всех примерах мы использовали это правило, опираясь на два важных предположения:

— приведённое уравнение, т.е. коэффициент при старшей степени равен единицы (это условие легко избежать. Можно использовать неприведенный вид уравнения, тогда будут допустимы следующие утверждения x1+x2=-b/a; x1*x2=c/a, но обычно сложнее решать :))

— когда уравнение будет иметь два различных корня. Мы предполагаем что неравенство верно и дискриминант строго больше нуля.

Поэтому, мы можем составить общий алгоритм решения по теореме Виета.

Общий алгоритм решения по теореме Виета

— Приводим  квадратное уравнение к приведённому виду, если уравнение дано нам в неприведённом виде. Когда коэффициенты в квадратном уравнении, которое раньше мы представили как приведённое,  получились дробными( не десятичными ), то в этом случае следует решать наше уравнение через дискриминант.

Также бывают случаи когда возврат к начальному уравнению позволяет нам работать с “удобными” числами.

— В случае когда коэффициенты уравнения являются целыми, следует решать уравнение по теореме Виета.

Примечание : Если в течении нескольких секунд, нам не удаётся найти корни по теореме Виета, то следует решать через дискриминант, это зачастую бывает быстрее.

Нужна помощь в учебе?

Предыдущая тема: Решение задач с помощью квадратных уравнений: алгоритм и примеры
Следующая тема:&nbsp&nbsp&nbspРешение дробных рациональных уравнений: схема и примеры

Все неприличные комментарии будут удаляться.

www.nado5.ru

Применение теоремы Виета.

Часто требуется найти сумму квадратов  (x₁²+x₂²)  или сумму кубов (x₁³+x₂³) корней квадратного уравнения, реже — сумму обратных значений квадратов корней или сумму арифметических квадратных корней из корней квадратного уравнения:

Помочь в этом может теорема Виета:

Сумма корней приведенного квадратного уравнения x²+px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

x₁+x₂=-p;  x₁∙x₂=q.

Выразим через p и q:

1) сумму квадратов корней уравнения x²+px+q=0;

2) сумму кубов корней уравнения x²+px+q=0.

Решение.

1) Выражение x₁²+x₂²  получится, если взвести в квадрат обе части равенства x₁+x₂=-p;

(x₁+x₂)²=(-p)²;  раскрываем скобки: x₁²+2x₁x₂+ x₂²=p²;  выражаем искомую сумму: x₁²+x₂²=p²-2x₁x₂=p²-2q. Мы получили полезное равенство: x₁²+x₂²=p²-2q.

2) Выражение x₁³+x₂³ представим по формуле суммы кубов в виде:

(x₁³+x₂³)=(x₁+x₂)(x₁²-x₁x₂+x₂²)=-p·(p²-2q-q)=-p·(p²-3q).

Еще одно полезное равенство: x₁³+x₂³=-p·(p²-3q).

Примеры.

3) x²-3x-4=0. Не решая уравнение, вычислите значение выражения  x₁²+x₂² .

Решение.

По теореме Виета сумма корней этого приведенного квадратного уравнения

x₁+x₂=-p=3, а произведение x₁∙x₂=q=-4. Применим полученное нами (в примере 1) равенство:

x₁²+x₂²=p²-2q. У нас -p=x₁+x₂=3 → p²=3²=9; q=x₁x₂=-4. Тогда x₁²+x₂²=9-2·(-4)=9+8=17.

Ответ: x₁²+x₂²=17.

4) x²-2x-4=0. Вычислить: x₁³+x₂³.

Решение.

По теореме Виета сумма корней этого приведенного квадратного уравнения x₁+x₂=-p=2, а произведение x₁∙x₂=q=-4. Применим полученное нами (в примере 2) равенство: x₁³+x₂³=-p·(p²-3q)=2·(2²-3·(-4))=2·(4+12)=2·16=32.

Ответ:  x₁³+x₂³=32.

Вопрос: а если нам дано не приведенное квадратное уравнение? Ответ: его всегда можно «привести», разделив почленно на первый коэффициент.

5) 2x²-5x-7=0. Не решая, вычислить: x₁²+x₂².

Решение. Нам дано полное квадратное уравнение. Разделим обе части равенства на 2 (первый коэффициент) и получим приведенное квадратное уравнение: x

2-2,5x-3,5=0.

По теореме Виета сумма корней равна 2,5; произведение корней равно -3,5.

Решаем так же, как пример 3), используя равенство: x₁²+x₂²=p²-2q.

x₁²+x₂²=p²-2q=2,5²-2∙(-3,5)=6,25+7=13,25.

Ответ: x₁²+x₂²=13,25.

6) x²-5x-2=0. Найти:

Преобразуем это равенство и, заменив по теореме Виета сумму корней через -p, а произведение корней через q, получим еще одну полезную формулу. При выводе формулы использовали равенство 1): x₁²+x₂²=p²-2q.

В нашем примере  x

1+x₂=-p=5; x₁∙x₂=q=-2. Подставляем эти значения  в полученную формулу:

7) x²-13x+36=0. Найти:

Преобразуем эту сумму и получим формулу, по которой можно будет находить сумму арифметических квадратных корней из корней квадратного уравнения.

У нас  x₁+x₂=-p=13; x₁∙x₂=q=36. Подставляем эти значения в выведенную формулу:

Совет: всегда проверяйте возможность нахождения корней квадратного уравнения по подходящему способу, ведь 4 рассмотренные полезные формулы позволяют быстро выполнить задание, прежде всего, в тех случаях, когда дискриминант — «неудобное» число. Во всех простых случаях находите корни и оперируйте ими. Например, в последнем примере подберем корни по теореме Виета: сумма корней должна быть равна

13, а произведение корней 36. Что это за числа? Конечно, 4 и 9. А теперь считайте сумму квадратных корней из этих чисел: 2+3=5. Вот так то!

 

 

www.mathematics-repetition.com

No related posts.