Модули свойства – Модуль числа — Youclever.org

Определение модуля

Свойства модуля

1. Модули противоположных чисел равны
2. Квадрат модуля числа равен квадрату этого числа
3. Квадратный корень из квадрата числа есть модуль этого числа
4. Модуль числа есть число неотрицательное
5. Постоянный положительный множитель можно выносить за знак модуля	,
6. Если , то
7. Модуль произведения двух (и более) чисел равен произведению их модулей

Числовые промежутки

Окрестность точки Пусть х_о—любое действительное число (точка на числовой прямой). Окрестностью точки хо называется любой интервал (a; b), содержащий точку x0. В частности, интервал (х_о-ε,х_о+ε), где ε >0, называется ε-окрестностью точки х_о. Число х_о называется центром.

3 ВОПРОС понятие функции Функцией называют такую зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение перемен­ной у.

Переменную х называют независимой переменной или аргументом.

Переменную у называют зависимой переменной.

Способы задания функции

Табличный способ.  заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.

При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. Для этого используют способ интерполяции.

Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.

Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.

Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами — наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом.

Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Это приводит к следующему способу задания функции.

Аналитический способ. Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у = f (х),  где f (х) — некоторое выражение с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически.

      Для аналитически заданной функции иногда не указывают явно область определения функции. В таком случае подразумевают, что область определения функции у = f (х) совпадает с областью определения выражения f (х), т. е. с множеством тех значений х, при которых выражение f (х) имеет смысл.

Естественная область определения функции

Область определения функции f – это множество X всех значений аргумента x, на котором задается функция.

Для обозначения области определения функции f используется краткая запись вида D(f). 

явное неявное параметрическое задание функции

Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).

Под неявным заданием

 функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.

Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.

studfiles.net

Модуль вещественного числа и его свойства

Определение. Модуль вещественного числа — это само число , если , и противоположное число , если .

   

Свойства модуля

1. ,

.

2. .

3. — это расстояние между точками и на числовой оси.

Доказательство.

1. Докажем сначала, что .

Рассмотрим несколько случаев (в этих случаях по-разному раскрываются модули):

   

Левая часть неравенства получается, если в доказанном неравенстве заменить на , — на , а затем — на , а — на .

2.

   

hijos.ru

Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Алгебра

Абсолютная величина (модуль) действительного числа

      Определение. Абсолютной величиной (модулем) действительного числа   a   называют неотрицательное число   | a | ,   которое определяется по формуле:

      Так, например,

| 5 | = 5,     | – 2 | = 2,    
| 0 | = 0.

Свойства модуля

      Если   x   и   y   – действительные числа, то справедливы равенства:

      Кроме того, справедливо соотношение:

      В то же время справедливы неравенства:

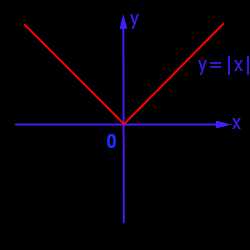
График функции   y = | x |

      График функции   y = | x |    имеет следующий вид:

Простейшее уравнение с модулем

      Рассмотрим простейшее уравнение с модулем, имеющее вид:

| f (x) | = g(x) .

      Поскольку

то данное уравнение эквивалентно совокупности двух систем:

      Для решения исходного уравнения остается лишь решить две этих системы и объединить полученные ответы.

      Замечание. Решение неравенств с модулями осуществляется аналогично.

      Желающим более глубоко освоить тему «Модули», мы рекомендуем изучить наши учебные пособия: «Уравнения и неравенства с модулями» и «Фигуры на координатной плоскости, заданные неравенствами».

      На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10

      Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит

      У нас также для школьников организованы

МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»

www.resolventa.ru

Общие модули в 1С 8.3 и 8.2

Общие модули 1С — объект метаданных конфигурации 1С 8.3 и 8.2, который хранит в себе программный код, который часто вызывается в конфигурации. Функцию/процедуру можно вызвать из любого места конфигурации (если она экспортная).

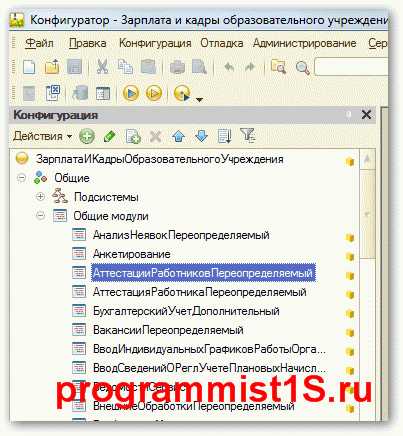
Как использовать общий модуль

Хороший тон — поместить процедуру или функцию  в общий модуль, если она вызывается в более чем одном месте. Во-первых, если процедура корректируется, её надо править только в одном месте. Во-вторых, этим достигается больший порядок в коде.

Типичный пример общего модуля — обработка проведения по какому-то регистру, получение количества разницы рабочих дней, пересчет курсов валют, пересчет количества/цены/суммы в табличной части и другие функции.

Свойства общих модулей

Одно из основных особенностей общих модулей от других модулей — нельзя объявлять общие переменные.

Получите 267 видеоуроков по 1С бесплатно:

Рассмотрим подробнее палитру свойств общего модуля:

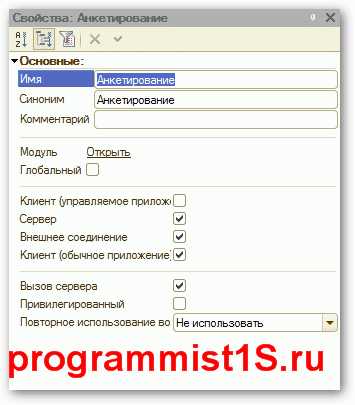
• Глобальный — если флаг установлен, функции и процедуры из этого модуля становятся доступны в глобальном контексте. Т.е. их можно вызвать в любом месте конфигурации, обращаясь без названия общего модуля. Однако добавляется условие — название процедур и функций в этом общем модуле должны быть уникальны в рамках глобального контекста.
• Сервер — процедуры и функции данного общего модуля могут быть выполнены на сервере.
• Внешнее соединение — программные коды данного общего модуля могут быть выполнены при подключении внешним источником (например, COM).
• Клиент (управляемое приложение) — процедуры и функции данного общего модуля могут быть использованы в толстом клиенте в режиме управляемого приложения.
• Клиент (обычное приложение) — программные коды данного общего модуля могут быть использованы в толстом клиенте в режиме обычного приложения.
• Вызов сервера  — флаг, разрешающий на клиенте использовать процедуры и функции из этого общего модуля.
• Привилегированный — если установлена Истина, в этом общем модуле будет отключена проверка прав доступа.
• Повторное использование — определяет настройки возвращаемых значений, если опция включена, то после первого выполнения система запомнит значение для данных входных параметров и будет возвращать уже готовое значение. Может принимать следующие значения: не используется — отключение, на время вызова — на время выполнения определенной процедуры, на время сеанса — пока пользователь не закрыл сеанс (программу).

Если Вы начинаете изучать 1С программирование, рекомендуем наш бесплатный курс (не забудьте подписаться на YouTube — регулярно выходят новые видео):

К сожалению, мы физически не можем проконсультировать бесплатно всех желающих, но наша команда будет рада оказать услуги по внедрению и обслуживанию 1С. Более подробно о наших услугах можно узнать на странице Услуги 1С или просто позвоните по телефону +7 (499) 350 29 00. Мы работаем в Москве и области.

programmist1s.ru

Свойства модуля и аргумента комплексного числа

Свойства модуля и аргумента комплексного числа:

1°. $|\bar z| = |z|$

Модуль числа, сопряженного числу $z$ равен модулю самого комплексного числа $z$.

2°. $z \cdot \bar z = |z|^2$

Произведение комплексного числа на сопряжённое ему равно квадрату модуля этого комплексного числа.

3°. $\mathrm{arg} \bar z = -\mathrm{arg} z$, $(\mathrm{arg} z \ne \pi)$

Аргумент числа, сопряжённого комплексному числу $z$ равен отрицательному аргументу комплексного числа $z$.

4°. $\mathrm{max} \{|x|, |y|\} \le |z| \le |x| + |y|$

Модуль комплексного числа больше либо равен наибольшему из модулей его действительной и мнимой части и не превосходит суммы этих модулей.

5°. $|z_1| — |z_2| \le |z_1 + z_2| \le |z_1| + |z_2|$

Модуль суммы двух комплексных чисел больше либо равен разности модулей этих чисел и меньше либо равен сумме модулей этих чисел.

6°. $|z_1 \cdot z_2| = |z_1| \cdot |z_2|$, $\mathrm{Arg} (z_1 \cdot z_2) = \mathrm{Arg} z_1 + \mathrm{Arg} z_2$

Модуль произведения двух комплексных чисел равен произведению модулей этих комплексных чисел, при этом аргумент произведения этих двух чисел равен сумме аргументов этих чисел.

7°. $\left| \frac{z_1}{z_2} \right| = \frac{|z_1|}{|z_2|}$, $\mathrm{Arg} \left( \frac{z_1}{z_2} \right) = \mathrm{Arg} z_1 — \mathrm{Arg} z_2$

Модуль частного двух комплексных чисел равен частности модулей этих комплексных чисел, при этом аргумент частности этих двух чисел равен разности аргументов этих чисел.

8°. $\left| z^n \right| = |z|^n$, $\mathrm{Arg} \left( z^n \right) = n \cdot \mathrm{Arg} z$

Аргумент комплексного числа $z$ в $n$-ой степени равен произведению показателя степени $n$ на аргумент комплексного числа.

9°. $\left| \sqrt[n]{z} \right| = \sqrt[n]{|z|}$, $\mathrm{Arg} \left( \sqrt[n]{z} \right) = \frac{\mathrm{Arg} z}{n}$.

Модуль корня n-ой степени комплексного числа z равен частномум аргумента комплексного числа и показателя степени $n$.

Теорема. Множество комплексных чисел $C$ есть метрическое пространство с метрикой $p(z_1, z_2) = |z_1 — z_2|$.

Следствие. Для множества комлексных чисел $C$ можно ввести все понятия, характерные для метрических пространств:

1) $\varepsilon$ — окружность с центром в точке $z_0$: $\bar u (z_0, \varepsilon) = \{z \in C: \; |z-z_0|< \varepsilon\}$;

2) проколотая $\varepsilon$ — окружность в точке $z_0$: $\bar u (z_0, \varepsilon) = \{z \in C: \; 0<|z-z_0|< \varepsilon\}$;

3) $G \subset C$, понятия внутренней, внешней, граничной точек множества $G$;

4) понятия открытого, замкнутого, связанного множеств.

Определение (предела последовательности $(z_n)$). Число $z_0$ называется пределом последовательности $(z_n)$ $z_0 = \lim_{n \to \infty} z_n$, если $\lim_{n \to \infty} p(z_n, z_0) = 0$ или $\lim_{n \to \infty} |z-z_0| = 0$.

Из соответствующих свойств модуля комплексного числа следует, что сходимость последовательности $(z_n)$ к точке $z_0$ равносильна содимости последовательности $(\mathrm{Re} z_n)$ к $\mathrm {Re} z_0$ и другой последовательнсти $(\mathrm{Im} z_n)$ к $\mathrm{Im} z_0$. Поэтому справедлива следующая теорема.

Теорема (Больцано-Вейерштрасса). Из любой ограниченной последовательности комплексных чисел можно выделить сходящуюся подпоследовательность.

Теорема (Критерий Коши). Для сходимости последовательности $(z_n)$ необходимо и достаточно, чтобы она была фундаментальной, то есть $\forall \varepsilon > 0 \; \exists n_0 \; \forall n, m ((n \le n_0) \& (m \le n_0) \rightarrow |z_n — z_m| < \varepsilon)$.

mathematike.ru

Модуль комплексного числа, формула и примеры

Если рассмотреть плоскость с прямоугольной системой координат, то любому комплексному числу можно сопоставить точку на этой плоскости с соответствующими координатами: , и радиус-вектор комплексного числа, т.е. вектор, соединяющий начало координат с точкой на плоскости, соответствующей числу.

Данная плоскость называется комплексной. Действительные числа располагаются на горизонтальной (вещественной) оси, мнимые части – на вертикальной (мнимой) оси.

Таким образом, модуль вычисляется как квадратный корень из суммы квадратов действительной и мнимой частей комплексного числа.

Если является действительным числом, то его модуль равен абсолютной величине этого действительного числа.

Например.

Свойства модуля

1. Модуль комплексного числа не отрицателен: , при этом в том и только том случае, если ;
2. Модуль суммы двух комплексных чисел меньше либо равен сумме модулей: ;
3. Модуль произведения двух комплексных чисел равен произведению модулей: , в том числе ;
4. Модуль частного двух комплексных чисел равен частному модулей: ;
5. , т.е. модуль разности комплексных чисел равен расстоянию между этими числами на комплексной плоскости.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Модуль числа Википедия

График вещественной функции Модуль |z|{\displaystyle |z|} и другие характеристики комплексного числа z{\displaystyle z}

Абсолю́тная величина́, или мо́дуль числа x{\displaystyle x} (в математике) — неотрицательное число, определение которого зависит от типа числа x{\displaystyle x}. Обозначается: |x|{\displaystyle |x|}.

В случае вещественного x{\displaystyle x} абсолютная величина есть непрерывная кусочно-линейная функция, определённая следующим образом:

 |x|={  x,x⩾0−x, x<0{\displaystyle \ |x|={\begin{cases}\ \ x,&x\geqslant 0\\-x,&\ x<0\end{cases}}}

Обобщением этого понятия является модуль комплексного числа z=x+iy,{\displaystyle z=x+iy,} также иногда называемый абсолютной величиной^[1]. Он определяется по формуле:

|z|=|x+iy|=x2+y2{\displaystyle |z|=|x+iy|={\sqrt {x^{2}+y^{2}}}}

Содержание

• 1 Основные свойства
  • 1.1 Вещественные числа
  • 1.2 Комплексные числа
• 2 Алгебраические свойства
• 3 История
• 4 В языках программирования
• 5 Обобщение
• 6 См. также
• 7 Примечания

Основные свойства[

ru-wiki.ru