Случайные величины
Учреждение образования «Белорусская государственная
сельскохозяйственная академия»
Кафедра высшей математики
Методические указания
по изучению темы «Случайные величины» студентами бухгалтерского факультета заочной формы получения образования (НИСПО)
Горки, 2013
Случайные величины
Дискретные и непрерывные случайные величины
Одним из основных понятий в теории вероятностей является понятие случайной величины. Случайной величиной называется величина, которая в результате испытания из множества возможных своих значений принимает только одно, причём заранее неизвестно, какое именно.
Случайные величины бывают
Случайные величины обозначаются заглавными буквами латинского алфавита X, Y, Z и т.д. Возможные значения случайных величин обозначаются соответствующими малыми буквами.
Запись означает «вероятность того, что случайная величинаХ примет значение, равное 5, равна 0.28».
Пример 1. Один раз бросают игральный кубик. При этом могут выпасть цифры от 1 до 6, обозначающие число очков. Обозначим случайную величину Х={число выпавших очков}. Эта случайная величина в результате испытания может принять только одно из шести значений: 1, 2, 3, 4, 5 или 6. Следовательно, случайная величина Х есть ДСВ.
Пример 2. При бросании камня он пролетает некоторое расстояние. Обозначим случайную величину X={расстояние полёта камня}. Эта случайная величина может принять любое, но только одно, значение из некоторого промежутка. Следовательно, случайная величина Х есть НСВ.
Закон распределения дискретной случайной величины
Дискретная случайная величина характеризуется значениями, которые она может принимать, и вероятностями, с которыми эти значения принимаются. Соответствие между возможными значениями дискретной случайной величины и соответствующими им вероятностями называется законом распределения дискретной случайной величины.
Если известны все возможные значения случайной величины
Закон
распределения ДСВ можно изобразить
графически, если в прямоугольной системе
координат изобразить точки  ,
, ,
…,
,
…, и
соединить их отрезками прямых линий.
Полученная фигура называется
многоугольником распределения.
и
соединить их отрезками прямых линий.
Полученная фигура называется
многоугольником распределения.
Пример 3. В зерне, предназначенном для очистки, содержится 10% сорняков. Наугад отобраны 4 зерна. Обозначим случайную величину X={число сорняков среди четырёх отобранных}. Построить закон распределения ДСВ Х и многоугольник распределения.
Решение. По условию примера . Тогда:
;
;
;
;
.
Запишем закон распределения ДСВ Х в виде таблицы и построим многоугольник распределения:
Х | 0 | 1 | 2 | 3 | 4 |
0.6561 | 0.2916 | 0.0486 | 0.0036 | 0.0001 |
Математическое ожидание дискретной случайной величины
Пусть известен закон распределения ДСВ Х:
Математическим ожиданием ДСВ Х называется сумма произведений каждого значения этой величины на соответствующую вероятность: .
Математическое ожидание случайной величины приближённо равно среднему арифметическому всех её значений. Поэтому в практических задачах часто за математическое ожидание принимают среднее значение этой случайной величины.
Пример 8. Стрелок выбивает 4, 8, 9 и 10 очков с вероятностями 0.1, 0.45, 0.3 и 0.15. Найти математическое ожидание числа очков при одном выстреле.
Решение. Обозначим случайную величину X={число выбитых очков}. Тогда . Таким образом, ожидаемое среднее значение числа выбитых очков при одном выстреле равно 8.2, а при 10 выстрелах – 82.
Основными свойствами математического ожидания являются:
 .
.
 .
.
 ,
где
,.
,
где
,.
 .
.
 ,
где Х и Y – независимые случайные величины.
,
где Х и Y – независимые случайные величины.
Разность называетсяотклонением случайной величины Х от её математического ожидания. Эта разность является случайной величиной и её математическое ожидание равно нулю, т.е. .
Дисперсия дискретной случайной величины
Для характеристики случайной величины, кроме математического ожидания, используется и дисперсия, которая даёт возможность оценить рассеяние (разброс) значений случайной величины около её математического ожидания. При сравнении двух однородных случайных величин с равными математическими ожиданиями «лучшей» считается та величина, которая имеет меньший разброс, т.е. меньшую дисперсию.
Дисперсией случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от её математического ожидания: .
В практических задачах для вычисления дисперсии используют равносильную формулу .
Основными свойствами дисперсии являются:


 .
.
 ,
где Х и Y – независимые случайные величины.
,
где Х и Y – независимые случайные величины.
Дисперсия характеризует разброс случайной величины около её математического ожидания и, как видно из формулы, измеряется в квадратных единицах по сравнению с единицами самой случайной величины. Поэтому для согласования единиц измерения разброса случайной величины с единицами измерения самой величины вводится среднее квадратическое отклонение .
Пример 9. Найти дисперсию и среднее квадратическое отклонение ДСВ Х, заданной законом распределения:
-5
2
3
4

0.4
0.3
0.1
0.2
Решение. Дисперсия ДСВ Х вычисляется по формуле
.
Найдём математическое ожидание данной
случайной величины:
.
Запишем закон распределения для случайной
величины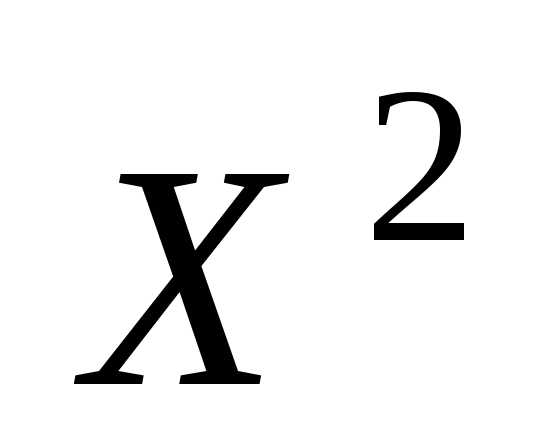 :
:

25
4
9
16

0.4
0.3
0.1
0.2
Тогда ,
, .
Вопросы для самоконтроля знаний
Что называется случайной величиной?
Какая случайная величина называется дискретной, а какая – непрерывной?
Что называется законом распределения дискретной случайной величины?
Что называется математическим ожиданием дискретной случайной величины и каковы его основные свойства?
Что называется отклонением случайной величины от её математического ожидания?
Что называется дисперсией дискретной случайной величины и каковы её основные свойства?
Для чего вводится среднее квадратическое отклонение и как оно вычисляется?
Задания для самостоятельной работы
В партии из 10 деталей имеется 8 стандартных. Наугад взяты 4 детали. Случайная величина Х={число стандартных деталей среди взятых}. Составить закон распределения этой случайной величины и найти .
Всхожесть семян пшеницы составляет 90%. Наугад взяты и посеяны 3 зерна. Случайная величина Х={число взошедших зёрен}. Составить закон распределения этой случайной величины и найти .
Стрелок выстрелил по мишени 4 раза. Вероятность поражения мишени при каждом выстреле равна 0.7. Случайная величина Х={число попаданий в мишень}. Составить закон распределения этой случайной величины и найти .
Рабочий обслуживает 3 станка. Вероятность выхода из строя в течение смены для первого станка равна 0.4, для второго – 0.5 и для третьего – 0.3. Случайная величина Х={число станков, вышедших из строя в течение смены}. Составить закон распределения этой случайной величины и найти .
Монета подбрасывается 4 раза. Случайная величина Х={число выпадений «герба»}. Составить закон распределения этой случайной величины и найти .
7
studfiles.net
Дискретные двумерные случайные величины. Пример решения задачи на Викиматик
Довольно часто при изучении случайных величин приходится иметь дело с двумя, тремя и даже большим числом случайных величин. Например, двумерной случайной величиной $\left(X,\ Y\right)$ будет описываться точка попадания снаряда, где случайные величины $X,\ Y$ абсцисса и ордината соответственно. Успеваемость наудачу взятого студента в период сессии характеризуется $n$-мерной случайной величиной $\left(X_1,\ X_2,\ \dots ,\ X_n\right)$, где случайные величины $X_1,\ X_2,\ \dots ,\ X_n$ — это оценки, проставленные в зачетной книжке по различным дисциплинам.
Набор $n$ случайных величин $\left(X_1,\ X_2,\ \dots ,\ X_n\right)$ называется случайным вектором. Мы ограничимся рассмотрением случая $\left(X,\ Y\right)$.
Пусть $X$ — дискретная случайная величина с возможными значениями $x_1,x_2,\ \dots ,\ x_n$, а $Y$ — дискретная случайная величина с возможными значениями $y_1,y_2,\ \dots ,\ y_n$.
Тогда дискретная двумерная случайная величина $\left(X,\ Y\right)$ может принимать значения $\left(x_i,\ y_j\right)$ с вероятностями $p_{ij}=P\left(\left(X=x_i\right)\left(Y=y_j\right)\right)=P\left(X=x_i\right)P\left(Y=y_j|X=x_i\right)$. Здесь $P\left(Y=y_j|X=x_i\right)$ — это условная вероятность того, что случайная величина $Y$ примет значение $y_j$ при условии, что случайная величина $X$ приняла значение $x_i$.
Вероятность того, что случайная величина $X$ примет значение $x_i$, равна $p_i=\sum_j{p_{ij}}$. Вероятность того, что случайная величина $Y$ примет значение $y_j$, равна $q_j=\sum_i{p_{ij}}$.
Если считать, что событие $Y=y_j$ произошло, то распределение случайной величины $X$ при условии $Y=y_j$ называется условным распределением случайной величины $X$ при условии $Y=y_j$. Тогда:
$$P\left(X=x_i|Y=y_j\right)={{P\left(\left(X=x_i\right)\left(Y=y_j\right)\right)}\over {P\left(Y=y_j\right)}}={{p_{ij}}\over {q_j}}.$$
Если считать, что событие $X=x_i$ произошло, то распределение случайной величины $Y$ при условии $X=x_i$ называется условным распределением случайной величины $Y$ при условии $X=x_i$. Тогда:
$$P\left(Y=y_j|X=x_i\right)={{P\left(\left(X=x_i\right)\left(Y=y_j\right)\right)}\over {P\left(X=x_i\right)}}={{p_{ij}}\over {p_i}}.$$
Пример 1. Задано распределение двумерной случайной величины:
$\begin{array}{|c|c|}
\hline
X\backslash Y & 2 & 3 \\
\hline
-1 & 0,15 & 0,25 \\
\hline
0 & 0,28 & 0,13 \\
\hline
1 & 0,09 & 0,1 \\
\hline
\end{array}$
Определим законы распределения случайных величин $X$ и $Y$. Найдем условные распределения случайной величины $X$ при условии $Y=2$ и случайной величины $Y$ при условии $X=0$.
Заполним следующую таблицу:
$\begin{array}{|c|c|}
\hline
X\backslash Y & 2 & 3 & p_i & p_{ij}/q_1 \\
\hline
-1 & 0,15 & 0,25 & 0,4 & 0,29 \\
\hline
0 & 0,28 & 0,13 & 0,41 & 0,54 \\
\hline
1 & 0,09 & 0,1 & 0,19 & 0,17 \\
\hline
q_j & 0,52 & 0,48 & 1 & \\
\hline
p_{ij}/p_2 & 0,68 & 0,32 & & \\
\hline
1 & 0,09 & 0,1 \\
\hline
\end{array}$
Поясним, как заполняется таблица. Значения первых трех столбцов первых четырех строк взяты из условия. Сумму чисел $2$-го и $3$-го столбцов $2$-й ($3$-й) строки укажем в $4$-м столбце $2$-й ($3$-й) строки. Сумму чисел $2$-го и $3$-го столбцов $4$-й строки укажем в $4$-м столбце $4$-й строки.
Сумму чисел $2$-й, $3$-й и $4$-й строк $2$-го ($3$-го) столбца запишем в $5$-й строке $2$-го ($3$-го) столбца. Каждое число $2$-го столбца делим на $q_1=0,52$, результат округляем до двух цифр после запятой и пишем в $5$-м столбце. Числа из $2$-го и $3$-го столбцов $3$-й строки делим на $p_2=0,41$, результат округляем до двух цифр после запятой и пишем в последней строке.
Тогда закон распределения случайной величины $X$ имеет следующий вид.
$\begin{array}{|c|c|}
\hline
X & -1 & 0 & 1 \\
\hline
p_i & 0,4 & 0,41 & 0,19 \\
\hline
\end{array}$
Закон распределения случайной величины $Y$.
$\begin{array}{|c|c|}
\hline
Y & 2 & 3 \\
\hline
q_j & 0,52 & 0,48 \\
\hline
\end{array}$
Условное распределение случайной величины $X$ при условии $Y=2$ имеет следующий вид.
$\begin{array}{|c|c|}
\hline
X & -1 & 0 & 1 \\
\hline
p_{ij}/q_1 & 0,29 & 0,54 & 0,17 \\
\hline
\end{array}$
Условное распределение случайной величины $Y$ при условии $X=0$ имеет следующий вид.
$\begin{array}{|c|c|}
\hline
Y & 2 & 3 \\
\hline
p_{ij}/p_2 & 0,68 & 0,32 \\
\hline
\end{array}$
Пример 2. Имеем шесть карандашей, среди которых два красных. Раскладываем карандаши в две коробки. В первую кладут $2$ штуки, а во вторую тоже два. $X$ — количество красных карандашей в первой коробке, a $Y$ — во второй. Написать закон распределения системы случайных величин $(X,\ Y)$.
Пусть дискретная случайная величина $X$ — количество красных карандашей в первой коробке, а дискретная случайная величина $Y$ — количество красных карандашей во второй коробке. Возможные значения случайных величин $X,\ Y$ соответственно $X:0,\ 1,\ 2$, $Y:0,\ 1,\ 2$. Тогда дискретная двумерная случайная величина $\left(X,\ Y\right)$ может принимать значения $\left(x,\ y\right)$ с вероятностями $P=P\left(\left(X=x\right)\times \left(Y=y\right)\right)=P\left(X=x\right)\times P\left(Y=y|X=x\right)$, где $P\left(Y=y|X=x\right)$ — условная вероятность того, что случайная величина $Y$ примет значение $y$ при условии, что случайная величина $X$ приняла значение $x$. Изобразим соответствие между значениями $\left(x,\ y\right)$ и вероятностями $P\left(\left(X=x\right)\times \left(Y=y\right)\right)$ в виде следующей таблицы.
$\begin{array}{|c|c|}
\hline
X\backslash Y & 0 & 1 & 2 \\
\hline
0 & {{1}\over {15}} & {{4}\over {15}} & {{1}\over {15}} \\
\hline
1 & {{4}\over {15}} & {{4}\over {15}} & 0 \\
\hline
2 & {{1}\over {15}} & 0 & 0 \\
\hline
\end{array}$
По строкам такой таблицы указываются значения $X$, а по столбцам значения $Y$, тогда вероятности $P\left(\left(X=x\right)\times \left(Y=y\right)\right)$ указываются на пересечении соответствующей строки и столбца. Рассчитаем вероятности, используя классическое определение вероятности и теорему произведения вероятностей зависимых событий.
$$P\left(\left(X=0\right)\left(Y=0\right)\right)={{C^2_4}\over {C^2_6}}\cdot {{C^2_2}\over {C^2_4}}={{6}\over {15}}\cdot {{1}\over {6}}={{1}\over {15}};$$
$$P\left(\left(X=0\right)\left(Y=1\right)\right)={{C^2_4}\over {C^2_6}}\cdot {{C^1_2\cdot C^1_2}\over {C^2_4}}={{6}\over {15}}\cdot {{2\cdot 2}\over {6}}={{4}\over {15}};$$
$$P\left(\left(X=0\right)\left(Y=2\right)\right)={{C^2_4}\over {C^2_6}}\cdot {{C^2_2}\over {C^2_4}}={{6}\over {15}}\cdot {{1}\over {6}}={{1}\over {15}};$$
$$P\left(\left(X=1\right)\left(Y=0\right)\right)={{C^1_2\cdot C^1_4}\over {C^2_6}}\cdot {{C^2_3}\over {C^2_4}}={{2\cdot 4}\over {15}}\cdot {{3}\over {6}}={{4}\over {15}};$$
$$P\left(\left(X=1\right)\left(Y=1\right)\right)={{C^1_2\cdot C^1_4}\over {C^2_6}}\cdot {{C^1_1\cdot C^1_3}\over {C^2_4}}={{2\cdot 4}\over {15}}\cdot {{1\cdot 3}\over {6}}={{4}\over {15}};$$
$$P\left(\left(X=2\right)\left(Y=0\right)\right)={{C^2_2}\over {C^2_6}}\cdot {{C^2_4}\over {C^2_4}}={{1}\over {15}}\cdot 1={{1}\over {15}}.$$
Поскольку в законе распределения (полученной таблице) все множество событий образует полную группу событий, то сумма вероятностей должна быть равна 1. Проверим это:
$$\sum_{i,\ j}{p_{ij}}={{1}\over {15}}+{{4}\over {15}}+{{1}\over {15}}+{{4}\over {15}}+{{4}\over {15}}+{{1}\over {15}}=1.$$
Функция распределения двумерной случайной величины
Функцией распределения двумерной случайной величины $\left(X,\ Y\right)$ называется функция $F\left(x,\ y\right)$, которая для любых действительных чисел $x$ и $y$ равна вероятности совместного выполнения двух событий $\left\{X < x\right\}$ и $\left\{Y < y\right\}$. Таким образом, по определению
$$F\left(x,\ y\right)=P\left\{X < x,\ Y < y\right\}.$$
Для дискретной двумерной случайной величины функция распределения находится путем суммирования всех вероятностей $p_{ij}$, для которых $x_i < x,\ y_j < y$, то есть
$$F\left(x,\ y\right)=\sum_{x_i < x}{\sum_{y_j < y}{p_{ij}}}.$$
Свойства функции распределения двумерной случайной величины.
1. Функция распределения $F\left(x,\ y\right)$ является ограниченной, то есть $0\le F\left(x,\ y\right)\le 1$.
2. $F\left(x,\ y\right)$ не убывающая для каждого из своих аргументов при фиксированном другом, то есть $F\left(x_2,\ y\right)\ge F\left(x_1,\ y\right)$ при $x_2>x_1$, $F\left(x,\ y_2\right)\ge F\left(x,\ y_1\right)$ при $y_2>y_1$.
3. Если хотя бы один из аргументов принимает значение $-\infty $, то функция распределения будет равна нулю, то есть $F\left(-\infty ,\ y\right)=F\left(x,\ -\infty \right),\ F\left(-\infty ,\ -\infty \right)=0$.
4. Если оба аргумента принимают значение $+\infty $, то функция распределения будет равна $1$, то есть $F\left(+\infty ,\ +\infty \right)=1$.
5. В том случае, когда ровно один из аргументов принимает значение $+\infty $, функция распределения $F\left(x,\ y\right)$ становится функцией распределения случайной величины, соответствующей другому элементу, то есть $F\left(x,\ +\infty \right)=F_1\left(x\right)=F_X\left(x\right),\ F\left(+\infty ,\ y\right)=F_y\left(y\right)=F_Y\left(y\right)$.
6. $F\left(x,\ y\right)$ является непрерывной слева для каждого из своих аргументов, то есть
$${\mathop{lim}_{x\to x_0-0} F\left(x,\ y\right)\ }=F\left(x_0,\ y\right),\ {\mathop{lim}_{y\to y_0-0} F\left(x,\ y\right)\ }=F\left(x,\ y_0\right).$$
Пример 3. Пусть дискретная двумерная случайная величина $\left(X,\ Y\right)$ задана рядом распределения.
$\begin{array}{|c|c|}
\hline
X\backslash Y & 0 & 1 \\
\hline
0 & {{1}\over {6}} & {{2}\over {6}} \\
\hline
1 & {{2}\over {6}} & {{1}\over {6}} \\
\hline
\end{array}$
Тогда функция распределения:
$F(x,y)=\left\{\begin{matrix}
0,\ при\ x\le 0,\ y\le 0 \\
0,\ при\ x\le 0,\ 0 < y\le 1 \\
0,\ при\ x\le 0,\ y>1 \\
0,\ при\ 0 < x\le 1,\ y\le 0 \\
{{1}\over {6}},\ при\ 0 < x\le 1,\ 0 < y\le 1 \\
{{1}\over {6}}+{{2}\over {6}}={{1}\over {2}},\ при\ 0 < x\le 1,\ y>1 \\
0,\ при\ x>1,\ y\le 0 \\
{{1}\over {6}}+{{2}\over {6}}={{1}\over {2}},\ при\ x>1,\ 0 < y\le 1 \\
{{1}\over {6}}+{{2}\over {6}}+{{2}\over {6}}+{{1}\over {6}}=1,\ при\ x>1,\ y>1 \\
\end{matrix}\right.$
wikimatik.ru
Примеры распределений дискретных случайных величин — Студопедия.Нет
Биномиальное распределение
, , ,
, .
Распределение Пуассона
, , , .
Примеры распределений непрерывных случайных величин
Равномерное распределение
, .
Нормальное распределение (с параметрами )
, , , , .
Запись означает, что случайная величина распределена нормально с параметрами и .
Показательное распределение
, , .
Распределение Релея
, .
Гамма-распределение с параметрами ,
Здесь – гамма-функция:
Пример 1.Изделия испытываются при перегрузочных режимах. Вероятности для каждого изделия пройти испытания, равны 0,8. Испытания заканчиваются после первого же изделия, не выдержавшего испытания.
1. Найти закон распределения вероятностей (ряд распределения) для числа испытаний (случайной величины ).
2. Построить многоугольник распределения.
3. Найти функцию распределения и построить её график.
4. Найти: а) , б) , в) .
Решение.Введем в рассмотрение случайную величину число изделий, прошедших испытания. Очевидно, что случайная величина может принимать значения от 1 и, теоретически, до бесконечности.
Случайная величина примет значение равное , если осуществится событие, состоящее в том, что изделия пройдут испытания, а –е изделие не пройдет. Если – вероятность того, что изделие пройдет испытание, а – вероятность того, что изделие не пройдет испытание, то по теореме умножения вероятностей случайных событий, , где .
Закон распределения вероятностей будет иметь вид
Для построения многоугольника распределения в декартовой прямоугольной системе координат построим точки и соединим их ломаной.
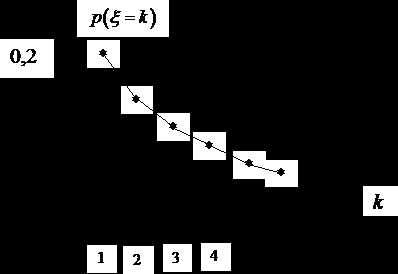
3. Функция распределения
Для решаемой задачи 
Строим график функции распределения
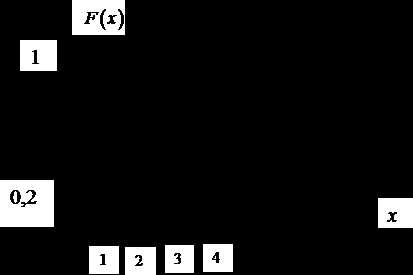
4. а)
.
б) ,
в) .
Пример 2.Дискретная случайная величина может принимать три значения , , . Вероятности этих значений соответственно равны , , . Найти математическое ожидание , дисперсию и среднее квадратическое отклонение .
Решение. Для дискретной случайной величины .
В данном случае .
.
.
Пример 3. Дискретная случайная величина может принимать три значения, два из которых известны , . Вероятности этих значений соответственно равны , . Найти закон распределения случайной величины , если известно её математическое ожидание .
Решение. Обозначим третье возможное значение случайной величины через . Так как для дискретной случайной величины , то . Значение найдем из условия , то есть из уравнения . Решив уравнение, найдем . Составим закон распределения
| 8 | 9 | 10 | |
| 0,4 | 0,5 | 0,1 |
Пример 4. Плотность распределения вероятностей случайной величины задается соотношением
Найти параметр , функцию распределения вероятностей случайной величины , , , и .
Решение. Значение параметра найдем из условия нормировки . Для заданной это условие примет вид . Интегрируя, получим , откуда . Следовательно
.
.
.
.
Пример 5.Поток заявок, поступающих на телефонную станцию, представляет собой простейший поток. Математическое ожидание числа вызовов за час равно 30. Найти вероятность того, что за минуту поступит не менее двух вызовов.
Решение.Так как поток заявок представляет собой простейший поток, то число заявок, поступающих на телефонную станцию, распределено по закону Пуассона
, , ,
с математическим ожиданием .
Следовательно, для решаемой задачи
Обозначим через событие, состоящее в том, что за минуту поступит не менее двух вызовов. Тогда
=
= .
Пример 6.Случайная величина имеет пуассоновское распределение и известно, что ее математическое ожидание и дисперсия связаны соотношением .
Найти вероятность , .
Решение.Известно, что математическое ожидание и дисперсия пуассоновского распределения совпадают и равны значению его пара-метра . Условие задачи приводит к уравнению относительно :
,
решениями которого являются числа , . Последнее значение не может быть параметром пуассоновского распределения в силу положительности параметра. Таким образом, случайная величина имеет ряд распределения
, .
Для искомой вероятности получаем
.
Известно, что . Из этого равенства . Для заданной случайной величины , . Следовательно, .
Пример 7.Время безотказной работы некоторого узла сложного агрегата – экспоненциальная случайная величина со средним . Для увеличения надежности агрегата узел дублируется – ставят параллельно несколько одинаковых, но функционирующих независимо узлов. Сколько узлов следует запараллелить, чтобы с вероятностью, не меньшей чем 0,9, по крайней мере один из них не вышел из строя за 10 часов работы?
Решение.По условию задачи– случайное время безотказной работы узла – имеет экспоненциальное (показательное) распределение. Это означает, что
,
Известно, что математическое ожидание экспоненциальной случайной величины есть величина, обратная параметру: . По условию задачи , следовательно, .
Таким образом, вероятность отказа узла в течение 10 часов будет равна .
Если запараллелено идентичных узлов, то событие {по крайней мере один из узлов не выйдет из строя за 10 часов} является противоположным событию {все узлы выйдут из строя за 10 часов}. Поэтому, . Узлы работают независимо, поэтому по теореме умножения вероятностей независимых событий
.
Искомое значение может быть найдено как наименьшее целое решение неравенства
.
Двумерные случайные величины
Вектор , координаты которого есть случайные величины, заданные на одном и том же вероятностном пространстве, называется случайным вектором, а функция называется функцией распределения вероятности случайного вектора или двумерной случайной величины .
Если координаты вектора – дискретные случайные величины, то называют дискретным случайным вектором.
Закон распределения дискретной двумерной случайной величины представляет собой таблицу
где Так же как и для одномерной дискретной случайной величины должно выполняться условие нормировки .
Зная закон распределения двумерной дискретной случайной величины, можно найти законы распределения составляющих, то есть случайных величин и . Для этого достаточно просуммировать вероятности по строкам и по столбцам соответственно. Знание законов распределения составляющих позволяет найти числовые характеристики составляющих, а также их корреляционный момент.
Если функцию распределения вероятности вектора можно представить в виде , то случайную величину называют непрерывной двумерной случайной величиной, а – ее плотностью распределения вероятности.
studopedia.net
Дисперсия дискретной случайной величины и ее свойства (с выводом). Примеры.
Определение. Дисперсией D(Х) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания: или , где |
Доказательство. С учетом того, что мат ожид М(Х) и квадрат мат-го ожид М2(Х) – величины постоянные, можно записать:
В качестве характеристики рассеяния нельзя брать математическое ожидание отклонения случайной величины от ее математического ожидания , ибо согласно свойству 6 математического ожидания эта величина равна нулю для любой случайной величины.
Выбор дисперсии, определяемой по формуле, в качестве характеристики рассеяния значений случайной величины Х оправдывается также тем, что, как можно показать, математическое ожидание квадрата отклонения случайной величины Х от постоянной величины С минимально именно тогда, когда эта постоянная С равна математическому ожиданию , т.е..
Если случайная величина Х — дискретная с конечным числом значений, то (3.11).
Если случайная величина Х — дискретная с бесконечным, но счетным множеством значений, то (если ряд в правой части равенства сходится).
Дисперсия D(Х)
имеет размерность квадрата случайной
величины, что не всегда удобно. Поэтому
в качестве показателя рассеяния
используют также величину 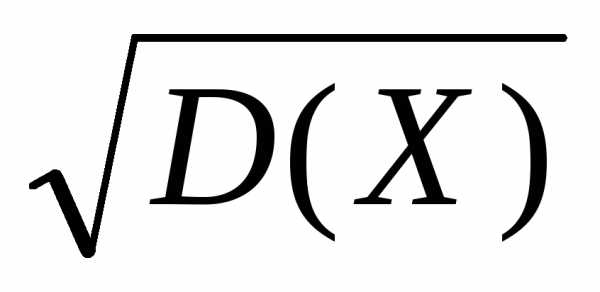 .
.
Определение.
Средним квадратическим отклонением
(стандартным отклонением или стандартом) |
Свойства дисперсии случайной величины.
Дисперсия постоянной величины равна нулю: .
□ . ■
2. Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат: .
□ Учитывая свойство 2 математического ожидания, получим . ■
3. Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания: (3.16) или где .
□ Пусть М(Х) = а. Тогда D(Х) = М(Х — а)2 = М(Х2 — 2аХ + а2). Учитывая, что а — величина постоянная, неслучайная, найдем
D(Х) = М(Х)2 — 2аМ(Х) + а2 = М(Х2) — 2а·а + а2 = M(X2) — a2.
Это свойство часто используют при вычислении дисперсии. Вычисление по формуле (3.16) дает, например, упрощение расчетов по сравнению с основной формулой (3.11), если значения xi случайной величины — целые, а математическое ожидание, а значит, и разности (xi — а) — нецелые числа.
4. Дисперсия алгебраической суммы конечного числа независимых случайных величин равна сумме их дисперсий: .
□ По свойству 3:
.
Обозначая,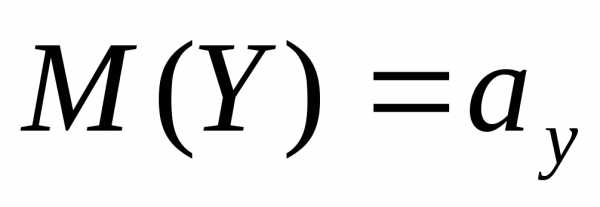 и учитывая, что для независимых случайных
величин М(ХУ)=М(Х)М(У), получим
и учитывая, что для независимых случайных
величин М(ХУ)=М(Х)М(У), получим
.■
Обращаем внимание на то, что дисперсия как суммы, так и разности независимых случайных величин Х и У равна сумме их дисперсий, т.е. .
Если использовать механическую интерпретацию распределения случайной величины, то ее дисперсия представляет собой момент инерции распределения масс относительно центра масс (математического ожидания).
3амечание.
Обратим внимание на интерпретацию
математического ожидания и дисперсии
в финансовом
анализе.
Пусть, например, известно распределение
доходности Х некоторого актива (например,
акции), т.е. известны значения доходности
xi
и соответствующие их вероятности pi
за рассматриваемый промежуток времени.
Тогда, очевидно, математическое ожидание
М(Х) выражает среднюю (прогнозную)
доходность актива, а дисперсия D(X) или
среднее квадратическое отклонение 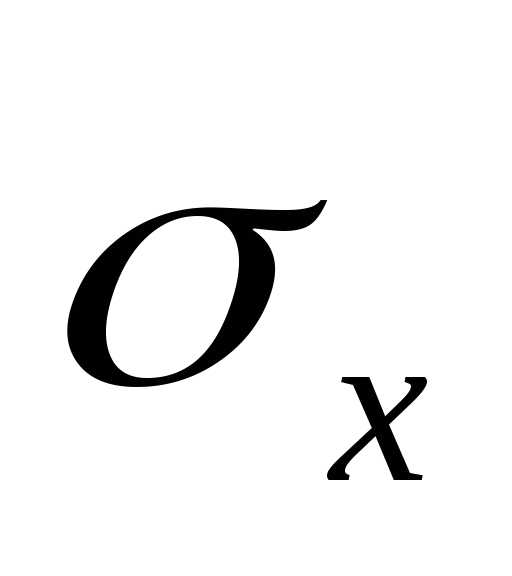 — меру отклонения, колеблемости доходности
от ожидаемого среднего значения, т.е.
риск данного актива.
— меру отклонения, колеблемости доходности
от ожидаемого среднего значения, т.е.
риск данного актива.
Математическое ожидание, дисперсия, среднее квадратическое отклонение и другие числа, призванные в сжатой форме выразить наиболее существенные черты распределения, называются числовыми характеристиками случайной величины.
Обращаем внимание на то, что сама величина Х — случайная, а ее числовые характеристики являются величинами неслучайными, постоянными.
studfiles.net
2.1.2. Дискретные случайные величины | Решение задач по математике и дру
Определение. Случайную величину x называют Дискретной, если множество ее возможных значений образует конечную или бесконечную последовательность чисел, т. е. конечно или счетно.
Пусть возможные значения дискретной случайной величины x упорядочены по возрастанию
X 1 ≤ X2 ≤¼≤ X N ≤¼. .
Рассмотрим события Ai, Содержащие все элементарные события w, приводящие к значению Xi:
A I={w: X = X I }, I=1, 2, ¼
Пусть Pi обозначает вероятность события Ai :
Pi = R (Ai)=R(w: x = xi ), i=1, 2, ¼ .
События Ai — несовместные События, которые составляют разбиение пространства элементарных событий Ω, т. е. Ω = Ai .
Тогда для вероятностей Pi выполняются свойства
P i ³ 0, i=1, 2, ¼ =1 . (2.2)
Закон распределения Дискретной случайной величины задается Рядом распределения.
Ряд распределения дискретной случайной величины x может быть представлен таблицей, в первой строке которой помещают возможные значения Xi , а во второй — вероятности Pi , соответствующие этим значениям.
X | X1 | X2 | …Xn… |
PI | P1 | P2 | …Pn… |
Кроме ряда распределения, дискретная случайная величина может быть задана с помощью Функции распределения.
Определение. Функция распределения F(X) случайной величины X это такая функция переменной X, которая равна вероятности того, что случайная величина примет значение, меньшее, чем заданное X,
F (X)=P(w:¦ (w) £ x) (2.3)
Для всех действительных чисел X.
Для дискретной случайной величины функция распределения определяется как сумма вероятностей для тех значений случайной величины, которые меньше заданного X. Обозначим через В(X) множество возможных значений случайной величины x, предшествующих числу X:
B(X) = {Xi: Xi £ X}. (2.4)
Тогда формулу (2.3) можно записать в виде
F (X) = . (2.5)
Приведем несколько примеров функций распределения дискретных случайных величин.
Пример 2.3. Правильный кубик подбрасывают один раз, и величина x обозначает число очков, выпавшее на его верхней грани. Построим функцию распределения этой случайной величины.
Решение. Обозначим через X возможные значения случайной величины x. В данном примере X={1,2,3,4,5,6}, и вероятность появления грани с любым количеством очков равна РI =.
Напишем ряд распределения этой дискретной случайной величины.
Построим функцию распределения по формуле (2.5). Для этого на числовой оси отметим точки из множества X. Они разбивают числовую ось OX На интервалы (-∞,1), [1,2) [2,3) [3,4) [4,5) [5,6) [6,+ ∞) .
Последовательно будем вычислять функцию распределения на каждом из указанных выше интервалов. При любом множество B(X)={Xi : Xi £X} не содержит возможных значений случайной величины, т. е. является пустым множеством. Тогда по формуле (2.5)
F(X)=0.
При любом множество будет состоять из одного значения — 1:
В(X)={Xi : Xi £ X}={1}. Тогда по формуле (2.5)
F(X)=P1 =.
При любом Множество B(X)={Xi : Xi £ X}={1,2}. Тогда по формуле
F(X)=P1+ P2=.
При любом множество B(X)={Xi : Xi £ X}={1,2,3}. Тогда
F(X)=P1+ p2+ p3=.
При любом Множество B(X)={Xi : Xi £ X}={1,2,3,4}. Тогда
F(X)=P1+ p2+ p3+ p4=.
При любом множество B(X)={Xi : Xi £ X}={1,2,3,4,5} .Тогда
F(X)=P1+ p2+ p3+ p4+ p5=.
При любом множество B(X)={Xi : Xi £ X}={1,2,3,4,5,6} =X. Тогда
F(X)=P1+ p2+ p3+ p4+ p5+ p6=1.
Заметим, что при переходе от одного интервала к другому множество B(X) расширяется на одно значение и от пустого множества переходит к множеству всех возможных значений X={1,2,3,4,5,6}.
Все вычисления можно объединить в формулу
. (2.6)
Пример 2.4. Построим функцию распределения для появления числа гербов при трех подбрасываниях монеты (Пример 2.1).
Решение. Ряд распределения был найден в Примере 2.1.
Обозначим через X множество всех возможных значений этой случайной величины X = { 0, 1, 2, 3 }. Заметим, что множество B(X) при любом X Является подмножеством X. Числа из множества X Разбивают числовую ось на интервалы (-¥,0), [0,1), [1,2), [2,3), [3,+¥).
Пусть X любое число из интервала (-¥,0). Тогда множество B(X) не содержит значений случайной величины x, т. е. B(X) = Ø , следовательно, F(X)=0 при всех X из (-¥,0).
Возьмем любое XÎ[0,1). Множество B(X) содержит значение 0:
B(X) ={0} и F(X)= P0 =.
Возьмем XÎ[1,2). Множество B(X) ={0,1}, и F(X) = P0+ P1= .
Для всех XÎ[2,3) множество B(X) ={0,1,2}, и F(X)=P0+ P1+P2= .
Для всех XÎ[3,¥) множество B(X)={0,1,2,3}=X . Отсюда следует
F(X)= P0+ P1+P2+P3= .
Запишем полученные значения функции распределения на отдельных интервалах в виде формулы
.
Построим график функции распределения F(X) дискретной случайной
Величины
F(X)
1
0 1 2 3 X
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Случайные величины — Теория вероятности — Математика — Каталог статей
Случайные величины
Случайные величины (с.в.) – численное значение появляющееся в результате опыта, и принимающее произвольное значение из заранее определенного множества.
Существует два типа случайных величин: дискретные и непрерывные.
Дискретные случайные величины принимают в результате испытания одно из изолированного дискретного множества значений. Они хорошо подходят для описания результатов измерений, связанных с подсчетом и выражаемых целыми числами.
Примеры дискретных случайных величин: оценка, полученная на экзамене, число попаданий в мишень в серии из 10 выстрелов и т. п.
Вероятность принятия дискретной случайной величиной каждого из возможных ее значений больше нуля. Эта вероятность может быть записана как
,P((X = xi)) = Pi
где i =… −1, 0, 1 …
Здесь X — обозначение случайной величины; xi— конкретные числовые значения, принимаемые дискретной случайной величиной; pi — вероятности этих значений.
Индекс i может в общем случае пробегать значения от −∞ до ∞.
Функция P((X = xi)), связывающая значения дискретной случайной величины с их вероятностями, называется ее распределением (законом распределения). Обычно закон распределения записывается в виде таблицы вида
Х | x1 | x2 | … | xn | … | |
Р | p1 | p2 | … | pn | … |
Пример Пусть Х – число очков выпавшее на игральной кости при одном броске. Тогда, эта с.в. распределена по закону
Х | 1 | 2 | 3 | 4 | 5 | 6 |
Р | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Непрерывные случайные величины в результате испытания могут принимать любые значения из некоторого интервала.
Примеры непрерывных случайных величин: спортивный результат в беге или прыжках, рост и масса тела человека, сила мышц и др.
Поскольку число возможных значений непрерывной случайной величины бесконечно велико и чаще всего нет оснований предположить, что одни значения появляются существенно чаще других, то вероятность принятия непрерывной случайной величиной каждого отдельного значения оказывается равной нулю. По этой причине нельзя описать распределение непрерывной случайной величины в виде вероятностей ее отдельных значений, как в случае дискретных случайных величин. Здесь необходимы другие подходы, которые рассмотрены в разделах 4.6 и 4.7.
Функция распределения
Рассмотрим вероятность того, что случайная величина X окажется меньше или равной некоторому заданному числу х, т. е.
F(x) = P((X≤ x))
. (4.11)
Эта вероятность, рассматриваемая как функция переменной х, называется функцией распределения случайной величины X. Она используется для записи распределений как дискретных, так и непрерывных случайных величин. Функция распределения непрерывной случайной величины будет непрерывной функцией (рис. 4.8).
Как было сказано ранее, вероятность принятия непрерывной случайной величиной какого-либо конкретного значения равна 0.
Для непрерывной случайной величины обычно интересует вероятность попадания ее в заданный интервал (x1;x2), которая по известной функции распределения находится как
P((x1 ≤ X,x2)) = F(x2)F(x1)
(4.12)
В этом выражении совершенно не обязательно записывать интервал таким образом. Можно было бы записать ,x1<X<x2,x1≤X≤x2 или x1<X ≤ x2 , при этом вероятность попадания случайной величины в интервал не изменится. Это связано с тем, что, как уже отмечалось, функция распределения случайной непрерывной величины не имеет скачков ни при каких значениях х.
Свойства функции распределения совпадает со свойствами эмпирической функции распределения (см. 2.3.4)
1. F(x) неубывающая функция.
2.
3.
График функция распределения представляет собой теоретический аналог полигона накопленных частот, рассмотренного в разделе 2.3.3.
Рис. 4.8. Функция распределения непрерывной случайной величины
Плотность распределения вероятностей
Для непрерывных случайных величин вводится понятие плотность распределения вероятностей, или «плотность вероятностей”, играющее исключительно важную роль при их описании.
Плотность вероятностей — это производная от функции распределения непрерывной случайной величины, т.е.
(4.14)
Более подробно при рассмотрении конкретных непрерывных распределений об этой функции рассказано в разделе 4.9. Типичный вид графика плотности вероятностей показан на рис. 4.9.
Вероятность попадания непрерывной случайной величины в интервал между значениями х1 и х2пропорциональная площади под кривой плотности вероятностей, заключенной между точками х1 и х2. Эта вероятность математически записывается в виде интеграла от f(x) в пределах х1 и х2.
. (4.15)
Свойства f(x) :
1.f(x) ≥ 0;
2. f(x) = 0 при x < xmin;
3. f(x) = 0 при x > xmin;
4. .
Рис. 4.9. Вид графика плотности распределения вероятностей
Числовые характеристики случайных величин
Распределение случайной величины, заданное в виде функции распределения или плотности вероятностей, полностью ее характеризует. Однако такая исчерпывающая характеристика случайной величины сложна и далеко не всегда необходима. Для решения многих практических задач не нужно знать распределение случайной величины, а достаточно иметь лишь некоторые обобщающие числовые характеристики этого распределения.
Математическое ожидание
Для более наглядного определения математического ожидания (среднего значения) случайной величины рассмотрим подход к этому понятию на конкретном примере.
Пусть имеется дискретная случайная величина X с возможными значениями и вероятностями этих значений . В качестве примера X рассмотрим случайную величину — количество правонарушений за сутки. Каждое из значений (отмечено 0; 1; … нарушений) будет наблюдаться некоторое число раз. Обозначим эти числа через . Очевидно, что сумма .
Таким образом, имеем n наблюдений за случайной величиной X, т. е. выборку объема n. Определим выборочное среднее арифметическое:
Здесь индекс n при обозначает, что среднее арифметическое вычислено по n наблюдениям.
Теперь представим, что испытание, состоящее в регистрации количества правонарушений, повторяется неограниченное число раз. Здесь, абстрагируясь от физической реализуемости такого эксперимента, будем считать, что наблюдению доступна вся теоретически бесконечная генеральная совокупность значений случайной величины X.
Согласно статистическому определению вероятности, данному в разделе 4.2.2, относительные частоты событий стремятся к их вероятностям при неограниченном повторении испытания.
Поэтому в пределе при n→∞
Таким образом, выборочное среднее арифметическое случайной величины X стремится при неограниченном повторении испытания (при неограниченном увеличении объема выборки) к некоторому постоянному числу, так как в последней сумме xi и рi — постоянные числа. Это число носит название математического ожидания (среднего значения) случайной величины.
Математическое ожидание обозначает как M(X) или mx.
Математическое ожидание дискретной случайной величины равно сумме всех ее возможных значений, умноженных на вероятности этих значений:
(4.16)
В этой записи означает, что суммирование производится по всем возможным i.
Только что рассмотренный пример показывает, что математическое ожидание — абстрактное понятие. Оно является теоретическим аналогом выборочного среднего арифметического.
Математическое ожидание равно среднему значению генеральной совокупности.
Для непрерывных случайных величин математическое ожидание определяется с помощью плотности вероятностей по формуле:
(4.17)
Свойства математического ожидания1. M(C)=C,
2. M(CX)=CM(X).
3. M(X+Y)= M(X)+M(Y),
4. M(X×Y)= M(X)M(Y), если X и Y – независимые C.B.
Дисперсия и стандартное отклонение
Точно так же, как математическое ожидание, являющееся теоретическим аналогом среднего арифметического, можно ввести теоретические аналоги всех числовых характеристик выборки, рассмотренных в гл. 3. Для этого нужно в соответствующих формулах для выборочных характеристик заменить все средние арифметические на математические ожидания.
Дисперсией случайной величины X называется математическое ожидание квадрата отклонений случайной величины от ее математического ожидания (сравните с определением п. 3.4.2). Дисперсия обозначается как D(Х), или σ².
.
Для дискретных случайных величин
(4.18)
т. е. дисперсия дискретной случайной величины равна сумме квадратов отклонений отдельных значений случайной величины от ее математического ожидания, умноженных на вероятности этих значений.
Для непрерывных случайных величин
(4.19)
Положительный корень квадратный из дисперсии называется средним квадратическим (стандартным) отклонением случайной величины.
Эта величина обозначается, как σx
σx=√D. (4.20)
Дисперсия и стандартное отклонение характеризуют изменчивость (вариативность) случайной величины. Чем сильнее случайная величина отклоняется от своего математического ожидания, тем больше величины D(X) и σx . Последнюю (σx) использовать удобнее, так как его размерность совпадает с размерностью случайной величины (например, если Х — кол-во долларов, выигранное в лотерею, то σx — измеряется в $.
Свойства дисперсии
1. D(C)=0,
2. D(CX)= C2D(X).
3. D(X+Y)= D(X)+D(Y),если X и Y – независимые с.в.
Обобщение 4.8.1 и 4.8.2.
Пусть – с.в., а – константы. Тогда . В частности . Если более того – независимые, то . В частности .
Пример
Играем в следующую игру: один раз бросаем игральную кость и получаем столько $, сколько выпало очков. Цена игры: 4$. Выгодно ли играть?
Пусть с.в. Х – количество очков, выпавшее при броске игральной кости. (см. пример 4.12)
Вычислим – именно столько очков
(а, значит, и $) ”в среднем” мы будем получать если играть достаточно долго.
Значит, игра невыгодна для нас. Мы ”в среднем” теряем 0.5$ в каждой игре.
Для вычисления D(X) обычно пользуются формулой D(X) = M(X2) – M2(X).
С.В. Х2 имеет следующее распределение
Х2 | 1 | 22=4 | 32=9 | 42=16 | 52=25 | 62=36 |
Р | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Вычислив М(Х2)=91/6 находим D(X) = 91/6 – 441/36 = 105/36 = .
Моменты
Математическое ожидание и дисперсия представляют собой частные случаи общих числовых характеристик случайной величины, называемых моментами.
Ниже кратко рассматриваются лишь так называемые центральные моменты случайной величины.
S-ым центральным моментом случайной величины X называется математическое ожидание s-й степени отклонения случайной величины от ее математического ожидания:
.
В частности, при s = 2 второй центральный момент случайной величины есть дисперсия.
На практике часто используются также третий и четвертый центральные моменты, позволяющие судить о симметричности и остроте вершины кривой распределения случайной величины.
Если μ3 = 0, то распределение симметрично относительно математического ожидания, если μ3>0, то преобладают положительные отклонения от математического ожидания, если μ3<0 — отрицательные. Для удобства применяется так называемый коэффициент асимметрии, который является безразмерной величиной и определяется как
(4.21)
Об остроте вершины кривой распределения судят по коэффициенту эксцесса:
(4.22)
Если γ4 >0, то распределение имеет острый пик, если γ4<0 (минимальное значение γ4= –2), то распределение имеет плосковершинную форму по сравнению с рассмотренным ниже нормальным распределением, для которого γ4 = 0.
alexlat.ucoz.ru
приведите примеры дискретных и непрерывных случайных величин
Если не вдаваться глубоко в математику, то СВ принимает численные значения, причем вещественные, этим СВ отличается от просто распределений. Бросаем раскрашенный кубик с пронумерованными гранями. Цвет грани — не СВ, а вот номер это — СВ. Вероятность того, что номер выпавшей грани будет больше 3, но меньше 5, можно посчитать. Вероятность того, что цвет будет больше синего, но меньше красного, считать смысла мало — цвета пока что никто даже не упорядочивал (пронумеруем цвета — получим СВ). Пример с номерами граней кубика описывает дискретную СВ. Бросаем дротик в мишень. Точка, куда он попадет, это вообще не СВ, это случайный вектор. А вот расстояние до центра — СВ, причем непрерывная. Сделаем вот что. Расстояние в метрах будем измерять. Количество знаков в расстоянии — дискретная СВ. Если к расстоянию прибавим количество знаков в нем, получим смесь дискретного и асболютно-непрерывного распределений, такая СВ не будет ни дискретной, ни непрерывной, но будет смесью дискретной и непрерывной СВ. Дискретная СВ не обязана принимать конечное кол-во значений, но если их бесконечно много, то ее возможные значения можно занумеровать в последовательность. Пример: за сутки человеку птицы могут накакать на голову случайное количество раз. Это количество сверху ничем не ограничено, но оно целое. Это тоже пример дискретной случайной величины. И еще: не всякую СВ можно представить в виде смеси дискретного и абсолютно-непрерывного распределений. Бывает еще сингулярное распределение. Но это уже экзотика.
любовницы. и жена
Результат бросания костей/кубиков/ и можно считать дискретной величиной. Потому что интуитивно ясно что каждая из сторон окажется сверху с равной вероятностью. Результат стрельбы по мишени можно считать непрерывной случайной величиной. Но ее распределение у каждого стрелка свое, индивидуальное.
Да, кубик, монета, карты — дискреты. А вот шум усилителя — случаен и непрерывен. Сюда же пойдет любой стационарный шум: шуршание колес по асфальту, деревьев на ветру, шифрованные сообщения (их делают шумоподобными до колоссальной степени, «чтоб никто не догадался», что идет передача).
touch.otvet.mail.ru

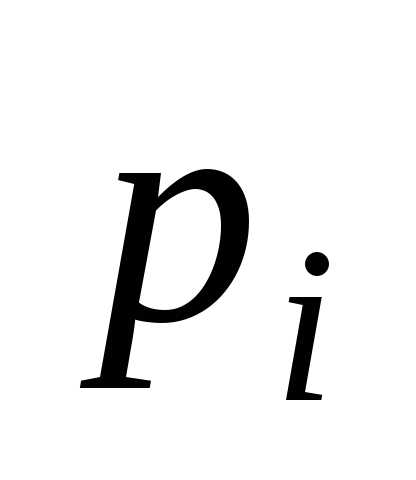

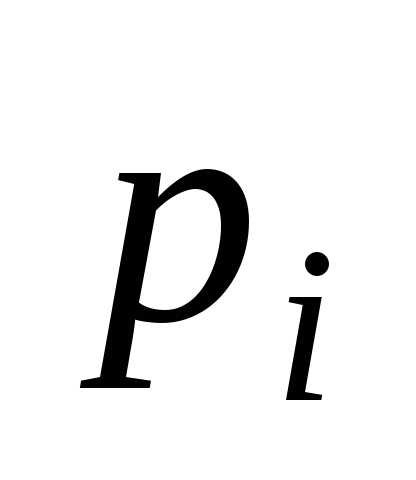
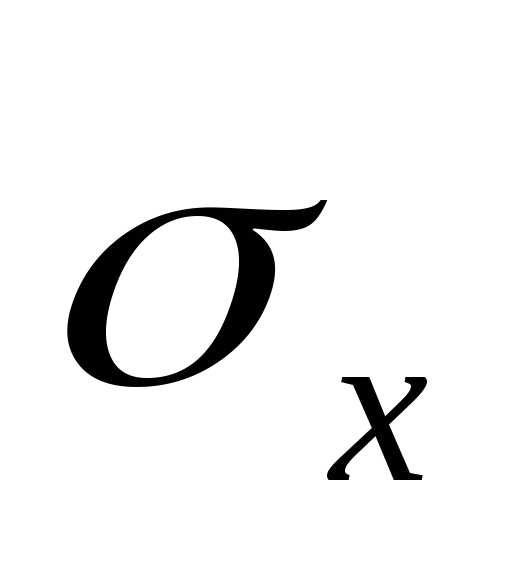 случайной величины Х называется
арифметическое значение корня
квадратного из ее дисперсии:
случайной величины Х называется
арифметическое значение корня
квадратного из ее дисперсии: