Разложение в степенной ряд функции – .

Тема 3. Разложение функций в степенной ряд

3.1. Постановка задачи. Ряд Тейлора

В теории функциональных рядов центральное место занимает раздел, посвященный разложению функции в ряд.

Таким образом, ставится задача: по заданной функции 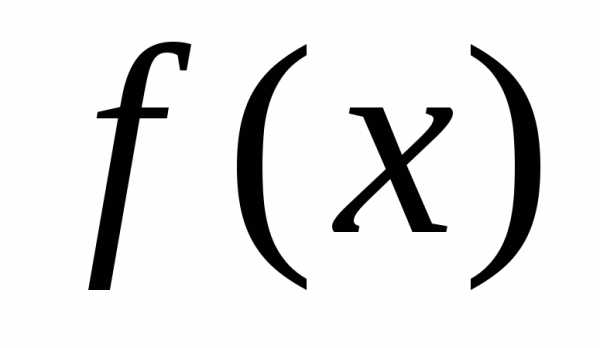требуется найти такой степенной ряд

,

который на некотором интервале сходился и его сумма была равна 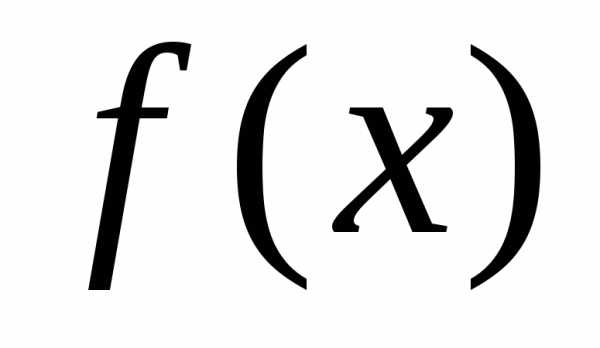, т.е.

= ..

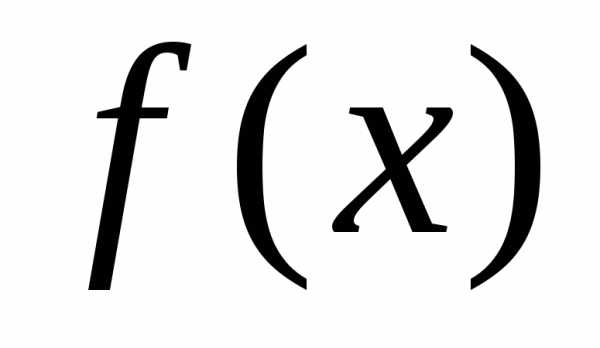Эта задача называется задачей разложения функции в степенной ряд.

Необходимым условием разложимости функции в степенной ряд является её дифференцируемость бесконечное число раз – это следует из свойств сходящихся степенных рядов. Такое условие выполняется, как правило, для элементарных функций в их области определения.

Итак, предположим, что функция 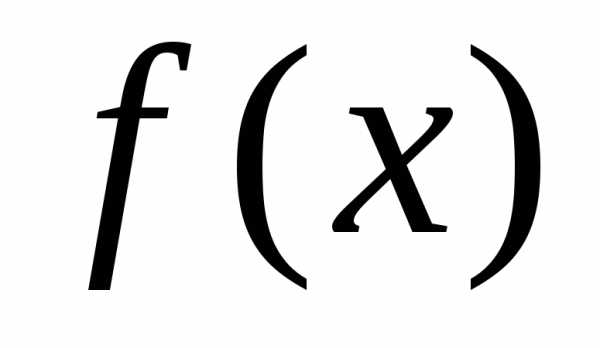имеет производные любого порядка. Можно ли её разложить в степенной ряд, если можно, то как найти этот ряд? Проще решается вторая часть задачи, с неё и начнем.

Допустим, что функцию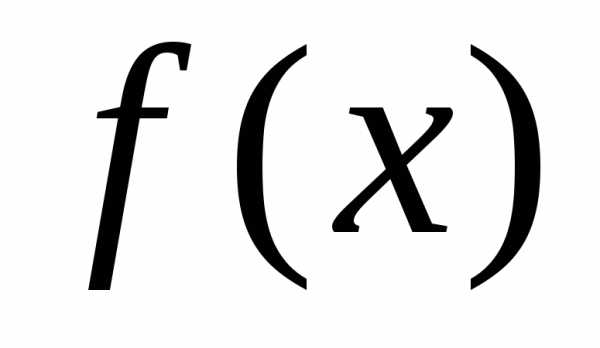можно представить в виде суммы степенного ряда, сходящегося в интервале, содержащем точкух₀:

= .. (*)

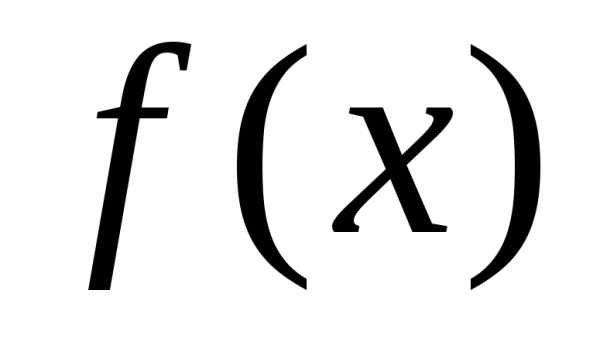где а₀,а₁,а₂,,…,а_п,… – неопределенные (пока) коэффициенты.

Положим в равенстве (*) значение х = х₀, тогда получим

.

Продифференцируем степенной ряд (*) почленно

= ..

и полагая здесь х = х₀, получим

.

При следующем дифференцировании получим ряд

= ..

полагая х = х₀, получим, откуда .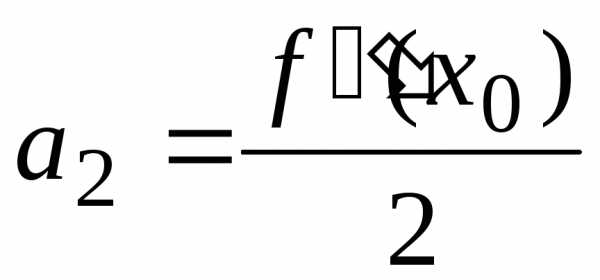

После п -кратного дифференцирования получим

Полагая в последнем равенстве х = х₀, получим , откуда

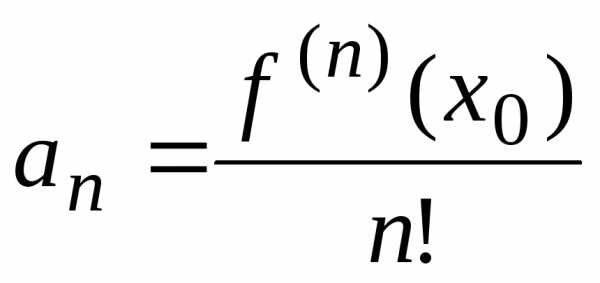
Итак, коэффициенты найдены

, , , …, ,….,

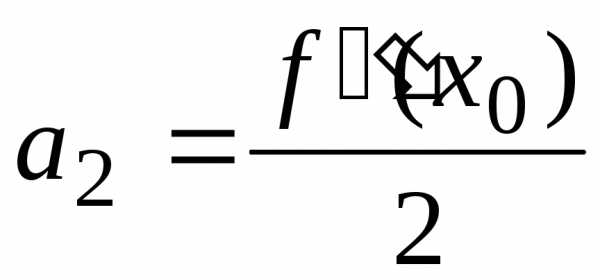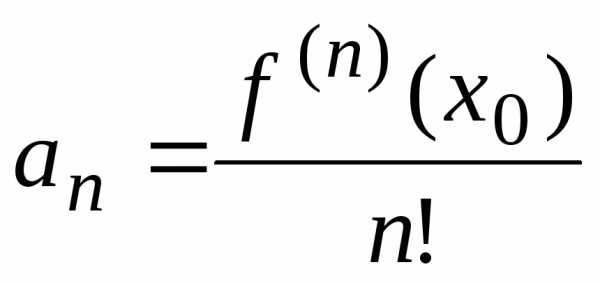подставляя которые в ряд (*), получим

Полученный ряд называется рядом Тейлора для функции .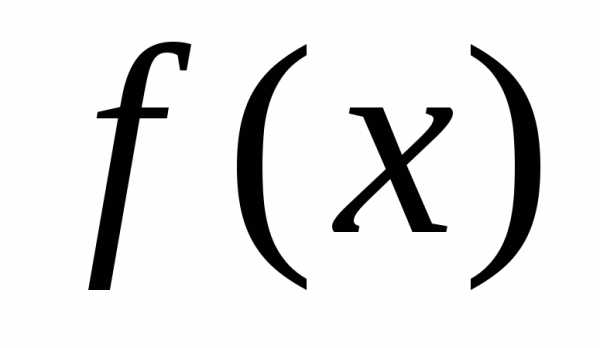

Таким образом, мы установили, что если функцию можно разложить в степенной ряд по степеням (х — х₀), то это разложение единственно и полученный ряд обязательно является рядом Тейлора.

Заметим, что ряд Тейлора можно получить для любой функции, имеющей производные любого порядка в точке х = х₀. Но это еще не означает, что между функцией и полученным рядом можно поставить знак равенства, т.е. что сумма ряда равна исходной функции. Во-первых, такое равенство может иметь смысл только в области сходимости, а полученный для функции ряд Тейлора может и расходиться, во-вторых, если ряд Тейлора будет сходиться, то его сумма может не совпадать с исходной функцией.

3.2. Достаточные условия разложимости функции в ряд Тейлора

Сформулируем утверждение, с помощью которого будет решена поставленная задача.

Если функция 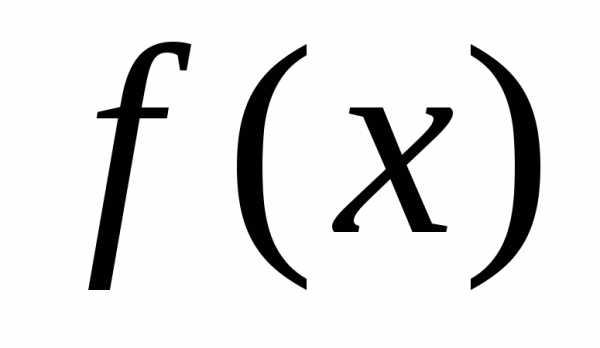в некоторой окрестности точки х₀ имеет производные до (n+1)-го порядка включительно, то в этой окрестности имеет место формула Тейлора

где R_n(х)-остаточный член формулы Тейлора – имеет вид (форма Лагранжа)

где точка ξ лежит между х и х

₀.

Отметим, что между рядом Тейлора и формулой Тейлора имеется различие: формула Тейлора представляет собой конечную сумму, т.е. п — фиксированное число.

Напомним, что сумма ряда S(x) может быть определена как предел функциональной последовательности частичных сумм S_п(x) на некотором промежутке Х:

.

Согласно этому, разложить функцию в ряд Тейлора означает найти такой ряд, что для любого х X

Запишем формулу Тейлора в виде, где

.

Заметим, что 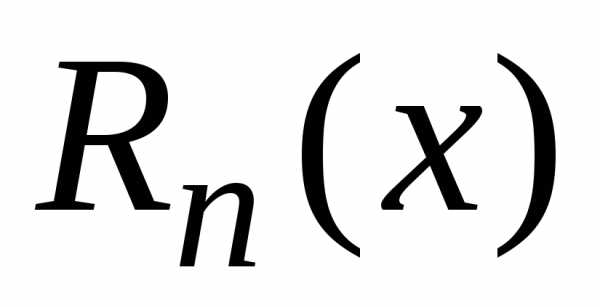определяет ту ошибку, которую мы получаем, заменяй функцию f(x) многочленом S_n(x).

Если , то,т.е. функция разлагается в ряд Тейлора. И наоборот, если , то.

Тем самым мы доказали критерий разложимости функции в ряд Тейлора.

Для того, чтобы в некотором промежутке функция f(х) разлагалась в ряд Тейлора, необходимо и достаточно, чтобы на этом промежутке , где R_n(x) — остаточный член ряда Тейлора.

С помощью сформулированного критерия можно получить достаточные условия разложимости функции в ряд Тейлора.

Если в некоторой окрестности точки х₀ абсолютные величины всех производных функции ограничены одним и тем же числом М ≥ 0, т.е.

, то в этой окрестности функция разлагается в ряд Тейлора.

Из вышеизложенного следует алгоритм разложения функции

f(x) в ряд Тейлора в окрестности точки х₀:

1. Находим производные функции f(x):

f(x), f’(x), f”(x), f’”(x), f⁽ⁿ⁾ (x),…

2. Вычисляем значение функции и значения её производных в точке х₀

f(x₀), f’(x₀), f”(x₀), f’”(x₀), f⁽ⁿ⁾ (x₀),…

3. Формально записываем ряд Тейлора и находим область сходимости полученного степенного ряда.

4. Проверяем выполнение достаточных условий, т.е. устанавливаем, для каких х из области сходимости, остаточный член R_n(x) стремится к нулю при или .

Разложение функций в ряд Тейлора по данному алгоритму называют разложением функции в ряд Тейлора по определению или непосредственным разложением.

studfiles.net

Разложение функций в степенные ряды

Если функция f(x) имеет на некотором интервале, содержащем точку а, производные всех порядков, то к ней может быть применена формула Тейлора:

,

где r_n – так называемый остаточный член или остаток ряда, его можно оценить с помощью формулы Лагранжа:

, где число x заключено между х и а.

Если для некоторого значения х r_n®0 при n®¥, то в пределе формула Тейлора превращается для этого значения в сходящийся ряд Тейлора:

Таким образом, функция f(x) может быть разложена в ряд Тейлора в рассматриваемой точке

х, если:

1) она имеет производные всех порядков;

2) построенный ряд сходится в этой точке.

 

При а=0 получаем ряд, называемый рядом Маклорена:

 

Пример 1. Разложить в степенной ряд функцию f(x)=2^x.

Решение. Найдем значения функции и ее производных при х=0

f(x) = 2^x, f(0) = 2⁰=1;

f¢(x) = 2^xln2, f¢(0) = 2⁰ ln2= ln2;

f¢¢(x) = 2^x ln²2, f¢¢(0) = 2⁰ ln²2= ln²2;

…

f⁽ⁿ⁾(x) = 2^x lnⁿ2, f⁽ⁿ⁾(0) = 2⁰ lnⁿ2= lnⁿ2.

Подставляя полученные значения производных в формулу ряда Тейлора, получим:

Радиус сходимости этого ряда равен бесконечности, поэтому данное разложение справедливо для -¥<x<+¥.

 

Пример 2. Написать ряд Тейлора по степеням (х+4) для функции f(x)=e^x.

Решение. Находим производные функции e^x и их значения в точке х=-4.

f(x) = е^x, f(-4) = е^-4;

f¢(x) = е^x, f¢(-4) = е^-4;

f¢¢(x) = е^x, f¢¢(-4) = е^-4;

…

f⁽ⁿ⁾(x) = е^x, f⁽ⁿ⁾( -4) = е^-4.

Следовательно, искомый ряд Тейлора функции имеет вид:

Данное разложение также справедливо для -¥<x<+¥.

 

Пример 3. Разложить функцию f(x)=lnx в ряд по степеням (х-1),

( т.е. в ряд Тейлора в окрестности точки х=1).

Решение. Находим производные данной функции.

…

Подставляя эти значения в формулу, получим искомый ряд Тейлора:

С помощью признака Даламбера можно убедиться, что ряд сходится при

½х-1½<1. Действительно,

Ряд сходится, если ½х-1½<1, т.е. при 0<x<2. При х=2 получаем знакочередующийся ряд, удовлетворяющий условиям признака Лейбница. При х=0 функция не определена. Таким образом, областью сходимости ряда Тейлора является полуоткрытый промежуток (0;2].

 

Приведем полученные подобным образом разложения в ряд Маклорена (т.е. в окрестности точки х=0) для некоторых элементарных функций:

(1) ,

(2) ,

(3) ,

(4) ,

(5) .

(последнее разложение называют биномиальным рядом)

 

Пример 4. Разложить в степенной ряд функцию

Решение. В разложении (1) заменяем х на –х², получаем:

.

 

Пример 5. Разложить в ряд Маклорена функцию

Решение. Имеем

Пользуясь формулой (4), можем записать:

;

подставляя вместо х в формулу –х, получим:

Отсюда находим:

Раскрывая скобки, переставляя члены ряда и делая приведение подобных слагаемых, получим

Этот ряд сходится в интервале

(-1;1), так как он получен из двух рядов, каждый из которых сходится в этом интервале.

 

Замечание.

Формулами (1)-(5) можно пользоваться и для разложения соответствующих функций в ряд Тейлора, т.е. для разложения функций по целым положительным степеням (х-а). Для этого над заданной функцией необходимо произвести такие тождественные преобразования, чтобы получить одну из функций (1)-(5), в которой вместо х стоит k(х-а)^m, где k – постоянное число, m – целое положительное число. Часто при этом удобно сделать замену переменной t=х-а и раскладывать полученную функцию относительно t в ряд Маклорена.

Этот метод иллюстрирует теорему о единственности разложения функции в степенной ряд. Сущность этой теоремы состоит в том, что в окрестности одной и той же точки не может быть получено два различных степенных ряда, которые бы сходились к одной и той же функции, каким бы способом ее разложение ни производилось.

 

Пример 6. Разложить функцию в ряд Тейлора в окрестности точки х=3.

Решение. Эту задачу можно решить, как и раньше, с помощью определения ряда Тейлора, для чего нужно найти производные функции и их значения при х=3. Однако проще будет воспользоваться имеющимся разложением (5):

Полученный ряд сходится при или –3<x-3<3, 0<x< 6 и является искомым рядом Тейлора для данной функции.

 

Пример 7. Написать ряд Тейлора по степеням (х-1) функции .

Решение.

Ряд сходится при , или -2 < x £ 5.

 

Пример 8. Разложить функцию в ряд Тейлора в окрестности точки x=2.

Решение. Сделаем замену t=х-2:

.

Воспользовавшись разложением (3), в котором на место х подставим , получим:

Полученный ряд сходится к заданной функции при , т.е. при .

Таким образом,

 

Решить: Разложить заданную функцию в ряд:

A 1) по степеням х 2) по степеням х

3) по степеням х 4) по степеням х

5) по степеням (х+1)6) по степеням (х-2)

7) по степ. х 8) в ряд Маклорена

9) в ряд Маклорена 10) в ряд Маклорена

 



infopedia.su

Разложение функции в степенной ряд. Единственность разложения

Лекция 6. Разложение функции в степенной ряд. Единственность разложения. Ряды Тейлора и Маклорена. Разложение в степенной ряд некоторых элементарных функций. Применение степенных рядов.

 

В предыдущих лекциях рассматривались степенные ряды, для которых в пределах области равномерной сходимости сумма ряда s(x) представляет собой непрерывную и бесконечно дифференцируемую функцию от х. Теперь поставим обратную задачу: найти степенной ряд, суммой которого является данная функция.

Определение 6.1. Представление функции в виде

                                                                  (6.1)

называется ее разложением в степенной ряд.

 

Теорема 6.1. Если функция  f(x) раскладывается в окрестности точки х0 в степенной ряд (6.1) с радиусом сходимости R, то:

1. функция f имеет на интервале (x0 – R , x0 + R) производные всех порядков, которые можно найти почленным дифференцированием ряда (6.1):                                                                    (6.2) 
2.                                     (6.3)
3. ряды (6.1), (6.2) и (6.3) имеют одинаковые радиусы сходимости.

Доказательство всех трех утверждений следует из общих свойств степенных рядов (теоремы 5.2 и 5.3).

 

Теорема 6.2. Если функция  f раскладывается в некоторой окрестности точки х0 в сте-пенной ряд (6.1), то  , и, следовательно, справедлива формула

                                                                                   (6.4)  

Доказательство.

Дифференцируя т раз равенство (6.1), получим:

 

Примем х = х0 , тогда  f(m)(x0) = m!am , что доказывает формулу (6.4).

 

Следствие. Если в некоторой окрестности заданной точки функция раскладывается в степенной ряд, то это разложение единственно.

Действительно, из теоремы 6.2 следует, что коэффициенты степенного ряда могут иметь только вид, задаваемый формулой (6.4).

   

Определение 6.2. Пусть функция  f(x) определена в некоторой окрестности точки х0 и имеет в этой точке производные всех порядков. Тогда ряд

                                                                                        

называется рядом Тейлора.

 

Пример. Найдем разложение в ряд Тейлора при х0 = 0 функции f(x) = 2x.

. Следовательно,

                      .

Определение 6.3. Если при разложении в ряд Тейлора принимается х0 = 0, то полученный ряд                                                             (6.5)

называется рядом Маклорена (см. предыдущий пример).

 

Разложение в степенной ряд некоторых элементарных функций.

 

В лекции 21 (1-й семестр) рассматривалось представление функции в виде многочлена Тейлора с остаточным членом. Поскольку коэффициенты ряда Тейлора и многочлена Тейлора вычисляются по одной и той же формуле, мы можем воспользоваться прове-денными в лекции 21 вычислениями для получения разложения в ряд Тейлора некото-рых элементарных функций. При этом обратим особое внимание на определение обла-сти сходимости полученных рядов.

1. . Сходимость полученного ряда исследовалась в примере 2 лекции 5, где показано, что он абсолютно сходится при любом х.

2. .

3. .

Используя формулу Даламбера для определения радиуса сходимости, найдем, что он равен бесконечности, то есть функции y = sin x и y = cos x раскладываются в ряд Тей-лора на всем множестве действительных чисел.

4. . Запишем остаточный член этой формулы в форме Лагранжа:

, и исследуем его поведение при для | x| < 1,

| x | > 1 и | x | = 1. При | x| < 1 , при | x | > 1 . Поэтому по теоре-ме 1.5 при  | x| < 1 ряд сходится, а при | x | > 1 расходится. При х = -1 ряд расходится, так как представляет собой гармонический ряд, все члены которого имеют знак «-», а при х = 1 получаем знакопеременный ряд, сходящийся условно по признаку Лейбница. Следовательно, областью сходимости полученного ряда является интервал (-1, 1].

5. . Найдем радиус его сходимости по формуле Даламбера: Следовательно, интервал сходимости – (-1, 1).

 

Формула Эйлера.

 

Используя разложения в ряд Тейлора функций ex, sin x и cos x , получим:

. Таким образом, доказана используемая в теории комплексных чисел формула Эйлера:

                    eiy = cos y + i sin y                                                               (6.6)

(см. лекцию 7, 2-й семестр).

 

Применение степенных рядов.

 

Возможность разложения функции в степенной ряд позволяет существенно упростить многие математические операции: вычисление приближенных значений данной функции, дифференцирование, интегрирование, поскольку степенной ряд можно заменить многочленом (с учетом того, что оценка остатка ряда не превысит заданного значения погрешности). В частности, можно приближенно вычислять «неберущиеся» интегралы, находить приближенные решения дифференциальных уравнений и т.д.

Рассмотрим вычисление интегралов с помощью рядов.

Примеры.

1. Для вычисления интеграла разложим подынтегральную функцию в ряд Тейлора, используя разложение функции ех:

Тогда =

С помощью этого равенства можно вычислить рассматриваемый интеграл при любом а с любой заданной точностью.

1. Вычислим интеграл , для чего разложим функцию в ряд:

– ряд, сходящийся при любом х. Интегрируя почленно, получим:

Приближенное решение дифференциального уравнения второго порядка   , удовлетворяющее начальным условиям .

Если предположить, что решение имеет вид: , то требуется найти значения производных от частного решения при х = х0 . Из начальных условий следует, что . Тогда из исходного уравнения получаем, что . Дифференцируя обе части исходного уравнения по х, найдем: откуда можно определить и т.д.

Пример. Найти решение уравнения при

Решение: и т.д.

Можно получить общую формулу для производных любого порядка:

. При х = 0 эта формула дает

                  .

Так как то в нуль обращаются все производные, порядок которых не кратен четырем. В конечном счете решение имеет вид:

 

support17.com

Разложение функций в степенные ряды — КиберПедия

 

Рассмотрим некоторые частные случаи разложения функции f(x) в степенной ряд. Например, степенной ряд

1 + x + x² + ¼ + xⁿ +¼

является геометрическим рядом со знаменателем xи, согласно доказанному в примере 3, сходится при | x| < 1; его сумма равна , т.е. = 1 + x + x² + ¼ + xⁿ +¼, (14)

Равенство (14) можно рассматривать как разложение функции в степенной ряд.

В качестве другого примера рассмотрим разложение в ряд функции . Заменяя в равенстве (14) xна -z, получим

= 1 —z + z²-¼ + (-1)ⁿzⁿ +¼ (15)

при 0 £ |z | < 1. Проинтегрируем равенство (15):

Тогда

или

(16)

при |x | < 1.

При x = 1 разложение (16) принимает вид

(17)

но ряд (17) сходится, значит разложение (16) справедливо для всех x£ 1.

Аналогично, можно записать разложение в степенной ряд функции . Положим в (14) x = —z², тогда

= 1 —z² + z⁴-¼ + (-1)ⁿz²ⁿ +¼ (18)

Проинтегрировав левую и правую часть (18), получим

,

или =

= (19)

при |x | < 1.

Это разложение верно и при x = 1, т.к. ряд (19) при x = 1 сходится. Известно, что , но

=

т.е. можно вычислить значение числа p с любой степенью точности.

Полученные разложения функций и являются частными случаями. В общем виде разложение функций в степенной ряд решено Маклореном и Тейлором.

 

Ряды Маклорена и Тейлора

Рассмотрим произвольную функцию f(x), определенную в заданном интервале |x-x₀ | <R, и предположим для нее, что в точке x₀ существуют производные всех порядков до n-го включительно. Будем искать многочлен n-степени с неизвестными пока коэффициентами, который наилучшим образом приближается к функцииf(x):

P_n(x) = a₀ + a₁( x— x₀ ) + a₂ ( x— x₀ )² + ¼ + a_n ( x— x₀ )ⁿ »f (x). (20)

 

 

Для этого потребуем, чтобы функция f(x) и ее n производных были равны значению многочлена P_n(x) и его производных в точке x₀. Еслиx₀ = 0, то

P_n(x) = a₀ + a₁x + a₂x² + ¼ + a_nxⁿ » f (x). (21)

Как видно из (21)

P_n(0) =a₀ = f(0).

Для нахождения коэффициентов a_i( i= 1, 2, ¼, n) продифференци-руем (21) почленно:

= a₁ + 2 a₂ x + 3 a₃ x² + 4 a₄ x³ + ¼ + n a_nx^n-1 +¼,

= 2 a₂+ 2×3 a₃ x + 3×4 a₄ x² + ¼ + n×(n-1) a_nx^{n-2 +}¼, (22)

……………………………………………………………

Как видно из (22) при x= 0: f¢(0) =a₁, f¢¢(0) = 2 a₂, f¢¢¢(0) = 2×3 a₃,

f⁽⁴⁾(0) = 2×3×4 a₄ , ¼, f⁽ⁿ⁾(0) = 2×3×4×¼×na_n. Отсюда для коэффициентов многочлена (21) получим:

a₀ = f(0), a₁ = f¢(0), a₂= , a₃ = , a₄ = , ¼,a_n = .

Приближение функции f(x) многочленом (21) примет вид (n! = 1×2×3×4×¼×n):

f(x) »f(0) + x + x² + x³ + ¼ + xⁿ. (23)

В тех случаях, когда функция f(x) или ее производные теряют смысл при x= 0, пользуются более общим представлением (20) функции в виде многочлена. Легко показать, что для приближения функции f(x) многочленом (20) справедливо выражение:

 

f(x) »f (x₀)+ (x—x₀)+ (x—x₀)² + (x—x₀)³ + ¼

¼+ (x—x₀)ⁿ. (24)

Многочлены (23) и (24) дают лишь некоторое приближение для функции f(x). В связи с этим возникает вопрос о степени близости f(x) и соответствующего многочлена. Разность

f (x) —P_n(x) = r_n(x) (25)

называется остаточным членом. Так как n мы можем брать сколь угодно большим, то выражения (23) и (24) приводят к разложению f(x) в бесконечный степенной ряд

f(x) = f (x₀) + (x —x₀) + (x —x₀)² + (x —x₀)³ + ¼

¼ + (x—x₀)ⁿ+ ¼(26)

при |x-x₀ | <R.

Впервые возможность представления функции в виде бесконечного ряда была доказана Тейлором. При x₀ = 0 такой ряд был выведен Маклореном:

f(x) = f(0) + x + x² + x³ + ¼ + xⁿ + ¼. (26¢)

Разность между f(x) и суммой (n+1) членов ряда, согласно (25), есть как раз остаточный член r_n(x). Тогда очевидно, что для того, чтобы при некотором значении xдействительно имело место разложение (26), необходимо и достаточно, чтобы

. (27)

Замечание.Для непрерывной вместе со своими производными функции f(x), как правило, условие (27) выполняется и функция f(x) разлагается в степенной ряд. Далее приведены примеры разложения элементарных функций в степенные ряды.

Пример 10. Разложить в ряд функциюf(x) =e^x. Все производные функции e^x равны e^x. Полагая x = 0, получим f(0) = = = = ¼ = 1. Подставляя эти значения в ряд (26¢), будем иметь разложение функции = e^x в ряд Маклорена:

(28)

Применяя к этому ряду признак Даламбера

.

Степенной ряд (28) сходится для любого x; интервал сходимости- (-¥, ¥).

Пример 11. Разложить в ряд функцию f(x) = .

, , , , ¼

При x = 0

, , , , , ¼

Подставляя в (26¢), получим

, (29)

где x измеряется в радианах.

Пример 12. Разложить в ряд функцию f(x) = .

, , , , ¼

При x = 0

, , , , , ¼

Подставляя в (26¢), получим

(30)

Разложение (30), также как и (29), справедливо при любом x.

Пример 13. Разложить в ряд функцию f(x) = . Функция не определена приx = 0, поэтому разложим ее в ряд Тейлора (26) по возрастающим степеням (x-1) (при x₀ = 1).

, , , , ¼

При x = 1

, , , , , ¼

Подставляя в (26), находим

Пример 14. Разложить в ряд функцию мнимого аргумента f(x) = . Обозначим z = ix. Зная разложение в ряд функции e^x, запишем

Разделяя действительную и мнимую часть, получим

. (31)

Согласно (29) и (30), равенство (31) можно записать в виде

. (32)

Заменяя x на —x и учитывая, что = , а = — , находим

. (33)

Формулы (32) и (33) были выведены Эйлером; разрешая (32) и (33) относительно и , получим

, .

cyberpedia.su

РАЗЛОЖЕНИЕ ФУНКЦИЙ В СТЕПЕННЫЕ РЯДЫ.

Рядом Тейлора для функции называется степенной ряд вида

Если а=0, то получим частный случай ряда Тейлора

Который называется рядом Маклорена.

Степенной ряд внутри его промежутка сходимости можно почленно дифференцировать и интегрировать сколько угодно раз, причём полученные ряды имеют тот же промежуток сходимости, что и исходный ряд.

Два степенных ряда можно почленно складывать и умножать по правилам сложения и умножения многочленов. При этом промежуток сходимости полученного нового ряда совпадает с общей частью промежутков сходимости исходных рядов.

Для разложения функции в ряд Маклорена необходимо:

1) вычислить значения функции и её последовательных производных в точке х=0, т.е. , ,

2) составить ряд Маклорена, подставив значения функции и её последовательных производных в формулу

3) найти промежуток сходимости полученного ряда по формуле

для разложения функции в ряд Тейлора необходимо:

1) Вычислить значения функции и её последовательных производных в точке х=а, т.е.

2) Составить ряд Тейлора, подставив значения функции и её последовательных производных в формулу.

3) Найти промежуток сходимости по формуле.

 

26. Разложить в ряд Маклорена функцию:

1) ; 2) ; 3) ; 4) ;

5) ; 6) ; 7) ; 8) ;

9) ; 10) .

1) Вычислим значения функции и её производных при х=0; имеем (n=1, 2, 3,…).

Подставив эти значения в формулу, получим разложение функции в ряд Маклорена:

Этот ряд называется экспоненциальным рядом.

Промежуток сходимости найдём по формуле

; ;

, т.е. .

Полученный ряд сходится к функции при любых значениях х, так как в любом промежутке функция и её производные по абсолютной величине ограничены одним и тем же числом.

2) Вычислим значения функции и её производных при х=0, имеем Заметим, что производные чётного порядка а производные нечетного порядка (n=1, 2, 3, 4, …)

Подставив эти значения в формулу, получим разложение синуса в ряд Маклорена:

Промежуток сходимости полученного ряда найдём по формуле

,

Т.е. ряд сходится в промежутке .

3) Рассуждая так же, как и в п. 2, аналогично получаем

Причём этот ряд сходится в промежутке .

4) Вычислим значения функции и её производных при х=0; имеем

Подставив эти значения в формулу, получим разложение функции в ряд Маклорена:

Или

Промежуток сходимости найдём по формуле: . Следовательно, -1<x<1.

При х=-1 и х=1 ряд расходится, поэтому область сходимости ряда – промежуток -1<x<1.

5)I способ. Вычислим значения функции и её производных при х=0; имеем Отсюда следует, что

(n=1, 2, 3, 4, … )

Подставив эти значения в формулу, получим разложение данной функции в ряд Маклорена:

Этот ряд называется логарифмическим рядом.

Промежуток сходимости найдём по формуле: ,

, т.е. -1<x<1.

Исследуем сходимость ряда в точках x=-1 и x=1. При х=-1 ряд расходится как гармонический. При х=1 имеем знакочередующийся ряд

,

Который сходится по признаку Лейбница. Итак, данный ряд сходится в промежутке -1<x<1.

 

Похожие статьи:

poznayka.org

Как разложить функцию в степенной ряд

Свернутое представление функции f(x) в виде степенного ряда в Wolfram|Alpha также можно получить, используя запрос вида: f(x) series representation

Wolfram|Alpha автоматически выбирает наиболее простой вид разложения функции в степенной ряд, если иное не задано. Так, в предыдущих примерах система Wolfram|Alpha использовала разложение экспоненциальной функции e^x в ряд Маклорена (в точке x=0). Если же применение ряда Маклорена невозможно (вспомните условия разложения функции в ряд Маклорена), то Wolfram|Alpha автоматически выводит разложение данной функции в ряд Тейлора в ближайшей точке, например в точке x=1:

При необходимости, Wolfram|Alpha может вывести определенное количество членов разложения функции в степенной ряд. Точнее, выводятся члены ряда до определенной степени (т. е. с коэффициентами до заданного порядка)  включительно. Это нужно указать явно следующим образом:

В настоящее время эта конструкция запроса срабатывает не всегда корректно — в некоторых случаях Wolfram|Alpha выводит больше членов ряда, чем указано в запросе.

Wolfram|Alpha позволяет получить разложение функции в степенной ряд в заданной точке. Соответствующий запрос выглядит так:

Кстати, эту форму запроса можно использовать также и для того, чтобы разложить некий многочлен по степеням одночлена (x-x0). Например, при x0=pi для заданного многочлена получим:

В теории рядов рассматривается следующая задача: найти коэффициенты разложения данной функции в ряд Тейлора (или Маклорена). Wolfram|Alpha позволяет подойти к решению этой задачи используя, например, запрос на табуляцию последовательности. К примеру, найдем таким образом первые шесть коэффициентов разложения функции cos(x) в ряд Тейлора. При этом, естественно, используем формулу коэффициентов ряда Тейлора (см. выше):

 Table [d^n/dx^n (cos x)/n!, {n,0,5}]

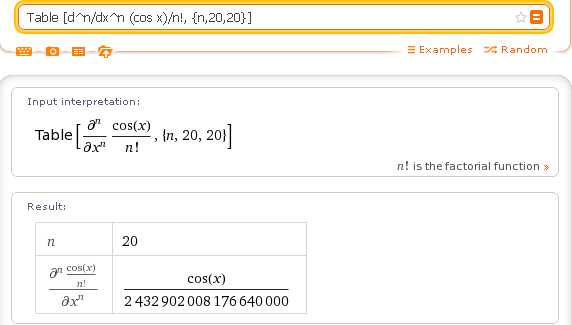
Здесь, чтобы получить шесть первых коэффициентов ряда мы указали их номера с n=0 по n=5 включительно, записав в запросе — {n,0,5}.Чтобы получить коэффициент ряда с заданным номером, эту запись следует изменить. Например, чтобы найти коэффициент с номером n=20, запишем — {n,20,20}, и получим:

Table [d^n/dx^n (cos x)/n!, {n,20,20}]

Если эта конструкция запроса покажется вам слишком сложной, тогда для получения коэффициентов ряда используйте более «естественные»запросы, соответственно:

table d^n/dx^n (cos x)/n! for n = 0 … 5 и d^n/dx^n (cos x)/n! for n = 20

Далее, можно подставить в найденные коэффициенты вместо аргумента x его конкретное значение, и таким образом Вы сможете получить коэффициенты разложения данной функции в степенной ряд в заданной точке.

Кроме того, в Wolfram|Alpha имеется специальный запрос для получения коэффициентов разложения функций в ряд Маклорена (в точке x=0). Например, найдем коэффициенты разложения в ряд Маклорена для функции e^x :

SeriesCoefficient[e^x, {x, 0, n}]

Обратите внимание, что в первой строке таблицы указаны степени x, начиная с 1 и далее. То есть свободный член разложения (коэффициент при x^0, равный f(0)/0!) здесь не выводится.

Чтобы убедиться в этом, посмотрите еще два аналогичных примера:

SeriesCoefficient[cos x, {x, 0, n}]

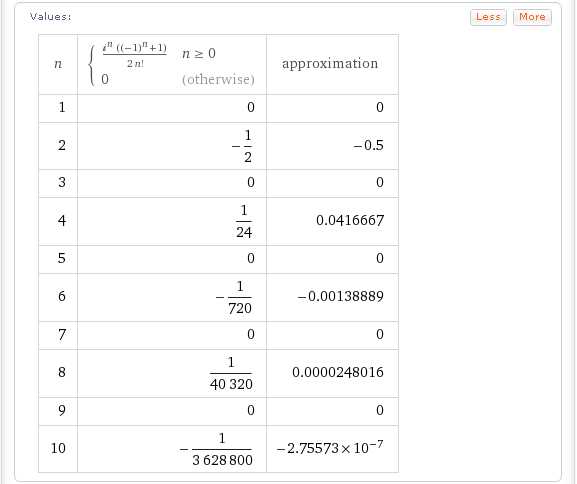
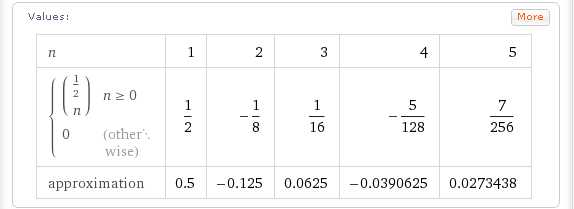
SeriesCoefficient[(1+x)^1/2, {x, 0, n}]

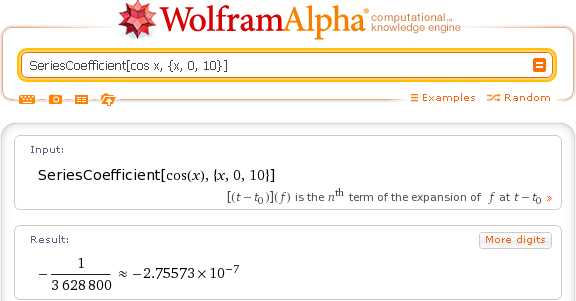
В том случае, когда нужно найти конкретный коэффициент ряда Маклорена для данной функции, например, коэффициент при x^10, используйте запрос вида:

SeriesCoefficient[cos x, {x, 0, 10}]

Наконец, если нужно найти несколько коэффициентов ряда для степеней n, например, с 6-й по 12-ю, запрос к Wolfram|Alpha формулируем так:

SeriesCoefficient[cos x, {x, 0, 6..12}]

Если хотите узнать, как выполнять приближенные вычисления при помощи степенных рядов в Wolfram|Alpha, читайте следующий пост.

www.wolframalpha-ru.com

Ряд Тейлора. Разложение функций в степенные ряды — КиберПедия

Для функции , имеющей все производные до -го порядка включительно, в окрестности точки (т. е на некотором интервале, содержащем точку ) справедлива формула Тейлора:

, (3.18)

где – так называемый остаточный член.

Если функция имеет производные всех порядков в окрестности точки и в этой окрестности, то справа в формуле получается степенной ряд, который называется рядом Тейлора:

(3.19)

Последнее равенство справедливо лишь в том случае, если при . В этом случае степенной ряд справа сходится и его сумма равна данной функции (говорят, что функция разложена в ряд по степеням ). Если же , то ряд не представляет данной функции, хотя может и сходиться (к другой функции).

Частный случай ряда Тейлора при иногда называют рядом Маклорена. Он имеет вид

(3.20)

Для каждой из элементарных функций существует такое и , что в интервале она разлагается в ряд Тейлора или (если ) в ряд Маклорена.

Разложение некоторых элементарных функций в ряд Маклорена:

· , ; (3.21)

· , ; (3.22)

· , ; (3.23)

· , ; (3.24)

· Биномиальный ряд

, (3.25)

где – произвольное постоянное число, .

 

Пример. Разложить в ряд Тейлора по степеням .

◄ Имеем: ;

…

Таким образом,

. ►

Ряды Фурье

Функциональный ряд вида

, (3.26)

называется тригонометрическим рядом. Постоянные числа и ( =1, 2, …) называются коэффициентами тригонометрического ряда.

Если ряд (3,26) сходится, то его сумма есть периодическая функция с периодом , т. е. , так как и являются периодическими функциями с периодом .

Рядом Фурье интегрируемой и периодической с периодом интегрируемой функции называется тригонометрический ряд (3.26) с коэффициентами и ( =1, 2, …), определяемыми формулами:

(свободный член), (3.27)

 

, ( =1, 2, …), (3.28)

, ( =1, 2, …). (3.29)

Определенные по формулам (3.27) ― (3.29) коэффициенты называются коэффициентами Фурье функции . Теория разложения функций в ряды Фурье называется гармоническим анализом.

Ряд Фурье функции может либо расходиться, либо сходиться, причем как к функции , так и к функции, отличной от нее. Условия сходимости ряда Фурье даются теоремой Дирихле.

Теорема Дирихле. Если функция непрерывна или имеет конечное число точек разрыва на отрезке и при этом монотонна или имеет конечное число экстремумов на , то ряд Фурье функции сходится для любых из и его сумма равна:

1) для всех точек непрерывности из интервала ;

2) для всех точек разрыва , где и – левосторонний и правосторонний предел функции в этих точках, соответственно;

3) при и .

 

Пример. Разложить в ряд Фурье периодическую функцию с периодом , определенную следующим образом: .

 

Рис. 1

 

 

◄ Эта функция кусочно монотонная и ограниченная. Следовательно, она допускает разложение в ряд Фурье. Вычисляем коэффициенты Фурье:

 

=

 

 

=

 

Окончательно получаем

.

В точках разрыва функции сумма ряда равна среднему арифметическому ее пределов справа и слева, т. е. в данном случае . ►

 

Если является четной функцией , то =0 ( =1, 2, …) и, следовательно, разложение четной функции в ряд Фурье будет содержать только косинусы:

,

где

 

, , ( =1, 2, …). (3.30)

Для нечетной функции коэффициенты ( =1, 2, …) и, следовательно, ряд Фурье для нечетной функции будет содержать только синусы:

,

где

 

, ( =1, 2, …). (3.31)

Эти формулы позволяют упрощать вычисления при нахождении коэффициентов Фурье в тех случаях, когда заданная функция является четной или нечетной. Но следует отметить, что не всякая периодическая функция является четной или нечетной.

 

Пример. Разложить в ряд Фурье периодическую функцию с периодом , определенную следующим образом: (рис. 2).

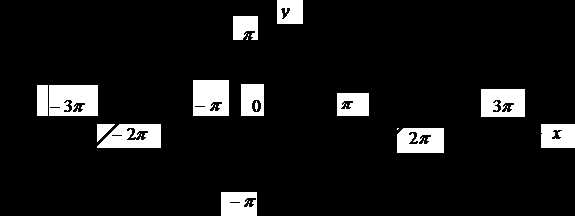
Рис. 2

◄ Заданная функция является нечетной. Следовательно, в ее разложении будут только синусы. По формуле (3.31) вычисляем коэффициенты :

.

Таким образом, получаем ряд

.

Это равенство имеет место во всех точках, кроме точек разрыва. В каждой точке разрыва сумма ряда равна среднему арифметическому ее пределов справа и слева, т. е. нулю. ►

 

cyberpedia.su

No related posts.