Скалярное, векторное и смешанное произведения векторов
1. Скалярное произведение векторов.
Скалярным произведением двух векторов называется число, равное произведению их длин на косинус угла между ними:
ab = |a||b|cos (5.1)
Скалярное произведение коммутативно и удовлетворяет свойству линейности по каждому из сомножителей.
Из определения скалярного произведения следует часто применяющаяся формула для вычисления длины вектора:
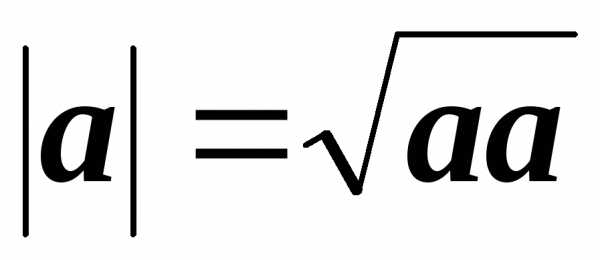 (5.2)
(5.2)
Пусть теперь векторы а и b заданы своими координатами: аи b. Скалярное произведение векторов равно сумме произведений соответствующих координат этих векторов:
ab = (5.3)
В
качестве следствия из этой теоремы
получаем формулу для вычисления косинуса
угла  между векторамиa и b:
между векторамиa и b:
(5.4)
2. Векторное произведение векторов.
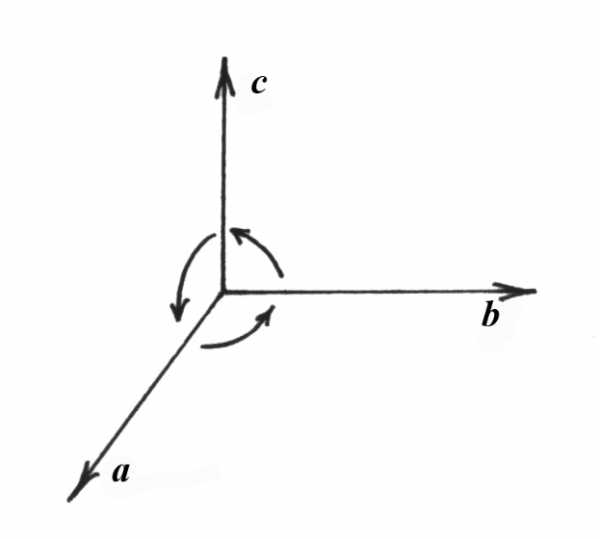
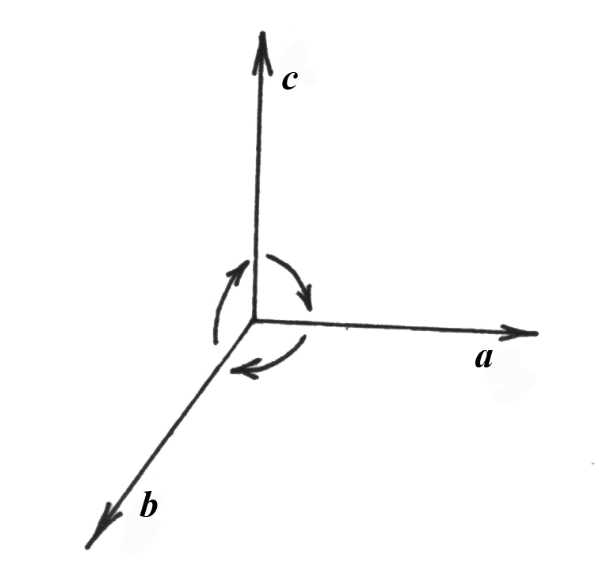
Упорядоченная тройка некомпланарных векторов (а, b, c), приведенных к общему началу, называется правой, если, находясь внутри трехгранного угла, образованного этими векторами, поворот от а к b, от b к с, от с к а виден против часовой стрелки (рис. 5.1). В противном случае тройка векторов называется левой (рис. 5.2).
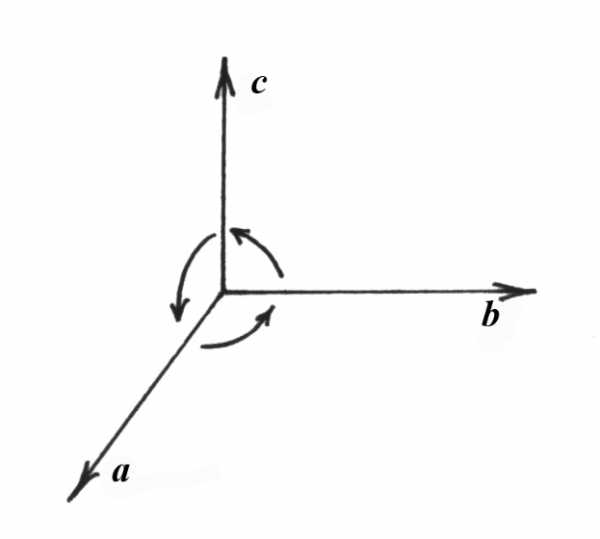

правая тройка левая тройка
Рис. 5.1 Рис. 5.2
Векторным произведением векторов а и b называется вектор с, удовлетворяющий условиям:
|c| = |a||b| sin , где – угол между векторами а и b;
вектор с перпендикулярен векторам а и b;
тройка векторов (а, b, c) является правой.
Мы будем обозначать векторное произведение следующим образом:
Свойства векторного произведения.
Векторы а и b коллинеарны тогда и только тогда, когда а b = 0, в частности, а а = 0.
Если векторы а и b привести к общему началу, то длина их векторного произведения |а b| будет равна площади S параллелограмма, построенного на векторах а и b (см. рис. 5.3) (геометрический смысл векторного произведения).
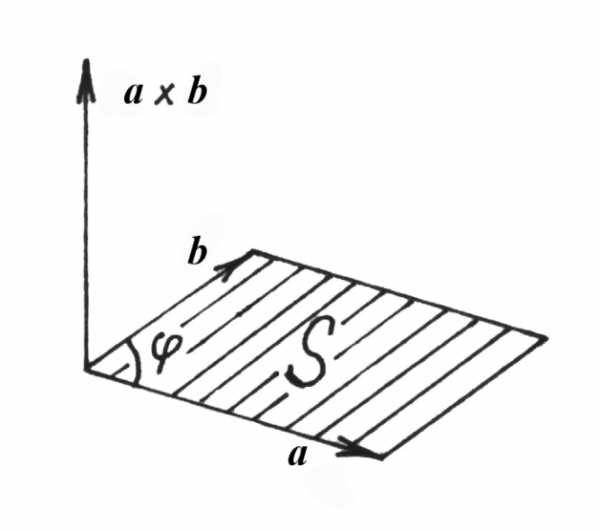
Рис. 5.3
Свойство антикоммутативности: а b = – b a.
Числовой множитель можно выносить за знак векторного произведения:
а b = (а b), а b = (а b).
Свойство дистрибутивности:
(a + b) c = a c + b c, a (b + c) = a b + a c.
Если известны координаты векторов аи b, то векторное произведение вычисляется по формуле:
a b = (5.5)
Для координатной записи векторного произведения удобно использовать символы определителя 2-го и 3-го порядков:
a b =(5.6)
или
a b =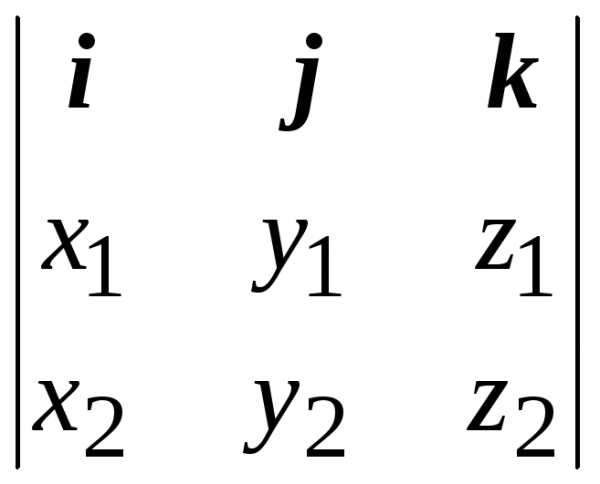 (5.7)
(5.7)
3. Смешанное произведение векторов.
Смешанным произведением трех векторов a, b и с называется скаляр (а b)c.
Геометрический смысл смешанного произведения: смешанное произведение (а b)c трех некомпланарных векторов равно объему параллелепипеда, построенного на векторах a, b и с, приведенных к общему началу, и взятому со знаком «+», если тройка (a, b, с) правая, и со знаком «–», если тройка (a, b, с) левая.
В связи с этим смешанное произведение принято обозначать abс = (а b)c = a(b c).
Заметим, что тройка векторов меняет свою ориентацию (т.е. будучи левой становится правой, и наоборот), если в ней переставляются любые два вектора. Поэтому справедливы равенства: abс = – baс = – сbа = –acb.
Если три вектора определены своими координатами: а, bи с, то смешанное произведение вычисляется по формуле:
abс = 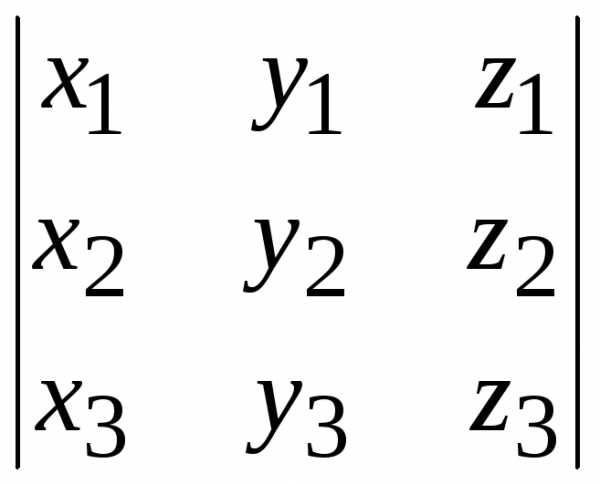
Используя смешанное произведение, можно сформулировать простое и удобное условие компланарности трех векторов: три вектора a, b и с компланарны тогда и только тогда, когда их смешанное произведение равно нулю. Следовательно, три вектора a, b и с компланарны тогда и только тогда, когда определитель, составленный из их координат, равен нулю:
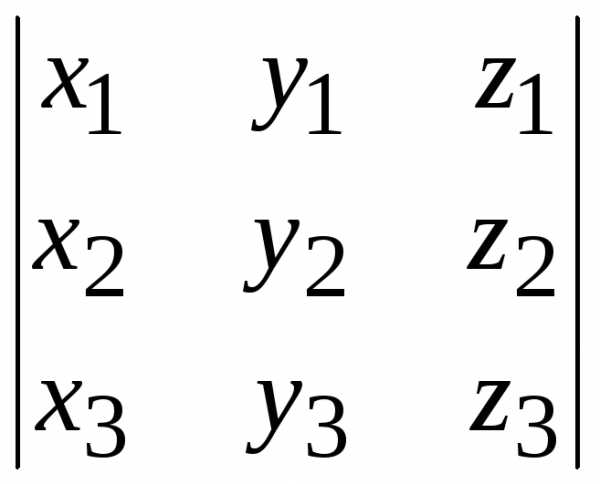 =
0
(5.9)
=
0
(5.9)
studfiles.net
Скалярное, векторное и смешанное произведения векторов
1. Скалярное произведение векторов.
Скалярным произведением двух векторов называется число, равное произведению их длин на косинус угла между ними:ab = |a||b|cos (5.1)
Скалярное произведение коммутативно и удовлетворяет свойству линейности по каждому из сомножителей.
Из определения скалярного произведения следует часто применяющаяся формула для вычисления длины вектора:
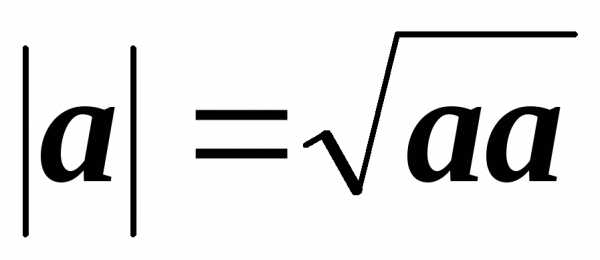 (5.2)
(5.2)
Пусть теперь векторы а и b заданы своими координатами: аи b. Скалярное произведение векторов равно сумме произведений соответствующих координат этих векторов:
ab =
В
качестве следствия из этой теоремы
получаем формулу для вычисления косинуса
угла  между векторамиa и b:
между векторамиa и b:
(5.4)
2. Векторное произведение векторов.
Упорядоченная тройка некомпланарных векторов (а, b, c), приведенных к общему началу, называется правой, если, находясь внутри трехгранного угла, образованного этими векторами, поворот от а к b, от b к с, от с к а виден против часовой стрелки (рис. 5.1). В противном случае тройка векторов называется левой (рис. 5.2).
правая тройка левая тройка
Рис. 5.1 Рис. 5.2
Векторным произведением векторов а и b называется вектор с, удовлетворяющий условиям:
|c| = |a||b| sin , где – угол между векторами а и b;
вектор с перпендикулярен векторам а и b;
тройка векторов (а, b, c) является правой.
Мы будем обозначать векторное произведение следующим образом: с = а b.
Свойства векторного произведения.
Векторы а и b коллинеарны тогда и только тогда, когда а b = 0, в частности, а а = 0.
Если векторы а и b привести к общему началу, то длина их векторного произведения |а b| будет равна площади S параллелограмма, построенного на векторах а и b (см. рис. 5.3) (геометрический смысл векторного произведения).
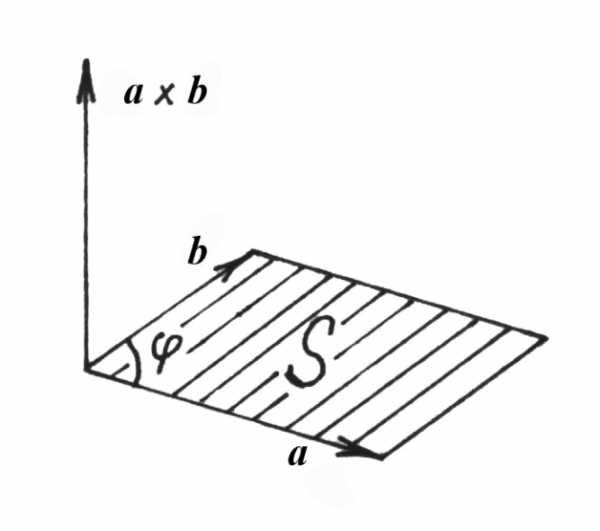
Рис. 5.3
Свойство антикоммутативности: а b = – b a.
Числовой множитель можно выносить за знак векторного произведения:
а b = (а b), а b = (а b).
Свойство дистрибутивности:
(a + b) c = a c + b c, a (b + c) = a b + a c.
Если известны координаты векторов аи b, то векторное произведение вычисляется по формуле:
a b = (5.5)
Для координатной записи векторного произведения удобно использовать символы определителя 2-го и 3-го порядков:
a b =(5.6)
или
a b =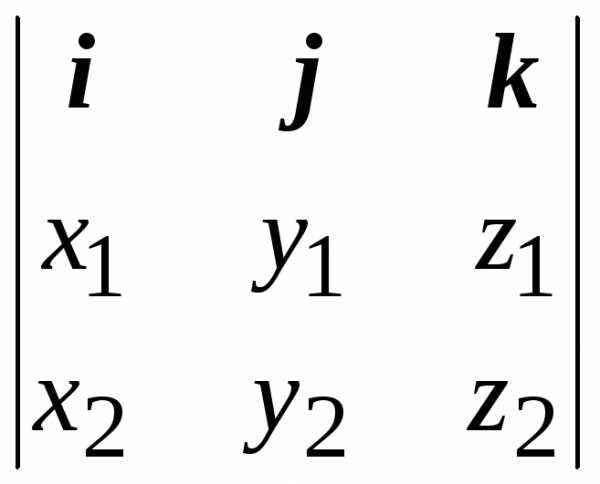 (5.7)
(5.7)
3. Смешанное произведение векторов.
Смешанным произведением трех векторов a, b и с называется скаляр (а b)c.
Геометрический смысл смешанного произведения: смешанное произведение (а b)c трех некомпланарных векторов равно объему параллелепипеда, построенного на векторах a, b и с, приведенных к общему началу, и взятому со знаком «+», если тройка (a, b, с) правая, и со знаком «–», если тройка (a, b, с) левая.
В связи с этим смешанное произведение принято обозначать abс = (а b)c = a(b c).
Заметим, что тройка векторов меняет свою ориентацию (т.е. будучи левой становится правой, и наоборот), если в ней переставляются любые два вектора. Поэтому справедливы равенства: abс = – baс = – сbа = –acb.
Если три вектора определены своими координатами: а, bи с, то смешанное произведение вычисляется по формуле:
abс = 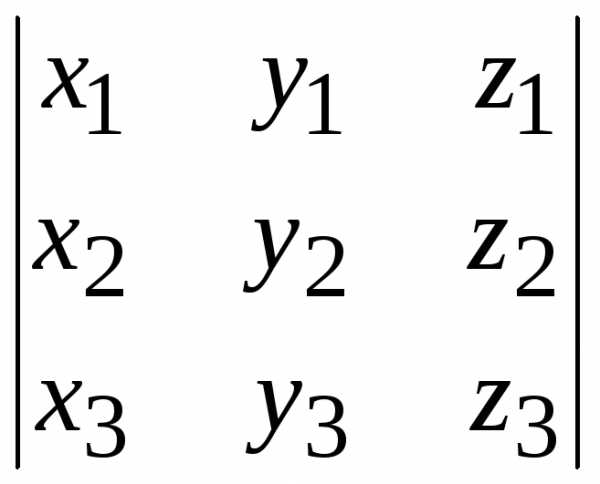 (5.8)
(5.8)
Используя смешанное произведение, можно сформулировать простое и удобное условие компланарности трех векторов: три вектора a, b и с компланарны тогда и только тогда, когда их смешанное произведение равно нулю. Следовательно, три вектора a, b и с компланарны тогда и только тогда, когда определитель, составленный из их координат, равен нулю:
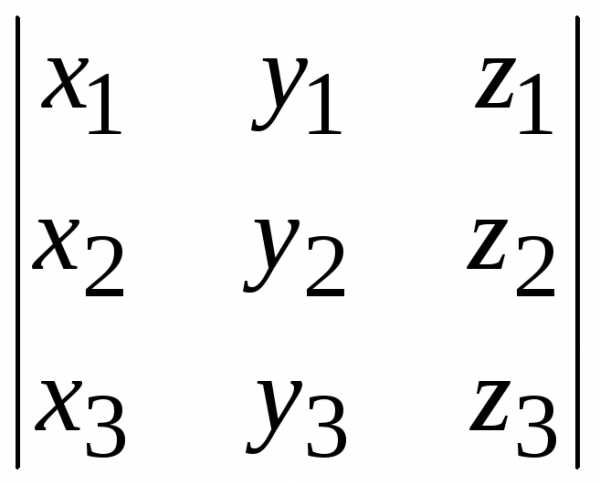 =
0
(5.9)
=
0
(5.9)
studfiles.net
4. Векторы. Скалярное и векторное произведения векторов.
п.1. Скалярное произведение векторов.
Определение. Скалярным произведением двух векторов называется произведение их модулей на косинус угла между ними.
Обозначение: .
Теорема. (Свойства скалярного произведения.)
1). Скалярное произведение подчиняется закону коммутативности:
, .
2). Скалярное произведение двух векторов равно нулю тогда и только тогда, когда хотя бы один из векторов нулевой или векторы ортогональны:
или или .
3). Скалярный квадрат вектора равен квадрату его модуля:
.
4). .
Доказательство. Все свойства очевидны из определения и их доказательства предоставляются читателям.
Теорема. (Свойство линейности скалярного произведения.)
1) Скалярное произведение дистрибутивно относительно сложениявекторов:
, .
2) Скалярный множитель можно выносить за знак скалярногопроизведения:
, , .
Доказательство. По свойству 4 предыдущей теоремы и по свойству проекции вектора на вектор (на ось) имеем:
.
Второе свойство доказывается аналогично.
Теорема доказана.
Замечание. Скалярное произведение можно рассматривать как числовую функцию от двух переменных, определенную на декартовом квадрате множества векторов :
,
т.е. , .
Тогда, свойства теоремы могут быть записаны так:
1) , ;
2) , , .
Первое из этих свойств называется свойством аддитивности функции f по первому аргументу, а второе – свойством однородности по первому аргументу. Если выполняются оба свойства, то говорят, что функция f линейна по первому аргументу. Отсюда происходит и название этих свойств скалярного произведения.
В силу коммутативности, скалярное произведение какфункция двух переменных линейна и по второму аргументу, т.е. справедливы еще два свойства:
3) , ;
4) , , .
Теорема. (Скалярное произведение векторов в координатной форме.) Скалярное произведение векторов равно сумме произведений соответствующих координат.
Другими словами, пусть , . Тогда
. (1)
Доказательство. Учитывая, что скалярное произведение ортогональныхвекторов равно нулю, а скалярный квадрат единичного вектора равен 1 , получаем:
, ч.т.д.
Теорема доказана.
Следствие 1. Пусть . Тогда .
Доказательство. Эта формула нам уже известна. Здесь ее можно получить, используя равенство (1), в котором положим :
,
откуда и следует доказываемая формула.
Следствие доказано.
Следствие 2. Пусть , . Тогда
.
Доказательство. Очевидно.
п.5. Смешанное и векторное произведения векторов в координатной форме.
Теорема. Пусть , , . Тогда:
1) ;
2) .
Доказательство. 1) Используем свойство линейности векторногопроизведения:
.
Далее, заметим, что векторные произведения коллинеарных векторов равны нулевому вектору:
.
Рассмотрим другие векторные произведения базисных векторов:
рис.4.
, , .
Эти равенства легко устанавливаются с помощью рис.4.
Отсюда следует:
, ч.т.д.
2) Воспользуемся только что доказанной формулой:
.
Теперь, по теореме о скалярном произведении векторов в координатной форме, получаем:
, ч.т.д.
Теорема доказана.
Замечание. Векторное произведение часто записывают в форме определителя:
.
Разумеется это не определитель, а лишь форма записи векторногопроизведения. Она компактна и удобна для запоминания.
Следствие. Определитель не изменяется при круговой перестановке строк (столбцов) определителя. При транспозиции двух строк (столбцов) определитель меняет знак.
Доказательство. С одной стороны,
.
С другой стороны,
.
Но, , откуда и следует утверждение. Далее, т.к. , то
.
Так как определитель не изменяется при транспонировании, то доказанное свойство справедливо и для столбцов определителя.
Следствие доказано.
it-iatu.ru
Физический смысл скалярного произведения векторов. Векторное произведение векторов » Аналитическая геометрия f(x)dx.Ru
п.2. Физический смысл скалярного произведения векторов. Работа постоянной силы.
Пусть материальная точка перемещается под действием постоянной силы вдоль вектора перемещения .
рис.1.
На рисунке 1 сила разложена на две ортогональные составляющие и , причем, из физики нам известно, что работа при перемещении материальной точки вдоль вектора создается составляющей и равна .
С другой стороны, , откуда получаем:
.
п.3. Векторное произведение векторов.
Определение. Векторным произведением вектора на вектор называется третий вектор , который удовлетворяет следующим трем условиям:
1) и ;
2) тройка векторов является правоориентированной;
3) .
рис.2.
Обозначение: .
Из определения следует, что, если векторы , и отложить от одной точки, то
1) вектор перпендикулярен плоскости, в которой лежат векторы и ;
2) кратчайший поворот вектора к вектору происходит против часовой стрелки, если смотреть «сверху», т.е. со стороны вектора ;
3) длина вектора численно равна площади параллелограмма, построенного на векторах и , как на его сторонах.
Теорема. (Свойства векторного произведения.)
1). Антикоммутативность:
, .
2). Условие коллинеарности векторов:
.
3). Модуль векторного произведения численно равен площади параллелограмма, построенного на векторах и , как на его сторонах.
Доказательство. 1) Пусть . Рассмотрим вектор . Этот вектор удовлетворяет всем трем условиям определения векторного произведения вектора на вектор .
Действительно, т.к. и , то и и . Далее, тройка векторов является правоориентированной, т.е. кратчайший поворот от вектора к вектору происходит против часовой стрелки, если смотреть на плоскость, в которой лежат векторы и «снизу», т.е. со стороны вектора .
И, наконец, , ч.т.д.
2) Если один из векторов или оба равны нулю, то они коллинеарные и их векторное произведение равно нулевому вектору, тут все очевидно. Пусть векторы и ненулевые. Тогда или , а это в свою очередь равносильно тому, что , ч.т.д.
3) Следует из формулы площади параллелограмма.
Теорема доказана.
Возможно найдутся ответы здесь:
fxdx.ru
Векторное произведение — это… Что такое Векторное произведение?
Векторное произведение в трёхмерном пространстве.Векторное произведение — это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном Евклидовом пространстве. Произведение не является ни коммутативным, ни ассоциативным (оно является антикоммутативным) и отличается от скалярного произведения векторов. Во многих задачах инженерии и физики нужно иметь возможность строить вектор, перпендикулярный двум имеющимся — векторное произведение предоставляет эту возможность. Векторное произведение полезно для «измерения» перпендикулярности векторов — длина векторного произведения двух векторов равна произведению их длин, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны либо антипараллельны.
Определить векторное произведение можно по-разному, и теоретически, в пространстве любой размерности n можно вычислить произведение n-1 векторов, получив при этом единственный вектор, перпендикулярный к ним всем. Но если произведение ограничить нетривиальными бинарными произведениями с векторным результатами, то традиционное векторное произведение определено только в трёхмерном и семимерном пространствах. Результат векторного произведения, как и скалярного, зависит от метрики Евклидова пространства.
В отличие от формулы для вычисления по координатам векторов скалярного произведения в трёхмерной прямоугольной системе координат, формула для векторного произведения зависит от ориентации прямоугольной системы координат или, иначе, её «хиральности».
Определение и история
Векторным произведением вектора на вектор в пространстве называется вектор , удовлетворяющий следующим требованиям:
Обозначение:
В литературе[1] определение векторного произведения может даваться по-разному. Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах в правой и левой прямоугольной системе координат. А далее выводится данное выше определение, а также определение правой и левой тройки векторов.
Также для исходного определения может быть взят набор алгебраических свойств векторного произведения, а из них выводиться остальное.
Векторное произведение было введено У. Гамильтоном в 1846 году[2] одновременно со скалярным произведением в связи с кватернионами — соответственно, как векторная и скалярная часть произведения двух кватернионов, скалярная часть которых равна нулю[3].
Правые и левые тройки векторов в трёхмерном пространстве
Рассмотрим упорядоченную тройку некомпланарных векторов в трёхмерном пространстве. Совместим начала этих векторов в точке (то есть выберем произвольно в пространстве точку и параллельно перенесём каждый вектор так, чтобы его начало совпало с точкой ). Концы векторов, совмещённых началами в точке , не лежат на одной прямой, так как векторы некомпланарны. Рассмотрим плоскость — единственную плоскость, проходящую через концы векторов, совмещённых началами в точке . Тогда можно в плоскости провести через концы векторов , совмещённых началами в точке , единственную окружность и выяснить направление обхода трёх точек на окружности, смотря на неё с одной из сторон от плоскости.
Упорядоченная тройка некомпланарных векторов в трёхмерном пространстве называется правой, если наблюдателю, находящемуся по одну сторону с точкой от плоскости , обход концов приведённых в общее начало векторов в указанном порядке кажется совершающимся в плоскости по часовой стрелке.
B противном случае — левая тройка. В этом случае наблюдателю, находящемуся с другой стороны от плоскости , обход концов таких векторов будет казаться совершающимся против часовой стрелки.
Другое определение связано с правой рукой человека (см. рисунок), откуда и берётся название.
Все правые между собой (и левые между собой) тройки векторов называются одинаково ориентированными.
Заметим, что определения «правой» и «левой» тройки векторов не зависят от хиральности рассматриваемой системы координат; более того, они вообще не требуют задания в рассматриваемом пространстве какой-либо системы координат, как и не требует этого само векторное произведение.
Свойства
Геометрические свойства векторного произведения
Рисунок 1: Площадь параллелограмма равна модулю векторного произведения. Рисунок 2: Объём параллелепипеда при использовании векторного и скалярного произведения векторов; пунктирные линии показывают проекции вектора c на a × b и вектора a на b × c, первым шагом является нахождение скалярных произведений.- При использовании векторного и скалярного произведений можно высчитать объём параллелепипеда, построенного на приведённых к общему началу векторах a, b и c (см. Рисунок 2). Такое произведение трех векторов называется смешанным.
На рисунке показано, что этот объём может быть найден двумя способами: геометрический результат сохраняется даже при замене «скалярного» и «векторного» произведений местами:
Величина векторного произведения зависит от синуса угла между изначальными векторами, поэтому векторное произведение может восприниматься как степень «перпендикулярности» векторов также, как и скалярное произведение может рассматриваться как степень «параллельности». Векторное произведение двух единичных векторов равно 1 (единичному вектору), если изначальные векторы перпендикулярны, и равно 0 (нулевому вектору), если векторы параллельны либо антипараллельны.
Алгебраические свойства векторного произведения
Выражение для векторного произведения в декартовых координатах
Если два вектора и определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисе
а система координат правая, то их векторное произведение имеет вид
Для запоминания этой формулы удобно использовать определитель:
или
где — символ Леви-Чивиты.
Если система координат левая, то их векторное произведение имеет вид
Для запоминания, аналогично:
или
Формулы для левой системы координат можно легко получить из формул правой системы координат, записав те же векторы и во вспомогательной правой системе координат ():
Обобщения
Кватернионы
Векторное произведение можно также записать в кватернионной форме, поэтому буквы , , — стандартные обозначения для ортов в : они рассматриваются как воображаемые кватернионы.
Заметим, что соотношения через векторное произведение между , и соответствуют правилам умножения для кватернионов , и . Если представить вектор как кватернион , то векторное произведение двух векторов получается взятием векторной части от произведения соответствующих им кватернионов. Скалярное произведение этих векторов противоположно скалярной части произведения этих кватернионов.
Преобразование к матричной форме
Векторное произведение двух векторов можно записать как произведение кососимметрической матрицы и вектора:
где
Пусть равен векторному произведению:
тогда
Такая форма записи позволяет обобщить векторное произведение на высшие размерности, представляя псевдовекторы (угловая скорость, индукция и т. п.) как такие кососимметричные матрицы. Ясно, что такие физические величины будут иметь независимых компонент в -мерном пространстве. В трёхмерном пространстве получаются три независимые компоненты, поэтому такие величины можно представлять как векторы этого пространства.
С такой формой записи также зачастую проще работать (например, в en:epipolar geometry).
Из общих свойств векторного произведения следует, что
- и
а так как кососимметрична, то
В такой форме записи легко доказывается тождество Лагранжа (правило «бац минус цаб»).
Распространение на матрицы
В трёхмерном случае можно определить векторное произведение матриц и произведение матрицы на вектор. Это делает очевидным указанный выше изоморфизм и позволяет упростить многие выкладки. Представим матрицу как столбец векторов, тогда
Умножение матрицы на вектор слева определяется аналогично, если представить как строку векторов. Транспонирование матрицы, соответственно, переводит строку векторов в столбец векторов, и наоборот. Легко обобщить многие соотношения для векторов на соотношения для векторов и матриц, например ( — матрица, , — векторы):
После этого можно изменить форму записи для векторного произведения:
— единичная матрица. Отсюда очевидны существование и вид матрицы, соответствующей векторному умножению на вектор слева. Аналогично можно получить выражение для матрицы умножения на вектор справа. Распространяя операции над векторами на матрицы покомпонентно, представляя их как «векторы из векторов», стандартные соотношения для векторов легко обобщаются на матрицы. Например, теорема Стокса в примет вид:
где ротор матрицы вычисляется как векторное произведение матрицы на оператор Гамильтона слева. В этих обозначениях очень легко доказать, например, следующие формы теоремы Стокса:
Размерности, не равные трём
Пусть — размерность пространства.
Векторное произведение, обладающее всеми свойствами обычного трёхмерного векторного произведения, то есть бинарное билинейное антисимметричное невырожденное отображение , можно ввести только для размерностей 3 и 7.
Однако есть простое обобщение на остальные натуральные размерности, начиная с 3, а если нужно — и на размерность 2 (последнее, правда, сравнительно специфическим образом). Тогда это обобщение, в отличие от невозможного, описанного чуть выше, вводится не для пары векторов, а лишь для набора векторов-сомножителей. Вполне аналогично смешанному произведению, естественно обобщаемому в -мерном пространстве на операцию с сомножителями. Используя символ Леви-Чивиты с индексами, можно явно записать такое -валентное векторное произведение как
Такое обобщение дает гиперплощадь размерности .
Если нужно ввести операцию именно для двух сомножителей, имеющую геометрический смысл, предельно близкий к смыслу векторного произведения (то есть представляющую ориентированную площадь), то результат уже не будет вектором, так как при не найдется единственной, однозначно определённой нормали к двумерной плоскости, натянутой на множители. Можно ввести бивектор, компоненты которого равны проекциям ориентированной площади параллелограмма, натянутого на пару векторов, на координатные плоскости:
- .
Эта конструкция называется внешним произведением.
Для двумерного случая операция
- .
называется псевдоскалярным произведением, так как получающееся пространство одномерно и результат есть псевдоскаляр. (Двухиндексное внешнее произведение, описанное выше, можно ввести и для двумерного пространства, однако оно, очевидно, достаточно тривиально связано с псевдоскалярным произведением, а именно внешнее произведение в этом случае представляется матрицей, на диагонали которой нули, а оставшиеся два недиагональных элемента равны псевдоскалярному произведению и минус псевдоскалярному произведению).
Алгебра Ли векторов
Векторное произведение вводит на структуру алгебры Ли (поскольку оно удовлетворяет обеим аксиомам — антисимметричности и тождеству Якоби). Эта структура соответствует отождествлению с касательной алгеброй Ли к группе Ли ортогональных линейных преобразований трёхмерного пространства.
См. также
Произведения векторов
Другое
Примечания
Литература
- Кочин Н. Е. Введение в векторный и тензорный анализ.
Ссылки
dic.academic.ru
Понятие скалярного, векторного и смешанного произведения векторов. Скалярное произведение векторов
Глава 3 Понятие скалярного, векторного и смешанного произведения векторов.
3.1 Скалярное произведение векторов.
В главе 1 была введена операция умножения вектора на число. Теперь же введём в рассмотрение скалярное произведение двух векторов и .
Определение:Скалярным произведением двух векторов и называется число равное произведению длин этих векторов на косинус угла между ними.
Будем обозначать скалярное произведение —
Таким образом:
-угол между векторами и
Скалярное произведение обладает следующими свойствами.
Свойство 1: переместительное свойство
Свойство 2: Скалярное произведение равно модулю одного из векторов умноженному на проекцию другого вектора на направление первого
Свойство 3: Распределительное свойство
Свойство 4: Пусть и — скаляры
Свойство 5: Чтобы векторы и были перпендикулярны необходимо и достаточно чтобы их скалярное произведение было равно нулю
Если векторы и заданы своими координатами, то можно получить правило вычисления скалярного произведения.
Пусть:
Используя полученную формулу, можно получить другие полезные формулы, часто применяемые при решении различных задач.
3.2 Векторное произведение
Пусть даны два вектора и .
Определение: Векторным произведением двух векторов и называется вектор , обладающий следующими свойствами.
1. Модуль вектора равен произведению модулей векторов и на синус угла между ними
2. Вектор перпендикулярен векторам и .
3. Вектор направлен таким образом, что для наблюдателя находящегося в его конце кратчайший поворот первого вектора к второму вектору должен происходить против хода часовой стрелки (см. рис. 3.1)
Рис 3.1
Будем обозначать векторное произведение проще .
Свойства векторного произведения.
Свойство 1: Если векторы и не коллинеарны, то модуль векторного произведения равен площади параллелограмма построенного на векторах и .
B C
A D
Рис 3.2
Свойство 2: Векторное произведение векторов и равно нулю тогда и только тогда когда векторы и коллинеарны.
Свойство 3: При перестановке векторов и векторное произведение этих векторов меняет знак на противоположенный.
Свойство 4: Пусть и — числа
Свойство 5: Распределительное свойство
Если векторы и заданы своими координатами , , то их векторное произведение:
- единичные векторы лежащие на осях ОХ, ОУ, OZ направленные вдоль оси декартовой системы координат.
3.3 Смешанное произведение трёх векторов.
Прежде чем дать определение смешанного произведения, введём в рассмотрение понятие правой и левой тройки векторов. Пусть три вектора с общим началом не лежат в одной плоскости.
Определение: Тройка векторов называется правой (левой) тройкой если для наблюдателя, находящегося в конце третьего вектора , кратчайший поворот от первого вектора ко второму вектору происходит против хода часовой стрелки. На Рис. 3.3 показана правая тройка , на Рис. 3.4 левая тройка .
Рис 3.3
Рис 3.4
Определение: Смешанным произведением трёх векторов называется число равное скалярному произведению векторов и .
Смешанное произведение трёх векторов обозначается или таким образом по определению
где — угол между векторами и .
Очень важным при решении задач является геометрический смысл смешанного произведения. Пусть три вектора имеют общее начало и не лежат в одной плоскости. Построим на этих векторах как на рёбрах параллелепипед (Рис. 3.5)
B1 C1
 |
A1 D1
B C
A D
Рис. 3.5
По определению смешанного произведения
Величина геометрически выражает площадь параллелограмма АВСD.
Величина является проекцией вектора на направление вектора , причём если угол — острый, то , если — тупой то , — высота параллелепипеда, таким образом
легко видеть, что если векторы образуют правую тройку то угол — острый и имеем знак плюс, в случае же если векторы образуют левую тройку то угол — тупой и имеет знак минус.
Таким образом, смешанное произведение трёх векторов равно объёму параллелепипеда, построенного на этих векторах, и взятого со знаком плюс, если векторы образуют правую тройку и со знаком минус если векторы образуют левую тройку.
Очень важно уметь вычислять смешанное произведение в случае если векторы заданы своими координатами.
,
,
Ещё одним свойством смешанного произведения является его связь с понятием компланарности векторов.
vunivere.ru
