Глава 8. Собственные значения и собственные векторы матрицы.
В этой главе рассматриваются вопросы о собственных векторах и собственных значениях произвольной квадратной матрицы, симметрической матрицы и подобных матриц.
1. Основные понятия.
Определение. Вектор 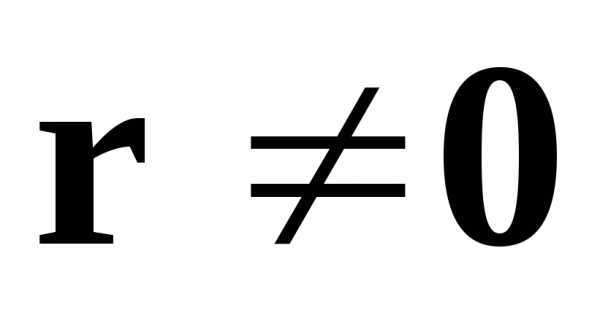 ,
называетсясобственным
вектором квадратной матрицы
,
называетсясобственным
вектором квадратной матрицы  ,
если существует такое число
,
если существует такое число ,
что
,
что
.
При
этом число называетсясобственным
значением матрицы
называетсясобственным
значением матрицы  ,
соответствующим собственному вектору
,
соответствующим собственному вектору
Уравнение может быть записано в виде
.
Определение. Если  — собственное значение матрицы
— собственное значение матрицы ,
а
,
а соответствующий ему собственный вектор,
то
соответствующий ему собственный вектор,
то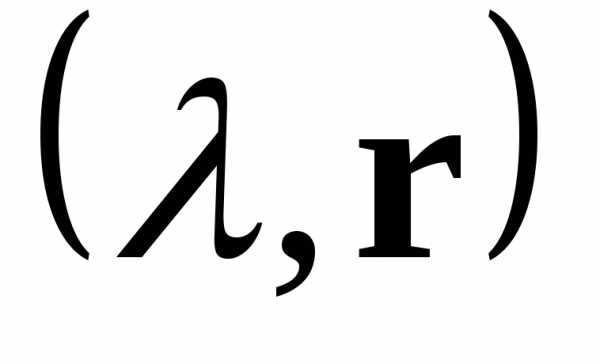 называютсобственной
парой матрицы
называютсобственной
парой матрицы  .
.
● Пример 1. Показать,
что вектор 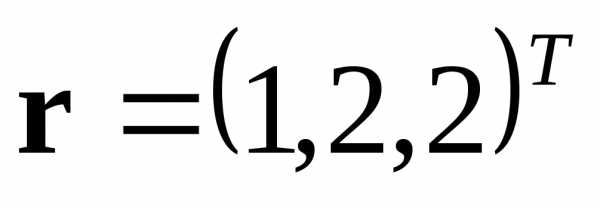 является собственным вектором матрицы
является собственным вектором матрицы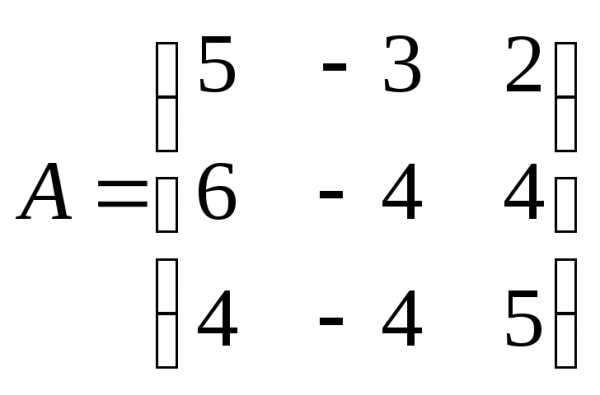 .
Найти
соответствующее ему собственное
значение.
.
Найти
соответствующее ему собственное
значение.
Решение.
Так как 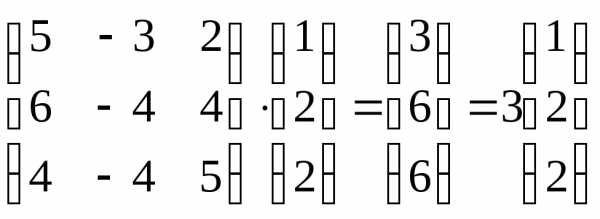
 ),
то
),
то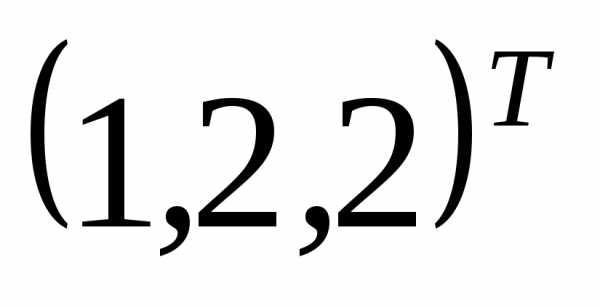 —
собственный вектор матрицы
—
собственный вектор матрицы ,
соответствующий собственному значению
,
соответствующий собственному значению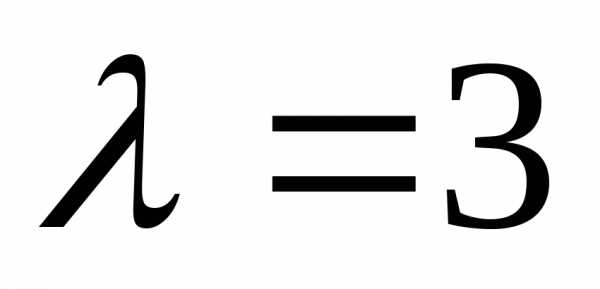 .●
.● ● Пример 2. Показать,
что если 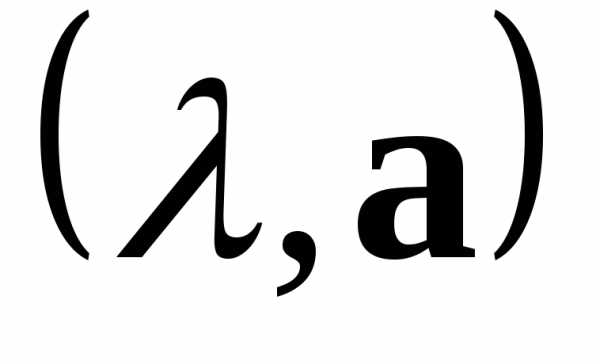 — собственная пара матрицы
— собственная пара матрицы ,
то
,
то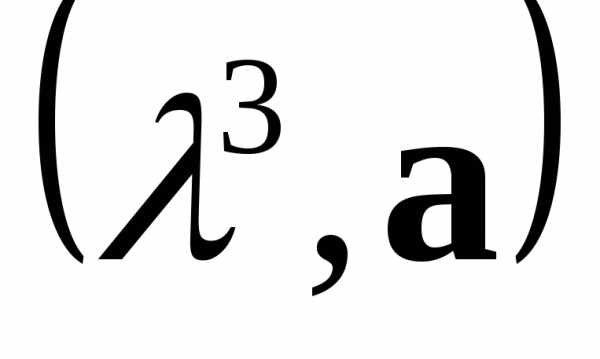 — собственная пара матрицы
— собственная пара матрицы .
.
Решение. Действительно,
,
т.е.
.
Из последнего следует, что — собственная пара матрицы
— собственная пара матрицы
● Пример 3. При каких 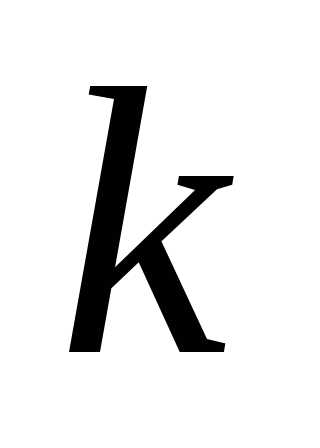 и
и векторявляется собственным вектором матрицы
векторявляется собственным вектором матрицы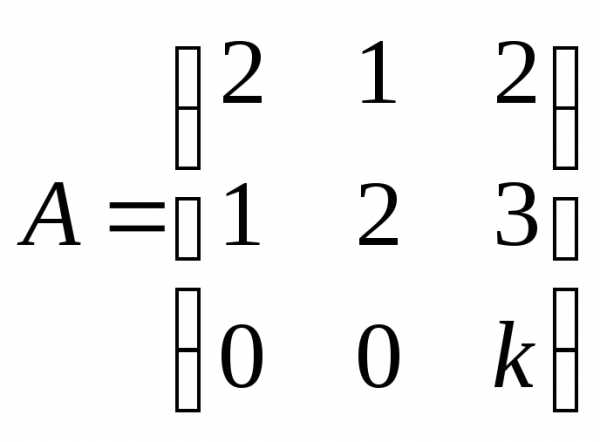 ?
?
Решение. Найдем вектор 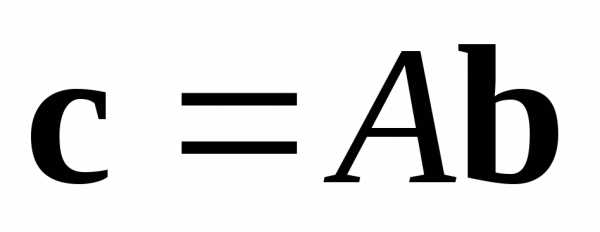 .
. .
.
Если  —
собственный вектор матрицы
—
собственный вектор матрицы  ,
то
,
то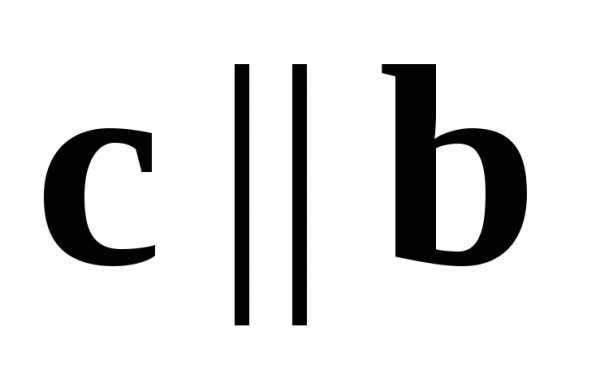 ,
откуда
,
откуда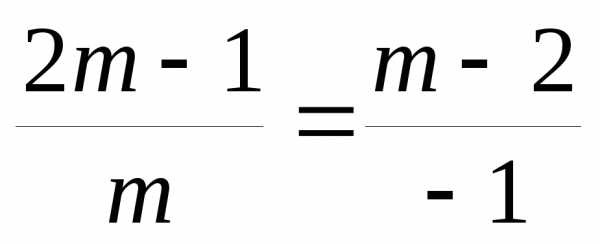 .
Из последнего имееми
.
Из последнего имееми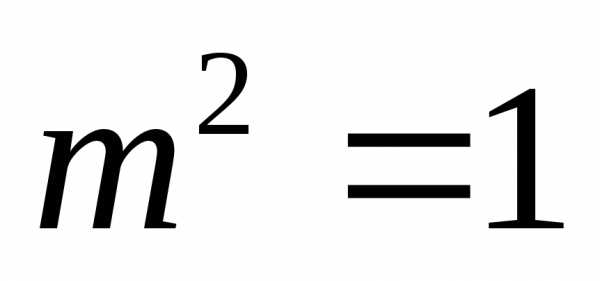
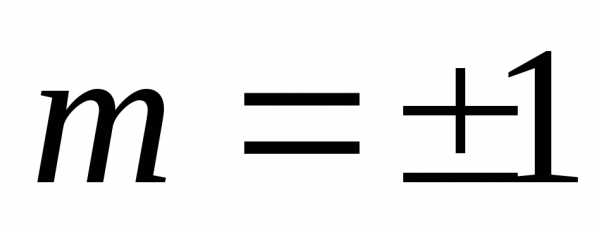 .
. Ответ:
при 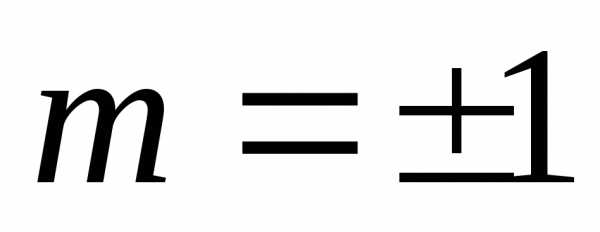 и произвольном
и произвольном векторсобственный вектор матрицы
векторсобственный вектор матрицы .
.
● Пример 4. Существует
ли  ,
при котором-
собственный вектор матрицы
,
при котором-
собственный вектор матрицы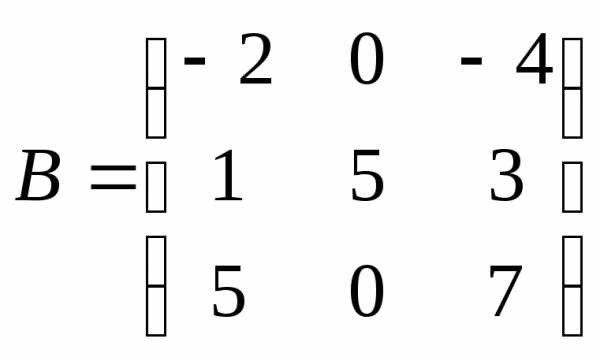 ?
Если существует, указать соответствующую
собственную пару.
?
Если существует, указать соответствующую
собственную пару.
Решение. Вычислим произведение 
Если  —
собственная пара матрицы
—
собственная пара матрицы
.
Из последнего
равенства имеем 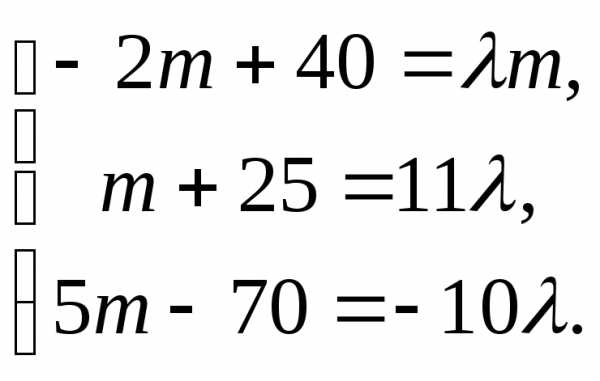 Откуда,
Откуда,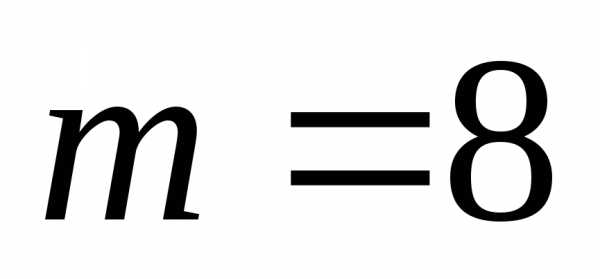 ,
,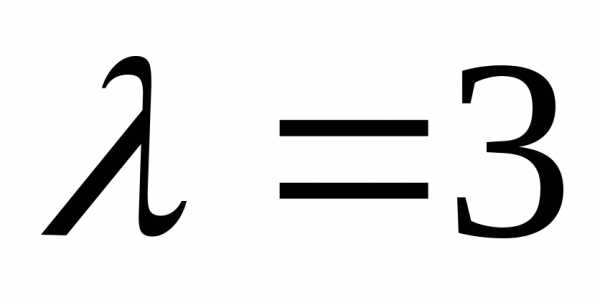 .
.
—
собственная пара матрицы .●
.●
2. Свойства собственных векторов.
1) Если  —
собственный вектор матрицы
—
собственный вектор матрицы  ,
а
,
а —
соответствующее ему собственное
значение, то при любом
—
соответствующее ему собственное
значение, то при любом вектор
вектор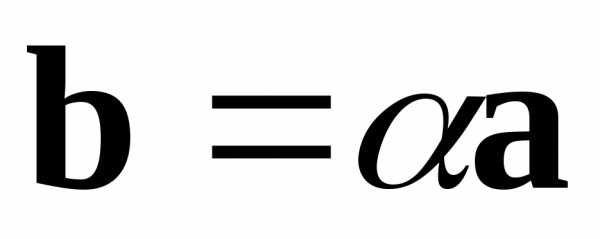 также является собственным вектором
этой матрицы, соответствующим этому же
собственному значению.
также является собственным вектором
этой матрицы, соответствующим этому же
собственному значению.
►Действительно, .◄
Замечание. Любой собственный вектор матрицы определяет целое направление собственных векторов этой матрицы с одним и тем же собственным значением.
2) Собственные векторы матрицы, соответствующие различным её собственным значениям, линейно независимы.
►Доказательство.
Пусть  и
и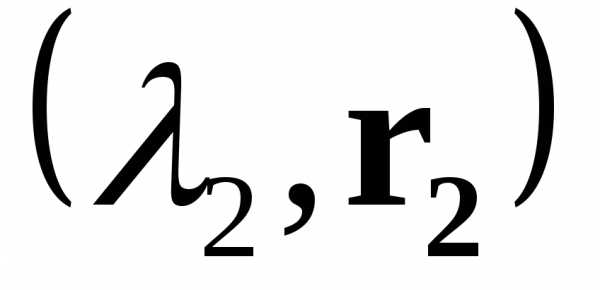 —
собственные пары матрицы
—
собственные пары матрицы ,
где
,
где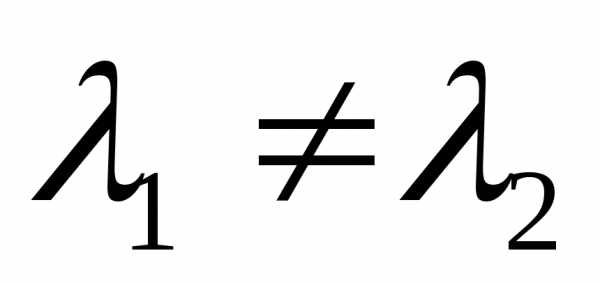 .
.
Предположим, что 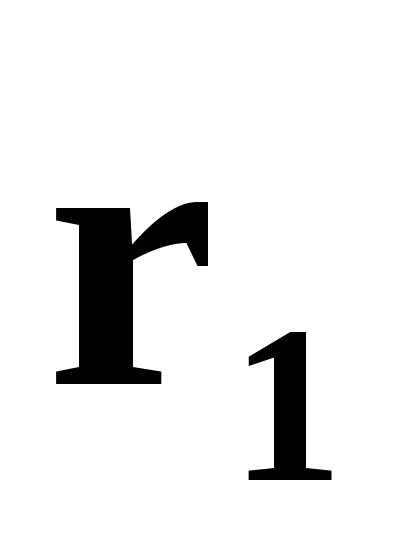 и
и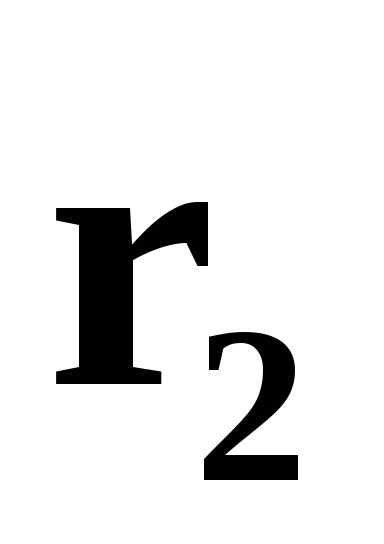 линейно зависимые векторы.
линейно зависимые векторы.
Если 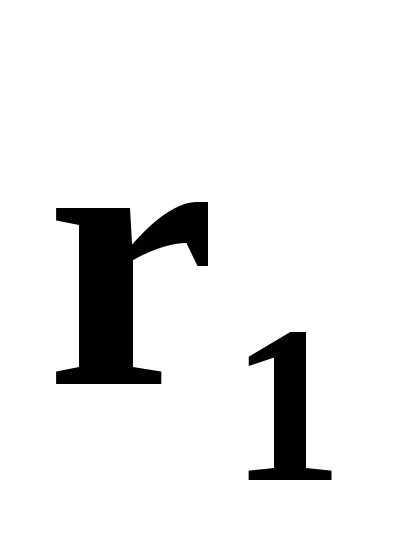 и
и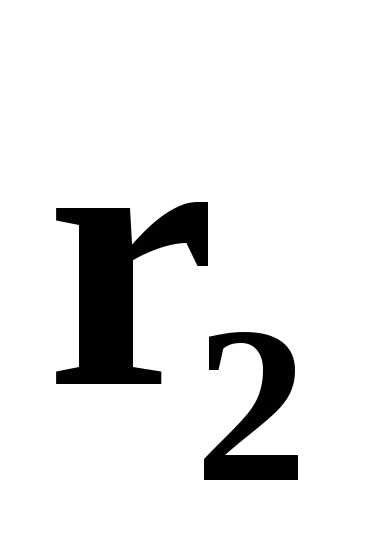 линейно зависимы, то хотя бы один из
этих векторов можно представить в виде
линейной комбинации другого (пусть
линейно зависимы, то хотя бы один из
этих векторов можно представить в виде
линейной комбинации другого (пусть ).
).
Тогда
,
откуда следует, что.
Так как ,
то
,
то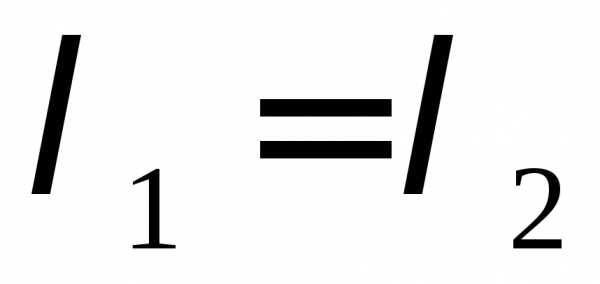 .
.
Полученное противоречие доказывает утверждение.◄
3) Если  и
и линейно независимые собственные векторы
матрицы
линейно независимые собственные векторы
матрицы ,
соответствующие одному и тому же
собственному значению
,
соответствующие одному и тому же
собственному значению
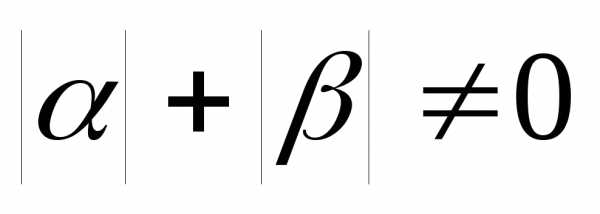 )
также является собственным вектором
этой матрицы, соответствующим этому же
собственному значению.
)
также является собственным вектором
этой матрицы, соответствующим этому же
собственному значению.►Действительно, , что и требовалось доказать.◄
4) Если матрица 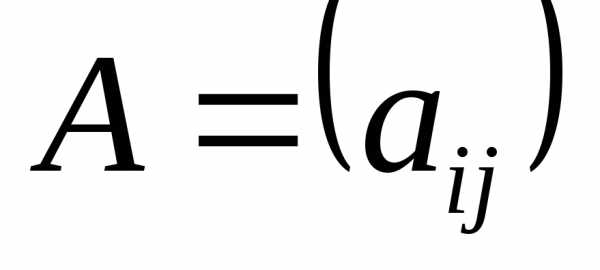 диагональная ,
то ее собственные значения совпадают
с диагональными элементами этой матрицы
(
диагональная ,
то ее собственные значения совпадают
с диагональными элементами этой матрицы
(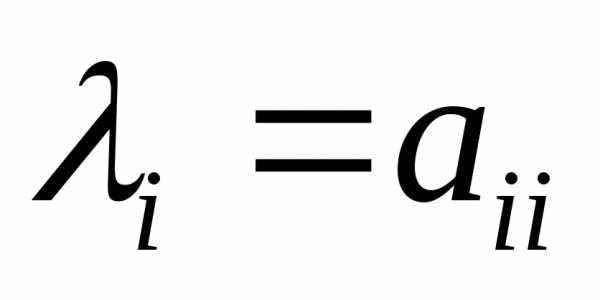 ),
а единичный вектор
),
а единичный вектор является собственным вектором,
соответствующим собственному значению
является собственным вектором,
соответствующим собственному значению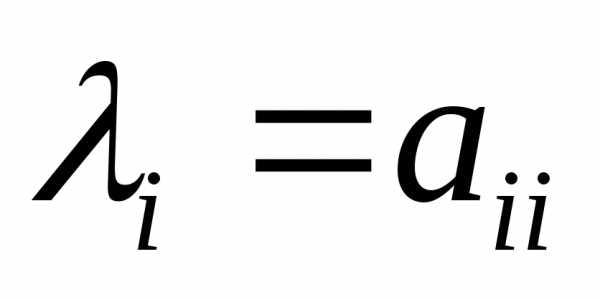 .
.
►Действительно, 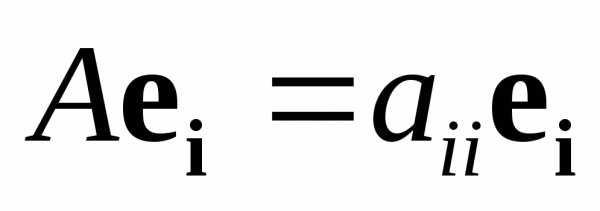 ◄
◄
3 Нахождение собственных значений и собственных векторов.
Собственные
значения и собственные векторы матрицы 
Если  собственный вектор матрицы
собственный вектор матрицы  ,
то однородная системаимеет нетривиальное решение, поэтому(
,
то однородная системаимеет нетривиальное решение, поэтому(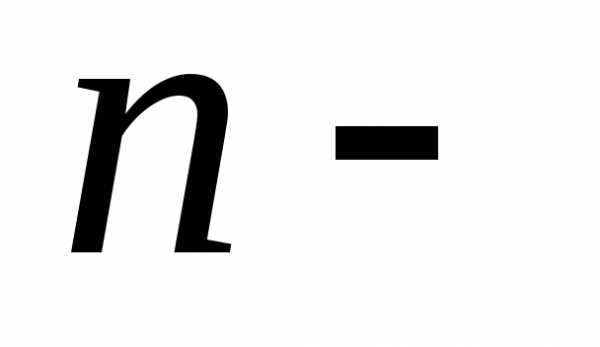 порядок
матрицы
порядок
матрицы и.
Последнее
уравнение позволяет найти собственные
значения матрицы
и.
Последнее
уравнение позволяет найти собственные
значения матрицы .
.
Определение. Многочлен называютхарактеристическим многочленомматрицы .
.
Определение. Уравнение
называется характеристическим уравнением
матрицы 
Корни характеристического уравнения
матрицы  являются собственными значениями
матрицы
являются собственными значениями
матрицы .
.
Характеристическое
уравнение матрицы 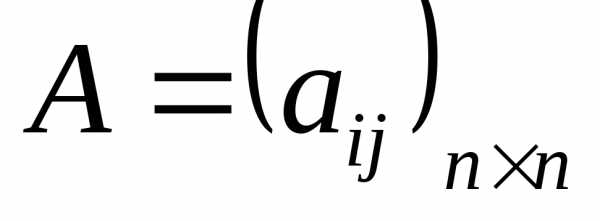 может быть записано в виде
может быть записано в виде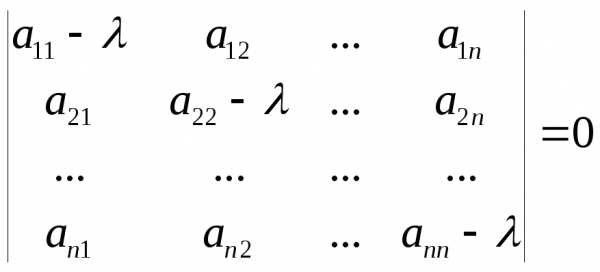 .
.
Определение. Множество всех собственных значений квадратной матрицы называется спектром этой матрицы.
Спектр матрицы 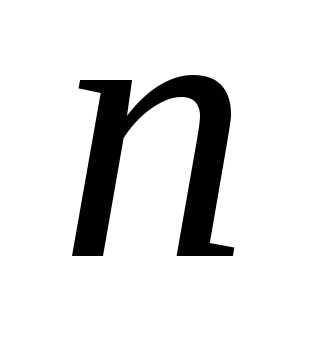 -го
порядка содержит
-го
порядка содержит собственных значений матрицы, которые
могут быть как действительными, так и
комплексными, простыми так и кратными.
собственных значений матрицы, которые
могут быть как действительными, так и
комплексными, простыми так и кратными.
Для матрицы 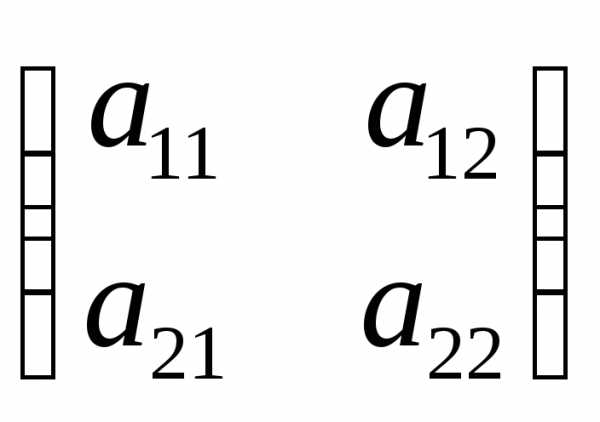 характеристическое уравнение
характеристическое уравнение может быть может быть преобразовано к
виду
.
может быть может быть преобразовано к
виду
.
,
поэтому характеристическое уравнение
матрицы  имеет вид
имеет вид
. (8.1)
При этом
,(8.2)
.(8.3)
Уравнение 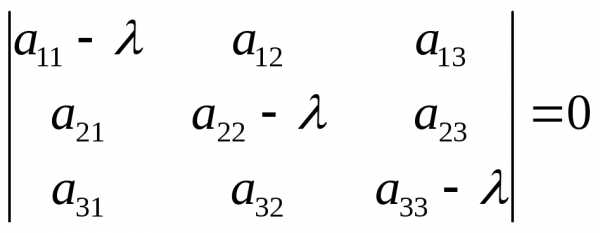 является характеристическим уравнением
матрицы
является характеристическим уравнением
матрицы .Это
уравнение может быть представлено в
виде
.Это
уравнение может быть представлено в
виде
или
, (8.4)
где
,
аминоры определителя .
.
Если  ,
, и
и корни характеристического уравнения
(8.4), то это уравнение может быть записано
в виде
корни характеристического уравнения
(8.4), то это уравнение может быть записано
в виде
. (8.5)
Сравнивая уравнения (8.4) и (8.5), можно записать следующее:
,(8.6)
,(8.7)
.(8.8)
Собственные векторы
матрицы  ,
соответствующие собственному значению
,
соответствующие собственному значению ,
удовлетворяют матричному уравнению,
которое может быть записана в форме
,
удовлетворяют матричному уравнению,
которое может быть записана в форме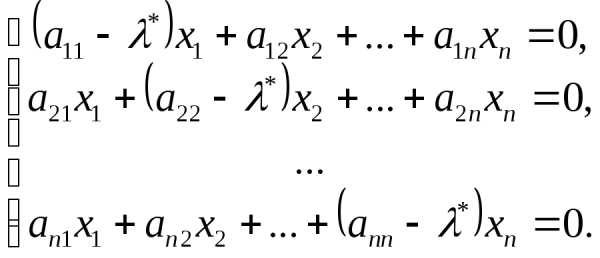 Так
как ранг матрицы этой системы меньше
числа неизвестных (=0),
то система имеет бесконечное множество
Так
как ранг матрицы этой системы меньше
числа неизвестных (=0),
то система имеет бесконечное множество
решений, каждое ненулевое из которых является собственным вектором,
соответствующим собственному значению  .
.
● Пример 5. Найти собственные значения и собственные
векторы матрицы 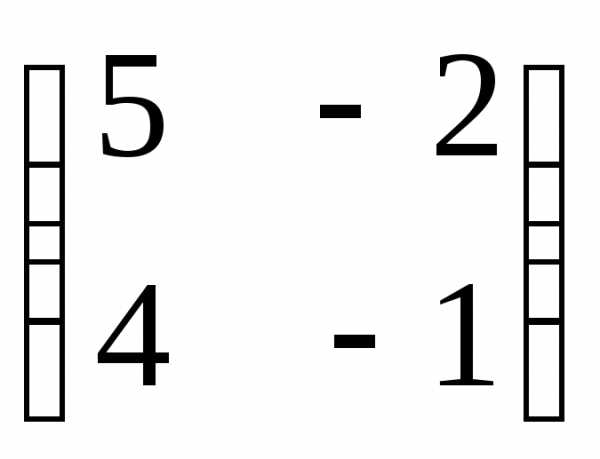 .
.
Решение. 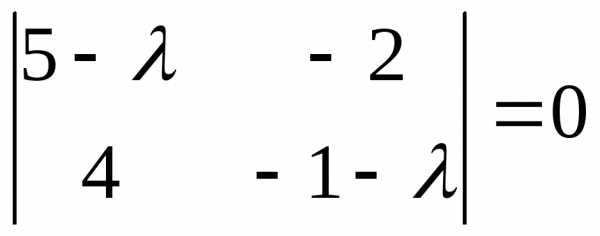 — характеристическое уравнение для
данной матрицы, откуда,
— характеристическое уравнение для
данной матрицы, откуда,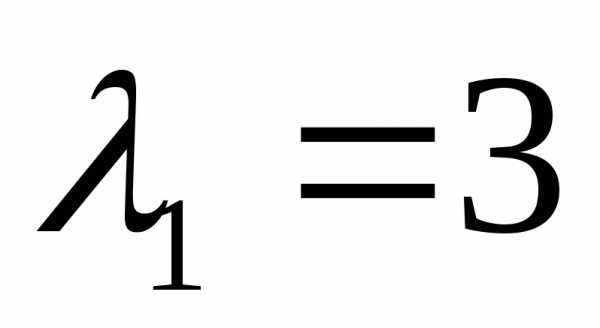 и
и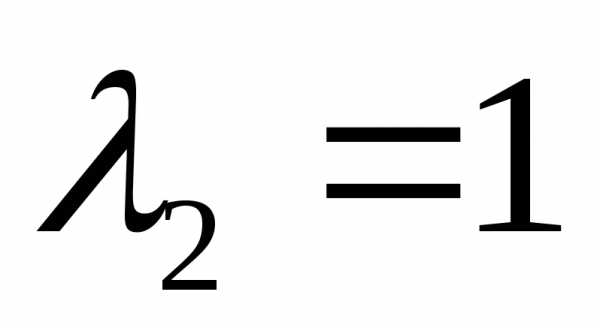 .
.
Для нахождения
собственных векторов, соответствующих
собственному
значению 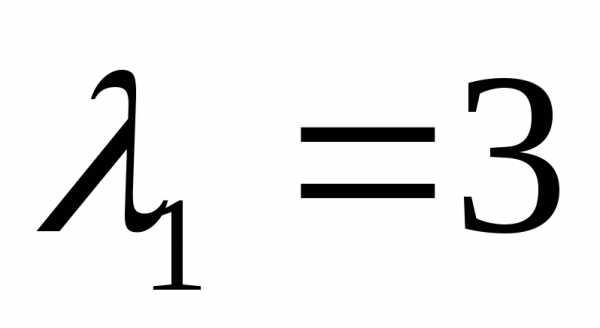 ,
имеем систему
,
имеем систему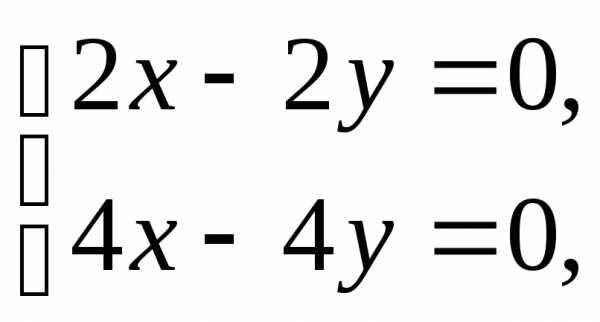 эквивалентную уравнению
эквивалентную уравнению .
Вектор
.
Вектор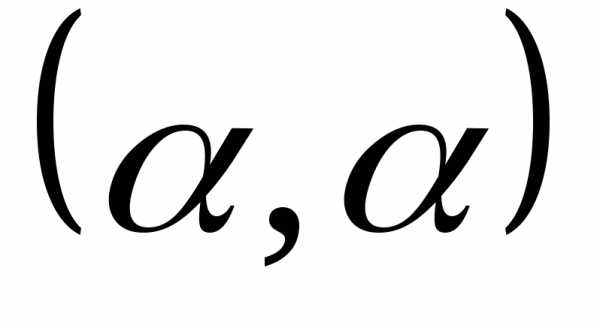 является решением этого уравнения, а
при
является решением этого уравнения, а
при вектор- искомый собственный вектор.
вектор- искомый собственный вектор.
Для
нахождения собственных векторов,
соответствующих собственному значению 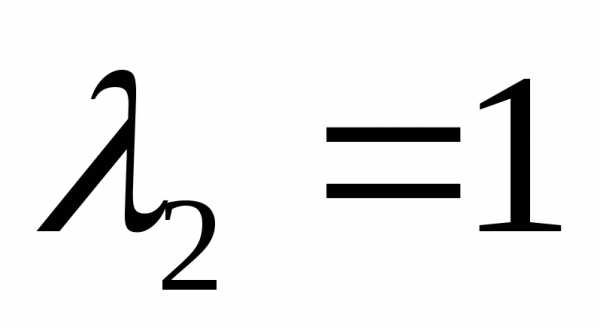 ,
имеем систему
,
имеем систему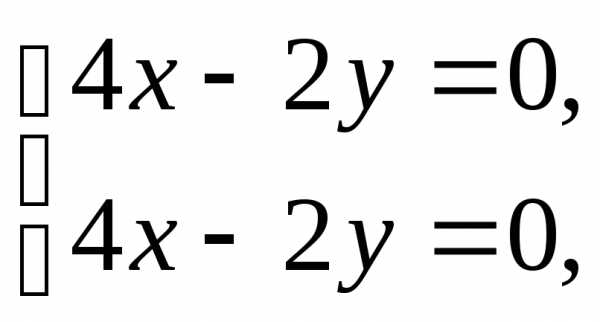 из которой следует, что векторпри
из которой следует, что векторпри является собственным вектором,
соответствующим собственному значению
является собственным вектором,
соответствующим собственному значению .
.
Ответ. 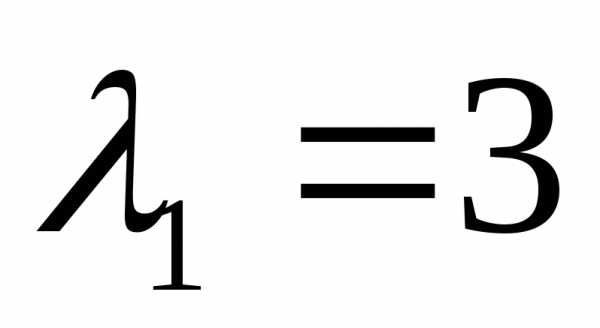 ,
,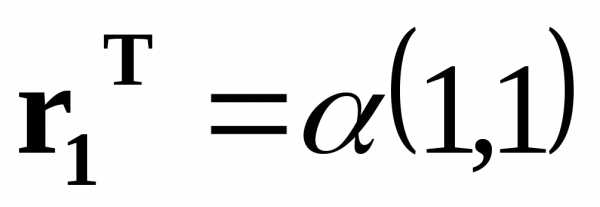 при
при ;
; ,при
,при .
.
● Пример 6.
Найти собственные
пары матрицы 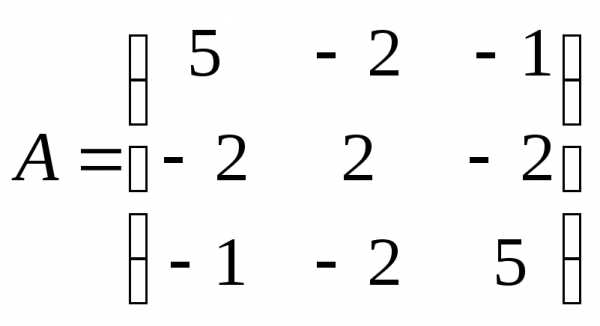 .
.
Решение. 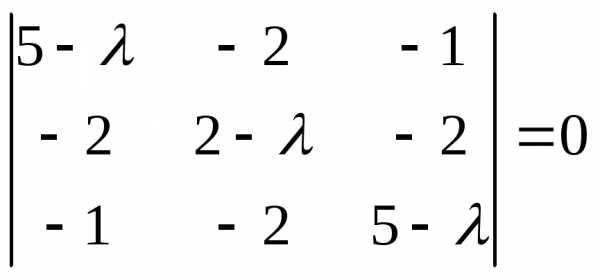 — характеристическоеуравнение
матрицы
— характеристическоеуравнение
матрицы  ,
которое может быть записано в виде,
где,
,
которое может быть записано в виде,
где, ,
,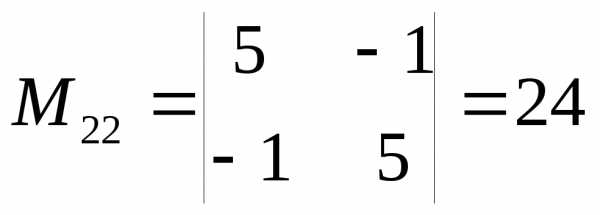 ,
,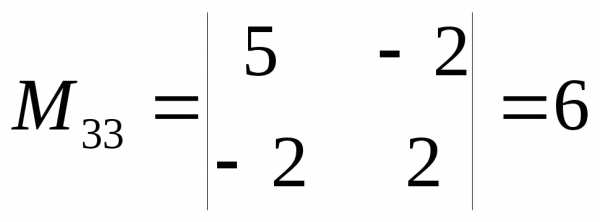 ,(проверьте).
,(проверьте).
—
характеристическое уравнение матрицы  ,
корни которого.
,
корни которого.
Собственные
векторы, соответствующие собственному
значению  ,
находим из системы.
Приимеем систему
,
находим из системы.
Приимеем систему 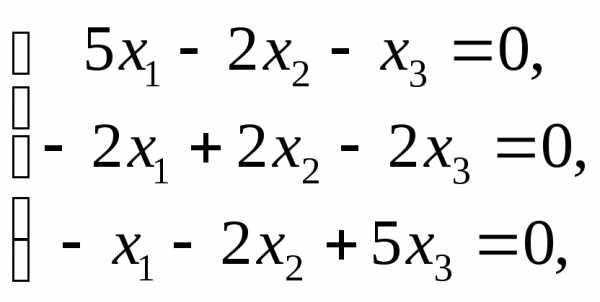 которая
равносильна системе
которая
равносильна системе 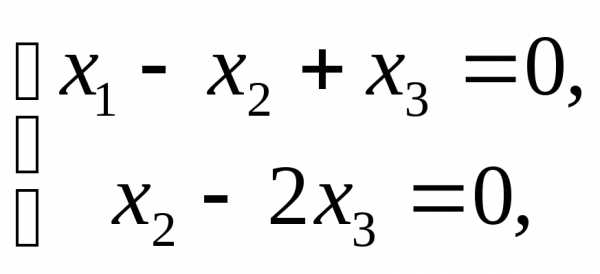 решение
которой
.
решение
которой
.
При 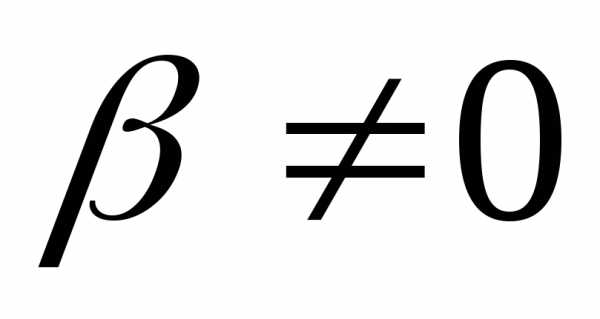 векторявляется собственным вектором матрицы
векторявляется собственным вектором матрицы ,
соответствующим собственному значению.
,
соответствующим собственному значению.
При
для нахождения собственных векторов
имеем систему которая равносильна одному уравнению.
которая равносильна одному уравнению.
При любых  и
и векторесть решение уравнения,
а при
векторесть решение уравнения,
а при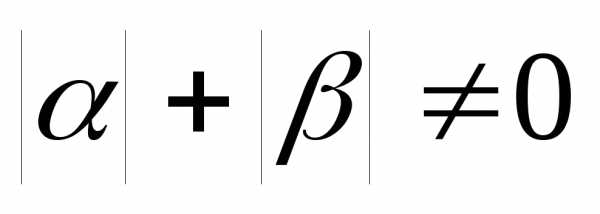
является собственным
вектором, который соответствует
собственному значению 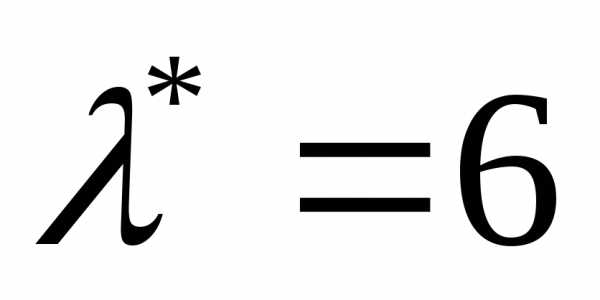 .
.
Ответ:
при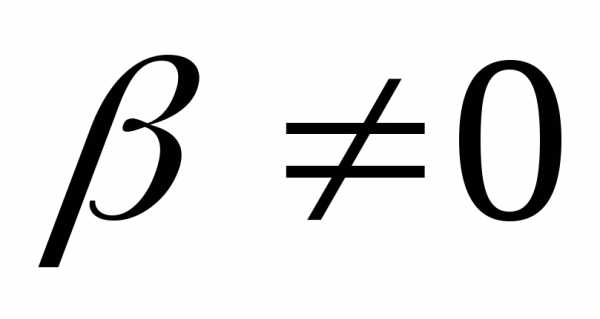 ;при
;при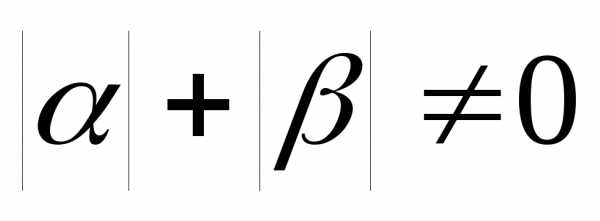 .
.
● Пример 7. Найти собственные значения и собственные
векторы матрицы  .
.
Решение.
Характеристическое уравнение для
указанной матрицы имеет вид  ,
откуда
,
откуда и
и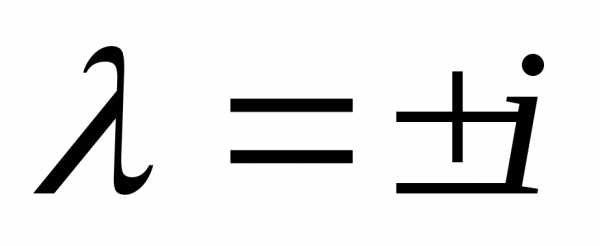 .
.
Для нахождения
собственных векторов, соответствующих
собственному значению 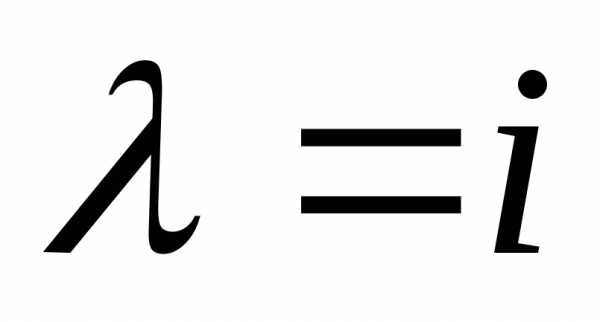 ,
имеем систему
,
имеем систему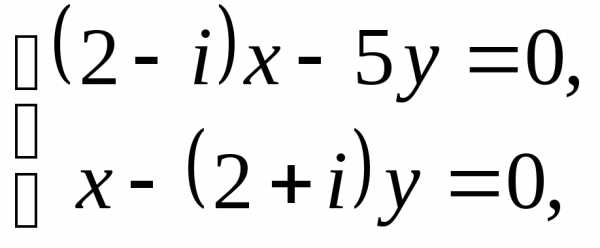 из которой следуетпри
из которой следуетпри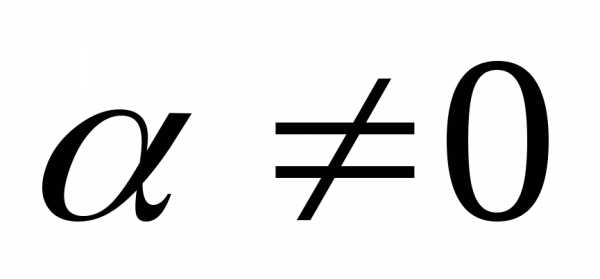 .
.
Для нахождения
собственных векторов, соответствующих
собственному значению 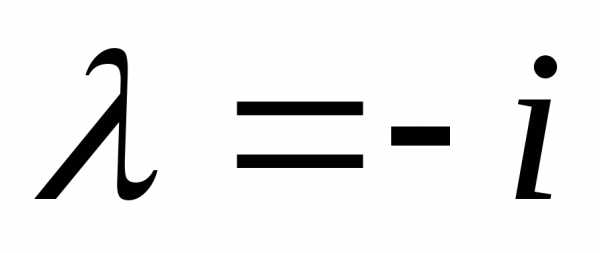 ,
имеем систему
,
имеем систему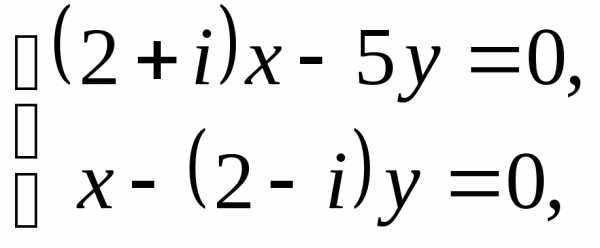 из которой следуетпри
из которой следуетпри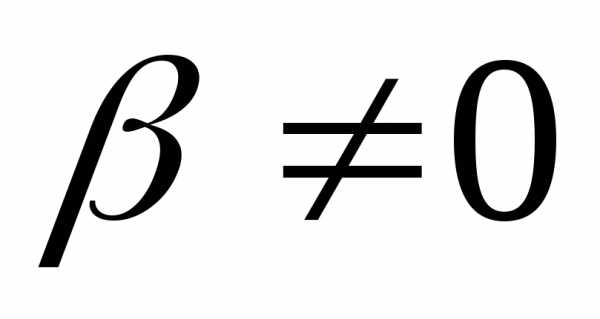 .
.
Ответ. 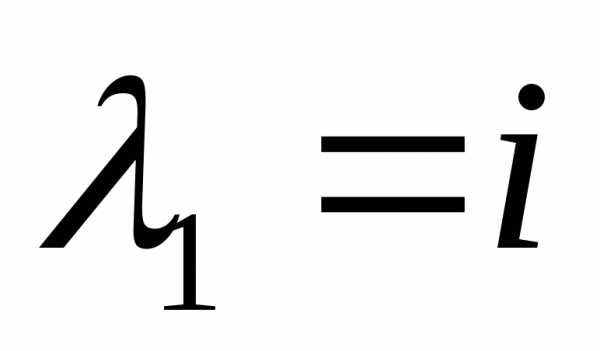 ,при
,при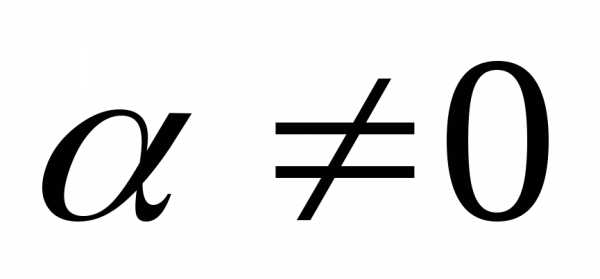 ;
;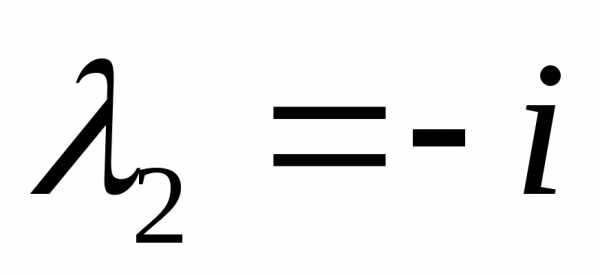 ,при
,при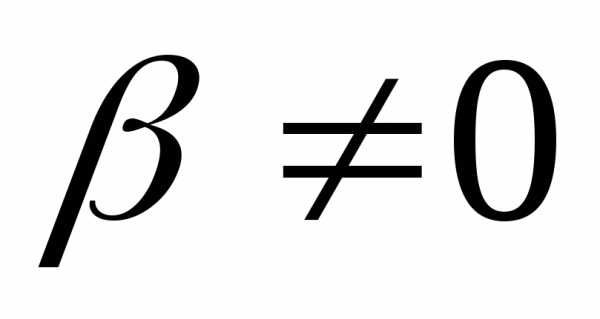 .
.
● Пример 8.
Доказать, что если 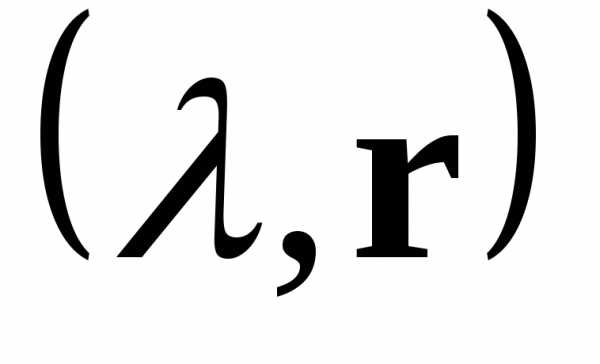 собственная
пара невырожденной матрицы
собственная
пара невырожденной матрицы  ,
то
,
то 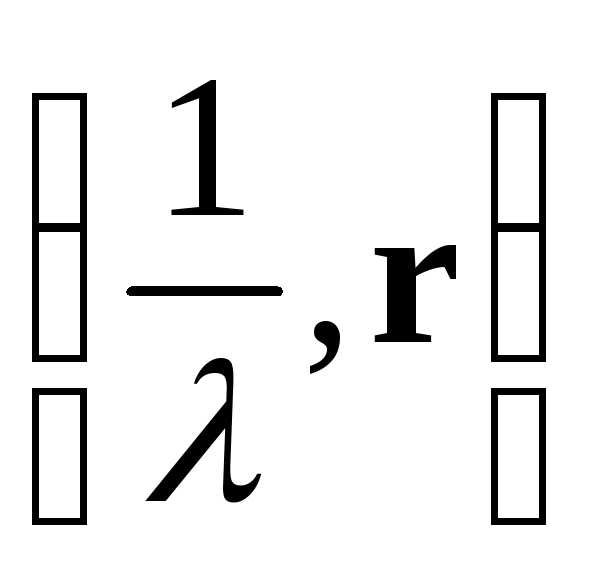 —собственная
пара матрицы
—собственная
пара матрицы  .
.
►Так матрица  невырожденная (),
то существует
невырожденная (),
то существует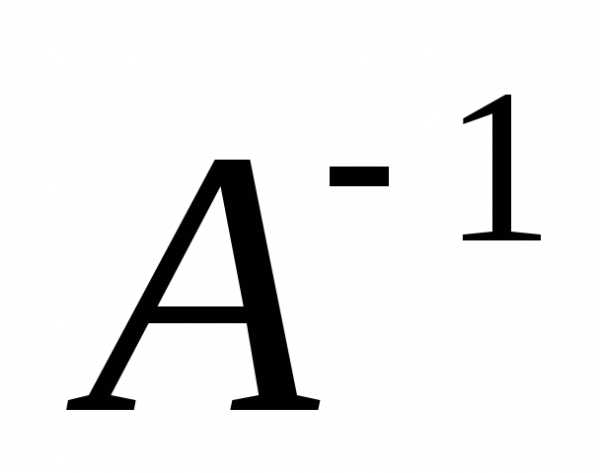 .
Произведение собственных значений
матрицы
.
Произведение собственных значений
матрицы равно
равно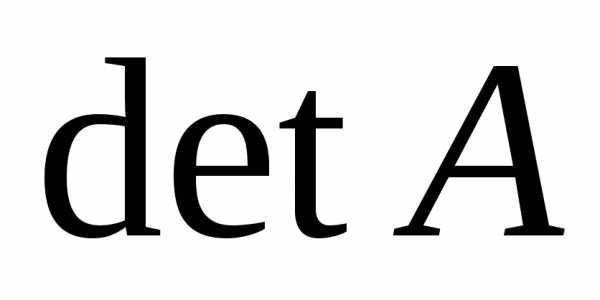 ,
а так как,
то собственное значение
,
а так как,
то собственное значение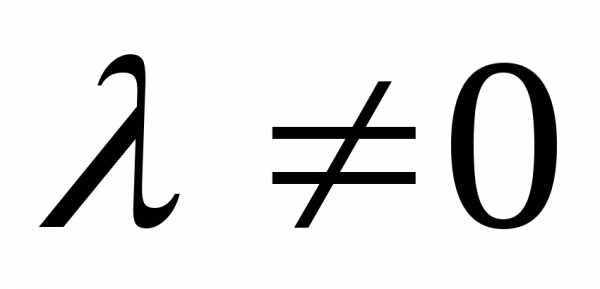 .
.
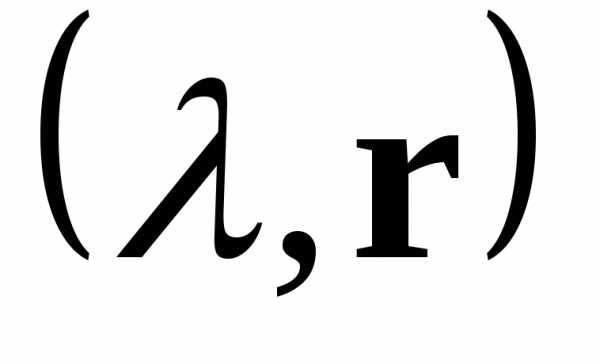 — собственная
пара матрицы
— собственная
пара матрицы  ,
поэтому.Умножив
последнее равенство слева на
,
поэтому.Умножив
последнее равенство слева на 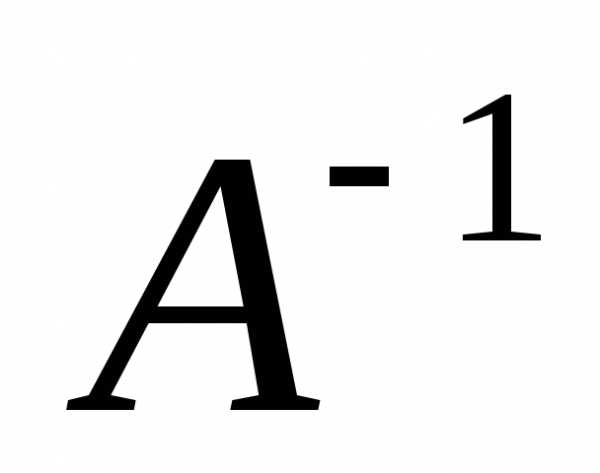 ,
имеем,
откуда,и
,
имеем,
откуда,и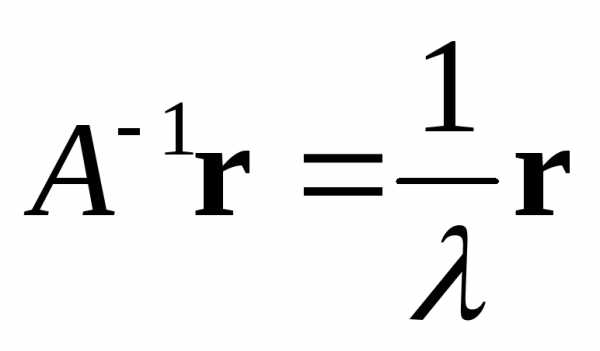 .
Последнее равенство означает, что
.
Последнее равенство означает, что  — собственная
пара матрицы
— собственная
пара матрицы 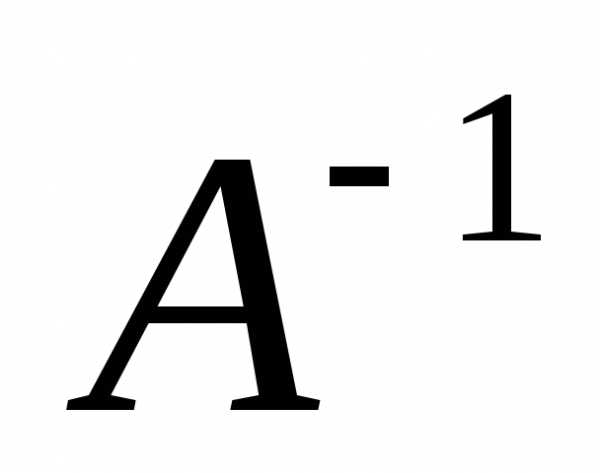 .◄
.◄
studfiles.net
Собственные числа и собственные векторы матрицы линейного преобразования (оператора)
Всякий ненулевой вектор х(а1,а2,…,аnназывается собственным вектором линейного преобразования, если
Ах=λx, (1.5.4) где λ -некоторое число, называемое собственным значением (числом) линейного преобразования.
Если матрица А имеет вид (1.5.2), то равенство (1.5.4) записывается в виде системы линейных алгебраических уравнений (Дц — Л)а^ -ь a^a^+…+а^а^ = О
(a11— λ)a1+a12a2+…+a1nan=0
a21a1+(a22— λ)a2+…+a2nan=0
———————————— (1.5.5)
an1a1+an2a2+…+(ann— λ)an=0
Система (1.5.5), однородная СЛАУ, имеет отличные от нуля (нетривиальные) решения только тогда, когда определитель равен нулю. Отсюда следует, что
det(A- λE)=0. (1.5.6) Уравнение (1.5.6) называется характеристическим уравнением матрицы данного линейного преобразования. Каждый действительный корень λ уравнения (1.5.6) является собственным числом. Соответствующие собственному числу координаты собственного вектора находятся из системы (1.5.5) методом, изложенном в теме 1.1 (см. пример 1.1.11).
Пример 1.5.4.Найти собственные числа и собственные векторы матрицы линейного преобразования.
Система однородных линейных алгебраических уравнений (1.5.5) для нахождения собственных векторов имеет вид:
(11-λ)а1+2а2-8а3=0
2а1+(2-λ)а2+10а3=0 (1.5.7)
-8а1+10а2+(5-λ)а3=0
Вычислим определитель (1.5.6) и решим соответствующее характеристическое уравнение
Характеристическое уравнение имеет вид
λ3-18 λ2-81 λ+1458=0, а его решение λ1=9, λ2=18, λ3=-9. Найденные значения λі, і=1,3 подставим в (1.5.7)
Решение этой системы х1= С(2,2,1)Т, С єR, а соответствующий единичный вектор х01 =(2/3, 2/3, 1/3) Т
При λ 2=18: х02=(-2/3, 1/3, 2/3)Тпри λ3=-9 х03 =(1/3, -2/3, 2/3)
Решения систем линейных уравнений рассмотрены в теме 1.1 (см. пример 1.1.11).
Необходимо отметить следующие свойства собственных значений и собственных векторов симметрической матрицы.
1.Корни характеристического уравнения вещественной симметрической матрицы вещественны.
2.Собственные векторы вещественной симметрической матрицы, отвечающие различным собственным значениям ортогональны. (Проверьте на собственных векторах матрицы примера 1.5.4).
Вопросы для самопроверки
1.Приведите примеры n-мерных векторов.
2.Что такое линейное векторное пространство, какое пространство
называется евклидовым?
З. Что такое базис в n -мерном пространстве?
4 . Как определяется линейное преобразование?
5.Докажите неравенство Коши-Буняковского.
6. Докажите неравенство ||x+y||≤||x||+||y||
7. При каком условии матрица линейного преобразования имеет диагональный вид?
8.Сформулируйте алгоритм нахождения собственных векторов.
Тема 1. 6 . Квадратичные формы. Приведение к каноническому виду уравнений линии и поверхности второго порядка
Квадратичной формой от трех переменных x,y,z называется однородный многочлен второй степени относительно этих переменных.
F(x,y,z)= a11x2 + 2a12xу+ а22у2 + 2a13xz+ 2a23yz+a22 z2 (1.6.1)
Если учесть, что а12 =a21, a13=a31, a23=a32 , тоF(x,y,z) записывается
в виде
F(x, у, z) = а11х2 + а12ху + а21ух + а22 у2 + a13xz + a31 zx + a23 yz + a32 zy + a22z2 .
называется матрицей квадратичной формы. Квадратичная форма имеет канонический вид, если она содержит члены только с квадратами переменных, т.е. аij = 0; i,j = 1,3; i≠ j . Матрица (1.6.2) квадратичной формы
(1.6.1) будет иметь диагональный вид, если в трехмерном пространстве перейти к. новому базису, состоящему из собственных векторов (см. тему 1.5) матрицы А, при этом на главной диагонали будут стоять собственные числа матрицы А.
Квадратичная форма в новом базисе будет иметь вид
F(x1, y1, z1)=λ1x12 + λ2 y12 + λ3z12 (1.6.3)
В случае двух переменных х, у квадратичная формаF(x,y) имеет вид
F(х,у) = а11х2 + 2а12 ху + а22 y2, (1.6.4)
причем а12 = a21 .
Методы приведения квадратичной формы к каноническому виду применяются при решении задач на приведение к каноническому виду уравнений кривых второго порядка
a11x2 + 2а12 ху + а22 у2 + b1х + b2 y + с = 0
и уравнений поверхностей второго порядка
a11x2 + 2а12 ху + а22 у2 + 2a13 xz+2a23 yz+a22 z2 +b1х + b2 y +b3 z + с = 0
Канонические уравнения основных кривых второго’ порядка были рассмотрены в теме 1.4 (1.4.6). Поверхности второго порядка делятся на центральные и нецентральные. Канонические уравнения некоторых поверхностей второго порядка приведены ниже.
megaobuchalka.ru
Найти матрицу в базисе из собственных векторов — КиберПедия
Если собственные векторы матрицы образуют базис, то она представима в виде:
, где – матрица составленная из координат собственных векторов, – диагональная матрица из собственных чисел.
…ничего не напоминает из заключительного параграфа статьи о линейных преобразованиях? 😉
Такое разложение матрицы также называют каноническим или диагональным.
Рассмотрим матрицу первого примера. Её собственные векторы линейно независимы и образуют базис. Составим матрицу из их координат:
На главной диагонали матрицы в соответствующем порядке располагаются собственные числа, а остальные элементы равняются нулю:
Подчёркиваю важность порядка: перестановка «двойки» и «тройки» недопустима!
По обычному алгоритму нахождения обратной матрицы либо методом Гаусса-Жордананетруднополучить . Это не опечатка – перед вами редкое, как солнечное затмение событие, когда обратная совпала с исходной матрицей.
Таким образом, матрица запишется в следующем виде:
Желающие могут перемножить три матрицы и удостовериться, что произведение равно .
Каноническое разложение матрицы выгодно использовать во многих задачах, и, кроме того, в нём сразу видны векторы, которые при данном линейном преобразовании не меняют направление. Это в точности векторы канонического базиса, т.е. собственные векторы.
Давайте вспомним заключительную часть урока о линейных преобразованиях. Там мы выяснили, что одному и тому же линейному преобразованию в разных базисах в общем случае соответствуют разные матрицы. И наиболее удобным из них как раз и является базис из собственных векторов! (в случае его существования). Более того, все матрицы конкретного линейного преобразования (в одном и том же векторном пространстве)имеют один и то же характеристический многочлен, и, скорее всего, именно по этой причине он и получил своё название. Так, в Примере 6 первой статьи по теме у исходной и итоговой матрицы «три на три» один и тот же характеристический многочлен – по той причине, что они задают одно и то же линейное преобразование трёхмерного пространства.
Пример 3
Записать матрицу в базисе из собственных векторов
Решение: найдем собственные значения. Составим и решим характеристическое уравнение:
– получены кратные собственные числа.
Мысленно либо на черновике подставим в определитель и запишем однородную систему линейных уравнений:
Вторая координата принудительно равна нулю: (иначе в первом уравнении получится неверное равенство). За «икс» можно принять любое ненулевое значение, в хорошем стиле положим, что .
Таким образом, кратным собственным числам соответствует единственный собственный вектор .
! Примечание: в общем случае такое утверждение неверно!
Канонические разложение матрицы имеет вид , и в нашей ситуации данного разложения не существует. Почему? Потому что невозможно записать матрицу , которая должна состоять из двух линейно независимых собственных векторов. Размерность вектора равна двум («икс» и «игрек»), но сам-то вектор – один-одинёшенек. Коллинеарный товарищ, например , в пару не годится (хотя бы по той причине, что и обратной матрицы попросту не существует).
У рассмотренного примера есть простое геометрическое объяснение: матрица определяет ни что иное, как «перекос Джоконды», у которого существует лишь одна группа коллинеарных векторов, сохраняющих своё направление. Направление же всех остальных ненулевых векторов данное линейное преобразование меняет.
Ответ: собственные векторы не образуют базиса, поэтому требуемое разложение неосуществимо.
Обратите внимание на корректность и точность ответа – нас никто не спрашивал о собственных значениях и собственных векторах.
Задача с матрицей «три на три» отличаются бОльшей технической сложностью:
Пример 4
Найти собственные векторы линейного преобразования, заданного матрицей
Решение: такая формулировка задачи смущать не должна – ведь это и есть «генеральная линия партии». Энтузиасты могут провести самостоятельные выкладки по аналогии с Примером №1, я же ограничусь «рабочим» решением примера.
По условию требуется найти собственные векторы, но алгоритм таков, что в первую очередь всё равно нужно найти собственные числа.
Вычтем «лямбду» из всех чисел главной диагонали матрицы и составим её характеристическое уравнение:
Определитель раскроем по первому столбцу:
На этом месте немного притормозим и познакомимся с очень полезным техническим приёмом, который значительно упростит дальнейшую жизнь. Практически во всех методических пособиях вам будет предложено раскрыть все скобки, получить слева многочлен 3-ей степени, затем подбором найти корень и стать жертвой долгих мытарств, описанных в Примере №1 урока Сложные пределы. За годы практики я отработал рациональную схему, позволяющую избежать этих неприятностей:
Сначала представим в виде произведения «хвост» левой части:
Выполненное действие не привело к заметному результату.
Поэтому пробуем разложить на множители квадратный трёхчлен . Решив квадратное уравнение, получаем .
Таким образом:
Вынесем за скобку и проведём дальнейшие упрощения:
Решаем ещё одно квадратное уравнение, в итоге:
Это была самая длинная ветка алгоритма, в большинстве случаев произведение получается значительно быстрее.
Собственные значения всегда стараемся расположить в порядке возрастания:
Найдем собственные векторы:
1) Мысленно либо на черновике подставим значение в определитель , с которого «снимем» коэффициенты однородной системы:
Систему можно решить с помощью элементарных преобразований и в следующих примерах мы прибегнем к данному методу. Но здесь гораздо быстрее срабатывает «школьный» способ. Из 3-го уравнения выразим: – подставим во второе уравнение:
Поскольку первая координата нулевая, то получаем систему , из каждого уравнения которой следует, что .
И снова обратите внимание на обязательное наличие линейной зависимости. Если получается только тривиальное решение , то либо неверно найдено собственное число, либо с ошибкой составлена/решена система.
Компактные координаты даёт значение
Собственный вектор:
Крайне желательно проверить, что найденное решение удовлетворяет каждому уравнению системы. В последующих пунктах и в последующих задачах рекомендую принять данное пожелание за обязательное правило.
2) Для собственного значения по такому же принципу получаем следующую систему:
Из 2-го уравнения системы выразим: – подставим в третье уравнение:
Поскольку «зетовая» координата равна нулю, то получаем систему , из каждого уравнения которой следует линейная зависимость .
Пусть
Проверяем, что решение удовлетворяет каждому уравнению системы.
Таким образом, собственный вектор: .
3) И, наконец, собственному значению соответствует система:
Второе уравнение выглядит самым простым, поэтому из него выразим и подставим в 1-ое и 3-е уравнение:
Всё хорошо – выявилась линейная зависимость , которую подставляем в выражение :
В результате «икс» и «игрек» оказались выражены через «зет»: . На практике не обязательно добиваться именно таких взаимосвязей, в некоторых случаях удобнее выразить и через либо и через . Или даже «паровозиком» – например, «икс» через «игрек», а «игрек» через «зет»
Положим , тогда:
Проверяем, что найденное решение удовлетворяет каждому уравнению системы и записываем третий собственный вектор
Ответ: собственные векторы:
Если бы по условию требовалось найти каноническое разложение – то здесь это возможно. Различным собственным числам соответствуют разные линейно независимые собственные векторы: составляем матрицу из их координат, диагональную матрицу из соответствующих собственных значений и находим обратную матрицу . Геометрически собственные векторы базиса указывают на три различных направления пространства, которые данное линейное преобразование не меняет.
Задача с более простыми вычислениями для самостоятельного решения:
Пример 5
Найти собственные векторы линейного преобразования, заданного матрицей
При нахождении собственных чисел постарайтесь не доводить дело до многочлена 3-ей степени. Кроме того, ваши решения систем могут отличаться от моих решений – здесь нет однозначности; и векторы, которые вы найдёте, могут отличаться от векторов образца с точностью до пропорциональности их соответствующих координат. Например, и . Эстетичнеепредставить ответ в виде , но ничего страшного, если остановитесь и на втором варианте. Однако всему есть разумные пределы, версия смотрится уже не очень хорошо.
Примерный чистовой образец оформления задания в конце урока.
cyberpedia.su
Собственные числа и собственные вектора
Для анализа внутренней структуры линейного преобразования целесообразно найти вектора, которые данное преобразование изменяет наиболее просто. Таким свойством обладают собственные вектора матрицы, удовлетворяющие соотношению
,
где l — коэффициент, показывающий изменения длины вектора, т.е. образ вектора совпадает с прообразом по направлению и отличается от него лишь длиной.
Умножим представленное соотношение слева на единичную матрицу E и перенесем все члены в левую часть.
Матрица называется характеристической матрицей. Очевидно, что она имеет вид:
Для вычисления вектора нужно решить систему . Эта система однородна (в правой части стоит нулевой вектор) и имеет ненулевое решение только тогда, когда определитель матрицы равен нулю ( ). В этом случае в матрице есть линейно зависимая строка, а в системе уравнений – линейно-зависимое уравнение. Удалив это уравнение и задав произвольное значение одной из координат вектора , решением оставшейся части системы можно найти остальные координаты .
Для того чтобы найти значение числа l, при котором определитель обратился в ноль, нужно аналитически выписать определитель матрицы, приводя подобные члены относительно степеней l. В общем случае для матрицы размерностью nполучим характеристическое уравнение степени n:
.
Известно, что решением уравнения степени nявляется n значений . Числа li называются собственными числами (значениями) матрицы. Обычно li располагают в ряд по уменьшению модуля, при этом максимальное значение обозначают через l1 , а минимальное через ln .
Пусть в качестве базиса принята совокупность собственных векторов и вектор имеет в этой системе координаты , . Тогда . Поскольку то , т.е. при линейном преобразовании координаты вектора по величине сокращаются (li < 1) или удлиняются (li > 1) пропорционально собственным числам. Линейное преобразование в базисе собственных векторов имеет диагональную матрицу
.
Если собственные числа li различны, то собственные вектора линейно-независимы. Отметим, что если является собственным вектором, то любой вектор также будет собственным вектором, т.е. для каждого li имеется не один собственный вектор, а бесчисленное множество векторов, лежащих на одном и том же направлении.
Таким образом, в базисе из линейно-независимых собственных векторов матрица линейного преобразования преобразует вектор путем растяжения, сжатия или разворота (l<0) координат вектора (умножение проекций на соответствующие собственные числа).
Пример: Найти собственные числа и собственные вектора матрицы .
Характеристическая матрица имеет вид
Приравнивая нулю определитель матрицы , получим характеристическое уравнение, из которого можно найти собственные числа
. Отсюда .
Вычисление собственных векторов. Первый собственный вектор может быть найден из уравнения , или
.
Последнее матричное уравнение эквивалентно системе:
.
Нетрудно видеть, что уравнения линейно-зависимы, следовательно, любое из них, например второе, можно удалить. Тогда . Задавая , получим . Отсюда вектор .
Уравнение для второго собственного вектора приводит к системе:
Отбрасываем второе уравнение, задав , получим , т.е. .
Найденные вектора представлены на рис. 7.7.
Т.к. матрица А симметрична, то исходный ортонормированный базис преобразуется в ортогональный (можно сделать ортонормированным, поделив каждый вектор нового базиса на его длину).
Рассмотрим некоторый вектор и найдем его образ под действием матрицы :
В результате получаем вектор большей длины, расположенный под углом с исходным вектором (рис. 7.8).
Тот же вектор можно получить другим способом. Найдем проекции (OB, CB) вектора на собственные вектора и (числа a и b). Линейное преобразование заключается в умножении первой проекции (a) на первое собственное число , и второй проекции на величину . Геометрически складывая преобразованные проекции (OD и DE), получаем тот же вектор . Аналогично преобразуется любой иной вектор, лежащий на плоскости .

| Рис. 7.8. Линейное преобразование в координатах собственных векторов |
Если взять множество векторов, лежащих концами на единичной окружности, то матрица линейного преобразования будет в 3 раза вытягивать проекции на вектор и оставлять неизменными (l2 = 1) проекции на . В результате окружность растягивается в эллипс. Таким образом, собственные числа и собственные вектора дают характеристику преобразования исходного пространства векторов.
Преобразование подобия
Совокупность линейно-независимых собственных векторов образует базис. При этом матрица перехода из исходного базиса в новый представляется совокупностью координат собственных векторов в исходном базисе
.
Соотношения в матричном виде можно представить как
| , | (7.8) |
где — диагональная матрица из собственных чисел: = .
Нельзя писать , так как , что не соответствует действительности, и, кроме того, при умножении матрицы H на справа действительно, каждый собственный вектор (столбец матрицы H) умножается на соответствующее собственное число
,
в то время как умножение на диагональную матрицу слева равносильно умножению на коэффициенты строк, а не столбцов, что противоречит математическому смыслу собственных векторов:
.
Умножив уравнение (7.8) сначала справа, а затем слева на матрицу , получим
| ; . | (7.9) |
МатрицыАи L представляют собой одно и то же линейное преобразование, записанное в различных системах координат. Матрица А показывает преобразование в координатах базиса , а матрица L показывает тоже преобразование в координатах базиса .
Итак, одному и тому же линейному преобразованию в разных базисах соответствует отличающиеся матрицы.
Базис1: – A, ,
Базис 2: — L ,
Базис 3: – , ,
где B= , (см.п.7.2)
Матрицы А и L называются подобными, т.к. соответствуют одному и тому же преобразованию. Определители этих матриц равны. Отсюда определитель матрицы равен произведению всех его собственных чисел
.
 Структурная диаграмма преобразования векторов представлена на рис. 7.9. В частности, если требуется преобразовать вектор из базиса в базис , то необходимо умножить его на матрицу H-1.
Структурная диаграмма преобразования векторов представлена на рис. 7.9. В частности, если требуется преобразовать вектор из базиса в базис , то необходимо умножить его на матрицу H-1.
| Рис. 7.9. Преобразование векторов |
С помощью данной диаграммы легко получается соотношение подобия (7.9), которое показывает переход от вектора к его образу по и против часовой стрелки.
Норма матрицы
Первое (максимальное) собственное число характеризует максимальное растяжение (при >1) или минимальное сжатие (при <1) вектора. Поскольку вычисления собственных чисел для матрицы большой размерности представляют значительные трудности, на практике часто используют оценку числовой характеристикой матрицы, называемой нормой матрицы , .
Норма матрицы является одной из характеристик матрицы. Поскольку матрица является отражением некоторого линейного преобразования, то неудивительно, что норма матрицы теоретически определяется через линейное преобразование верхней границей изменения длины вектора (представленный ниже оператор sup обозначает точную верхнюю границу)
,
т.е. норма матрицы характеризуется максимальным по модулю образом единичного вектора. Отсюда понятно соотношение .
Используются три способа вычисления нормы матрицы.
1. Кубическая норма (норма по строкам) равна максимальной сумме модулей элементов строк ,.
2. Октаэдрическая норма (норма по столбцам) равна максимальной сумме модулей элементов столбцов, .
3. Сферическая норма (Евклидова норма). .
Свойства норм матрицы:
Для любой симметричной матрицы .
Сжимающее отображение
Преобразование (отображение) называется сжимающим, если . Это справедливо при или .
Для оценки , характеризующего максимальную степень сжатия, необходимо отметить, что переход от образа к прообразу связан с матрицей А-1.
.
В правой части записано представление прообраза вектора через его образ. Поскольку матрице А-1 соответствует матрица -1 с элементами , то — максимальное собственное число для обратной матрицы А-1 и .
stydopedia.ru
Собственные значения и собственные векторы матрицы
Комплексное число называется собственным числом квадратной матрицы , если существует ненулевой вектор (матрица-столбец) , такой, что выполнено равенство
. (13)
Вектор называется в этом случае собственным вектором матрицы , соответствующим числу .
Такой собственный вектор – не единственный, т.к., если удовлетворяет уравнению (13), то и вектор — тоже удовлетворяет, где t – любое число, не равное нулю. Следовательно, собственный вектор определяется с точностью до множителя.
Матричное уравнение (13) эквивалентно однородной системе
(14)
Для того чтобы система (14) имела ненулевое решение, необходимо и достаточно, чтобы определитель этой системы был равен нулю:
(15)
Уравнение (15) называется характеристическим для матрицы и представляет собой алгебраическое уравнение — ой степени относительно . Его корни и являются собственными числами матрицы .
Если матрица — диагональная, т.е.
, (16)
с разными числами по диагонали ( ), то собственные числа совпадают с диагональными элементами матрицы .
Как известно из курса алгебры (см, например, ), уравнение (15) имеет, по крайней мере, один корень, а пример с матрицей (16) показывает, что у матрицы размера максимум собственных чисел. Чтобы найти собственные числа, надо решить уравнение (15). Для нахождения собственных векторов решается система (14) при найденных значениях .
►Пример 14.Найти собственные числа матрицы .
Решение.
Составим характеристическое уравнение
.
Вычисляем определитель
Уравнение имеет три действительных корня: , которые и являются собственными числами. ◄
Для того чтобы найти собственный вектор, соответствующий собственному числу , надо решить систему (14), подставив в нее значение числа .
►Пример 15.Найти собственные векторыдля матрицыпримера 14.
Решение.
Найдем собственный вектор для числа . Для этого решим однородную систему
Ранг матрицы этой системы равен двум, на единицу меньше числа неизвестных. Решение найдем через миноры матрицы :
Итак, собственный вектор имеет вид , где любое число, не равное нулю. Ответ можно писать при t=1, помня замечание, приведенное выше.
Аналогично находятся два других вектора. Советуем студентам найти их самостоятельно. ◄
Упражнения.
Найти собственные числа, и для действительных собственных чисел найти собственные векторы матриц:
1) , 2) , 3) , 4) , 5) , 6) , 7) .
Ответы:
1) ;
2) ;
3) ;
4) ;
5) ;
6) ;
7) .
Индивидуальное задание
1. Вычислить определители:
, , .
2. Даны матрицы:
, , , .
Вычислить:
a) , где — единичная матрица.
b) (вычисления проводить, сохраняя три знака после запятой).
3. Решить матричное уравнение (найти матрицу ).
.
4.Решить системы уравнений двумя способами: по формулам Крамера и с помощью обратной матрицы.
а) б)
5.Исследовать системы уравнений и найти решение, если оно существует.
а)
б)
в)
6. Исследовать и решить системы уравнений.
а)
б)
в)
Приложение
В приложении приведены примеры работы с матрицами и примеры решения систем с использованием математического пакета MATHEMATICA Первоначально студент должен ознакомиться с работой интерфейса. Для любой работы необходимо знать операции ввода, вывода результатов; команды для выполнения операций.
Ввод данных осуществляется через знак «=». Программа подтверждает ввод строкой «In[1]:=…». Результат выполнения операции находится в строке, начинающейся словом «Out[1]=». Номера в квадратных скобках ввода и вывода совпадают.
Выполнение любой операции происходит по команде со строгим выполнением заданного формата.
Найти эти форматы можно в справке VIRTUAL BOOK. Там же приведены примеры выполнения операций. Ниже приведен ряд команд для выполнения заданий по теме.
Ввод матрицы.
In[4]:= m1 = {{2, -5, 4}, {3, -1, 8}, {2, 6, 1}, {-1, 3, 4}}
Out[4]= {{2, -5, 4}, {3, -1, 8}, {2, 6, 1}, {-1, 3, 4}}
Имя матрицы m1. Сама матрица вводится построчно с использование фигурных скобок.
Умножение матриц.
In[1]:= m2 = {{1, 6, 4}, {-4, -2, 4}, {3, 1, 8}}
In[1]:= m3 = {{2, -1, 2, 6}, {-5, 5, -2, 3}
Out[1]= {{1, 6, 4}, {-4, -2, 4}, {3, 1, 8}}
Out[2]= {{2, -1, 2, 6}, {-5, 5, -2, 3}}
In[7]:= m1.m2
Out[7]= {{34, 26, 20}, {31, 28, 72}, {-19, 1, 40}, {-1, -8, 40}}
Команда для умножении «.».
Вычисление определителя.
In[10]:= Det[m2]
Out[10]= 252
Матрица m2 введена выше.
Нахождение обратной матрицы.
In[8]:= Inverse[m2]
Out[8]= {{-(5/63), -(11/63), 8/63}, {11/63, -(1/63), -(5/63)}, {1/126, 17/252, 11/ 126}}
Вычисление собственных чисел и собственных векторов.
In[14]:= Eigenvalues[{{1, 2}, {2, 1}}]
Out[14]= {3, -1}
In[16]:= Eigenvectors[{{1, 2}, {2, 1}}]
Out[16]= {{1, 1}, {-1, 1}}.
m4 = {{2, 1}, {8, 7}, {3, -5}, {-4, 6}}
Определение ранга матрицы.
In[18]:= MatrixRank[m1]
Out[18]= 3
Решение систем линейных уравнений.
In[17]:= Solve[{2 x + y — z + 2 t == 12, -x + 2 y + 4 z + 3 t == 4,
2 x + y + 4 z — 2 t == -10, x + 3 y + 5 z + 2 t == 3}, {x, y, z, t}]
Out[17]= {{x -> 1, y -> 2, z -> -2, t -> 3}}.
В этом примере система имеет единственное решение. Вместо знака равенства в ответе используется « ->». Ниже система, имеющая множество решений и система, не имеющая решений.
In[20]:= Solve[{x + y + z == 4, 2 x + y + z == 5, 3 x + 2 y + 2 z == 9}, {x, y, z}]
Equations may not give solutions for all»solve»,
In[20]:= Solve[{x + y + z == 4, 2 x + y + z == 5, 3 x + 2 y + 2 z == 10}, {x, y, z}]
Out[20]= {{x -> 1, y -> 3 — z}}
Out[21]= {}
Наряду со строчной записью ввода вывода использоваться записью матриц и других математических объектов в привычном виде. Для этого можно использовать команду TraditionalForm
infopedia.su
Собственные числа и собственные векторы матрицы.
Образование Собственные числа и собственные векторы матрицы.просмотров — 91
Определение 9.3. Вектор х принято называть собственным векторомматрицы А, если найдется такое число λ, что выполняется равенство: Ах= λх, то есть результатом применения к х линейного преобразования, задаваемого матрицей А, является умножение этого вектора на число λ. Само число λ принято называть собственным числомматрицы А.
Подставив в формулы (9.3) x`j = λxj, получим систему уравнений для определения координат собственного вектора:
.
Отсюда
. (9.5)
Эта линейная однородная система будет иметь нетривиальное решение только в случае, если ее главный определитель равен 0 (правило Крамера). Записав это условие в виде:
получим уравнение для определения собственных чисел λ, называемое характеристическим уравнением. Кратко его можно представить так:
| A — λE | = 0, (9.6)
поскольку в его левой части стоит определитель матрицы А-λЕ. Многочлен относительно λ | A — λE| принято называть характеристическим многочленомматрицы А.
Свойства характеристического многочлена:
1) Характеристический многочлен линейного преобразования не зависит от выбора базиса. Доказательство. (см. (9.4)), но следовательно, . Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, не зависит от выбора базиса. Значит, и |A-λE| не изменяется при переходе к новому базису.
2) В случае если матрица А линейного преобразования является симметрической (ᴛ.ᴇ. аij=aji), то все корни характеристического уравнения (9.6) – действительные числа.
Свойства собственных чисел и собственных векторов:
1) В случае если выбрать базис из собственных векторов х1, х2, х3, соответствующих собственным значениям λ1, λ2, λ3 матрицы А, то в этом базисе линейное преобразование А имеет матрицу диагонального вида:
(9.7) Доказательство этого свойства следует из определения собственных векторов.
2) В случае если собственные значения преобразования А различны, то соответствующие им собственные векторы линейно независимы.
3) В случае если характеристический многочлен матрицы А имеет три различных корня, то в некотором базисе матрица А имеет диагональный вид.
Пример.
Найдем собственные числа и собственные векторы матрицы Составим характеристическое уравнение: (1- λ)(5 — λ)(1 — λ) + 6 — 9(5 — λ) — (1 — λ) — (1 — λ) = 0, λ³ — 7λ² + 36 = 0, λ1 = -2, λ2 = 3, λ3 = 6.
Найдем координаты собственных векторов, соответствующих каждому найденному значению λ. Из (9.5) следует, что если х(1)={x1,x2,x3} – собственный вектор, соответствующий λ1=-2, то
— совместная, но неопределенная система. Ее решение можно записать в виде х(1)={a,0,-a}, где а – любое число. В частности, если потребовать, чтобы |x(1)|=1, х(1)=
Подставив в систему (9.5) λ2=3, получим систему для определения координат второго собственного вектора — x(2)={y1,y2,y3}:
, откуда х(2)={b,-b,b} или, при условии |x(2)|=1, x(2)=
Для λ3 = 6 найдем собственный вектор x(3)={z1, z2, z3}:
, x(3)={c,2c,c} или в нормированном варианте
х(3) = Можно заметить, что х(1)х(2) = ab – ab = 0, x(1)x(3) = ac – ac = 0, x(2)x(3) = bc — 2bc + bc = 0. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, собственные векторы этой матрицы попарно ортогональны.
Читайте также
Число называется собственным числом матрицы , если существует ненулевой вектор такой, что . При этом вектор называется собственным вектором матрицы , соответствующим собственному числу . Характеристическим уравнением матрицы называется уравнение . (10) Корни этого… [читать подробенее]
Определение 9.3. Вектор х называется собственным векторомматрицы А, если найдется такое число &… [читать подробенее]
oplib.ru
Собственные векторы и собственные значения линейного оператора
Обратная связь
ПОЗНАВАТЕЛЬНОЕ
Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса — ваш вокал
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший «Салат из свеклы с чесноком»
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Линейные операторы
Определение.Пусть и два линейных пространства. Если дано правило, по которому каждому элементу ставится в соответствие элемент , , то говорят, что задан оператор (отображение, закон), действующий из пространства в пространство
Записывают: или
Говорят: «Оператор переводит вектор в вектор ».
Принято называть образом , а — прообразом .
Оператор называется линейным, если выполняются условия:
1. — свойство аддитивности оператора;
2. — свойство однородности оператора.
Если пространства и совпадают, то оператор отображает пространство в себя.
Пример 52.Проверить линейность оператора
Выберем в пространстве базис
Запишем разложение произвольного вектора по данному базису:
В силу линейности оператора получаем:
Так как также вектор из , то его можно разложить по базису
Тогда (5)
С другой стороны, вектор , имеющий в том же базисе координаты можно записать так:
(6)
Так как любой вектор можно разложить по базису, причем единственным образом, получаем равенство правых частей в (5) и (6).
Отсюда
Матрица называется матрицей оператора в базисе , а ранг матрицы – рангом оператора .
Утверждение. Каждому линейному оператору соответствует матрица в данном базисе.
Собственные векторы и собственные значения линейного оператора
Определение. Пусть R – заданное — мерное линейное (векторное) пространство. Ненулевой вектор R называется собственным вектором линейного оператора , если найдется такое число , что выполняется равенство:
(7)
Число называется собственным числом (значением) линейного оператора (матрицы ), соответствующим вектору .
Собственный вектор под действием линейного оператора переходит в вектор, коллинеарный самому себе.
Равенство (7) можно представить в матричной форме:
,
где вектор представлен в виде вектора-столбца, или в развернутом виде
Перепишем систему так, чтобы в правых частях были нули:
(8)
Или в матричном виде
Полученная однородная система всегда имеет нулевое решение. Для существования ненулевого решения необходимо и достаточно, чтобы определитель системы был равен нулю:
(9)
Определитель системы является многочленом –го порядка относительно . Этот многочлен называется характеристическим многочленом оператора или матрицы , а уравнение (9) – характеристическим уравнением оператора или матрицы . Это уравнение имеет степень относительно , равную порядку матрицы линейного оператора (т.е. ).
По основной теореме алгебры, уравнение -й степени имеет корней. Таким образом, для нахождения собственных чисел надо составить характеристическое уравнение и найти его действительные корни. Затем, подставляя каждое собственное число в систему (8), находим для каждого собственного числа соответствующий собственный вектор.
Характеристический многочлен линейного оператора не зависти от выбора базиса.
Пример 53. Найти собственные числа и собственные векторы линейного оператора заданного матрицей .
Решение
Составим характеристическое уравнение, используя формулу (9):
Вычислим полученный определитель (понижением порядка):
— собственные числа (значения) линейного оператора (собственные числа матрицы оператора).
Найдем собственные векторы.
Если , то для определения координат собственного вектора составим и решим соответствующую систему уравнений:
Пусть (свободная переменная), тогда , .
Составим собственный вектор .
Если , то .
Пусть , тогда и .
Составим собственный вектор .
Если , то .
Пусть , тогда и .
Составим собственный вектор .
Пример 54 . Найти собственные числа матрицы .
Решение
Составим характеристическое уравнение матрицы, ,используя формулу (9):
— характеристическое уравнение оператора (матрицы) .Разложив левую часть уравнения на множители, получим . Следовательно, матрица имеет два собственных числа: .
Пример 55. Найти собственные векторы матрицы
Решение
Впримере выше были найдены собственные числа матрицы :
1)Если , то для определения координат собственного вектора получаем систему уравнений , которая имеет вид:
Решим данную систему методом Гаусса:
~ ~ ~
Пусть , тогда и .
Получим собственный вектор .
2) Если , тогда .
Решаем систему:
~ ~
Находим , и
Получим собственный вектор .
megapredmet.ru
