24. Производные высших порядков
Билет 24
Производные высших порядков явно заданной функции
Производная у’=ƒ'(х) функции у=ƒ(х) есть также функция от х и называется производной первого порядка.
Если функция ƒ'(х) дифференцируема, то ее производная называется производной второго порядка и обозначается у»
Итак, у»=(у’)’.
Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается у'» (или ƒ'»(х)). Итак, у'»=(y»)’
Производной n-го порядка (или n-й производной) называется производная от производной (n-1) порядка:
y(n)=(y(n-1)) .
Производные порядка выше первого называются производными высших порядков.
Начиная с производной четвертого порядка, производные обозначают римскими цифрами или числами в скобках (уν
<< Пример 23.1
Найти производную 13-го порядка функции у=sinx.
Решение:

ФОРМУЛА ТЕЙЛОРА
В определении функции у=ƒ(х) не говорится о том, при помощи каких средств находятся значения у по значениям х. В тех случаях, когда функция является формулой вида у=х3/5-5х+7, значения функции найти легко с помощью четырех арифметических действий. Но как найти значения, например, функций у=sinx, у=ln(1+х) при любых (допустимых) значениях аргумента?
Для того, чтобы вычислить значения данной функции у=ƒ(х), ее заменяют многочленом Рn(х) степени n, значения которого всегда и легко вычисляемы. Обоснование возможности представлять функцию многочленом дает формула Тейлора.
26.1. Формула Тейлора для многочлена
Пусть функция ƒ(х) есть многочлен Рn(х) степени n:
ƒ(х)=Р n(х)=а0+а1х+а2х2+…+аnхn.
Преобразуем этот многочлен также в многочлен степени n относительно разности х-х0, где х0 — произвольное число, т. е. представим Рn(х) в виде
Рn(х)=А0+A1(x-х0)+А2(х-х0)2+…+Аn(х-х0)n (26.1)
Для нахождения коэффициентов А0, А1 ,…, Аn продифференцируем n раз равенство (26.1):
Р’n(х)=А1+2А2(х-x0)+3A3(x-x0)2+…+nAn(x-x0)n-1,
Рn»(х)=2А2+2•3А3(х-х0)+…+n(n-1)Аn(х-х0)n-2,
Рn«‘(х)=2•3А3+2•3•4А4(х-х0)+…+n(n-1)(n-2)Аn
— — — — — — — — — — — — — — — — — —
Рn(n)(х)=n(n-1)( n-2)…2•1Аn
Подставляя х=х0 в полученные равенства и равенство (26.1), имеем:
Подставляя найденные значения A0,A1,…,An в равенство (26.1), получим разложение многочлена n-й степени Рn(х) по степеням (х-х0):
Формула (26.2) называется формулой Тейлора для многочлена Рn(х) степени n.
<< Пример 26.1
Разложить многочлен Р(х)=-4х3+3х2-2х+1 по степеням х+1.
Решение: Здесь х0=-1, Р'(х)=-12х2+6х-2, Р»(х)=-24х+6, Р'»(х)=-24. Поэтому Р(-1)=10, Р'(-1)=-20, Р»(-1)=30, Р'»(-1)=-24. Следовательно,
т. е. -4х3+3х2-2х+1=10-20(х+1)+15(х+1)2-4(х+1)3.
Ряд Тейлора. Разложение функции в ряд Тейлора.
Оказывается, большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания. Например, в окрестности точки х=1:
При использовании рядов, называемых рядами Тейлора, смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование.
Ряд Тейлора в окрестности точки a имеет виды:
1), где f(x) — функция, имеющая при х=а производные всех порядков. Rn — остаточный член в ряде Тейлора определяется выражением
2)
k-тый коэффициент (при хk) ряда определяется формулой
3) Частным
случаем ряда Тейлора является ряд
Маклорена (=Макларена)
при a=0
члены ряда определяются по формуле
Условия применения рядов Тейлора.
1. Для того, чтобы функция f(x) могла быть разложена в ряд Тейлора на интервале (-R;R) необходимо и достаточно, чтобы остаточный член в формуле Тейлора (Маклорена (=Макларена)) для данной функции стремился к нулю при k→∞ на указанном интервале (-R;R).
2. Необходимо чтобы существовали производные для данной функции в точке, в окрестности которой мы собираемся строить ряд Тейлора.
Свойства рядов Тейлора.
Если f есть аналитическая функция, то ее ряд Тейлора в любой точке а области определения f сходится к f в некоторой окрестности а.
Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности а. Например:
Ряды Тейлора применяются при аппроксимации ( приближение — научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми) функции многочленами. В частности, линеаризация ((от linearis — линейный), один из методов приближённого представления замкнутых нелинейных систем, при котором исследование нелинейной системы заменяется анализом линейной системы, в некотором смысле эквивалентной исходной.) уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Таким образом, практически любую функцию можно представить в виде полинома с заданной точностью.
studfiles.net
Производные высших порядков для студентов
Аналогично, если производная существует и дифференцируема, то можно найти третью производную рассматриваемой функции:
Таким образом, понятие производной -го порядка вводится индуктивно путем последовательного вычисления производных, начиная с производной первого порядка. Переход к производной следующего, более высокого порядка производится с помощью рекуррентной формулы:
Замечание. Порядок производной, чтобы не путать с показателем степени, пишут в круглых скобках либо записывают римскими цифрами. Например, производная четвертого порядка
При нахождении производных высшего порядка используются следующие соотношения:
Примеры вычисления производных высших порядков
| Понравился сайт? Расскажи друзьям! | |||
третья производная — Смысл третьей производной? — 22 ответа
В разделе Наука, Техника, Языки на вопрос Смысл третьей производной? заданный автором BUMER лучший ответ это Позволяет найти угол наклона на графике второй производной или точки перегиба на графике первой…
Кроме того, есть понятие гладкости функции. Функция называется гладкой, если у нее существует производная любого порядка…
В противном случае говорят, что она гладкая только до производной такого-то порядка…
Привет! Вот подборка тем с ответами на Ваш вопрос: Смысл третьей производной?
Ответ от Двутавровый[гуру]
Радиус кривизны смещения точки перегиба…
Ответ от Добросердечный[гуру]
Вторая производная — кривизна графика.
Ответ от ? ?[гуру]
Полностью согласен со всем выше сказанным, но хочу заметить что кроме геометрического смысла производной существует ещё и физический смысл а понять необходимость производных высщего порядка проще всего поняв физическую суть…
К примеру для уравнения движения производная пути по времени — это скорость
вторая производная — ускорение, но не всякое движение может быть равноускоренным
характеристикой изменения ускорения будет третья производная,
но и скорость изменения ускорения может быть не равномерной :)) и т.д.
Кроме того оперируя с производными нельзя мыслить «плоско», очень часто их используют для пространственных характеристик моделей.
Мне очень нравятся задачи с применением производной где требуется оптимизировать процесс или маршрут, или снизить себестоимость…
Простенькая задачка на эту тему для размышления…
Определить оптимальные размеры цилиндрической консервной банки с крышкой для обьёма V=1литр выполненной из жести толщиной S=0.2 мм из условия минимального веса металла 🙂
Ответ от хромосомы[гуру]
Поддерживаю ответ Григория Милонова, а ещё производные высших порядков нужны для разложения функций в ряды — Тейлора, Маклорена. В некоторых методах приближенного решения систем нелинейных уравнений без них тоже никак
Ответ от 2 ответа[гуру]
Привет! Вот еще темы с нужными ответами:
Производная функции на Википедии
Посмотрите статью на википедии про Производная функции
Ответить на вопрос:
22oa.ru
Производная высших порядков
В этой статье познакомимся с понятием производной высшего порядка от функции одной переменной. Начнем с определения и рассмотрим несколько примеров. Будем исходить из того, что Вы уже не имеете проблем с вычислением первой производной.
Итак, пусть дана некоторая функция , и пусть она имеет конечную производную первого порядка в интервале , то есть также является функцией на данном интервале. Если эта функция дифференцируема, то можно найти вторую производную исходной функции . Обозначается следующим образом:
То есть для нахождения второй производной достаточно продифференцировать первую производную.
Производные более высокого порядка (в случае их существования) функции задаются так:
, , …, .
Таким образом, для вычисления производной -го порядка от какой-то функции необходимо продифференцировать последовательно раз. Переход к производной более высокого порядка осуществляем по формуле:
Покажем теперь на примерах процесс нахождения производных высших порядков.
Пример 1. Найти вторую производную функции .
Решение
Шаг первый. Находим :
Шаг второй. Находим искомую , применив представленную выше формулу:
Ответ:
[свернуть]
Пример 2. Найти третью производную функции .
Решение
Находим последовательно производные, не забывая, что имеем дело со сложной функцией (косинус зависит не просто от , а от выражения ).
Ответ:
[свернуть]
Пример 3. Найти с первой по третью производные от функции .
Решение
При нахождении второй производной избавимся от дроби.
И работаем теперь с производной произведения.
[свернуть]
Пример 4. Найти десятую производную функции .
Решение
Чтобы дать ответ, необязательно находить последовательно с первой по десятую производные. Достаточно открыть таблицу производных и найти там производную от ,
.
Отсюда можем сделать следующий вывод:
.
Ответ:
[свернуть]
Пример 5. Найти третью производную функции
Решение
Находим последовательное три производные. Не забываем, что перед нами дробь.
Ответ:
[свернуть]
Понятно, что сложности с этой темой могут возникнуть только в том случае, если у Вас западает техника нахождения производной. Вопрос нахождения производных высшего порядка от неявно и параметрически заданных функций читайте в следующих статьях:
На этом всё, удачи в освоении матана! 🙂
higher-math.ru
1. Производные высших порядков Понятие производных высших порядков
Пусть
функция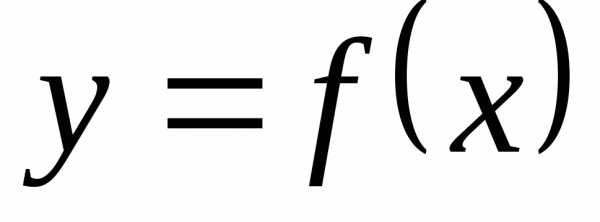 дифференцируема в некотором интервале.
Тогда её производная
дифференцируема в некотором интервале.
Тогда её производная 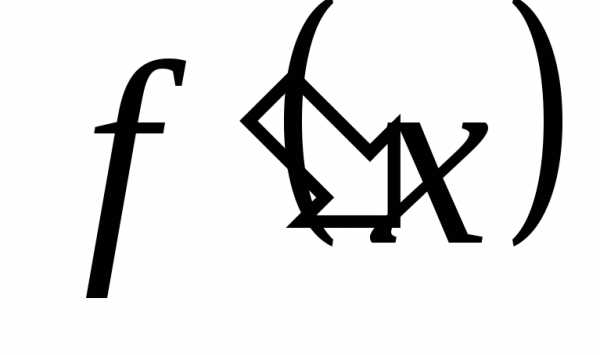 ,
вообще говоря, зависит отх , то есть
является функцией от х.
Следовательно, по отношению к ней снова
можно ставить вопрос о существовании
производной.
,
вообще говоря, зависит отх , то есть
является функцией от х.
Следовательно, по отношению к ней снова
можно ставить вопрос о существовании
производной.
Определение. Производная
от первой производной называется производной
второго порядка или второй производной
и обозначается символом 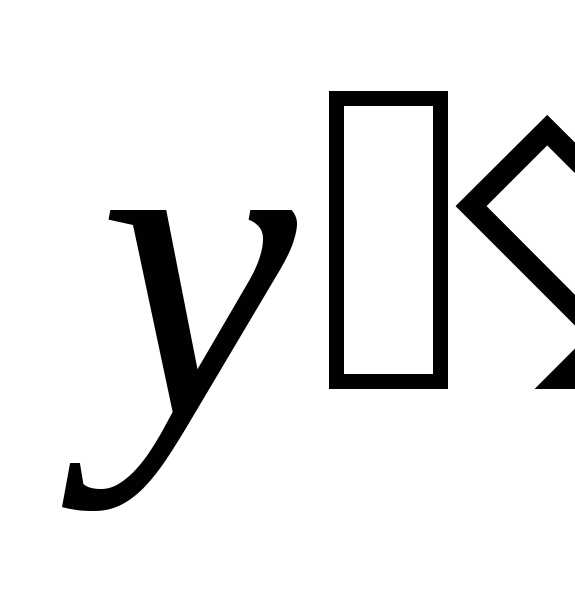 или
или ,
то есть
,
то есть
.
Пример
1. Найти
вторую производную от функции  .
.
Решение. Найдем первую производную функции:
.
Находим вторую производную как производную первой производной:
.
Определение. Производная
от второй производной называется
производной третьего порядка или третьей
производной и обозначается символом  или
или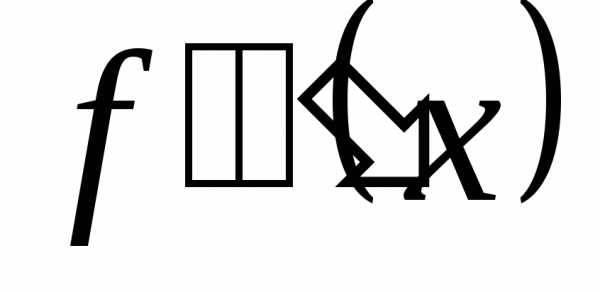 .
.
Определение. Производной n-ого
порядка функции 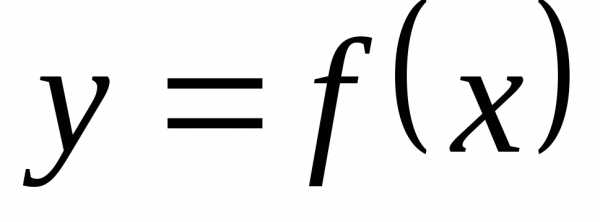 называется
первая производная от производной
(n-1)-го
порядка данной функции и обозначается
символом
называется
первая производная от производной
(n-1)-го
порядка данной функции и обозначается
символом  или
или :
:
.
Определение. Производные порядка выше первого называются высшими производными.
Пример
2. Найти
производную четвертого порядка функции 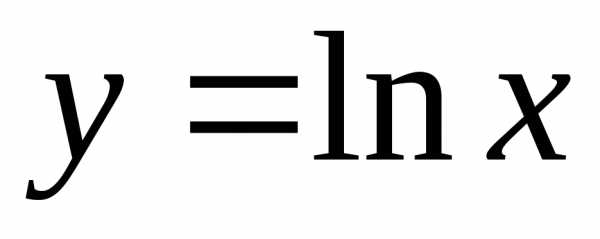 .
.
Решение. Находим последовательно первую, вторую, третью и четвертую производные:
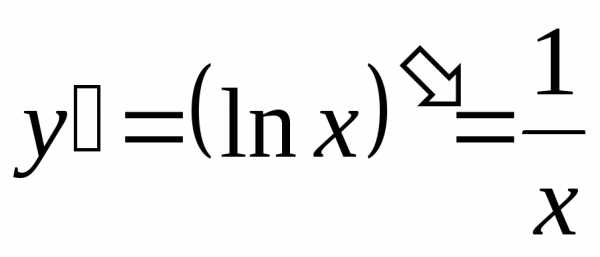 ,
, 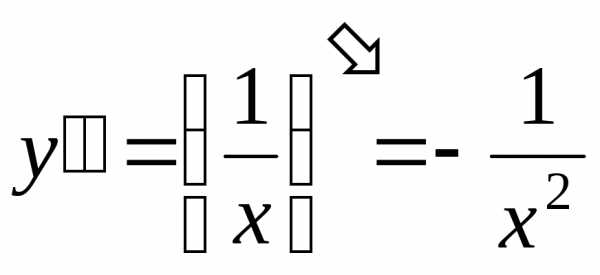 ,,
,,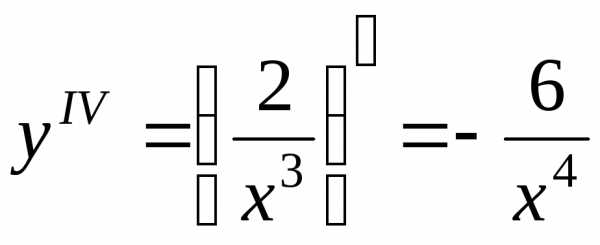 .
.
Пример
3.Найти
производную n-ого
порядка для функции 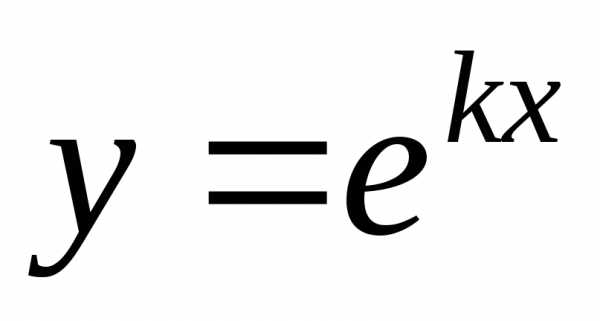 (k—const).
(k—const).
Решение. Имеем:
,
, ,.
,.
Пример
4. Найти
производную n-ого
порядка для функции  .
.
Решение. Имеем:

 ,
,
 ,
,
 ,
,
 ,
,

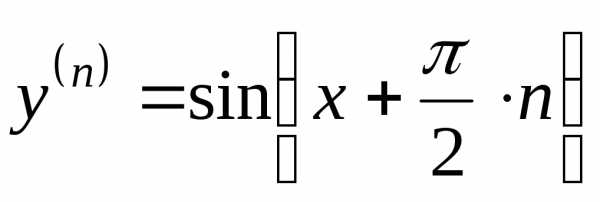 .
.
 Замечание.
Аналогично можно получить формулу n-ой
производной функции
:
Замечание.
Аналогично можно получить формулу n-ой
производной функции
:
 .
.
 Пример
5. Найти
производную n-ого
порядка для степенной функции
Пример
5. Найти
производную n-ого
порядка для степенной функции 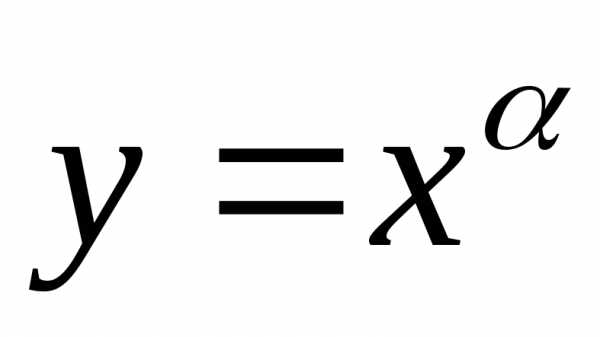 , где
, где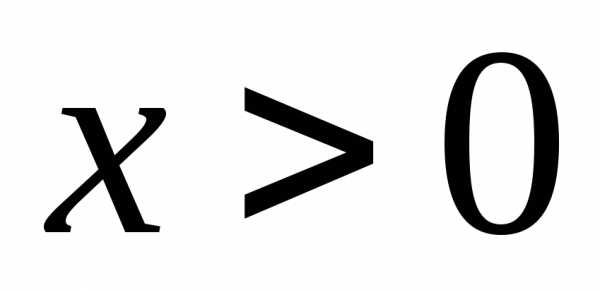 и
и — любое вещественное число.
— любое вещественное число.
 Решение.
Дифференцируя последовательно, получим:
Решение.
Дифференцируя последовательно, получим:

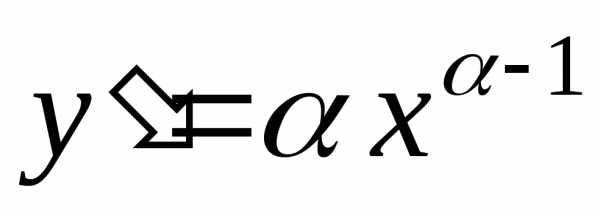 ,
,
,
, ,
,
 .
.
В частном случае, когда , гдеm – натуральное число, получим:
 ,
, 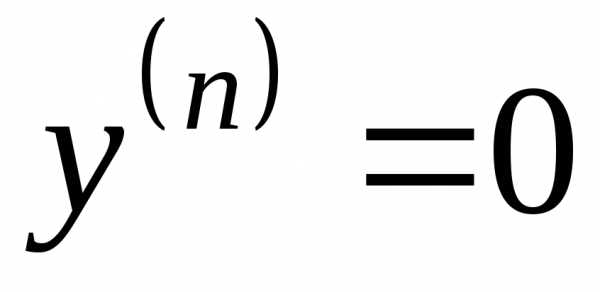 при
при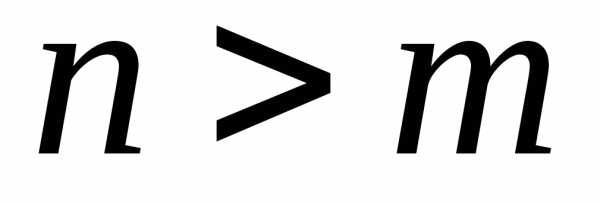 .
.
 Замечание. При строгом выводе формулы для производной n-ого
порядка следует применять метод
математической индукции.
Замечание. При строгом выводе формулы для производной n-ого
порядка следует применять метод
математической индукции.

 Вторая
производная параметрически заданной
функции
Вторая
производная параметрически заданной
функции
Если функция задана параметрически уравнениями , то для нахождения производной второго порядка нужно продифференцировать выражение для её первой производной, как сложной функции независимой переменной.
Так
как 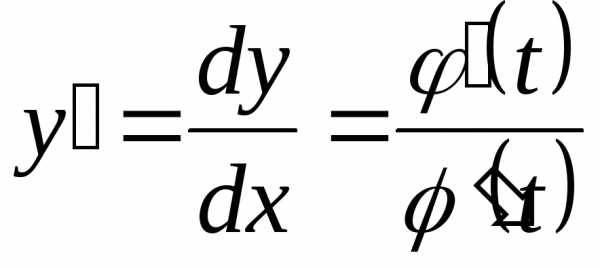 ,
то
,
то
,
и с учетом того, что
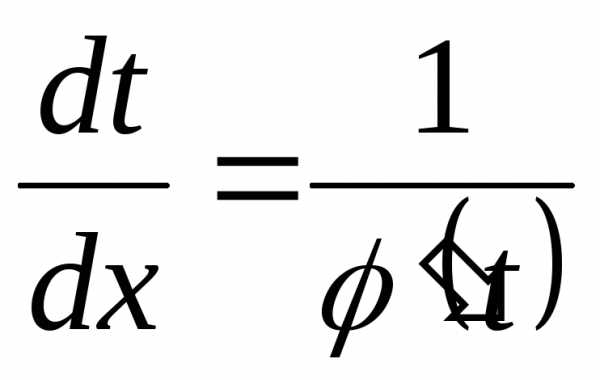 ,
,
получим
, то есть
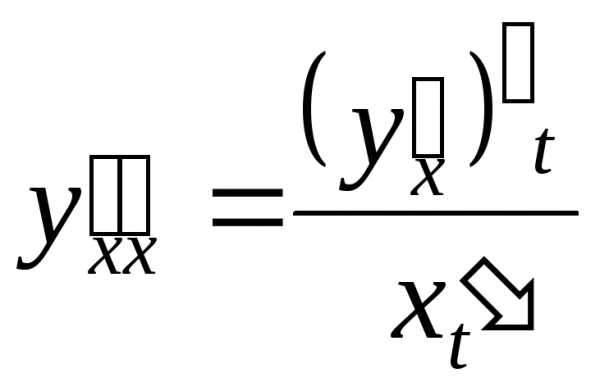 .
.
Аналогично можно найти третью производную

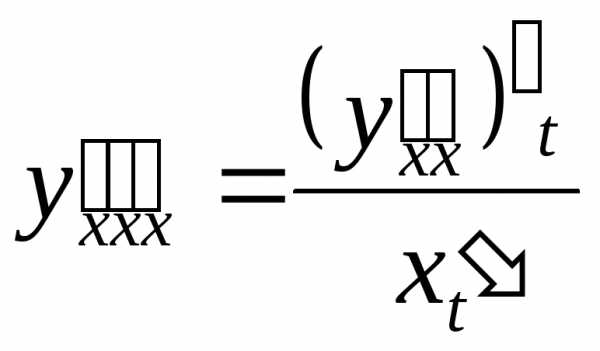 .
.
Пример
7. Найти
вторую производную параметрически
заданной функции  ,
,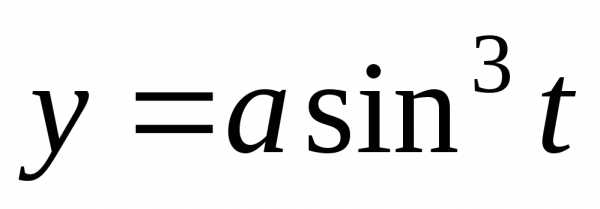 .
.
Решение.,
.
Формула Лейбница
Для нахождения производной n-ого порядка от произведения двух функций большое практическое значение имеет формула Лейбница.
Пусть u и v — некоторые функции от переменной х, имеющие производные любого порядка и y=uv. Выразим n-ую производную через производные функцийu и v.
Имеем последовательно
,
,
.
Легко подметить аналогию между выражениями для второй и третьей производных и разложением бинома Ньютона соответственно во второй и третьей степенях, но вместо показателей степени стоят числа, определяющие порядок производной, а сами функции можно рассматривать как «производные нулевого порядка». Учитывая это, получим формулу Лейбница:
. (2)
Эту формулу можно доказать методом математической индукции.
Пример. Найти пятую
производную функции 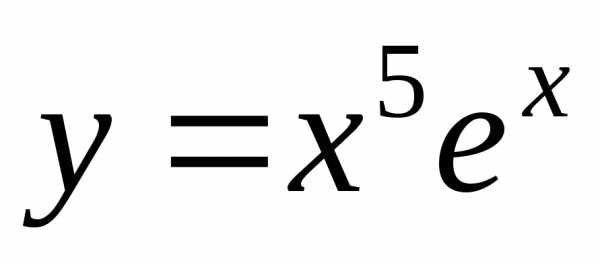 .
.
Решение.
Положим 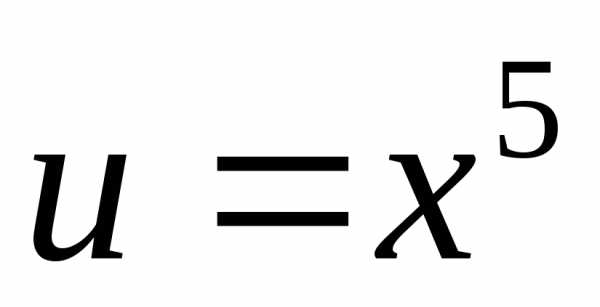 и
и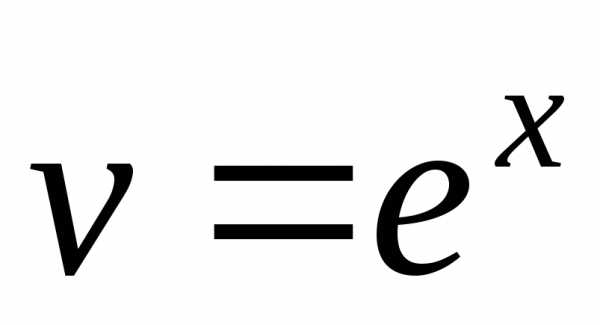 .
Найдем
.
Найдем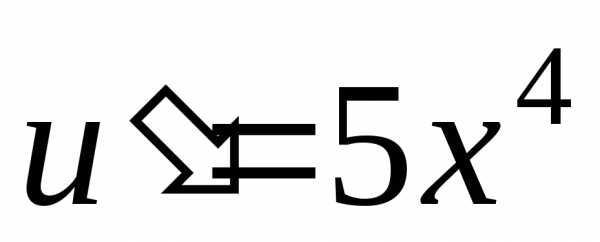 ,,,,;.
Подставляя эти выражения в формулу
Лейбница при
,,,,;.
Подставляя эти выражения в формулу
Лейбница при ,
получим
,
получим
.
studfiles.net
Производные высших порядков, формулы и примеры решения задач
Задание. Найти $y^{(4)}(x)$, если $y(x)=e^{4 x} \sin 3 x$
Решение. Так как заданная функция представляет собой произведение двух функций $u(x)=e^{4 x}$, $v(x)=\sin 3 x$, то для нахождения производной четвертого порядка целесообразно будет применить формулу Лейбница:
$y^{(4)}(x)=\left(e^{4 x}\right)^{(4)} \cdot \sin 3 x+C_{4}^{1}\left(e^{4 x}\right)^{(3)} \cdot(\sin 3 x)^{\prime}+$
$+C_{4}^{2}\left(e^{4 x}\right)^{\prime \prime} \cdot(\sin 3 x)^{\prime \prime}+C_{4}^{3}\left(e^{4 x}\right)^{\prime} \cdot(\sin 3 x)^{(3)}+e^{4 x}(\sin 3 x)^{(4)}$
Найдем все производные и посчитаем коэффициенты при слагаемых.
1) Посчитаем коэффициенты при слагаемых:
$C_{4}^{1}=\frac{4 !}{1 ! \cdot(4-1) !}=\frac{4 !}{3 !}=\frac{3 ! \cdot 4}{3 !}=4$
$C_{4}^{2}=\frac{4 !}{2 ! \cdot(4-2) !}=\frac{4 !}{2 ! \cdot 2 !}=\frac{2 ! \cdot 3 \cdot 4}{2 ! \cdot 2 !}=\frac{3 \cdot 4}{2}=6$
$C_{4}^{3}=\frac{4 !}{3 ! \cdot(4-3) !}=\frac{4 !}{3 !}=\frac{3 ! \cdot 4}{3 !}=4$
2) Найдем производные от функции $u(x)$:
$u(x)=e^{4 x}, u^{\prime}(x)=\left(e^{4 x}\right)^{\prime}=e^{4 x} \cdot(4 x)^{\prime}=e^{4 x} \cdot 4 \cdot(x)^{\prime}=4 e^{4 x}$
$u^{\prime \prime}(x)=\left(u^{\prime}(x)\right)^{\prime}=\left(4 e^{4 x}\right)^{\prime}=4 \cdot\left(e^{4 x}\right)^{\prime}=16 e^{4 x}$
$u^{\prime \prime \prime}(x)=\left(u^{\prime \prime}(x)\right)^{\prime}=\left(16 e^{4 x}\right)^{\prime}=64 e^{4 x}$
$u^{(4)}(x)=\left(u^{\prime \prime \prime}(x)\right)^{\prime}=\left(64 e^{4 x}\right)^{\prime}=256 e^{4 x}$
3) Найдем производные от функции $v(x)$:
$v(x)=\sin 3 x, v^{\prime}(x)=(\sin 3 x)^{\prime}=\cos 3 x \cdot(3 x)^{\prime}=3 \cos 3 x$
$v^{\prime \prime}(x)=\left(v^{\prime}(x)\right)^{\prime}=(3 \cos 3 x)^{\prime}=3 \cdot(\cos 3 x)^{\prime}=$
$=3 \cdot(-\sin 3 x) \cdot(3 x)^{\prime}=-9 \sin 3 x$
$v^{\prime \prime \prime}(x)=\left(v^{\prime \prime}(x)\right)^{\prime}=-27 \cos 3 x, v^{(4)}(x)=\left(v^{\prime \prime \prime}(x)\right)^{\prime}=81 \sin 3 x$
Тогда
$y^{(4)}(x)=256 e^{4 x} \cdot \sin 3 x+4 \cdot 64 e^{4 x} \cdot 3 \cos 3 x+$
$+6 \cdot 16 e^{4 x} \cdot(-9 \sin 3 x)+4 \cdot 4 e^{4 x} \cdot(-27 \cos 3 x)+e^{4 x} 81 \sin 3 x=$
$=e^{4 x}(336 \cos 3 x-527 \sin 3 x)$
Ответ. $y^{(4)}(x)=e^{4 x}(336 \cos 3 x-527 \sin 3 x)$
www.webmath.ru
Производные высших порядков. Правила и примеры
Под производной высших порядков понимают дифференцирования функции более одного раза. Если производнуюповторно дифференцировать, то получим производную второго порядка, или вторую производную функции , и она обозначается
Производная третьего порядка будет иметь вид
Аналогично получают формулы для нахождения производных высших порядков. При нахождении производной порядке необходимо иметь производную порядка. Исключение составляют функции для которых можно заметить тенденцию изменения производных. Это степенные, некоторые тригонометрические и экспоненциальные функции:
В других случаях, для нахождения производных высших порядков от заданной функции нужно последовательно находить все ее производные низших порядков. Для практического усвоения материала рассмотрим примеры.
Пример 1.
Вычислить производные второго порядка
1)
2)
3)
4)
Решение.
1) По правилам дифференцирования параметрических функций имеем
Применим к заданной функции. Найдем производную
Дифференцируем второй раз. По правилу дифференцирования получим
По формуле вычисляем
2)Определяем первую производную для функции
Вычисляем вторую производную
3)Вычислим первую производную
а потом вторую
При нахождении производной второго и высших порядков для данного примера и ему подобных можно пользоваться следующим правилам:
1) если степень функции меньше порядка производной , то она вклада не дает
2) все старшие степени дают вклад
По такой схеме вторую производную можно было найти так:
Для практики второй способ эффективнее, особенно если нужно найти производные гораздо более высоких порядков чем второй.
4) Производную функции первого порядка будет иметь вид
второго порядка
По аналогии можно вывести формулу для производной экспоненциальной функции порядка
Решая примеры для синус и косинус функций можно заметить сходство при исчислении старших производных и вывести следующие зависимости
Пользуйтесь и пусть не возникают проблемы с производными высших порядков.
yukhym.com
