Простая физика — EASY-PHYSIC
В этой статье приведены две задачи, которые помогут вам научиться определять радиус кривизны траектории при движении тела под углом к горизонту. Каждая из задач представляет собой целый набор, поэтому неясностей не должно остаться.
Задача 1.
Тело брошено со скоростью 10 м/с под углом к горизонту. Найти радиусы кривизны траектории тела в начальный момент его движения, спустя время 0,5 с и в точке наивысшего подъема тела над поверхностью земли.
Как известно, радиус кривизны траектории связан с нормальным ускорением и скоростью формулой:
Откуда :
То есть, чтобы найти радиус кривизны траектории в любой точке, необходимо лишь знать скорость и нормальное ускорение, то есть ускорение, перпендикулярное вектору скорости. Рассмотрим все заданные точки и определим в них скорости и нужные составляющие ускорения.
К задаче 1
Самое простое – это определение этих величин в точке наивысшего подъема.
Действительно, вертикальная составляющая скорости здесь равна нулю, поэтому скорость тела в данной точке равна горизонтальной составляющей, а ускорение, нормальное к вектору этой скорости – это ускорение свободного падения, поэтому
Вторая по простоте расчета – точка начала движения. Скорость в ней нам уже известна, осталось с ускорением разобраться. Ускорение свободного падения разложим на две составляющие: и . Первая – перпендикулярна скорости, она-то нам и нужна. Определяем радиус:
Наконец, точка, в которой тело окажется через пол-секунды.
Наше тело будет лететь по горизонтали с постоянной скоростью, равной . По вертикали тело будет двигаться равнозамедленно до середины траектории (наивысшей точки), а затем равноускоренно. Определим, успеет ли тело добраться до апогея:
Простой прикидочный расчет показывает, что нужная нам точка находится на первой половине траектории, где тело еще двигается вверх. Тогда его скорость по оси :
Определим полную скорость тела в момент времени :
Угол наклона вектора скорости к горизонту в этот момент равен:
А можно было сразу и косинус найти:
Тогда искомый радиус кривизны траектории равен:
Ответ: м, м, м.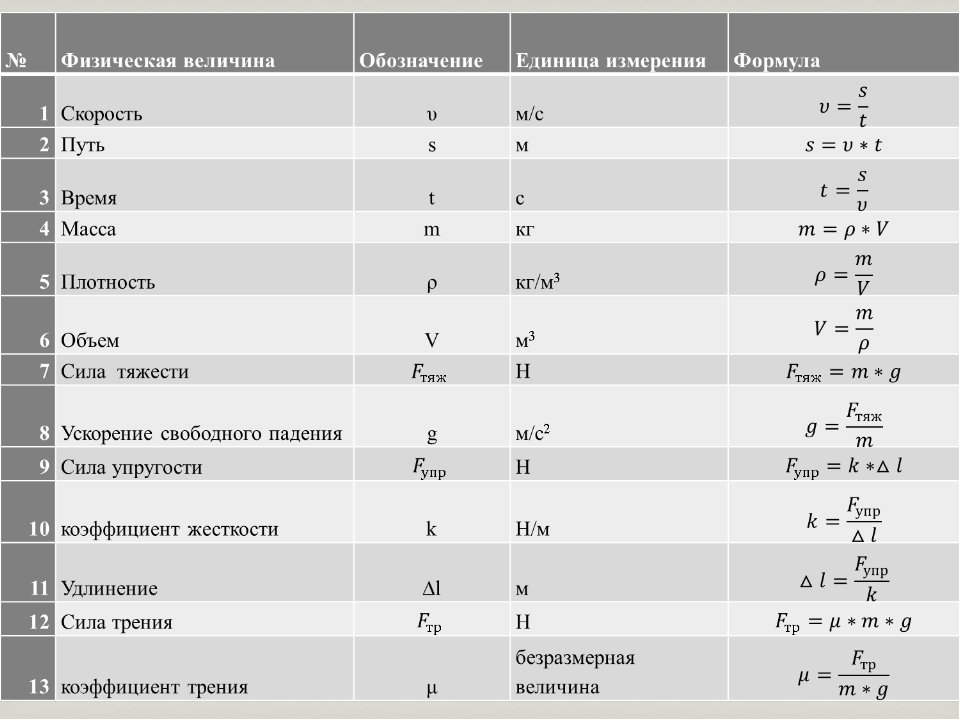
Задача 2.
Под каким углом к горизонту нужно бросить шарик, чтобы а) радиус кривизны траектории в начальный момент времени был в 8 раз больше, чем в вершине; б) центр кривизны вершины траектории находился бы на поверхности земли?
Запишем условие задачи так: а) , б).
а)Как и в предыдущей задаче, определяем радиус кривизны траектории в точке броска. Скорость нам известна, а нормальным ускорением будет проекция ускорения свободного падения:
Определим теперь радиус кривизны в вершине:
По условию :
б) Мы уже определили , осталась максимальная высота подъема.
Время определяем из условия равенства нулю вертикальной составляющей скорости так же, как мы это делали в предыдущей задаче:
Приравниваем и :
Откуда .
Ответ: а) , б) .
Центрифугирование: как определить ускорение (число g) в зависимости от скорости вращения и диаметра ротора
Центрифугирование – способ разделения неоднородных, дисперсных жидких систем на фракции по плотности под действием центробежных сил.
Центрифугирование осуществляют в центрифугах, принцип работы которых основан на создании центробежной силы, увеличивающей скорость разделения компонентов смеси по сравнению со скоростью их разделения только под влиянием силы тяжести. Разделение веществ с помощью центрифугирования основано на разном поведении частиц в центробежном поле. В центробежном поле частицы, имеющие разную плотность, форму или размеры, осаждаются с разной скоростью.
Скорость осаждения, или седиментации, зависит от центробежного ускорения (g), прямо пропорционального угловой скорости ротора (w, рад/с) и расстоянию между частицей и осью вращения (r, см): g =
Угловая скорость – характеристика скорости вращения тела, измеряется обычно в радианах в секунду, полный оборот (360°) составляет 2π радиан.
Центробежное ускорение тогда будет равно: g =p2x r x n2/900.
Центробежное ускорение обычно выражается в единицах g (ускорение свободного падения, равное 980 м/с2) и называется относительным центробежным ускорением (ОЦУ), т.е. ОЦУ=g/980 или ОЦУ = 1,11 x 10-5 x r x n2 .
Относительное ускорение центрифуги (rcf) задается, как кратное от ускорения свободного падения (g). Оно является безразмерной величиной и служит для сравнения производительности разделения и осаждения.
Относительное ускорение центрифуги (rcf) зависит от частоты вращения и радиуса центрифугирования.
Существует номограмма, выражающая зависимость относительного ускорения центрифуги (rcf) от скорости вращения ротора (n) и радиуса (r) – среднего радиуса вращения столбика жидкости в центрифужной пробирке (т.е. расстояния от оси вращения до середины столбика жидкости). Радиус измеряется (
Номограмма для определения относительного ускорения центрифуги (rcf) в зависимости от скорости вращения и диаметра ротора
r – радиус ротора, см
n – скорость вращения ротора, оборотов в минуту
rcf (relative centrifuge force) – относительное ускорение центрифуги
Радиус центрифугирования rmax– это расстояние от оси вращения ротора до дна гнезда ротора.
Для определения ускорения с помощью линейки совмещаем значения радиуса и числа оборотов на и на шкале rcf определяем его величину.
Пример: на шкале А отмечаем значение rрадиуса для ротора – 7,2 см, на шкале С отмечаем значение скорости ротора –14,000 об/мин, соединяем эти две точки. Точка пересечения образованного отрезка со шкалой В показывает значение ускорения для данного ротора. В данном случае ускорение равно 15’000.
Измерение радиуса Земли в 240 г. до н.э. – e=mc2andallthat
Мозг шире неба,
Эмили Дикинсон, «Мозг»
Ибо, поставь их рядом,
Одно другое включит 6 С легкость, и ты рядом.
Большинство учителей естествознания считают, что «Космос» является одной из самых увлекательных тем для многих студентов: чувство чуда, возникающее по мере того, как наша родная планета теряется в пустых просторах Солнечная система, которая затем теряется в бескрайних звездных просторах галактики Млечный Путь, доставляет удовольствие.
Но ученики часто задают вопрос: откуда мы все это знаем? Откуда мы знаем, что расстояние до ближайшей к Солнцу звезды равно 4 световым годам? Или как узнать расстояние до Солнца? Или Луна?
Со смущением признаюсь, что я обычно отвечал небрежным и непреднамеренно-пренебрежительным «Ну что ж, ученые их измерили!», что (хотя и верно) должно было звучать скорее как исповедание веры, чем как трезвый рассказ о эмпирический факт. Что, если честно, так оно и было; просто потому, что я еще не пытался выяснить, как эти измерения были сделаны впервые.
Технологические ресурсы, доступные нашим предкам, кажутся нам примитивными и рудиментарными, но в сочетании с глубоким колодцем человеческой изобретательности, который, как мне нравится, является отличительной чертой нашего вида, он оказался не просто «лучшим в мире», а « побеждающий вселенную».
Надеюсь, вам понравится эта обзорная экскурсия по этому малопосещаемому уголку научной глубинки, и вы захотите поделиться этими историями со своими учениками.
Хорошо знать, что мозг действительно «шире неба».
Я представил это в стиле и формате, подходящих для обмена и обсуждения со студентами KS3/KS4 (11-16 лет).
Бешеные псы и Эратосфен выходят в полуденное Солнце…
Начнем с самого начала: первое достоверное измерение размеров Земли было сделано в 240 г. до н.э., а началось все (по крайней мере, в этом пересказе) с тот факт, что Эратосфен любил общаться с туристами. («Err-at-oss-THen-ees» с «TH» произносится как «термометр» — никогда не забывайте, что ученики всех возрастов часто приветствуют помощь в обучении произношению незнакомых слов)
Александрия (на территории современного Египта) была процветающим городом и притягивала туристов. Эратосфен взял за правило разговаривать с как можно большим количеством посетителей. Их истории, взятые с долей скептицизма, были бесценным источником информации о мире в целом. Эратосфен был главным библиотекарем Александрийской библиотеки, считавшейся в то время одним из семи чудес света, и считал своим долгом собрать, каталогизировать и классифицировать как можно больше информации.
Один посетитель, присутствовавший в Александрии в самый длинный день в году (21 июня по нашему календарю), мимоходом упомянул Эратосфену что-то, что Библиотекарю было трудно забыть: «Знаете, — сказал посетитель, — в полдень в этот день в моем родном городе теней нет .’
Как же так? задумался Эратосфен. Объяснение было только одно: в тот день в Сиене (родном городе туриста, ныне известном как Асуан) Солнце было прямо над головой.
То же самое не было в Александрии. В полдень появилась небольшая, но заметная тень. Эратосфен измерил угол тени в полдень самого длинного дня. Было семь градусов.
Нет теней в Сиене, но в то же самое время в Александрии 7-градусная тень. Объяснение опять-таки было только одно: Александрия была «наклонена» на 7 градусов по отношению к Сиене.
Семь степеней разделения
Сферичность Земли была признана астрономами с ок. 500 г. до н.э., так что эта разница не была неожиданностью для Эратосфена, но он понял, что, поскольку он сравнивал длину теней в двух местах на поверхности Земли одновременно, то 7 o не было просто углом тени.
: 7 o — угол, образуемый в центре Земли радиальными линиями, проведенными из обоих мест.
Эратосфен заплатил человеку, чтобы тот прошел расстояние между Александрией и Сиеной. (Это была не такая странная просьба, как кажется нам: в древнем мире были профессионалы, называемые бематистами, которых обучали измерять расстояния, считая шаги.)
Бематисту понадобился почти месяц, чтобы пройти это расстояние, и по нашим измерениям оно составило 5000 стадий или 780 км.
Затем Эратосфен использовал метод простого отношения для расчета окружности Земли, C :
Тогда:
Современное значение радиуса Земли составляет 6371 км.
Если и но…
До сих пор ведутся споры относительно фактической длины одного греческого стадиона, но измерения Эратосфена, как правило, согласуются в пределах 1-2% от современного значения.
К сожалению, ни один из экземпляров книги, в которой Эратосфен объяснял свой метод под названием «О измерении земли », не сохранился с древних времен, поэтому представленная здесь версия является упрощенной, изложенной Клеомедом в более поздней книге.
За дальнейшими подробностями читатели могут обратиться к превосходной статье в Википедии об Эратосфене.
Астроном Карл Саган также незабываемо объяснил этот метод в своем телевизионном документальном сериале 1980 года Космос .
Вы можете прочитать…
Это часть серии статей о том, как люди «измерили размер неба»:
Часть 2: Как Аристарх измерил расстояние между Землей и Луной
Часть 3: Как Аристарх измерил расстояние между Землей и Луной Солнце
Нравится:
Нравится Загрузка…
Измерение радиуса протона | Институт креационных исследований
Измерение радиуса протона
BY ВЕРНОН Р. КАППС, доктор философии. * |
СРЕДА, 31 ЯНВАРЯ 2018 ГОДА
Когда мы хотим что-то измерить в нашей повседневной жизни, мы прикладываем линейку к рассматриваемому объекту и считываем его размеры по маркировке.
Поскольку протоны и нейтроны очень малы, мы не можем напрямую наблюдать их взаимодействие с помощью какого-либо измерительного прибора. Мы должны наблюдать результаты этого взаимодействия и вывести их размеры из этих результатов. Действительно, на субатомном уровне результаты измерения зависят не только от того, как выполняется измерение, но и от энергии, при которой оно производится, и от типа зонда, используемого для измерения. В более ранней статье Acts & Facts мы ясно увидели, как эти вещи могут повлиять на измерение радиуса протона. 1
Рисунок 1. Схематическая диаграмма двух возможных событий, которые могут произойти, когда электрон рассеивается на кварках, составляющих протон.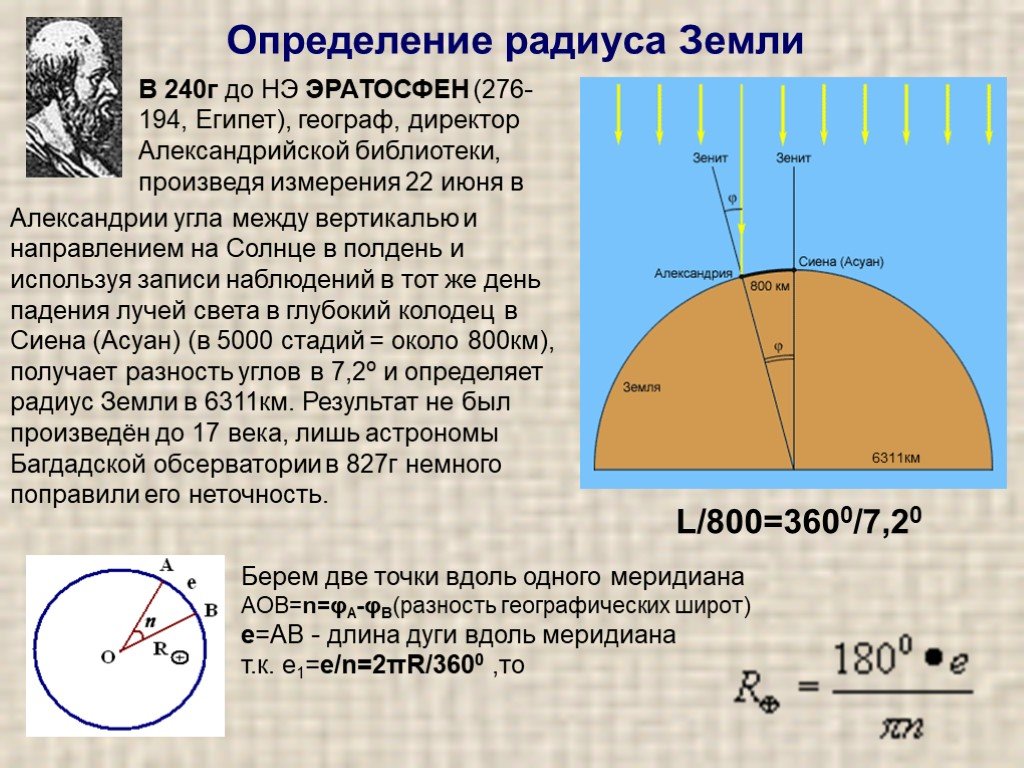
В недавней статье в Physics Today была предпринята попытка согласовать различия между двумя более ранними измерениями радиуса протона. 2 Несколько месяцев спустя в последующей статье в Science News указывалось, что различия между двумя измерениями — т. е. прямым рассеянием электронов на протоне по сравнению с измерением лэмбовского сдвига в мюонном водороде — все еще оставались после обширных усилий. при согласовании с теоретическими моделями. 3
Итак, откуда вся неуверенность в размерах радиуса протона? Протон представляет собой составную частицу, состоящую из двух верхних кварков и одного нижнего кварка, при этом глюоны постоянно обмениваются между кварками (см. рис. 1). Если мы используем фермионную частицу, например, электрон или мюон, для измерения радиуса протона, мы будем эффективно измерять протяженность электромагнитного поля протона 
радиус. С другой стороны, если мы используем электрически нейтральную адронную частицу, например, нейтрон или нейтральный пи-мезон, мы эффективно измеряем степень сильное поле , или диапазон сильного ядерного взаимодействия (~ 1,4 фм), а не фактический физический радиус.
Гравитационная сила на много порядков слишком мала на субатомных расстояниях, чтобы быть подходящим зондом. Слабое ядерное взаимодействие примерно на три порядка (10 -3 ) слишком мало, чтобы быть эффективным зондом для этого измерения.
Есть много способов, которыми налетающий электрон может взаимодействовать с протоном-мишенью. 4 Он может столкнуться с кварком и отскочить назад. Он может быть направлен вокруг верхнего кварка (+ заряд) или от нижнего кварка (- заряд). Или он может взаимодействовать с двумя или тремя составляющими его кварками до того, как покинет электромагнитное поле ядра. Если фотон, испускаемый электроном при взаимодействии с кварками, имеет достаточную энергию, он может «спарить» электрон и позитрон в электромагнитном поле ядра.
Все эти потенциальные взаимодействия теоретически возможны и поэтому должны учитываться любой моделью/гипотезой, пытающейся объяснить результаты наблюдений и извлечь радиус протона из данных. На сегодняшний день ни одна из предложенных моделей/гипотез не смогла адекватно объяснить наблюдаемые расхождения между двумя наборами данных. Ясно, что Стандартная модель физики еще не все объясняет.
Наука — прекрасный инструмент для исследования мира природы, в котором мы живем, но мы всегда должны помнить, что наука выполняется и интерпретируется людьми, которые могут ошибаться.
Наука — прекрасный инструмент для исследования мира природы, в котором мы живем, но мы всегда должны помнить, что наука выполняется и интерпретируется людьми, которые могут ошибаться. Таким образом, в душе человека всегда есть место для веры. Главный вопрос для каждого человека: во что вы собираетесь верить — в человека или в Бога?
Каталожные номера
- Куппс, В.
Р. 2014. Протонные проблемы: вера в теории или реальность? Деяния и факты . 43 (4): 9. - Блау, С.К. 2017. Структура протона в новом свете. Физика сегодня . 70 (5): 14-15.
- Коновер, Э. 2017. Размер протона по-прежнему вызывает недоумение, несмотря на новое измерение. Новости науки. 192 (8): 14.
- Протон в атоме в тысячи раз меньше самого атома, а электроны и кварки в тысячи раз меньше протона, возможно, бесконечно меньше, если они точечные частицы.
Р. 2014. Протонные проблемы: вера в теории или реальность? Деяния и факты . 43 (4): 9.* Д-р Куппс является научным сотрудником Института креационных исследований и получил степень доктора философии. по ядерной физике в Университете Индианы в Блумингтоне. Он работал в Лос-Аламосской национальной лаборатории, а затем занял должность физика-радиолога в Национальной ускорительной лаборатории Ферми, где он руководил лабораторией радиохимического анализа с 1988 по 2011 год. Он является опубликованным исследователем с 73 публикациями.
Процитируйте эту статью: Vernon R.
Cupps, Ph.D. 2018. Измерение радиуса протона. Акты и факты . 47 (2).
Последние новости
НОВОСТИ АКТЫ И ФАКТЫ ПОДКАСТЫ
НОВОСТИ
Вариант бабочки
Бабочки снова попали в новости науки, на этот раз в отношении основного гена под названием WntA: «объединенная группа исследователей из Корнельского университета…
АВТОР: FRANK SHERWIN, D.SC. (HON.)
CREATION PODCAST
Сколько лет Вселенной? | Подкаст о создании: серия 35
Многие ученые утверждают, что Вселенной примерно 13,8 миллиарда лет, путем реинжиниринга Большого Взрыва с предположением, что эта теория…
В двух отдельных исследованиях утверждается, что массивные цунами и землетрясения, вызванные ударом астероида, сильно повлияли на каменную летопись. Одна исследовательская группа смоделировала…
АВТОР: TIM CLAREY, PH.D.
АКТЫ И ФАКТЫ
Деревья и листья
Майкл Стэмп и Сьюзан Виндзор*
Вы никогда не слишком молоды, чтобы быть ученым-креационистом! Дети, узнайте интересные факты о Божьем творении с помощью.
..
ОТ: РАЗЛИЧНЫХ АВТОРОВ
АКТЫ И ФАКТЫ
Центр открытий ICR отмечает свою третью годовщину!
Центр открытий ICR в Далласе, штат Техас, торжественно открылся 2 сентября 2019 года. С тех пор через наши двери прошли тысячи людей…
ОТ: СОТРУДНИКА
ИЗВИНЕНИЯ
Когда летучие мыши ужинают ночью
Летучие мыши — загадочные, чудесные хищники даже в падшем мире, где всеядное хищничество является обычным явлением. 1 Поскольку летучие мыши в основном ведут ночной образ жизни,…
АВТОР: JAMES J. S. JOHNSON, J.D., TH.D.
АКТЫ И ФАКТЫ
Птичий таз не произошел от динозавра
Большинство зоологов и палеонтологов позвоночных пришли к воображаемому консенсусу: птицы на самом деле являются летающими динозаврами. Это убеждение включает в себя…
АВТОР: ФРЭНК ШЕРВИН, D.SC. (HON.)
АКТЫ И ФАКТЫ
Гора Хермон образовалась в результате наводнения
Гора Ермон — это тема, которая, кажется, все чаще всплывает в наши дни, особенно среди христианских пророчеств и учителей последнего времени.