Внеклассный урок — Квадратичная функция. Функция y = ax2, ее график и свойства
Квадратичная функция. Функция y = ax2, ее график и свойства
Квадратичная функция – это функция, которую можно задать формулой вида
y = ax2 + bx + c,
где x – независимая переменная, a, b и c – некоторые числа, причем а ≠ 0.
Областью определения квадратичной функции является множество всех чисел. (Напомним: областью определения функции называется совокупность значений независимой переменной, см.раздел «Функции и их графики»)
Функция y = ax2.
Функция y = ax2 – это частный случай квадратичной функции.
Графиком функции y = ax2 является парабола.
Свойства функции y = ax2 при a > 0:
1. Если x = 0, то y = 0. График функции проходит через начало координат.
2. Если x ≠ 0, то y > 0. График функции расположен в верхней полуплоскости.
3. Противоположным значениям аргумента соответствуют равные значения функции. Пояснение: допустим, x = –2, y = 8. При x = 2 значение y не меняется и составляет 8.
4. В промежутке (–∞; 0] функция убывает, а в промежутке [0; +∞) — возрастает.
5. Наименьшее значение функции равно нулю. Это значение она принимает при x = 0 (см. Наибольшего значения функция не имеет. Т.е. областью значений функции является промежуток [0; +∞). |
Свойства функции y = ax2 при a < 0:
1. Если x = 0, то y = 0. График функции проходит через начало координат.
2. Если x ≠ 0, то y < 0. График функции расположен в нижней полуплоскости.
3. Противоположным значениям аргумента соответствуют равные значения функции. График функции представляет собой симметричную фигуру относительно оси y. Пояснение: допустим, x = –4, y = –8. При x = 4 значение y не меняется и составляет –8.
4. В промежутке (–∞; 0] функция возрастает, а в промежутке [0; +∞) — убывает.
5. Наибольшее значение функции равно нулю. Это значение она принимает при x = 0 (см.пункт 1). Наименьшего значения функция не имеет. Т.е. областью значений функции является промежуток (–∞; 0]. |
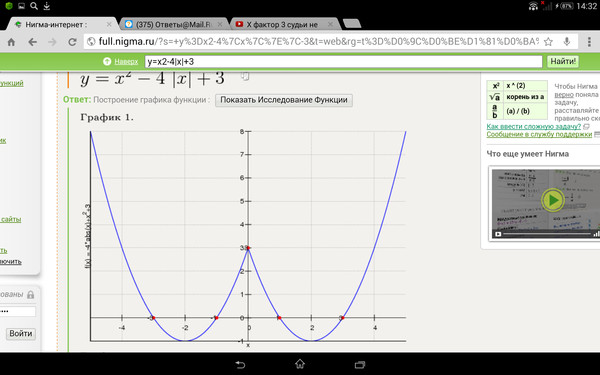
2.Квадратичная функция y=x² — Функции и их графики
В уравнении квадратичной функции: a – старший коэффициент b – второй коэффициент с — свободный член. Графиком квадратичной функции является квадратичная парабола, которая для функции имеет вид: Точки, обозначенные зелеными кружками – это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции , составим таблицу: Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции при любых значениях остальных коэффициентов. График функции имеет вид: Для нахождения координат базовых точек составим таблицу:
Обратите внимание, что график функции симметричен графику функции относительно оси ОХ. Итак, мы заметили: Если старший коэффициент a>0, то ветви параболы напрaвлены вверх. Если старший коэффициент a<0, то ветви параболы напрaвлены вниз. Второй параметр для построения графика функции – значения х, в которых функция равна нулю, или нули функции. На графике нули функции — это точки пересечения графика функции с осью ОХ. Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение . В случае квадратичной функции нужно решить квадратное уравнение . В процессе решения квадратного уравнения находим дискриминант: , который определяет число корней квадратного уравнения. И здесь возможны три случая: 1. 2. Если ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. Если ,то график функции выглядит примерно так: 3. Если ,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ: , Если ,то график функции выглядит примерно так: Следующий важный параметр графика квадратичной функции – координаты вершины параболы:
Прямая, прохдящая через вершину параболы параллельно оси OY является осью симметрии паработы. И еще один параметр, полезный при построении графика функции – точка пересечения параболы с осью OY. Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: . То есть точка пересечения параболы с осью OY имеет координаты (0;c). Итак, основные параметры графика квадратичной функции показаны на рисунке: |
x=\frac{-5±\sqrt{25-4\times 4\left(-y\right)}}{2\times 4}
Square 5.
x=\frac{-5± \sqrt{25-16\left(-y\right)}}{2\times 4}
Умножить -4 раза 4.
x=\frac{-5±\sqrt{25+16y}}{2 \times 4}
Умножить -16 раз -y.
x=\frac{-5±\sqrt{16y+25}}{2\times 4}
Прибавьте 25 к 16y.
x=\frac{-5±\sqrt{16y+25}}{8}
Умножить 2 раза на 4.
x=\frac{\sqrt{16y+25}-5}{8}
Теперь решите уравнение x=\frac{-5±\sqrt{16y+25}}{8}, когда ± равно плюсу. Добавьте -5 к \sqrt{25+16y}. 9{ 2 } — 4 x — 5 = 0
Тригонометрия
4 \sin \theta \cos \theta = 2 \sin \theta
Линейное уравнение
y = 3x + 4
Арифметика 3 0 3 0 9
90Матрица
\left[ \begin{array} { l l } { 2 } & { 3 } \\ { 5 } & { 4 } \end{array} \right] \left[ \begin{array} { l l l } { 2 } & { 0 } & { 3 } \\ { -1 } & { 1 } & { 5 } \end{массив} \right]
Одновременное уравнение
\left.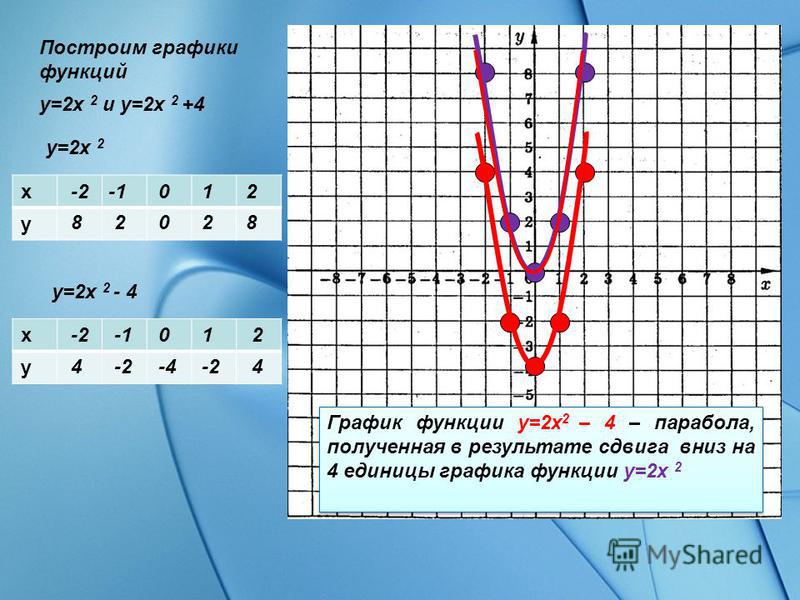 \begin{cases} { 8x+2y = 46 } \\ { 7x+3y = 47 } \end{cases} \right. 9{2}+2 x-3}
\begin{cases} { 8x+2y = 46 } \\ { 7x+3y = 47 } \end{cases} \right. 9{2}+2 x-3}
Как построить график \\[y = 4x
Ответ
Подтверждено
184,5 тыс.+ просмотров
Подсказка: Чтобы решить это, нам нужно задать значения ‘x ‘, и мы можем найти значения ‘y’. В противном случае мы можем найти координату данного уравнения, лежащую на линии оси x, мы можем найти это, подставив значение «y» равным нулю (х-пересечение). Точно так же мы можем найти координату уравнения, лежащую на линии оси y, мы можем найти это, подставив значение «x», равное нулю (отрезок y).
Полное пошаговое решение:
Дано, \[y = 4x — 2\].
Чтобы найти точку пересечения. Это значение «x» в \[y = 0\]. Подставляя это в данное уравнение. Имеем
\[0 = 4x — 2\]
\[4x = 2\]
Делим на 4 с обеих сторон,
\[x = \dfrac{2}{4}\]
\[x = \ dfrac{1}{2}\]
\[x = 0.5\]
Таким образом, мы имеем координату уравнения, которая лежит на линии оси x. Координата \[(0.5,0)\].
Координата \[(0.5,0)\].
Чтобы найти точку пересечения с осью y. Это значение «y» при \[x = 0\]. Подставляя это в данное уравнение, мы имеем,
\[y = 4(0) — 2\]
\[y = — 2\].
Таким образом, у нас есть координата уравнения, которая лежит на линии оси y. Координата \[(0, — 2)\].
Таким образом, у нас есть координаты \[(0.5,0)\] и \[(0, — 2)\]. Этого достаточно, чтобы нарисовать график.
Возьмем масштаб по оси абсцисс = 1 единица = 1 единица; ось Y= 1 единица = 1 единица
Все, что мы сделали, это расширили линию, касающуюся координат \[(0,5,0)\] и \[(0, — 2)\], на прямую линию.
Используя график, мы нашли другие координаты, которые равны \[( — 1, — 6),\] и \[(1,2)\]
Примечание: Метод пересечения является простым и более точным методом для построить график любого уравнения. Если точки пересечения равны нулю, то данное уравнение проходит через начало координат, и мы находим координатные точки, задавая случайные значения, такие как 1, 2, 3,… для «x», мы находим соответствующее значение «y».

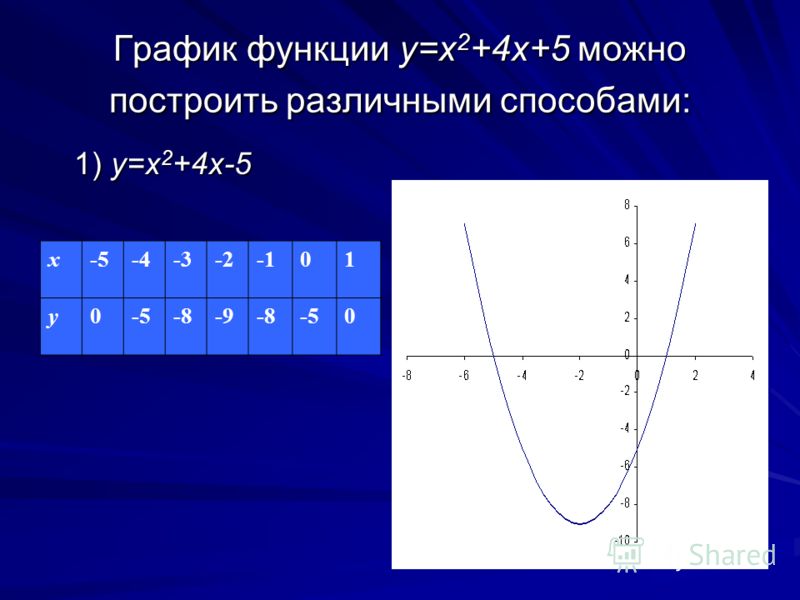 пункт 1).
пункт 1).