где $\binom{n}{k} = \frac{n!}{(n-k)!k!}$ – биномиальный коэффициент.
Биномиальное распределение – это распределение числа успехов $k$ в серии из независимых $n$ опытов, при условии, что вероятность успеха в каждом опыте есть $p$.
Математическое ожидание и дисперсия, соответственно, равны
$$\mathrm{E}(X)=np$$ $$\mathrm{V}(X)=np(1−p)$$
При больших $n$ биномиальное распределение хорошо приближается нормальным.
Рис. 2 плотность вероятности и функция распределения биномиального распределения
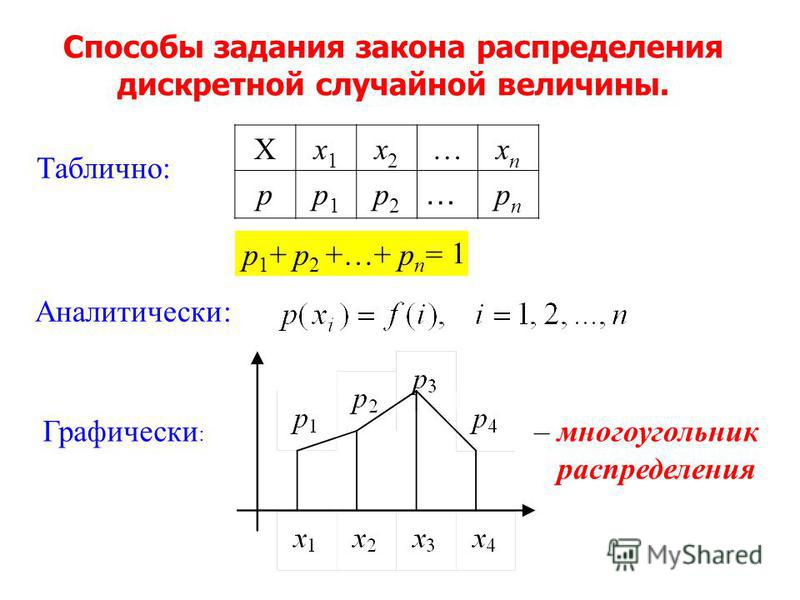
Для вычисления биномиального распределения в Excel используется стандартная функция BINOMDIST (БИНОМРАСП):
BINOMDIST(number_s=k, trials=n, probability_s=p,cumulative=TRUE|FALSE)
Если cumulative=TRUE, то возвращается кумулятивная функция распределения, а если cumulative=FALSE, то возвращается плотность вероятности.
Рис. 3 Пример вычисления биномиального распределения
Равномерное распределение
Случайная величина $X$ распределена равномерно на отрезке $[a, b]$, если ее функция распределения $U(x|a,b)$ и, соответственно, плотность вероятности $u(x|a,b)$ имеют вид
$$U(x|a,b) = \begin{cases} 0, x≤a, \\ \frac{x-a}{b-a}, a < x ≤ b \\ 1, x > b\end{cases}$$ $$u(x|a,b) = \begin{cases} 0, x≤a, \\ \frac{1}{b-a}, a < x ≤ b \\ 0, x > b\end{cases}$$
Математическое ожидание и дисперсия, соответственно, равны
$$\mathrm{E}(X)=0.
{–1}(X)$$
имеет функцию распределения $F$.
Таким образом, если получить набор случайных величин, распределенных равномерно, то эти случайные величины можно превратить в новые, имеющие другое, заданное распределение.
Для генерации случайных чисел в Excel имеется стандартная функция: RAND (СЛЧИС).
RAND()
Возвращает случайное число, равномерно распределенное на отрезке $[0,1]$. Новое случайное число возвращается при каждом вычислении рабочего листа.
На листе Random рабочей книги Statistics.xls приведен пример генерации случайных чисел для разных распределений.
Рис.13 Пример генерации случайных чисел
Нормальное распределение (3.5)
§ 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
3.5. Нормальное распределение.
Говорят, что случайная величина нормально распределена или подчиняется закону распределения Гаусса, если ее плотность распределения имеет вид
| (28) |
где a — любое действительное число, а >0.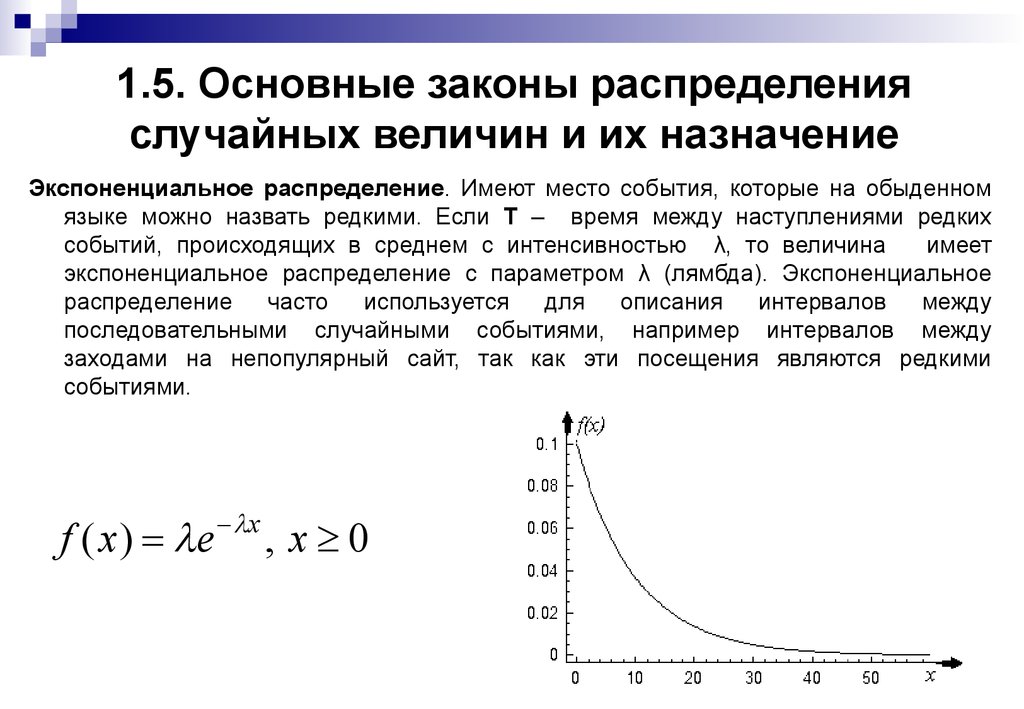
Смысл параметров
a и будет установлен в дальнейшем (см. §4, п. 2).
Исходя из связи между плотностью распределения и функцией распределения F(x) [см. формулу (22)], имеем
График функции симметричен относительно прямой
На рис. 11 изображены два графика функции y=. График I соответствует значениям a=0, =1, а график II — значениям a=0, =1/2.
Покажем, что функция удовлетворяе условию (24), т.
е. при
любых a и выполняется соотношение
В самом деле, сделаем в этом интеграле замену переменной, полагая . Тогда
В силу четности подинтегральной функции имеем
Следовательно,
Но,
В результате получим
| (29) |
Найдем вероятность . По формуле (23) имеем
Сделаем в этом интеграле замену переменной, снова полагая . Тогда , и
| (30) |
Как мы знаем, интеграл не берется в элементарных функциях. Поэтому для вычисления определенного интеграла (30) вводится функция
| (31) |
называемая интегралом вероятностей. Для этой функции составлены таблицы ее значений для различных значений аргумента (см.
Итак,
| (32) |
Легко показать, что функция Ф(х) (интеграл вероятностей) обладает следующими свойствами.
1°. Ф(0)=0
2°. ; при величина практически равна 1/2 (см. табл. II).
3°. Ф(-x)=-Ф(х), т.е. интеграл вероятностей является нечетной функцией.
График функции Ф(х) изображен на рис. 12.
Таким образом, если случайная величина нормально распределена с параметрами a и , то вероятность того, что случайная величина удовлетворяет неравенствам , определяется соотношением (32).
Пусть >0. Найдем вероятность того, что нормально распределенная случайная величина отклонится от параметра a по абсолютной величине не более, чем на , т.е. .
Так как неравенство равносильно неравенствам , то полагая в соотношении (32) , получим
Вследствие того, что интеграл вероятностей — нечетная функция, имеем
| (33) |
Пример 1.
Пусть случайная величина подчиняется нормальному закону распределения вероятностей с параметрами
a=0, =2.
Определить: (Решение)
1) ;
2) ;
Пример 2. В каких пределах должна изменяться случайная величина, подчиняющаяся нормальному закону распределения, чтобы (Решение)
Из последнего примера следует, что если случайная величина подчиняется нормальному закону распределения, то
можно утверждать с вероятностью, равной
Случайное распределение данных
❮ Предыдущий Далее ❯
Что такое распространение данных?
Распределение данных — это список всех возможных значений и частота передачи каждого значения.
имеет место.
Такие списки важны при работе со статистикой и наукой о данных.
Случайный модуль предлагает методы, которые возвращают случайно сгенерированные данные дистрибутивы.
Случайное распределение
Случайное распределение представляет собой набор случайных чисел, следующих за определенным функция плотности вероятности
.Функция плотности вероятности: Функция, описывающая непрерывную вероятность. то есть вероятность всех значения в массиве.
Мы можем генерировать случайные числа на основе определенных вероятностей, используя выбор() метод случайный модуль .
Метод selection() позволяет указать вероятность для каждого значения.
Вероятность задается числом от 0 до 1, где 0 означает, что значение никогда не будет встречаться, а 1 означает, что значение будет встречаться всегда.
Пример
Создать одномерный массив, содержащий 100 значений, где каждое значение должно быть 3, 5,
7 или 9.
Вероятность значения 3 устанавливается равной 0,1
Вероятность значения 5 устанавливается равной 0,3
Вероятность значения 7 устанавливается равной 0,6
Вероятность того, что значение равно 9, установлена равной 0
из numpy import random
x = random.choice([3, 5, 7, 9], p=[0.1, 0.3, 0,6, 0,0], размер=(100))
print(x)
Попробуйте сами »
Сумма всех чисел вероятности должна быть равна 1.
Даже если вы запустите приведенный выше пример 100 раз, значение 9 никогда не появится.
Вы можете вернуть массивы любой формы и размера, указав форму в размер параметр.
Пример
Тот же пример, что и выше, но возвращает двумерный массив с 3 строками, каждая из которых содержит 5 значений.
из numpy import random
x = random.choice([3, 5, 7, 9], р=[0,1, 0,3, 0.6, 0.0], size=(3, 5))
print(x)
Попробуйте сами »
❮ Предыдущая Далее ❯
НОВИНКА
Мы только что запустили
Узнать
ВЫБОР ЦВЕТА
КОД ИГРЫ
Играть в игру
Top Tutorials
Учебное пособие по HTMLУчебное пособие по CSS
Учебное пособие по JavaScript
Учебное пособие
Учебное пособие по SQL
Учебное пособие по Python
Учебное пособие по W3.
CSS Учебник по Bootstrap
Учебник по PHP
Учебник по Java
Учебник по C++
Учебник по jQuery
Лучшие ссылки
Справочник по HTMLСправочник по CSS
Справочник по JavaScript
Справочник по SQL
Справочник по Python
Справочник по W3.CSS
Справочник по Bootstrap
Справочник по PHP
Цвета HTML
Справочник по Java
Справочник по Angular
Справочник по jQuery
Примеры HTML
Примеры CSS
Примеры JavaScript
How To Примеры
Примеры SQL
Примеры Python
Примеры W3.CSS
Примеры Bootstrap
Примеры Java
Примеры XML
Примеры jQuery
FORUM | О
W3Schools оптимизирован для обучения и обучения. Примеры могут быть упрощены для улучшения чтения и обучения.
Учебники, ссылки и примеры постоянно пересматриваются, чтобы избежать ошибок, но мы не можем гарантировать полную правильность всего содержания.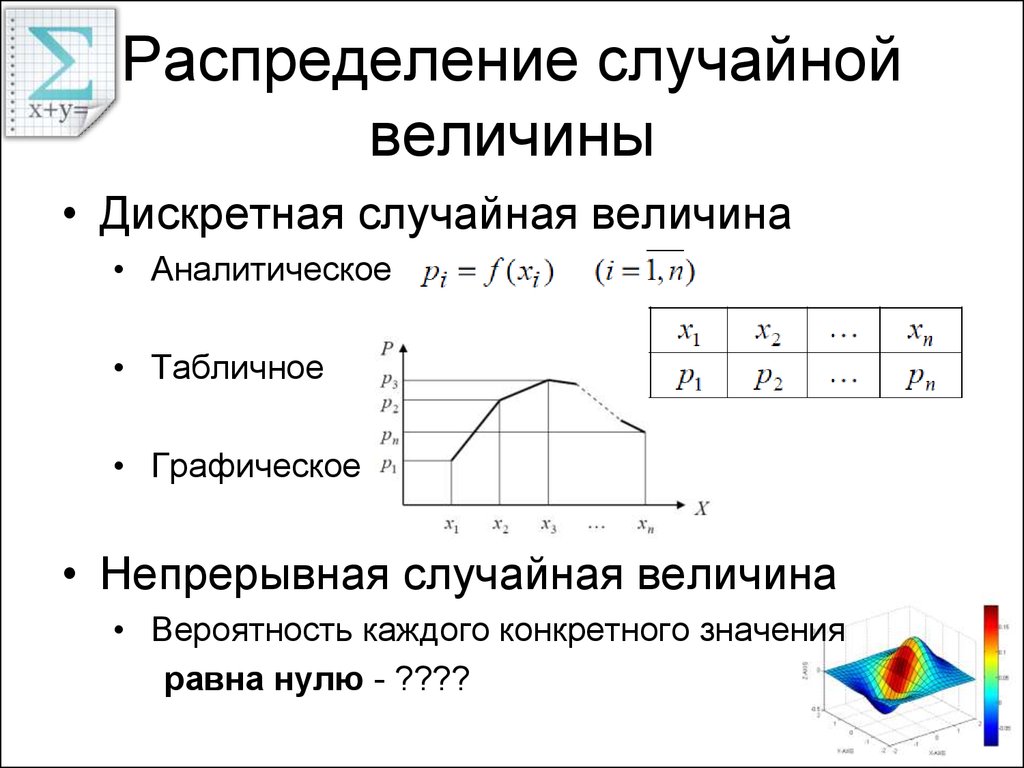
Используя W3Schools, вы соглашаетесь прочитать и принять наши условия использования,
куки-файлы и политика конфиденциальности.
Copyright 1999-2022 Refsnes Data. Все права защищены.
W3Schools работает на основе W3.CSS.
Непрерывные распределения вероятностей — веб-сайт обзора статистики ENV710
Непрерывное распределение вероятностей : Распределение вероятностей, при котором случайная величина X может принимать любое значение (непрерывно). Поскольку существует бесконечное множество значений, которые X может принимать, вероятность того, что X примет любое конкретное значение, равна нулю. Поэтому мы часто говорим в диапазонах значений (p(X>0) = 0,50). Нормальное распределение является одним из примеров непрерывного распределения. Вероятность того, что X попадет между двумя значениями (a и b), равна интегралу (площади под кривой) от a до b:
Распределение вероятностей формируется из всех возможных исходов случайного процесса (для случайной величины X) и вероятности, связанной с каждым исходом.
Распределения вероятностей могут быть либо дискретными (отдельные/отдельные результаты, например количество детей), либо непрерывными (континуум результатов, например рост). Функция плотности вероятности определяется таким образом, что вероятность значения X между a и b равна интегралу (площади под кривой) между a и b. Эта вероятность всегда положительна. Далее, мы знаем, что площадь под кривой от отрицательной бесконечности к положительной бесконечности равна единице.
Нормальное распределение вероятностей, одно из фундаментальных непрерывных статистических распределений, на самом деле представляет собой семейство распределений (бесконечное число распределений с разными средними значениями (μ) и стандартными отклонениями (σ). Поскольку нормальное распределение является непрерывным распределение, мы не можем рассчитать точную вероятность исхода, но вместо этого мы вычисляем вероятность для диапазона исходов (например, вероятность того, что случайная величина X больше 10)9.
0037
Нормальное распределение симметрично и сосредоточено на среднем значении (таком же, как медиана и мода). В то время как ось X находится в диапазоне от отрицательной бесконечности до положительной бесконечности, почти все значения X находятся в пределах +/- трех стандартных отклонений от среднего (99,7% значений), в то время как ~ 68% находятся в пределах +/-1 стандартное отклонение и ~95% находятся в пределах +/- двух стандартных отклонений. Это часто называют правилом трех сигм или правилом 68-95-99,7. Нормальная функция плотности показана ниже (на диагностике этой формулы не будет!)
Как показано вверху этой страницы, стандартная нормальная функция вероятности имеет среднее значение, равное нулю, и стандартное отклонение, равное единице. Часто значения x стандартного нормального распределения называются z-показателями. Мы можем рассчитать вероятности, используя таблицу нормального распределения (z-таблицу). Вот ссылка на нормальную таблицу вероятностей.
Важно отметить, что в этих таблицах вероятности представляют собой область СЛЕВА от z-показателя. Если вам нужно найти область справа от z-показателя (Z больше некоторого значения), вам нужно вычесть значение в таблице из единицы.
Используя эту таблицу, мы можем вычислить p(-1
Мы можем преобразовать любое нормальное распределение в стандартное нормальное распределение, используя приведенное ниже уравнение. Z-показатель равен X минус среднее значение генеральной совокупности (μ), деленное на стандартное отклонение (σ).
Мы хотим определить вероятность того, что случайно выбранный синий краб будет весить больше 1 кг. Основываясь на предыдущих исследованиях, мы предполагаем, что распределение веса (кг) взрослых синих крабов нормально распределено со средним значением популяции (μ) 0,8 кг и стандартным отклонением (σ) 0,3 кг. Как определить эту вероятность? Во-первых, мы вычисляем показатель z, заменяя X на 1, среднее значение (μ) на 0,8 и стандартное отклонение (σ) на 0,3. Мы рассчитываем наш z-показатель как (1-0,8)/0,3=0,6667. Затем мы можем посмотреть в нашу таблицу z, чтобы определить, что p(z>0,6667) составляет примерно 1-0,748 (взято из диаграммы, где-то между 0,7454 и 0,7486) = 0,252. Следовательно, исходя из нашего предположения о нормальности, мы заключаем, что вероятность того, что случайно выбранный взрослый синий краб весит более одного килограмма, составляет примерно 25,2% (область, заштрихованная синим цветом).
Подобно нормальному распределению, t-распределение представляет собой семейство распределений, которые варьируются в зависимости от степеней свободы.
