+50 формул по физике за 7-11 класс с пояснением
О чем статья
Основные формулы по физике: кинематика, динамика, статика
Итак, как говорится, от элементарного к сложному. Начнём с кинетических формул:
Также давайте вспомним движение по кругу:
Медленно, но уверенно мы перешли более сложной теме – к динамике:
Уже после динамики можно перейти к статике, то есть к условиям равновесия тел относительно оси вращения:
После статики можно рассмотреть и гидростатику:
Куда же без темы “Работа, энергия и мощность”. Именно по ней даются много интересных, но сложных задач. Поэтому без формул здесь не обойтись:
Нужна помощь в написании работы?
Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Заказать работу
Основные формулы термодинамики и молекулярной физики
Последняя тема в механике – это “Колебания и волны”:
Теперь можно смело переходить к молекулярной физике:
Плавно переходим в категорию, которая изучает общие свойства макроскопических систем.
Это термодинамика:
Основные формулы электричества
Для многих студентов тема про электричество сложнее, чем про термодинамика, но она не менее важна. Итак, начнём с электростатики:
Переходим к постоянному электрическому току:
Далее добавляем формулы по теме: “Магнитное поле электрического тока”
Электромагнитная индукция тоже важная тема для знания и понимания физики. Конечно, формулы по этой теме необходимы:
Ну и, конечно, куда же без электромагнитных колебаний:
Основные формулы оптической физики
Переходим к следующему разделу по физике – оптика. Здесь даны 8 основных формул, которые необходимо знать. Будьте уверены, задачи по оптике – частое явление:
Основные формулы элементов теории относительности
И последнее, что нужно знать перед экзаменом. Задачи по этой теме попадаются реже, чем предыдущие, но бывают:
Основные формулы световых квантов
Этими формулами приходится часто пользоваться в силу того, что на тему “Световые кванты” попадается немало задач.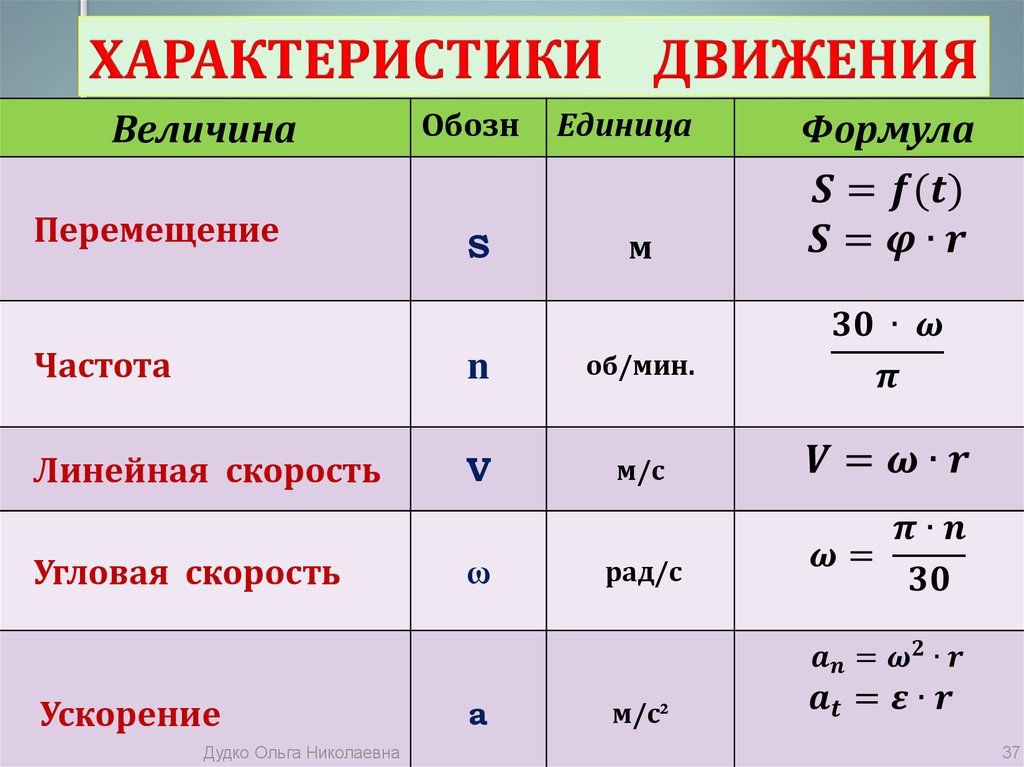
Итак, рассмотрим их:
На этом можно заканчивать. Конечно, по физике есть ещё огромное количество формул, но они вам не столь не нужны.
Это были основные формулы физики
В статье мы подготовили 50 формул, которые понадобятся на экзамене в 99 случая из 100.
Совет: распечатайте все формулы и возьмите их с собой. Во время печати, вы так или иначе будете смотреть на формулы, запоминая их. К тому же, с основными формулами по физике в кармане, вы будете чувствовать себя на экзамене намного увереннее, чем без них.
Надеемся, что подборка формул вам понравилась!
P.S. Хватило ли вам 50 формул по физике, или статью нужно дополнить? Пишите в комментариях.
Средняя оценка 4.7 / 5. Количество оценок: 32
Поставьте вашу оценку
Сожалеем, что вы поставили низкую оценку!
Позвольте нам стать лучше!
Расскажите, как нам стать лучше?
78473
Закажите помощь с работой
Не отобразилась форма расчета стоимости? Переходи по ссылке
Не отобразилась форма расчета стоимости? Переходи по ссылке
Как с помощью школьных формул по физике я вычислил разгон автомобиля BMW M5 Competition / Хабр
Немного теории.
Для начала разберемся с тем, что такое лошадиные силы и устроим небольшой экскурс в школьную физику.
1 л.с. — это мощность, затрачиваемая при вертикальном подъёме груза массой 75 кг со скоростью 1 м/с.
Как известно, мощность показывает, какую работу совершает тело в единицу времени:
Работа равна произведению силы на перемещение: A = F*S. Учитывая, что скорость V=S/t, получим:
Получаем формулу для перевода лошадиных сил в принятую в международной системе СИ единицу измерения мощности — Ватт:
Перейдем к основной части, а именно — к техническим характеристикам автомобиля.
Некоторые характеристики и расчёты будут приводиться приближенно, поскольку мы не претендуем на умопомрачительную точность расчетов, важнее понять физику и математику процесса.
m = 2 тонны = 2000 кг — масса автомобиля (масса авто 1940 кг, считаем что в ней водитель массой 60 кг и больше ничего/никого).
P = 670 л.с. (по паспорту 625 л.
с., но реально мощность выше — измерено на динамометрическом стенде в ролике DSC OFF https://www.youtube.com/watch?v=ysg0Depmyjc. В этой статье мы ещё обратимся к замерам отсюда.)
Разгон 0-100 км/ч: 3.2-3.3 с (по паспорту, замерам)
Разгон 100-200 км/ч: 7.5-7.6 с (по паспорту, замерам)
Мощность двигателя генерируется на маховике, потом через сцепление передается в КПП, далее через дифференциалы, привода, карданный вал передается на колёса. В результате эти механизмы поглощают часть мощности и итоговая мощность, поставляемая к колесам, оказывается меньше на 18-28%. Именно мощность на колесах определяет динамические характеристики автомобиля.
У меня нет сомнений в гениальности инженеров БМВ, но, для начала, возьмем для удобства потери мощности 20%.
Вернемся к нашим физическим баранам. Для вычисления разгона нам нужно связать мощность со скоростью и временем разгона. Для этого воспользуемся вторым законом Ньютона:
Вооружившись этими знаниями, получим конечную формулу:
Выражая отсюда t, получим итоговую формулу для вычисления разгона:
На самом деле в паспорте автомобиля указывается максимальная мощность, достигаемая двигателем при определенном числе оборотов.
Ниже приведена зависимость мощности двигателя от числа оборотов (синяя линия). Строго говоря, параметры этой кривой зависят от номера передачи, так что для определенности скажем, что график для 5й передачи.
Главное, что мы должны усвоить из этого графика — мощность автомобиля не постоянна во время движения, а увеличивается по мере роста оборотов двигателя.
Перейдем к расчету разгона от 0 до 100 км/ч. Переведем скорость в м/с:
При разгоне от 0 до 100 км/ч автомобиль практически сразу переключается с первой передачи на вторую, и при достижении около 90 км/ч переключается на третью. Будем считать, что на всём протяжении разгона автомобиль разгоняется на второй передаче, причем максимальная мощность будет меньше 670 л.с., поскольку передача ниже пятой. Возьмём в качестве начальной мощности при 0 км/ч мощность 150 л.с. (при 2000 об/мин), конечную — 600 л.с. (7000 об/мин):
Чтобы не считать сложные интегралы для вычисления средней мощности, скажем следующие слова: учитывая приближенный характер наших расчетов, проскальзывание авто при ускорении, а также сопротивление воздуха (хотя при разгоне от 0 до 100 оно играет не такую большую роль, как при разгоне до 200 км/ч), будем считать, что мощность зависит от скорости линейно, тогда средняя мощность при разгоне от 0 до 100 км/ч составляет:
Пришло время учесть потери мощности, о которых было сказано ранее, а заодно перевести мощность в кВт (1 кВт = 1000 Вт) для удобства.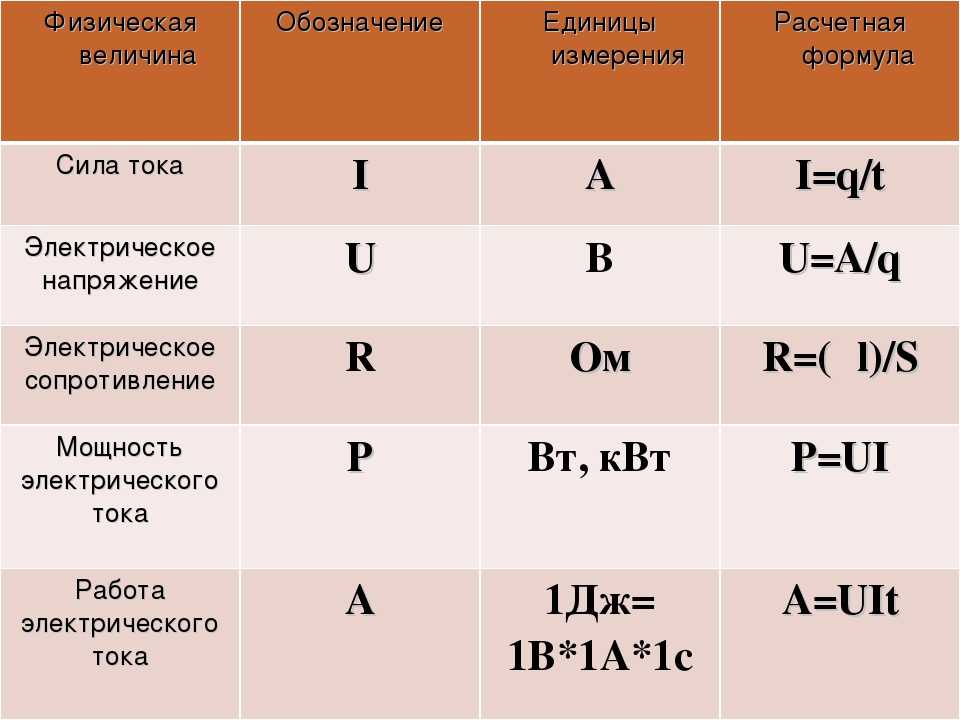
Потери мощности 20%, значит эффективность 80%=0.8:
Теперь подставляем всё в конечную формулу:
Получили довольно близкий к «паспортным» 3.3 с результат, ура! Специально не стал ничего дополнительно подгонять, дабы подчеркнуть приближенный характер расчёта, хотя это было довольно просто сделать, взяв, например, чуть больше мощность.
Теперь, ради интереса и проверки самих себя, вычислим разгон 100-200 км/ч.
С ростом скорости растёт трение воздуха, для движения используются более высокие передачи КПП (3-я, 4-я, 5-я), но при этом уменьшается проскальзывание колес. Так что оставим среднюю мощность 375 л.с.
Так делать конечно же нельзя! После 2-й передачи двигатель работает на «комфортных» для себя оборотах 4000-7000 об/мин, поэтому средняя мощность будет гораздо выше, поскольку выше будет начальная мощность для каждой передачи. Здесь уже не получится считать, что автомобиль едет только на 4-й передаче на всем протяжении разгона, но можно считать, что он проехал одинаковые промежутки времени на 3-й, 4-й и 5-й передаче, и пусть график зависимости мощности от числа оборотов для них одинаков, поэтому построим общую условную кривую зависимости мощности от скорости:
Опять же, считаем для простоты зависимость мощности от скорости линейной, тогда получаем среднюю и реальную мощность:
Тогда итоговое время разгона 100-200 км/ч:
Время разгона «по паспорту» 7.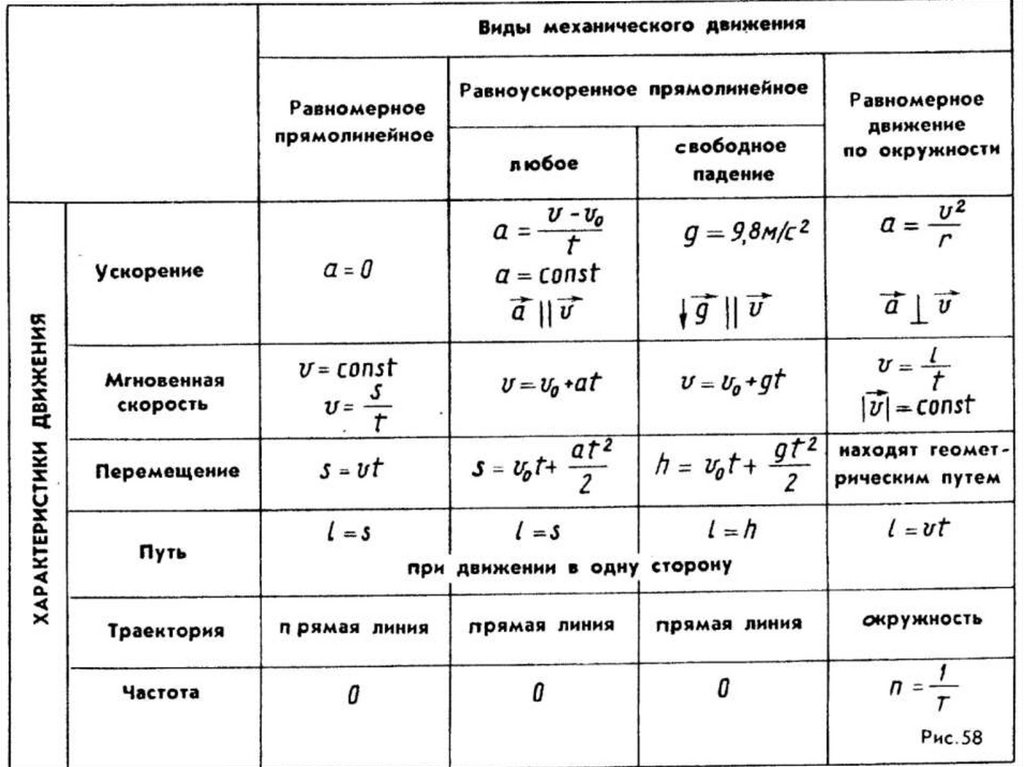
2), можете повыводить на досуге 🙂
Ну и в общем-то всё. Приведенные рассуждения и вычисления не претендуют на истину в последней инстанции и большую точность, но показывают, что зная «школьные» формулы по физике, можно решать такие интересные задачки, связанные с жизнью.
Уравнения в физике: значение и расчет
Какая польза от уравнений в реальном мире? Почему физики описывают физику на языке математических уравнений? Что такого особенного в математике, что мы можем использовать ее в окружающем нас мире? Какие есть примеры физических уравнений, что они нам говорят и как мы их решаем? Узнайте об этом в этой статье!
Определение уравнения в физике
Существует определение уравнения (будь то в физике или нет), но оно очень техническое и совсем не информативное. что мы может сказать об уравнениях физики то, что они делают . Уравнения в физике описывают отношения между физическими величинами. Уравнение всегда содержит знак «равно», =.
В физике существует уравнение, описывающее зависимость между вашей скоростью, продолжительностью вашего путешествия и пройденным расстоянием. Чем больше ваша скорость, тем большее расстояние вы преодолеваете за то же время. Уравнение скажет:. Мы видим, что удвоение времени в пути означает удвоение пройденного расстояния, если скорость остается неизменной, и что удвоение скорости означает удвоение пройденного расстояния, если время в пути остается прежним.
Уравнение физики, которое мы ввели выше, выглядит немного неясным: букв так много, что отношения (знаки умножения и равенства) отходят на второй план. Однако отношения очень важны в физике. Вот почему люди присваивают символы количествам. Важно объяснить другим людям, что означают ваши символы, и удобно использовать стандартные символы для вещей, которые имеют стандартные символы.
Чтобы уравнение выглядело яснее, мы можем дать названия величинам, участвующим в задаче. Предположим, что пройденное расстояние (для расстояния), наша скорость (для скорости) и продолжительность нашего путешествия (для времени).
Уравнение сейчас.
Мы опустили крестик умножения, потому что ясно, что это две разные вещи. Ничего не помещая между двумя величинами, мы умножаем их. Это уравнение выглядит намного яснее, и нетрудно сразу же вспомнить, что означает, например, расстояние. Это хорошо, мы только что записали уравнение физики!
Уравнение, которое всегда верно (также называемое тавтологией), StudySmarter Originals.
Типы физических уравнений
У вас может сложиться впечатление, что существует много разных типов физических уравнений, потому что все они выглядят по-разному. Хотя верно, что во многих областях физики есть свои собственные уравнения, каждое уравнение в физике имеет одну и ту же цель, а именно описание отношения между величинами. Однако мы можем провести различие между уравнениями, основываясь на том, как представляются величины в уравнении, как показывают следующие примеры.
- Линейное уравнение содержит величины только в первой степени, например уравнение для расстояния,.
- Квадратное уравнение также содержит величины, возведенные в квадрат, например уравнение кинетической энергии,.
У нас также есть дифференциальные уравнения (содержащие производные величин), тензорные уравнения (содержащие величины с несколькими входными данными, как векторы) и многие другие способы, которыми величины могут появляться в уравнениях.
Примеры физических уравнений
Уравнения Эйнштейна о гравитации, StudySmarter Originals.
Соотношение между силой, которую вы прикладываете к объекту, массой объекта и скоростью, с которой объект будет ускоряться (описывается ускорением ) в результате приложения силы, задается уравнением
Это Второй закон Ньютона. Например, мы видим, что нам нужно приложить большую силу, чтобы произошло большее ускорение, или чтобы сдвинуть объект с большей массой с тем же ускорением.
Связь между кинетической энергией объекта, его массой и скоростью определяется уравнением
.
Это говорит нам о том, что удвоение массы объекта приведет к удвоению его кинетической энергии, а удвоение его скорости приведет к четырехкратному увеличению его кинетической энергии. Чтобы убедиться в этом, предположим, что конечная скорость в два раза больше начальной скорости, т. е. Тогда конечная энергия, деленная на начальную энергию, равна
.
Мы видим, что действительно энергия увеличивается в четыре раза, если скорость удваивается. Это основная причина того, почему автомобиль разгоняется медленнее на высоких скоростях, чем на низких: ему нужно добавить больше энергии, чтобы получить ту же скорость из-за квадрата в уравнении выше!
Мы видели большое количество физических уравнений, но теперь пришло время поработать с ними и решить их.
Решение уравнений в физике
Эдвард Виттен пишет уравнения по теории струн на доске, Wikimedia Commons Public Domain.
Решение уравнений в физике очень похоже на решение уравнений в математике, за исключением двух основных отличий.
- В физике всегда есть контекст, поэтому физическое уравнение следует из небольшой истории. Мы должны распаковать историю и преобразовать ее в разрешимое уравнение.
- Мы должны быть осторожны с юнитами. В общем, мы включаем единицы в все расчеты .
Давайте посмотрим, как это работает на примере задачи.
В: Джон всегда ходит со скоростью (миль в час). В прошлое воскресенье он гулял по городу и в итоге покрыл в общей сложности. Сколько времени у него ушло?
A: Первый шаг — преобразовать эту историю в разрешимое уравнение. Начнем с присвоения имен нужным нам величинам. Мы называем скорость ходьбы Джона, пройденное им расстояние и время, которое ему потребовалось. Тот факт, что это было воскресенье и что он гулял по городу, не имеет значения для вопроса. Из рассказа мы знаем и то, и то. Теперь нам нужно найти уравнение, которое относится к и . К счастью, мы это знаем. Как и в случае с математическими уравнениями, мы изолируем, разделив обе части на , и у нас остается уравнение.
Мы знаем и, значит, это разрешимое уравнение, значит, шаг 1 выполнен! Давайте решим ее, соблюдая осторожность с единицами измерения. Заполняем:
.
Теперь давайте обязательно ответим на вопрос полностью. Джону потребовалось 3 часа (чтобы прогуляться по городу в прошлое воскресенье).
В приведенном выше примере у нас не было проблем с единицами измерения, потому что информация, предоставленная нам, была в единицах, которые «хорошо сочетаются». Если это не так, нам придется использовать наши знания о преобразованиях единиц измерения, как показано в примере ниже.
В: Анна хочет толкнуть машину, о которой мы можем предположить, что она не имеет трения и не находится ни на каком уклоне. Она толкает с силой, масса автомобиля равна, а масса Анны равна. Каково ускорение автомобиля?
A: Мы называем приложенную силу, массу автомобиля , ускорение автомобиля и массу Анны. Мы это знаем, поэтому изолируем ускорение и получаем уравнение. Мы знаем и, поэтому шаг 1 выполнен.
Решим, заполнив данные (включая единицы!):
Мы видим, что нам понадобилось преобразование между кг и фунтами, именно это, чтобы ответить на вопрос. Ответ заключается в том, что ускорение автомобиля равно .
Надеюсь, эти примеры прояснили, как язык математических уравнений полезен в реальном (физическом) мире.
Резюме: шаг за шагом
- Читая вопрос, дайте названия указанным величинам и запишите их значения (с указанием единиц).
- Определите, какую величину вам нужно знать, чтобы ответить на вопрос, и запишите уравнение физики, связывающее эту величину с записанными вами величинами.
- Решите уравнение (будьте осторожны с единицами измерения) и ответьте на вопрос полным предложением и с правильными единицами измерения.
Уравнения движения в физике
Уравнение Шредингера, описывающее квантовую механику, StudySmarter Originals.
В конце концов, все, к чему стремится физика, — это предсказывать движение объектов.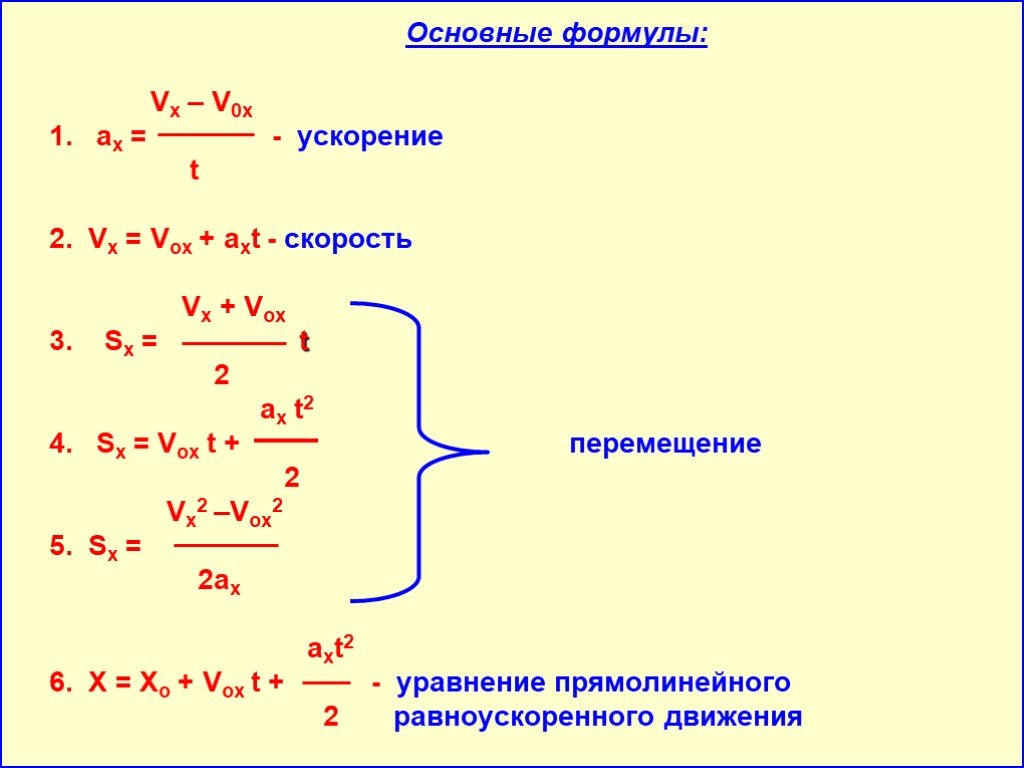
Следовательно, мы можем утверждать, что все уравнения в физике в некотором роде являются уравнениями движения. Однако некоторые уравнения описывают только движение объектов, а не причины движения. Давайте посмотрим на эти уравнения.
Сначала рассмотрим уравнение, описывающее движение с постоянной скоростью. Для начальной точки, скорости и продолжительности движения местоположение объекта задается как
.
Из предыдущего мы знаем, что пройденное расстояние равно, поэтому это логично: местоположение объекта равно его начальному местоположению плюс пройденное расстояние.
Объект также может ускоряться. Для постоянного ускорения, начальной скорости, начальной точки и продолжительности движения местоположение объекта определяется как
.
У нас уже есть некоторое интуитивное представление о том, почему он здесь, но давайте рассмотрим остальное. Скорость, полученная через время, равна, поэтому через время скорость нашего объекта равна. Это означает, что средняя скорость нашего объекта равна среднему значению и , т.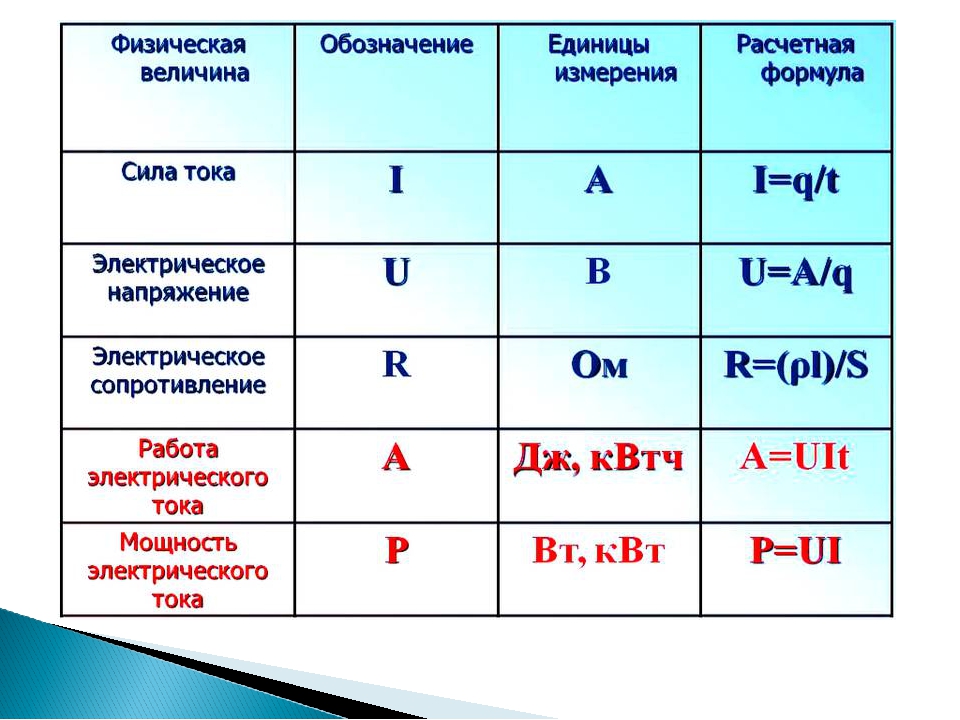
е. Пройденное расстояние равно
,
, и мы приходим к приведенному выше уравнению! Обратите внимание, что для нулевого ускорения мы снова приходим к уравнению для постоянной скорости, что и ожидаем найти.
Уравнения в физике – Ключевые выводы
- Уравнение в физике описывает отношение между физическими величинами.
- Уравнение всегда содержит знак «равно», =.
- Мы присваиваем величинам символы, чтобы уравнения были читабельными.
- Решение уравнений в физике во многом похоже на решение уравнений в математике, с двумя отличиями:
- Часто нам приходится самим составлять уравнения из рассказа. Читая рассказ, мы даем названия соответствующим величинам и перечисляем их значения.
- Мы всегда учитываем единицы в наших расчетах. Когда уравнение решено, мы даем ответ в правильных единицах.
- Уравнение движения объектов с постоянной скоростью.
- Уравнение движения объектов с постоянным ускорением.
[1] Источник изображения Виттена: https://commons.wikimedia.org/wiki/File:Witten_Blackboard.jpg.
Уравнения физики
Эти все
Экзаменационные комиссии по английскому языку теперь ДАЮТ вам уравнения, так что вы больше не будете получать оценки за их повторение. Однако я бы сказал, что на самом деле , зная их , облегчают вам объяснение физического принципа.
Например, если вы ЗНАЕТЕ, что F=ma, то, отвечая на вопрос «Что включает в себя наличие действующей силы?», вы знаете, что результирующая сила заставит тело ускоряться.
Имея математический склад ума, я считаю, что изучение уравнений является сокращенным способом изучения физики!
Марка
убедитесь, что вы знаете правильные единицы измерения.
Запомнить
быть осторожным, когда вы пишете буквы уравнения… это символы
НЕ часть вашего почерка!
Особый уход с I
по текущему нельзя спутать с л для
длина или 1 (номер один)!
| Год | Ключ Сцена | ||
| скорость
= пройденное расстояние затраченное время | В = д/т | Y7 | КС3 |
ускорение = изменение скорости затраченное время | а = Дв/т | Y8 | КС3 |
плотность
= масса | р = м/В | Y7 | КС3 |
| сила = масса х ускорение | Ф = | млн летY9 | КС3 |
| работа done = сила x расстояние, пройденное в направлении этой силы | Вт = Фс | Y9 | КС3 |
| импульс = масса х скорость | р = мв | Y12 | КАК |
мощность
= переданной энергии затраченное время | П = Э/т | Y8 | KS3 |
мощность
= выполненная работа затраченное время | П = Вт/т | Y9 | KS3 |
| вес
= масса x гравитационное поле сила | Вт = мг | Y7 | KS3 |
| кинетический энергия = половина x масса x (квадрат скорости) | Э К = 1 / 2 мв 2 | Y12 | KS4 |
| изменение в гравитационной потенциальной энергии = масса x гравитационное поле сила x разница в росте | Y9 | KS3 | |
| давление
= приложенная сила площадь контакта | П
= F A | Y7 | KS3 |
| Газ Закон: давление х объем газа = количество молей х моль газовая постоянная x абсолютная температура | пВ = нРТ | Y12 | КАК |
| Газ Закон: комбинация закона Бойля и закона Чарльза | П 1 В 1 = П 2 В 2 T 1 T 2 | Y11 | КС4 |
| плата = текущее х время | Дисквалификация = I Dt | Y10 | KS4 |
| Ом Закон: Разность потенциалов = ток x сопротивление | В = I R | Y8 | |
| Ом Закон применяется к полному контуру : Электродвижущая сила = ток x (сумма сопротивления цепи и внутреннего сопротивления ячейка) | ЭДС = л( р +р) | Y12 | КАК |
| мощность = ток x разность потенциалов | П = И В | Y8 | KS3 |
| энергия переданный в компоненте = заряд, прошедший через него x потенциал разница во всем | Вт = QV | Y10 | KS4 |
| сопротивление
= удельное сопротивление x длина площадь поперечного сечения | Р
= r l A | Y12 | КАК |
| скорость волны = частота x длина волны 90 198 | v
= fl для электромагнитного излучение v = c дает: c = fl | Y8 | KS3 |
| центростремительный
сила = масса x скорость 2 радиус пути | r | Y13 | А2 |
| Электрика энергия превратилась в тепло = разность потенциалов х ток х время | Е = V I т | Y9 | KS3 |
| Обратный квадратичный закон для силы, действующей на массу в гравитационном поле другая масса: сила пропорциональна произведению масс и обратно пропорциональна квадрату расстояния между их | Ф Г = — G м 1 м 2 r 2 НБ знак минус означает, что это ВСЕГДА привлекательно | Y13 | А2 |
| Обратный Закон квадрата для силы, действующей на заряд в электрическом поле другого заряд: сила пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними | F E = 1 Q 1 Q 2 4PE0195 2 41 4PE0.  9.0356 2 НБ общий знак, указывающий, является ли он привлекательным (отрицательный)
или отталкивающее (положительное) происходит от знаков зарядов. | Y13 | А2 |
| емкость
= сохраненный заряд разность потенциалов | С = В В | Y13 | А2 |
| соотношение напряжения на катушках трансформатора = отношение витков на катушках | В 1 = N 1 V 2 N 2 NB 1 может быть P для первичного и 2 может быть s для вторичного — это не имеет значения что есть что! | Y11 | КС4 |
LOJ Ноябрь 2000 г.