Законы математики. Математические формулы
Конвертер Брайля
С помощью конвертера Брайля вы легко и просто можете конвертировать текст в азбуку Брайля.
Поддерживается несколько языков (включая числа и знаки препинания).
- Главная
- Статьи Законы математики, математические формулы
Ниже расписаны основные правила действий с цифрами и записи формул из общей и высшей математики.
Целые числа. Математика начинается с обозначения простых целых чисел, которые выделяются цифровым точечным знаком (прим. — дальше признак) (точки 3, 4, 5, 6). Сразу за цифровым знаком без пробелов и тире прописывается само значение цифры в один или несколько символов.
Десятичные дроби. Десятичная дробь представляет собой более сложное число. Написание десятичной дроби начинается с записи целого числа (см. выше). После его написания в форме одной или нескольких цифр ставится запятая без пробела, а после запятой также без пробела продолжается запись десятичных знаков.
Простые дроби. Простая дробь записывается сложнее, нежели обычные целые числа и десятичные дроби. Обозначение простой дроби в точечной системе Брайля также начинается с цифрового признака. Затем без пробела в цифровом варианте прописывается числитель. Далее без использования пробела и цифрового знака идет знаменатель. Вот здесь запись несколько усложняется. Знаменатель изображается специальными «сниженными цифрами», которые указывают на уменьшение числа. Помимо использования в простых дробях, сниженные цифры применяют для использования в старших классах математики – для записи верхних и нижних индексов. Сниженные цифры записываются сочетаниями точек нижней части брайлевского шеститочия: 2, 3, 5, 6.
Проценты. Процентное значение может выделяться просто знаком % в системе брайлевских символов: (точки 3, 4, 5, 6), а затем без пробелов пишется сниженный ноль (точки 3, 5, 6). Важно, что между числом и знаком процента пробел не ставится.
Рациональные сложные выражения. Оформление дроби, где в числителе и знаменателе одновременно находятся какие-нибудь выражения, состоит из указания нескольких признаков: начало дроби, дробная черта и конец дроби.
ПОМНИТЕ! Точечная система Брайля не позволяет записывать символы со смещением уровня основной строки. Поэтому любая степень или дробь записывается линейно. При этом перед каждым новым элементом математического выражения ставятся определенные точечные признаки.
- Признак «начало дроби» пишется точками 2, 3. После него без пробела записывается числитель (если возникла необходимость, то его можно переносить по строкам). После окончания числителя обязательно делается пробел, а затем идет признак «дробная черта». Это точки 1, 2, 5, 6. Далее уже без пробела записывается знаменатель (при необходимости его также можно переносить по строкам). После последнего знака знаменателя обязательно проставляется признак «конец дроби»: (точки 5, 6).
- Верхний и нижний индексы. Для определения при прочтении и записи математического выражения в виде верхнего или нижнего индекса также используется точечный код (признак). Он прописывается точками 1, 6. после чего без пробела записывается число, буквенный символ или целое выражение. Окончание нижнего индекса также обособляется признаком конца индекса: точки 1, 5, 6. В свою очередь, верхний индекс обозначается точками 3, 4.
А дальше – по той же схеме.
А дальше – по той же схеме.Знаки операций (математические символы).
- Сложение («плюс») обозначается точками 2, 3, 5. Перед ним проставляется пробел, отделяющий плюс от предыдущих символов или выражений. После плюса может стоять цифровой знак, буква или левая круглая скобка.
- Вычитание («минус») обозначается точками 3, 6. К нему применяются те же правила, что и при сложении.
- Умножение («точка» или «крестик») записывается одной точкой 3. При умножении пробелы не оставляются ни до, ни после знака. В некоторых случаях знак умножения можно опустить.
- Знак деления «две точки» записывается сочетанием точек 2, 5, 6. На него распространяются те же правила, как и на знаки « плюс» и «минус».
- Знак «равенство» прописывается точками 2, 3, 5, 6. При этом перед знаком «равно» ставится пробел, а после – нет.
- Знаки «меньше» и «больше» пишутся точками 2, 4, 6 и 1, 3, 5 соответственно. В данном случае пробел ставится и до, и после каждого знака.
Перенос математических формул. По стандарту в одной строке вмещается 24 символа, напечатанных в точечной системе Брайля. Поэтому в такой строке нельзя уместить длинную математическую формулу или выражение. В точечной системе для переноса последним на строке проставляют математическое действие, ставят точку 5, а все остальное переносят на следующую строку. Важное условие, если перенос приходится делать в действии «умножение», его следует обязательно поставить в конце строки, потому что, если в этом месте не было бы переноса, знак умножения можно было бы опустить.
Использование неизвестных переменных и их признаки. Математические, химические и физические формулы, часто записываются в виде символов латинского алфавита, английского и другого алфавита. Для их обозначения в точечном шрифте Брайля также используются специальные признаки. Такой признак ставится перед буквой или сочетанием букв. Если дальше встречается буква другого алфавита, то перед ней ставится новый соответствующий признак.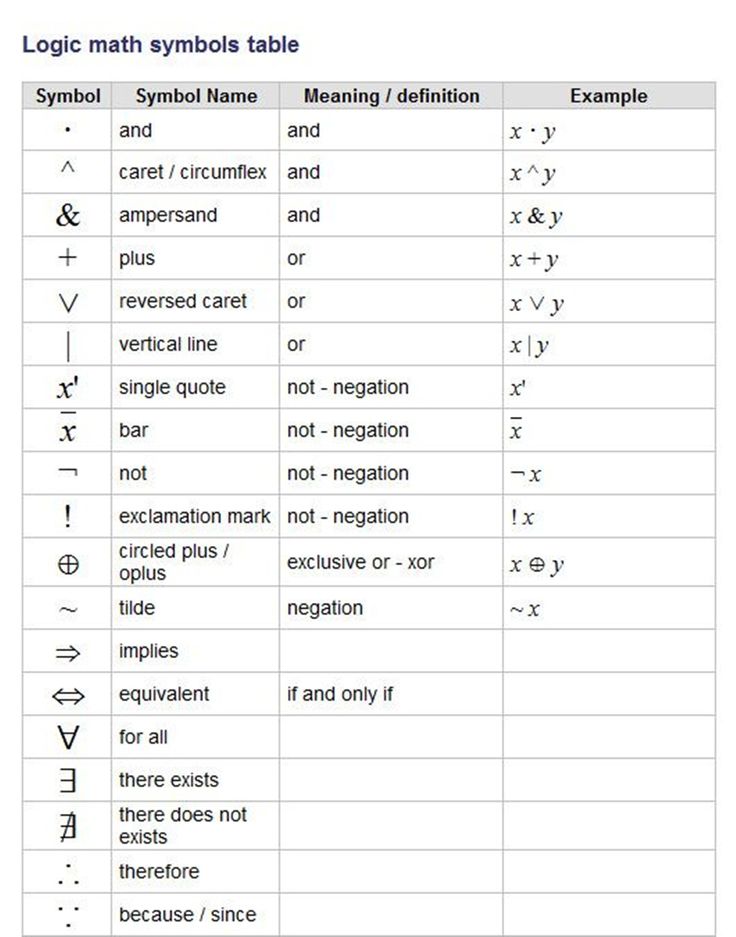
ПРИМЕРЫ ПРИЗНАКОВ АЛФАВИТА:
- Перед заглавной буквой русского алфавита ставится признак с сочетанием точек — 4, 5, но в большинстве случаев он не используется, так как считается, что по умолчанию текст написан на русском языке. Если буква строчная, то достаточно поставить перед ней одну точку – 5.
- Перед заглавной латинской буквой прописывается признак с сочетанием точек-, а признак малой соответственно – 6.
- Перед заглавной греческой буквой указывается признак точками 4, 5, 6, а признак малой – двумя точками 5, 6.
Правило прочтения буквы и понимания формулы, определяется признаком, который стоит перед буквой.
Тригонометрические функции и логарифмы
Тригонометрические формулы – более сложная часть точных наук. Но и в ней для обозначения предусмотрены специальные обозначения для прочтения шрифта Брайля, правда немного сложные для восприятия. Названия функции всегда прописывается с буквы русского алфавита «я».
Это связано с тем, что последняя буква русского алфавита не встречается в формулах. Поэтому, если в тексте точных наук встречается признак, обозначенный точками 1,2,4,6. После проставления признака записывается сама функция (имя функции).
Сама функция или логарифм прописывается первой буквой от своего традиционного написания. К примеру, синус — яs, яl, натуральный логарифм – яln.
Но стоит помнить, что перед буквой названия функции обязательно следует прописывать еще и алфавитный признак. Без него прочтение функции станет затруднительно.
Словарь терминов по математике от А до Я – ПОЧЕМУХА.РУ ответы на вопросы.
Аксиома — утверждение, принимаемое 6ез доказательств.
Алгебраическое выражение — некоторое количество чисел, обозначенных буквами или цифрами и соединенных при помощи действий сложения, вычитания, умножения, деления, возведения в степень и извлечения корня.
Абцисса (французское слово).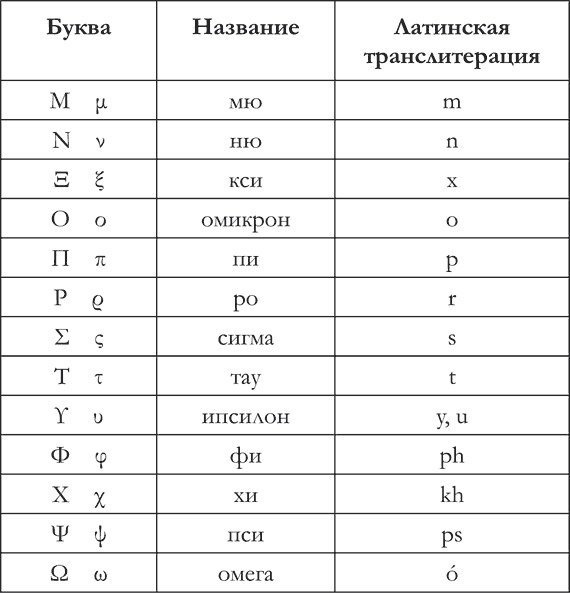
Одна из точек декартовых координат. Является первой. Обозначается, обычно, символом «X». Впервые употреблено Г. Лейбницем в 1675 году (немецкий ученый).
Аддитивность. Некоторое свойство величин. Говорит о следующем: значение определенной величины соответствующее полноценному объекту, равно сумме значений такой величины, которые соответствуют его частям в любом разбиении полноценного объекта на части.
Адъюнкта. Полностью соответствует алгебраическому дополнению.
Аксонометрия. Один из способов изображения на плоскости пространственных фигур.
Алгебра. Часть математики, которая изучает задачи и решения алгебраических уравнений. Термин впервые возможно было увидеть в 11-м веке. Применил Мухам меда бен-Муса ал-Хорезми (математик и астроном).
Аргумент (функции). Переменная величина (независимая), с помощью которой определяется значение функции.
Арифметика. Наука, которая изучает действия над числами.
Возникла в Вавилоне, Индии, Китае, Египте.
Ассиметрия. Отсутствие или нарушение симметрии (обратное значение симметрии).
Бесконечно большая величина — больше любого наперед заданного числа.
Бесконечно малая величина — меньше любой конечной.
Биллион. Одна тысяча миллионов (единица с девятью нулями).
Биссектриса. Луч, имеющий начало в вершине угла (делит угол на две части).
Вектор. Направленный отрезок прямой. Один конец — начало вектора; другой — конец вектора. Впервые термин употребил У. Гамильтон (ирландский ученый).
Вертикальные углы. Пара углов, которая имеет общую вершину (образуется за счет пересечения двух прямых таким образом, что стороно одного угла — это прямое продолжение второго).
Вектор — величина, характеризующаяся не только своим числовым значением, но и направлением.
График — чертеж, наглядно изображающий зависимость одной величины oт другой, линия, дающая наглядное представление о характере изменения функции.
Гексаэдр. Шестигранник. Термин впервые был употреблен Паппой Александийским (древнегреческий ученый).
Геометрия. Часть математики, которая изучает пространственные формы и отношения. Термин впервые употребили в Вавилоне/Египте (5 ве до н. э.).
Гипербола. Незамкнутая кривая (состоит при помощи двух неограниченных ветвей). Термин появился благодаря Апполонию Пермскому (древнегреческий ученый).
Гипоциклоида. Это кривая, которую описывает точка окружности.
Гомотетия. Расположение между собой фигур (подобных), при которых прямые, соединяющие точки этих фигур, пересекаются в одной и той же точке (это называется центр гомотетии).
Градус. Единица измерения для плоского угла. Равна 1/90 части прямого угла. Измерять углы в градусах начала больше 3 веков назад. Впервые такие измерения применили в Вавилоне.
Дедукция. Форма мышления. С ее помощью какое-либо утверждение выводят логически (исходя из правил современной науки «логики»).
Диагональ. Отрезок прямой, который между собой соединяет вершины треугольника (они не лежат на одной стороне). Впервые употребил термин Евклид (3 век до нашей эры).
Дискриминант. Выражение, составленное из величин, определяющих функцию.
Дробь — число, составленное из целого числа долей единицы. Выражается отношением двух целых чисел m/n, где m — числитель, показывающий, сколько долей единицы содержится в дроби, а n знаменатель, показывающий, на сколько долей разделена единица.
Знаменатель. Числа, из которых составляют дробь.
Золотое сечение — деление отрезка на две части так, что большая часть, относится к меньшей так, как весь отрезок — к большей части. Приблизительно равно 1,618. Критерий красоты, используется в архитектуре и др. Термин ввел Леонардо да Винчи.
Индекс. Буквенный либо числовой указатель. С его помощью снабжается математические выражения (делается это для того, чтобы отличать друг от друга).
Индукция. Метод доказательства математического уравнения.
Интеграл. Основное понятие математического анализа. Возникло из-за того, что понадобилось измерять объемы и площади.
Иррациональное число. Число, которое не является рациональным.
Катет. Одна из сторон прямоугольного треугольника, которая прилежит к прямому углу.
Квадрат. Правильный четырехугольник (либо ромб). Каждый угол квадрата прямой. Все углы в квадрате равны (по 90 градусов).
Математическая константа. Величина, которая никогда не изменяется в своем значении. Константа — противоположное число для переменной.
Конус. Тело, которое ограничено одной полостью при помощи конической поверхности. Оно пересекает плоскость (плоскость перпендикулярна ее оси).
Косинус. Является одной из тригонометрических функций. Обозначение в математике/высшей математике — cos.
Корень уравнения — решение, значение неизвестного, найденное через известные коэффициенты.
Константа — постоянная величина.
Координаты — числа, определяющие положение точки на плоскости, поверхности или в пространстве.
Логарифм. Показатель степени «m». Его следует возвести в степень «а» для того, чтобы получить некоторое число NT. Впервые логарифм предложил Дж. Непер.
Линия — общая часть двух смежных областей поверхности.
Максимум. Наибольшее значение функции.
Масштаб. Отношение двух линейных размеров по отношению друг к другу. Используется во многих современных отраслях. Основная — картография, геодезия.
Матрица. Прямоугольная таблица. Образуется при помощи множества числа (определенного). Включает в себя столбцы и строки (структура матрицы). Впервые термин «матрица» появилась у ученого Дж. Сильвестра.
Медиана. Отрезок, который соединяет вершину треугольника и его середину противоположной стороны.
Минимум. Наименьшее значение функции.
Многоугольник. Геометрическая фигура. Определение — замкнутая ломаная.
Модуль. Абсолютная величина (действительного числа).
Множество — совокупность элементов, объединенных по какому-нибудь признаку.
Норма. Абсолютная величина числа.
Неравенство — два числа или выражения, соединенных знаками (больше) или (меньше).
Овал. Выпуклая, замкнутая фигура (плоская).
Окружность. Многочисленные точки, расположенные на плоскости.
Ордината. Одна из декартовых координат. Обозначается, обычно, второй.
Октаэдр. Геометрическая фигура. Один из пяти многогранников (правильных). Октаэдр включает в себя 8 граней (правильных), 6 вершин и 12 ребер.
Параллелепипед. Призма. Основание — параллелограмм или многогранник (равносильные понятия). Имеет 6 граней. Каждая грань — параллелограмм.
Параллелограмм. Четырехугольник. Противолежащие стороны у него параллельны (попарно). На данный момент присутствует 2 частных случая параллелограмма: ромб и квадрат. Главное свойство данной геометрической фигуры:
• Противоположные стороны равны;
• Противоположные углы равны.
Периметр. Сумма всех сторон геометрической фигуры. Впервые удалось встретить у Архимеда и Герона (древнегреческие ученые).
Перпендикуляр. Прямая, которая пересекает плоскость (любую), находящуюся под прямым углом.
Пирамида. Многогранник. Его основание — это многоугольник. Любая другая грань — треугольник (эти грани имеют общую вершину). На данный момент пирамиды могут быть различных типов: треугольные, четырехугольные и так далее (различают таковые при помощи определения числа углов).
Планиметрия. Одна из наиболее важных частей элементарной (простой) геометрии. Планиметрия изучает свойства фигур, которые находятся на плоскости. Впервые термин был обозначен Еквлидом (древнегреческий ученый).
Плюс. Знак, который обозначает математическое действие — сложение. Кроме того, при помощи плюса обозначаются положительные числа. Впервые знак ввел Я. Видман (знаменитый чешский ученый).
Предел. Основное понятие математики. Обозначает: переменная величина неограниченно приближается к постоянному значению (определенному). Впервые термин использовал известный ученый Ньютон.
Призма. Многогранник. Первые 2 грани — равные угольники (это есть основания призмы). Остальное — боковые грани.
Проекция. Один из способов изображения пространственных и плоских фигур.
Переменная — величина, числовое значение которой изменяется по определенному, известному или неизвестному закону.
Плоскость — простейшая поверхность. Любая прямая, соединяющая две ее точки, целиком принадлежит ей.
Прямая — совокупность точек, общих для двух пересекающихся плоскостей.
Процент — сотая часть числа.
Радиан. Единица для измерения углов.
Ромб. Параллелограмм. Все стороны у данной фигуры равны. Ромб, имеющие прмые углы, имеет термин «квадрат».
Сегмент. Часть круга (таковую ограничивают при помощи хорды, которая соединяет концы дуги).
Секанс. Тригонометрическая функция. Обозначение в математике/высшей математике — sec.
Сектор. Часть круга. Ограничивается при помощи окружности + двух радиусов (соединяет концы одной дуги с центром круга).
Симметрия — соответствие.
Синус. Тригонометрическая функция. Обозначение в математике/высшей математике — sin.
Стереометрия. Часть элементарной геометрии. Занимается изучением полноценных пространственных фигур.
Тангенс. Тригонометрическая функция. Обозначение в математике/высшей математике — tg.
Тетраэдр. Многогранник, включает в себя 4 треугольные грани. В каждой вершине по 3 грани (сходятся в вершинах). Тетраэдр имеет 4 грани + 6 ребер + 4 вершины.
Точка. Не имеет определенного и окончательного понятия. Любая точка обозначается при помощи букв A, B, C.
Треугольник. Многоугольник (простой). Включает в себя 3 вершины + 3 стороны;
Теорема — утверждение, которое нужно доказать исходя из аксиом и ранее доказанных теорем.
Тождество — равенство, справедливое при всех значениях входящих в него коэффициентов.
Топология — раздел математики, изучающий свойства фигур, не изменяющиеся при любых деформациях, проводимых 6ез разрывов и склеиваний.
Уравнение — математическая запись задачи о разыскании значений неизвестных, при которых значения двух данных функций равны.
Угол. Геометрическая фигура (плоская). Образуется двумя лучами, которые выходят из одной точки (точки — вершины угла).
Факториал — произведение натуральных чисел от 1 до какого-либо данного натурального числа n. Обозначается n!. Факториал нуля о! = 1.
Формула — комбинация математических знаков, выражающая какое-нибудь предложение.
Функция — числовая зависимость между элементами двух множеств, при котором одному элементу одного множества соответствует определенный элемент другого множества. Может быть задана формулой или графиком.
Хорда. Отрезок, который соединяет между собой 2 точки, находящиеся на окружности.
Цифры — знаки для обозначения чисел.
Центр. Середина чего-либо (например: круга).
Цилиндр. Тело, которое ограничено цилиндрической поверхностью + параллельными плоскостями (двумя).
Впервые понятие «цилиндр» возможно было встретить у Евклида и Аристарха.
Циркуль. Специальный прибор, разработанный для того, чтобы чертить дуги, линейные измерения и окружности.
Числитель. Определенное число, при помощи которого составлена дробь. Впервые термин применил Максим Плануда (византийский ученый).
Число — одно из основных понятий математики, возникшее в связи со счетом отдельных предметов.
Шар. Геометрическое тело. Представляет из себя общую совокупность всех точек определенного пространства.
Экспонента. Является одним и тем же, что и экспоненциальная функция. Впервые термин ввел Г. Лейбниц (немецкий ученый).
Эллипс. Овальная кривая. Впервые данный термин ввел Апполоний Пергский (древнегреческий ученый).
Список арифметических и общепринятых математических символов
В базовой математике существует множество различных символов, которые широко используются.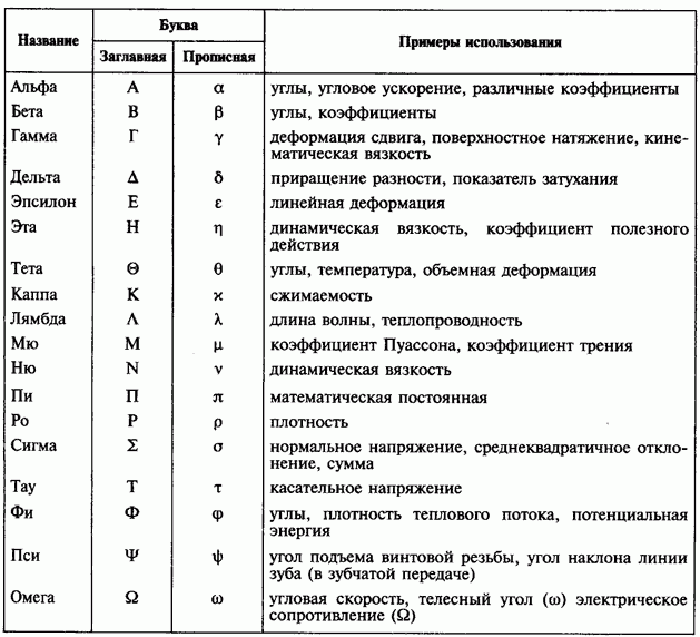
Ниже приводится подборка наиболее часто используемых символов в арифметике и общей математике , а также других символов, использование которых охватывает несколько подполей математики.
В целях удобочитаемости эти символы разделены по их функциям на таблицы. Другие полные списки символов — с разбивкой по темам и типам — также можно найти на соответствующих страницах ниже (или на панели навигации).
Содержание
Предпочитаете версию в формате PDF?
Получите основную сводку математических символов в форме электронной книги — вместе с использованием каждого символа и кодом LaTeX.
Да. Это было бы полезно.
Математические константы
В обычной математике константы часто используются для обозначения ключевых натуральных чисел, целых чисел, действительных чисел и комплексных чисел. В следующей таблице описаны наиболее распространенные из них, а также их названия, использование и функции.
| Symbol Name | Explanation | Example |
|---|---|---|
| $0$ ( Zero ) | Additive identity of common numbers | $5 + 0 = 0 + 5 = 5$ |
| $1 $ ( One ) | Мультипликативное тождество обычных чисел | $6 \times 1 = 6$ |
| $\sqrt{2}$ ( Квадратный корень из $2$ ) | Положительное число $. Постоянная Пифагора. Приблизительно $1.414$. 92 = -1$ |
Разделители
Разделители — это символы, используемые для обозначения разделения между различными независимыми математическими объектами. К ним относятся общие разделители, такие как скобки, скобки и фигурные скобки, а также использование разделителей в контексте интервалов.
Общие разделители
| Название символа | Объяснение | Пример |
|---|---|---|
$. $ | Десятичный сепаратор | $ 15,35 + 8,25 = 23,60 $ |
| $, $ | Разделитель объекта | $ \ {5, 0, 2 \} $ | $4 : 3 = 1024 : 768$ |
| $(), [], \{ \}$ | Индикаторы порядка работы | $\left[(2+3) + 4 \right] + 5$ |
| $( )$ | Кортеж-индикатор | $ (4, 7, 11, 15) $ |
Интервалы
| Название символа | Объяснение | Пример |
|---|---|---|
| $ | ||
| $ | ||
| $ | ||
| $. от $a$ до $b$ | $\pi \in [3, 5]$ | |
| $(a, b)$ | Открытый интервал от $a$ до $b$ | $( 1, 9) =$ $\{x \in \mathbb{R} \mid \\ 1 < x < 9\}$ |
| $[a, b)$ | Правый открытый интервал от $a$ до $b$ | $[e, \pi) \subseteq [1, \infty)$ |
| $(a, b]$ | Лево- открытый интервал от $a$ до $b$ | $0 \notin (0, 100]$ |
Операторы
Операторы — это символы-заполнители, используемые для обозначения математических операций , которые переводят один или несколько математических объектов в другой подобный объект.
В обычной математике к ним относятся арифметические операторы и другие унарные операторы, связанные с числами.
Арифметические операторы
| Название символа | Объяснение | Пример |
|---|---|---|
| $ x + y $ | Суме {5} + \dfrac{2}{3} = \dfrac{19}{15}$ | |
| $x-y$ | Разница ($x$ минус $y$) | $13-1.\ overline{3} = 11.\overline{6}$ |
| $-x$ | Аддитивное обратное (отрицательное $x$) 95$ | |
| $\pm$ | Оператор плюс-минус | Используя квадратичную формулу, мы получаем, что $x = \dfrac{-b \pm \sqrt{\Delta}}{2a} $. |
| $ \ MP $ | Оператор Minus-and-Plus | $ 5 \ PM (-3) = 5 \ MP 3 $ |
СИБЛИЦА, СИМОРИТЕЛЬНЫЕ НАПРАВЛЕНИЕ
| 8. | Объяснение | Пример |
|---|---|---|
| $\sqrt{x}$ | Главный квадратный корень из $x$ | $\sqrt{30}= \\ \sqrt{2 \cdot 3 \cdot 5}$ |
| $\sqrt[n]{x}$ | Корень n-й степени из $x$ | $\sqrt[3]{125}=5$ |
| $|x|$ | Абсолютное значение из $x$ | $|-5| = |5| = 5$ |
| $x \%$ | $x$ процента | $5 \% \doteq \dfrac{5}{100}$ |
В математике реляционные символы используются для обозначения математических отношений , которые принимают один или несколько математических объектов для формирования полных математических предложений.
В арифметике и общей математике к ним относятся относительные символы, связанные с равенством и сравнением.
Символы отношения, основанные на равенстве
| Имя символа | Объяснение | Пример |
|---|---|---|
| $x \dotex y$, $x \doteq y$, $x \doteq y$, $x \doteq y$,0216 $x := y$ | $x$ равно , определяемому как $y$ | $\mathbb{R}_+ \doteq \\ \{ x \in \mathbb{R} \mid x > 0 \ }$ |
| $x = y$ | $x$ равно $y$ | $ \pi = \dfrac{C}{d}$ |
| $x \ne y$ 9004 | $x$ равно не равно до $y$ | $\sqrt{3} \ne 1.7$ |
| $x \приблизительно y$ | $x$ равно приблизительно равно от до $y$ | $\dfrac{5}{7} \примерно 0,714$ 92$ |
Comparison-based Relational Symbols
| Symbol Name | Explanation | Example |
|---|---|---|
| $x < y$ | $x$ is less than $y$ | $2 < e$ |
| $x > y$ | $x$ на больше, чем $y$ | $\dfrac{13}{4} > 3$ |
| $x y$ $ | $x$ на меньше или равно 9n$ for $n \ge 4$ |
Нотационные символы
Нотационные символы часто являются соглашениями и сокращениями , которые не попадают в категории констант, разделителей, операторов и реляционных символов.
В следующей таблице приведены некоторые из них в контексте общей математики, а также их использование и значение.
| Символ Название | Пояснение | Пример | |
|---|---|---|---|
| $ \ ldots, \ cdots $ | Символы горизонтального эллипсиса | $ 3 + 7 + 11 + \ CDOTS + 43 $ | |
| $ \ Infty $ | Infinity Symbol 944449 | $ | SIMBLIN {1} + \dfrac{1}{2} + \cdots = \infty$ |
| $Q. E. D.$, $\square$, $\blacksquare$ | QED / Символы конца доказательства | Следовательно, $1 + \cdots + n = \frac{n(n+1)}{2}$ , по желанию. $\, \blacksquare$ | |
| ※, ⨳ | Символы противоречия | Возведение обеих частей уравнения в квадрат дает $2 < 1$. ⨳ |
Основной список символов см. в разделе Математические символы. Списки символов, классифицированных по типу и предмету , см.