Что такое угол в геометрии определение: понятие, определение и виды углов на рисунках

Отрезок, угол, луч — геометрия и искусство

• Точки и прямые
• Геометрические фигуры
• Отрезок, угол, луч
• Линии
• Классификация
• Многоульники
• Окружность
• Параллельность и перпендикулярность

Плоские фигуры

Отрезок — часть прямой, ограниченная двумя точками (концы отрезка)

Длина отрезка — положительное число, показывающее, сколько раз единичный отрезок и его части укладываются в данном отрезке. Длину отрезка АВ также называют расстоянием ммежду точками А и В.

Свойства:
1) Длины равных отрезков равны
2) Длина суммы отрезков равнв сумме их длин

Луч (полупрямая) – часть прямой, имеющая начало и не имеющая конца.

Угол — фигура образованная двумя лучами, исходящими из одной точки (вершина угла). Общая вершина называется вершиной угла, а лучи — сторонами угла.

Обычно под углом понимают плоский угол, но есть другие виды углов — многогранные.

Виды углов

Острый	Прямой	Тупой	Развёрнутый

Угол, меньший прямого, называется острым.

Угол, равный смежному с ним, называется прямым.

Угол, больший прямого, называется тупым

.

Угол называется развёр- нутым, если его стороны сместе составляют прямую.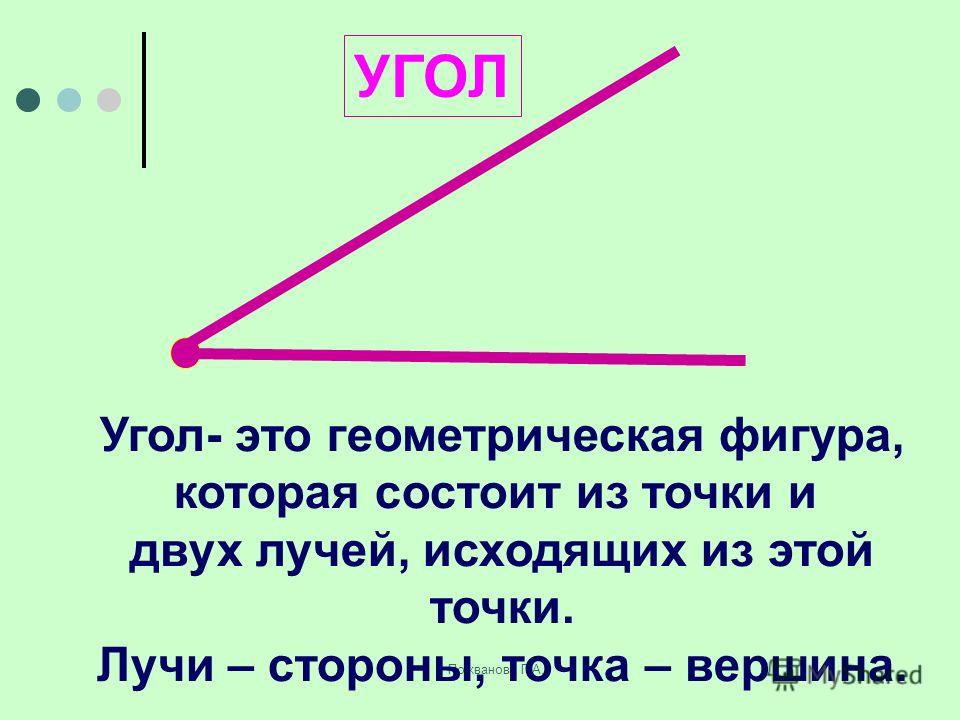

Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными.
Теорема. Сумма смежных углов равна 180°.
Следствие. Если смежные углы равны, то они прямые.

Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
Теорема. Вертикальные углы равны.
Угловая мера меньшего из вертикальных углов называется углом между прямыми.

Итак, сформулируем определения понятий луча, отрезка и фигуры:
• Лучом называется часть прямой, ограниченная одной из её точек.
• Отрезком называется часть прямой, заключенная между двумя её точками.
• Под фигурой понимают некоторое сочетание определенным образом расположенных в одной плоскости (а иногда и в пространстве) элементов: точек, прямых, лучей, отрезков (иногда и плоскостей).

Olle Baertling

Найди разные виды углов на рисунке и картине:

Из истории. Единицы измерения углов.
Градусное измерение углов возникло в Древнем Вавилоне задолго до новой эры. Жрецы считали, что свой дневной путь Солнце совершает за 180 «шагов», и, значит, один «шаг» равен 1/180 развернутого угла.

В Вавилоне была принята шестидесятиричная система счисления, т. е. фактически числа записывались в виде суммы степеней числа 60, а не 10, как это принято в нашей десятеричной системе. Естественно поэтому, что для введения более мелких единиц измерения углов один «шаг» последовательно делился на 60 частей.

Вавилонская система измерения углов оказалась достаточно удобной, и ее сохранили математики Греции и Рима.

Термины, которыми мы пользуемся для названия угловых величин, имеют латинские корни. Слово

«градус» происходит от латинского gradus (шаг, ступень). В переводе с латинского minutus означает «уменьшенный». Наконец, secunda переводится как «вторая». Имеется в виду следующее: деление градуса на 60 частей, т. е. минуты,— это первое деление; деление минуты на 60 секунд — второе деление градуса. Малоупотребительное название 1/60  секунды — терцина, латинское tercina означает «третье» (деление градуса).

Принятая сейчас система обозначения величин углов получила широкое распространение на рубеже XVI и XVII вв.; ею уже пользовались такие известные астрономы, как Н. Коперник и Т. Браге. Но еще К. Птолемей (II в. н. э.) количество градусов обозначал кружком, число минут — штрихом, а секунд — двумя штрихами.

Другая единица измерения углов — радиан — введена совсем недавно. Первое издание (это были экзаменационные билеты), содержащее термин «радиан», появилось в 1873 г. в Англии. Сначала в обозначениях указывалось, что имеется в виду радианная мера , но вскоре инадекс R (или г) стали опускать. Сам термин «радиан» происходит от латинского radius (спица, луч).

Если вспомнить определение угла в один радиан (центральный угол, длина дуги которого равна радиусу окружности), то выбор корня «рад» для названия такого угла представляется совершенно естественным.

 

Главная | Геометрия и искусство | Плоские фигуры | Пространственные фигуры | Движения и преобразования | Орнаменты и стили | Доклад | Разное | Галерея | Главная Карта Сайта

Каковы элементы угла? / математика | Thpanorama

Элементы угла они — вершина, которая является общей точкой; и два луча или стороны.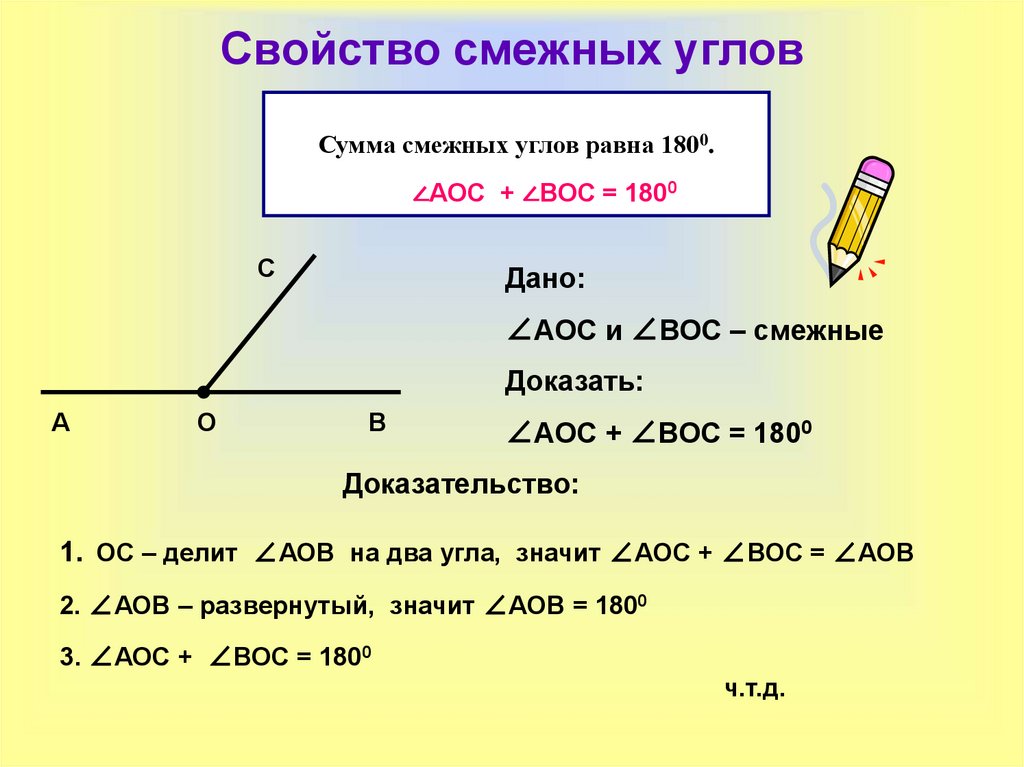 Геометрически, угол — это часть плоскости, которая включена между двумя лучами, начинающимися из общей точки.

Прямые линии определяются как линии, начинающиеся в точке и продолжающиеся бесконечно в одном направлении. Углы обычно измеряются в градусах или радианах (π).

Элементы угла те, которые появляются в его определении, а именно:

— Общая точка, называемая вершиной.

— Два луча, называемые сторонами. Лучи также называют лучами.

Формальное определение угла в геометрии гласит следующее: «это отношение между длиной окружности дуги, проведенной между двумя лучами, и ее радиусом (расстоянием до вершины)».

Евклид определил угол как наклон между двумя линиями, которые пересекаются друг с другом в плоскости, но не находятся на одной прямой; то есть линии обрезаются в одной точке.

5 основных типов углов

Все типы углов присутствуют в геометрии и широко используются при работе с полигонами..

По мере измерения углы классифицируются как:

1- Высокий

Это углы, которые составляют менее 90 градусов (

2- Прямо

Это углы, измерения которых равны 90 градусам (90º). Когда угол прямой, говорят, что стороны, которые его формируют, перпендикулярны.

3- тупой

Это углы, которые измеряют более 90 градусов, но менее 180 градусов (90º

4- Обычный

Это те углы, которые измеряют 180 градусов (180º).

5- Полный или перигональный

Это углы, измерения которых равны 360 градусам (360º).

Примеры углов

— Название «треугольник» объясняется тем, что эта геометрическая фигура имеет 3 угла, которые образованы сторонами треугольника и 3 вершинами. Треугольники классифицируются в соответствии с мерой каждого угла.

— На стрелках часов видно, как меняются углы. Центр часов представляет вершину, а стрелки — стороны. Если часы показывают 3 часа дня, то угол между иглами равен 90º.

Если часы показывают 6:00 утра, то угол между иглами составляет 180º.

— В физике использование углов очень важно знать, как определенные силы действуют на тело, или наклон, с которым должен быть запущен снаряд, чтобы достичь определенного места назначения. .

наблюдение

Углы формируются не только двумя лучами или лучами. В общем, они могут быть сформированы между двумя прямыми. Разница в том, что в этом последнем случае появляются 4 угла.

Если у вас есть ситуация, подобная предыдущей, появляются определения углов, противоположных вершине и дополнительным углам..

Вы также можете определить угол между кривыми и поверхностями, для которого необходимо знать о касательных линиях и касательных плоскостях.

ссылки

1. Бурк. (2007). Угол по геометрии Математике Рабочая тетрадь. NewPath Learning.
2. C., E. Á. (2003). Элементы геометрии: с многочисленными упражнениями и геометрией компаса. Университет Медельина.
3. Clemens, S.R., O’Daffer, P.G. & Cooney, T.J. (1998). геометрия. Пирсон Образование.
4. Lang, S. & Murrow, G. (1988). Геометрия: курс средней школы. Springer Science & Business Media.
5. Лира А. , Хайме П., Чавес М., Гальегос М. и Родригес С. (2006). Геометрия и тригонометрия. Порог издания.
6. Moyano, A.R., Saro, A.R. & Ruiz, R.M. (2007). Алгебра и квадратичная геометрия. Netbiblo.
7. Palmer, C.I. & Bibb, S.F. (1979). Практическая математика: арифметика, алгебра, геометрия, тригонометрия и правила скольжения. Реверте.
8. Салливан, М. (1997). Тригонометрия и аналитическая геометрия. Пирсон Образование.
9. Вингард-Нельсон, Р. (2012). геометрия. Enslow Publishers, Inc.

геометрия — Определение угла и измерение угла

Задавать вопрос

спросил 5 лет, 11 месяцев назад

Изменено 5 лет, 11 месяцев назад

Просмотрено 5к раз

$\begingroup$

Определение угла в евклидовой геометрии дается следующим образом:

Угол. Определение: Фигура, образованная двумя линиями или лучами, расходящимися из общей точки (вершины).

Однако определение нигде не указывает, как определять измерение угла. Немного покопавшись/подумав, становится очевидным, что определение измерения выглядит примерно так:

.

Нарисуйте единичный круг вокруг вершины. Затем угол измеряется как длина дуги между пересечением двух линий и окружностью. (в радианах)

Кажется, что именно так всегда определяется измерение угла, но, учитывая, что в определении угла прямо не говорится, что это единственный способ измерения, мне интересно, можно ли использовать другие измерения, которые согласуются с евклидовой геометрией. . Например:

(Таким образом, измерением угла $\alpha$ в каждом случае является длина нарисованной от руки стрелки — как если бы она была идеально нарисована поверх дуги/линий).

Теперь, для любого измерения, не основанного на окружности, может показаться, что всякий раз, когда «измерительный прибор» вращается, углы меняются, а это означает, что они всегда должны использоваться параллельно некоторой базовой линии.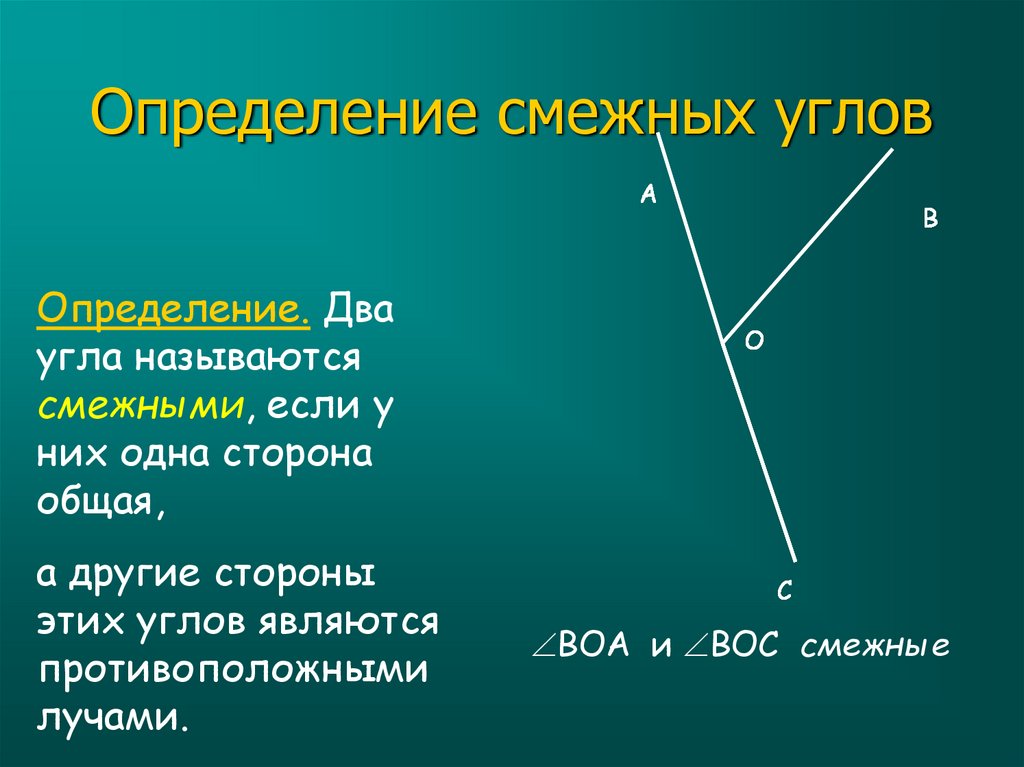 С другой стороны, вычисление sin() и т. д. становится очень простым.

Вопрос: Есть ли что-то серьезное в изменении методологии измерения угла, что может нарушить евклидову геометрию? Является ли определение угла «круг» единственно допустимым?

• геометрия
• евклидова геометрия

$\endgroup$

1

$\begingroup$

Сложение двух углов определяется без учета меры. Определение меры $m(\alpha)$ угла $\alpha$, чтобы иметь смысл, должно удовлетворять соотношению $m(\alpha+\beta)=m(\alpha)+m(\beta)$, которое ваши альтернативные определения этого не делают.

РЕД.

Поскольку вышеизложенное кажется недостаточно ясным, приведу пример (см. схему ниже). Возьмем точку $C$ на оси $x$ и луч $OD$ с $OD=OC$. Пусть $E$ — середина $CD$: хорошо известна теорема элементарной геометрии, что в равнобедренном треугольнике $OCD$ медиана $OE$ также делит пополам угол $\angle COD$, так что $\angle COD= 2\угол COE$.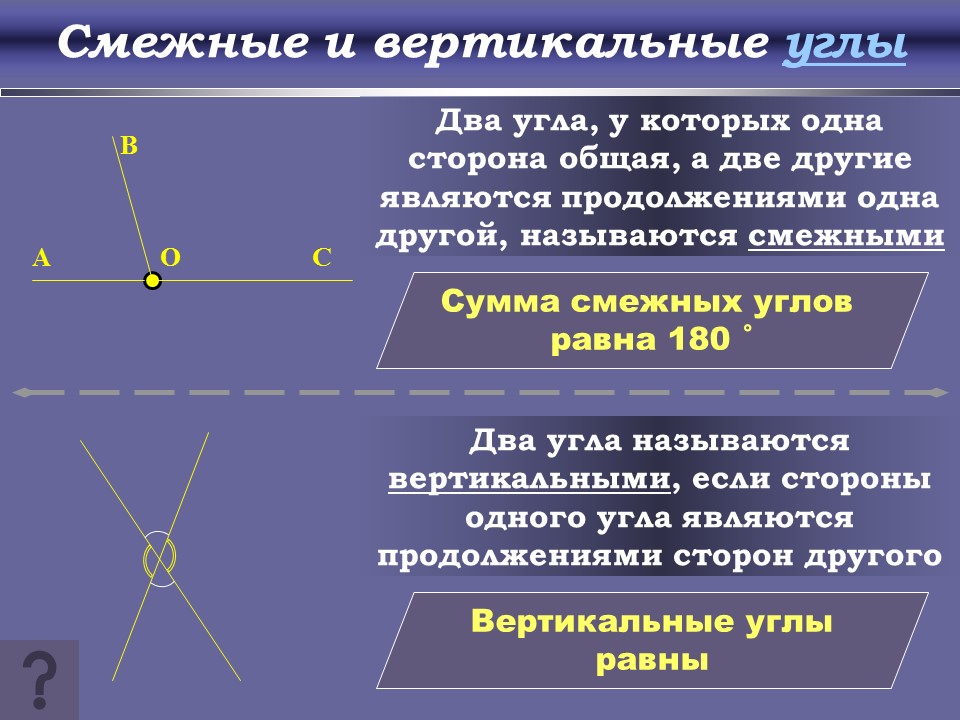

Но с вашим треугольным определением, например, мера $\угла COD$, вообще говоря, не является удвоенной мерой $\угла COE$, потому что $AE’>E’D’$.

$\endgroup$

5

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.